Abstract
Mathematical models based on ordinary differential equations (ODE) have had significant impact on understanding HIV disease dynamics and optimizing patient treatment. A model that characterizes the essential disease dynamics can be used for prediction only if the model parameters are identifiable from clinical data. Most previous parameter identification studies for HIV have used sparsely sampled data from the decay phase following the introduction of therapy. In this paper, model parameters are identified from frequently sampled viral-load data taken from ten patients enrolled in the previously published AutoVac HAART interruption study, providing between 69 and 114 viral load measurements from 3–5 phases of viral decay and rebound for each patient. This dataset is considerably larger than those used in previously published parameter estimation studies. Furthermore, the measurements come from two separate experimental conditions, which allows for the direct estimation of drug efficacy and reservoir contribution rates, two parameters that cannot be identified from decay-phase data alone. A Markov-Chain Monte-Carlo method is used to estimate the model parameter values, with initial estimates obtained using nonlinear least-squares methods. The posterior distributions of the parameter estimates are reported and compared for all patients.
Introduction
Many researchers have analyzed the dynamics of human immunodeficiency virus (HIV) using nonlinear ordinary differential equation (ODE) models [1]–[5]. Using various mathematical models, they sought to simulate the dynamics of the virus or to help design a treatment. Many of these studies have attempted to identify model parameters from patient data, but the sparsity of measurements resulted in very large confidence intervals in the parameter estimates. Furthermore, the experimental data used only included the period of viral decay following the introduction of therapy. Identification of the HIV model parameters under these conditions requires assuming that the drug efficacy is known, which in turn affects the estimates of the remaining parameters.
The amount of data normally available for HIV model identification is sparse. Typically, a patient on effective therapy has his or her viral load tested every 3 or 4 months, a rate too slow to accurately capture the dynamic characteristics accurately. In this paper, the data used to identify model parameters are from the AutoVac study conducted at the IrsiCaixa HIV research foundation in Barcelona [6]. In the AutoVac study, 12 patients underwent a series of about 30-day treatment interruptions, followed by resumption of suppressive therapy, and viral load measurements were taken at 3-day intervals during the interruption. This resulted in between 69 and 114 viral load measurements per patient, with between 38 and 77 data points per patient above the limit of detection. Therefore, data gathered from this particular experiment are sufficiently rich for model identification. All patients enrolled in the AutoVac study had maintained undetectable viral loads on therapy for at least two years prior to the study, and had baseline CD4+ T-Cell counts over 700. Patient nine and twelve both had interruptions without measurable viral load rebound, and were excluded from this study due to insufficient usable data.
Full-state measurements are not available for HIV model identification, so the problem of identifiability must be considered. For HIV models, Stafford et al. [7] have studied the identifiability of a 3 state model. Xia and Moog [8] analyzed the theoretical identifiability of a 4 state model and determined the minimal number of state measurements needed for estimating all model parameters. Frequently, only viral load data are available and in this case, not all parameters can be identified independently [7], [9]. Recently, Miao et al. also investigated some identifiability issues for viral dynamics [10].
For identifying the parameters of a viral dynamics model, two major methods are commonly used: nonlinear least squares [11] and Bayesian estimation [12]–[16]. In this paper, we employ a Bayesian Markov-Chain Monte Carlo technique as in [12], [16], with nonlinear least-squares used to generate initial conditions for the MCMC technique. The primary difference between this work and previous works is the quality of the data used for estimation. The data used in [16] consists of 10 measurements from 12 patients taken at 5 time points. The data used in [12] consists of seven measurements from 42 patients taken at seven time points. The data used in [15] consists of 9 viral load measurements from 42 patients taken at nine time points, plus a single baseline measurement of phenotypic drug susceptibility and survey data on patient adherence. The data used in [17] used 18 measurements of viral load from 18 time points. All four of these studies only included data from a single virus decay phase following treatment initiation. As a result of the sparse data, these previous studies had to make a number of simplifying assumptions about parameter values in order to preserve identifiability. By contrast, the AutoVac patient study provides us with between 69 and 114 viral load measurements from 10 patients from between 3 to 5 treatment interruptions cycles per patient. The high quality of the data used in this study allows reliable estimation of parameter values without resorting to the simplifying assumptions used in previous studies.
We consider the following mathematical model characterizing the viral dynamics for a patient:
 |
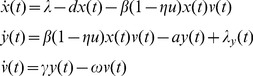(1) |
There are three states: 
, the concentration of target CD4+ T cells; 
, the concentration of actively infected CD4+ T cells; 
, the viral load. 
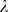is the proliferation rate and 
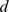is the death rate of target CD4+ T cells; 
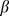is the infection rate; 
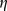is the drug efficacy; 
is the death rate of actively infected cells;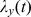 
is the contribution of the reservoir to actively infected CD4+ T cells; 
is the rate of free virus production by infected cells;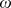 
is the clearance rate for the free virus. The drug application 
is 0 during interruptions and 1 during treatment. This is a variation of a model first proposed in [18], with the addition of the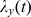 
term describing the additional contribution of infected cells from all viral reservoir processes. This model is essentially the same as the model identified against patient data in the previous studies [11]–[15].
Highly active antiretroviral therapy (HAART) has proven effective to reduce the active viral load [19], [20] and is standard care for HIV patients. However, it cannot eradicate the virus completely [21], [22]. Although scientists suspect that the existence of long-term latent reservoirs in patients is the main reason for viral persistence [23], [24], there is little quantitative understanding of their contribution, mainly because of the difficulty measuring the virus reservoir directly. Some HIV investigators have proposed mathematical models to describe the dynamics of long-term latent reservoirs [25]–[27]. Little research has been done to estimate the parameters of these models quantitatively based on clinical data.
In this study, the total contribution of the reservoir processes to the actively infected CD4+T cells is estimated from standard viral-load time-series data. We analyze the identifiability for each parameter in Model 1 using differential algebra tools. The implementation of Bayesian estimation method is presented, and the joint posterior parameter distributions calculated by the Bayesian methods for each patient are reported.
Methods
Experimental Methods
Ethics statement
The previously published clinical study [6] was carried out in accordance with a human subjects protocol approved by the institutional ethics review committee at the University Hospital Germans Trias i Pujol in Barcelona, Spain. Written informed consent was obtained from all study participants. De-identified patient data was shared in accordance with a protocol approved by the University of Delaware Institutional Review Board.
Study design
This research described here uses data from a previously published study. The measurements which are the focus of this work have been previously described in [6]. Briefly, a randomized prospective Structured Treatment Interruption study enrolled 26 HIV-1 positive asymptomatic adults with no detectable virus for at least two years prior to entering the study (limit of detection 50 virions per ml). 14 were randomized to a control group, continuing their previous cART regimens. 12 were randomized to the experimental group, and underwent between three and five cycles of interrupted antiviral therapy, remaining off therapy until two consecutive viral load measurements above 3000 virions/mL were reached, or for a maximum of 30 days, then re-initiating the original cART regimen for 90 days before the next interruption cycle began. HIV-1 RNA PCR quantitative analysis was performed on samples collected three times weekly following treatment interruption, and then weekly for the two months following re-initiation of treatment.
Modeling Persistence of Latent Reservoirs
Although highly active antiretroviral therapy (HAART) efficiently suppresses viral load to undetectable levels, current regimens cannot eradicate the virus completely [21], [26], [28]–[30]. One possible reason is the persistent replication of HIV at a very low level, even under HAART conditions [26], [31], [32]. Another possible reason is the existence of stable reservoirs of latently infected cells [26], [33], [34]. These two possibilities are not mutually exclusive, and it is likely that a combination of persistent viremia and reservoir activation combine to maintain the reservoirs and prevent eradication [26].
Rong and Perelson proposed models to describe the dynamics of the latent reservoir [26]. However, in order to be identifiable from viral-load data, the models must be simplified. Siliciano et al. [35] found that the average half-life of the latent reservoir in resting CD4
T cells is 44 months, which means it is extremely stable. There is no strong evidence that the activation rate of the reservoir is constant, however, and a combination of various factors may contribute to the maintenance of a residual virus load during effective antiviral suppression. Therefore, in Equation 1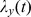 
represents the total average contribution of reservoir dynamics to the active infected cell compartment 
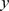during the treatment period. The time between ceasing antiviral therapy and the viral load reaching measurable levels (the rebound time) is very sensitive to the value of 
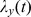, and consequently the goodness of fit for the entire model is also very sensitive to 
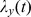. Surprisingly, as shown in our results, a patient-specific constant value for 
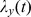provided an excellent fit for all ten patients for all interruption cycles, implying that the average contribution of reservoir dynamics to the active infected cell compartment is relatively constant across several interruption cycles.
Identifiability Analysis
Equation 1 is a special case of the following general nonlinear model:
 |
(2) |
In this study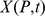 
is the state vector 
, 
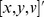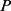is the parameter vector 
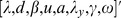, and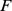 
is the function which describes system dynamics.
We adapt the following concepts of identifiability from [36]–[38]:
Definition 1. Equation 2 is said to be globally identifiable from the given states if the equation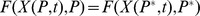 
has only one solution 
.
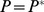Definition 2. Equation 2 is said to be locally identifiable from the given states if in some open neighborhood,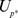 
, around the true parameter vector, the equation 
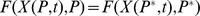has only one solution 
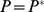and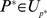 
.
The identifiability of HIV dynamic models has been analyzed previously [8], [10]; however, these previous works assumed more than one state could be measured. Here, only the viral load data are assumed to be available. Differential algebra is used to analyze the identifiability issue of Model 1. Details of the differential algebraic techniques are found in [37]–[39]. The steps in this analysis are as follows:
We choose the following order relation for Equation 1:
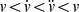.- Based on the above order, the normalized characteristic polynomial of
is calculated:
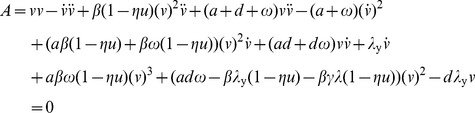
(3)
Equation 3 is generated by a) solving for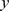 
from the last equation of Equation 1, b) substituting for 
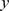in the middle equation of Equation 1, c) solving for 
from that equation and d) substituting for 
in the first equation of Equation 1. Knowledge of 
allows one to estimate the coefficients in Equation 3. This characteristic polynomial does not contain the states 
, 
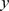and their derivatives, but still describes the viral dynamics of Equation 1.
iii) By extracting the coefficients in the above polynomial we obtain the following set of identifiable parameters:
iv) The identifiability of each parameter can be checked by checking the injectivity of the the map defined in Equation 4. All parameters except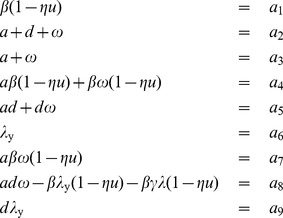
(4) 
and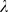 
are uniquely identifiable; the product 
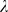is uniquely identifiable. Since the patients enrolled in the AutoVac study had all maintained undetectable viral loads on therapy for at least two years prior to the study, it is reasonable to assume that the initial conditions of this study are the steady states in Equation 1. Therefore, the steady state of 
in Equation 1, 
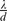, is set as the concentration of CD4+ T Cells at the beginning of this study. Under this assumption, the value of 
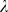is defined as the product of the initial number of target cells 
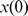and the estimated decay rate of target cell 
.
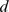Although theoretically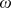 
is uniquely identifiable, the current best estimate of 
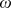is between 
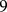and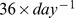 
[40]. Estimation of 
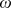would require very high frequency measurements (several measurements per hour, much faster than our data). Therefore the value of 
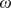is set as 
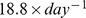(corresponding to the geometric mean of the estimated half-lives in [40]), and the virus dynamics are treated as a singular perturbation to the system. Assuming that the true value of 
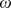is sufficiently large that the singular perturbation approximation is valid, the only identified parameter that depends on this assumption is 
; the posterior distribution of estimated values for 
would shift in a inversely proportional manner with a change in the assumed value of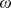 
, with no change in the posterior distributions of any other parameter.
The identifiability analysis described above does not take into account the number of measurements or the sampling rate; it simply states that for a sufficiently large number of measurements taken at a sufficiently fast sampling rate, the set of parameters described are identifiable. The uncertainty in the estimated parameter values will depend on the actual number of measurements and their frequency.
Bayesian Estimation
Initial estimates
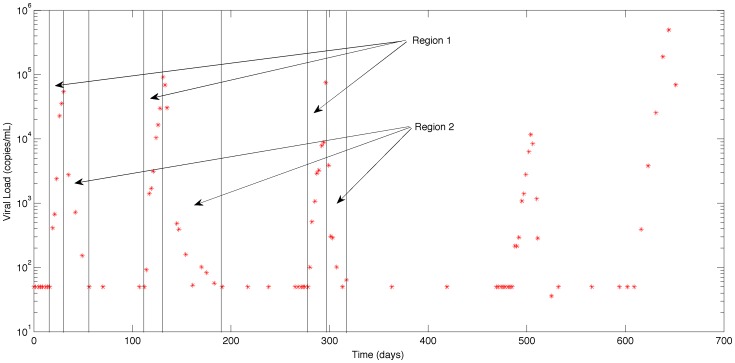
During the AutoVac study treatment for each patient was interrupted and after a period of time, restarted. This cycle of interruption and reinstating the treatment is repeated 3 to 5 times. In order to generate an acceptable initial value for the MCMC method, a two-step least-squares method was used, using data from the first three interruption cycles. The data from the period in which the treatment is interrupted, region 1, is used to estimate the 5 parameters,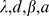 
and 
using a constrained nonlinear least squares method. The data from region 2, where treatment is reinstated, contains information about the drug efficacy. With the value of the six parameters fixed to those values found by least squares in region 1 (as shown in Fig. 1), the data of region 2 is used to estimate the drug efficacy. The initial values obtained using this two-step procedure are used as the kernel for the MCMC methodology described below; the MCMC methodology identifies all six parameters against all data from both regions of all treatment interruptions.
Figure 1. The viral load data for Patient 1.
MCMC methodology
From the steady-state values of Equation 1, the relationship between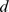 
and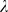 
can be written as:
 |
(5) |
Where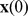 
is the initial measurement of CD4+ T cells taken for each patient at the beginning of the study (as in [16]). Therefore, in this method, the parameter set 
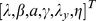are estimated. 
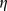is calculated for each iteration by least-squares subject to the values of the other five parameters. The MCMC approach taken here is based on the Metropolis-Hasting algorithm [13]. Assume that the 
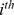subject, we have 
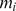measurements of viral load. We denote the parameters as:
 |
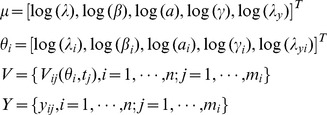The logarithm is used to ensure that all estimates of the parameters are positive. The vectors,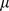 
and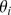 
are the logarithm of the parameters for the population level and the logarithm of the parameters for the 
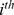individual respectively. The initial values of 
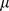and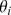 
are set as the results of Patient 2 from the nonlinear least-square method described above, which are 
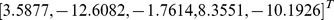. The matrix 
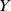is the matrix of the logarithm of available measurements to base 10 for all the patients. Let 
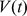denote the solution of the differential equation and 
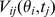denote the value of 
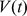for the 
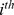patient using parameters 
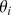at time 
.
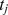Following the iterative MCMC algorithm of [13], the implementation can be written as:
1. Initialize the chain with initial values
.-
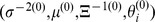2. Use Gibbs sampling steps to update
, 
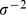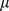, and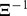 
and use Metropolis-Hastings algorithm to update 
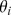:- (a)
;
.
.
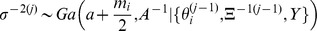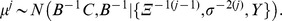
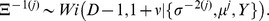
where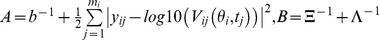 
, 
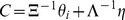and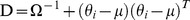 
.
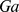is the gamma distribution and 
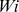is the Wishart prior distribution. The hyper-parameters, 
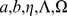and 
are known with the following values:
 |
The hyper-prior values for the initial variance of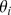 
, 
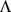, are sufficiently large that this may be considered a non-informative prior distribution. For comparison, the analysis in [16] had initial variance for 
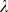and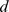 
of 0.12 and 0.016 respectively, heavily biasing the posteriors to the priors, and the analysis in [15] had initial variance for the parameters 
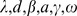of 0.005, also substantially biasing the posterior distributions of these parameter estimates to the prior distributions.
(b) Generate a prospective value
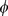for 
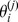from the previous iterative value 
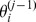where
 |
(c) Evaluate the acceptance probability of this move by applying Metropolis-Hastings algorithm. If this move is accepted,
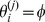. If not, 
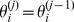.3. Repeat step 2 until the chain converges.
To obtain reasonable results from the MCMC method, good initial estimates of 
are needed. The constrained least squares approach described previously is used to get an initial estimate. The parameters are constrained so that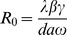 
, which is the basic reproduction ratio during treatment interruptions, is greater than 1. If 
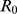were less than 1, then the virus would not have successfully established infection.
The above procedure was applied to the data for 10 patients with sufficient data. The MCMC procedure produced 200,000 possible sets of parameters for each patient that are consistent with the patients’ data. For the purposes of analysis, the first 50,000 iterations were discarded to allow the chain to converge, leaving 150,000 parameter sets per patient for the final analysis. From this result, the marginal probability densities for of the six parameters can be established.
Results
Nonlinear Least Squares Estimation
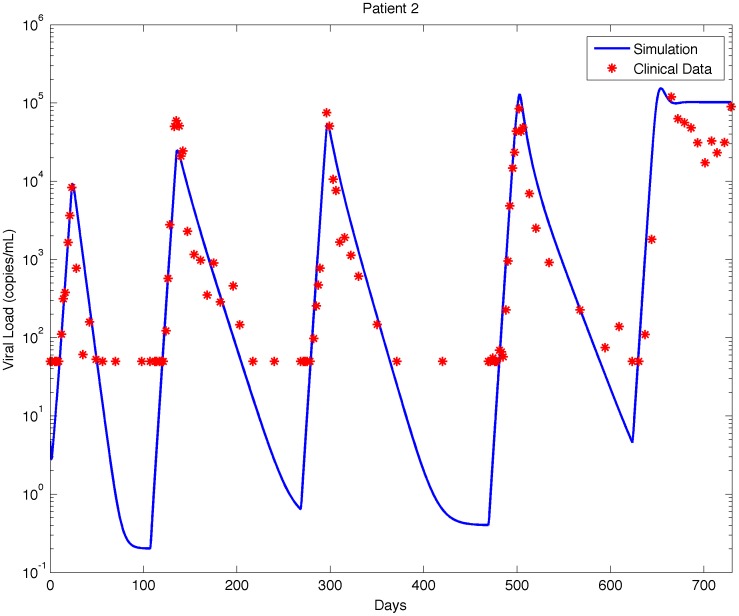
Parameter estimates were generated for each of 10 patients using the nonlinear least squares method. Of the 12 patients in the study, 2 had no detectable virus after an interruption, leaving insufficient data above the measurement threshold to identify model parameters. Although the nonlinear least-square method cannot guarantee globally optimal results, it can provide good initial estimates for the prior distribution of the MCMC method. Simulated viral load curves based on the identified parameter values using this method are compared to the measured data from Patient 2 in Fig. 2.
Figure 2. Model fitting for identified patients.
Red star: experimental data (detection limit: 50 copies/mL); solid line: simulation based on estimated parameters.
Bayesian Estimation
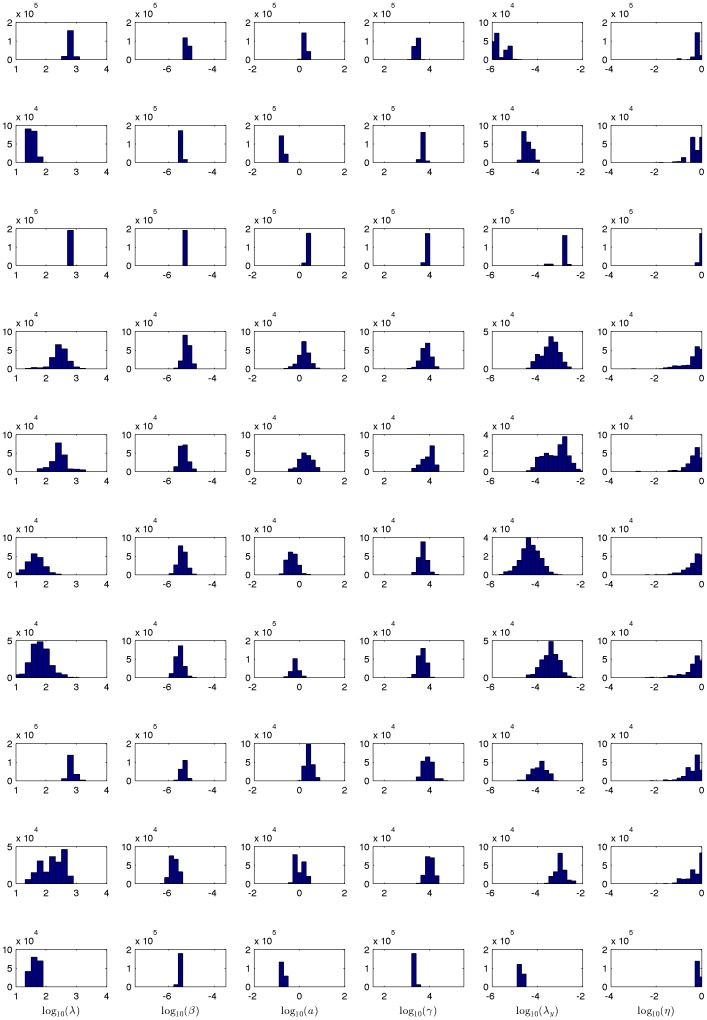
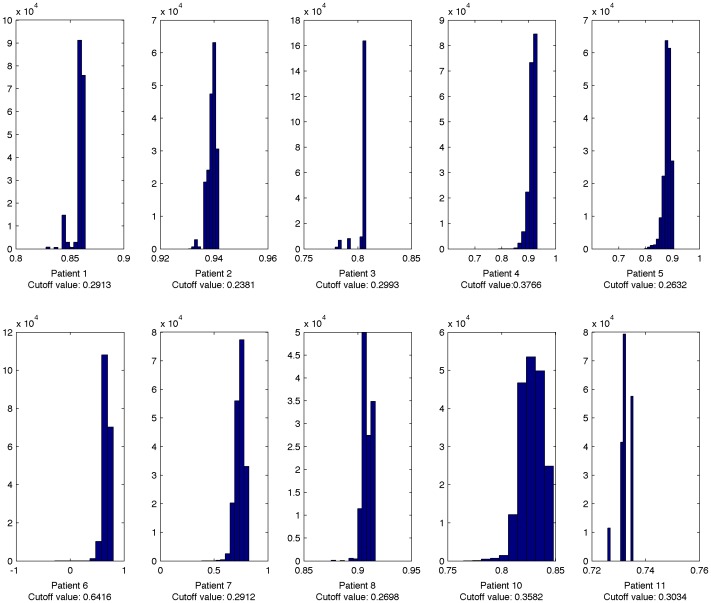
The MCMC model fitting procedure was run for each of the 10 patients with sufficient data. Histograms of the marginal posterior distributions for the six parameters for each of the 10 patients are shown in Fig. 3.
Figure 3. The marginal posterior distribution of each parameter for ten different patients.
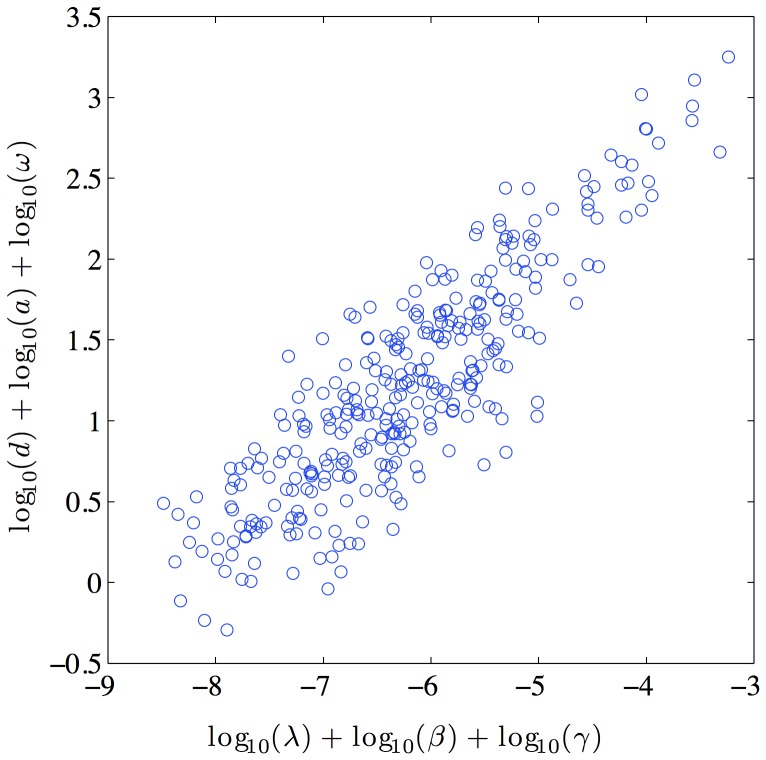
Note that the parameters are not independent, and the parameter vectors should be considered as complete sets. Table 1 shows the average correlation coefficient among each different pair of parameters; it is clear that most pairs of parameters would be considered highly correlated. In addition to this first-order correlation between parameters, there are also higher order nonlinear correlations. Fig. 4 shows the high level of correlation between the product of the parameters which form the numerator and denominator of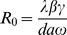 
, further emphasizing the need to consider parameter vectors rather than individual parameters. Values chosen independently from each parameter’s distribution can easily generate a parameter set which is a particularly poor representation of the data. Consequently, we also report as tables in the supplementary material the entire posterior distribution for each of the 10 patients (shown in supplementary tables S1, S2, S3, S4, S5, S6, S7, S8, S9, S10). The posterior distribution generated by this MCMC method provides a database for testing the robustness of treatment optimization strategies, such as those described in [25], [41]–[43].
Table 1. The average correlation coefficients between parameters for all ten patients.
|
|
|
|
|
|
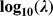
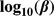
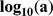
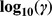
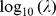
1 | 0.0953 | 0.6632 | 0.4278 |
|
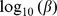
0.0953 | 1 | 0.1228 | −0.6421 |
|
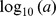
0.6632 | 0.1228 | 1 | 0.5817 |
|
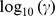
−0.6421 | 0.5817 | 0.6632 | 1 |
Figure 4. Typical scatter plot of R 0 correlation.
The heavy correlation between the elements in the numerator and denominator of R 0 demonstrates the strong higher-order correlation between parameters.
The histograms in Fig. 3 show the range of values of each parameter, and Table 2 gives the maximum likelihood estimate for each parameter. From the histograms it is clear that the distributions for the parameters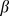 
,
, and 
vary little between patients, indicating that the infection rate and burst size of the virus and the death rate of infected cells may be consistent across the patient population. By contrast, the parameters 
, 
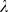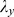, and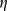 
vary substantially between patients, indicating that the regeneration rate of CD4+ T cells, the reservoir contribution rate, and the drug efficacy may vary significantly across the patient population.
Table 2. Parameter identification results for each patient, reported as mean(standard deviation).
| Parameter | Unit | Patient 1 | Patient 2 |
|
|
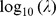
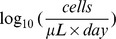
2.77(0.07) | 1.54(0.12) |
|
|
|
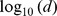
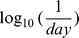
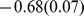
−1.33(0.12) |
|
|
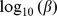
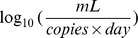
−5.26(0.09) | −5.48(0.06) |
|
|
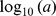
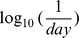
0.23(0.08) | −0.76(0.07) |
|
|
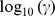
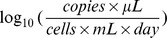
3.45(0.12) | 3.69(0.05) |
|
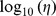
– | −0.14(0.18) | −0.10(0.28) |
|
|
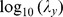
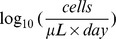
−5.67(0.30) | −4.43(0.17) |
| Parameter | Unit | Patient 3 | Patient 4 |
|
|
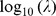
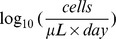
2.88(0.04) | 2.45(0.27) |
|
|
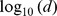
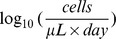
−0.34(0.04) | −0.61(0.27) |
|
|
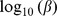
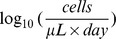
−5.35(0.01) | −5.23(0.15) |
|
|
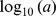
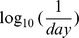
0.37(0.04) | 0.19(0.24) |
|
|
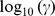
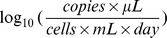
3.84(0.03) | 3.82(0.22) |
|
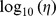
– | −0.05(0.03) | −0.17(0.43) |
|
|
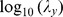
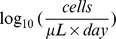
−2.94(0.20) | −3.45(0.38) |
| Parameter | Unit | Patient 5 | Patient 6 |
|
|
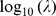
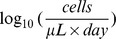
2.43(0.27) | 1.64(0.29) |
|
|
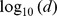
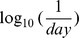
−0.64(0.27) | −1.28(0.29) |
|
|
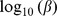
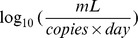
−5.36(0.16) | −5.42(0.18) |
|
|
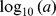
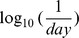
0.26(0.28) | −0.32(0.21) |
|
|
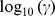
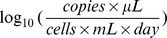
3.90(0.25) | 3.70(0.17) |
|
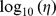
– | −0.17(0.37) | −0.15(0.38) |
|
|
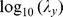
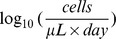
−3.18(0.51) | −4.33(0.43) |
| Parameter | Unit | Patient 7 | Patient 8 |
|
|
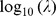
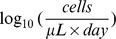
1.79(0.31) | 2.83(0.11) |
|
|
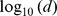
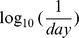
−1.33(0.31) | −0.44(0.11) |
|
|
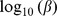
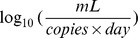
−5.54(0.18) | −5.36(0.12) |
|
|
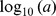
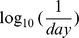
−0.18(0.15) | 0.42(0.14) |
|
|
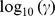
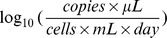
3.66(0.16) | 3.91(0.21) |
|
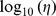
– | −0.17(0.42) | −0.22(0.36) |
|
|
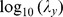
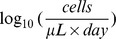
−3.46(0.36) | −3.90(0.31) |
| Parameter | Unit | Patient 10 | Patient 11 |
|
|
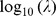
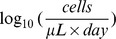
2.21(0.37) | 1.65(0.10) |
|
|
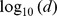
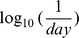
−0.96(0.37) | −1.35(0.10) |
|
|
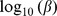
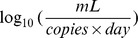
−5.78(0.17) | −5.54(0.04) |
|
|
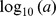
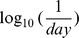
0.00(0.21) | −0.74(0.07) |
|
|
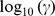
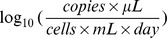
4.00(0.17) | 3.39(0.01) |
|
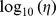
– | −0.11(0.34) | −0.13(0.06) |
|
|
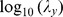
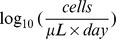
−3.00(0.24) | −4.65(0.09) |
Table 3 gives a summary of the estimated population parameters (the average value of the 10 identified patients), compared with those from previously published papers [15], [16].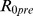 
is the basic reproductive ratio 
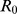of the virus without treatment. 
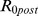is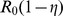 
, the reproductive ratio of the virus under treatment conditions. The values for parameters 
,
,
,
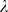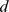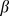, and 
are consistent with the previously published best estimates for these parameters. In particular, the maximum likelihood estimates for the death rate of target cells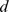 
ranged from 
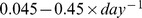, in perfect agreement with the estimates obtained from patient data in [15]. This estimate is considerably higher than the decay rate estimated in [16], but careful examination of the methods in that previous work show that the value of 
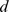was essentially constrained to the prior distribution. The ratio 
is consistent between all three studies. Our maximum likelihood estimates for the death rate of infected cells 
ranged from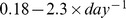 
, in agreement with the current best estimate of 
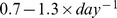[17], [26], as well as the data from the two comparable studies [15], [16]. Our maximum likelihood estimate of the density-dependent infection rate 
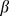ranged from 
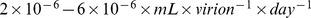, compared to 
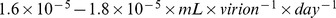[13] and 
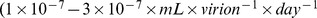[16]. Our maximum likelihood estimates of the target cell recruitment rate 
ranged from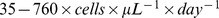 
, higher than the comparable range of 
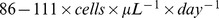reported in [15]; however, this is expected, as the inclusion criteria for our experiment resulted in patients with much healthier immune systems overall compared to the patients in [15]. The much lower rate of 
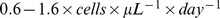reported in [16] is a direct result of that study’s unrealistically low prior value for 
. Our estimates of the virus production rate 
range from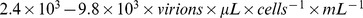 
, higher than the 
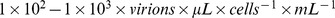range reported in [15]; however, this is due to the estimate in [15] of 
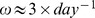, as opposed to our fixed estimate of 
.
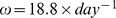Table 3. Result comparison between this paper and previous studies.
| Source | ||||
| Luo et al. | Huang et al. [15] | Putter et al. [16] | ||
| Average MLE | Posterior Mean | Posterior Median | ||
| (Interpatient Range) | (95% CI) | (Interpatient Range) | ||
| Parameter | Units | |||
|
|
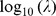
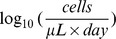
2.47 | 1.97 | 0.11 |
| (1.54, 2.88) | (1.93,2.05) | (−0.24,0.21) | ||
|
|
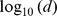
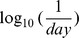
−0.74 | −0.96 | −2.99 |
| (−1.35, −0.34) | (−1.01, −0.40) | (NA) | ||
|
|
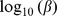
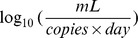
−5.41 | −4 | −6.80 |
| (−5.78, −5.23) | (−4.00, −3.15) | (−6.94, −6.53) | ||
|
|
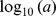
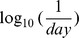
0.01 | −0.42 | −0.50 |
| (−0.76,0.42) | (−0.49, −0.22) | (−0.62,0.26) | ||
|
|
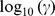
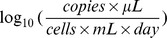
3.77 | 2.51 | 4.87 |
| (3.39,4.00) | (NA) | (4.83,4.89) | ||
|
– | 0.73 | NA | 0.71 |
| (0.60,0.89) | (NA) | (0.63,0.84) | ||
|
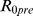
– | 1.93 | NA | 3.90 |
| (1.16,3.68) | (NA) | (1.72,4.86) | ||
|
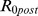
– | 0.56 | NA | 0.34 |
| (0.13,0.76) | (NA) | (0.05,0.60) | ||
| # of patients | 10 | 42 | 12 | |
| # of measurements per patient | 98 | 9 | 5 | |
The maximum likelihood values of the reservoir contribution rate ranged over three orders of magnitude, from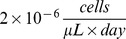 
for Patient 1 to 
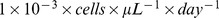for Patients 3 and 10. This suggests that the replenishment of the active compartment by the viral reservoirs is very heterogenous between patients. However, it is noteworthy that a single constant value of 
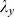was able to accurately predict rebound time across multiple interruption cycles for the same patient despite variation in interruption length, indicating that the replenishment rate for a given patient is relatively constant over the course of the experiment.
The efficacy of the antiviral drugs is estimated directly from the viral load data. To our knowledge, this is the first time this has been done. Previous estimates of model parameters have typically inferred drug efficacy from PK/PD data in the plasma, resulting in estimates of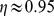 
[15], or relied heavily on the assumption that the first measurement was at steady-state [16], resulting in estimates between 
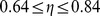. By contrast, our direct estimate of 
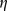from the viral load data give us maximum likelihood estimates ranging from 
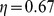to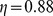 
. This indicates that the estimates based on plasma pharmacokinetic data may overestimate the true drug efficacy, though the estimates which relied exclusively on the first measurement were consistent with our results.
Fig. 5 shows the histograms of the coefficient of determination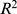 
for each of the 10 patients. The statistical significance threshold for the fit relative to an average measurement model was calculated using the F-test (
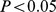is considered statistically significant); this shows that, for all patients except Patient 6, all 150,000 parameter vectors in the posterior distribution would be considered a statistically significant fit to the data if considered in isolation.
Figure 5. The histogram of coefficient of determination.
R 2 Cutoff values: The value of R 2 corresponding to P = 0.05.
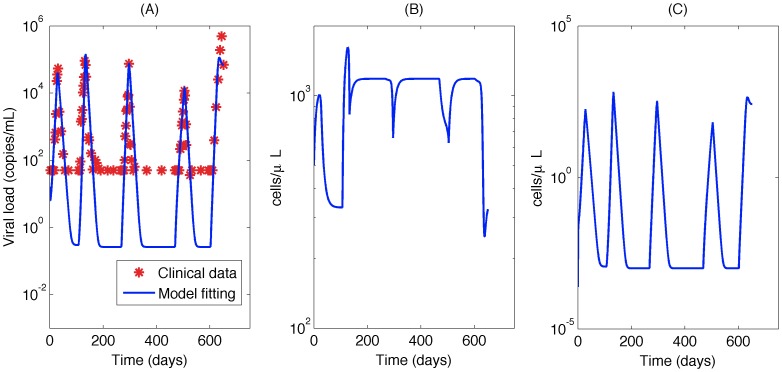
The viral load fitted by the model using the maximum likelihood estimates of the parameters and simulation results for Patient 1 are shown in Fig. 6.
Figure 6. Typical Bayesian Posterior Mean Results.
(A)The fitted viral load curve and viral load data for patient 1; (B)Target cell simulation using fitted parameters; (C)Infected cell simulation using fitted parameters.
Discussion
As shown in this study, the parameters in the HIV dynamics model are heavily correlated. The strong correlation between parameters in this model mean that only the distribution of complete parameter sets (as opposed to independent distributions of each parameter) can be considered to accurately represent the fit of the model to the data. The quality and extent of the data available in this study was considerably higher than any previously published parameter estimation study, allowing for the accurate estimation of the model parameters without using the simplifying assumptions necessitated by the sparsity of data in previous studies. Furthermore, the level of excitation of the dynamics provided by the multiple interruption schedules allowed us to directly identify two parameters not previously identifiable from patient data. The results agree for the most part with previously published data, but the results are more reliable and significant given the dramatic increase in the amount of data available for identification.
This paper presents, for the first time, the posterior distribution of parameters for a commonly used HIV infection model identified against measured patient data. Analysis of this distribution shows good representation of the data. As shown in the histograms of Fig. 5, all parameter estimates in the posterior distributions for all patients except a subset of patient 6 would be considered statistically significant by the standard F Test (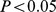
), implying that the reported posterior distribution describes the range of feasible parameter values based on the measured data well. Inspection of the data from patient 6 shows the data available above the limit of detection are limited compared to the other patients, which can explain the high value of 
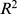corresponding to an F-test P value of 0.05 for that patient. However, even for this patient, more than half of estimates are still statistically significant, and there were 39 measurement points above the limit of detection, substantially more measurements than were available for any previously published parameter estimation study.
The multiple interruptions in the patient data provided the opportunity to quantify the contribution rate of viral reservoirs to the active infected cell compartment. These rates varied widely from patient to patient. The rate was characterized in terms of number of productively infected cells produced per day, and equally well describes such diverse potential reservoir processes as low-level persistent replication, viral blipping, and spontaneous reactivation of quiescent cells. The overall fit is highly sensitive to the rebound time, and the rebound time is uniquely determined by the reservoir contribution rate. It is surprising, therefore, that a single value for the reservoir contribution rate was able to describe the data well over multiple interruptions in the same patient; this strongly suggests that the underlying process represented by the parameter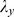 
is continuous rather than bursting in nature. The quantification and understanding of the viral reservoir dynamics is of critical importance to understanding the nature of ongoing viral evolution under conditions of effective suppression, and will be a necessary precursor to any attempts to flush the reservoirs and achieve a functional cure for HIV.
The results presented here also show that the overall drug efficacy is between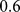 
and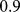 
, and that the effective reproductive ratio of the virus while on therapy is between 
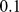and 0.8, verifying the results presented in [16]. It is important to emphasize that, while the antiviral drug regimens are very successful at suppressing overall virus load, they are not perfect in inhibiting infection, and de novo infection events continue to occur even under highly effective therapy. The results presented here also verify the previously reported findings in [15] that uninfected CD4+ target cells have a half-life of approximately 
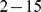days in vivo, which is substantially shorter than estimates obtained in vitro. This is likely due to the higher state of activation of the CD4+ T-cells during active viremia in vivo, but whatever the cause, it is a consistent finding across multiple experiments.
In addition to being the most accurate way of describing the fit of a model to data with high levels of measurement uncertainty, the publication of complete parameter distributions identified from patient data also has significant practical importance. A growing number of model-based interventions using variations of the model described in Equation 1 are being proposed, including our own methods designed to minimize the risk of resistance emerging during antiviral regimen switching [25], [41], [42], [44]–[47]. Most of these methods have used either nominal parameters or a single parameter set. The parameter distributions published in this work provide a parameter set against which the robustness of a proposed model-based method to expected patient variation can be tested. The data used in this paper came from a cohort restricted to patients with good immunological control of the virus under antiviral suppression, so the distribution of parameters can only be said to be representative of such a subgroup of HIV-infected persons. However, the publication of the identification methods will likely lead to the publication of parameter distributions from patients in other studies in the future, leading to a growing library of virtual patients.
Supporting Information
The posterior distribution { θi } for Patient 1. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 2. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 3. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 4. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 5. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 6. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 7. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 8. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 10. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 11. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
Acknowledgments
We thank the researchers and participants in the AutoVac study for the data used in this work.
Footnotes
Competing Interests: JMP has received research funding, consultancy fees, or lecture sponsorships from GlaxoSmithKline, Merck and Roche. There are no other conflicts to declare. This does not alter the authors' adherence to all the PLoS ONE policies on sharing data and materials.
Funding: The project described was supported by Award Number R21AI078842 from the National Institute Of Allergy And Infectious Diseases. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institute Of Allergy And Infectious Diseases or the National Institutes of Health. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Wei X, Ghosh SK, Taylor ME, Johnson VA, Emini EA, et al. Viral dynamics in human immunodeficiency virus type 1 infection. Nature. 1995;373:117–122. doi: 10.1038/373117a0. [DOI] [PubMed] [Google Scholar]
- 2.Ho DD, Neumann AU, Perelson AS, Chen W, Leonard JM, et al. Rapid turnover of plasma virions and CD4 lymphocytes in HIV-1 infection. Nature. 1995;373:123–126. doi: 10.1038/373123a0. [DOI] [PubMed] [Google Scholar]
- 3.Nelson GW, Perelson AS. Modeling defective interfering virus therapy for AIDS: conditions for HIV survival. Math Biosci. 1995;125:127–153. doi: 10.1016/0025-5564(94)00021-q. [DOI] [PubMed] [Google Scholar]
- 4.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271:1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 5.Bortz DM, Nelson PW. Model selection and mixed-effects modeling of HIV infection dynamics. Bull Math Biol. 2006;68:2005–2025. doi: 10.1007/s11538-006-9084-x. [DOI] [PubMed] [Google Scholar]
- 6.Ruiz L, Carcelain G, Martnez-Picado J, Frost S, Marfil S, et al. HIV dynamics and t-cell immunity after three structured treatment interruptions in chronic HIV-1 infection. AIDS. 2001;15:F19–F27. doi: 10.1097/00002030-200106150-00001. [DOI] [PubMed] [Google Scholar]
- 7.Stafford MA, Corey L, Cao Y, Daar ES, Ho DD, et al. Modeling plasma virus concentration during primary HIV infection. J Theor Biol. 2000;203:285–301. doi: 10.1006/jtbi.2000.1076. [DOI] [PubMed] [Google Scholar]
- 8.Xia X, Moog CH. Identifiability of nonlinear systems with application to HIV/AIDS models. IEEE T Automat Contr. 2003;48:330–336. [Google Scholar]
- 9.Wu H, Zhu H, Miao H, Perelson AS. Parameter identifiability and estimation of HIV/AIDS dynamic models. Bull Math Biol. 2008;70:785–799. doi: 10.1007/s11538-007-9279-9. [DOI] [PubMed] [Google Scholar]
- 10.Miao H, Dykes C, Demeter LM, Wu H. Differential equation modeling of HIV viral fitness experiments: model identification, model selection, and multimodel inference. Biometrics. 2009;65:292–300. doi: 10.1111/j.1541-0420.2008.01059.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liang H, Miao H, Wu H. Estimation of constant and time-varying dynamic parameters of HIV infection in a nonlinear differential equation model. Ann Appl Stat. 2010;4:460–483. doi: 10.1214/09-AOAS290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Wu H, Huang Y, Acosta EP, Rosenkranz SL, Kuritzkes DR, et al. Modeling long-term HIV dynamics and antiretroviral response: effects of drug potency, pharmacokinetics, adherence, and drug resistance. J Acquir Immune Defic Syndr. 2005;39:272–283. doi: 10.1097/01.qai.0000165907.04710.da. [DOI] [PubMed] [Google Scholar]
- 13.Huang Y, Liu D, Wu H. Hierarchical bayesian methods for estimation of parameters in a longitudinal HIV dynamic system. Biometrics. 2006;62:413–423. doi: 10.1111/j.1541-0420.2005.00447.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Huang Y. Long-term HIV dynamic models incorporating drug adherence and resistance to treatment for prediction of virological responses. Computational Statistics & Data Analysis. 2008;52:3765–3778. [Google Scholar]
- 15.Huang Y, Wu H, Acosta EP. Hierarchical bayesian inference for HIV dynamic differential equation models incorporating multiple treatment factors. Biom J. 2010;52:470–486. doi: 10.1002/bimj.200900173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Putter H, Heisterkamp SH, Lange JMA, de Wolf F. A Bayesian approach to parameter estimation in HIV dynamical models. Stat Med. 2002;21:2199–2214. doi: 10.1002/sim.1211. [DOI] [PubMed] [Google Scholar]
- 17.Markowitz M, Louie M, Hurley A, Sun E, Di Mascio M, et al. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J Virol. 2003;77:5037–5038. doi: 10.1128/JVI.77.8.5037-5038.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Perelson A. Dynamics of HIV infection of CD4+ T cells. Mathematical Biosciences. 1993;114:81–125. doi: 10.1016/0025-5564(93)90043-a. [DOI] [PubMed] [Google Scholar]
- 19.Perelson AS, Essunger P, Cao Y, Vesanen M, Hurley A, et al. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature. 1997;387:188–191. doi: 10.1038/387188a0. [DOI] [PubMed] [Google Scholar]
- 20.Gulick RM, Mellors JW, Havlir D, Eron JJ, Gonzalez C, et al. Treatment with indinavir, zidovudine, and lamivudine in adults with human immunodeficiency virus infection and prior antiretroviral therapy. N Engl J Med. 1997;337:734–739. doi: 10.1056/NEJM199709113371102. [DOI] [PubMed] [Google Scholar]
- 21.Dornadula G, Zhang H, VanUitert B, Stern J, Livornese L, et al. Residual HIV-1 RNA in blood plasma of patients taking suppressive highly active antiretroviral therapy. JAMA. 1999;282:1627–1632. doi: 10.1001/jama.282.17.1627. [DOI] [PubMed] [Google Scholar]
- 22.Palmer S, Wiegand AP, Maldarelli F, Bazmi H, Mican JM, et al. New real-time reverse transcriptase-initiated PCR assay with single-copy sensitivity for human immunodeficiency virus type 1 RNA in plasma. J Clin Microbiol. 2003;41:4531–4536. doi: 10.1128/JCM.41.10.4531-4536.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Finzi D, Hermankova M, Pierson T, Carruth LM, Buck C, et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science. 1997;278:1295–1300. doi: 10.1126/science.278.5341.1295. [DOI] [PubMed] [Google Scholar]
- 24.Chun TW, Stuyver L, Mizell SB, Ehler LA, Mican JA, et al. Presence of an inducible HIV-1 latent reservoir during highly active antiretroviral therapy. Proc Natl Acad Sci U S A. 1997;94:13193–13197. doi: 10.1073/pnas.94.24.13193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Luo R, Piovoso M, Zurakowski R. A generalized multi-strain model of HIV evolution with implications for drug-resistance management. In: Proc. American Control Conference. 2009. pp. 2295–2300. doi: 10.1109/ACC.2009.5160358.
- 26.Rong L, Perelson AS. Modeling latently infected cell activation: viral and latent reservoir persistence, and viral blips in HIV-infected patients on potent therapy. PLoS Comput Biol. 2009;5:e1000533. doi: 10.1371/journal.pcbi.1000533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Rong L, Perelson AS. Modeling HIV persistence, the latent reservoir, and viral blips. Journal of Theoretical Biology. 2009;260:308–331. doi: 10.1016/j.jtbi.2009.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Smith DM, Wong JK, Shao H, Hightower GK, Mai SHT, et al. Long-term persistence of transmitted HIV drug resistance in male genital tract secretions: implications for secondary transmission. J Infect Dis. 2007;196:356–360. doi: 10.1086/519164. [DOI] [PubMed] [Google Scholar]
- 29.Gunthard HF, Havlir DV, Fiscus S, Zhang ZQ, Eron J, et al. Residual human immunodeficiency virus (HIV) type 1 RNA and DNA in lymph nodes and HIV RNA in genital secretions and in cerebrospinal uid after suppression of viremia for 2 years. J Infect Dis. 2001;183:1318–1327. doi: 10.1086/319864. [DOI] [PubMed] [Google Scholar]
- 30.Palmer S, Maldarelli F, Wiegand A, Bernstein B, Hanna GJ, et al. Low-level viremia persists for at least 7 years in patients on suppressive antiretroviral therapy. Proc Natl Acad Sci U S A. 2008;105:3879–3884. doi: 10.1073/pnas.0800050105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Blankson JN, Persaud D, Siliciano RF. The challenge of viral reservoirs in HIV-1 infection. Annu Rev Med. 2002;53:557–593. doi: 10.1146/annurev.med.53.082901.104024. [DOI] [PubMed] [Google Scholar]
- 32.Schrager LK, D’Souza MP. Cellular and anatomical reservoirs of HIV-1 in patients receiving potent antiretroviral combination therapy. JAMA. 1998;280:67–71. doi: 10.1001/jama.280.1.67. [DOI] [PubMed] [Google Scholar]
- 33.Chun TW, Carruth L, Finzi D, Shen X, DiGiuseppe JA, et al. Quantification of latent tissue reservoirs and total body viral load in HIV-1 infection. Nature. 1997;387:183–188. doi: 10.1038/387183a0. [DOI] [PubMed] [Google Scholar]
- 34.Chun TW, Finzi D, Margolick J, Chadwick K, Schwartz D, et al. In vivo fate of HIV-1-infected T cells: quantitative analysis of the transition to stable latency. Nat Med. 1995;1:1284–1290. doi: 10.1038/nm1295-1284. [DOI] [PubMed] [Google Scholar]
- 35.Siliciano JD, Kajdas J, Finzi D, Quinn TC, Chadwick K, et al. Long-term follow-up studies confirm the stability of the latent reservoir for HIV-1 in resting CD4+ T cells. Nat Med. 2003;9:727–728. doi: 10.1038/nm880. [DOI] [PubMed] [Google Scholar]
- 36.Ljung L, Glad S. On global identifiability for arbitrary model parameterizations. Automatica. 1994;30:265–76. [Google Scholar]
- 37.Saccomani MP, Audoly S, D’Angio L. Parameter identifiability of nonlinear systems: the role of initial conditions. Automatica. 2003;39:619–632. [Google Scholar]
- 38.Saccomani MP, Audoly S, Bellu G, D’Angio L. Examples of testing global identifiability of biological and biomedical models with the daisy software. Computers in Biology and Medicine. 2010;40:402–407. doi: 10.1016/j.compbiomed.2010.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ritt JF. Differential algebra. Providence, R.I.: American Mathematical Society. 1950.
- 40.Ramratnam B, Bonhoeffer S, Binley J, Hurley A, Zhang L, et al. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. The Lancet. 1999;354:1782–1785. doi: 10.1016/S0140-6736(99)02035-8. [DOI] [PubMed] [Google Scholar]
- 41.Luo R, Zurakowski R. A new strategy to decrease risk of resistance emerging during therapy switching in HIV treatment. In: Proc. American Control Conference. 2008. pp. 2112–2117. doi: 10.1109/ACC.2008.4586804.
- 42.Luo R, Cannon L, Hernandez J, Piovoso M, Zurakowski R. Controlling the evolution of resistance. J Process Control. 2011;21:367–378. doi: 10.1016/j.jprocont.2010.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Luo R, Piovoso MJ, Martinez-Picado J, Zurakowski R. Optimal Antiviral Switching to Minimize Resistance Risk in HIV Therapy. PLoS ONE. 2011;6:e27047. doi: 10.1371/journal.pone.0027047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Martinez-Cajas JL, Wainberg MA. Antiretroviral therapy : optimal sequencing of therapy to avoid resistance. Drugs. 2008;68:43–72. doi: 10.2165/00003495-200868010-00004. [DOI] [PubMed] [Google Scholar]
- 45.Cardozo EF, Zurakowski R. Robust Closed-Loop Minimal Sampling Method for HIV Therapy Switching Strategies. Biomedical Engineering, IEEE Transactions on 59: In press. 2012. doi: 10.1109/TBME.2012.2201479. [DOI] [PMC free article] [PubMed]
- 46.Ferreira J, Hernandez-Vargas EA, Middleton RH. Computer simulation of structured treatment interruption for HIV infection. Comput Methods Programs Biomed. 2011;104:50–61. doi: 10.1016/j.cmpb.2011.07.011. [DOI] [PubMed] [Google Scholar]
- 47.Hernandez-Vargas E, Colaneri P, Middleton R, Blanchini F. Discrete-time control for switched positive systems with application to mitigating viral escape. International Journal of Robust and Nonlinear Control. 2011;21:1093–111. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
The posterior distribution { θi } for Patient 1. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 2. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 3. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 4. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 5. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 6. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 7. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 8. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 10. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)
The posterior distribution { θi } for Patient 11. The first 50,000 rows were excluded from analysis to allow for convergence of the Markov Chain.
(XLSB)