A Familiar-Size Stroop Effect: Real-World Size Is an Automatic Property of Object Representation

Abstract

When we recognize an object, do we automatically know how big it is in the world? We employed a Stroop-like paradigm, in which two familiar objects were presented at different visual sizes on the screen. Observers were faster to indicate which was bigger or smaller on the screen when the real-world size of the objects was congruent with the visual size than when it was incongruent— demonstrating a familiar-size Stroop effect. Critically, the real-world size of the objects was irrelevant for the task. This Stroop effect was also present when only one item was present at a congruent or incongruent visual size on the display. In contrast, no Stroop effect was observed for participants who simply learned a rule to categorize novel objects as big or small. These results show that people access the familiar size of objects without the intention of doing so, demonstrating that real-world size is an automatic property of object representation.

Every object in the world has a physical size which is intrinsic to how we interact with it (Gibson, 1979); we pick up small objects like coins with our fingers, we throw footballs and swing tennis rackets, we orient our body to bigger objects like chairs and tables and we navigate with respect to landmarks like fountains and street signs. When we learn about objects, our experience is necessarily situated in a three-dimensional context. Thus, the real-world size of objects may be a basic and fundamental property of visual object representation (Konkle & Oliva, 2011) and of object concepts (Setti, Caramelli, & Borghi, 2009; Sereno & O’Donnel, 2009; Rubinsten & Henik, 2002).

One of the most fundamental properties of object representation is category information; we rapidly and obligatorily recognize objects and can name them at their basic-level category (Grill-Spector & Kanwisher, 2005; Thorpe, Fize, & Marlot, 1996). This indicates that when visual information about an object is processed, it automatically makes contact with category information. Here we examined whether our knowledge of an object’s real-world size is also accessed automatically; as soon as you see a familiar object, do you also know how big it typically is in the world?

We designed a Stroop-like paradigm to test whether the real-world size of the object is automatically accessed when you recognize a familiar object. In what is commonly referred to as the “Stroop effect” (Stroop, 1935; see MacLeod, 1991), observers are faster to name the ink color of a presented word when the word is congruent with the ink color than when it is incongruent (the word pink in pink ink or green ink). Even though the word itself is irrelevant to the task, fluent readers automatically and obligatorily read the word, even at a cost to performance. Stroop paradigms have been used as a tool to understand how we automatically draw meaning from words, and this has been extended to understand how we draw meaning from pictures (MacLeod, 1991).

Here we present images of familiar big or small objects (e.g., chair, shoe) at big and small visual sizes on the screen. Critically, in the following paradigms, we have people perform a visual size judgment (e.g., “which of two items is bigger on the screen?”). For this visual size judgment, the identities of the objects, and their real-world sizes, are completely irrelevant to the task. Thus, if the real-world size of objects speeds or slows performance on this basic visual size task, this would be strong evidence that as soon as you recognize an object, you automatically access its real-world size as well.

Experiment 1: Familiar Object Stroop Task

In Experiment 1, we presented images of two real-world objects, one big and one small, at two different sizes on the screen. The real-world size of the objects could be congruent or incongruent with their visual sizes. Observers made a judgment about the visual size of the object (“which is smaller/bigger on the screen?”) with a speeded key press response.

Pictures of real-world objects vary along a number of dimensions, from their aspect ratio to their pixel area within their bounding frame. These measures affect the visual size that objects appear on the screen; for example, a wide object tends to look smaller than a tall object, even if they are equated on other dimensions such as the diagonal extent or fit inside similar bounding circles, and big objects tend to fill more of their bounding box than small objects, thus covering more area even when matched for height and width. To account for these factors, in Experiment 1a we paired big and small objects by aspect ratio and set the visual sizes of each object based on the diagonal length of the bounding box (Kosslyn, 1978; Konkle & Oliva, 2011), and in Experiment 1b we set the visual sizes of objects based on their total pixel area (see Figure 1).

Figure 1.

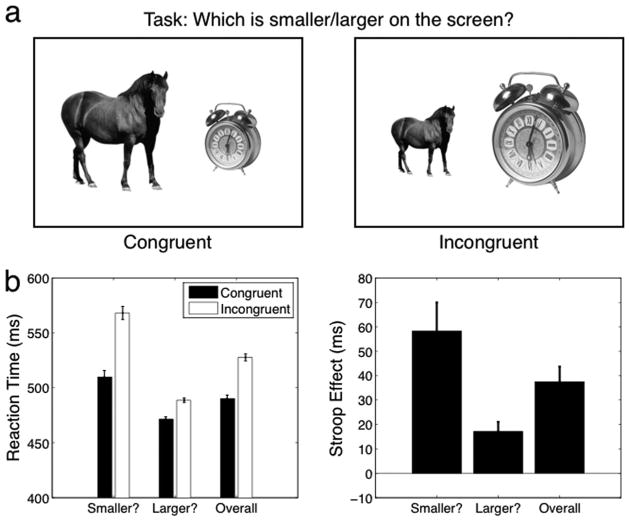
Experiment 1 sample displays: In Experiment 1, two familiar objects were presented side by side, and observers’ task was to indicate which object was smaller or larger on the screen. The real-world size of the objects could either be congruent or incongruent with the presented size. Example displays are shown for congruent and incongruent conditions, for Experiment 1a (A) and Experiment 1b (B). In Experiment 1a, the big and small objects were matched by aspect ratio and their visual size was set by adjusting the diagonal extent relative to the size of the screen. In Experiment 1B, the visual size of the objects was set by adjusting the object pixel area relative to the area of the screen.

Method

Participants

Thirty-four participants (n = 18 in Experiment 1a, n = 16 in Experiment 1b), age 18 –35, gave informed consent and completed the experiment.

Apparatus

Observers sat 57 cm from a computer screen (29 × 39.5 cm) and viewed stimuli presented using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997).

Design

Each trial started with a fixation cross for 700 ms, then color images of real-world objects were presented on the screen, with one at a visually large size and the other at a visually small size. The task was to make a judgment about the visual size of the object (“which is visually bigger on the screen?”) as fast as possible while maintaining high accuracy. Participants were positioned with their left index finger over the c key and their right index finger over the m key, and indicated whether the left or the right image was bigger on the screen with the spatially corresponding button. The images were present on the display until the observer responded. The task was counterbalanced so participants also performed the other size judgment (“which is visually smaller on the screen?”) on the same displays. Correct responses were followed by a 900-ms interval before the next trial began. Incorrect responses were followed by error feedback and a 5-second interval before the next trial began.

In congruent trials, the real-world size of the familiar objects was congruent with the visual size. For example, an alarm clock would be presented small while a horse was presented big. In incongruent trials, this was reversed and the horse was small on the screen while the alarm clock was big on the screen (Figure 2a).

Figure 2.

Experiment 1a: Familiar-size Stroop effect: (A) Two familiar objects were presented side by side, and observers indicated which object was smaller or larger on the screen. The real-world size of the objects could either be congruent or incongruent with the presented size. Congruent and incongruent example displays are shown. (B) The left panel shows overall reaction times for congruent trials (black bars) and incongruent trials (white bars), plotted for each task (smaller/larger visual size judgment) and combined across tasks. The right panel shows the difference between incongruent and congruent reaction times (Stroop effect). Error bars reflect ±1 SEM. A reliable familiar-size Stroop effect was observed.

In both Experiment 1a and 1b, the big and small objects were counterbalanced to appear in both congruent/incongruent trials with the correct answer on the left/right side of the screen, across bigger/smaller visual size tasks. In Experiment 1a, there were 576 trials (36 pairs of objects × 2 congruent/incongruent conditions × 2 left/right sides of screen × 2 bigger/smaller tasks × 2 different pairings of objects; yielding 288 congruent/288 incongruent trials). In Experiment 1b, there were ×20 trials (20 pairs of objects × 2 congruent/incongruent conditions × 2 left/right sides of the screen × 2 bigger/smaller tasks × 2 different pairings of objects; yielding 160 congruent/160 incongruent trials). Observers completed both tasks (which is visually smaller/larger?) for the first set of object pairs (e.g., refrigerator– garlic), and the repeated both tasks for the second set of object pairs (e.g., refrigerator–seashell). The order of the tasks was counterbalanced across observers.

Stimuli: Experiment 1a

In Experiment 1a, a set of 36 big and 36 small object stimuli were gathered and paired by matching aspect ratio, such that the difference between width/height between the big and small item was within 0.2 (e.g., car–pizza cutter, ladder– hammer). To make each display, the visual sizes were set so that the diagonal extent of the bounding box around each object was either 35% or 60% of the screen height, for visually small and big, respectively (~11 and 18 degrees visual angle). This method of setting the visual size has been used before to take into account variations in aspect ratio across objects (Konkle & Oliva, 2011; Kosslyn, 1978).

In the first half of the experiment, all trials contained pairs of objects that were matched in aspect ratio. Thus all observers saw these same pairs. To double the number of trials to increase power, we pseudorandomly paired the big and small objects, and this pairing was different for each observer. Here, we ensured that if a tall big object was paired with a wide small object (e.g., door–harmonica), then there would also be a tall small object paired with a wide big object (e.g., bottle–train). Thus, the aspect ratio of two items on any given display could be different, but across trials the ratio of aspect ratios was balanced across congruent and incongruent conditions. This stimulus-pairing method ensured that the aspect ratio (or ratio of aspect ratios) was completely balanced across congruent and incongruent trial types. Thus, any differences in RTs between these two conditions cannot be driven by effects of aspect ratio on perceived visual size.

Stimuli: Experiment 1b

Even when the aspect ratio of an object’s bounding box is matched, big objects tend to fill more pixels within this frame than small objects (e.g., Consider a tree vs. a flower). Thus when big objects are presented at a big size, they tend to have a greater pixel area than the small objects, even though the diagonal extents are matched. To control for this factor, in Experiment 1b we constructed a new set of 20 big and 20 small object stimuli that were matched for pixel area.

Unlike in the image set for Experiment 1a, here we specifically avoided objects with internal holes (e.g., ring, grocery cart) or long extended parts forming partial holes (e.g., slide, nut cracker), to avoid the issue of whether background pixels internal to the contour of the object should be included in measures of total object pixel area. Object images were sized so that the object pixel area was either 20% or 48% of a 440 × 440 image. Objects which could not fill 48% of a 440 × 440 frame, namely objects with more extreme aspect ratios (e.g., pen, floor lamp), were automatically excluded by this criterion. When two images were placed on a 1,024 × 768 screen during a trial, the pixel area of the smaller image was 4.9% of the total screen area, while the pixel area of the bigger image was 11.8% of the total screen area. Thus in Experiment 1b, the relative pixel area between the visually big and visually small item was exactly the same across the congruent or incongruent displays. Stimuli from both Experiment 1a and 1b are available for download on the first author’s website.

Results

Incorrect trials and trials in which the reaction time (RT) was shorter than 200 ms or longer than 1500 ms were excluded, removing 3.8% of the trials in Experiment 1a and 1.4% of trials in Experiment 1b. One participant was excluded in Experiment 1a due to a computer error.

The results for Experiment 1a are plotted in Figure 2. Overall, RTs for incongruent trials were significantly longer than for congruent trials (38 ms, SEM = 6 ms; Cohen’s d = 1.5; 2 × 2 repeated measures ANOVA, main effect of congruency: F(1, 67) = 18.2, p < .001). All 17 observers showed an effect in the expected direction.

This Stroop effect was reliably observed in both visual size tasks, with paired t tests showing significant Stroop effects (visually smaller task: 58 ms, SEM = 12 ms; t(16) = 4.98, p = .0001; visually larger task: 17 ms, SEM = 4 ms, t(16) = 4.40, p = .0004). We also observed an effect of task on RT: people were faster to judge which was bigger on the screen than which was smaller (main effect of task: F(1, 67) = 14.6, p = .001). This result is consistent with classic findings of faster RTs for visually larger items (Osaka, 1976; Payne, 1967; Sperandio, Savazzi, Gregory, & Marzi, 2009). The magnitude of the Stroop effect was significantly different across these tasks (task × congruency interaction: F(1, 67) = 8.9, p = .009), with a larger effect when people were judging which object was smaller on the screen. Finally, while overall accuracy was high (98%), when errors were made they were significantly more often for the incongruent than congruent displays (incongruent error count: 8.6, SEM = 1.6; congruent error count: 3.1, SEM = 0.8; t(16) = 4.35, p < .001).

We additionally examined whether the method of aspect ratio pairing was important; as in the first half, both items on a display had a matched-aspect ratio, whereas items were paired on a display without regard to their aspect ratio, with aspect ratio only balanced across trials. Stroop effects were found for both matched-aspect ratio trials and pseudopaired-aspect ratio trials, in both RT and error counts (matched-aspect ratio on a display: Stroop RT = 34.0, SEM = 8.7, t(16) = 3.94, p = .001; Stroop error count: t(16) = 3.84, p = .001; pseudopaired-aspect ratio: Stroop RT = 28.6, SEM = 8.7, t(16) = 3.29, p < .005; Stroop errors: t(16) = 3.61, p < .005). There was no difference in the overall RT, t(16) = 0.32, ns or magnitude of the Stroop effect, t(16) = 0.53, ns across these stimulus pairing conditions.

Experiment 1b showed the same pattern of results as Experiment 1a. We observed a significant Stroop effect in RTs (21 ms, SEM = 3.8 ms; Cohen’s d = 1.4; 2 × 2 ANOVA main effect of congruency: F(1, 63) = 31.0, p < .001), and all 16 participants showed an effect in the expected direction. As before, people were faster overall to judge which was bigger on the screen (main effect of task: F(1, 63) = 19.4, p = .001), with a bigger Stroop effect in that task (task × congruency interaction: F(1, 63) = 17.7, p = .001). Finally, more errors were made on the incongruent than congruent displays (incongruent error count: 3.1, SEM = 0.8, congruent error count: 0.8, SEM = 0.3; SEM = 1.6; t(15) = 2.99, p = .009).

Comparing the two experiments, the magnitude of the Stroop effect in Experiment 1b was smaller than in Experiment 1a (16.5 ms difference, t(31) = 2.26, p = .03). However, we also observed that participants in Experiment 1b were reliably faster and more accurate than participants in Experiment 1a (Overall RT E1a: 509 ms; E1b: 414 ms; t(31) = 2.26, p < .05; Overall Errors E1a = 12; E1b = 4; t(31) = 3.28, p < .005). The better speed and accuracy in Experiment 1b suggests that the two visual sizes used for the displays were overall more perceptually distinguishable than in Experiment 1a. Thus, despite the fact it was significantly easier to make a visual size judgment in Experiment 1b, we still observed a highly reliable Stroop effect.

Overall, the results of both experiments demonstrate a familiar-size Stroop effect: people are slower to complete a basic visual judgment when the familiar size of the object is incongruent with the visual size. The overall pattern of results was replicated in two experiments, and the effect was observed in expected direction in every single subject (N = 34).

Experiment 2: Single-Item Stroop Task

In Experiment 2, a single item was presented on the screen at a visually small or big size, and observers again performed a visual size judgment, where the identity and real-world size of the object is irrelevant. This experiment tests whether the perceptual comparison of two items required in Experiment 1 was critical for eliciting the familiar-size Stroop effect. During the initialization phase, observers learned the big and small visual sizes while judging filled rectangles presented on the screen, and subsequently pictures of big or small real-world objects were presented at the same big and small visual sizes. We note that judging whether a single item on the screen is big or small still relies on a comparison, with respect to memory of the items that have come before and/or the item relative to the screen size. However, this task does remove any requirement for the direct perceptual comparison of two real-world objects.

Method

Participants

Nineteen participants (between ages 18 –35) gave informed consent and completed the experiment.

Stimuli

The set of 36 big and 36 small objects from Experiment 1a were used in this experiment. The same specifications for setting their visual size was employed.

Procedure

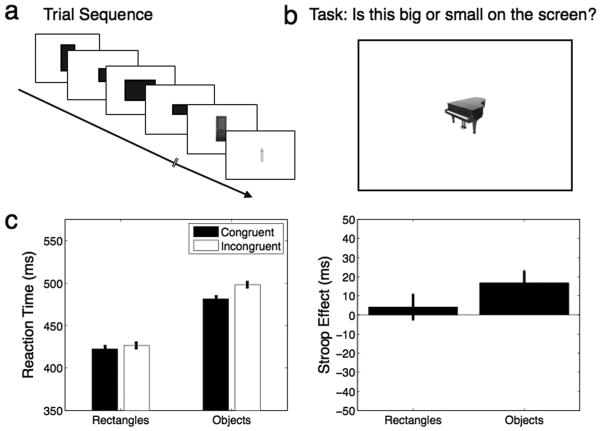
On each trial, a single item was presented on the screen, and the task was to make a judgment about the visual size of the object (“is this small or big on the screen?”) as fast as possible, while maintaining high accuracy. Observers were told to keep track of the average size and to judge whether each item was smaller or larger than the average. For the first 24 trials, black filled rectangles were presented, alternating in visual size systematically, and familiarizing observers with the big and small visual sizes. For the next 48 trials, the visual sizes of the presented rectangles was randomized from trial to trial, and observers were told to practice responding with accuracy and speed. Following these initialization blocks, pictures of real-world objects were presented instead of rectangles, and observers continued the same task (Figure 3a, 3b). To respond, observers used their two index fingers on the c and m keys to indicate either “big on the screen” or “small on the screen” with the response-key assignment counterbalanced across observers. The rest of the trial design and timing was the same as in Experiment 1.

Figure 3.

Experiment 2: Single-item Stroop task: (A) Observers were presented with a black rectangle on the screen and indicated whether it was bigger or smaller than the average of the previous trials. After initialization phase with rectangles, images of real-world objects were shown. (B) An example incongruent trial is shown, with a big piano shown at a small visual size. Because the black rectangles covered the images of big or small real-world objects, there were also congruent and incongruent trials in the initialization phase, but the observers were blind to these conditions. (C) The left panel shows overall reaction times congruent trials (black bars) and incongruent trials (white bars), plotted for the initialization phase and object stimuli. The right panel shows the difference between incongruent and congruent reaction times. Error bars reflect ±1 SEM. There was a significant Stroop effect for single items on the screen, and no effect when observers made the judgments on rectangles that covered images of real-world objects.

For the initialization trials that established the visual sizes using black rectangles, we filled the bounding box of a subset of the object pictures. In the alternating trials, 6 big and 6 small objects were presented, alternating big and small visual sizes and big and small real-world sizes. These same trials were repeated for the next two practice blocks in a randomized order. This method exposed observers to a range of visual sizes in an unbiased way, and further allowed us to measure RTs for “congruent” and “incongruent” trials where observers were blind to condition, as they only saw black rectangles. Following the practice blocks, there were 288 total trials (36 objects × 2 real-world sizes × 2 retinal sizes × 2 repetitions; yielding 144 congruent/144 incongruent trials).

Results

Incorrect trials and trials in which the RT was shorter than 200 ms or longer than 1,500 ms were excluded, removing 3.9% of the trials.

The results are plotted in Figure 3. Reaction times for incongruent trials were significantly longer than for congruent trials (17 ms, SEM = 6 ms; Cohen’s d = 0.65; 2 × 2 repeated measures ANOVA, main effect of congruency: F(1, 75) = 8.1, p < .05). Seventeen of 19 observers showed an effect in the expected direction. People were faster overall to respond to big real-world objects (e.g., piano, main effect of real-world size: F(1, 75) = 7.2, p < .05), with no interaction between real-world size and congruency, F(1, 75) = 1.1, ns.

Examining the initialization trials in which people judged black rectangles that covered real-world object images, there was no “hidden” Stroop effect (7 ms, SEM = 5 ms; t(18) = 1.38, ns). This further confirms that the obligatory effect of real-world size on visual size judgments relies on automatic recognition of the object and activation of real-world size information.

Experiment 3: Rule-Learning Stroop Task

One account of this familiar-size Stroop effect is that our knowledge about object size arises from extensive visual experience with objects in the world, and this expertise is required to automatically activate familiar size. However, an alternate explanation is that the interference between known size and visual size arises only at a very conceptual level. For example, if this effect is cognitively penetrable (Pylyshyn, 1999), then it would be sufficient to simply instruct people that some objects are big and others are small in order to observe a Stroop effect. We test this possibility in Experiment 3.

We introduced participants to novel bicolor objects from a “block world”, where observers were told that all objects in this world fall into two classes: big objects made out of blue and red blocks, and small objects made of yellow and green blocks. Here we taught observers a simple rule with minimal experience, to see if this quick learning of abstract regularities from exposure to a minimal set of stimuli was sufficient to drive a Stroop effect. If observers show a Stroop effect on objects whose size is based on a rule, this would suggest that known size can be rapidly incorporated into our object knowledge. Alternatively, if observers do not show a Stroop effect, this would suggest that more experience with the objects is required for automatic known size processing.

Method

Participants

Seventeen new participants (between ages 18 –35) gave informed consent and completed the experiment.

Procedure

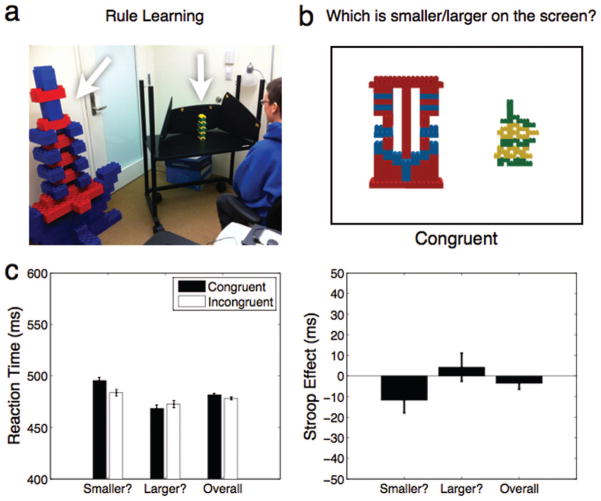
Observers were introduced to two example physical objects in the testing room, one small (approx. 120 cm × 75 cm) and one large (approx. 30 cm × 18 cm), depicted in Figure 4a. Participants were told that these were example objects from a block-world, where all blue-red block objects were big and all yellow-green block objects were small. Observers completed a 30-min familiarization phase to expose them to the example objects in the testing room and to the pictures of the other bicolored objects presented on the screen. Following this familiarization phase, observers completed a block-world Stroop task (Figure 4b).

Figure 4.

Experiment 3: Rule-learning Stroop task. (A) Observers were familiarized with one bicolor big object and one bicolor small object, and were told that in block world, all big objects were made of blue and red blocks, and all small objects were made of yellow and green blocks. Another testing room contained the reference objects with the opposite color–size pairing, counterbalancing this rule across observers. (B) During the Stroop task, two bicolor objects were presented side by side, and observers indicated which object was smaller or larger on the screen. The implied real-world size of the objects could either be congruent or incongruent with the presented size. An example display that is congruent with the familiarization in (A) is shown. (C) The left panel shows overall reaction times for congruent trials (black bars) and incongruent trials (white bars), plotted for each task (smaller/larger visual size judgment) and combined across tasks. The right panel shows the difference between incongruent and congruent reaction times (Stroop effect). Error bars reflect ±1 SEM. No reliable rule-learning Stroop effect was observed.

Familiarization Methods

Observers were given a sheet of paper, a pencil, and markers, and had 3 minutes to create a colored drawing of each reference object. Next, participants were given 10 seconds to study the reference object, after which they closed their eyes and one or more blocks were added to the object. They then had three guesses to indicate which blocks were added and were given feedback. Added blocks were always of the same colors as the reference objects. Observers completed three change-detection trials per reference object. This task ensured observers had ample time to engage with the reference objects, providing further exposure to learn the color–size rule.

We next familiarized the participants to pictures of other objects from block world, presented on the screen. For each trial, the participant was instructed to turn and look at the big or small reference object, after which they looked back at the screen and a picture of a new object from block world presented. This picture was always of the same real-world size class (e.g., a “small” object also made out of green and yellow blocks). Observers’ task was to determine if the depicted object was slightly taller or slightly shorter than the reference object, were it in the world alongside the reference object. Each depicted object was presented for 500 ms, which did not allow sufficient time for observers to count the number of rows of blocks. The 32 novel bicolor object pictures were presented in random order. This task ensured that participants were familiarized with each depicted object on the screen, and further required them to conceive of its physical size in the world.

Stimuli

Thirty-two bicolor block objects were created using LEGO Digital Designer software (http://ldd.lego.com/). All objects shapes were made out of both blue-red and yellow-green blocks. Each observer saw 16 unique yellow-green objects and 16 unique blue-red objects. These objects were paired in aspect ratio as in Experiment 1a.

Design

The trial design was as in Experiment 1, except that pictures of bicolor block objects were presented on the display rather than images of real-world objects (Figure 4b). There were 512 total trials (16 pairs of objects × 2 congruent/incongruent trial type × 2 left/right sides of screen × 2 smaller/larger task × 4 repetitions), yielding 256 congruent/256 incongruent trials.

To counterbalance for the pairing of color and real-world size, the same reference objects as seen in Figure 4a were constructed from blocks of the other colors, and half of the observers were familiarized with the alternate set of reference objects. Thus, across observers, each display of two block objects served as both a congruent and incongruent trial. Additionally, we counterbalanced at the item level, such that across observers, each object appeared in both blue-red or yellow-green as both an implied big and implied small object, ensuring that object shapes were fully counterbalanced across conditions.

Results

Incorrect trials and trials in which the RT was shorter than 200 ms or longer than 1,500 ms were excluded, removing 3.7% of the trials.

The results are shown in Figure 4c. Overall, we observed no difference in RT between congruent and incongruent trials (−4 ms, SEM = 3 ms; Cohen’s d = −0.3; 2 × 2 ANOVA, main effect of congruency: F(1, 67) = 1.7, p = .21; Figure 4c). The Stroop effect was not present in either task (smaller task: −12 ms, SEM = 6 ms; larger task: 4 ms, SEM = 7 ms; task × congruency interaction: F(1, 67) = 1.9, p = .19). Of the 17 observers, 7 showed an effect in the expected direction and 10 showed an effect in the opposite direction. A power analysis indicated this study had very high power (>99%) to detect a Stroop effect of similar magnitude as in Experiment 1, and high power (83%) to detect an effect of half the size. At a power of 99% this study could detect an effect size of d = 1.0 (~12 ms Stroop effect).

We next compared the Stroop effect between real-world objects and block-world objects, conducting a 2 × 2 ANOVA with familiar/bicolor objects as a between-subjects factor, and congruency as a within-subject factor. There was a significant main effect of congruency, F(1, 67) = 25.1, p < .001 and a significant interaction between experiments and congruency, F(1, 67) = 36.7, p < .001. That is, people in the familiar object experiment showed a Stroop effect (38 ms, SEM = 6) while people in the rule learning experiment did not (−4ms, SEM = 3). Two-sample t tests confirmed this result, t(32) = 6.06, p < .0001. Further, there was no difference in overall RT between the two experiments, F(1, 67) = 0.4, p = .53, indicating that across experiments participants were not any faster or slower overall to make visual size judgments. The exact same pattern of results was obtained whether comparing the rule-learning group with the group from Experiment 1a (statistics reported above) or the group from Experiment 1b (main effect of congruency: F(1, 65) = 12.6, p < .001, no effect of familiar/bicolor objects: F(1, 65) = 3.2, p = .09, interaction: F(1, 65) = 27.2, p < .001; two sample t test between familiar object and bicolor object Stroop effects: t(31) = 5.21, p < .0001).

These across-experiment comparisons show that there is a robust Stroop effect with familiar objects that was not detected for stimuli whose real-world size is implied based on an explicitly learned rule. Even though observers know this rule with certainty, the data show that this fact-based knowledge was not sufficient to generate a detectable Stroop effect within the reasonable power of the current design. This suggests that in order for known size to have a strong and automatic impact performance, more extensive experience and learning is required.

General Discussion

A hallmark of our object recognition system is that object processing automatically connects with stored knowledge, allowing for rapid recognition (Thorpe et al., 1996). Nearly as soon as we are able to detect an object, we can also name it at the basic-category level (Grill-Spector & Kanwisher, 2005; Mack, Gauthier, Sadr, & Palmeri, 2008). Here we show that even when object information is completely task-irrelevant, familiar size gives rise to a Stroop effect. These results suggest that we not only identify objects automatically, but we also access their real-world size automatically.

A previous study used similar displays as in Figure 1, but observers judged which object was bigger in the world (Srinivas, 1996). They also found a Stroop effect, with observers faster to make a real-world size judgment when the visual size was congruent. Thus, Srinivas demonstrated that a perceptual feature (visual size) influenced the speed of a conceptual/semantic judgment (which is bigger in the world), which makes sense as visual size may be a route to accessing real-world size more quickly. The current study demonstrates the complementary effect: real-world size facilitates/interferes with a visual size judgment, revealing the speed and automaticity with which task-irrelevant semantic information is brought to bear on a very basic perceptual task. Together, these results speak to the integral nature of perceptual and semantic features, demonstrating a direct and automatic association between real-world size and visual size.

What is the underlying relationship between real-world size and visual size that gives rise to a Stroop effect? One possibility is that interference occurs at a relatively high-level concept, arising from a common abstract concept of size. However, the data from the rule-learning experiment are not wholly consistent with pure conceptual interference. Had we found that teaching people a simple size rule led to a Stroop effect, this would be strong evidence supporting a more abstract locus of interference. However, we observed that simply being able to state whether something is big or small with minimal experience did not lead to strong interfere with visual size judgments. Instead, the data imply that the association between an object and its real-world size has to be learned with repeated experience before it can automatically interfere with a visual size task.

A second possibility is that interference in this task arises in more perceptual stages of processing. Consistent with this idea, a number of researchers have claimed that stored information about real-world size is represented in a perceptual or analog format (Moyer, 1973; Paivio, 1975; Rubinsten & Henik, 2002). Further, objects have a canonical visual size, proportional to the log of their familiar size, where smaller objects like alarm clocks are preferred at smaller visual sizes, and larger objects like horses are preferred at larger visual sizes (Konkle & Oliva, 2011; Linsen, Leyssen, Sammartino, & Palmer, 2011). On this more perceptual account of interference, in the congruent condition both objects have a better match to stored representations, which include visual size information, facilitating and/or interfering with visual size judgments.

Certainly, these two accounts of the familiar-size Stroop effect are not mutually exclusive. As is the case with the classic color–word Stroop task, it is likely that there is interference at multiple levels of representation, from more perceptual ones (realized in visual-size biases) to more conceptual ones (e.g., semantic facts that a horse is big). The present data do suggest, however, that strong interference effects are not granted in one shot by learning a rule, but instead must be grounded in repeated perceptual experience. This mirrors the results for the classic Stroop effect, where intermediate or fluent reading ability is required to show interference with color naming (Comalli, Wapner, & Werner, 1962; MacLeod, 1991). In the current studies, we tested the two ends of an experiential continuum, from rich and structured real-world object representations to novel objects lacking specific visual experience and semantic content. It is a more extensive endeavor to understand how much experience, and critically what kind of experience or knowledge, (e.g., of object functions, purpose, categories labels, or natural real-world viewing) is necessary before real-world size becomes an intrinsic and automatic aspect of object recognition. It is important to note that regardless of the sources of interference between real-world size and visual size and the nature of experience required, the present data clearly show that the real-world size of objects is automatically activated when an object is recognized.