Sequencing Cyclic Peptides by Multistage Mass Spectrometry

Abstract

Some of the most effective antibiotics (e.g., Vancomycin and Daptomycin) are cyclic peptides produced by non-ribosomal biosynthetic pathways. While hundreds of biomedically important cyclic peptides have been sequenced, the computational techniques for sequencing cyclic peptides are still in their infancy. Previous methods for sequencing peptide antibiotics and other cyclic peptides are based on Nuclear Magnetic Resonance spectroscopy, and require large amount (miligrams) of purified materials that, for most compounds, are not possible to obtain. Recently, development of mass spectrometry based methods has provided some hope for accurate sequencing of cyclic peptides using picograms of materials. In this paper we develop a method for sequencing of cyclic peptides by multistage mass spectrometry, and show its advantages over single stage mass spectrometry. The method is tested on known and new cyclic peptides from Bacillus brevis, Dianthus superbus and Streptomyces griseus, as well as a new family of cyclic peptides produced by marine bacteria.

1 Introduction

Sequencing cyclic peptides, once a heroic effort, remains difficult today. The dominant technique for sequencing cyclic peptides is 2D nuclear magnetic resonance (NMR) spectroscopy, which requires large amount (miligrams) of highly purified materials that are often nearly impossible to obtain [2]. Tandem mass spectrometry (MS/MS) provides an attractive alternative to NMR since it allows one to sequence a peptide from picograms of non-purified material. However, the algorithms for interpreting mass spectra of cyclic peptides are still in infancy.

In addition to ribosomal cyclic peptides (that are encoded in a proteome), many cyclic peptides are nonribosomal [1], (and thus are not directly encoded by codons). Also, some cyclic peptides are chimeric, i.e., they are generated by concatenation and cyclization of peptides from different proteins (e.g., θ-defensins [9]). MS/MS database search against protein databases is inapplicable to nonribosomal peptides leaving de novo peptide sequencing as the only option in this case. Moreover, algorithms for searching spectra of ribosomal (let alone chimeric) cyclic peptides against a protein database have not been developed yet. As a result, natural product researchers have to reserve to searching spectra of new cyclic peptides against databases of amino acid sequences of all known cyclic peptides produced by various organisms. However, the existing databases of cyclic peptides (e.g. NORINE [10]) are very limited and represent only a small fraction of cyclic peptides present in various organisms. Thus, in difference from linear peptides, de novo sequencing rather than database search represents the primary mode for analyzing cyclic peptides.

De novo sequencing by mass spectrometry can be tricky even for linear peptides [4, 5, 6], let alone for cyclic peptides. In the case of linear peptides, mass spectrometrists usually reserve to database search since it is more accurate than de novo sequencing [7, 8]. The database search approach (dereplication) for spectra of cyclic peptides (Ng et al. [3]) can usually resequence a new variants of a cyclic peptide family differing from a known member by one or two mutations. However, this approach only works if an identical or very close variant is present in a database of cyclic peptides.

Two approaches has emerged to improve accuracy of de novo sequencing of linear peptides: multistage mass spectrometry [11, 12] and spectral networks [13]. Both approaches use information about related peptides (either generated during multistage mass spectrometry experiment or naturally present in the sample) to synergistically sequence a peptide of interest. Both multistage mass spectrometry and spectral networks enable an ability to distinguish between C-terminal and N-terminal ion series [12, 14], a major obstacle in interpreting mass spectra [15].

While spectra of linear peptides are characterized by two ion series (N-terminal and C-terminal ions), spectra of cyclic peptides of length k have k ion series (each series correspond to subpeptides starting at position i of a cyclic peptide, 1 ≤ i ≤ k). Thus, de novo sequencing of cyclic peptides is more complex than sequencing of linear peptides. Similar to the case of linear peptides, one can think of two approaches for de novo sequencing of cyclic peptides: multistage mass spectrometry and spectral network analysis. While Ng et al., [3] presented the first algorithm for de novo sequencing of individual cyclic peptides, and Mohimani et al., [16] improved on [3] by applying the idea of spectral networks to cyclic peptides, the application of multistage mass spectrometry remains poorly explored for sequencing of cyclic peptides. In our experiments, in addition to tandem (MS2) spectrum, multistage spectra include MS3 and MS4 spectra and thus contain more information for spectral interpretation. Our aim is to develop the first algorithm for de novo sequencing of cyclopeptides by multistage mass spectrometry and benchmark it on peptides with known and still unknown amino acid sequences. We show that multistage mass spectrometry improves the quality of de novo sequencing of cyclic peptides (as compared to single stage mass spectrometry) and illustrate its application to Reginamides, Etamycins, Dianthins and Tyrocidines.

Our results demonstrate that multistage sequencing is a promising approach for cyclopeptide sequencing. However, multistage mass spectrometry datasets for cyclopeptides remian scarce making it difficult to optimize the scoring model using machine learning approaches. An important aim of this paper is to encourage natural product researchers to generate such datasets.

2 Materials and methods

Spectral datasets

We analyzed cyclic peptides from Reginamides, Tyrocidines, Etamycins and Dianthins families using multistage mass spectrometry.

The Reginamides represent a newly isolated family of cyclic octapeptides isolated from a marine Streptomyces strain that also produces secondary metabolites with anti-asthma activities (Splenocins). Mohimani et al., 2010 [16], sequenced ten variants of Reginamides using spectral networks. In this paper we analyze these ten variants of Reginamides using multistage mass spectrometry.

The antibiotic Tyrothricin, isolated from the soil microbe Bacillus brevis by Rene Dubos in 1939, is a classic example of a mixture of related cyclic decapeptides whose sequencing proved to be difficult and took over two decades to complete. Tang et al., [17] listed 28 known peptides from B. brevis. Mohimani et al. [16] showed how to sequence multiple variants of Tyrocidines, and even discover new variants from a single mass spectrometry experiment. In this paper we analyze six variants of Tyrocidines.

Etamycin is an antibiotic isolated from terrestrial actinomycete S. griseus alongside the streptogramin A antibiotic, and the two molecules together displayed bactericidal activity against some Gram-positive bacteria [18]. Recently, Etamycin is shown to be active against Methicillin-Resistant Staphylococcus aureus [19]. In this paper we analyse four variants of Etamycins.

Dianthins are cyclic peptides of variable length isolated from plant Dianthus superbus, which is used as a traditional Chinese medicine for the treatment of urethritis, carbuncles, and carcinoma [20, 21]. In this study we investigate five known dianthins (Dianthins B–F) and discover six new variants. While Dianthins B–F show some faint sequence similarities with each other, this level of similarity is insufficient for construction of the spectral network of dianthins, thus making the approach from [16] inapplicable.

While to of the peptide families investigated in this study (Reginamides and Tyrocdines) have also been studied in [16], their spectral dataset used in this paper is multistage, in contrast to the single stage spectral datasets used in [16].

Tandem Mass Spectrometry Data Acquisition and Preprocessing

For the ion-trap data acquisition, each compound was prepared to a 1 M solution using 50:50 MeOH:H2O with 1% AcOH as solvent, and underwent nanoelectrospray ionization on a Biversa Nanomate (pressure: 0.3 p.s.i., spray voltage: 1.41.8 kV). Ion trap spectra were acquired on a Finnigan LTQ-MS (Thermo-Electron Corporation) running Tune Plus software version 1.0. Ion tree datasets were collected using automatic mode, in which, the [M+H]+ of each compound was set as the parent ion. MSn data were collected with the following parameters: maximum breadth, 20; maximum MSn depth, 4. At n = 2, isolation width, 4; normalized energy, 50. At n = 3, isolation width, 4; normalized energy 30. At n = 4, isolation width, 4; normalized energy 30. Thermo-Finnigan files (in RAW format) were then converted to an mzXML file format using the ReAdW (http://tools.proteomecenter.org/).

Spectra generation: from individual spectra to ion trees

Since multistage mass spectrometry improves the accuracy of de novo sequencing of linear peptides [12], we decided to use multistage mass spectrometry to improve the quality of de novo sequencing of cyclic peptides as well. For each of the above peptides, MS³ and MS⁴ spectra were collected by data dependent acquisition [22] using Thermo Scientific linear ion trap mass spectrometers. Thermo LTQ instrument was configured for the acquisition of up to 20 MS³ spectra for each MS² spectra and up to 20 MS⁴ spectra for each MS³ spectra. Figure 1(a) shows an example of MS³ and MS⁴ spectra acquisition and represents the spectra as an ion tree. For each peptide Peptide, IonTree is a collection of a single MS², 20 MS³ and 400 MS⁴ spectra. We filtered each MS³ and MS⁴ spectrum to 20 highest intensity peaks, and each MS² spectrum to 100 highest intensity peaks. For Tyrocidines, MS² Time of Flight (TOF) spectra is used in addition to MSⁿ ion trap (IT) spectra.

Figure 1.

(a) Illustration of ion tree of Reginamide A, a peptide with amino acid sequence AIIKIFLI and mass 912.59 (plus charge). 686.42 is the mass of AIIKIF and KIFLIA. 728.47 is the mass of IKIFLI and IIKIFL. 445.28 is the mass of FLIA. 558.37 is the mass of IFLIA. 615.46 is the mass of IKIFL, KIFLI and IIKIF. 487.40 is the mass of IFLI. (b) Corresponding tags for the TITM between the 8-tag AIIKIFLI and the ion tree shown on the left.

Cyclic tags and linear subtags

Consider the cyclic peptide VOLFPFFNQY (Tyrocidine A) with integer masses (99, 114, 113, 147, 97, 147, 147, 114, 128, 163). One may partition this peptide into three parts as OLF-PFF-NQYV with integer masses 374, 391 and 504 respectively. In general, a k-partition is a decomposition of a peptide P into k subpeptides with integer masses m₁ …m_k (we refer to mass$\left(P\right){\sum }_{i=1}^k{m}_i$ as the parentmass of peptide P). A k-tag of a peptide P is an arbitrary partition of mass(P) into k integers. A k-tag of a peptide P is correct if it corresponds to masses of a k-subpartition of P, and incorrect otherwise. For example, (374, 391, 504) is a correct 3-tag, while (100, 1000, 169) is an incorrect 3-tag of Tyrocidine A. We emphasize that the notion of a k-tag defined in this paper is different from the notion of a peptide sequence tag [23], not to mention that peptides we investigate may include non-standard amino acids like Ornithine in VOLFPFFNQY. Below, when we use the term tag, we refer to k-tags rather than peptide sequence tags.

A (linear) subtag of a cyclic k-tag (m₁,…, m_k) is a (continuos) linear substring m_i…m_j of the cyclic k-tag (we assume m_i…m_j = m_i…m_km₁…m_j in the case j < i). There are k(k − 1) subtags of a k-tag. The mass of a subtag is the sum of all elements of the subtag. The length of a subtag is the number of elements in the subtag. For example, 114, 260, 244, 147 is a subtag of cyclic 7-tag (99, 114, 260, 244, 147, 242, 163) of Tyrocidine A with length 4 and mass of 765Da.

For a Subtag = m_i…m_j, all the subtags contained in Subtag that either start at m_i or end at m_j are called children of the Subtag and the Subtag is called their parent. A subtag of length k has 2(k − 1) children. For example, subtag 260, 244, 147 is a child of subtag 114, 260, 244, 147, and 114, 260, 244, 147 is parent of 260, 244, 147.

Ion tree

A multistage MS experiment generates multiple spectra of related peptides (MS², MS³, MS⁴, etc.). The ion tree reveals the dependencies between these spectra by organizing them into a tree-like structure. A vertex (spectrum) S in the ion tree is connected to a vertex (spectrum) S′ by a directed edge if S′ is a product spectra generated from a peak with mass m in S. In this case we set PrecursorMass(S′) = m and PrecursorSpectrum(S′) = S. The MS² spectrum of the original cyclic peptide, S_r, is called the root of the ion tree. We define depth(S) as the distance from the root to vertex S in the ion tree.

Figure 1 (a) illustrates (part of) ion tree of Reginamide A consisting of MS², MS³ and MS⁴spectra. The complete ion tree of Reginamide A consists of 20 MS³ and 400 MS⁴ spectra. In this ion tree, the leftmost MS⁴ spectrum in Figure 1 (a) (precursor mass 445.12) is connected to the leftmost MS³ spectrum (precursor mass 686.36) by an edge because it is a product spectrum generated from a peak with mass 445.12 in the MS³ spectrum. PrecursorMass of the former spectrum is 445.12, and its PrecursorSpectrum is the latter spectrum. The depth of the former (MS⁴) spectrum is 2, and the depth of the latter (MS³) spectrum is 1.

Tag-Ion Tree Match (TITM)

A (cyclic) tag Tag and a spectrum Spectrum of a cyclic peptide define a cyclic Tag-Spectrum Match (CyclicTSM). Similarly, for a linear tag Tag and spectrum of a linear peptide, we define a linear Tag-Spectrum Match (LinearTSM). Since a peptide of length k represents a k-tag, the standard Peptide-Spectrum Matches (PSM) represent a particular case of a TSM. Given a (cyclic) tag Tag and an ion tree IonTree we also define a Tag-IonTree Match (TITM(Tag, IonTree)).

Given a TITM(Tag, IonTree) and a spectrum S from the IonTree, we define Tag(S) as follows. We first initialize Tag(S_r) = Tag and recursively (from root to leaves) define tags Tag(S) for all spectra S in the ion tree as follows. Let S′ be a spectrum (with unassigned Tag(S′) and let S be its precursor spectrum with already defined Tag(S). We define Tag(S′) as a a child of Tag(S) with mass equal to the PrecursorMass(S′) (if such a child exist). If such a child does not exist, we define Tag(S′) = Null (with linearTSMScore(Null,.) = 0).

In some cases, there exist multiple children of Tag(S) with mass equal to PrecursorMass(S′). If more than one subtag satisfies this condition, we define Tag(S′) as a subtag of Tag(S) satisfying this condition and maximizing linearT SMScore(Tag(S′), S′)). An alternative approach would be summing up the score of all such children. However such scoring tends to favor symmetric peptide (i.e., palindromes) and peptides with repeated patterns. Figure 1(b) shows all the tags Tag(S) for the TITM between the 8-tag (peptide) AIIKIFLI and the IonTree shown in Figure 1(a).

Tag Ion Tree Match Score (TITMScore)

Assume we are given a CyclicTSM Score CyclicTSMScore(Tag, Spectrum) for CyclicTSMs and a LinearTSMScore LinearTSMScore(Tag, Spectrum) for linearTSMS. Since comprehensive training samples for cyclopeptides are not available, we define very simple scoring functions for a cyclic TSM or a linear TSM (Tag, Spectrum) as the number of peaks in Spectrum explained by the theoretical spectrum of Tag (see [16] for an example of cyclic TSM score).

Given a TITM(Tag, IonTree), we define TITMScore(Tag, IonTree), as:

$$TITMScore(Tag,IonTree)=CyclicTSMScore(Tag,S_r)+\sum _{SinIonTree\text{and}S\ne S_r}{c}_{depth\left(S\right)}\cdot LinearTSMScore(Tag\left(S\right),S)$$

The TITMScore depends on parameters c₁…c_n that scale contributions of TSMs depending on their depth. Ideally, one should learn and optimize these parameters from a larger collection of TITMs. However, due to unavailability of a large training set of TITMs, we simply assume c₁ = c₂ = … = c_n = 1.

Now we define the Multistage Cyclic Peptide Sequencing Problem.

• Goal: Given an ion tree, reconstruct the cyclic peptide (tag) that generates this ion tree.

• Input: An ion tree IonTree, and a parameter k (tag length).

• Output: A cyclic k-tag Tag that maximizes TITMScore(Tag, IonTree).

To find the tag with maximum score against the given ion tree, we adapt the branch and bound approach, which is briefly described below.

A tag is valid if all its elements are larger than or equal to 57 Da (minimal mass of an amino acid). A valid (k + 1)-tag derived from a k-tag Tag by breaking one of its masses into 2 masses is called an extension of Tag. For example, a 4-tag (374, 100, 291, 504) is an extension of a 3-tag (374, 391, 504). All possible tag extensions can be found by exhaustive search since for each k-tag (m₁…m_k) there exist at most ${\sum }_{i=1}^k{m}_i$ extensions¹. We remark that in practice, all possible 3-tags can be enumerated and ranked by brute-force (a 3-tag can be represented as (a, b, PrecursorMass−a−b), where a and b are integers satisfying a > = 57, b > = 57 and a + b < = PrecursorMass − 57).

Our algorithm for sequencing cyclic peptides starts from scoring all 3-tags and selecting t top-scoring 3-tags, where t is a parameter (t equals to 100 by default). We start from tags of length 3 that proved to be an adequate starting point for tag extensions in previous study [16]. It further iteratively generates a set of all extensions of all top-scoring k-tags, combines all the extensions into a single list, score each (k + 1)-tag using TITMScore, and extracts t top scoring extensions from this list. The pseudocode in Figure 2 outlines the main steps of the algorithm.

Figure 2.

A branch-and-bound algorithm for finding high scoring k-tags. It start from tags of length 3 and iteratively generates a set of all extensions of all top-scoring k-tags, combines all the extensions into a single list, score each (k + 1)-tag using TIT MScore, and extracts t top scoring extensions from this list.

3 Results

First, we tested multistage de novo sequencing on Reginamides, Tyrocidines, Etamycins and Dianthins (Table 1), and showed that our results are consistent with the previously published NMR results that represent the golden standard in the field of natural products. (Table 2).

Table 1.

Multistage sequencing results. Masses that are verified by NMR are shown in bold. PM stands for Parent Mass of the peptide. Rank 1 … 3 for the highest scoring tag of Reginamide 925 means the three high scoring tags of Reginamide 925 have equal scores, and one of them is the tag shown. Asterisk on 147Da and 113Da means if we exchange these masses, the score wouldnt change. 222 − 18 and 147 + 18 masses for Etamycin 878 means instead of returning the correct masses 222Da and 147Da, the algorithm has returned 204Da and 165Da (this alternative breakage is also reported in [24]). ⇆ between 128Da and 113Da residues of Reginamide A means the algorithm has made a mistake in the order of those two residues, compared to previous reconstructions.

Peptide	Multistage reconstruction										PM	rank
Reginamide A	71	113	128 ⇆	113	113	147	113	113			911	4 … 6
Reginamide 897	71	113	99	128	113	113	147	113			897	2 … 3
Reginamide 925	71	113	99	156	113	147*	113*	113			925	1 … 3
Reginamide 939	71	113	113	156	113	147*	113*	113			939	4 … 6
Reginamide 953	71	113	170	113	113	147	113	113			953	3 … 4
Reginamide 967	71	113	184	113	113	147	113	113			967	24 … 30
Reginamide 981	71	113	113	85	226	147	113	113			981	1 … 2
Reginamide 995	113	113	331	226	212						995	3 … 4
Reginamide 1009	113	113	297	147	113	226					1009	1 … 5
Reginamide 1023	113	113	797								1023	5 … 15
Tyrocidine A	99	114	[113+	147]	[97+	147]	147	114	128	163	1269	20 … 44
Tyrocidine A1	99	128	[113+	147]	97	147	147	114	128	163	1283	22 … 49
Tyrocidine B	99	114	[113+	147]	97	186	147	[114+	128]	163	1308	11 … 19
Tyrocidine B1	99	128	[113+	147]	97	186	147	[114+	128]	163	1322	37 … 105
Tyrocidine C	99	114	[113+	147]	97	186	[186+	114]	128	163	1347	67 … 169
Tyrocidine C1	99	128	113	147	97	186	186	114	128	163	1361	10 … 33
Etamycin 878	71	141	71	113	113	222 − 18	147 + 18				878	5 … 8
Etamycin 864	71	127	71	113	113	222 − 18	147 + 18				864	1 … 3
Etamycin 862	71	141	71	97	113	222 − 18	147 + 18				862	9 … 12
Etamycin 858	71	141	71	113	113	222 − 18	127 + 18				858	11 … 12
Dianthin F	57	97	99 ⇆	147	147						547	13 … 20
Dianthin 564	57	113	113	71	97*	113*					564	6 … 14
Dianthin E	113	87	[147+	99+	57+	97]					600	7 … 36
Dianthin 610	97	99	[97+	57]	113	147					610	7 … 11
Dianthin 624	57	97	147	113	97	113					624	5 … 9
Dianthin 640	57	113	113	[97+	147]	113					640	25 … 66
Dianthin 644	57	97	99	147	147	97					644	1
Dianthin B	113	147	[147	97	57	97]					658	1
Dianthin 672	113	559									672	1 … 6
Dianthin C	57	147 ⇆	97	163	99	113					676	5 … 7
Dianthin D	87	113	97	97	113	[147+	57]				711	13 … 18

Table 2.

Previous reconstructions for Reginamide A [16], Etamycin 878 [19], Dianthins [20, 21] and Tyrocdines [17]. For Etamycin 878, Reginamide A and Dianthins B and C the sequences are determined by NMR, while for Dianthis D–F the sequence ois determined by ESI-MS2. Orn stands for amino acid Ornithine. Hyp stands for HydroxyProline. Phg stands for Phenylglycine.

Peptide/Compound	NMR reconstruction
Reginamide A	71 (Ala)	113 (Ile)	113 (Ile)	128 (Lys)	113 (Ile)	147 (Phe)	113 (Leu)	113 (Ile)
Tyrocidine A	99 (Val)	114 (Orn)	113 (Lue)	147 (Phe)	97 (Pro)	147 (Phe)	147 (Phe)	114 (Asn)	128 (Gln)	163 (Tyr)
Tyrocidine A1	99 (Val)	128 (Lys)	113 (Lue)	147 (Phe)	97 (Pro)	147 (Phe)	147 (Phe)	114 (Asn)	128 (Gln)	163 (Tyr)
Tyrocidine B	99 (Val)	114 (Orn)	113 (Lue)	147 (Phe)	97 (Pro)	186 (Trp)	147 (Phe)	114 (Asn)	128 (Gln)	163 (Tyr)
Tyrocidine B1	99 (Val)	128 (Lys)	113 (Lue)	147 (Phe)	97 (Pro)	186 (Trp)	147 (Phe)	114 (Asn)	128 (Gln)	163 (Tyr)
Tyrocidine C	99 (Val)	114 (Orn)	113 (Lue)	147 (Phe)	97 (Pro)	186 (Trp)	186 (Trp)	114 (Asn)	128 (Gln)	163 (Tyr)
Tyrocidine C1	99 (Val)	128 (Lys)	113 (Lue)	147 (Phe)	97 (Pro)	186 (Trp)	186 (Trp)	114 (Asn)	128 (Gln)	163 (Tyr)
Etamycin 878	71 (Ala)	141 (N,β-MeLeu)	(71 N-MeGly)	113 (Hyp)	113 (Leu)	222 (Thr+Hpca)	147 (N-MePhg)
Dianthin B	113 (Ile)	147 (Phe)	147 (Phe)	97 (Pro)	57 (Gly)	97 (Pro)
Dianthin C	57 (Gly)	97 (Pro)	147 (Phe)	163 (Tyr)	99 (Val)	113 (Ile)
Dianthin D	57 (Gly)	87 (Ser)	113 (Leu)	97 (Pro)	97 (Pro)	113 (Ile)	147 (Phe)
Dianthin E	57 (Gly)	97 (Pro)	113 (Ile)	87 (Ser)	147 (Phe)	99 (Val)
Dianthin F	57 (Gly)	97 (Pro)	147 (Phe)	99 (Val)	147 (Phe)

We are able to empirically compare the peptides reconstructed by nutistage MS with peptides reconstructed by single stage MS using published NMR reconstructions as the standard of truth. Multistage MS results typically resemble corrects peptides better the single-stage MS. We further completed this empirical analysis by estimating p-value and showing that the multistage approach performs better than MS² approach [16, 3] by estimating the p-values. Table 3 compares the results of the mutistage analysis with the results of the single stage (MS²) spectral analysis². We use the shorthands Score = CyclicTSMScore(Peptide, S_r), MultiScore = TITMScore(Peptide, IonTree). p_e is the emprical p-value of score of correct peptide among 10⁶randomly generated valid tags with length and parent mass equal (up to error tolerance) to Peptide. Table 3 compares empirical p-values of single-stage and multistage scores for peptides with available reconstructions. Lower p-values for multistage score means multistage score outperforms single-stage score. Since the number of randomly generated tags is limited to 10⁶, many empirical p-values are zero, making it difficult to reliably compare single stage scores with multi-stage scores.

Table 3.

Comparison of scores of Single Stage and Multi Stage spectra. MultiScore refers to multistage score, while Score refers to single stage score. Empirical p-value of multistage scoring is lower than single scoring, which shows multistage scoring is better for sequencing of cyclic peptides. For some of the peptides empirical p-value is zeros for both both scores, and we are unable to compare the p-values. Instead we use Marcov chain based p-value, p_m.

Compound	Single Stage (M S2)			Multistage (M S2, M S3 and M S4)
	Score	Pe	Pm	MultiScore	Pe	Pm
Reginamide A	22	2.0 × 10−6	2.9 × 10−8	178	0	0
Tyrocidine A	30	0	1.5 × 10−8	45	0	8.0 × 10−14
Tyrocidine A1	30	0	1.6 × 10−9	42	0	1.4 × 10−13
Tyrocidine B	28	0	4.1 × 10−10	50	0	2.4 × 10−13
Tyrocidine B1	27	0	1.5 × 10−9	27	0	1.4 × 10−13
Tyrocidine C	27	0	1.7 × 10−9	26	0	1.5 × 10−9
Tyrocidine C1	32	0	3.5 × 10−13	25	0	1.5 × 10−12
Etamycin 878	22	0	6.4 × 10−8	64	0	4.6 × 10−9
Dianthin F	11	2.3 × 10−4	2.6 × 10−4	17	4.0 × 10−6	9.0 × 10−7
Dianthin E	9	0.054	0.058	6	2.4 × 10−3	2.3 × 10−3
Dianthin B	5	0.43	0.43	9	2.4 × 10−3	1.4 × 10−4
Dianthin C	14	5.3 × 10−5	4.8 × 10−5	39	0	6.2 × 10−9
Dianthin D	20	1.0 × 10−6	1.0 × 10−6	40	0	3.3 × 10−9

The difficulty with estimating empirical p-values is caused by the fast decrease of p-value with score increase, forcing us to analyze an impractically large number of tags to accurately estimate small p-values. Indeed, even sampling a billion tags does not allow one to accurately estimate p-values below 10⁻. A better approach would be to sample only high-scoring tags (rather than all tags), resulting in a better estimation of the tail of the probability distribution of scores. Below we describe such an approach.

We start with a set of 1000 randomly generated tags, and a score threshold (initial score threshold is zero). In each iteration, we delete all tags with score below the threshold and further mutate the remaining tags. A random mutation of a tag (m₁ …,m_i,m_i+1, …,m_k) results in a tag (m₁ …,m_i +δ,m_i+1 −δ…,m_k), where i and δ are chosen at random. We call the former tag the mother tag, and the latter tag the daughter tag. By gradually increasing the score threshold, the tags in the set evolve to have higher scores and maintain the probability distribution characteristic for high-scoring tags.

To estimate the probability distribution of scores (and eventually compute p-values), we keep track of the transitions between various scores in the course of mutation and construct a Markov chain on the set of scores. Whenever a mutation happens, we keep track of the transition from the score of the mother tag to the score of the daughter tag. We use the fraction of such transitions to estimate the transition probability for each pair of scores in the Markov chain. The probability distribution of scores (needed for computing p-values) can be estimated as the equilibrium distribution of this Markov chain [25]. We denote the p-value estimated by this approach as p_m. In addition to the empirical probability p_e (that can only be estimated for relatively high p-values), Table 3 also provides values of p_m (that can be estimated for both high and low p-values).

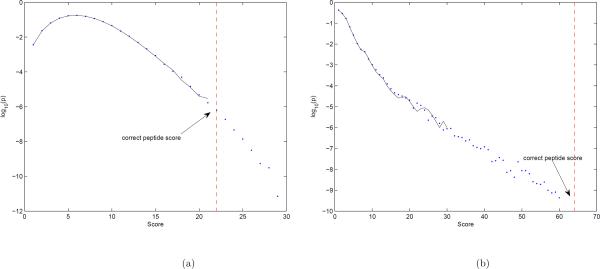
To evaluate the accuracy of the Markov chain approach to computing p-values, we compared the estimated probability distributions of scores of tags against Etamycin 898 spectra with two approaches: (i) using a million randomly generated peptides (for p_e estimation), and (ii) using the Markov chain estimator (for p_m estimation). Figure 2 demonstrates that these approaches produce similar results for probabilities higher than 10⁻⁶.

Text S1 describes how to combine information from all high scoring tags to generate a spectral profiles, and Figure S1 shows a comparison of MS2 and MS4 results using spectral profiles. Text S2 shows a more comprehensive comparison of single-stage and multi-stage sequencing on synthetic data.

Our analysis showed that the branch and bound approach can successfully sequence four cyclic peptide families. The correct sequences were ranked high, but often not the highest one. However, this is a very challenging problem: even for linear peptides de novo peptide sequencing remains inaccurate. On top of that, large mass spectrometry data for cyclic peptides are unavailable for the training required for the development of the cyclic peptide sequencing algorithms. Nevertheless, even partially accurate de novo reconstructions help researchers to probe the diversity of cyclic peptides produced by various organisms.

4 Discussion

Sequencing cyclic peptides adds two fundamental difficulties to the already challenging task of de novo peptide sequencing: the amino acid masses are not known in advance and the peptides are cyclic rather than linear. Current de novo sequencing algorithms do not adequately address these difficulties. Using multistage mass spectrometry leads to multiple lower-quality spectra from shorter subpeptides that need to be integrated to reveal the sequence of the cyclic peptide. Although the theoretical problem of an interpretation of a multistage spectrum is difficult, we have shown that a tag-based approach works well in practice.

De novo sequencing of cyclic peptides results in arguably the most difficult spectral interpretation problem in mass spectrometry. As a result, papers reporting new cyclic peptides typically discuss a single cyclic peptide per paper. In contrast, this paper is an attempt to analyze a large set of cyclic peptides in a single study: six tyrocidines, ten reginamides, eleven dianthins, and four etamycins. All the six tyrocidines discussed here have been well characterized. Among ten reginamides, only Reginamide A has been validated by NMR (due to insufficient quantities of purified materials for other reginamides). For dianthins, Dianthin D has been validated by NMR, and masses of Dianthins B, C, E and F have been previously reported. The other six dianthins have novel parent masses, not reported in the literature. Among the four Etamycins, only Etamycin 878 has been NMR validated. The tags generated by multistage sequencing are consistent with NMR sequences (in the cases the NMR experiments have been done). The sequence given by NMR is usually ranked high in our multistage sequencing.

The aim of this paper is to demonstrate that multistage sequencing is a promising new application for cycopeptide sequencing. While the initial analysis is promising, the lack of large multistage datasets for cyclopeptides is a great deficiency. thus an important aim of this paper is to encourage natural product researchers to generate such datasets.

As has been the case with de novo sequencing of linear peptides, large MS samples can be used to derive elaborate statistical models. Since cyclic peptides are implicated in many biologically important processes (see [26, 27] for the role of cyclic peptides in chemical defense and communication), the time has come to generate large datasets of annotated spectra of cyclic peptides.

Figure 3.

(a) Estimating the probability distribution of score of Etamycin 878 (single-stage MS). Solid line shows distribution of scores of randomly generated 10⁶ peptides, and the dots show the estimates based on the Markov chain approach. (b) Similar results for the multi stage score. In each case, the score of correct peptide is also shown. The gure shows the p-values given by markov chain approach are similar to empirical p-values. Moreover, the p-value of correct peptide scorein multistage case is lower than p-value of score of the same peptide in single-stage case.