Abstract
The tissue contrast of a magnetic resonance (MR) neuroimaging data set has a major impact on image analysis tasks like registration and segmentation. It has been one of the core challenges of medical imaging to guarantee the consistency of these tasks regardless of the contrasts of the MR data. Inconsistencies in image analysis are attributable in part to variations in tissue contrast, which in turn arise from operator variations during image acquisition as well as software and hardware differences in the MR scanners. It is also a common problem that images with a desired tissue contrast are completely missing in a given data set for reasons of cost, acquisition time, forgetfulness, or patient comfort. Absence of this data can hamper the detailed, automatic analysis of some or all data sets in a scientific study. A method to synthesize missing MR tissue contrasts from available acquired images using an atlas containing the desired contrast and a patch-based compressed sensing strategy is described. An important application of this general approach is to synthesize a particular tissue contrast from multiple studies using a single atlas, thereby normalizing all data sets into a common intensity space. Experiments on real data, obtained using different scanners and pulse sequences, show improvement in segmentation consistency, which could be extremely valuable in the pooling of multi-site multi-scanner neuroimaging studies.
Keywords: compressed sensing, magnetic resonance imaging (MRI), image synthesis, phantom, standardization, segmentation, intensity normalization, histogram matching, histogram equalization
1 Introduction
Magnetic resonance (MR) imaging (MRI) is a noninvasive imaging modality that is the gold standard for imaging the brain. MR image processing, particularly segmentation of brain structures, has been used to further the understanding of normal aging or the progression of diseases such as multiple sclerosis, Alzheimer’s disease, and schizophrenia. Large multi-site and multi-center studies are often used to gather more data across a broader population or to carry out follow-up imaging in longitudinal studies [12,16]. Because the intensities in conventional MR images do not have specific numerical units (unlike those in computed tomography (CT) images), there is a major concern about the consistency of quantitative results obtained in these studies due to the different pulse sequences [5] and scanners [11] that are used. In fact, because the intensity scale and the tissue contrast are dependent on the MR acquisition pulse sequence as well as the underlying T1, T2, , PD values in the tissue (cf. Fig. 1), any image processing task that is carried out on these data cannot normally be expected to behave quite the same across subjects. In this work, we focus on the consistency of image processing tasks—particularly on the task of image segmentation—using conventionally acquired MR data.
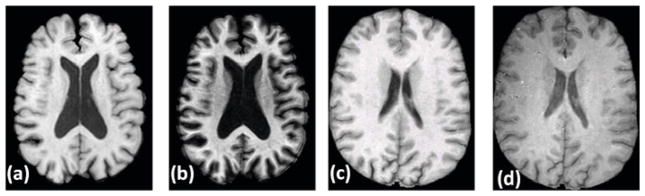
Fig. 1.
Data acquired under different pulse sequences or different scanners: (a) An acquisition of a Spoiled Gradient Recalled (SPGR) sequence in GE 3T scanner [16], (b) same subject with Magnetization Prepared Rapid Gradient Echo (MPRAGE) sequence in GE 3T scanner, (c) another subject [12], SPGR, GE 1.5T scanner, (d) same subject with MPRAGE sequence in a Siemens 3.0T scanner. Evidently, tissue contrast is dependent on the choice of pulse sequences, as well as on the choice of scanner. The contrast is intrinsically dependent on the choice of MR acquisition parameters, like flip angle, repetition time, echo time etc.
Numerous methods have been proposed to find the segmentation of cortical and sub-cortical structures of the human brain. Some of these methods assume a statistical model [17] for the probability distribution function (pdf) of the image intensity and generate a segmentation rule based on a maximum likelihood (ML) estimation [8] or maximum a-priori (MAP) estimation of the pdf parameters. Another popular class of segmentation method is based on Fuzzy C-Means (FCM) [2] and its modifications [1]. But all of these methods are intrinsically dependent on the tissue contrast of the image, which is dependent on the acquisition parameters. Accordingly, the same data acquired under different pulse sequences or different scanners, having different contrasts, yielding inconsistent segmentations [5].
One way of reducing the segmentation inconsistency is intensity normalization. Some popular ways to do this are histogram equalization or histogram matching by non-rigid registration [15], intensity scaling based on landmarks [18], intensity correction by a global piecewise linear [19] or a polynomial mapping [14]. A common problem with these methods is that the histogram matching is never perfect with discrete valued images. Also landmark based methods are mostly initialized by manually chosen landmarks, which are time consuming to create and lack robustness. Another way to normalize involves the use of the peak intensities of white matter (WM) or gray matter (GM) [4] to match the image histogram to a target histogram by information theoretic methods [25]. Histograms of the segmented sub-cortical structures can also be matched to the individual histograms of the sub-cortical structures of a registered atlas [13]. It has been shown to produce consistent sub-cortical segmentation over datasets acquired under different scanners. In spite of their efficiency, all these methods are intrinsically dependent on the accuracy of the underlying segmentation of the image and the atlas-to-subject registration method. Another group of techniques have been proposed to include the MR acquisition physics into the segmentation methodology [21,11] to normalize all intensity images by their underlying T1, T2, and PD values. They suffer from the fact that many images are to be acquired with precise acquisition parameters, which is often not possible in large scale studies.
In this paper, we propose an MR image example-based contrast synthesis (MIMECS) method, that addresses the problem of intensity standardization over pulse sequences or scanners. We build upon the concepts of compressed sensing [3,9] to develop a patch matching approach, that uses patches from an atlas to synthesize different MR contrast images for a given subject. The primary purpose of MIMECS synthesis—and therefore the application for evaluation of its efficacy—is consistent segmentation across pulse sequences and scanners.
There are a few key differences with previous methods of intensity normalizations [19,18,25,4,13,11,21]. MIMECS is a pre-processing step to the segmentation. It neither needs to estimate T1, T2, PD values, nor does it need the intrinsic MR acquisition parameters, like echo time (TE) or repetition time (TR). It also does not need landmarks or any atlas-to-subject registration, thus being fully automatic and independent of the choice of registration methods used in any subsequent processing. We use it to normalize a dataset which is acquired under different pulse sequences and on different scanners [12], thus having diverse contrasts. On this dataset, we show that MIMECS can normalize all the images to a particular contrast, that produce more consistent cortical segmentations compared to their original contrasts.
The paper is organized as follows. First, we briefly summarize compressed sensing in Sec 2.1. Then we describe the imaging model in Sec. 3.1 and the contrast synthesis algorithm is explained in Sec. 3.3. A validation study with phantoms is described in Sec. 4.1. Then, we use MIMECS to simulate alternate pulse sequences and show its applicability as an intensity normalization and histogram matching process on a set of multi-site and multi-scanner data in Sec. 4.2.
2 Background
2.1 Compressed Sensing
We use the idea of compressed sensing in our MIMECS approach. Compressed sensing exactly recovers sparse vectors from their projections onto a set of random vectors [9,3] that need not form a basis. The idea behind compressed sensing comes from the fact that most of the signals that we observe are usually sparse, thus it is better not to observe the full signal, but a part of it, and reconstruct the whole signal from those small number of measurements.
Suppose we want to reconstruct a signal x ∈ ℝn which is s-sparse, i.e. has at most s non-zero elements. We want to observe another vector y ∈ ℝd, s < d < n, such that each element of y can be obtained by an inner product of x and another vector from ℝn. Then, compressed sensing can be used to reconstruct x ∈ ℝn exactly from y ℝd, with y = Φx, d < n, x being s-sparse, Φ ∈ ℝd×n. Thus, compressed sensing is also a way to reduce the dimension of the observed sparse data in a lossless way.
One approach for finding x is to solve
| (1) |
where ε1 is the noise in the measurement and || · ||0 indicates the number of non-zero elements in the vector. Although this approach provides some simple conditions on Φ [10], it is an NP-hard problem. Another approach is to solve
| (2) |
where ||x||1 is the L1 norm of a vector. This is a convex problem and can be transformed into a linear program that can be solved in polynomial time. If ε2 is unknown, Eqn. 2 can be written in the following form,
| (3) |
where λ is a weighing factor. The sparsity on x̂ increases as λ increases.
It has been shown that if Φ follows the global restricted isometry property (RIP) [3], then the solutions to Eqn. 1 and Eqn. 2 are identical and the optimal solution can be obtained by an L1 minimization problem using Eqn. 3. This result is interesting because it has been shown that random subsets of incoherent matrices satisfy the RIP [24]. Thus, to reconstruct x, it is possible to observe its projections onto a set of previously chosen incoherent vectors. We use this idea to find a sparse vector for each patch and then use that sparse vector as an index into the atlas.
3 Method
3.1 Imaging Model
Consider two MR images Y1 and Y2 of the same person, acquired at the same time, but having two different MR contrasts, C1 and C2, labeled as 1 and 2. E.g. Y1 and Y2 can be either T1-w, T2-w or PD-w images. They could be either 2D slices or 3D volumes. The imaging equations can be written as,
| (4) |
| (5) |
where Θ1 and Θ2 are the intrinsic imaging parameters, like TR, TE, flip angle etc for that particular acquisition,
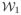 and
and
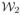 are imaging equations [7] corresponding to the contrast or the pulse sequence used, η1 and η2 are random noise. T1, T2 and PD are relaxation times and the proton density maps of the tissues. They could be 2D or 3D maps, according to Y1 and Y2.
are imaging equations [7] corresponding to the contrast or the pulse sequence used, η1 and η2 are random noise. T1, T2 and PD are relaxation times and the proton density maps of the tissues. They could be 2D or 3D maps, according to Y1 and Y2.
Ideally, if a number of C1 contrast images of the subject is acquired, with the Θ’s known for all the acquisitions, then an estimate of the underlying T1, T2 and PD maps can be obtained by either directly inverting
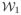 in Eqn. 4 [11] or by a least square estimate [21]. Then Y2 can directly be synthesized using Θ2 and the estimates of T1, T2 and PD ’s using Eqn. 5.
in Eqn. 4 [11] or by a least square estimate [21]. Then Y2 can directly be synthesized using Θ2 and the estimates of T1, T2 and PD ’s using Eqn. 5.
There are several drawbacks for this strategy. Θ1 and Θ2 are often not known,
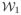 and
and
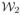 are difficult to model accurately or multiple acquisitions are not taken. Therefore, it is almost impossible to reconstruct Y2 from Y1 using the straight-forward approach. We will try to synthesize Y2 from Y1 using an atlas.
are difficult to model accurately or multiple acquisitions are not taken. Therefore, it is almost impossible to reconstruct Y2 from Y1 using the straight-forward approach. We will try to synthesize Y2 from Y1 using an atlas.
3.2 Atlas Description
Define an atlas
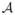 as a pair of images,
as a pair of images,
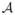 = {φ1, φ2}, where φ1 and φ2 are C1 and C2 contrasts of the same subject having the same resolution. We assume that φ1 and φ2 are co-registered. Also assume that φ1 and φ2 are made of p × q × r 3D patches. For convenience, we assume that each of the 3D patches is stacked into a 1D vector of size d × 1, d = p × q × r. The patches are then denoted by d ×1 vectors φ1(i) and φ2(i), i ∈ Ωφ. Ωφ is the image domain of both φ1 and φ2, as they are co-registered. Then we define the C1 and C2 contrast dictionaries Φ1 and Φ2 ∈ ℝd×N, where the columns of Φ1 and Φ2 are patches φ1(i) and φ2(i), i ∈ Ωφ from the atlas and N = |Ωφ| is the number of patches from
= {φ1, φ2}, where φ1 and φ2 are C1 and C2 contrasts of the same subject having the same resolution. We assume that φ1 and φ2 are co-registered. Also assume that φ1 and φ2 are made of p × q × r 3D patches. For convenience, we assume that each of the 3D patches is stacked into a 1D vector of size d × 1, d = p × q × r. The patches are then denoted by d ×1 vectors φ1(i) and φ2(i), i ∈ Ωφ. Ωφ is the image domain of both φ1 and φ2, as they are co-registered. Then we define the C1 and C2 contrast dictionaries Φ1 and Φ2 ∈ ℝd×N, where the columns of Φ1 and Φ2 are patches φ1(i) and φ2(i), i ∈ Ωφ from the atlas and N = |Ωφ| is the number of patches from
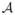 . Clearly, a column of Φ1 corresponds to the same column in Φ2.
. Clearly, a column of Φ1 corresponds to the same column in Φ2.
3.3 Contrast Synthesis
Now, given a subject image Y1 of contrast C1, we want to generate its C2 contrast using Φ’s. Y1 is first decomposed into d × 1 patches y1(j), j ∈ ΩY, ΩY is the input image domain. The primary idea of MIMECS is that each subject patch y1(j) can be matched to one or more patches from the dictionary Φ1, because they are of the same C1 contrast. The matching patches have their own C2 contrast counterparts in Φ2, which are then used to synthesize the C2 contrast version of y1(j). As a result, the need of any atlas to subject registration is eliminated. This idea of patch matching can be explained efficiently using the idea of sparse priors [26] in a compressed sensing paradigm.
From Eqn. 4 and Eqn. 5, if
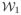 and
and
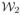 are linear operators of
, then a pseudo-inverse on Eqn. 4 will provide Y2 from Y1. Ignoring noise, the reconstruction of Y2 can be written as,
are linear operators of
, then a pseudo-inverse on Eqn. 4 will provide Y2 from Y1. Ignoring noise, the reconstruction of Y2 can be written as,
| (6) |
This inverse problem is ill-posed because G is almost always never known. The problem is regularized by assuming that any patch y1(j) can be found from a rich and over-complete dictionary Φ1, having the same contrast as y1(j), by
| (7) |
|| · ||0 is the L0 norm, denoting number of non-zero elements in a vector. Intuitively, the sparsest representation x1(j) denotes an index of Φ1, such that y1(j) is matched to a particular column of Φ1. This regularized problem is written in a compressed sensing paradigm following Eqn. 3,
| (8) |
where λ is a weighing factor, as defined in Eqn. 3. A positivity constraint on the sparse representation x1(j) is enforced to impose a valid anatomical meaning on the elements of x1(j), such that an element of x1(j) denotes a positive weight of how much a column of Φ1 contributes in reconstructing y1(j). This positivity constraint was previously explored in Lasso [23].
With the sparse representation of y1(j), we simply reconstruct the C2 contrast patch as,
| (9) |
Then the C2 contrast image Y2 is reconstructed by combining all the ŷ2(j)’s thus obtained.
3.4 Contrast Synthesis with Modified Dictionary
Typically for a 256 × 256 × 198 image volume, number of example patches N ≈ 100, 0000. It is computationally very intensive to work with Φ1 that is of the order of 27×100, 0000. To reduce the computation overhead, we use a dictionary selection procedure that uses an approximate segmentation of the input image. The rationale can be seen from the fact that if a patch y1(j) is known to come from a certain tissue type, e.g., pure white matter (WM), the computation of Eqn. 8 can be reduced by choosing a subset of Φ1 that contains only pure WM patches.
We break down Φ1, as well as Φ2, into several sub-dictionaries of separate tissue classes, which are obtained from a topology preserving anatomy driven segmentation, called TOADS [1]. The atlas φ1 is segmented into 6 tissue classes, namely cerebro-spinal fluid (CSF), ventricles, gray matter (GM), white matter (WM), basal ganglia and thalamus, labeled l ∈ L = {1, …, 6}, respectively. The segmentation of φ1, denoted as Sφ, is similarly decomposed into patches sφ(i), i ∈ Ωφ. The sub-dictionaries and for each tissue class l are generated as,
| (10) |
Fig. 2(a)–(c) show atlas SPGR and MPRAGE contrasts (φ1 and φ2) and their segmentation (Sφ).
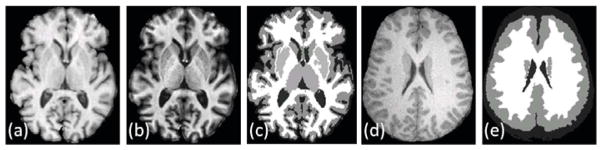
Fig. 2.
Modified dictionary using segmentation: (a) An example SPGR T1-w contrast atlas image φ1 [16] from a GE 3T scanner, (b) its MPRAGE T1-w contrast φ2, (c) their TOADS [1] segmentation Sφ, used to generate the sub-dictionaries and according to Eqn. 10, (d) An SPGR T1-w subject image Y1 [12], (b) an approximate hard segmentation SY (obtained from TOADS), used to choose a reduced sub-dictionary
In our experiments, typically, for a 256 × 256 × 198 image. With the smaller atlas sub-dictionaries, we modify Eqn. 8 so as to reduce the search space for y1(j)’s. An approximate segmentation of Y1, denoted as SY, is computed using one iteration of TOADS (e.g., Fig.2(d)–(e)). SY is again decomposed into patches sY (j), j ∈ ΩY, so that the information about the tissue classes for y1(j) is obtained from sY (j). Now, the contrast synthesis algorithm described in Eqn. 8–9 is modified with the inclusion of the sub-dictionaries,
Divide the atlases φ1, φ2 and the segmentation Sφ into d × 1 patches, and generate the sub-dictionaries and according to Eqn. 10.
Find an approximate segmentation of the input C1 contrastY1 as SY. Divide the Y1 and SY into d × 1 patches y1(j)’s and sY (j)’s, j ∈ ΩY.
For each j, find all the tissue classes ℓ that sY (j) contains, ℓ ∈ L.
For each j, generate patch specific dictionaries Φ1(j) by concatenating all ’s and Φ2(j) by concatenating ’s , ℓ ∈ L. Thus Φ1(j) contains all the potential classes that y1(j) could belong to, according to its atlas based approximate segmentation. Clearly, Φ1(j), Φ2(j) ∈ ℝd×Nj with Nj ≪ N. At this point, if Φ1(j) becomes too large, we randomly choose a d × N0 random subset of Φ1(j) and the corresponding subset of Φ2(j) for further analysis to minimize computational overhead, N0 < Nj.
Solve Eqn. 8 with y1(j) and Φ1(j) to get x1(j).
Solve Eqn. 9 with Φ2(j) and x1(j) thus obtained.
Repeat for every j ∈ ΩY.
4 Results
4.1 Estimation of λ
We use 3 × 3 × 3 patches in all our experiments. All the images are normalized so that their peak WM intensities are unity. The optimal value of λ is obtained using a cross-validation study on the Brainweb phantoms [6] following the idea of homotopy methods [20]. We use the atlas C1 contrast as a T1-w (φ1) and C2 as a T2-w (φ2) phantom having 0% noise, shown in Fig. 3(a)–(b). Now, using these two phantoms as atlas, we use the same φ1 phantom as the test image Y1 and try to reconstruct its T2-w contrast Ŷ2, while the true T2-w contrast is already known as φ2 = Y2. The optimal λ is obtained by,
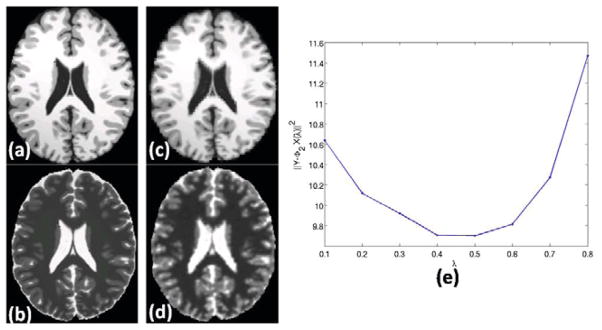
Fig. 3.
Optimal λ: (a) A T1-w Brainweb phantom φ1 [6], (b) original T2-w version φ2, they are used as atlas. (c) Reconstructed T1-w image Φ1X(λ̂), from Eqn. 11, (d) Reconstructed T2-w image (Ŷ2 = Φ2X(λ̂)) using Y1 = φ1, (e) plot of λ vs. the reconstruction error .
| (11) |
while Φ1 and Φ2 are obtained from φ1 and φ2 as defined earlier. λ is varied from [0.1, 0.8] and the optimal λ = 0.5 from Fig. 3(d). Using this λ, we generate a T2 contrast of the phantom shown in Fig. 3(c). Ideally, if we are to use all the patches from Φ1 instead of creating sub-dictionary , λ̂ ≈ 0. However, the use of a reduced sized dictionary gives improvement in computational efficiency with a sub-optimal performance, as seen from the reconstructed image (Fig. 3(c)). We use this lambda for all the subsequent experiments.
4.2 Experiment on BIRN Data
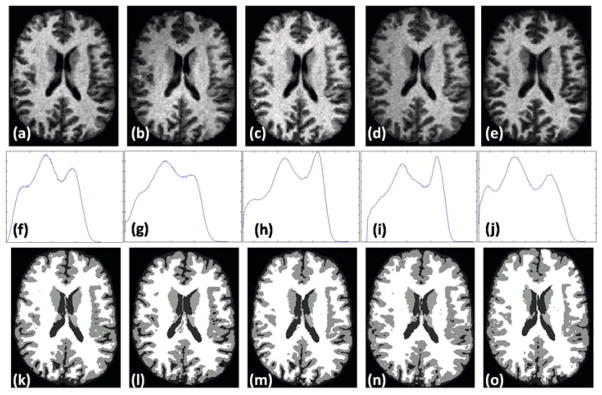
There has been concerns over consistency of the segmentations arising from scanner variability. To show that synthetic contrasts can produce consistent segmentations, we use the “traveling subject” data [12] that consists of scans of the same person under different pulse sequences and different scanners. These data were downloaded from the BIRN data repository, project accession number 2007-BDR-6UHZ1. We use the scans of 3 subjects, each consisting of one SPGR acquisitions from 1.5T GE, 4T GE, 1.5T Philips and 3T Siemens scanners each and one MPRAGE acquisition from a 1.5T Siemens scanner, each of them having 0.86 × 0.86 × 1.2 mm resolution. One of the subjects is shown in Fig. 4(a)–(e). Their histograms are quite different (cf. Fig. 4(f)–(j)), and the Kullback-Leibler distance (KL distance) between each pair of the normalized histograms (Table 1) affirms this fact. This difference in histograms affect the consistency in the segmentations, shown in Fig. 4(k)–(o).
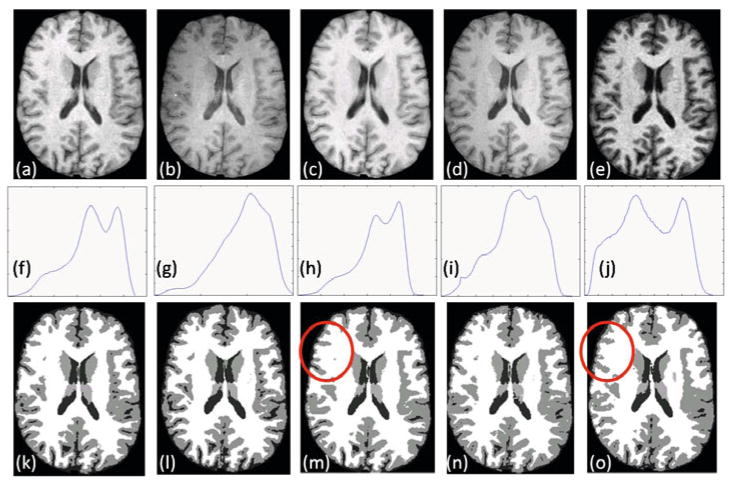
Fig. 4.
BIRN data: T1-w SPGR contrasts from (a) GE 1.5T, (b) GE 4T, (c) Philips 1.5T, (d) Siemens 3T scanner, (e) T1-w MPRAGE contrast from Siemens 1.5T. Their histograms are shown in (f)–(j) and the hard segmentations [1] are shown in (k)–(o). The histograms are quite different which is reflected on the difference in the segmentations.
Table 1.
KL distances between original/synthesized image histograms for images acquired under 5 different scanners, averaged over 3 subjects
| GE 1.5T | GE 4T | Philips 1.5T | Siemens 3T | Siemens 1.5T | |
|---|---|---|---|---|---|
| GE 1.5T | · | 0.28/0.04 | 0.39/0.06 | 0.30/0.02 | 0.49/0.03 |
| GE 4T | 0.72/0.04 | · | 1.22/0.02 | 0.11/0.06 | 0.91/0.07 |
| Philips 1.5T | 0.48/0.05 | 0.85/0.23 | · | 0.88/0.04 | 0.07/0.07 |
| Siemens 3T | 0.53/0.01 | 0.07/0.04 | 0.98/0.03 | · | 0.88/0.06 |
| Siemens 1.5T | 0.62/0.03 | 1.01/0.06 | 0.05/0.01 | 1.04/0.08 | · |
With the aim of having consistent segmentation of these images, we want to normalize the intensities of all the images to a particular target contrast. The purpose of choosing MPRAGE as the target C2 contrast is to have better delineation of cortical structures, because the GM-WM contrast is very poor on SPGR acquisitions. We use a GE 3T T1-w SPGR and its MPRAGE acquisitions from the BLSA study [16] as atlas φ1 and φ2, shown in Fig. 2(a)–(b). The synthesized images are shown in Fig. 5(a)–(e). It is seen from the images that they have more similar contrasts than the original images, and this is visually confirmed by the histograms in Fig. 5(f)–(j). Also, Table 1 shows that the the histograms of the synthetic MPRAGEs are more similar, having the KL distances being an order of magnitude less.
Fig. 5.
Synthesizing MPRAGE contrast from BIRN data: Synthetic MPRAGE contrasts of the data shown in Fig. 4(a)–(e) using the atlas shown in Fig. 2(a)–(c). The histograms of the synthetic MPRAGEs are shown in (f)–(j) and the hard segmentations [1] are shown in (k)–(o).
To show the improvement in segmentation consistency, we compare our method with a registration based approach, where we deformably register the SPGR atlas φ1 to the SPGR input image Y1 by ABA [22] and use that transformation on φ2 to generate the Ŷ2. Then the segmentation is performed on the registered images. If Y1 is MPRAGE (e.g. in Siemens 1.5T scanner), φ2 is simply registered to Y1 to get Ŷ2. The Dice coefficients for the original, registered and transformed images and the synthetic images are shown in Table 2. Original images usually show poor consistency, especially between SPGR and MPRAGE acquisitions, which was already reported in literature [5]. Table 2 also shows that the Dice between SPGR and MPRAGE sequences is improved between the synthetic MPRAGE versions of the images compared to their original scans.
Table 2.
Consistency comparison: Segmentation consistency is measured on original 4 SPGR and 1 MPRAGE scans, their MPRAGE registered and transformed versions (described in Sec. 4.2) and synthesized MPRAGEs. Mean Dice coefficients, averaged over CSF, GM and WM, are reported between the segmentations of (original, registered, synthetic) images acquired under 5 different scanners/pulse sequences (GE 1.5T SPGR, GE 4T SPGR, Philips 1.5T SPGR, Siemens 3T SPGR and Siemens 1.5T MPRAGE) averaged over 3 subjects.
| GE 1.5T | GE 4T | Philips 1.5T | Siemens 3T | Siemens 1.5T | |
|---|---|---|---|---|---|
| GE 1.5T | · | 0.81, 0.78, 0.84 | 0.77, 0.83, 0.85 | 0.86, 0.87, 0.89 | 0.82, 0.80, 0.87 |
| GE 4T | · | · | 0.70, 0.71, 0.79 | 0.79, 0.77, 0.84 | 0.76, 0.77, 0.82 |
| Philips 1.5T | · | · | · | 0.78, 0.83, 0.84 | 0.74, 0.75, 0.84 |
| Siemens 3T | · | · | · | · | 0.78, 0.81, 0.85 |
5 Conclusion
We have developed a compressed sensing based method, called MIMECS, that uses multiple contrast atlases to generate multiple contrasts of MR images. It is a patch-based method, where a patch in the subject C1 contrast image is matched to an atlas to generate a corresponding C2 contrast patch. An application of MIMECS is to normalize intensities between MR images taken from different scanners and different pulse sequences to generate synthetic images, while the synthetic images produce more consistent segmentation. In all our experiments, we have used only one pair of images as atlas to generate patch dictionaries. Also we have not particularly taken into account the topology of the structures. Our future work includes inclusion of features like topology and labels as a matching criteria, instead of only using intensities. Also we would like to explore the possibility of including more atlases and more contrasts.
Acknowledgments
Some data used for this study were downloaded from the Biomedical Informatics Research Network (BIRN) Data Repository (http://fbirnbdr.nbirn.net:8080/BDR/), supported by grants to the BIRN Coordinating Center (U24-RR019701), Function BIRN (U24-RR021992), Morphometry BIRN (U24-RR021382), and Mouse BIRN (U24- RR021760) Testbeds funded by the National Center for Research Resources at the National Institutes of Health, U.S.A.
This research was supported in part by the Intramural Research Program of the NIH, National Institute on Aging. We are grateful to Dr. Susan Resnick for providing the data and all the participants of the Baltimore Longitudinal Study on Aging (BLSA), as well as the neuroimaging staff for their dedication to these studies.
Contributor Information
Snehashis Roy, Email: snehashisr@jhu.edu.
Aaron Carass, Email: aaron_carass@jhu.edu.
Jerry Prince, Email: prince@jhu.edu.
References
- 1.Bazin PL, Pham DL. Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans on Medical Imaging. 2007;26(4):487–496. doi: 10.1109/TMI.2007.893283. [DOI] [PubMed] [Google Scholar]
- 2.Bezdek JC. A Convergence Theorem for the Fuzzy ISO-DATA Clustering Algorithms. IEEE Trans on Pattern Anal Machine Intell. 1980;20(1):1–8. doi: 10.1109/tpami.1980.4766964. [DOI] [PubMed] [Google Scholar]
- 3.Candes EJ, Romberg JK, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Comm on Pure and Appl Math. 2006;59(8):1207–1223. [Google Scholar]
- 4.Christensen JD. Normalization of brain magnetic resonance images using histogram even-order derivative analysis. Mag Res Imaging. 2003;21(7):817–820. doi: 10.1016/s0730-725x(03)00102-4. [DOI] [PubMed] [Google Scholar]
- 5.Clark KA, Woods RP, Rottenber DA, Toga AW, Mazziotta JC. Impact of acquisition protocols and processing streams on tissue segmentation of T1 weighted MR images. NeuroImage. 2006;29(1):185–202. doi: 10.1016/j.neuroimage.2005.07.035. [DOI] [PubMed] [Google Scholar]
- 6.Cocosco CA, Kollokian V, Kwan RKS, Evans AC. BrainWeb: Online Interface to a 3D MRI Simulated Brain Database. NeuroImage. 1997;5(4):S425. http://www.bic.mni.mcgill.ca/brainweb/ [Google Scholar]
- 7.Deichmann R, Good CD, Josephs O, Ashburner J, Turner R. Optimization of 3-D MP-RAGE Sequences for Structural Brain Imaging. NeuroImage. 2000;12(3):112–127. doi: 10.1006/nimg.2000.0601. [DOI] [PubMed] [Google Scholar]
- 8.Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of Royal Stat Soc. 1977;39:1–38. [Google Scholar]
- 9.Donoho DL. Compressed sensing. IEEE Trans Inf Theory. 2006;52(4):1289–1306. [Google Scholar]
- 10.Elad M, Bruckstein AM. A Generalized Uncertainty Principle and Sparse Representation in Pairs of Bases. IEEE Trans Inf Theory. 2002;48(9):2558–2567. [Google Scholar]
- 11.Fischl B, Salat DH, van der Kouwe AJW, Makris N, Segonne F, Quinn BT, Dale AM. Sequence-independent segmentation of magnetic resonance images. NeuroImage. 2004;23(1):69–84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 12.Friedman L, Stern H, Brown GG, Mathalon DH, Turner J, Glover GH, Gollub RL, Lauriello J, Lim KO, Cannon T, Greve DN, Bockholt HJ, Belger A, Mueller B, Doty MJ, He J, Wells W, Smyth P, Pieper S, Kim S, Kubicki M, Vangel M, Potkin SG. Test-Retest and Between-Site Reliability in a Multicenter fMRI Study. Human Brain Mapping. 2008;29(8):958–972. doi: 10.1002/hbm.20440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Han X, Fischl B. Atlas Renormalization for Improved Brain MR Image Segmentation Across Scanner Platforms. IEEE Trans Med Imag. 2007;26(4):479–486. doi: 10.1109/TMI.2007.893282. [DOI] [PubMed] [Google Scholar]
- 14.He R, Datta S, Tao G, Narayana PA. Information measures-based intensity standardization of MRI. Intl Conf Engg in Med and Biology Soc. 2008 Aug;:2233–2236. doi: 10.1109/IEMBS.2008.4649640. [DOI] [PubMed] [Google Scholar]
- 15.Jager F, Nyul L, Frericks B, Wacker F, Hornegger J. Bildverarbeitung für die Medizin 2008 Informatik aktuell. ch 20. Springer; Heidelberg: 2007. Whole Body MRI Intensity Standardization. [Google Scholar]
- 16.Kawas C, Gary S, Brookmeyer R, Fozard J, Zonderman A. Age-specific incidence rates of Alzheimer’s disease: the Baltimore Longitudinal Study of Aging. Neurology. 2000;54(11):2072–2077. doi: 10.1212/wnl.54.11.2072. [DOI] [PubMed] [Google Scholar]
- 17.Leemput KV, Maes F, Vandermeulen D, Suetens P. Automated Model-Based Tnumber Classification of MR Images of the Brain. IEEE Trans on Med Imag. 1999;18(10):897–908. doi: 10.1109/42.811270. [DOI] [PubMed] [Google Scholar]
- 18.Madabhushi A, Udupa JK. New methods of MR image intensity standardization via generalized scale. Med Phys. 2006;33(9):3426–3434. doi: 10.1118/1.2335487. [DOI] [PubMed] [Google Scholar]
- 19.Nyul LG, Udupa JK. On Standardizing the MR Image Intensity Scale. Mag Res in Medicine. 1999;42(6):1072–1081. doi: 10.1002/(sici)1522-2594(199912)42:6<1072::aid-mrm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 20.Osborne MR, Presnell B, Turlach BA. A new approach to variable selection in least squares problems. IMA J Numerical Analysis. 2000;20(3):389–403. [Google Scholar]
- 21.Prince JL, Tan Q, Pham DL. Optimization of MR Pulse Sequences for Bayesian Image Segmentation. Medical Physics. 1995;22(10):1651–1656. doi: 10.1118/1.597425. [DOI] [PubMed] [Google Scholar]
- 22.Rohde GK, Aldroubi A, Dawant BM. The adaptive bases algorithm for intensity-based nonrigid image registration. IEEE Trans on Med Imag. 2003;22:1470–1479. doi: 10.1109/TMI.2003.819299. [DOI] [PubMed] [Google Scholar]
- 23.Tibshirani R. Regression Shrinkage and Selection via the Lasso. J Royal Stat Soc. 1996;58(1):267–288. [Google Scholar]
- 24.Tropp JA, Gilbert AC. Signal recovery from random measurements via orthogonal matching pursuit. IEEE Trans Inform Theory. 2007;53:4655–4666. [Google Scholar]
- 25.Weisenfeld NI, Warfield SK. Normalization of Joint Image-Intensity Statistics in MRI Using the Kullback-Leibler Divergence. Intl Symp on Biomed Imag (ISBI) 2004 Apr;1:101–104. [Google Scholar]
- 26.Yang J, Wright J, Huang T, Ma Y. Image Super-Resolution Via Sparse Representation. IEEE Trans Image Proc. 2010;19(11):2861–2873. doi: 10.1109/TIP.2010.2050625. [DOI] [PubMed] [Google Scholar]