Intrinsic energy landscapes of amino acid side chains

Abstract

Amino acid side chain conformational properties influence the overall structural and dynamic properties of proteins and, therefore, their biological functions. In this study, quantum mechanical (QM) potential energy surfaces for the rotation of side chain χ₁ and χ₂ torsions in dipeptides in the alphaR, beta and alphaL backbone conformations were calculated. The QM energy surfaces provide a broad view of the intrinsic conformational properties of each amino acid side chain. The extent to which intrinsic energetics dictates side-chain orientation was studied through comparisons of the QM energy surfaces with χ₁ and χ₂ free energy surfaces from probability distributions obtained from a survey of high resolution crystal structures. In general, the survey probability maxima are centered in minima in the QM surfaces as expected for sp³ (or sp² for χ₂ of Asn, Phe, Trp, and Tyr) atom centers with strong variations between amino acids occurring in the energies of the minima indicating intrinsic differences in rotamer preferences. High correlations between the QM and survey data were found for hydrophobic side chains except Met, suggesting minimal influence of the protein and solution environments on their conformational distributions. Conversely, low correlations for polar or charged side-chains indicate a dominant role of the environment in stabilizing conformations that are not intrinsically favored. Data also link the presence of off-rotamers in His and Trp to favorable interactions with the backbone. Results also suggest that the intrinsic energetics of the side-chains of Phe and Tyr may play important roles in protein folding and stability. Analyses on whether intrinsic side chain energetics can influence backbone preference identified a strong correlation for residues in the AlphaL backbone conformation. It is suggested that this correlation reflects the intrinsic instability of the AlphaL backbone such that assumption of this backbone conformation is facilitated by intrinsically favorable side-chain conformations. Together our results offer a broad overview of the conformational properties of amino acid side-chains and the QM data may be used as target data for force field optimization.

INTRODUCTION

The primary sequence of a protein largely dictates the ensemble of secondary, tertiary, and quaternary interactions, which work in concert with environmental factors to modulate a protein’s biological functions. Central to the role of the primary sequence in determining tertiary and quaternary structure are the properties of the amino acid side chains. As observed in the first globular proteins for which 3D structures were resolved, hemoglobin and myoglobin,^{1, 2} side-chain interactions between adjacent helices stabilize the helix-bundle topology and allows formation of the functional tetramer in hemoglobin.³ Accordingly, understanding the physical properties of side chains, including their conformational properties, is essential to understanding the relationship of structure and function in proteins.

The conformations of amino acid side chains are influenced by both their intrinsic conformational energies and by interactions with the surrounding environment. While conformations of side chains in folded structures can be determined using NMR and X-ray crystallography, quantification of the relative contributions of intrinsic vs. environmental factors to the observed conformations of amino acids using experimental methods alone is difficult. Alternatively, the intrinsic energetics may be investigated using computational methods, which include quantum mechanics (QM). QM data can be used to help investigate the energy landscape of side chains in the absence of environmental effects, allowing the intrinsic contributions to observed conformational preferences of side chains to be determined.

To date, a range of studies have used computational methods to investigate the conformational properties of amino acid side chains. Side chain conformations in bovine pancreatic trypsin inhibitor (BPTI) were extensively analyzed by Gelin & Karplus ⁴ using empirical potential energy calculations on model dipeptides more than three decades ago. Previous studies have linked intrinsic energies to occurrences of rotamers in protein structures.^{5, 6} Of particular interest was the study of Butterfoss and Hermans. In their work it was shown that the observed rotamer frequencies for Met and Lys correlate well with the estimated populations obtained by Boltzmann weighting of the torsion energies derived from QM calculation on the model compounds ethylmethyl sulfide and butane, respectively. However, the above studies involved calculations of the χ₁ and χ₂ dihedrals using empirical force field evaluations of dipeptides or QM calculations on model compounds that lack the peptide backbone. In the present study we extend those efforts by employing QM methods to provide a more accurate and complete picture of the relationship between intrinsic energetics and conformational properties of side chains in proteins.

In this work, backbone-dependent energy landscapes are calculated for the amino acid side-chain χ₁ and χ₂ dihedrals angles using QM methods on dipeptides. Performing the calculations on dipeptide representations of the amino acids yields profiles for the intrinsic conformational energies where only local interactions of the side-chain with the adjacent peptide bonds in the backbone can occur. The QM results are then compared with observed distributions for χ₁ and/or χ₂ obtained from a survey of the RCSB Protein Data Bank (PDB) ⁷ to determine the degree by which intrinsic energies contribute to the prevalence of side chain conformations in crystal structures. In addition, results from the presented QM calculations can serve as a set of reference data for the refinement of side-chain torsion parameters in empirical force fields.^{8, 9}

METHODS

QM Calculations

Molecular mechanics calculations were used to generate starting geometries for the χ₁/χ₂ 1- and 2-dimensional (2D) QM potential energy surface (PES) calculations. N-acetylated and N′-methylamidated dipeptides were first constructed with the program CHARMM ¹⁰ and optimized with the CHARMM22/CMAP force field ^{11, 12} with the following methodology. Backbone φ/ψ angles were restrained at the AlphaR (−60.0/−45.0), Beta (−120.0/120.0), or AlphaL (63.5/34.8) conformations. Initial geometries were generated with χ₁ restrained from 0 to 360° in 15° increments with χ₂ harmonically restrained at 180° with a force constant of 10⁴ kcal/mol/rad². In order to limit the dimensionality of the conformational space for the longer amino acids the remaining χ torsions were restrained to the following values based on a previous rotamer study ¹³: χ₃ = 0° for Gln, 180° for Glu, 67° for Met, χ_3,4 = 180° for Lys and χ_3,4,5 = 180° for Arg. A harmonic force constant of 10⁴ kcal/mol/rad was used in all cases. Each generated conformation was energy minimized for 500 steps of conjugate-gradient (CONJ) followed by 500 steps of adopted basis Newton-Raphson (ABNR), each with a convergence criteria of the gradient < 10⁻⁵ kcal/mol/Å. Coordinates of the optimized geometries were then used to initiate the QM χ₁, χ₂ scans.

QM PES calculations were performed starting with the geometries from the MM calculations. With Val 1D torsion scans were performed about χ₁ while 2D χ₁, χ₂ scans were performed for the remaining studied amino acids. 2D scans involved a series of 1D torsion scans for χ₂ with constrained φ, ψ and χ₁ kept at its initial on-grid values of 15° increments. χ_3, χ₄ and χ₅ were constrained to values listed above for the larger side chains. In the individual 1D scans χ₂ was incremented in 15° steps from the −180° conformation for a full 360° rotation about the torsion. Calculations were performed using the GAUSSIAN 03 ¹⁴ program with the 6-31G* ¹⁵ and 6-31+G* ¹⁶ basis sets, with the latter used for Glu and Asp, at the MP2 ¹⁷ level of theory. During the scans all non-constrained degrees of freedom were allowed to relax to the default convergence criteria. Because several conformations contain steric clashes that led to problems with convergence, reverse scans were performed and data from the forward and reverse scans combined by selecting the lowest energy conformations to yield the complete 1D χ₂ surfaces. In a number of cases, the QM optimization failed to converge. This was generally caused by “flat” local energy regions such that the minimizer algorithm “hovers” around the true minimum but never achieves the convergence criteria. In such cases, the average of the coordinates from the last three optimization steps was used as the input geometry for an additional QM energy minimization. The use of the average structure was designed to move the molecule out of the quasi-minimum geometry, thereby allowing the molecule to relax into the correct minimum. Single point energy calculations of the optimized geometries were performed with the program QCHEM ¹⁸ at the RIMP2/cc-pVTZ ^{19, 20} level of theory. The final RIMP2 energies were extracted for analysis. The energy surface for each side chain was offset to its respective global minimum. With redundant points removed, this procedure yields 576 data points for each backbone conformation, yielding a total of 1728 conformations per residues except Val, for which 3×24 = 72 conformations were obtained. The energies and conformations from the QM calculations for all the studied amino acids may be access from the MacKerell web page at http://mackerell.umaryland.edu/MacKerell_Lab.html.

Protein structure survey

All protein structures were obtained from the RCSB Protein Data Bank ⁷ and only structures with a resolution ≤ 1.5 Å were considered. A sequence similarity filter was applied using the RCSB’s PDB query functionality with a 50% BlastClust²¹ sequence identity threshold to avoid systematic bias due to the presence of redundant proteins. Any residue with a side chain that had one or more missing atoms was discarded. To further improve the quality of the data included in the analysis χ entries from amino acids that contain at least one atom with B-factor > 40 and with occupancy ≠ 1.0 were removed. In addition, amino acid residues with a B-factor of 0.0 were discarded as that value is typically assigned due to the unavailability of the B-factors. To minimize the possibility of errors from incorrect B-factors amino acids that involve one or more atoms with B-factor < 1 were removed. Furthermore, only the first occurrence of duplicate residue entries, which were rare, was included. As hydrogens are not visible in protein X-ray structures only χ₁ data is available for Cys, Ser and Thr, though the 2D QM surfaces were obtained for these amino acids. PDB entries with non-standard residue names were also removed. The final survey results were also parsed as a function of secondary structure (AlphaR, Beta, and AlphaL) based on secondary structure assignment determined by the program STRIDE ²² for AlphaR and Beta or based phi/psi values for AlphaL as described below. A PDB survey statistics is presented in Table S1 of supporting information.

Definitions of dihedral angles

The χ torsion angles were defined as follows: χ₁ = N-Cα-Cβ-Xγ and χ₂ = Cα-Cβ-Xγ-Xδ where X is a side chain-dependent atom type. In Asn, χ₂ is defined as Cα-Cβ-Cγ-Nδ. A rotamer is a conformer of the side chain defined by a specific combination of torsion angles. Thus, each torsion angle was classified into three generic orientations annotated as gauche⁻ (m) at −60°, gauche⁺ (p) at +60°, and anti (t) at ±180°, a nomenclature employed by Lovell et al. ²³ for the construction of rotamer libraries. For Asn and Trp, where χ₂ involves an sp³-sp² type bond, rotamers definitions are trans (t) at 180°, cis (c) at 0°, gauche⁻ (m) at −90°, and gauche⁺ (p) at +90° with window sizes of ±45° used to define χ₂. For the symmetric side chains of Asp/Phe/Tyr, the χ2 nomenclatures of gauche (g) at ±90° and χ₂ = trans (t) at 0° or ±180° was used to define and compare rotamer populations. The boundaries of each of these two rotamers were defined with a window size of ±45°. To present our QM results, we adhered to the generic m, p, and t definitions.

Definitions of backbone conformation

Backbone φ/ψ in the QM calculations were defined as AlphaR (−60,−45), Beta (−120,120), and AlphaL (63.5, 34.8). To obtain comparable crystal distributions, backbone φ/ψ angles were collated using helix/strand definitions determined from the program STRIDE ²². Backbone dihedrals in the φψ ranges of [0,150] and [−30,120], respectively, were considered for comparisons with the AlphaL data. Note that this definition does not identify alphaL helicies (ie. 4 or more consecutive residues in the alphaL backbone conformation) but rather just residues with the alphaL backbone conformation.

Comparisons of QM and protein survey data

To compare the QM and survey data the calculated QM energies for each conformation were converted to probability values p_ij conforming to a Boltzmann distribution

$$p_{ij}=\frac{e^{-\mathrm{\Delta }{E}_{ij}/kT}}{{\displaystyle \sum _{\mathit{backbone}}}{\displaystyle \sum _{ij}}{e}^{-\mathrm{\Delta }{E}_{ij}/kT}}$$ (1)

where the relative potential energies are calculated as

$$\mathrm{\Delta }{E}_{ij}^{\mathit{local}}=E_{ij}-E_{min}^{\mathit{bkb}}$$ (2)

for a given (i,j)=(χ₁,χ₂) with χ ∈ [−180, −165, −150, …, 165} where $E_{min}^{\mathit{bkb}}$ is the global minimum of the three energy surfaces associated with the studied backbone conformations. $E_{min}^{\mathit{local}}$, the local minimum on the individual backbone surfaces, was used in place of $E_{min}^{\mathit{bkb}}$ to remove the backbone-dependency in comparisons of individual backbone types. A temperature T of 300K was used in the calculations.

The crystal distributions for χ₁ and χ₂ angles were calculated from the selected protein structures using a bin size of 15° centered on each QM χ₁ and χ₂ grid point. Populations of each of the rotamers were calculated by summing the probabilities at intervals χ ∈ [−120, 0) for m, χ ∈ [0, 120) for p, and χ ∈ [−180, −120) ∪ [120, 180) for t rotamers. Absent from these populations is backbone dependence as the probability distributions were calculated independently for each backbone type.

The 1D and 2D overlap coefficients (OC) for two probability distributions were calculated over the sampled grid points using equation 3 as previously described ^24–28.

$$OC=\frac{\sum p_m·p_n}{\sqrt{\sum {(p_m)}^2·\sum {(p_n)}^2}}$$ (3)

The OC is indicative of how well two probability distributions overlap and serves as a metric to compare probability distributions derived from the QM surfaces and the survey data distributions.

Secondary Structure Propensities

The propensity (or likelihood) for a side chain to assume a particular secondary structure was calculated from the crystallographic survey using the following definition:

$$P_{\mathit{conf}}^{AA,\mathit{survey}}=\frac{A_{\mathit{conf}}/A_{\mathit{tot}}}{N_{\mathit{conf}}/N_{\mathit{tot}}}$$ (4)

where the propensity for residue A to be in conformation conf is the fraction of this type of residue in a certain secondary structure conformation normalized over the fraction of all residues in this conformation ²⁹. To allow for comparisons an analogous approach was applied for the determination of propensity based on the QM-calculated intrinsic energies. The QM-based propensity score is a sum over the normalized Boltzmann weighted probabilities for a defined backbone conformation conf as follows in Equation 5:

$$P_{\mathit{conf}}^{AA,QM}=\sum _{\mathit{conf}}{p}_{ij}$$ (5)

where p_ij is the Boltzmann factor normalized over the sum of all backbone conformations, as described in Equation 1.

RESULTS AND DISCUSSION

In the present study, blocked dipeptides were used as model compounds for computing the intrinsic conformational properties about the χ₁ and χ₂ dihedral angles of the side chains using QM calculations. Dipeptides have been widely used in both experimental and theoretical work to characterize the behavior of the amino acid side chains.³⁰ 1D or 2D energy surfaces were obtained for three backbone conformations for side chains in their physiologically relevant protonation states. Pro was not studied due to it being a constrained imino acid. As the intrinsic pKa of His is around 6.5, which is close to physiological pH, the charged state (Hsp) was included in addition to the two neutral protonation states, δ-His (Hsd) and ε-His (Hse). We define the intrinsic conformational properties as those due to the chemical connectivity of the side chains and their interactions with the adjacent peptide bonds in the backbone in the absence of any interactions with the surrounding environment (i.e. in the gas phase). To understand the contribution of the intrinsic properties to the conformations of side chains seen in proteins, the QM calculated energies were converted to probabilities based on a Boltzmann distribution and compared to PDB survey data obtained as part of the present work. Accordingly, it should be emphasized that in this study computed conformational potential energies are being compared to conformational free energies from the survey data.

The energy landscape of amino acid side chains

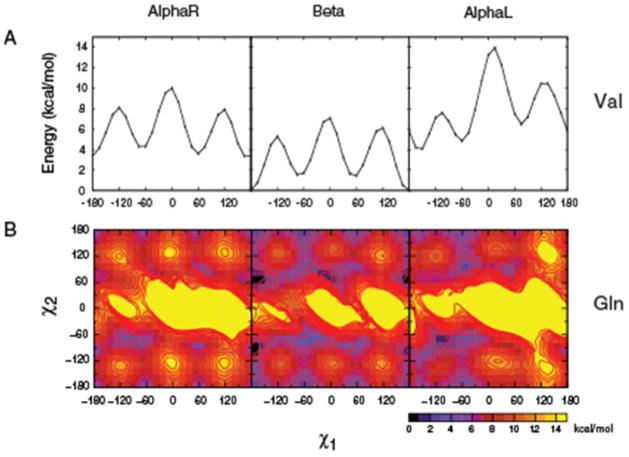
Step one was the generation of a library of ab initio QM energy profiles for the amino acid side-chains using blocked dipeptide models. Full 1D χ₁ or 2D χ₁, χ₂ QM energy surfaces allowed the energy landscape for the rotation of the side-chain moieties to be mapped. The 15° increment for the surfaces was selected as a compromise between resolution and computational cost. Likewise, fixed backbone geometries were used on the basis that given the computational demand of the QM calculations, it is necessary to make the assumption that a single backbone conformation is representative of a type of secondary structure or backbone conformation in the case of AlphaL. Example 1D surfaces for Val and 2D surfaces for Gln are shown in Figure 1. In each case the energy surfaces are presented for the AlphaR, Beta and AlphaL backbone conformations offset to the global minima for all (All) conformations, in which the energy of the global minima for all three surfaces was used as the offset. The energy surfaces for the remaining studied amino acids are included as part of Figure S1 of the supporting information. Table I presents the relative energies for each of the t, m, or p conformations for all the studied dipeptides.

Figure 1.

Val χ₁ and Gln 2D χ₁, χ₂ QM energy surfaces for the three backbone conformations based on the dipeptide model. Energies are offset to the global minima for all three backbone conformations.

Table I.

Relative QM energies of model residues at exact sp³ rotamer conformations.

Alpha										Global Minimum
Rotamer/Residue	tt	tm	tp	mt	mm	mp	pt	pm	pp	χ1	χ2	energy
arg	9.99	8.06	5.75	14.87	12.22	17.74	14.19	17.00	15.93	−150	−45	4.08
asn	11.76	6.54	6.81	3.10	3.85	10.68	2.64	8.91	5.97	60	120	0.66
asp	24.59	22.65	22.62	8.22	11.00	5.52	1.21	1.91	7.30	45	−180	0.00
cys	6.70	4.80	5.98	3.52	1.73	5.20	5.00	6.02	2.44	−60	−60	1.73
gln	5.36	10.70	7.18	5.04	5.23	14.95	5.35	10.15	13.01	−90	−75	2.62
glu	19.83	21.11	21.36	17.14	16.98	2.55	17.82	1.99	16.95	90	−60	0.00
hsd	4.42	10.26	9.05	8.31	6.85	7.33	11.23	6.06	8.40	−165	150	3.23
hse	12.86	5.90	6.32	4.15	3.29	8.29	3.17	8.44	5.18	60	120	0.00
hsp	8.43	17.99	16.27	21.65	24.38	24.07	20.39	21.83	24.37	−165	150	6.98
ile	4.40	7.68	3.25	3.98	3.65	6.05	4.68	6.20	9.05	−180	60	3.25
leu	5.66	5.58	2.26	2.99	5.44	5.76	5.34	8.79	8.70	−180	60	2.26
lys	10.44	7.63	4.56	15.01	11.93	17.88	14.29	17.42	16.64	165	60	3.60
met	4.51	16.47	5.21	5.34	7.32	4.03	6.01	12.06	10.44	−60	75	2.97
phe	7.63	6.92	5.62	5.62	2.91	7.68	10.34	6.46	6.40	−60	−75	2.65
ser	9.33	6.06	7.48	3.84	3.52	8.23	4.67	10.14	2.55	60	60	2.55
thr	10.92	8.09	8.73	4.05	4.08	8.62	5.54	11.14	3.58	45	60	3.46
trp	13.03	6.95	6.40	6.85	3.75	8.14	13.41	6.71	6.00	−60	−90	2.50
tyr	7.36	6.95	5.63	5.58	2.92	7.50	10.41	6.28	6.30	−60	105	2.53
val	3.34				4.30				3.60	165		3.34
avg(Alpha)	8.81
	Beta
arg	8.07	7.86	8.22	6.59	3.04	7.01	7.37	8.09	7.04	−90	30	1.19
asn	1.26	2.85	4.01	5.12	3.44	4.20	7.26	5.72	4.01	−60	−30	0.64
asp	10.63	14.13	13.64	15.84	15.47	13.85	19.75	14.47	26.46	−165	−180	10.38
cys	2.32	0.34	0.71	2.83	1.56	1.63	5.39	5.12	1.56	−180	−75	0.00
gln	1.83	4.37	0.70	2.04	4.59	7.51	3.69	7.02	9.97	−15	75	0.00
glu	18.61	16.89	13.13	19.93	17.80	11.06	21.91	10.76	28.46	−60	75	7.54
hsd	6.64	3.81	2.37	1.31	5.40	5.77	5.07	6.33	7.84	45	−120	0.00
hse	2.27	3.16	3.98	5.93	3.14	3.75	7.78	5.69	5.14	−180	−135	0.88
hsp	14.86	15.42	14.57	3.47	12.83	13.81	8.18	13.10	13.95	−60	165	3.36
ile	1.90	4.25	1.45	0.45	0.00	2.37	2.21	3.89	5.99	−60	−60	0.00
leu	2.53	2.62	0.38	0.00	2.26	3.01	3.91	6.89	6.25	−60	−180	0.00
lys	8.08	8.72	8.49	7.02	1.72	6.46	7.72	8.37	7.84	−45	−60	1.27
met	2.28	13.25	0.34	2.48	6.94	4.90	3.52	10.42	11.03	−180	45	0.00
phe	5.33	2.17	0.93	3.74	2.07	3.99	8.14	5.29	6.10	−180	−90	0.00
ser	3.14	3.04	3.80	4.91	3.83	3.16	7.00	6.28	0.69	60	45	0.00
thr	4.45	5.04	5.37	5.16	4.22	3.07	7.04	6.77	0.79	60	45	0.00
trp	10.50	3.08	2.38	9.15	3.05	4.46	11.71	6.25	5.47	−180	−105	0.00
tyr	5.41	2.07	0.86	3.62	2.17	3.97	8.09	5.27	6.08	−180	−90	0.00
val	0.00				1.53				1.44	−180		0.00
avg(Beta)	6.33
	AlphaL
arg	7.69	8.75	8.26	9.34	12.48	13.04	6.62	12.56	0.00	60	60	0.00
asn	10.67	7.11	9.43	0.00	3.99	6.23	14.18	15.66	3.54	−60	−180	0.00
asp	33.67	40.34	30.90	10.26	14.01	11.61	27.66	26.27	28.80	−60	−165	9.79
cys	9.81	5.17	9.75	2.46	1.66	1.82	8.23	9.35	5.71	−60	−75	1.47
gln	6.84	16.18	8.10	2.71	3.91	9.44	6.41	14.66	7.67	−105	−75	1.03
glu	29.11	51.56	23.27	22.41	15.15	12.46	27.60	21.53	41.69	−90	60	7.41
hsd	10.30	13.73	8.41	10.77	4.32	4.92	9.49	10.29	10.82	60	−105	1.16
hse	12.66	9.38	10.79	1.35	4.55	6.04	17.05	13.59	4.22	−75	−135	1.34
hsp	9.14	14.47	9.82	19.35	16.27	17.18	7.99	11.52	9.93	75	−120	0.00
ile	10.43	18.39	8.65	6.92	6.95	9.14	5.74	11.24	6.60	−30	−180	4.40
leu	13.58	13.30	5.18	2.82	4.87	5.09	10.26	10.46	6.57	−60	−180	2.82
lys	8.09	9.80	8.21	9.41	13.05	13.88	7.27	11.88	0.00	60	60	0.00
met	6.45	24.68	5.43	4.53	7.46	3.16	6.73	25.91	9.65	−75	60	2.23
phe	11.44	12.78	7.79	6.26	2.42	4.85	14.78	10.91	6.39	−45	−75	1.52
ser	12.38	2.31	11.76	3.56	5.18	5.04	10.32	10.05	4.45	−165	−60	1.34
thr	16.08	6.12	15.52	6.39	8.40	7.98	11.30	11.11	5.09	−165	−60	4.56
trp	14.13	10.85	10.04	7.70	2.95	5.72	23.62	12.26	4.21	−45	−75	1.69
tyr	11.52	12.81	7.82	6.50	2.48	4.76	14.59	10.80	6.48	−45	−75	1.57
val	4.09				4.86				6.49	−150		4.09
avg(AlphaL)	10.77

Energies in kcal/mol correspond to the exact rotamer conformations (ie. χ1/χ2 = −60, 180 or 60°) and offset with respect to the global minimum for all three surfaces of each residue. While symmetry in χ₂ dihedrals involving sp² atom centers in Asp, Phe, and Tyr is present, energies for all sp³ rotamer geometries, as defined in the Methods section, are shown.

In general, the expected energy minima m, p, and t for sp³ carbons and, in the case of Phe/Trp/Tyr/Asn χ₂, minima at t and ±90° for sp² carbons are reflected in the 2D energy maps. Due to the symmetry of their side chains, the m and p rotamers for Asp, Phe and Tyr are structurally equivalent. However, results from the full continuous 360° scans of Asp/Phe/Tyr’s side chains are included in the QM energy surfaces. As shown in Figure S1 of Supporting Information, the two halves on the χ₂ space are not entirely symmetric, as is expected for symmetric moieties. Although minute, the differences are an indication of structural changes during QM geometry optimizations that are not fully relaxed due to the longer side chains being trapped in local minima and present a potential limitation in direct comparisons of QM data with crystallographic surveys. We include the full data to highlight this limitation. However, for further analysis and comparisons with the crystallographic survey, only the (−180,0) range data was used for χ₂ for Asp/Phe/Tyr.

The extended (Beta) conformation yields energies that are systematically more favorable than AlphaR and AlphaL (Table I), which are evident in the Val energy surfaces shown in Figure 1. This is consistent with the AlphaR and AlphaL energies being 2 or more kcal/mol higher than that of the extended C5 conformation in the alanine dipeptide ^{12, 31}. However, with Asp, Glu, and Hse the global minimum occurs in AlphaR while with Arg, Lys, Asn, and Hsp it is occurs in the AlphaL backbone conformation. Thus, interactions of the polar and charged side chains with the local backbone can intrinsically alter the ordering of the relative energies of the backbone conformations. Interactions with the backbone also lead to deep energy minima on the surfaces; such minima, which in certain cases do not correspond to conformations observed in the PDB survey, mask the presence of relatively shallower but energetically relevant minima as well as leading to high-energy regions. This effect is most obvious in the charged residues Asp and Glu, where deep energy minima are located on Asp’s χ₁ = m and p and Glu’s mp and pm regions of the AlphaR backbone conformation (Figure S1, Supporting Information). The Asp QM surfaces contains low-energy conformations at χ₂ = 0/180° (or t). Analysis of the structure of the Asp dipeptide shows a favorable hydrogen bond between the acid group and the peptide bond stabilizing the χ₂ = t conformation (Figure S2A). In Hsp, the energy surface is perturbed due to highly favorable interactions with the backbone at the χ₁ = p region of the AlphaL backbone (Figure S1, Supporting Information). This is an inherent property of the dipeptide representations of side chains in vacuum where the effects of the solvent as well as the protein environment are omitted. Their presence, however, indicates the importance of environmental contributions to the conformational properties of side chains observed in protein structures as will be discussed below. Together these data reflect the presence of intrinsic differences in rotamer preferences for the different amino acids.

Protein Databank Survey

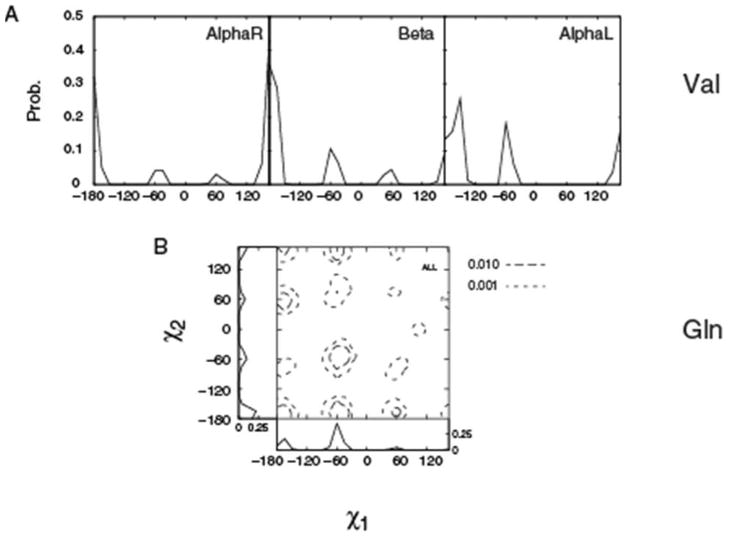
Analyses of dihedral distributions of protein side chains have been the subject of numerous studies ^{23, 32–34} and, as a result, there exists several compilations of protein survey data, including the recent compilation by Shapovalov and Dunbrack.³⁵ However, because of the accelerated increase of high-resolution structures deposited in the Protein Databank we performed a new survey. The survey identified 2106 non-redundant (similarity < 50%) high resolution (≤ 1.5Å) PDB entries. The final data set is summarized in Table 2, with the results separated into distributions for the AlphaR, Beta and AlphaL backbone conformations as well as for all backbone conformations. To test the statistical significance of the data set, it was randomly split into 5 sets and the populations of the different rotamers compared (Table S2, Supporting Information). The results show the populations to be nearly identical for the 5 sets with the standard deviations of the populations being 0.02 or less. This indicates that the size of the sample is an adequate representation of χ distributions in protein crystal structures. Presented in Figure 2 are 1D Val and 2D Gln χ distributions from the crystallographic survey. Also presented are 1D distributions along χ₁ and χ₂ degrees of freedom for Gln, which are appended to the respective axes of the 2D surface. Comparison of the energy surfaces in Figure 1 and the distributions in Figure 2 show the location of the QM-calculated minima to generally correspond to the survey maxima, respectively, as the probability distributions for both χ₁ and χ₂ have the expected minima corresponding to the t, m, and p rotamers. However, significant differences are also present as expected since the intrinsic conformational energies of the side chains do not solely dictate the conformations sampled in the heterogeneous environments encountered in protein structures. In the following section, details of the QM and survey differences will be presented allowing for an improved understanding of the relative contribution of intrinsic and environmental factors to be obtained.

Table II.

Relative SASA for side-chains in the AlphaR, Beta, and AlphaL backbone conformations.

	Average SASA	SD	N
all	32.63	0.08	428089
alpha	30.74	0.08	139629
beta	18.46	0.23	98692
alphaL	60.08	0.74	20192

SD: standard deviation calculated from 5 random and non-overlapping subsets

Figure 2.

A) Val χ₁ and B) Gln 2D χ₁, χ₂ PDB probability distributions. For Val the data is for the individual backbone conformations such that the sum of the probabilities for each surface equal 1. For Gln, only the All surface is presented along with χ₁ and χ₂ 1D distributions along the respective axes.

Relationship between Intrinsic Energetics and Rotamer Populations in Protein Structures

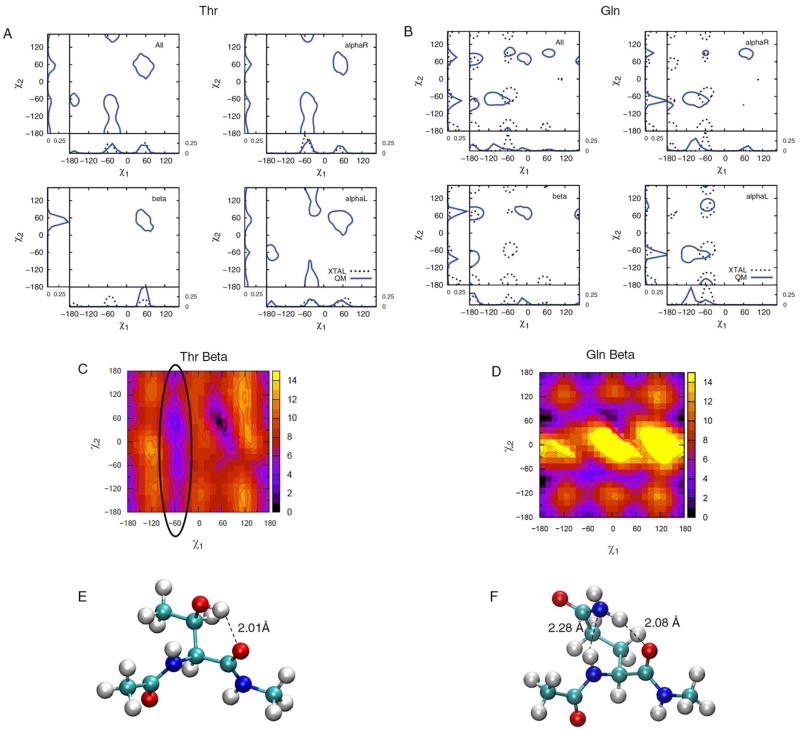
To allow for comparison of the potential energy surfaces with data from the PDB survey, the QM energies were converted to probabilities based on a Boltzmann distribution using Equations 1 and 2. The resulting QM probabilities were then overlaid onto the PDB distributions producing “combined QM/PDB probability” plots including the 1D χ₁ and χ₂ summed representations along the x and y axes, respectively. For comparisons of data in different backbone types, we offset each QM surface to the minimum of respective backbone conformations in order to remove the relative energy contributions originating from the backbone itself. Figure 3 shows the combined QM/PDB probability plots for Thr and Gln. The corresponding plots for all the amino acids can be found in Figure S3 of the Supporting Information. In general, the heterogeneity in PDB rotamer distributions is apparent. For example, rotamer t is nearly absent in Thr χ₁ whereas m and p occur at approximately the same probabilities. The short and negatively charged side chain of Asp is predominantly in the χ₁ = t, m and, interestingly, the χ₂ = 0° (fully eclipsed) geometries. The χ₂ torsion of the His and Trp side-chains also exhibit a weak but noticeable population at 0°. In Asn/Phe/Tyr/Trp, where χ₂ involves rotation about an sp² atom, a notable population at 0° occurs when χ₁ = m. Fully eclipsed conformations for these residues are generally not energetically favorable and their presence is discussed in conjunction with intrinsic energetics in the following section.

Figure 3.

Combined QM/PDB survey probability plots for A) Thr and B) Gln. Crystal distributions for Thr χ₂ are absent as they involve a proton. The probabilities for the three backbone conformations are over those individual surfaces such that the sum of the probabilities for each surface equal 1. 2D QM energy surfaces containing the global minimum is shown for each residue (C and D). Structures of model dipeptides Thr (60°, 45°) (E) and Gln (−15°, 75°) (F) at their global minima show short hydrogen-bonding interactions with the backbone. 2D-plots are made with probability contours of 0.005.

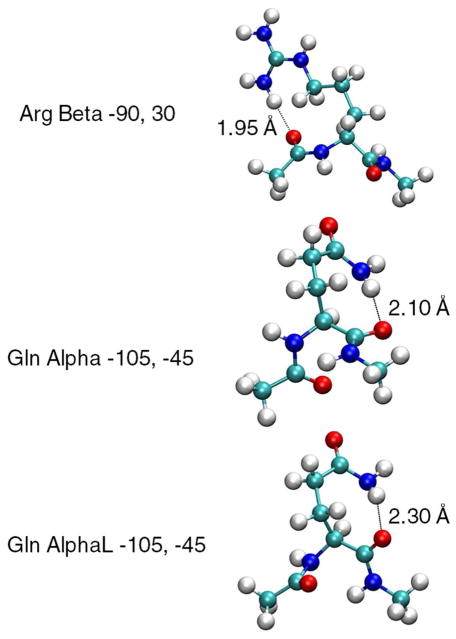
Along with the combined QM/PDB probability plots for Thr and Gln in Figure 3, shown are the QM 2D energy surface for the Beta backbone conformation and selected side-chain conformations for the dipeptides that correspond to deep minima on the energy surfaces. Comparison of the Beta energy surface and the corresponding probability distribution shows the difficulty in simply converting the QM potential energy surfaces to probabilities and using those directly for analysis. In the Beta surface of Thr there is a deep minimum around pp associated with a strong hydrogen bond between the hydroxyl and the backbone carbonyl as indicated in Figure 3C. Similarly, deep minima are found around the off-rotamer location χ₁,χ₂ = (−15°, p) for Gln (Figure 3D). Structures corresponding to other minima for Gln and Arg are shown in Figure 4 to further exemplify the type of strong electrostatic interactions that can occur in the QM surface of residues with long side chains. As calculation of the QM probabilities is based on the Boltzmann distribution of energies relative to the global minimum, the presence of these deep minima can obscure the presence of other local minima in the QM surface. This effect is emphasized by the significantly different rotamer populations of selected amino acids when they are calculated for the QM data offset to the global minima (Table S3 of the supporting data) and when the survey probability of the rotamers are determined over all the backbone conformations (Table S4 of the supporting information). Such limitations need to be considered when comparing the QM and PDB distributions. For example, the Beta QM energy surface of Thr contains an extensive low-energy valley at χ₁ = m (circled in Figure 3C), which is not accurately reflected in the QM probability distribution. However, sampling of that region is evident in the PDB survey data in the 1D χ₁ plots in Figure 3A.

Figure 4.

Structures of Arg and Gln showing favorable interactions with the backbone resulting in non-rotameric minimum in QM surfaces.

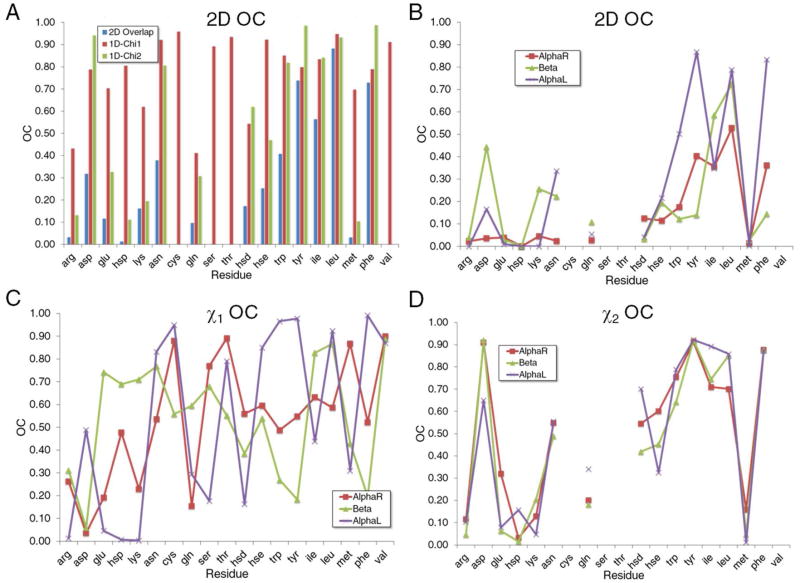
Quantitative comparisons of the QM and survey probability distributions were achieved using OC values calculated from Equation 4. This was performed in both 1 and 2 dimensions for all the amino acids with the results shown in Figure 5. In the figure the amino acids were ordered along the x axis based on physicochemical properties starting from charged, to polar, to polar cyclic, and to hydrophobic. The degree of overlap between the QM and PDB distributions range from near zero for Hsp and Met to higher values for Asn, Ile, and Trp, with the largest OC values occurring with Leu, Phe and Tyr. In general, we observe that simultaneous consideration of the χ₁ and χ₂ yields overall poor agreement with polar or charged side chains such as Arg, Asp, Glu, His (Hsp/Hsd/Hse), Lys, Asn, and Gln while hydrophobic side-chains such as Phe, Tyr, and Ile are located in the upper spectrum in terms of correlations with survey distributions. In the case of polar side chains, which can form favorable intramolecular interactions with the backbone, smaller OC values indicate that their experimentally observed conformations are stabilized by the protein or solution environment. For hydrophobic residues, high OC values indicate a dominance of intrinsic over environmental contributions to their orientations in protein structures. Because hydrophobic interactions are an important feature in stabilizing the core of proteins ³⁶, this data suggests that intrinsic energetics of hydrophobic residues may make an important contribution to the folding and stabilization of proteins (see below). Furthermore, the QM calculated χ₁ distributions correlate better with crystal occurrences than χ₂. This is expected as χ₁ modulates the orientation of moieties that interact directly with the backbone in contrast to the functional groups defined by the χ₂ dihedral that are removed from the backbone such that their conformations are more strongly influenced by interactions with their environment. Simply put, the further away from the backbone the less interactions with the backbone, and therefore the lower the contribution of the intrinsic conformational properties to the sampling of rotamer populations in protein 3D structures. Taken together, these data demonstrate that the extent that environmental effects shift sampled conformations away from the intrinsically favored conformations is highly side chain dependent. Specific cases will be discussed in the following paragraphs.

Figure 5.

Overlap coefficients (OC) for A) all surfaces associated with the three backbone conformations and for the three individual backbone conformations for the B) 2D χ₁, χ₂, C) 1D χ₁ and D) 1D χ₂ OC values as a function of residue type. Residues are arranged along the x axis based on physicochemical properties.

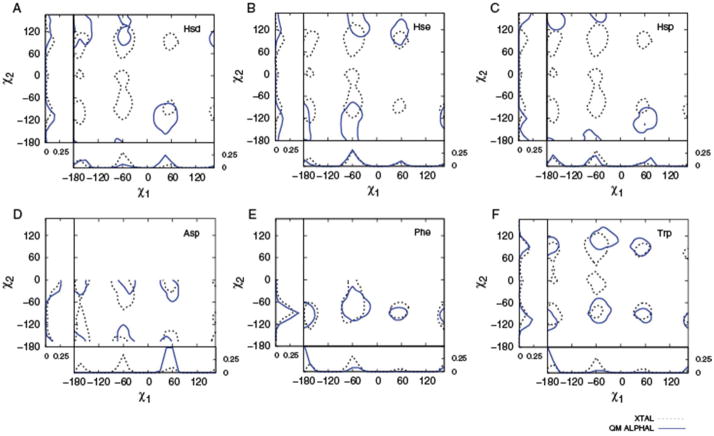
With a pKa of 6.5, the imidazole ring can exist in either the neutral (Hsd or Hse) or +1 charged state under physiological conditions. Therefore, all three protonation states of the His side chain were considered in the QM calculations and each was compared to the crystallographic His distributions. From the OC graphs (Figure 5) and combined QM/PDB probability plots (Figure 6) the neutral species, Hse, is in better agreement with the PDB survey data than Hsd. While speculative, this suggests that the Hse species occurs at a higher probability in crystal structures than the δ-His counterpart. The charged species Hsp shows little 2D overlap with the crystal distribution. In general, the moderate correlation of the His survey and QM distributions, especially evident in the 2D OC values, is likely associated with the often specialized role of His in proteins. For example, His residues are often involved in well-defined non-covalent interactions associated with chemical catalysis ^37–39 or ligating metals ⁴⁰ where His is acting as a general acid or base. Such interactions may be expected to dominate the conformation of the side-chain, overcoming the intrinsic orientational contribution. This appears to be particularly true with Hsp, where its charged nature is suggested to lead to the environment having a larger role in dictating its conformation in proteins.

Figure 6.

Combined QM/PDB survey probability plots for A) Hsd, B) Hse, C) Hsp, D) Asp, E) Phe, and F) Trp. QM (solid) and crystallographic survey (dashed) probabilities are shown. Probability contour lines are of 0.005. See Supporting Information for backbone-dependent plots.

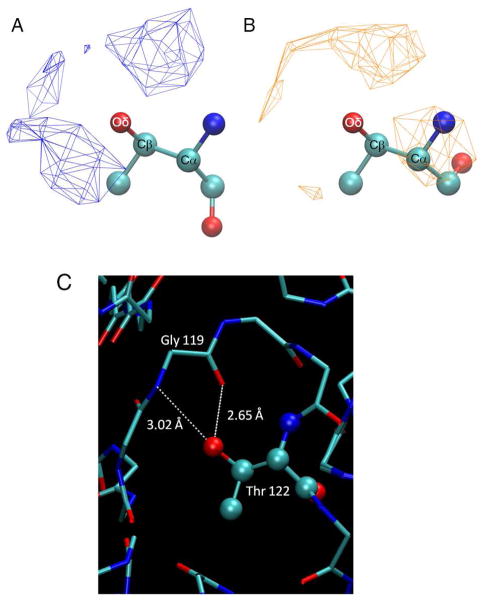
Intrinsic energies of both Phe and Tyr show high correlation with crystal distributions yielding 2D-OC values of 0.73, χ₁OC of 0.80, and χ₂OC of 0.98 for Phe with the Tyr OC values nearly identical to those of Phe, consistent with the structural and chemical similarity of their side-chain moieties. The high correlation between intrinsic energies and crystal distributions is an indication that the protein environment has a minimal effect on the orientation of the side-chains. To further investigate this we overlaid all occurrences of Phe within the selected protein structures based on side-chain atoms (Cβ and beyond) and identified aliphatic and aromatic carbon atoms within 5.0 Å of the Phe side-chain non-hydrogen atoms. A 3D occupancy map was then constructed at a grid resolution of 1.0 ų and normalized over the total number of atoms that satisfy the distance criteria. This yielded a 3D probability density map (Figure 7) representative of the overall shape of the environment in which the phenyl moieties are embedded. As is evident in Figure 7 the environment surrounding the Phe side chains forms an approximately isotropic cage-like hydrophobic distribution around the phenyl ring. This is consistent with the high OC values such that the environment generally does not offer specific interactions that dictate the conformational properties of the phenyl ring in protein structures. These results suggest a model where the side-chain conformations of Phe and Tyr are dominated by the intrinsic energetics, with the surrounding protein structure accommodating those conformations. For example, an important role of three Phe residues in controlling both the folding rate and the stability of the Villin Head Piece has been documented.^{41, 42} While this was attributed to aromatic-aromatic interactions the intrinsic conformational properties of that residue may contribute to the entropy barrier to folding as well as the entropic contribution to protein stability.

Figure 7.

3D probability distribution of aliphatic and aromatic carbons around the Phe side-chain atoms derived from the crystallographic survey. Densities were calculated by normalizing each occupancy point over the total number of atoms within 5Å of the phenyl ring’s non-hydrogen atoms and displayed with a cut off density of 0.001. An arbitrarily chosen backbone conformation (transparent) is displayed for convenience.

For Thr χ₁ = m is highly populated in protein structures for all backbone types (Figure 3A). However, based on intrinsic energies, AlphaR and AlphaL backbones produce energetically accessible m regions but not Beta. As discussed above, due to intramolecular hydrogen bonding, a deep energy well at [χ₁, χ₂] = [45°, 60°] or pp is present in the Beta backbone conformation. It is therefore clear that the protein environment must compete for these interactions. To investigate this, all Thr residues in the χ₁ = m orientation were obtained from the selected crystal structures and further divided into AlphaR and Beta backbone classes. For each of the two classes we calculated the occurrence of hydrogen-bond donor/acceptor atoms (O, N, S) within 5 Å of the side-chain oxygen atom, excluding O or N atoms in the peptides bonds covalently linked adjacent to the side chain (self) and normalized that data to the total number of hydrogen-donor atoms that satisfy the distance criterion. No significant sampling of well defined regions in the vicinity of the side chain was found in the resulting distribution (not shown). We then further classified neighboring atoms based on their origin: water, backbone (non-self), or side chains. Of particular interest was the distribution obtained from non-self backbone atoms. Shown in Figure 8 is an overlay of resulting 3D distributions of backbone hydrogen-bond donor/acceptor atoms around Thr for χ₁ = m summed over the AlphaR and Beta backbone conformations. Analysis of the probability distributions show well-defined densities where the Thr hydroxyl can act as both a hydrogen donor and acceptor. The χ₁ = m conformation in the Beta backbone, which intrinsically interacts favorably with its own backbone, appears to find strong coordinating interactions with N/O atoms of the neighboring protein backbone. This would mean that the intrinsic conformational preference of Thr for χ₁ = m is effectively overcome by hydrogen bond interactions with other backbone groups. Interestingly, this type of interaction is also present in AlphaR, although intrinsic energetics alone was sufficient to explain its occurrence. This indicates a more “passive” role of the environment in dictating the side-chain orientations of Thr in alphaR helices. An example of the type interaction is shown in Figure 8C where the ability of a selected Thr hydroxyl to act as both a hydrogen bond donor and an acceptor in interactions with the peptide backbone is evident. This observation is a well-defined example of how the protein environment can stabilize specific side-chain rotamers and provides a new insight into the complexity of structural properties of Thr residues.

Figure 8.

3D Probability distribution for non-self backbone N/O atoms around the Thr side-chain Oδ at χ₁ = m derived from crystallographic survey. Densities were calculated by normalizing each occupancy point by the total number of atoms within 5 Å of O_δ of Thr and displayed with a cutoff density of 0.001. Shown are Thr structures in the AlphaR (A) and Beta (B) backbone conformations along with corresponding N/O densities represented as wireframes. C) Thr122 of 1BYI forms hydrogen bonds with the backbone atoms from Gly119.

Effects of Local Environment

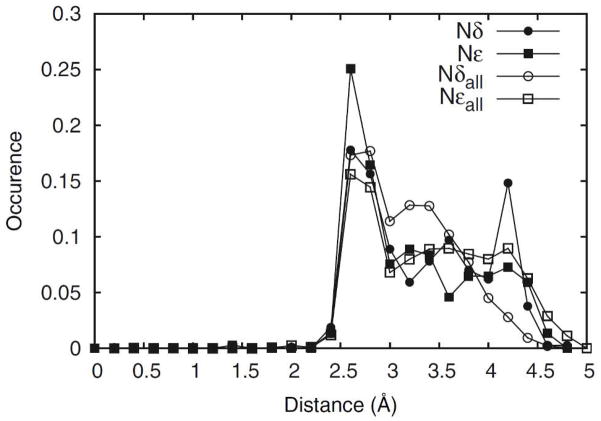
The effect of local environment on rotamer population has previously been discussed in a number of studies ^{4, 43–45}. It has been observed that the protein and aqueous environments provide stabilizing interactions to the side chain and selects from a pool of intrinsically low-energy orientations ⁴. In fact, it has been proposed by Schrauber et al. ⁴³ that in some cases individual side chains can adapt high-energy orientations as a compromise to allow the protein as a whole to access low free energy conformations. However, Petrella and Karplus ⁵ stipulated that for Val, Ile, Leu, Phe, Trp and Met, the presence of off-rotamers can be attributed to internal energetics of the isolated side chain. From the database survey, in addition to the probability peaks at locations corresponding to the energy minima associated with the sp³ Cα and Cβ atoms, off-rotamers at χ₂ = 0° are present in His and Trp (Figure 6). Although the QM energy surfaces for these residues indicate presence of local minima at χ₂ = 0° converted QM probabilities do not contain significant populations for His or Trp in this conformation suggesting a dominant role of environmental effects. However, intrinsic effects are playing a role in the observed off-rotamer conformations of His and Trp. Previous computational studies ⁴⁵ have attributed the occurrence of this Trp off-rotamer to C-H moieties on the indole ring acting as hydrogen bond donors interacting with hydrogen bond acceptors in the surrounding environment. In the case of His, the χ₂ = 0° population appeared only in the QM probability distribution for Hse in the χ₁ = m rotamer associated with the Beta backbone, albeit at relatively low levels (Figure S3, Supporting Information). In this conformation a hydrogen bond between C=O and C_δ-H of the side-chain is formed, therefore stabilizing this orientation (Figure S2B). The presence of shallow local minima at or near χ₂ = 0° in the QM energy surfaces across all three protonation states of histidine (Figure S1, Supporting Information) indicate that similar interactions are also present in Hsd and Hsp. However, the presence of deep energy wells near (t,−120°) of Hse/Beta and (m,−120°) and (p,120°) of Hse/Alpha, (p,−120°) and (t,120°) of Hsd/Beta, and (p,−120°) of Hsp/AlphaL leads to the χ₂ orientation at 0° not being significantly populated upon conversion of the QM surface to a probability distributions, as discussed above. In fact, nearly all the probability peaks observed in the crystallographic survey have corresponding local minima in Hsd/Hse QM energy surfaces, though they are obscured in the QM probability surfaces due to deep energy minima. This data suggests that interactions of the His side chain with the environment strongly compete for the deep energy minima, as indicated by the weak 2D OC value (Figure 5a). In fact, close examination of the QM energy surfaces (Figure S1, Supporting Information) reveals energy minima near the specific off-rotamer location (m,0°). To understand the structural implications of the local protein environment in crystal occurrences of these off-rotamers we calculated the shortest distances of O, N or S atoms with respect to the Nδ or Nε of the imidazole ring. A histogram was constructed using a bin size of 0.2 Å. In Figure 9, the distribution of O/N/S atom distances are shown across all His residues versus those across conformations corresponding to the above-defined off-rotamer. It is clear that both nitrogens participate in strong hydrogen-bonding interacions, as seen in probability spikes in the 2.5–3.5Å range. However, a marked rise in probability of closely interacting (2.5–3.0Å) hydrogen-bonding partners around off-rotameric Nε, but not Nδ, provides evidence that stabilization of Nε is important at these conformations. The above-presented evidence provides a link between the occurrences of off-rotamers and intrinsic conformational as well as environmental effects.

Figure 9.

Distribution of O, N, or S atoms around the N atoms of the His side chains. Distances of the nearest atoms to each Nδ (closed circles) or Nε (closed squares) of His side-chain that are in the χ₂ = 0°±10° conformation (371 data points) were binned to 0.2 Å and compared with those for all (10101 data points) His entries (open circles and squares for Nδ and Nε, respectively).

Backbone Dependency of Intrinsic Conformational Energetics

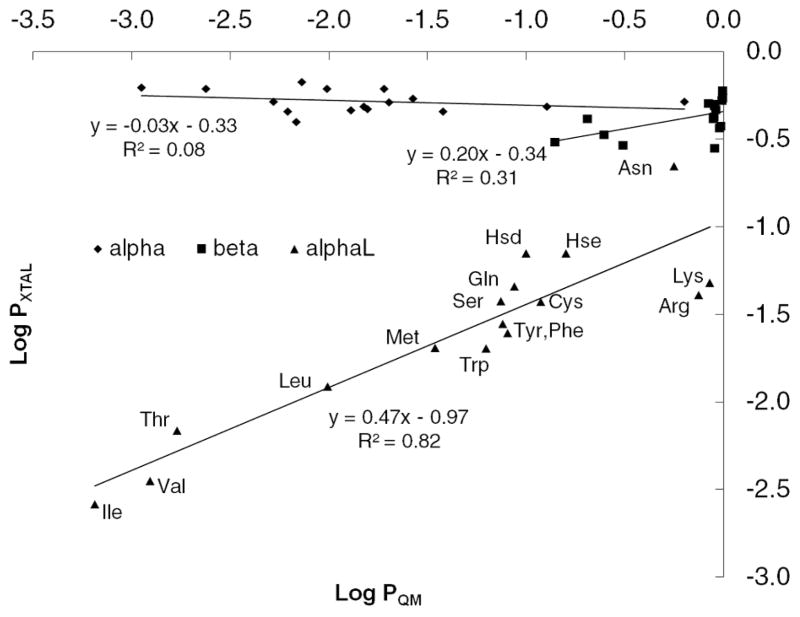
It has been previously discussed that the prevalence of rotamers is dependent on backbone conformation.⁴⁴ To investigate the extent by which local backbone conformation impacts the contribution of intrinsic energetics to side-chain conformation, the crystallographic data was partitioned into three backbone classes corresponding to the three backbone conformations used in the QM calculations. Figure 5 includes the backbone-dependent OC values for all the studied amino acids. With the 2D OC values, AlphaR offers the least agreement with the survey results with an average 2D OC over all the studied amino acids of 0.15 versus 0.21 and 0.28 for Beta and AlphaL, respectively. One explanation could be that the Beta and AlphaL conformations offer more potential for side chain-self-backbone interactions, leading to larger intrinsic contributions. The intrinsic contribution is largest for Asp, Lys, Gln, and Ile when they are in the Beta backbone conformation. For Asn, Trp, Tyr, Leu, and Phe, higher OC values are seen at the AlphaL orientation, with values of 0.34, 0.50, 0.87, 0.79, and 0.83, respectively. These data indicate that the extent to which intrinsic energetics dictates conformational sampling is backbone dependent.

Secondary structure propensity

The preference for a residue to assume a particular backbone conformation has been a popular topic in structural bioinformatics (reviewed in Ref. ⁴⁶). Early work by Blout et al. ⁴⁷ established the first correlation between amino acid sequence and secondary structure using synthetic homopolymers. Such a correlation has led to the development of numerous secondary structure prediction methods that can be divided into two approaches: physicochemical and probabilistic. With the increasing number of available protein structures, the probabilistic approach has seen significant improvement ⁴⁶ in terms of accuracy since the first propensity scales derived from observed frequencies were published (reviewed in ⁴⁸). Results obtained in the present study allow us to investigate the intrinsic conformational energies of the side chains, which contribute to their physicochemical properties, with their secondary structure propensity. To address this for each residue in backbone conformation conf the ratio of the sum of Boltzmann probabilities of the χ_1,2,conf energy surface is calculated relative to the sum of Boltzmann weights for all three backbone conformations (Equation 5). This yields the probability of each residue occupying the different types of secondary structure based on the intrinsic conformational energies alone. These probabilities were then compared with analogous values from the survey data calculated using Equation 4. To remove the likelihood of bias from strong side chain-backbone electrostatic interactions contributing to the QM results side chains with charged moieties that can interact directly with the local backbone (ie. Asp, Glu, Hsp) were excluded from the analysis. A linear regression model was built for each of the three backbone conformations (Figure 10) with the data presented in Table S5 of Supporting Information. For AlphaR or Beta there is negligible correlation between the crystallographic and intrinsic propensities, indicating the intrinsic conformational properties to not play a role in conformational preference. However, a correlation is found for AlphaL with a slope of 0.47 and R² of 0.82, indicating that the intrinsic energetics are contributing to the propensity of the different amino acids to assume that backbone conformation in protein structures. This result is consistent with a previously established relationship⁴⁹ between J-coupling constants of blocked residues (dipeptides) in solution and occurrences in coils.

Figure 10.

Correlation of secondary structure propensities calculated from crystallographic survey and from intrinsic energies. Charged residues Asp, Glu, and Hsp were omitted from the analysis.

Analyses of the results for individual residues reinforce the above observation. Selected amino acids that have the high propensities for AlphaL in the survey, Asn, Lys and Arg, all have the global minimum in AlphaL (Table I). In contrast, some of the amino acids with the least favorable average energies over all the AlphaL minima relative to the AlphaR and Beta minima, Thr and Ile, have some of the lowest AlphaL experimental propensities. These results suggest a model where intrinsically favorable interactions of the side chain with the backbone in the alphaL conformation lead to enhanced sampling of that backbone conformation in proteins. Interestingly, only short (less than 5 residues) left-handed helical regions of polypeptides are found in nature and are typically functionally important components of the protein.⁵⁰ Along with the suggestion that neighboring residue effects ⁵¹ play a role in these regions, the present observation of the role of intrinsic conformational energies in sampling the alphaL backbone conformation offers another example of how primary sequence can play an important role in protein function by favoring biologically important conformations. It’s important to bear in mind that, due to the alphaL backbone definition used in this study, no direct relationship can be drawn between our alphaL and true left-handed alpha helices. However, our results provide an insight as to how a relatively unusual backbone conformation such as alphaL can be stabilized.

Solvent accessibility

Additional analysis of the crystallographic survey data involved the solvent accessible surface area (SASA) for the side-chains in different backbone types (Table II). The AlphaL set clearly stands out as being more solvent-exposed than AlphaR or Beta. As presented above the average 2D OC value for AlphaL, 0.28, was higher than the values for Beta and AlphaR, with OCs of 0.15 and 0.21, respectively, and side chain type is indicated to influence assumption of the AlphaL conformation. These observations suggest a simple model where the additional impact of the intrinsic conformational energies in AlphaL is due to a decrease in the number of specific interactions of the side chains with the surrounding protein.

SUMMARY

Presented are the intrinsic energy landscapes for amino acid side chains calculated using QM calculations on representative dipeptide models. The data offers insights into the role of intrinsic energetics on side chain sampling of the χ₁ and χ₂ torsions. The locations of local minima are in good agreement with observed conformations in protein structures. However, the extent to which they agree, as measured by OC values, depends on the type of amino acid as well as the backbone conformation. Strong electrostatic interactions with the backbone resulting in deep energy minima on QM surfaces contribute to the low OC values seen in charged or polar side-chains. However, the protein environment can effectively compete with the intrinsic interactions, as evidenced by the absence of observed rotamer populations in the protein survey data that correspond to deep minima within the QM surfaces. Information is also provided that support previously discussed occurrences of off-rotamers, with new evidence suggesting that intrinsic energetics of His and Trp lead to the stabilization of local minima corresponding to observed off-rotamer populations. Another interesting observation was the high 2D-OC values for Leu, Phe and Tyr, indicating a dominant role of intrinsic energetics in their conformational properties. While speculative, based on the known role of these amino acids in protein folding the present results suggest that their intrinsic conformational properties make an entropic contribution to both protein folding rates and protein stability. Finally, a correlation for the propensities of side chains to occur in the AlphaL backbone conformation is found between intrinsically determined preferences and those occurring in proteins. This observation suggests that the identity of a side chain plays a more prominent role in influencing assumption of the AlphaL conformation as compared to the AlphaR or Beta backbone conformations.

The presented QM calculations will be important in empirical force field optimization. At the time of this writing, there is no published data on high level ab initio calculations of the complete energy profiles associated with side chain χ₁ and χ₂ torsions for the relevant amino acids residues. Accordingly, the calculated QM energy surfaces will be of utility as target data for the optimization of protein force fields.