Mechanisms of Inferential Order Judgments in Humans (Homo sapiens) and Rhesus Monkeys (Macaca mulatta)

Abstract

If A > B, and B > C, it follows logically that A > C. The process of reaching that conclusion is called transitive inference (TI). Several mechanisms have been offered to explain transitive performance. Scanning models claim that the list is scanned from the ends of the list inward until a match is found. Positional discrimination models claim that positional uncertainty accounts for accuracy and reaction time patterns. In Experiment 1, we trained rhesus monkeys and humans on adjacent pairs (e.g. AB, BC, CD, DE, EF) and tested them with previously untrained nonadjacent pairs (e.g. BD). In Experiment 2, we trained a second list, and tested with nonadjacent pairs selected between lists (e.g. B from list 1, D from list 2). We then introduced associative competition between adjacent items in Experiment 3 by training two items per position (e.g. B₁C₁, B₂C₂) before testing with untrained nonadjacent items. In all three Experiments, humans and monkeys showed distance effects in which accuracy increased, and reaction time decreased, as the distance between items in each pair increased (e.g. BD vs. BE). In Experiment 4, we trained adjacent pairs with separate 9- list and 5-item lists. We then tested with nonadjacent pairs selected between lists to determine whether list items were chosen according to their absolute position (e.g. D, 5-item list > E, 9-item list), or their relative position (e.g. D, 5-item list < E, 9-item list). Both monkeys’ and humans’ choices were most consistent with a relative positional organization.

As defined by the principle of transitivity, if given the premise that A is greater than B, and that B is greater than C, it logically follows that A must also be greater than C. Piaget argued that the ability to make transitive inferences (TI) is a defining feature of concrete operational thinking in young children (Piaget, 1954; Piaget, Inhelder & Szeminska, 1960). This ability is useful because it allows hierarchical relationships to be organized using minimal information. TI may also be useful to animals, particularly to those animals whose social structure is organized by a linear dominance hierarchy. Because dominance relationships are often established through aggressive physical encounters, the chances of injury or death may be reduced if the animal can learn its ranking with the fewest number of necessary encounters. Inferring dominance relationships by watching dyadic interactions would eliminate the need to physically engage each animal in the group (Bond, Kamil, & Balda, 2003; Grosenick, Clement, & Fernald, 2007).

To investigate transitivity in animals, McGonigle and Chalmers (1977) developed a nonverbal testing technique in which pairs of adjacent and arbitrarily selected list items were presented to squirrel monkeys e.g., AB, BC, CD, DE (see also Bryant & Trabasso, 1971). Selection of the "correct" item from a given pair produced a reward; selection of the incorrect item, a time-out (TO). Once a criterion level of performance was reached, a previously untrained, nonadjacent pair was presented (e.g. BD). If the animal could extrapolate an overall list order from relationships between adjacent pairs, then accuracy to nonadjacent pairs (e.g. BD, BE, CE, etc.) should be greater than that predicted by chance. McGonigle and Chalmers (1977) showed that this was the case for squirrel monkeys. Additional evidence for TI has been found in a many other species as well [Bond, Kamil, & Balda, 2003 (pinyon jays); D’Amato & Colombo, 1990 (Cebus monkeys); Davis, 1992 (rats); Gillan 1981 (chimpanzees); Grosenick, Clement, & Fernald, 2007 (fish); Lazareva et al., 2004 (crows); MacLean, Merritt, & Brannon, 2008 (lemurs); Treichler & van Tilburg, 1996 (rhesus monkeys); von Fersen et al., 1991 (pigeons)].

These studies are significant because they extend the scope of animal cognition in a new direction. They also pose the challenge of identifying a nonverbal mechanism that can account for the behavioral signatures commonly observed during training and testing of TI. One is the serial position effect (SPE) that occurs during adjacent-pair training; the other is the distance effect that is observed during testing with nonadjacent pairs (D’Amato & Colombo, 1990). The SPE refers to the fact that during training, accuracy is greatest for pairs that contain an end item, e.g., AB and EF from a 6-item list, and lowest for pairs that only contain middle items, e.g. CD. The distance effect refers to the fact that accuracy increases and RT decreases as the distance between items during testing increases, e.g., BC, BD, BE.

The SPE and distance effects have been cited as evidence that, like humans, monkeys integrate list items into a linear representation (D’Amato & Colombo, 1990; Treichler & van Tilburg, 1996; Treichler, Raghanti, & van Tilburg, 2003). Others have argued that elementary conditioning processes and reinforcement history can account for the SPE and distance effects (Couvillon & Bitterman, 1992; Delius & Siemann, 1998; Frank, Rudy, & O’reilly, 2003; Frank et al., 2005; Wynne et al., 1992).

Reinforcement-based theories can indeed account for some of the qualitative response patterns observed during both training and test. During training, selection of each non-end item produces reinforcement half of the time, e.g. C in a CD pair, and does not produce reinforcement the other half of the time, e.g. C in a BC pair. A challenge for reinforcement-based models is explaining transitive performance for these middle pairs, which are reinforced equally often. One of the most frequently cited models is based on Value Transfer Theory (VTT), which asserts that positive value is transferred from the reinforced item (e.g. A) to the nonreinforced item (e.g. B) in any given pairing (von Fersen, et al. 1991). Thus, even though middle items are all reinforced equally, the transferred positive values create the ordering B > C > D. Accordingly, B is chosen over D in a transitive test. Other models can predict TI performance, but usually only under very specific training conditions (Couvillon & Bitterman, 1992; Lazareva et al., 2004; Wynne, 1995).

Because conditioning models are based on reward history, there are some data for which any conditioning model would seem inadequate. For example, Paz-y-Mino et al. (2004), showed that pinyon jays were able to infer their rank within a social dominance hierarchy simply by watching known conspecifics interact with novel birds. Conditioning models have difficulty explaining this result because pinyon jays had no history of reinforcement with the birds in question. In another study, Treichler and van Tilburg (1996) trained monkeys on two separate 5-item lists (e.g. A+B−, B+C−, C+D−, D+E−, and F+G−. G+H−, H+I−, I+J−) and later linked these lists by training the single pair (E+F−). Accurate performance on test pairs that were composed of items from each list demonstrated that the monkeys connected the two lists to form a single 10-item list, as opposed to two separate lists organized by their within-list associative values. The linking of two lists via training on a single pair presents difficulties for any model that bases its predictions on differences in the associative strength of list items. These experiments, and others in which monkeys learned various serial tasks (Chen, Swartz, & Terrace, 1997; Terrace, 1991, 1993; Terrace, Son, & Brannon, 2003), suggest that monkeys may solve transitivity problems by forming a linear representation of the list items.

How can serial position and distance effects be explained if monkeys use a linear representation to make transitive choices? For humans, it has been proposed that transitive choice might result from an ends-inward serial scan. Two scan processes are initiated, one from each end of the list, and the scan proceeds inwardly until one of the processes finds a match (Holyoak and Patterson 1981; Jou 1997; Merikle & Coltheart 1972; Parkman, 1971; Trabasso, Riley, & Wilson, 1975; Trabasso & Riley, 1975; Woocher, Glass, & Holyoak, 1978). If the scan process that starts at the beginning of the list is first to reach an item, then a response occurs to that item. Conversely, if the scan that starts at the end of the list reaches an item first, a response occurs to the other item by default. This process can explain both the SPE and distance effect because items that are separated by a larger distance will, on average, have an item closer to one of the ends than items that are separated by smaller distances. If the time needed to scan through the list is the primary determinant of response latency, and if the probability of error increases with each scanned item, then accuracy should increase, and RT should decrease with increasing separation distance between the pairs. By using the same logic, an ends-inward scan can also account for the SPE. For example, on a 7-item list, fewer transitions are needed for pairs near one end of the list (such as BC, EF) than for pairs located in the middle (such as CD).

Positional discriminability models can also account for the SPE and distance effect (Holyoak & Patterson, 1981). During training, the beginning and end items are typically learned first. Some models suggest that they serve as positional reference points for the other items. As a result, new items are given two-dimensional position codes (beginning and end) based on their proximity to the beginning and end items (Henson, 1998, 1999). These codes are imprecise, forming a normal distribution centered on the item's veridical position. Once a code is generated for each item, a comparison process computes the difference between the two position codes. This information sampling process is iterative, occurring repeatedly until it reaches a cumulative difference threshold, at which point one of the two items is selected (Holyoak & Patterson, 1981; Jou, 1997).

Because items that are close together, e.g. CD, have more positional overlap than items that are farther apart (e.g. BE), more information sampling is required in order to make a decision. Items that are farther apart will thus be discriminated more quickly and easily than items that are close together (i.e. the distance effect). Positional uncertainty can also explain the SPE. By mere proximity, the positional uncertainty distributions for middle items will have more overlap with the distributions of other items than will beginning and end items. It is also the case that in many models, the distributions of middle items are wider and flatter than those of beginning and end items (Bower, 1971; Henson, 1999; Murdock, 1960; Trabasso & Riley, 1975). Thus, one would expect more errors and longer RT’s for middle items than for end items.

We conducted four experiments to investigate which of these underlying mechanisms might be responsible for transitive performance. During each experiment, humans and rhesus monkeys were trained with various types of adjacent pairs and then tested on nonadjacent pairs that were composed of the items used during the training phase. The purpose of Experiment 1 was to verify that our method for training transitive inference would produce the standard SPE and distance effects previously observed in other experiments. Each of the subsequent experiments was designed so that successes and failures were diagnostic of the manner in which list items were organized and represented in memory. Although previous experiments have demonstrated that humans and monkeys show similar response patterns, the present experiments go one step further by asking whether these patterns are also governed by similar mechanisms.

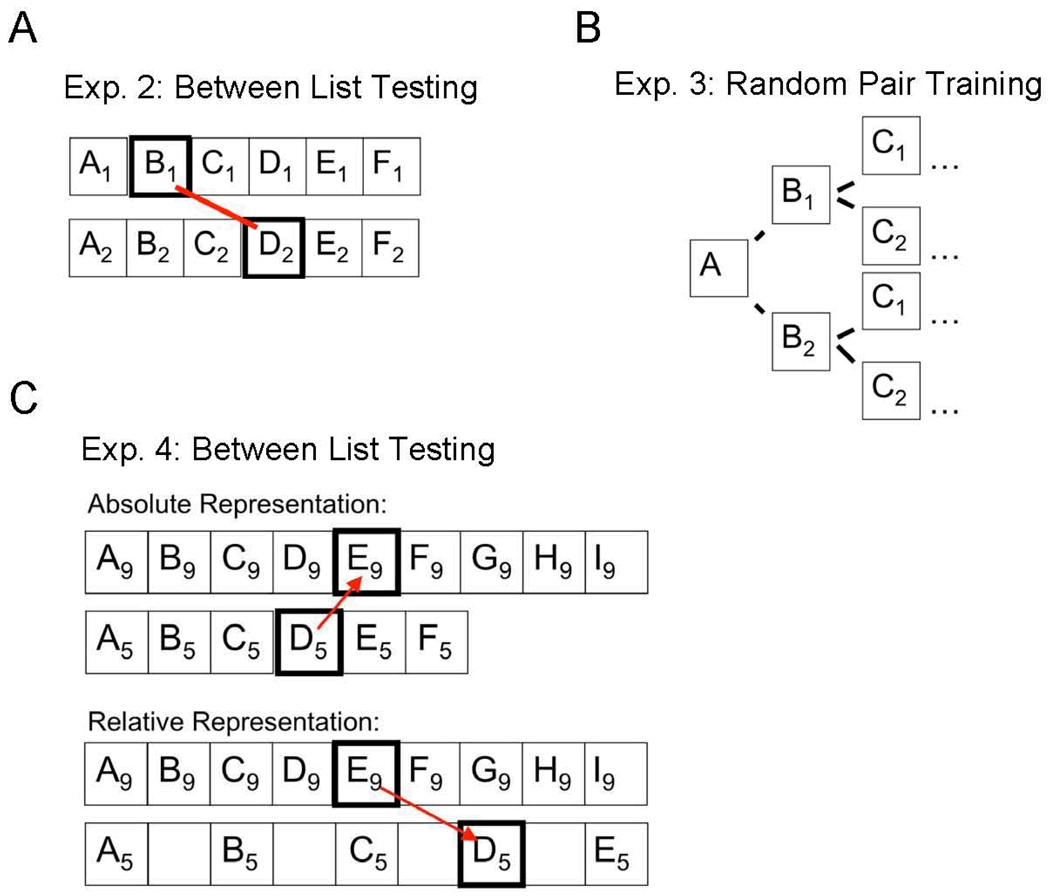
The purpose of Experiment 2 was to determine whether the human and non-human participants in Experiment 1 were able to make accurate ordinal judgments when pairs of items were selected from different lists (see Treichler, Raghanti, & van Tilburg, 2003). For example, given the presentation of pair B₁D₂, where B₁ was selected from List 1, and item D₂ was selected from List 2, would participants correctly order the items of the B₁D₂ test pair by selecting item B₁ (Figure 1A)? Failure to do so would suggest that accurate ordinal judgments were restricted to within-list pairs, and that the probable mechanism was an ends-inward associative scan that could only be performed on a single list at a time.

Figure 1.

(A) During between-list testing, test pairs were composed of items drawn from different lists. The subscripts represent the list number. (B) There were two items per position, with each item having a 50% chance of appearing for any given position. For example, “A” was randomly paired with one of two “B” items (e.g. B₁ and B₂). (C) A five and a nine-item list arranged spatially according to the between-list subjective similarities that are predicted from a relative versus absolute positional representation. The subscripts represent the list length.

Notably absent from most scanning models, is mention of the connective linkage that allows the scan process to transition from one item to the next. Experiment 3 tested the hypothesis that participants used positional information when making order judgments. If transitions from one item to the next were mediated by associative linkages (Jou, 1997), associative competition between list items should make it very difficult for such linkages to operate (Figure 1B). Failure to make accurate judgments during testing would suggest that subjects did not understand the positions of the items, and instead, relied on associative links in order to guide an ends-inward scan.

Although successful test performance during Experiment 3 would suggest that associative scanning was not used, it still leaves open the possibility that scanning by ordinal position occurred. Under this scenario, each list item is placed into an ordinal slot or bin, whose contents could later be scanned for content (see Conrad, 1965, Henson, 1998, Orlov et al., 2006). This is functionally very similar to an associative scanning process, but it differs with respect to the suggested linkage that allows scanning to proceed from one item to the next. Rather than associative linkages, the slots themselves have a fixed order which dictate how scanning will proceed. This results in a very different type of positional representation than that described for the positional discriminability model. Because the memory slots are fixed, the nature of the positional representation will be ordinal, such as "first", "second", and "third" (Orlov, et al. 2000; Orlov et. al. 2006). In contrast, if the beginning and end items serve as salient anchor points by which other list items are organized (e.g. Henson, 1999), then items should be represented with respect to their relative positions ("beginning", "middle", and "end").

In Experiment 4 we asked whether item positions were represented by their absolute or relative value. A simple way to compare the absolute and relative models is to visually map a comparison of two lists of different lengths, say a 5-item and a 9-item list. Absolute and relative representations would give rise to different judgments of subjective similarity. If judgments are made by scanning ordinal memory slots, one would expect item C from the 5-item list (A, B, C, D, E) to be subjectively most similar to item C from the 9-item list (A, B, C, D, E, F, G, H, I). However, if the items were organized relative to the beginning and end of the list (as assumed by the positional discriminability model), then subjective similarity should be greatest when item C from the 5-item list is compared with item E from the 9-item list. This is because they both occupy the middle position within their respective lists (cf. Figure 1C).

Experiment 1

Within list training and within list testing

The purpose of Experiment 1 was to verify that our training methods would produce the SPE and distance effects observed in previous experiments (e.g. Moyer & Landauer, 1967; Trabasso & Riley, 1975). We also wanted to compare RT and accuracy functions obtained from humans and monkeys to determine the extent to which they were qualitatively similar.

Subjects

Three male rhesus monkeys (Macaca mulatta) and 15 adult humans participated in this experiment¹. One monkey (Benedict) was 7 years old, and had approximately 5 years of previous cognitive testing before these experiments began. The other two monkeys (Ebbinghaus and Lashley) were both 5 years old with approximately 3 years of previous cognitive testing with numerical stimuli (Brannon & Terrace, 1998). The 15 undergraduate students from Columbia University were paid to participate in all 4 experiments conducted in this study. As with monkeys, a within-group design was used to train and test human participants.

Apparatus

Humans were tested with a Macintosh G4 computer that was connected to a 15-inch computer monitor. A 15-inch Magictouch touch screen was affixed to the computer monitor in order to record selections made by the participant. The monkeys were transferred from their home cages to the experimental apparatus prior to each testing session. Training and testing took place in a chamber (23" wide × 27" long × 28.5" deep) that contained a 15" touch sensitive video monitor and a reinforcement hopper. The test chamber was completely enclosed in a sound-attenuated booth. All software was written in the RealBasic programming language.

Procedure

The stimuli were digitized photographs of natural objects and artificial structures (e.g. animals, people, scenery, flowers, cars, bridges etc.). Each photograph measured 1.5" × 1.5" in size, and was arbitrarily selected from a library of approximately 2500 photographs. The screen was divided into a 4×4 matrix that provided 16 locations for presenting photographs. However, in the present experiment, only 3 locations were used; specifically, the 3 locations in the top row of the matrix, starting from the left edge of the matrix. The positions of the photographs used during each trial were chosen at random. All of the stimuli were presented on a blue background. The start-stimulus was a 2" × 2" white square that was presented in the center of the screen.

At the onset of each trial, the start-stimulus was presented. A response to the start-stimulus caused it to disappear. After a 0.5 sec delay, monkeys and humans were presented with a pair of adjacent items randomly selected from a 6-item list (A+B−, B+C, C+D−, D+E−, and E+F−). Selection of the correct item (+) caused the screen to turn red, and a reward to be delivered (the word “CORRECT!” for humans, and a banana flavored pellet for the monkeys). Selection of the incorrect item (−) produced a 3-sec timeout (TO) during which the screen was black. For humans, the word “INCORRECT!” was flashed across the screen. Differential auditory feedback was provided both for correct responses and errors. Correct responses produced a “positive” sound; incorrect responses, a “negative” sound. If a selection was not made before a 5-sec time limit expired, the trial ended with a TO.

The monkeys were trained daily, 100 trials per session. Correct and incorrect choices had to be learned by trial and error. The testing phase began once monkeys reached a criterion performance of 80% correct, for each adjacent pair, for two consecutive sessions. During testing, non-adjacent pairs were presented for the first time, randomly intermixed with adjacent items.

Human participants had a single 300 trial training session. Participants were told that some pictures were “better” than others, and that they would learn these relationships through trial and error. No mention was made of the inherent order of the items. Accuracy was analyzed in blocks of 50 trials. In order to be eligible for testing, participants were required to reach a criterion performance of 80% correct for all training pairs by the fifth block. For humans, training accuracy was assessed during the criterion block and the block that immediately preceded criterion performance. For monkeys, the last 5 sessions (including the criterion session) were assessed.

Pair Testing

The monkeys were given six 105-trial test sessions in which all possible pairs were drawn from the 6-item list (AB, AC, AD, AE, AF, BC, BD, BE, BF, CD, CE, CF, DE, DE, EF). The pairs were drawn at random with the constraint that all pairs had to be presented an equal number of times during the 105-trial session. Choices were non-differentially reinforced (i.e. both correct and incorrect choices were rewarded), and no time-outs were given for any of the responses. Because the non-differential contingency created the possibility that monkeys could learn to select any item to obtain reward, test- and training-sessions alternated every day (i.e. test sessions and training sessions were given every other day). Testing of the human participants was identical to that of the monkeys, with the exception that human participants were only given a single 105-trial test session.

Results and Discussion

Training

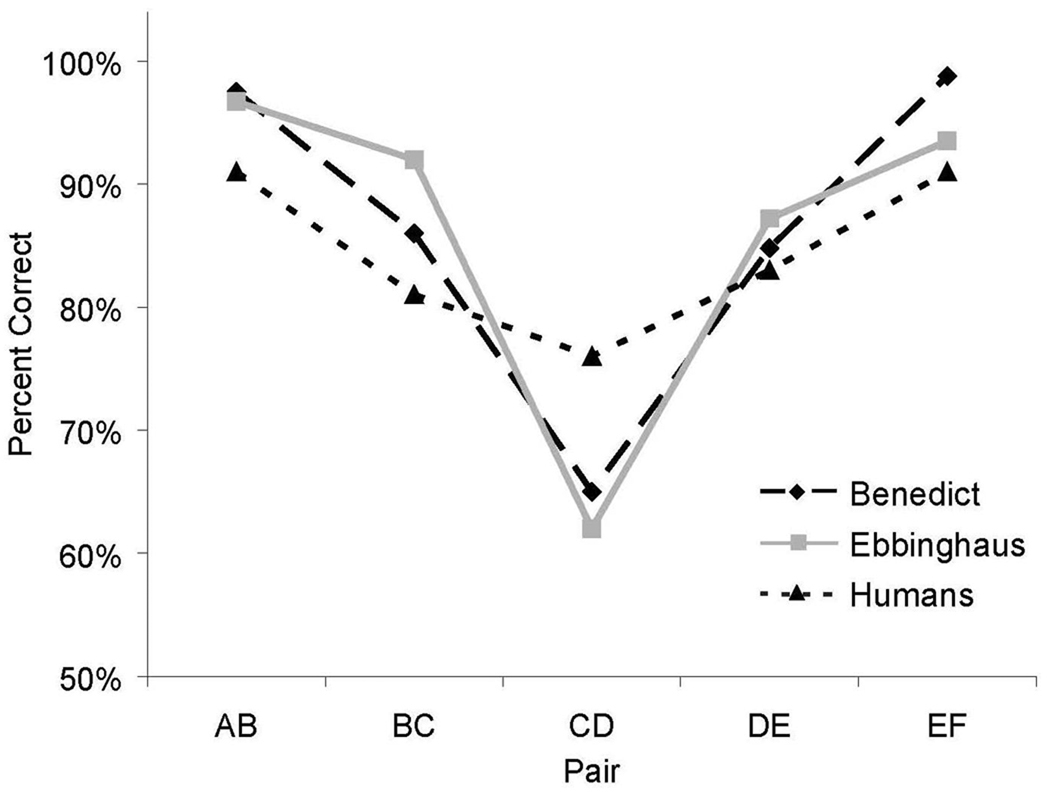
Serial position effects were obtained from both humans and monkeys. As shown in Figure 2, an SPE was obtained from both Benedict and Ebbinghaus. Accuracy for middle pairs, e.g. CD, was lower than accuracy for end pairs, e.g. AB, EF. Although the both humans and monkeys showed a U-shaped accuracy function, the serial position effect for the human participants was much smaller than it was for monkeys. One reason may be that the human participants had much greater experience processing symbolic sequential information compared to monkeys, and therefore may have developed strategies to improve performance on the difficult middle pairs.

Figure 2.

The serial position effect during training for humans and monkeys. For humans, the data include mean accuracy for the criterial 50-trial block combined with the immediately preceding 50-trial block. For monkeys, the data include the last five sessions of training including the criterial session.

Pair Testing

Because responses to the first item (A) were always rewarded, and responses to the last item (F) were never rewarded, it is possible that reinforcement alone could explain the differences in accuracy and reaction time for pairs with those items. This could explain distance effects because pairs with end items are separated (on average) by larger distances than non-end pair items. To eliminate this confound, only internal (non-end) pairs from the list were used for reaction time and accuracy analyses.

Statistical analyses were the same as Experiment 1 for all four experiments. For monkeys, linear regressions were conducted on median session RT’s of internal test items, and one-way analyses of variance (ANOVA) were conducted on mean session accuracies of internal test pair items. For humans, within-subject ANOVAs were conducted on the accuracy and the median RT for internal test pairs.

Accuracy

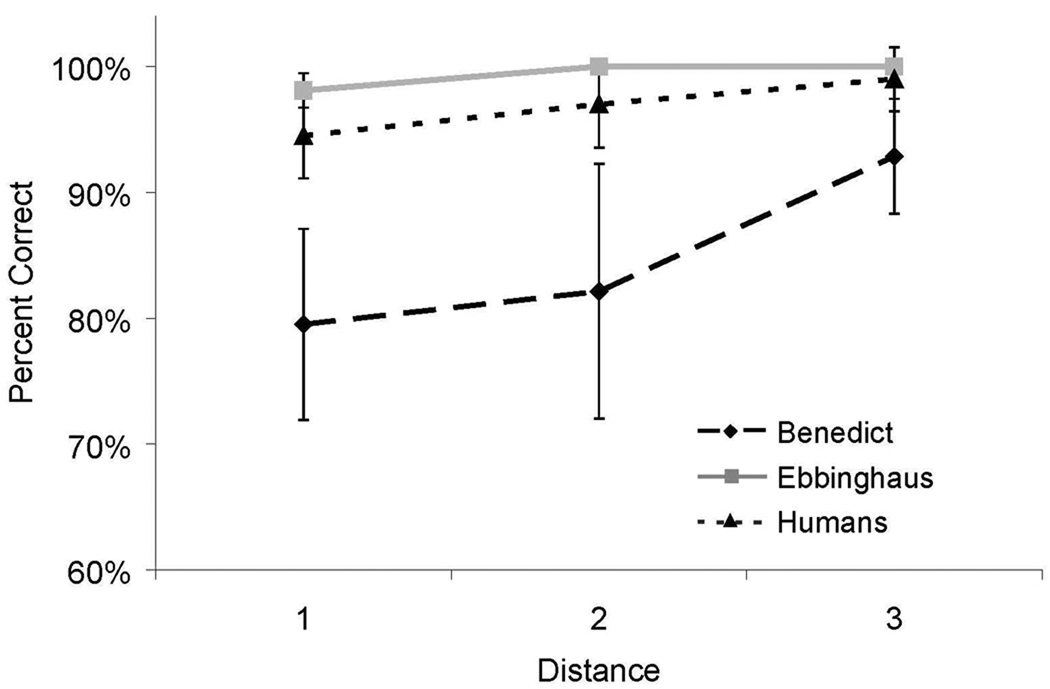
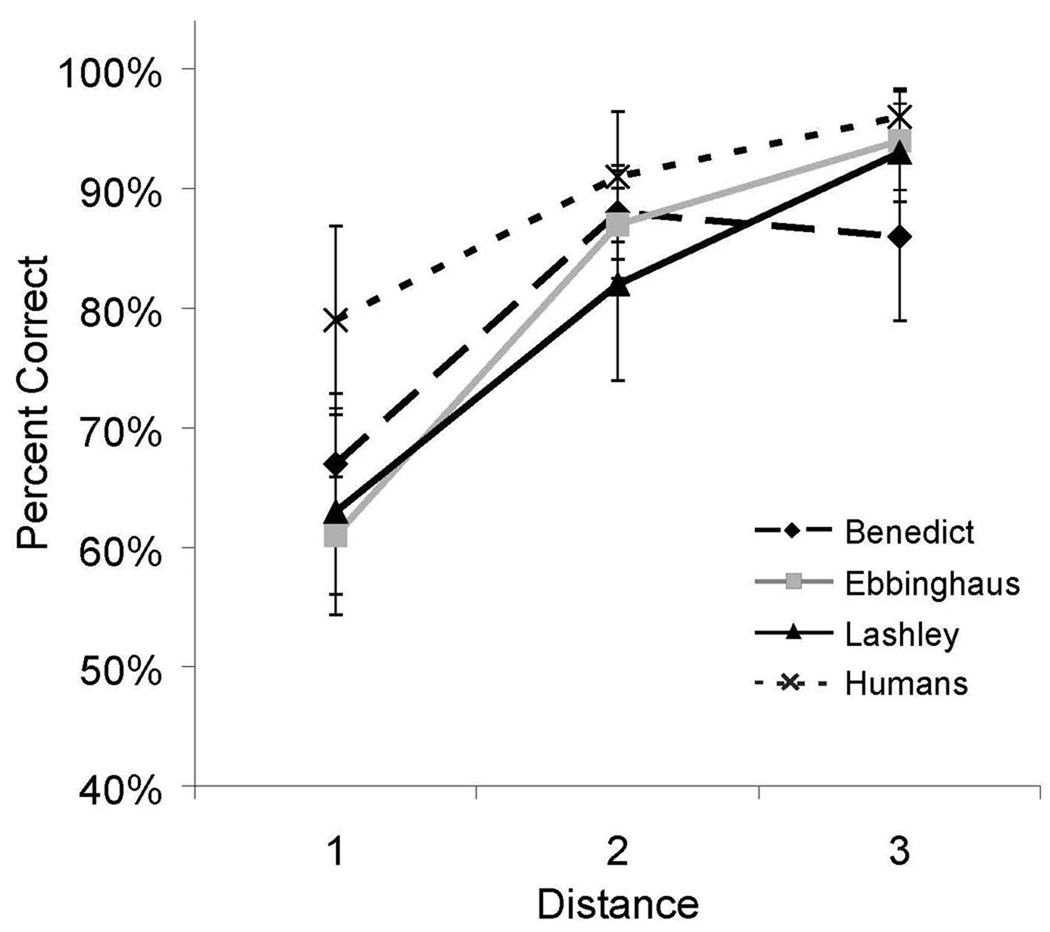
As shown in Figure 3, a distance effect was obtained for both humans and monkeys. Accuracy increased as the distance between items increased. However, for humans, the accuracy distance effect was only borderline statistically significant [Benedict, F(2,27) = 3.57, p < .05, η² = 0.21; Ebbinghaus, F(2,27) = 6.00, p < .05, η² = 0.21; Humans, F(2,26) = 3.12, p = .06, , η² = 0.12]. As in other studies of transitivity (e.g. D’Amato & Colombo, 1990), accuracy was higher on the novel pairs with non-differential feedback than on adjacent pairs on which participants had received extensive training.

Figure 3.

Accuracy for all internal (non-end) test pairs in Experiment 1 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

Reaction Time

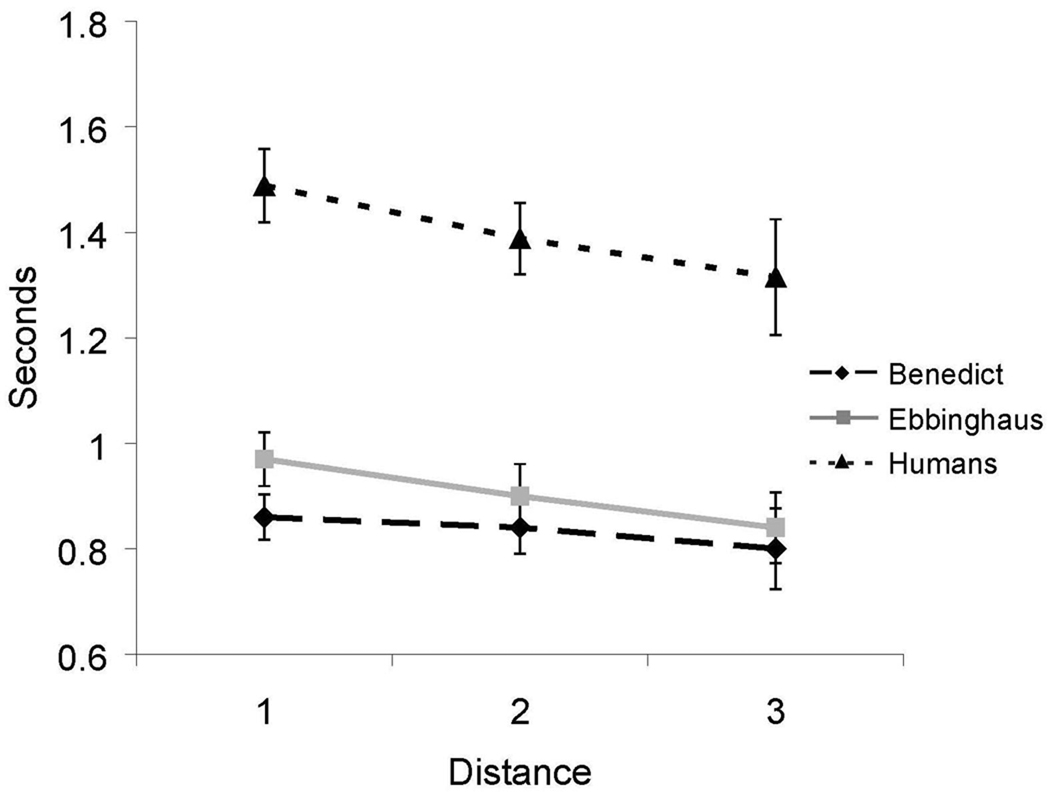
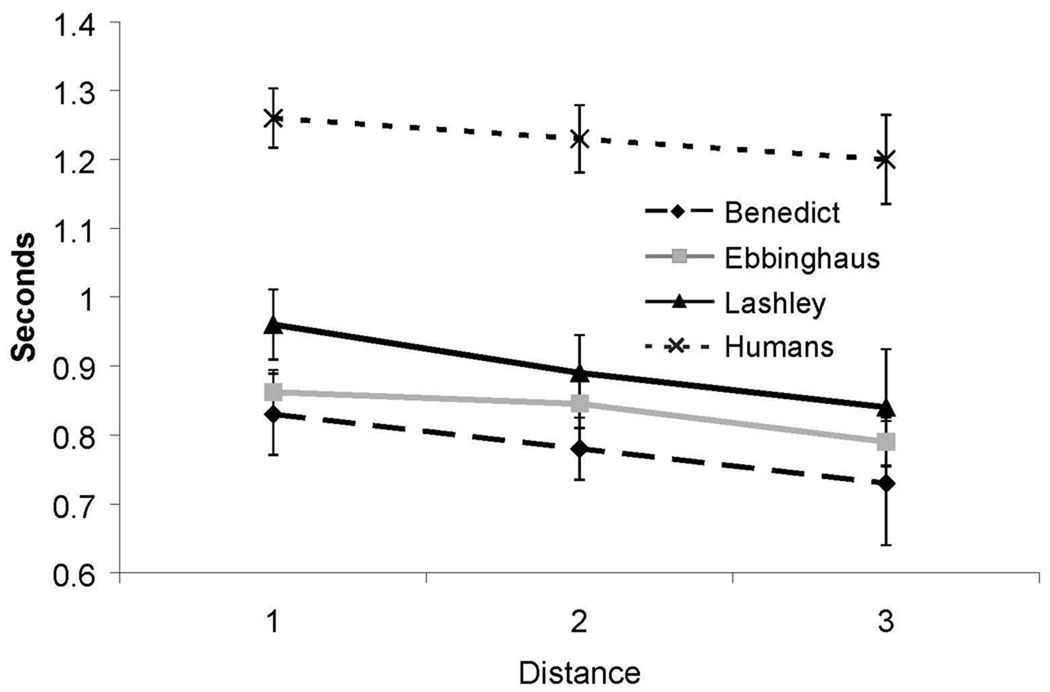
As shown in Figure 4, a distance effect, based on RTs, was also obtained from both humans and from one monkey. RT decreased as the distance between the test pairs increased [Ebbinghaus, F(1,28) = 6.82, p < .05, R² = 0.20; Humans, F(2,26) = 4.2, p < .05, η² = 0.06]. While Benedict showed a similar pattern of decreasing RTs with increases in distance between test items, that difference fell short of statistical significance [F(1,28) = 1.66, p = .21].

Figure 4.

Reaction time for all internal (non-end) test pairs in Experiment 1 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

Given that non-differentially reinforced testing sessions were interspersed with regular training sessions, it is possible that the multiple sessions with non-differentially reinforced items may have affected performance over the course of testing. In order to examine this possibility, the first five test sessions (Session Block 1) and the last five test sessions (Session Block 2) were compared using a two-way ANOVA (Distance X Session Block) for accuracy and RT. We found no main effect of session block for either Benedict (Accuracy, F(1, 24) = 0.001, p = 0.97; RT, F(1, 24) = 1.05, p = 0.36) or Ebbinghaus (RT, F(1, 24) = 0.16, p = 0.69), and no interaction between session block and distance for Benedict (Accuracy, F(2, 24) = 0.41, p = 0.67; RT, F(2, 24) = 0.12, p = 0.88) or Ebbinghaus (F(2, 24) = 0.20, p = 0.82). Because Ebbinghaus’ accuracy was at ceiling for all pairs, his accuracy was not assessed for trends.

The results of Experiment 1 achieved two goals. It provided baseline accuracy and RT functions that were used to assess participants’ performance in Experiments 2–4. They also provided evidence that qualitatively similar patterns in accuracy and RT could be obtained from humans and monkeys during both training and testing.

Experiment 2

Within list training and between list testing

Experiment 2 was designed to determine whether participants were engaged in an associative ends-inward serial scan when making judgments of relative order. The participants, both humans and monkeys were the same as the ones used in Experiment 1. In Experiment 2, they were trained on a second list, and were then tested with nonadjacent pairs (Figure 1A), one item from list 1; the other from list 2, e.g., B₁D₂, C₂E₁, etc. List number indicated by subscripts, 1 or 2. If a self-terminating search process was used to scan a single list at a time (e.g. Sternberg, 1969), then it should not be possible to make between-list comparisons.

Method

Participants and Apparatus

The participants were the same as those used in Experiment 1, as was the apparatus.

Procedure

Monkeys

Testing occurred in two stages. During the first stage of testing, monkeys were trained, and then tested on adjacent and non-adjacent pairs from their new list using procedures identical to those of the previous experiment. This was done to confirm that the monkeys were able to make transitive choices on the second list as well. Following the first phase of testing, 3 sessions of retraining were given on their old list (from Experiment 1) intermixed with 2 training sessions from their new list. They were then given 5 sessions of within-session mixed training where either the new list, or the old list was presented during the first half of the session, and the other list was presented during the last half of the session (e.g. new/old, old/new). The order of new and old within-session presentations was switched for each session.

During the second phase of testing, monkeys were tested using the same procedures as described in Experiment 1, with the exception that items in each pair were drawn from different lists, e.g., A₁B₂, B₁D₂. Ten 105-trial test sessions were given, with all pairs presented an equal number of times (15 pairs, presented 7 times each). Choices were non-differentially reinforced, and no TOs were given for any of the responses. As in Experiment 1, test sessions were interspersed with training sessions in order to minimize any effect of non-differential reinforcement on accuracy.

Humans

Human participants were trained on a second list (Day 2) using the same procedures that were used in Experiment 1 (Day 1) with the following exceptions. Participants were given a 50 trial review of the list from Experiment 1, and were trained for 250 trials on a new 6-item list composed of novel stimuli. After participants had completed training on the second list, they were tested during a 105-trial session in which they were shown all possible pairs between lists. The procedure used for selecting test pairs was identical to that of the monkeys.

Results and Discussion

Pair Testing

The results of between-list pair-testing were very similar to the results of the within-list pair testing that were described in Experiment 1. As shown in Figure 5, accuracy exceeded chance levels on all pairs for both monkeys and humans. There was also a strong distance effect with regard to accuracy. As in Experiment 1, accuracy increased as distance between the test pairs increased (Humans, F(2, 26) = 21.3, p < .05, η² = 0.28; Benedict, F(2,27) = 15.11, p < .05, η² = 0.53; Ebbinghaus, F(2,27) = 48.33, p < .05, η² = 0.78; and Lashley, F(2,27) = 17.55, p < .05, η² = 0.57). The human participants and one monkey showed a statistically significant decrease in RT as the distance between pairs increased [Humans, F(2,26) = 4.4, p < .05, η² = 0.02; Lashley, F(1,28) = 5.67 , p < .05, R² = 0.17]. As can be seen in Figure 6, RT decreased with distance for the other two monkeys, but that decrease was not statistically significant [Benedict, F(1,28) = 1.37, p = .25; Ebbinghaus, F(1,28) = .07, p = .79]. As compared with the results of Experiment 1, there was a large drop in accuracy for adjacent-position test pairs at a distance of 1 (Figure 5). This was most likely due to the fact that, in Experiment 2, there was no explicit training on items from different lists that occupied adjacent positions.

Figure 5.

Accuracy for all internal (non-end) between-list test pairs in Experiment 2 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

Figure 6.

Reaction time for all internal (non-end) between-list test pairs in Experiment 2 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

The ability of humans and monkeys to order the between-list test pairs, cannot be explained by a single-list ends-inward associative scan. Although this suggests that monkeys and humans knew the positions of the items, it is possible that multiple lists were scanned simultaneously. This hypothesis seems plausible given that an ends-inward scan of a single list would require the parallel activation of two scanning processes, one at each end of the list. On this view, two self-terminating searches that were initiated simultaneously from the ends of both lists could account for the results obtained in Experiment 2. The results are also consistent with models based on positional scanning and also positional comparison.

Experiment 3

Can positional information be used in the absence of associative information?

The purpose of Experiment 3 was to determine whether positional information was used when making judgments of relative order. Our strategy was to interfere with associative scanning by eliminating item-item associations while at the same time preserving the order information provided by the individual pairs so that an overall order could still be extrapolated in a test for transitivity. The general training procedure was similar to that used in Experiments 1 and 2. The main difference was that for each position, one of two items appeared, with each having a 50% probability of appearing (see Methods). The resulting associative competition between items should effectively eliminate in item-item associative scan mechanism. If the participants used the information between training pairs to infer the order of nonadjacent pairs, it would suggest judgments were based on positional information.

Method

Participants and Apparatus

Participants and apparatus were the same as that used in Experiments 1 and 2.

Procedure

Both monkeys and humans were trained on a 7-item list using a training procedure similar to that used in Experiment 1. While the response contingencies and parameters remained the same as in Experiment 1, training differed in that participants were presented with one of two items per position for non-end items (e.g. B₁ or B₂ for second position, C₁ or C₂ for third position, etc.). Items that occupied the same position (e.g. B₁ B₂) were not presented. Each item in a given pair had a 50% probability of appearing (Figure 1B). For example, there were four possible "BC" pairs (B₁C₁, B₁C₂, B₂C₁, B₂C₂). Unlike the interior items, each end item (A and G) was represented by only one item. Overall, there were 20 possible pairings, and each pair was presented 5 times per 100 trial session. Monkeys were trained daily until they obtained an accuracy of 70% correct on all pairs for two consecutive sessions, after which, they were given ten 105-trial (21 pairs, 5 trials each) testing sessions. All test sessions were interleaved with training sessions, so that test sessions and training sessions occurred every other day.

Human participants were trained for two consecutive days. On the first day, participants were given 400 training trials. On the second day, they were given 300 training trials that were followed by a 105-trial test session in which all possible pairs were tested. In order to be eligible for testing, participants were required to make correct choices 70% of the time for all possible pairs in a given 100-trial training block.

Pair Testing

During testing, items were drawn from adjacent and nonadjacent positions. All pairs were drawn at random with the constraint that all pairs had to be presented an equal number of times. As described earlier, each set of non-end pairs had four possible configurations (x₁y₁, x₂y₁, x₁y₂, x₂y₂). All configurations were selected at random, and were not necessarily presented with equal frequency within a particular session, but were approximately equal over the course of all sessions. As with the previous experiments, end-items were not included in pair testing analysis².

Results and Discussion

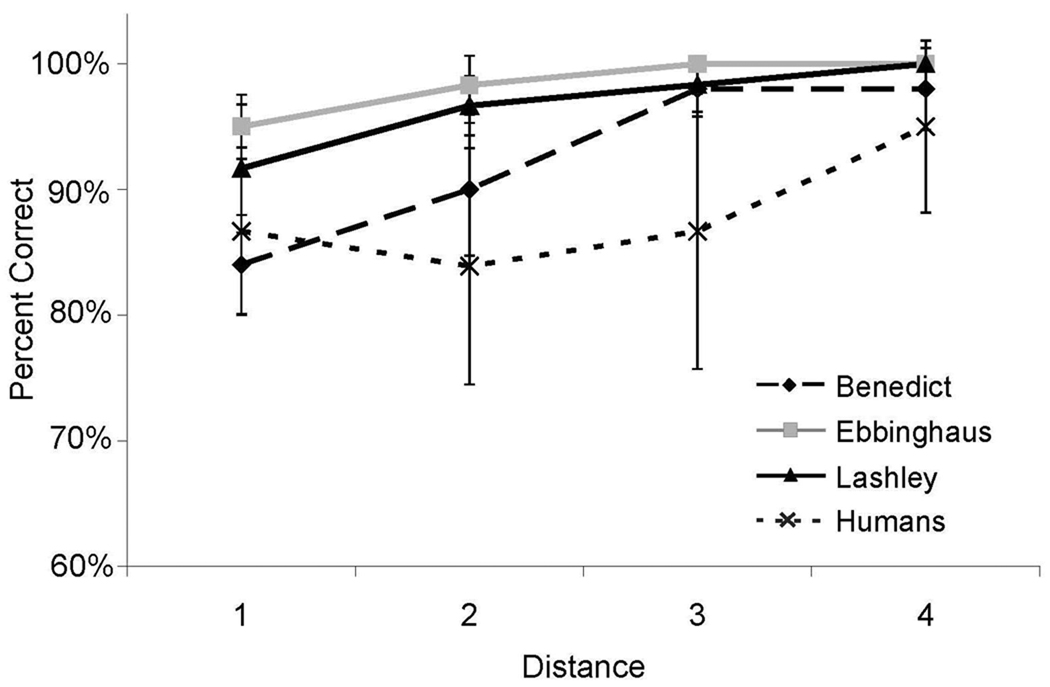
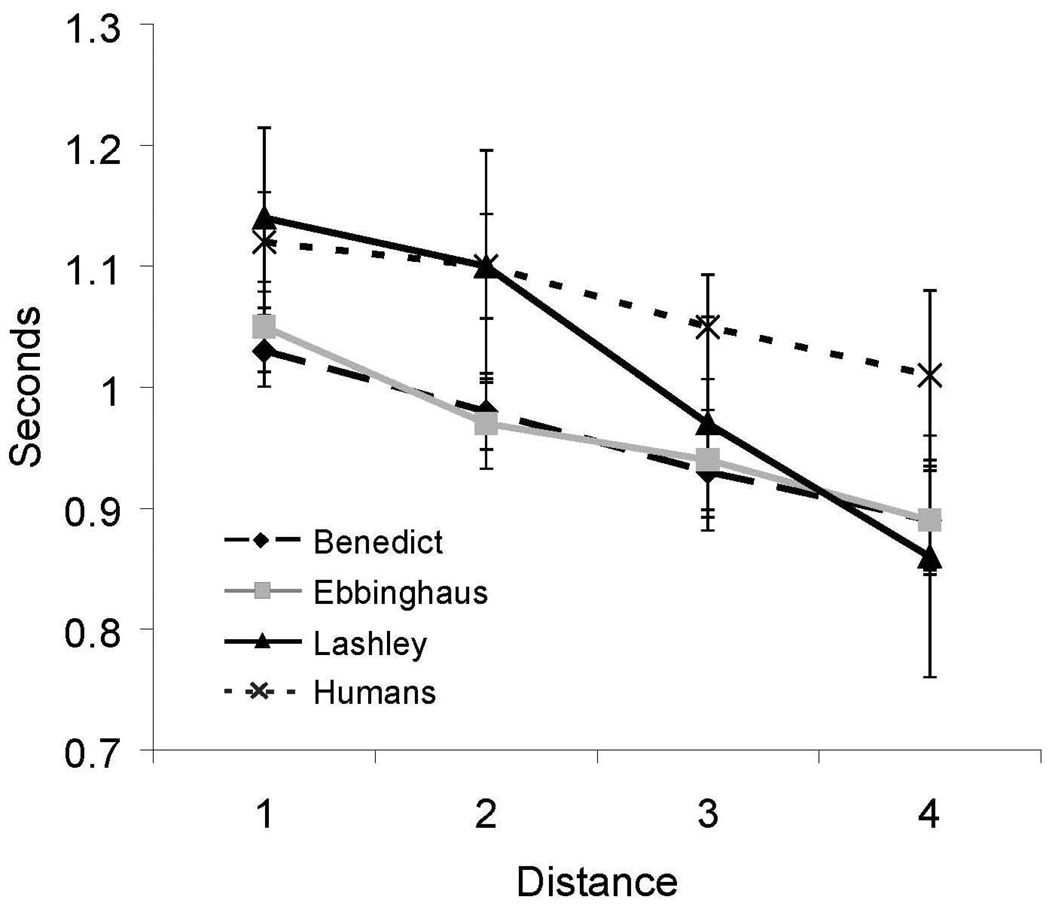
Even though there were two items for each position, Ebbinghaus was able to reach criterion performance in 8 sessions, Lashley in 29 sessions, and Benedict in 37 sessions. As in Experiments 1 and 2, monkeys and humans responded correctly to test pairs at a greater than chance level of accuracy (cf. Figure 7). Both species showed distance effects with respect to accuracy [Humans, F(3,39) = 4.6, p < .05, η² = 0.09; Benedict, F(3,44) = 12.58, p < .05, η² = 0.46; Ebbinghaus, F(3,44) = 6.74, p < .05, η² = 0.31; Lashley, F(3,44) = 5.24, p < .05, η² = 0.26); and as shown in Figure 8, also with respect to RT [Humans, F(3,39) = 4.7, p < .05, η² = 0.06; Benedict, F(1, 46) = 45.73, p < .05, R² = 0.50; Ebbinghaus, F(1, 46) = 13.93, p < .05, R² = 0.23; Lashley, F(1, 46) = 40.12, p < .05, R² = 0.47]. One notable difference in the accuracy function obtained from humans in Experiment 3, is that the lowest accuracy occurred at a distance of 2 (rather than at a distance of 1). There is no obvious explanation for that outcome. We expect that further experimentation examining amount of training, list length, and other variables that equate overall list difficulty between the two species may help explain this finding.

Figure 7.

Accuracy for all internal (non-end) between-list test pairs in Experiment 3 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

Figure 8.

Reaction time for all internal (non-end) between-list test pairs in Experiment 3 as a function of distance between items for both humans and monkeys. Error bars represent 95% confidence intervals.

When interpreting the results of Experiment 3, it may seem reasonable to ask, why couldn’t multiple serial scans, as discussed at the end of Experiment 2, operate during the random-pair training and testing phases of Experiment 3? To answer this question, it is important to remember that the only "connection" one item has to another is an associative link. In Experiment 2, when participants were presented with two discrete lists, there were single well-defined and unambiguous paths (determined by associative links) that each scanning process could follow. That allowed each list to be scanned independently of the other. Such independence however, is not possible on a random-pair list. For such a mechanism to work, additional non-associative mechanisms would be required to insure all items could be scanned, not just the ones with the strongest associative links.

We therefore concluded that an associative scanning mechanism could not account for the findings in Experiment 3. However, as mentioned earlier, this does not rule out the possibility of a positional scanning mechanism, where the items are given ordinal position codes, or are placed in ordinal bins whose contents can be scanned. Although we have established that positional information is used when making relative order judgments, the nature of this information is unclear. Are items placed in fixed ordinal positions (i.e. first, second, third, etc.), or are they organized by their relative positions (i.e. beginning, middle, end)?

Experiment 4

In Experiment 4 we asked whether list items were coded according to relative or absolute position. The training procedure was similar to that used in Experiment 2. Two lists were trained, and participants were then tested on pairs of items drawn from both lists. In Experiment 4 however, the lists were of different lengths; a 5-item and a 9-item list (See Figure 1C). If item position is represented via absolute position codes, then items from each list that occupy identical ordinal positions should also appear to have identical subjective positions (i.e. C₅C₉; subscript indicates list length). However, if order is represented by relative position codes, then items that occupy similar positions with respect to the ends of their list should appear subjectively most similar, i.e., C₅E₉. Thus, if the list is organized on the basis of relative position as shown in Figure 1C, the participants should prefer item E₉ to D₅ in the D₅E₉ pair. Alternatively, if a list is organized on the basis of absolute position, participants should prefer item D₅ to item E₉.

Method

Participants and Apparatus

The participants and apparatus were the same as those in the previous experiments.

Procedure

Humans

Human participants were trained on two new lists. Training and testing occurred over the course of two consecutive days, with one session per day. During the first session, participants were trained on new five- and nine-item lists. The training order for each list was randomized. During nine-item training, participants were given 296 trials of quasi-randomly drawn pairs from the list (37 trials for 8 pairs) using the same procedures that we used in Experiment 1. During five-item list training however, participants were trained with a procedure similar to that used in Experiment 3. This method was used because there are only four pairs in a 5-item list (AB, BC, CD, DE). For such a small number of pairs, it could be easier to learn a set of conditional discriminations than to learn the ordinal relationships between the items. Therefore, one of two possible items per position (e.g. B₁ or B₂ for second position, C₁ or C₂ for third position, etc.) was presented at random. As in Experiment 3, the end items were only represented by a single item. Thus, during adjacent-pair training, there were 12 unique pair combinations that were presented 8 times each for a total of 96 trials.

During session 2, participants were given more training trials on both the five and nine item lists, for 180 (15 trials/12 unique pairs) and 120 trials (15 trials/8 pairs) respectively. Training order for the five- and the nine-item lists was randomized. During testing, participants were presented with 60 test trials and 16 probe trials. The test trials included the critical test pair D₅E₉, and the pairs B₅B₉, C₅C₉, D₅D₉, & E₅E₉. The probe trials consisted of pairs D₅I₉, C₅H₉, B₅G₉, and A₅F₉. The probes were used to make sure that monkeys and humans were not biased against selecting items from the five-item list.

Monkeys

Monkeys received the same general training procedure on the 9- and 5-item lists as the human participants. The 9-item list was trained using a procedure identical to that of Experiment 1. Each session was 104 trials, with 13 trials for each of the 8 pairs. After meeting a training criterion of 70% correct for all adjacent pairs during two consecutive sessions, monkeys were tested on all 36 possible pairs that could be drawn from a 9-item list. Response contingencies during testing were the same as those of Experiment 1.

Preliminary Testing

Prior to training on the 5-item list, two of our monkeys (Ebbinghaus and Benedict) were given preliminary cross-list testing using the 7-item list from Experiment 3 and the newly trained 9-item list. The monkeys were given 6 test sessions, with each session containing 105 trials. The test sessions used non-differentially reinforced test pairs C₇C₉, D₇D₉, E₇E₉, F₇F₉, G₇G₉, E₇F₉ and F₇G₉. However, because the “G” items were never reinforced in the 7-item list, the G₇G₉ was excluded from data analyses.

Second List Training

All monkeys were trained on a 5-item list also using procedures that were identical to those used in Experiment 3. That is, positions B, C, and D all had two stimuli associated with them, one of which appeared randomly on a given trial. As with the human participants, this method was used to reduce the possibility of conditional discrimination learning given that there were only four pairs (AB, BC, CD, DE). Monkeys were given 96 trials per session (12 pairs and 8 trials per pair). Once a criterion level of 80% was reached for all adjacent pairs over the course of 2 consecutive sessions, the second testing phase began in which non-adjacent pairs were used as test items. The second testing phase was designed simply to verify that the monkeys were able to respond transitively on the 5-item list.

Retraining

Following the second testing phase, the monkeys were given 3 sessions of re-training on the 9-item list followed by 2 sessions of retraining on the 5-item list. During subsequent sessions, they were given mixed within-session training in which either the 9-item list pairs or the 5-item list pairs were presented during the first half of the session (i.e. 5-item list → 9-item list, 9-item list → 5-item list). The order in which the 9-item and 5-item lists were presented was alternated daily. The monkeys were given 56 trials per session during training on the 9-item list, and 48 trials/session on the 5-item list. Once the monkeys had reached criterion, between-list testing began.

Between-list testing

Once retraining was finished, the monkeys were tested between lists without differential reinforcement, in a manner similar to that described in Experiment 2. During testing, they were presented with 60 test trials and 16 probe trials. The testing trials consisted of the critical test pair D₅E₉, and also pairs B₅B₉, C₅C₉, D₅D₉, E₅E₉. The probe trials consisted of pairs D₅I₉, C₅H₉, B₅G₉, A₅F₉. Again, testing and training sessions were interspersed in order to prevent monkeys from learning that either item in the test pair could be selected to earn a reward.

Results and Discussion

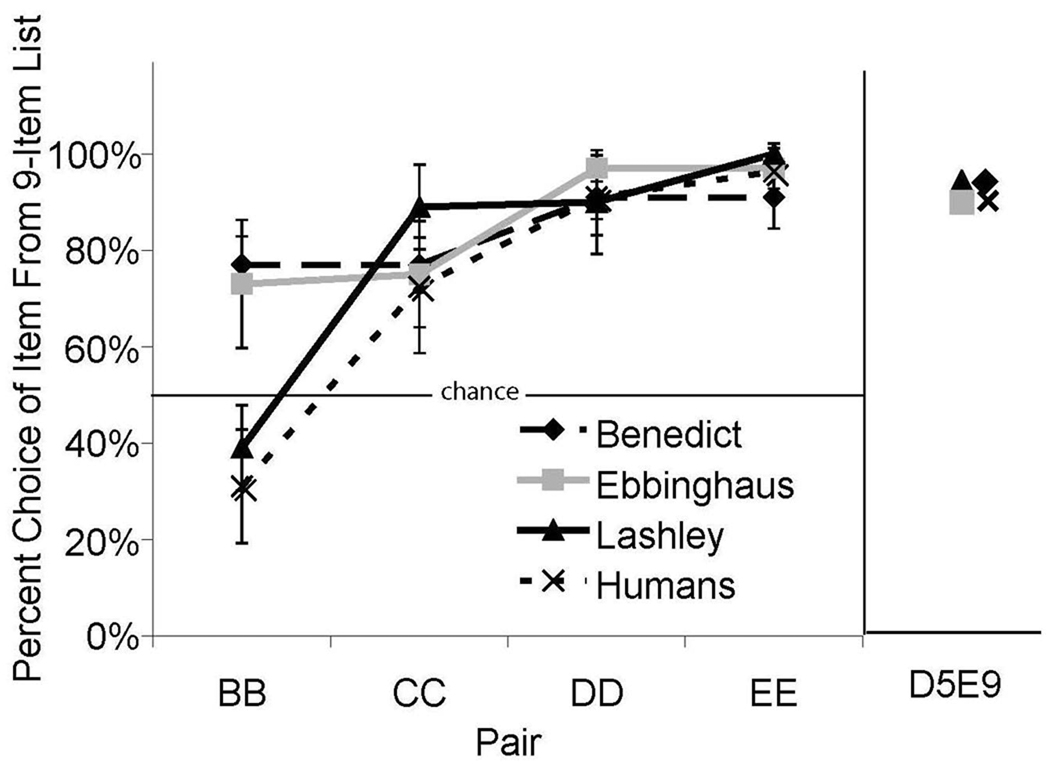
In general, the performance of both monkeys and humans supported the view that list items were represented by their relative positions. The relevant data are shown in Figure 9. With the exception of item B (for the human participants and Lashley), there was a strong preference for the item from the longer list when testing the same absolute positions across lists. If the end-points of the list are used as salient markers to assign position codes, then items occupying the same absolute position should begin to appear subjectively farther apart as one moves further into the list. For example, the subjective distance between C₅C₉ should appear smaller than D₅D₉. Our data confirmed this pattern. Preference increased for the item from the longer list as distance from the beginning of the list increased [Humans: F(3,39) = 14.49, p < .05, η² = 0.34; Benedict, F(3,44) = 8.15, p < .05, η² = 0.36; Ebbinghaus, F(3,44) = 12.40, p < .05, η² = 0.46; and Lashley, F(3,44) = 43.42, p < .05, η² = 0.75].

Figure 9.

Preference for item from the longer list when absolute position is held constant (e.g. B from the 5-item list versus B from the 9-item list). The D5 – E9 comparison represents a comparison of D from the 5-item list versus E from the 9-item list. Error bars represent 95% confidence intervals.

We have noted previously that representations based on the absolute and relative positions of list items predict opposite choices for the critical between-list pair D₅E₉. The bases for these predictions can be seen in Figure 1C. There should be a strong preference for item D₅ if list items were organized by absolute position. Conversely, there should be a strong preference for item E₉ if items were organized by relative position. As shown in the right-hand panel of Figure 9, both monkeys and humans chose E₉ more than D₅.

Data from the preliminary tests (9-item vs. 7-item) with Benedict and Ebbinghaus also fit with relative as opposed to absolute position. Preferences for the 9-item list increased with distance in a manner consistent with relative position. Preference for items from the 9-item list for pairs C₇C₉, D₇D₉, E₇E₉, F₇F₉ were 61.9% (CI_.95 = 51.1% – 71.7%), 73.8% (CI_.95 = 63.4% – 84.2%), 69.2% (CI_.95 = 61.2% – 77.2%), and 85.7% (CI_.95 = 81.0% – 90.4%), respectively for Benedict, and 4.8% (CI_.95 = 0% – 12.3%), 23.8% (CI_.95 = 15.8% – 31.8%), 66.7% (CI_.95 = 58.7% – 74.7%), and 100% respectively for Ebbinghaus. In addition, there were two pairs for which absolute and relative positional representations predict opposite patterns: pairs E₇F₉ and F₇G_9. If positions encoded in absolute terms, monkeys should prefer items from the shorter list. In contrast, if positions are encoded in relative terms, then they should prefer items from the longer list. Further, preference should be stronger for F₇G₉ than in pair E₇F₉, given that the subjective distance should be greater. Both Benedict and Ebbinghaus preferred the item from the longer list, and further, both monkeys showed a greater preference for the long-list item in pair F₇G₉ (Benedict = 82.9%, CI_.95 = 77.4% – 88.4%; Ebbinghaus = 100%) than to pair E₇F₉ (Benedict = 76.2%, CI_.95 = 63.4% – 89.0%; Ebbinghaus = 88.1%, CI_.95 = 73.6% – 100%).

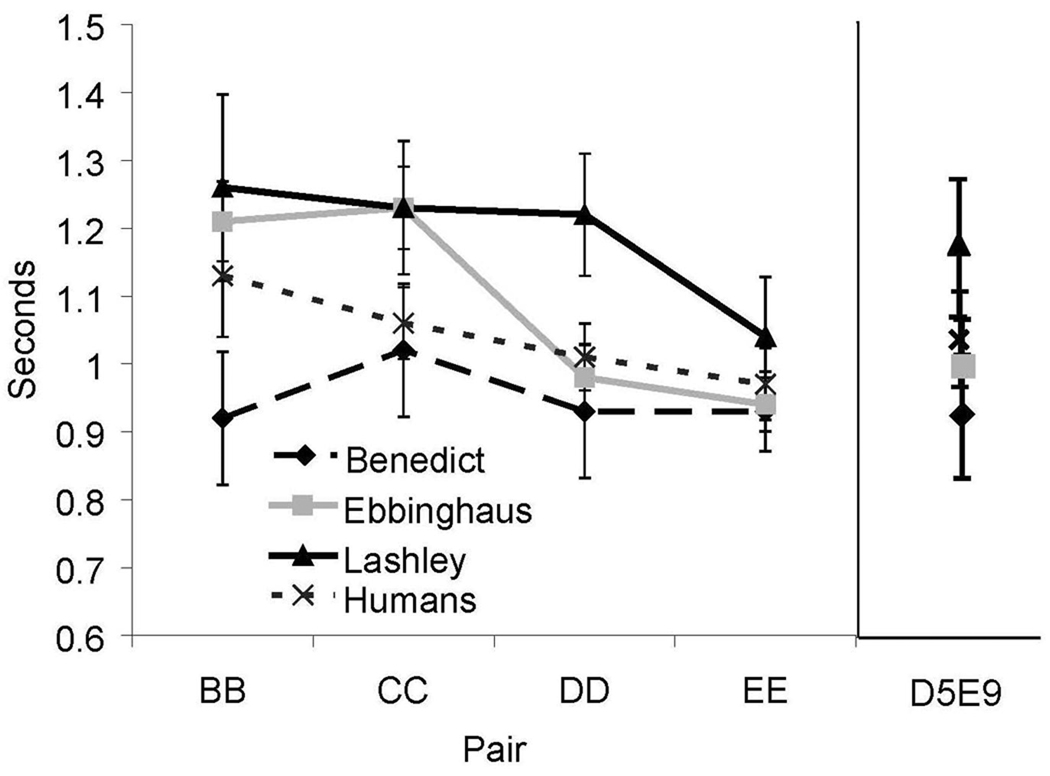
The distance effects we described above suggest that when participants make choices that are inconsistent with a relative positional organization, that those “incorrect” choices represent errors in positional discrimination. If so, we would expect that for all “correct” relative choices, there would be a reaction time distance effect that followed the pattern B₅B₉ > C₅C₉ > D₅D₉ >E₅E₉ in the 9-item vs. 5-item lists (see Figure 1C). As shown in Figure 10, that prediction was confirmed. For human participants, RT’s decreased as the subjective distance increased between the items from each pair (F(3,39) = 4.1, p < .05, η² = 0.08), and for Ebbinghaus (F(1,46) = 28.7, p < .05, R² = 0.38), but the decrease in RT only approached significance for Lashley (F(1,46) = 2.7, p = 0.10) and it was not significant for Benedict (F(1,46) = 0.36, p = 0.55).

Figure 10.

Reaction time for selections that were consistent with relative position. Error bars represent 95% confidence intervals.

Another explanation for these results is that participants had a general preference for items from the 9-item list. To test this hypothesis, 16 probe items were included in every 76 trial test session. The probe items were selected randomly from the set D₅I₉, C₅H₉, B₅G₉, and A₅F₉. If participants organized the list by relative position, they should prefer items from the shorter list. For humans, the choices for pairs D₅I₉, C₅H₉, B₅G₉, and A₅F₉ were 82.1%, 76.9%, 88.1%, and 85.7% respectively in favor of the items from the 5-item list. For monkeys, choices for pairs D₅I₉, C₅H₉, B₅G₉, and A₅F₉ also favored the 5-item list, with preferences of 83.3%, 81.25%, 94.44%, and 95.83% respectively for Benedict; 95.83%, 91.67%, 91.67%, and 97.92% for Ebbinghaus; and 87.50%, 100%, 94.44%, and 100% for Lashley. Thus, both humans and monkeys strongly preferred items from the shorter list. These data show that the performance we observed during our tests for absolute versus relative position cannot be attributed to a general preference for items from the longer list.

General Discussion

Previous accounts of transitive performance in animals focused primarily on associative models. A major limitation of these models is that they can predict performance accurately only under a very limited set of conditions (Lazareva, et al., 2004, Wynne, 1995), and none is able to account for some examples of transitivity in rhesus monkeys, (e.g. Treichler, Raghanti, & van Tilburg’s (2003) list linking procedure). Indeed, given the recent suggestion that humans and monkeys share a common system for some types of ordering tasks (Cantlon & Brannon, 2006), it is possible they may also share a common mechanism for determining relative order in a transitive inference task. Thus, we asked which type of model could explain transitivity in humans, and, whether the same mechanism could be used to explain transitivity in rhesus monkeys.

Our strategy was to challenge participants with progressively more difficult versions of the TI task that addressed the adequacy of different types of scanning and positional models as explanations of serial position and distance effects. Experiment 1 confirmed that serial position and distance effects could be obtained reliably following training on the TI paradigm that we used in all four experiments. Experiment 2 showed that both monkeys and humans could accurately order items that were selected from two different lists of equal length. In Experiment 3, associative competition was introduced to evaluate whether list items were associatively scanned.

The outcome of Experiment 3 suggested that positional information was used when making judgments of order. It was unclear, however, whether position was absolute e.g., first, second, third, or relative e.g., beginning, middle, end. This question was addressed in Experiment 4 by training participants on 9- and 5-item lists. Relative position was pitted against absolute position by assessing preference for E from the 9-item list versus D from the 5-item list. We also examined preferences for items that occupied the same absolute position (e.g. C from the 9-item list versus C from the 5-item list). In general, performance on these tests favored the view that participants’ choices were based on relative position as opposed to absolute position. This suggests that list items were organized and scaled relative to the end points of the list, and that list items were represented much like “beginning”, “middle”, or “end” rather than “first”, “second”, “third”, etc.

Awareness, associative models and transitivity

Recent research has focused on the role of “awareness” in the ability to make transitive inferences. Greene et al. (2001) found that human adults were able to make transitive inferences even when they were not explicitly aware of an underlying hierarchy. These results have led some researchers to conclude that humans solve transitive problems in two ways. When aware of the hierarchy, they use logical reasoning processes to infer the relative order of non-adjacent pairs. However, when they are unaware, they rely on simple associative mechanisms that are used to commonly explain transitivity in animals (Frank et al., 2005, Martin & Alsop, 2004). Thus far, the data are conflicting. Leo & Greene (2008) have shown that when end-items do not have differential reward values, unaware participants can still make accurate transitive choices – suggesting that unaware humans do not rely on associative mechanisms. Other studies have found that when humans are unaware of an existing hierarchy that performance falls to chance or near chance levels (Moses, Villate, & Ryan, 2006; Smith & Squire, 2005).

Could both humans and monkeys be solving transitivity problems by simple associative means, thereby explaining the similarities that we found? Frank et al., (2005) contend that while aware humans use logical reasoning processes to solve transitive problems, unaware humans and animals solve them by using differences in associative strength among the list items. Frank et al. argue that, even though reinforcement values for internal (non-end) items are roughly equal, a blocking effect (Kamin, 1968) of end items causes differences in excitatory associative strength that can explain transitive choices. Because end items perfectly predict response outcomes, (e.g. A and F in a 6-item list), participants do not have to pay attention to their adjacent items, e.g. B and E. Therefore, conditioning to these items is effectively “blocked”. This means that B is not decremented when selected incorrectly, and that E receives very little excitatory strength when it is selected correctly. However, B receives a lot of excitatory associative strength when paired with C, and E receives a lot of negative associative strength when paired with D. The net result of the anchor blocking effect is that B has much more excitatory associative strength than E, and therefore, participants will be more likely to select B than E, which is the correct transitive choice. Frank et al. offer several predictions from their model.

Because responses to test pairs occur on the basis of individual elemental associative strengths, accuracy to pairs that share a specific element should be correlated (Frank et al., 2005). For example, performance on BD should be correlated with pair BE, but should not be correlated with performance on pair CE. In order to investigate whether this was true of our data, we examined all pairs that shared an element in the human and monkey data in Experiment 1, as well as the combined data for all three monkeys in Experiment 2. We found no significant correlations between any pairs that shared an element except for pair CE and CD in Experiment 2 (r = 0.49, p = 0.008).

Frank et al.’s model also predicts that accuracy to middle pairs for longer lists should be particularly low because the differences in associative strength between middle items are small. In fact, they mention that the middle nonadjacent pair from a 7-item list (CE) should be particularly difficult and produce very low accuracy. We would therefore expect that on a 9-item list, the difficulty would be even greater for the middle pair DF, and that accuracy should be at or near chance. However, we did not find this to be true. For pair DF, Benedict, Ebbinghaus, and Lashley obtained accuracies of 83.3%, 95.8% and 75%, respectively.

Given the conflicting findings in the literature with regard to implicit versus explicit processing in humans, it is unclear whether humans truly use different mechanisms when they are aware than when they are unaware. We did not find any evidence that a common associative mechanism could explain the similarity in performance between humans and monkeys.

Conclusions

Humans and monkeys performed similarly in all four experiments, and members of both species organized list items according to relative, as opposed to their absolute positions. Similarities in the performance of humans and monkeys also suggest that, as with other continua (e.g. Cantlon & Brannon, 2006), both species share a common mechanism for organizing transitive information. Given that monkeys cannot formulate verbal representations, it is possible that both species co-opt existing mechanisms used for making decisions in perceptual space, and use those systems for making judgments about relative order. Indeed, recent experiments have established critical behavioral and neurobiological linkages between space and other continuous dimensions such as time (Basso et al., 1996; Boroditsky, 2000; Casasanto & Boroditsky, 2008; Merritt, Casasanto & Brannon, in press), number (Dehaene, Bossini, & Giraux, 1993; Hubbard et al., 2005; Walsh 2003), and even serial order (Previtali, de Hevia, & Girelli, 2009). Other studies have found similar behavioral signatures between spatial discrimination tasks and transitivity tasks (Holyoak & Patterson, 1981). If monkeys also link abstract continuous dimensions to space (e.g. Walsh, 2003), then we might expect relative position to transfer from one type of continuum (e.g. size) to another type of continuum (e.g. brightness). The degree to which the similarities between humans and monkeys are captured by a common spatial system, is an interesting question to pursue in future research.