Piecewise HIV virus dynamic model with CD4⁺ T cell count-guided therapy: I

Abstract

The strategies of structured treatment interruptions (STIs) of antiretroviral therapies have been proposed for clinical management of HIV infected patients, but clinical studies on STIs failed to achieve a consistent conclusion for this strategy. To evaluate the STI strategies, in particular, CD4⁺ T cell count-guided STIs, and explain these controversial conclusions from different clinical studies, in this paper we propose to use piecewise HIV virus dynamic models to quantitatively explore the STI strategies and investigate their dynamic behaviors. Our analysis results indicate that CD4⁺ T cell counts can be maintained above a safe level using the STI with a single threshold or a threshold window. Numerical simulations show that the CD4⁺ T cell counts either fluctuate or approach a stable level for a patient, depending on the prescribed upper or lower threshold values. In particular, the CD4⁺ T cell counts can be stabilized at a desired level if the threshold policy control is applied. The durations of drug-on and drug-off are very sensitive to the prescribed upper or lower threshold levels, which possibly explains why the on-off strategy with fixed schedule or a STI strategy with frequent switches is associated with the high rate of failure. Our findings suggest that it is critical to carefully choose the thresholds of CD4⁺ T cell count and individualize the STIs for each individual patient based on initial CD4⁺ T cell counts.

1 Introduction

Although the introduction of highly active antiretroviral therapy (HAART) has improved quality of life and morbidity and slowed down the disease progression of HIV infected patients, lifelong HAART continues to be associated with problems such as adverse effects, imperfect adherence and drug resistance (Ananworanich et al., 2006; Perelson et al., 1999; El-Sadr et al., 2006; Maggioloa et al., 2009; Tirelli and Bernardi, 2001). The inherent risks and problems associated with HAART have led to strategies of scheduled treatment interruptions (STIs), in particular, CD4⁺ T cell counts-guided STIs, that might provide a good strategy to ameliorate these problems (Ananworanich et al., 2006; El-Sadr et al., 2006; Maggioloa et al., 2009). Several clinical studies have been done with aims to compare STI strategies with continuous antiretroviral therapy, but conflicting results have been reported (Ananworanich et al., 2006; El-Sadr et al., 2006; Maggioloa et al., 2009).

The Staccato study (Ananworanich et al., 2006) has designed to assess CD4⁺ T cell count-guided treatment and fixed-cycle week-on/week-off strategies compared with continuous treatment, but week-on/week-off arm was stopped early due to high rate of failure. In this study, the patients continued their therapy until CD4⁺ T cell counts went over to 350 cells/μl, and then stopped until they dropped back to 350 cells/μl. They concluded that the STI arm (compared with the continuous arm) had no difference in new AIDS-associated illnesses and the emergence of drug resistance, but was associated with more HIV-related diseases (Ananworanich et al., 2006).

The Strategies for Management of Antiviral Therapy (SMART) study (El-Sadr et al., 2006) used CD4⁺ T cell counts to determine the starting and stopping point of STIs(Hirschel and Flanigan, 2009), i.e., HAART was started when the CD4⁺ T cell count dropped below a certain threshold, 200 cells/μl, while stopped when it increased above a certain level, 350 cells/μl. The investigators concluded that patients in the STI arm had higher rates of death and higher rates of HIV disease progression.

More recently, the Long Term Treatment Interruption (LOTTI) study (Maggioloa et al., 2009) pointed out that the long-term clinical outcome of a CD4⁺ T cell count-guided strategy might be equivalent to continuous HAART. The results indicate that CD4⁺ T cell count-guided STI is a good alternative choice for some chronically infected individuals who may need to take drugs for lifelong time, and it is beneficial for the patients’ immune reconstruction during drug-off period. In order to make the STI strategy safe and effective, CD4⁺ T cell count-guided STI treatment should be designed to preserve the immune function when patients are off therapy and to ensure that the CD4⁺ T cell counts can be maintained above a safe level. The lower threshold and upper threshold of CD4⁺ T cell counts chosen for restarting and stoping therapy in the LOTTI study are 350 cells/μl and 700 cells/μl, respectively.

More controversial studies include the Trivacan study (Danel et al., 2006) which used a CD4⁺ T cell threshold of 250 cells/μl (the same as the SMART study) to restart HAART and they observed an increment in serious morbidity in the STI arm. Several other studies (Ananworanich et al., 2006; Ananworanich and Hirscel, 2007; Hirschel and Flanigan, 2009; Maggiolo et al., 2004) used a CD4⁺ T cell count threshold of 350 cells/ml to restart HAART and did not report an increased risk of serious morbidity for patients in the STI arm. Ruiz et al. (Ruiz et al., 2007) designed the experiments to evaluate the safety of CD4 cell count and plasma HIV-1 RNA-guided STIs with aims to maintain CD4⁺ T cell counts higher than 350 cells/μl and plasma HIV-1 RNA less than 100,000 copies/μl. So far, there are no good explanations for the clinical differences from above studies (Hirschel and Flanigan, 2009; Maggioloa et al., 2009), and more studies are needed to justify the benefits and risks of STIs.

All these studies indicate that the CD4⁺ T cell count threshold selected to reintroduce HAART is crucial to maintain the CD4⁺ T cell count above a safe threshold (Danel et al., 2006; DART Trial Team, 2008; Ruiz et al., 2007). But it remains uncertain what is the best CD4⁺ T cell count threshold to guide the STI due to the controversial reports from different studies (International et al., 2005; Maggiolo et al., 2004). The purpose of this paper is to develop and extend the classical HIV virus dynamic models (Nowak and May, 2000; Perelson et al., 1999) to the piecewise dynamic model representing the CD4⁺ T cell count-guided therapy to explore the possible treatment outcomes and potentially explain why the controversial results were obtained from different clinical studies.

HIV dynamic studies have significantly contributed to the understanding of HIV pathogenesis and antiretroviral (ARV) treatment strategies. Both deterministic and stochastic models have been developed to describe the immune response to HIV infection and the decline in CD4⁺ T cell counts in HIV infected patients (Perelson et al., 1999; Nowak and May, 2000; Rong et al., 2007). A number of studies (Blower et al., 2000; Huang et al., 2003; Rong et al., 2007) explored long-term viral dynamic models with constant or time-dependent drug efficacy incorporating clinical factors such as drug adherence and drug resistance. HIV dynamic models and control theory have been used to study both non-adaptive and adaptive STI strategies (Rosenberg et al., 2007). The optimal control method which minimizes side effects while keeping virus on check, is actively being examined (Adams et al., 2004; Hadjiandreou et al., 2011). Adams et al.(Adams et al., 2004) considered a complicated HIV dynamic model and used control theory to design non-adaptive STI strategies that involve a short-term pattern of several interruptions after infection. They showed that such strategies could lead to long-term control of the virus in some patients. Hadjiandreou et al. (Hadjiandreou et al., 2011) formulated the non-adaptive STI therapy into a dynamic optimization problem and showed that STIs could control disease progression. Park et al. (Park et al., 2006) used a mathematical model to describe an ‘incomplete’ adaptive STI strategy, in which the drug dose was administered (interrupted) when the healthy CD4 T cell count was less (greater) than a threshold. When the healthy CD4 T cell count was between the two thresholds, the non-adaptive STI strategy is maintained. They showed that not only the entire treatment period but also the total drug dose administered were reduced.

To authors’ best knowledge, no mathematical model has been formulated to represent the use of CD4⁺ T cell counts as a guider to trigger or suspend the therapy. Our proposed piecewise HIV viral dynamic models shall explore HIV dynamic behaviors under (1) the continuous therapy (Ananworanich et al., 2006; Maggioloa et al., 2009; Perelson et al., 1999; El-Sadr et al., 2006); (2) the STI with frequent switching such as week-on/week-off approach (Ananworanich et al., 2003, 2006; Dybul et al., 2001; Montaner et al., 2005); and (3) the STI with sparse switching in which a patient continues his/her antiretorviral therapy until his/her CD4⁺ T cell count goes over a predefined threshold value to stop the therapy, and only restarts the therapy when his/her CD4⁺ T cell count dips below a predefined threshold value (Hirschel and Flanigan, 2009; Maggiolo et al., 2004; Maggioloa et al., 2009; Oxenius et al., 2002; El-Sadr et al., 2006; Tebas et al., 2002). In particular, we will focus on the effects of CD4⁺ T cell count thresholds or width of threshold windows on the durations of drug on and drug off (i.e. the number of drug-on/off switches), which can help us to determine in what cases the continuous therapy or STI treatment is necessary for an HIV infected patient. Furthermore, some key issues on how to evaluate the benefits and risks of STIs by using piecewise HIV virus dynamic models will be addressed.

2 Methods

2.1 A basic HIV viral dynamics model with antiretroviral therapy

On the basis of the administration of at least three antiretroviral drugs highly active antiretroviral therapy(HAART) has proved extremely effective in suppressing HIV below detection. The HAART treatment reduces the amount of virus in the body of a patient to a very low level, allowing the immune system to recover its strength. Generally two classes of antiretroviral (ARV) drugs are popularly used as the first line of HIV treatment: reverse transcriptase inhibitors (RTIs) and protease inhibitors (PIs). RTIs can effectively block RT’s enzymatic function and prevent completion of synthesis of the viral DNA from HIV-1 RNA. Protease inhibitors prevent HIV protease from cleaving the HIV polyprotein into functional units, causing infected cells to produce immature virus particles that are non-infectious. The basic model of viral dynamics usually consists of a set of ODEs describing the interactions between susceptible cells, infected cells and virions. Considering the effects of both RTIs and PIs, denoted by η_RT and η_{P I} respectively, the basic deterministic model for the quantification of HIV-1 dynamics in vivo can be written as follows

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-(1-{\eta }_{RT}){kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}=(1-{\eta }_{RT}){kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=(1-{\eta }_{PI})\lambda T^{\ast }-{cV}_I,\hfill \\ \frac{{dV}_{NI}}{dt}={\eta }_{PI}\lambda T^{\ast }-{cV}_{NI},\hfill \end{array}$$ (1)

where T(t) and T^*(t) denote the number of uninfected and infected CD4⁺ T cells at time t while V_I(t) and V_NI (t) are the concentration of infectious and noninfectious virus particles in the blood, respectively. Parameter s is the rate at which uninfected cells are generated from a source, d is the death rate of uninfected cells, d is the death rate of infected cells, c is the clearance rate of free virus, k is the infectivity rate, and λ is the rate of production of virions by infected cells. The parameter definitions and initial conditions are summarized in Table 1.

Table 1.

Definitions of the parameters used in the model

	Variable, parameter and description	Initial or default values
Variables
T	Uninfected CD4+ cell population size	1200 cells/μl
T*	Infected CD4+ helper cell population size	0
VI	concentration of infectious virus particles	10−6 copies/μl
VNI	concentration of non-infectious virus particles	0
Parameters
s	Generation rate for uninfected CD4+ T cell	15 μl−1 day−1
d	Death rate of uninfected CD4+ T cells	0.01 day−1
k	Infection rate for CD4+ T cells by virus	2.4 × 10−6 μl−1 day−1
δ	Death rate of infected CD4+ cells	0.35 day−1
λ	Number of free virus produced by lysing a CD4+ cell	3000 day−1
c	Death or clearance rate of free virus	3 day−1
ηRT	RTI drug efficacy	0.5–1
ηPI	PI drug efficacy	0.5–1

Many researchers investigated this system (Chun et al., 1997; Perelson et al., 1999; Nowak and May, 2000) and examined the basic reproductive ratio R₀ = (1 − η_RT )(1 − η_{P I})ksλ/δdc, which determines whether HIV pathogen can persist or not. In particular, let Ē = (T̄, T̄^*, V̄_I ) be equilibrium of system (1) (we ignored the variable V_NI since it is independent). Then we can define the Lyapunov function V as follows

$$V_1(T,T^{\ast },V_I)=\overline{T}\left(\frac{T}{\overline{T}}-ln\frac{T}{\overline{T}}\right)+{\overline{T}}^{\ast }\left(\frac{T^{\ast }}{{\overline{T}}^{\ast }}-ln\frac{T^{\ast }}{{\overline{T}}^{\ast }}\right)+\frac{\delta }{\lambda }\overline{V}\left(\frac{V_I}{\overline{V}}-ln\frac{V_I}{\overline{V}}\right).$$ (2)

Following the methods proposed by Korobeinikov (Korobeinikov, 2004), it is easy to prove that the equilibrium Ē is globally and asymptotically stable if R₀ > 1, otherwise the infection-free equilibrium is globally and asymptotically stable.

Standard continuous combination therapies have resulted in dramatic reduction in HIV-related morbidity and mortality. However, there are some significant limitations with continuous administration of HAART such as side effects and drug resistance (Ananworanich et al., 2006; DART Trial Team, 2008; Hirschel and Flanigan, 2009; Maggioloa et al., 2009; Maggiolo et al., 2004). In order to avoid these problems due to long-term drug exposure while preserving CD4⁺ T cell counts at a relatively high level, it is reasonable to design a STI strategy to trigger or suspend ARV treatment using the CD4⁺ T cell count as a guide.

2.2 Models for STI strategy with a single threshold

On the basis of the Staccato study (Ananworanich et al., 2006) that the patients on antiretroviral therapy continued until their CD4⁺ T cell count went to 350 cells/μl, and then the therapy was stopped until it dropped below 350 cells/μl, we propose a piecewise smooth HIV virus dynamic model to investigate the STI strategies, address important issues related to determination of thresholds and drug on/off periods, and possibly explain why the drug-on/off period is associated with high failure rate of ARV treatment (Ananworanich et al., 2003, 2006). Here we assume that there is a threshold value C_T below which antiretroviral therapy will be triggered and above which the therapy will be stopped. Then the viral dynamics models for drug-off and drug-on states can be written respectively as (by ignoring non-infectious virus):

Drug-off state

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-{kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}={kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=\lambda T^{\ast }-{cV}_I,\hfill \end{array}T+T^{\ast }>C_T;$$ (3)

Drug-on state

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-(1-{\eta }_{RT}){kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}=(1-{\eta }_{RT}){kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=(1-{\eta }_{PI})\lambda T^{\ast }-{cV}_I,\hfill \end{array}T+T^{\ast }<C_T.$$ (4)

First we review the dynamics of drug-off state, in which there exists a unique steady state, denoted by $E_{\mathit{off}}=({\overline{T}}_{\mathit{off}},{\overline{T}}_{\mathit{off}}^{\ast },{\overline{V}}_{\mathit{off}})$, where

$${\overline{T}}_{\mathit{off}}=\frac{s}{R_{0}d},{\overline{T}}_{\mathit{off}}^{\ast }=\frac{(R_0-1)dc}{k\lambda },{\overline{V}}_{\mathit{off}}=\frac{(R_0-1)d}{k}$$

and R₀ = ksλ/δdc, and E_off exists and is locally stable if R₀ > 1 (Nowak and May, 2000). For the drug-on state, similarly, there exists a unique steady state, denoted by $E_{on}=({\overline{T}}_{on},{\overline{T}}_{on}^{\ast },{\overline{V}}_{on})$, where

$${\overline{T}}_{on}=\frac{s}{R_{c}d},{\overline{T}}_{on}^{\ast }=\frac{(R_c-1)dc}{(1-{\eta }_{RT})(1-{\eta }_{PI})k\lambda },{\overline{V}}_{on}=\frac{(R_c-1)d}{(1-{\eta }_{RT})k}$$

and R_c = R₀η, η= (1 − η_RT )(1 − η_{P I} ), and E_on exists and is locally stable if R_c > 1 (Nowak and May, 2000). It is easy to get ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$.

Drug-off and drug-on models (3) and (4) together can be used to explore the STI strategies and to investigate when to trigger ARV therapy or when to suspend the therapy. We will focus on studying the possible treatment outcomes by using theories of the piecewise continuous system in the following (Filippov, 1988).

Let H(Z) = T + T^* − C_T with vector Z = (T, T ^*, V_I)′, where ′ denotes the transpose of the vector, and

$$\begin{array}{l}{F}_{S_1}(Z)={(s-dT-{kV}_{I}T,{kV}_{I}T-\delta T^{\ast },\lambda T^{\ast }-{cV}_I)}^{\prime },\\ F_{S_2}(Z)={[s-dT-(1-{\eta }_{RT}){kV}_{I}T,(1-{\eta }_{RT}){kV}_{I}T-\delta T^{\ast },(1-{\eta }_{PI})\lambda T^{\ast }-{cV}_I]}^{\prime },\end{array}$$

then the systems (3) and (4) can be integrated in the following piecewise smooth virus dynamic model (Filippov, 1988; Utkin et al., 2009)

$$\stackrel{.}{Z}(t)=\{\begin{array}{ll}{F}_{S_1}(Z),\hfill & Z\in S_1,\hfill \\ F_{S_2}(Z),\hfill & Z\in S_2,\hfill \end{array}$$ (5)

where $S_1=\{Z\in R_{+}^3:H(Z)>0\},S_2=\{Z\in R_{+}^3:H(Z)<0\}$ and $R_{+}^3=\{Z=(T,T^{\ast },V_I):T\ge 0,T^{\ast }\ge 0,V_I\ge 0\}$. Furthermore, the manifold Σ separating the two regions S₁ and S₂ is defined by

$$\mathrm{\sum }=\{Z\in R^3:H(Z)=0\}$$

and H is a smooth scale function with a nonvanishing gradient H_Z on Σ. From now on, we call the Filippov system (5) defined in region S₁ as System S₁ (i.e. drug-off state (3)) and in region S₂ as System S₂ (i.e. drug-on state (4)). In order to determine the sliding domain Σ_S (⊂ Σ), we take the vector n = (1, 1, 0)′ which is perpendicular to Σ and we can verify whether or not the set

$${\mathrm{\sum }}_S=\{Z\in \mathrm{\sum }:\langle n,F_{S_1}\rangle \langle n,F_{S_2}\rangle <0\}$$

is empty. Simple calculations show that this set is indeed empty, which indicates that the sliding mode does not exist. So System (5) is a non-sliding piecewise system. Note that a ‘sliding mode’ may occur if there are regions in the vicinity of manifold Σ where the vectors for the two different structures of the system (5) are directed towards each other. More detailed discussions can be found in (Bernardo et al., 2008; Kuznetsov et al., 2003).

Threshold policy control

If we only consider the CD4⁺ T cell threshold policy control in (5), i.e., we choose the CD4⁺ T cell as a guider to initiate the ARV therapy for T < C_T and suspend the therapy for T > C_T, then the non-sliding piecewise system (5) becomes a Filippov system with a sliding mode. In such a scenario, we may control the number of healthy CD4⁺ T cells to stabilize at a desired level. Here, we only consider a single enzyme reverse transcriptase (RT) treatment (i.e., η_{P I} = 0) to illustrate the idea. In this case, the system can be written as

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-\epsilon {kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}=\epsilon {kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=\lambda T^{\ast }-{cV}_I,\hfill \end{array}$$ (6)

in which

$$\epsilon =\{\begin{array}{ll}1,\hfill & H(Z)>0,\hfill \\ 1-{\eta }_{RT},\hfill & H(Z)<0.\hfill \end{array}$$

The manifold Σ is defined as Σ = {Z ∈ R³ : H(Z) = 0} with H(Z) = T − C_T.

Simple calculations imply that the set Σ_S is not empty, hence the sliding mode does exist. Then the interior of the sliding mode Σ_S is given by the following set

$$\mathit{int}{\mathrm{\sum }}_S=\left\{Z\in \mathrm{\sum }:\frac{s-{dC}_T}{{kC}_T}<V_I<\frac{s-{dC}_T}{(1-{\eta }_{RT}){kC}_T}\right\}.$$ (7)

To examine the sliding dynamics (Utkin et al., 2009), we let dT (t)/dt = 0, which yields

$$\epsilon =\frac{s-{dC}_T}{{kV}_I{C}_T}.$$

Then the dynamics in the sliding domain is described by

$$\{\begin{array}{l}\frac{{dT}^{\ast }}{dt}=s-{dC}_T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=\lambda T^{\ast }-{cV}_I.\hfill \end{array}$$ (8)

So there exists a unique pseudoequilibrium of model (8) provided s − dC_T > 0, denoted by $E_P=({\overline{T}}_P^{\ast },{\overline{V}}_I)$, and

$${\overline{T}}_P^{\ast }=\frac{s-{dC}_T}{\delta },{\overline{V}}_I=\frac{\lambda }{c}\frac{s-{dC}_T}{\delta },$$

which is globally and asymptotically stable in the plane T = C_T for model (8).

2.3 Models for STI strategy with two thresholds

The recent clinical studies, SMART and LOTTI initiated the ARV therapy once the CD4⁺ T cell counts dipped below a lower threshold (denoted by C_TH, say 200 or 350 cells/μl) and suspended the treatment once the CD4⁺ T cell counts climbed above an upper threshold (denoted by C^TH, say 600 cells/μl or more), where [C_TH, C^TH] is called as a threshold window of treatment decision. In this case, we can extend models (3) and (4) by replacing the single threshold C_T by a lower threshold and an upper threshold, which can be written as,

Drug-off state

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-{kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}={kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=\lambda T^{\ast }-{cV}_I,\hfill \end{array}\text{until}T+T^{\ast }\downarrow C_{TH};$$ (9)

Drug-on state

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT-(1-{\eta }_{RT}){kV}_{I}T,\hfill \\ \frac{{dT}^{\ast }}{dt}=(1-{\eta }_{RT}){kV}_{I}T-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=(1-{\eta }_{PI})\lambda T^{\ast }-{cV}_I,\hfill \end{array}\text{until}T+T^{\ast }\uparrow C^{TH}.$$ (10)

Note that according to the above models, for a new patient, if T (t₀) + T^*(t₀) > C^TH, this patient could be in the drug-off state; if T (t₀) + T^*(t₀) < C_TH, he/she could be in the drug-on state; and if C_TH < T (t₀) + T^*(t₀) < C^TH, he/she may either be in the drug-off state or be in the drug-on state which depends on the increasing or decreasing trend of CD4⁺ T cell counts. Further, if ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C^{TH}$, then the system reverts to the drug-off state before it can reach the equilibrium E_on; while if ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }<C_{TH}$, then the system must switch to the drug-on state before it can reach the steady state E_off. Combining these two observations, we find that the system will persistently alternate between drug-off state and drug-on state provided

$${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }<C_{TH}<C^{TH}<{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }.$$ (11)

In the following analyses, we will investigate how the threshold values C_T, C_TH and C^TH as well as the threshold window affect the durations of drug-on and drug-off, and consequently we can quantitatively evaluate different treatment strategies including continuous therapy without any treatment switch, continuous therapy with multiple treatment switchings, and STI strategies. Using these mathematical models, we would also possibly explain why the controversial conclusions were obtained from different clinical studies.

3 Results

First we introduce the concept of the real and virtual equilibria. Generally speaking, if any equilibrium lies in the region governed by the structure that it originates from, this equilibrium is defined as a real equilibrium point, whereas if it is located in another region, it is said to be a virtual equilibrium (Bernardo et al., 2008; Kuznetsov et al., 2003). In more details, considering the following system

$$\frac{dZ(t)}{dt}=f(Z,u_{\tau }),$$ (12)

where Z (Z ∈ R²) is the state vector, f ∈ C(R², R²) is a continuous function and the control u_τ is defined as

$$u_{\tau }=\{\begin{array}{cc}0,& \tau (Z)<0,\\ u_1(Z,t),& \tau (Z)>0,\end{array}$$ (13)

where u₁ is a continuous function, τ (Z) : R² → R is a threshold which is dependent on the state vector, and u_τ is discontinuous. The ‘controlled system’ is the one in which the control u_τ = u₁ is applied; while the ‘free system’ is the one in which no control (i.e. u_τ = 0) is applied. The manifold Σ is defined as

$$\mathrm{\sum }:=\{Z\in R^2:\tau (Z)=0\},$$ (14)

then Σ is the set of points in R². Let G¹ = {Z ∈ R² : τ(Z) < 0}, G² = {Z ∈ R² : τ(Z) > 0}. Let $Z_{G^i}^{eq}$ be such that $f_i(Z_{G^i}^{eq},u_i)=0$ for some u_i in (12). Then $Z_{G^i}^{eq}$ is called a real equilibrium if it belongs to Gⁱ and a virtual equilibrium if it belongs to G^j, j ≠ i.

Results for the STI with a single threshold

Numerical simulations of models (3) and (4) show that the total CD4⁺ T cell population either oscillates persistently or stabilizes at the equilibrium endemic states for drug-on/off states, depending on the choice of the threshold C_T (see details in Fig. 1 and Fig. 3). Note that the equilibrium endemic states E_on and E_off for drug-on/off states could be virtual or real, depending on the relationship of ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast },{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$ and the threshold level C_T. We consider the following three scenarios:

$$\begin{array}{l}\text{Case}1:{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C_T>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast },\\ \text{Case}2:{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }>C_T,\\ \text{Case}3:C_T>{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }.\end{array}$$

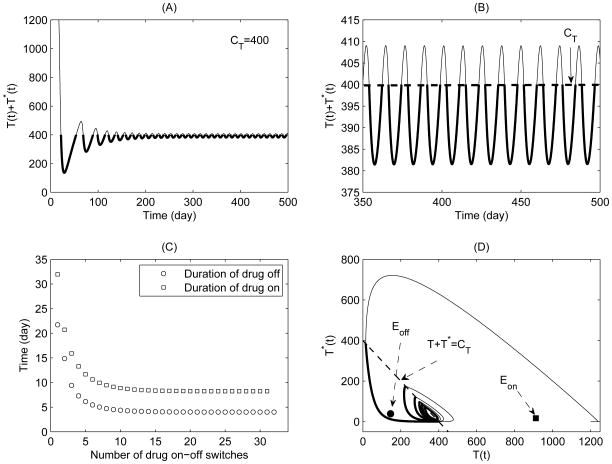
Figure 1.

A simulation of typical solutions of the non-sliding piecewise system (5) for Case 1 with C_T = 400. The initial conditions and parameter values are given in Table 1 with η_RT = η_{P I} = 0.6. (A) Total CD4⁺ T cell population; (B) Expanded view of late stage of (A); (C) Durations of drug-on (square) and drug-off (circle) for each drug-on/off switch; (D) Phase plane plot of healthy CD4⁺ T cell and infected CD4⁺ T cell populations.

Figure 3.

Two simulations of typical solution of non-sliding piecewise system (5) with threshold value $C_T={\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$ in (A–C) for Case 2 and $C_T={\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$ in (D–F) for Case 3. The initial values and parameter values are given in Table 1 with η_RT = η_{P I} = 0.6.

The equilibria E_on and E_off are virtual equilibria for Case 1. Fig. 1(A) and (B) show that the total CD4⁺ T cell population oscillates about the threshold T + T ^* = C_T = 400 (thick solid curves for drug-on and thin solid curves for drug-off phases respectively). It shows that the system switches back and forth between the drug-on and drug-off states forever, and there is a periodic solution which is the attractor for Case 1. Fig. 1(C) shows that the durations of drug-off and drug-on are quickly stabilized at fixed levels with the number of drug-on/off switches increases. In particular, the stable duration of drug-on is approximately double the duration of drug-off. The phase plane plot for healthy CD4⁺ T cell and infected CD4⁺ T cell populations is given in Fig. 1(D). The simulation results indicate that the CD4⁺ T cell counts could be successfully maintained above a certain level, which is in a good agreement with the observations for HIV patients under the STI therapies from clinical studies (Ananworanich et al., 2003, 2006).

To investigate how the threshold value C_T affects the durations of drug-on and drug-off, we fix all parameter values and initial conditions as those in Table 1 and let C_T vary from ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$ to ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$ (only Case 1 is considered here). We integrate system (5) from t = 0 to 2000, and record the durations of drug-on/off and the number of drug-on/off switches, as shown in Fig. 2. For a given threshold value C_T, the durations of both drug-on and drug-off decrease and stabilize at certain values as time goes on. It follows from Fig. 2(A) and (B) that the duration of drug-off decreases and the duration of drug-on dramatically increases, as C_T increases. In particular, if we would like to maintain CD4⁺ T cell count at the level of 500 (or 600) or above, the STI strategy needs about 11.8 (or 16) days of drug-on and 3.33 (or 2.8) days of drug-off. Fig. 2(A) and (B) further show that the duration of drug-on is more sensitive to the variation of the threshold value C_T compared to that of drug-off. It indicates that in order to maintain CD4⁺ T cell counts above a certain level, the careful choice of durations of drug-on/off is pivotal. This possibly explains why the on-off strategy with a fixed schedule (Ananworanich et al., 2003) or the earlier frequent switching STI strategy has a high rate of failure (presumably due to improper choice of the durations of drug-on or drug-off). Although the frequent switching STI strategy can theoretically maintain CD4⁺ T cell counts from declining, its final clinical or virological outcome is significantly dependent on the durations of drug-on and drug-off states, which are determined by the pre-subscribed threshold level C_T and the initial states of a patient.

Figure 2.

The effects of the threshold value C_T on the number of drug-on/off switches and durations of drug-on and drug-off, where the threshold value C_T varies from ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$ to ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$. The initial conditions and parameter values are given in Table 1 with η_RT = η_{P I} = 0.6

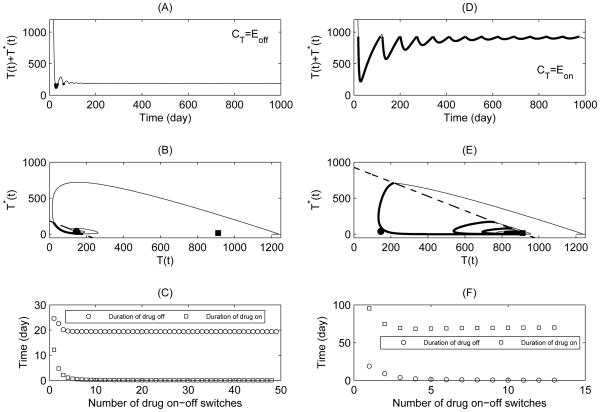
If the threshold value C_T is too small (smaller than or equal to ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$, Case 2), E_on is a virtual equilibrium and E_off is a regular equilibrium. If the threshold value C_T is too large (larger than or equal to ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$, Case 3), E_on is a regular equilibrium and E_off is a virtual equilibrium. Further, numerical simulations show that E_off and E_on are globally stable for Case 2 and Case 3, respectively (Fig. 3). Consequently, we conclude that, if the threshold value C_T is too small, the patient will be free from drug treatment after several treatment switches (Fig. 3(A–C)), i.e., the duration of drug-on tends to zero, as shown in Fig. 3(C). It suggests that the threshold C_T should be carefully chosen. Otherwise, for a low threshold, ARV treatment cannot be triggered even if a patient’s CD4⁺ T cell count is relatively low. Whereas, for a high threshold value C_T, the duration of drug-off approaches zero after several treatment switches (Fig. 3(F)). It indicates that, if a patient hopes to maintain a high level of CD4⁺ T cell counts, a very long time of continuous treatment is needed, as shown in Fig. 3(D–F).

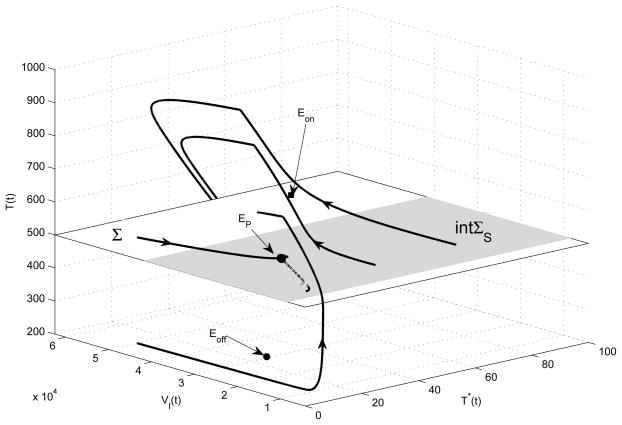
Here we provide a more detailed illustration for the case of T̄_on > C_T > T̄_off. In such a scenario, the equilibria E_on and E_off are virtual and only the pseudoequilibrium E_P is a feasible equilibrium. Any trajectory initiating from {T ∈ R₊ : T > C_T} ultimately hits the manifold Σ since the globally stable equilibrium E_off is in the region {T ∈ R₊ : T < C_T }, so is any trajectory initiating from {T ∈ R₊ : T < C_T}. In addition, any trajectory initiating from the domain of sliding Σ_S will slide in this region and ultimately approach the pseudoequilibrium E_P. Numerical simulations further confirm that the pseudoequilibrium E_P is globally and asymptotically stable (as shown in Fig. 4). It follows, seen from Fig. 4, that four solutions with different initial values approach the pseudoequilibrium E_P. It indicates that the number of heathy CD4⁺ T cells can stabilize at a desired level for a long time by choosing a suitable HAART strategy guided by CD4⁺ T cell counts.

Figure 4.

Four solutions of Filippov system (6) which starts from different initial values, where the sliding region Σ_S is shaded and crossing region Σ is unshaded. The solutions switch their directions at T = C_T = 500, and orbits slide along the shaded region which corresponds to mechanical sticking. The parameter values are given in Table 1 with η_RT = 0.8 and η_{P I} = 0.

Results for the STI strategy with a threshold window

The STI strategy with a single threshold inevitability induces frequent drug-on/drug-off switches, which consequently results in frequent fluctuations of CD4⁺ T cell counts. At the same time, the STI strategy with multiple threshold values or with a threshold window is also proposed to reduce the frequent drug-on/drug-off switches. In particular, as discussed in Section 2.3, the STI with a threshold window allows a patient to continue the ARV therapy until his/her CD4⁺ T cell count goes over the upper threshold value C^TH, then suspend the therapy; while the ARV therapy is only restarted when the CD4⁺ T cell count drops down to the lower threshold value C_TH. It would be interesting to investigate how the threshold window governs the durations of drug-on and drug-off, dynamics of CD4⁺ T cell counts and viral loads, in addition to clinical outcomes. We use the proposed models (9) and (10) for this purpose.

Note that, based on models (9) and (10), we have ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$. Generally we assume that ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C_{TH}$ and ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }<C^{TH}$. According to relationships among ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast },{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }$, the lower threshold value C_TH and the upper threshold value C^TH, we have the following possible cases:

$$\begin{array}{l}\text{Case}1:{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C^{TH}>C_{TH}>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast },\\ \text{Case}2:C^{TH}>{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C_{TH}>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast },\\ \text{Case}3:C^{TH}>{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }>C_{TH},\\ \text{Case}4:{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }>C^{TH}>{\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }>C_{TH}.\end{array}$$

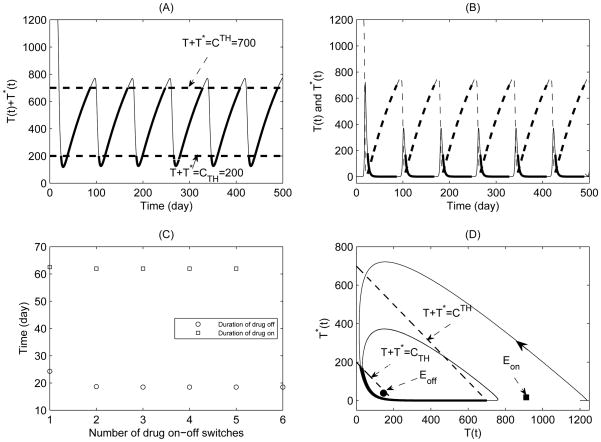
For Case 1 we can easily see that both equilibria E_on and E_off are virtual (see Fig. 5(D)). It is clear that these stable but virtual equilibria can never be actually attained. For example, a trajectory starting, say, in S₁ and approaching a stable virtual equilibrium E_off located in S₂ will never reach E_off since the dynamics changes as soon as it crosses the threshold H(Z). This indicates that the system may switch between drug-off state (9) and drug-on state (10) forever. Let η_RT = η_{P I} = 0.6 and fix all parameter values as those listed in Table 1. Simple calculations give ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }=928.27\mu l^{-1}$ and ${\overline{T}}_{\mathit{off}}+{\overline{T}}_{\mathit{off}}^{\ast }=184.52\mu l^{-1}$. We choose C_TH = 200 cells/μl and C^TH = 700 μl⁻¹. Fig. 5(A) shows that, for the given threshold window, the CD4⁺ T cell counts fluctuate periodically during the whole treatment cycles. The variations of healthy and infected CD4⁺ T cells are also given, respectively, in Fig. 5(B). The durations of drug-on and drug-off are shown in Fig. 5(C), which suggests that the durations of each drug-on/off are stabilized at fixed values and the duration of drug-on is much longer than that of drug-off. In the presence of a perfect RT inhibitor (i.e. η_RT = 1), it is easy to obtain how fast the number of CD4⁺T cells rebounds to the upper threshold value C^TH (see details in the Appendix). However, RT inhibitors, like other drugs, are not perfect, in this case we can show that the durations of drug-on/off are dependent on the threshold level and the initial level of the CD4⁺T cells.

Figure 5.

A simulation of typical solution of systems (9) and (10) with C_TH = 200 and C^TH = 700 for Case 1. The parameter values are given in Table 1 with η_RT = η_{P I} = 0.6. (A) Time series of total CD4⁺ T cell population; (B) Time series of healthy CD4⁺ T cell population (dashed line) and infected CD4⁺ T cell population (solid line); (C) Durations of drug on and drug off for each drug-on/off switch; (D) Phase plane plot of healthy CD4⁺ T cell and infected CD4⁺ T cell populations

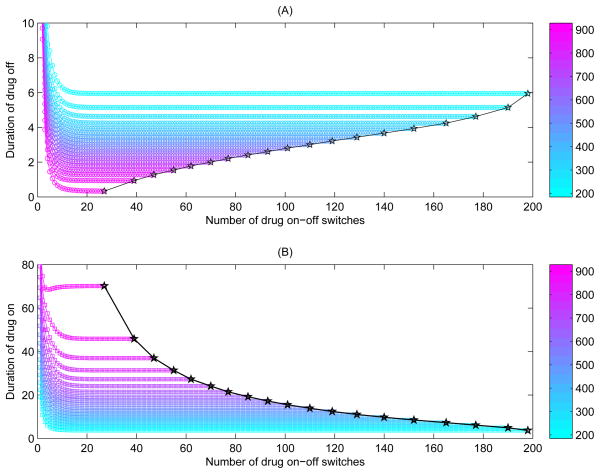
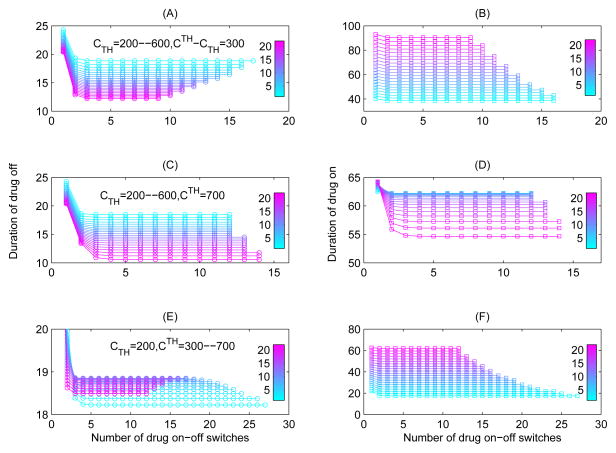
In order to further show the effect of threshold windows on the durations of drug-on/off or number of drug-on/off switches for Case 1, we consider the following different settings for threshold windows (as shown in Fig. 6). First, we fixed the width of threshold window such that C^TH − C_TH = 300 μl⁻¹, and let the lower threshold value C_TH increase from 200 to 600 μl⁻¹, where C_TH = 200 + 20(n − 1) μl⁻¹ for n = 1, 2, ··· 21 (see Fig. 6(A,B)). For the same width of threshold window, it is interesting to note that as C_TH increases, the duration of drug-off decreases (Fig. 6(A)) while the duration of drug-on increases dramatically (Fig. 6(B)). This indicates that, for the same width of threshold window, the larger the lower threshold value C_TH, the more time for the CD4⁺ T cell counts needed to rebound to the upper threshold and the less time for the CD4⁺ T cell counts needed to fall down to the lower threshold. Secondly, we fixed the upper threshold value C^TH = 700 μl⁻¹, and let the lower threshold value C_TH vary from 200 to 600 μl⁻¹ with C_TH = 200 + 20(n − 1) μl⁻¹ for n = 1, 2, ··· 21 (see Fig. 6(C,D)). It follows that, as C_TH increases (and consequently as the threshold window becomes narrower), it took less time for the CD4⁺ T cell counts to rebound or fall down, as shown in Fig. 6(D). Finally, we fixed the lower threshold value C_TH = 200 μl⁻¹, and let the upper threshold value C^TH increase from 300 to 700 μl⁻¹ with C^TH = 300 + 20(n − 1) μl⁻¹ for n = 1, 2, ··· 21 (see Fig. 6(E,F)). It is seen that, as C^TH increases (and consequently as the threshold window becomes wider), the CD4⁺ T cell counts took more and more time to rebound to the upper threshold or fall down to the lower threshold. It is interesting to observe that as C^TH further increases, the duration of drug-off reaches a maximum and then decreases as C^TH exceeds a certain critical value, as shown in Fig. 6(E–F).

Figure 6.

The effects of width of threshold window on the durations of drug-on (or drug-off) and number of drug-on/off switches. The parameters are fixed as those in Table 1 with η_RT = η_{P I} = 0.6. (A–B) We fixed the width of threshold window, i.e., let C^TH − C_TH be a constant as 300 μl⁻¹, and C_TH increases from 200 to 600 μl⁻¹; (C–D) We fixed the upper threshold value C^TH as 700 μl⁻¹ and let the lower threshold value C_Th vary from 200 to 600 μl⁻¹; (E–F) We fixed the lower threshold value C_TH as 200 μl⁻¹ and let the upper threshold value C_Th increase from 300 to 700 μl⁻¹.

It follows from Fig. 6(A–B) and (E–F) that, as the upper threshold value C^TH increases, the duration of drug-on monotonically increases whilst the drug holiday decreases and is much shorter than the duration of drug-on. So an interesting issue arising from Fig. 6 is whether there is a certain value of the upper threshold value C^TH above which the STI strategy with a threshold window cannot maintain the periodical fluctuation of CD4⁺ T cell counts. In another word, could a high level of CD4⁺ T cell counts be maintained by using this STI strategy? To answer this question, we focus our discussions on Cases 2–4 in the following.

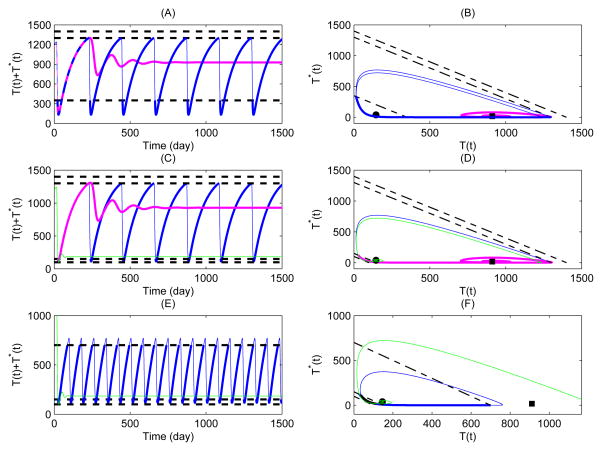
For Case 2, the drug-on equilibrium E_on becomes a regular steady state, which is globally stable for the drug-on system (10) only. It is interesting to examine for the whole system (9) and (10) how the CD4⁺ T cell counts behave. It follows from Fig. 7(A,B) that one trajectory (pink curve) initiating from the initial data listed in Table (1) approaches the regular equilibrium E_on for C^TH = 1400 μl⁻¹, whereas another trajectory (blue curve) starting from the same initial data oscillates periodically if choosing C^TH = 1300 μl⁻¹. It indicates that for a patient with a different upper threshold for stopping ARV treatment may result in completely different outcomes such as oscillated CD4⁺ T cell counts for a STI strategy or a constant CD4⁺ T cell level for a continuous therapy. Further, extensive numerical simulations imply that, under the same treatment regime (i.e., the upper or lower thresholds fixed), the CD4⁺ T cell counts in some patients may oscillate, while others may approach a fixed level, which depends on the initial levels of the CD4⁺ T cell counts of a particular patient.

Figure 7.

Numerical simulations of solutions of drug-on/off state systems (9) and (10) with different lower and upper threshold values. The parameter values are given in Table 1 with η_RT = η_{P I} = 0.6. For Case 2: (A–B) Blue cure for the solution with C_TH = 350 μl⁻¹ and C^TH = 1300 μl⁻¹, pink curve for the solution with C_TH = 350 μl⁻¹ and C^TH = 1400 μl⁻¹; For Case 3: (C–D) Blue cure for the solution with C_TH = 150 μl⁻¹ and C^TH = 1300 μl⁻¹, pink curve for the solution with C_TH = 150 μl⁻¹ and C^TH = 1400 μl⁻¹, and green curve for the solution with C_TH = 100 μl⁻¹ and C^TH = 1300 μl⁻¹; For Case 4: (E–F) Blue cure for the solution with C_TH = 150 μl⁻¹ and C^TH = 700 μl⁻¹, and green curve for the solution with C_TH = 100 μl⁻¹ and C^TH = 700 μl⁻¹.

It is also interesting to explain why we can still observe periodical oscillations of CD4⁺ T cell counts for this STI strategy with a threshold window. For the scenario of $C^{TH}>{\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$, the maximum level, to which the CD4⁺ T cell counts under the drug-on state will rebound, may be either greater or lower than the upper threshold value C^TH. If the former occurs, the drug-on state switches to the drug-off state and then it possibly oscillates between these two states; while if the latter occurs, switches do not happen and consequently the continuous therapy is required for the HIV infected patients. In this case, the CD4⁺ T cell counts are stabilized to the regular equilibrium of the drug-on state ${\overline{T}}_{on}+{\overline{T}}_{on}^{\ast }$. It suggests that the best choice of a treatment strategy (a continuous or STI strategy) for a given patient should depend on the CD4⁺ T cell counts at the initiating time and the proposed upper threshold level.

For Case 3, we have that both equilibria E_on and E_off are regular and globally stable for their own system. Fig. 7(C,D)) shows that the CD4⁺ T cell counts will approach certain levels represented by the equilibrium E_on or E_off, corresponding to a continuous treatment strategy (pink curve) or free from therapy (green curve), under thresholds C_TH = 150 μl⁻¹, C^TH = 1400 μl⁻¹ or C_TH = 100 μl⁻¹, C^TH = 1300 μl⁻¹, respectively. Interestingly, oscillation of the CD4⁺ T cell counts can also be observed under C_TH = 150 μl⁻¹ and C^TH = 1300 μl⁻¹, suggesting a STI strategy with a threshold window is required (blue curve). This indicates that the STI strategy with different thresholds may result in different treatment regimes such as drug-on/off, continuous therapy, and free from ARV treatment.

For Case 4, we have the virtual equilibrium E_on and the real drug-off equilibrium E_off, which is globally stable for the drug-off system (9) only. Similar to Case 2, the CD4⁺ T cell counts either approach a certain value (green curve), corresponding to free from therapy, or oscillate (blue curve), corresponding to a drug-on/off treatment, as shown in Fig. 7(E, F).

4 Discussion

The significant challenge of different HAART strategies is how to balance the risks of HIV disease progression against adverse events associated with long-term HAART. Meanwhile, the benefits and risks of the STI strategies are unclear. Researchers from different disciplines have designed different treatment strategies to carefully evaluate the advantages and disadvantages of continuous and discontinuous treatments, and conflicting results have been reported (Ananworanich et al., 2003, 2006; Dybul et al., 2001; Hirschel and Flanigan, 2009; El-Sadr et al., 2006; Oxenius et al., 2002; Maggioloa et al., 2009). Many investigators suggested that in order to evaluate the benefits and risks of STIs, long-term studies are necessary and the choice of CD4⁺ T cell count threshold may be pivotal for successful STIs (Hirschel and Flanigan, 2009; Maggioloa et al., 2009).

Based on the clinical results, in this paper we proposed the piecewise HIV virus dynamic models for CD4⁺ T cell count-guided STI strategies, which extended the standard HIV virus dynamic models (Nowak and May, 2000; Perelson et al., 1999). Hence the formulated models can better describe the CD4⁺ T cell count-guided STI treatment strategy with a single threshold (which results in frequent switches between drug-on and drug-off states) and a threshold window (which results in a longer period of drug-on or drug-off states or even a continuous therapy or completely free from ARV treatment). This modeling approach allows us to investigate how the threshold value of CD4⁺ T cell counts or the width of the threshold window affect the durations of drug-on/off. Our main results indicate that different conclusions are reached due to different prescribed thresholds, threshold windows or different status of enrolled patients (associated with different initial levels of CD4⁺ T cell counts), and consequently we provide a potential explanation on why controversial conclusions were obtained from different clinical studies (Ananworanich et al., 2003, 2006; Dybul et al., 2001; Hirschel and Flanigan, 2009; El-Sadr et al., 2006; Oxenius et al., 2002; Maggioloa et al., 2009).

For the STI strategy with a single threshold, the dynamic system becomes as either a non-sliding piecewise or a Filippov dynamic model for different switching surfaces. Our theoretical analysis and simulation results show that CD4⁺ T cell counts can either fluctuate around the threshold or stabilize at a desired level for different choices of the threshold. The duration of drug-on state is more sensitive to the threshold value compared to that of the drug-off state (Fig. 2). Therefore, it is critical to choose the appropriate threshold of CD4⁺ T cell counts for the CD4⁺ T cell count-guided STI strategies so that a reasonable duration of drug-on/off states for a patient can be achieved in order to maintain the CD4⁺ T cell count to a certain level. Otherwise, it may result in an improper duration of drug-on or drug-off state, which may more likely lead to treatment failure. This provides a possible explanation on why the drug-on/off strategy with a fixed schedule (Ananworanich et al., 2003) or a STI strategy with frequent switches (Ananworanich et al., 2006) has a higher rate of failure.

The CD4⁺ T cell count-guided STI strategy with a threshold window (two thresholds: the lower threshold and upper threshold) has also been experimentally investigated by many investigators (Maggioloa et al., 2009; El-Sadr et al., 2006; Ruiz et al., 2007). We have studied several different scenarios based on the relations among the thresholds and equilibria using the proposed models. Our results show that the CD4⁺ T cell counts can either fluctuate around the two thresholds or stabilize at an equilibrium for drug-on or drug-off state. In particular, the bistability of either a periodic oscillation or an equilibrium depends on the initial CD4⁺ T cell count of the patient and the two threshold values. For example, for a patient with a fixed level of CD4⁺ T cells count at the treatment starting time, it requires either a continuous therapy or drug-on/off treatment regime to maintain the CD4 cell counts above a certain level for different choices of the threshold values. This conclusion is consistent with that in LOTTI (Maggioloa et al., 2009). This further consolidates that the continuous HAART and CD4⁺ T cell count-guided STI strategy with a threshold window may achieve similar clinical outcomes if the threshold window for the STI strategy is appropriately selected for each patient based on their baseline CD4⁺ T cell count. Also notice that, for a fixed threshold window, whether a patient needs a continuous therapy or STI strategy depends on the initial CD4⁺ T cell count of the patient at the treatment starting time. Further numerical studies show that the STI strategy is needed for a patient with a relatively high or low initial CD4⁺ T cell count, while the continuous therapy is required to maintain CD4⁺ T cell count above a safe level (Fig. 7(C–D)) if the initial CD4⁺ T cell count of a patient is in the middle (data not shown here). This further confirms that it is important to individualize the treatment strategy for different patients at different stage of their disease progression with different initial CD4⁺ T cell count levels. If the CD4⁺ T cell count-guided STI strategy is used, the threshold window needs to be individualized for different patient based on the patient’s baseline CD4⁺ T cell count level and the treatment goal.

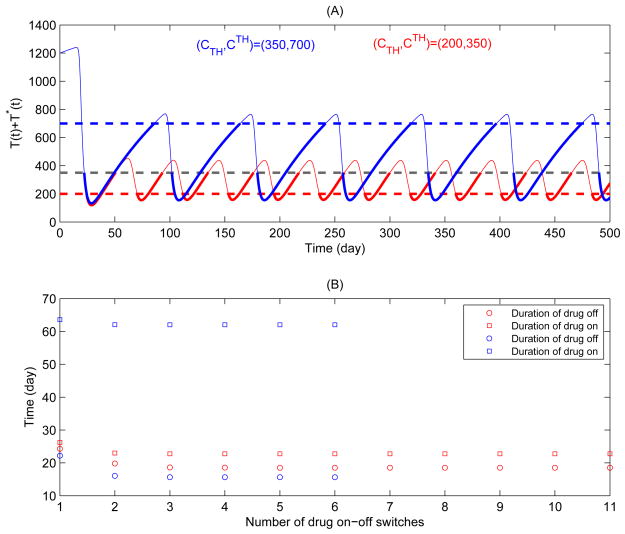
We have also shown (Fig. 6(C–F)) that the effects of the threshold values and the width of threshold window on the durations of drug-on and drug-off states are complex. The duration of drug-on state is more sensitive to the variation of thresholds compared to that of drug-off state. For example, using C_TH = 200 cells/ul and C^TH = 350 cells/ul as the thresholds to trigger/suspend HAART as the SMART study did, our numerical study indicates that drug-on and drug-off states should last 22.77 and 18.54 days, respectively; whilst using C_TH = 350 cells/ul and C^TH = 700 cells/ul as the thresholds to trigger/suspend HAART as the LOTTI study did, it should last 62.02 and 15.62 days for drug-on and drug-off states, respectively. Further, it can be seen from Fig. 8 that treatment switches occur more frequently under the regime with C_TH = 200 and C^TH = 350 cells/ul than that under the regime with C_TH = 350 and C^TH = 700 cells/ul. In the former case, the CD4⁺ T cell counts may be kept in a low level for a relatively long time (as shown in Fig. 8), which inevitably increases the risk of opportunistic infections or death from any cause. This may partially explain why the SMART study had a higher rate of death in the STI arm (El-Sadr et al., 2006).

Figure 8.

Numerical simulations of solutions corresponding to SMART and LOTTI studies. The parameter values are identical to Fig. 7. (A) Blue cure for the solution with C_TH = 350 μl⁻¹ and C^TH = 700 μl⁻¹, pink curve for the solution with C_TH = 200 μl⁻¹ and C^TH = 350 μl⁻¹; (B) The durations of drug-on and drug-off corresponding to (A) are given.

Note that the outcomes of the STI strategies may also be affected by the selected values of kinetic parameters listed in Table 1. More sensitivity analyses of these parameters on the outcomes may be needed. In practice, these parameters can be estimated for each individual patient based on viral load and CD4⁺ T cell counts data (Liang et al., 2010). In addition, the proposed models neither intend to quantify the whole HIV disease progression trajectory (Hadjiandreou et al., 2009; Perelson et al., 1999) nor explicitly consider drug resistance, drug side effects, HIV latency (Rong and Perelson, 2009), quality of life of patients and cost-effectiveness of the treatment strategies.

Further, there is strong evidence that drug effectiveness does depend on the treatment progression (Buchbinder et al., 1994; Park et al., 2006; Perelson et al., 1999), and the longer treatment the less drug effectiveness. Note that drugs not only provides an effective treatment of infections with HIV, but also plays an important role in virus dynamics. This indicates that the different drug efficacies may result in different treatment outcome. Thus, the drug effectiveness affects the durations of drug-on and drug-off of STI therapy and consequently be one of the crucial factors which can help us to determine the thresholds of CD4⁺ T cell count.

Therefore, the benefits and risks of CD4⁺ T cell count-guided STI treatments cannot be comprehensively evaluated in present work. So future extension of our work is warranted to investigate different treatment strategies by considering more practical factors using the proposed piecewise HIV virus dynamic models.

Appendix: The minimum duration of drug-on state

In the presence of a perfect RT inhibitor (i.e. η_RT = 1), the drug-on state (10) becomes

$$\{\begin{array}{l}\frac{dT}{dt}=s-dT,\hfill \\ \frac{{dT}^{\ast }}{dt}=-\delta T^{\ast },\hfill \\ \frac{{dV}_I}{dt}=(1-{\eta }_{PI})\lambda T^{\ast }-{cV}_I,\hfill \end{array}\text{until}T+T^{\ast }\uparrow C^{TH}.$$ (15)

In this special case, it is interesting to examine how fast the number of CD4⁺T cells rebounds to the upper threshold value C^TH. We assume, without loss of generality, that the first time of the number of CD4⁺ T cells dropped and reached at the lower threshold value C_TH at time τ₁ after infected, i.e., we have T (τ₁) + T ^*(τ₁) = C_TH. Note that the analytical solution of the first two equations of the model (15) with initial values of T (τ₁) and T ^*(τ₁) can be obtained by direct integration, i.e.,

$$\begin{array}{l}T(t)=\frac{s}{d}-e^{-d(t-{\tau }_1)}\left(\frac{s}{d}-T({\tau }_1)\right)\\ =T({\tau }_1)e^{-d(t-{\tau }_1)}+\frac{s}{d}\left(1-e^{-d(t-{\tau }_1)}\right),t\ge {\tau }_1,\\ T^{\ast }(t)=T^{\ast }({\tau }_1)e^{-\delta (t-{\tau }_1)},t\ge {\tau }_1,\end{array}$$ (16)

which indicates that

$$\begin{array}{l}T(t)+T^{\ast }(t)=T({\tau }_1)e^{-d(t-{\tau }_1)}+T^{\ast }({\tau }_1)e^{-\delta (t-{\tau }_1)}+\frac{s}{d}\left(1-e^{-d(t-{\tau }_1)}\right)\\ =T({\tau }_1)e^{-d(t-{\tau }_1)}+[C_{TH}-T({\tau }_1)]e^{-\delta (t-{\tau }_1)}+\frac{s}{d}\left(1-e^{-d(t-{\tau }_1)}\right),t\ge {\tau }_1.\end{array}$$

Suppose the number of CD4⁺ T cells went to the upper threshold C^TH at time μ₁, i.e., we have T (μ₁) + T ^*(μ₁) = C^TH, then we have the following equation

$$C^{TH}=T({\tau }_1)e^{-d({\mu }_1-{\tau }_1)}+[C_{TH}-T({\tau }_1)]e^{-\delta ({\mu }_1-{\tau }_1)}+\frac{s}{d}\left(1-e^{-d({\mu }_1-{\tau }_1)}\right).$$ (17)

Solving the above equation (17) with respect to μ₁ gives the minimum time (μ₁ − τ₁) of the number of CD4⁺T cells rebounding from the lower threshold C_TH to the upper threshold C^TH. For example, if we fix C_TH = 200 cells/μl with T (τ₁) = 150 (or 350 cells/μl with T (τ₁) = 250) and C^TH = 600 cells/μl and other parameters are given as those in Table 1, then the minimum duration of drug-on is μ₁ − τ₁ = 40.55 days (or 32.85 days).