Quantitative comparison of randomization designs in sequential clinical trials based on treatment balance and allocation randomness

Abstract

To evaluate the performance of randomization designs under various parameter settings and trial sample sizes, and identify optimal designs with respect to both treatment imbalance and allocation randomness, we evaluate 260 design scenarios from 14 randomization designs under 15 sample sizes range from 10 to 300, using three measures for imbalance and three measures for randomness. The maximum absolute imbalance and the correct guess (CG) probability are selected to assess the trade-off performance of each randomization design. As measured by the maximum absolute imbalance and the CG probability, we found that performances of the 14 randomization designs are located in a closed region with the upper boundary (worst case) given by Efron’s biased coin design (BCD) and the lower boundary (best case) from the Soares and Wu’s big stick design (BSD). Designs close to the lower boundary provide a smaller imbalance and a higher randomness than designs close to the upper boundary. Our research suggested that optimization of randomization design is possible based on quantified evaluation of imbalance and randomness. Based on the maximum imbalance and CG probability, the BSD, Chen’s biased coin design with imbalance tolerance method, and Chen’s Ehrenfest urn design perform better than popularly used permuted block design, EBCD, and Wei’s urn design.

1. INTRODUCTION

Random treatment allocation prevents selection biases in clinical trials [1,2]. Simple randomization (SR) provides the highest level of randomness, but may result in treatment imbalances that could bring accidental bias to the trial result [3,4]. Initially introduced by Hill in 1951 [5], the permuted block design (PBD) balances treatment allocation within each block at the cost of a certain proportion of deterministic assignments. Efron proposed the biased coin design (BCD) in 1971, in which a biased probability p_bias ∈(0.5, 1) is used to reduce the imbalance when it is occurring and an equal probability of 0.5 is used otherwise [6]. Wei proposed the adaptive biased coin design (ABCD) and the urn design (UD), both aim to control the imbalance relative to the number of subjects randomized [7]. In 1983, Sores and Wu proposed the big stick design (BSD) where a deterministic assignment is applied when imbalance reaches a pre-specified limit, and a pure random assignment is used otherwise [8]. After that, Smith proposed a generalized biased coin design (GBCD) as a large class of randomization designs covering both Efron’s BCD and Wei’s UD [9]. In 1999, Chen developed the biased coin design with imbalance tolerance (BCDWIT), which combined the BCD and the BSD [10]. In 2000, Chen proposed an Ehrenfest urn design (EUD), in which the total number of balls in the urn remains constant [11]. In 2004, Antognini proposed the symmetric extension of EUD (Sym-EUD) and the asymmetric extension of EUD (Asym-EUD) [12]. Other designs described in literatures include the random allocation rule (RAR), the truncated binomial design (TBD), and variable block design (VBD) [2]. Although all these designs differ in mathematical mechanisms and statistical properties, they have a common purpose of pursuing treatment balancing and allocation randomness and face the same trade-off dilemma. The tightest treatment balance can be achieved by PBD with a block size of 2, which has the maximum imbalance of 1 associated with 50% deterministic assignments. At the other end, SR has the highest randomness and the weakest imbalance control. Although neither of these two extreme scenarios is desirable, both provide anchors to assess the performance of a variety of restricted randomization designs using the criteria of both treatment balance and allocation randomness.

Among the 14 randomization designs described above, the PBD is the most commonly used method. However, its performance compared with other designs remains unknown to many investigators. Several authors addressed the performance of restricted randomization designs. Rosenberger and Lachin [2] provided a comprehensive review of many randomization designs, covering SP, RAR, TBD, PBD, VBD, BCD, BSD, UD, and GBCD based on thorough probabilistic analysis of the conditional allocation probability distribution under previous assignments. They compared treatment imbalance and allocation randomness based on the variance of the treatment arm size and the correct guess (CG) probability, respectively, through both analytical and computer simulation approaches. However, they limited the comparisons to a few parameter setting points, and the trade-off relationship between randomness and balance remains unclear. Kundt [13] evaluated the treatment imbalances for PBD, BCD, BSD, and UD under different parameter settings and trial sample sizes, but did not include the evaluation of treatment allocation randomness. Chen [11] compared BCDWIT with EUD and concluded that EUD is more balanced than BCDWIT with the same level of randomness. However, this conclusion is obtained under specific conditions. It does not hold in general. Antognini [12,14] compared Chen’s EUD with Wei’s UD based on the speed of convergence measured by the variance of treatment imbalance, and recognized the conflicting demands for balance and randomness without further analysis on the randomness.

In this paper, we review the measures of treatment imbalance and allocation randomness in Section 2 and define the conditional allocation probabilities for 14 different randomization designs in Section 3. Computer simulation plan is presented in Section 4, followed by results in Section 5. Discussions are included in Section 6.

2. MEASURES OF TREATMENT IMBALANCE AND ALLOCATION RANDOMNESS

Consider a two-arm trial with a balanced allocation ratio. Let T₁; T₂; …; T_n be a sequence of random treatment assignment, where T_i = j if subject i is assigned to treatment j (j = 1, 2). After subject i is randomized, let N_j(i) be the number of subjects assigned to treatment j, and D_i = N₁(i)−N₂(i) be the difference between the two treatment arm sizes. Commonly used measures for treatment imbalance include the probability of achieving exact balance (EB), Pr(D_i = 0|i > 1), the standard deviation of treatment imbalance at the end of the trial (Dn), and the maximum absolute imbalance in the entire sequence (MI). In practice, EB is rarely needed, particularly for trials with large sample sizes. The standard deviation of treatment imbalance at the end of the trial is important when imbalance is affected by the sample size. The maximum absolute imbalance has special value when treatment balance is required throughout the execution of the trial in order to prevent possible biases associated with the subject enrollment time sequence.

The randomness of treatment allocation is the fundamental characteristic of randomized controlled clinical trials to prevent selection bias and to ensure the validity of statistical inference. SR offers the highest degree of randomness. All restricted randomization designs have to sacrify certain levels of randomness in order to gain the benefit in treatment balance. Commonly used measures for allocation randomness include entropy of treatment assignment (ET), probability of deterministic allocation (DA), and probability of CG. Entropy is originally introduced by Klotz [15]. For two-arm trials with a balanced allocation ratio, it can be evaluated with:

$$\text{Entropy}(T_i)=-p_{i1}\text{ ln }{p}_{i1}-(1-p_{i1})\text{ ln}(1-p_{i1})$$ (1)

where p_i1 is the probability assigning subject i to treatment 1. Entropy is zero when the allocation is deterministic and is maximized to ln(2) = 0.6931 when p_i1 = 0.5. Allocation is considered deterministic if only one possible outcome exists, i.e. p_i1 = 0 or p_i1 = 1. Entropy is a quantitatively sound measure of randomness, but it is not intuitive. Probability of deterministic assignments has been used by many authors [16–18]. Matts and Lachin indicated that the probability of DA for PBD with a block size of b is 1/(b/2 + 1). DA does not occur in BCD or UD.

Arguably, the most commonly used measure for allocation randomness is the CG probability proposed by Blackwell and Hodges [19]. The optimal guess approach is guessing the next allocation as the treatment with the fewest prior allocations. Let n_ij be the actual number of subjects assigned to treatment j after the randomization for subject i. The probability of CG for a randomization sequence of n subjects is evaluated by:

$$\text{CG}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\text{CG}}_i$$

with

$${\text{CG}}_i=\{\begin{array}{cc}1\hfill & \text{if }(n_{i-1,1}<n_{i-1,2}\text{ and }{T}_i=1)\text{ or }(n_{i-1,1}>n_{i-1,2}\text{ and }{T}_i=2)\hfill \\ 0.5\hfill & \text{if }(n_{i-1,1}=n_{i-1,2})\hfill \\ 0\hfill & \text{if }(n_{i-1,1}<n_{i-1,2}\text{ and }{T}_i=2)\text{ or }(n_{i-1,1}>n_{i-1,2}\text{ and }{T}_i=1)\hfill \end{array}$$ (2)

3. CONDITIONAL ALLOCATION PROBABILITY OF RANDOMIZATION DESIGNS

The conditional allocation probability is fully determined by the randomization algorithm and the current treatment distribution:

$$p_{1,1}=1/2,p_{i1}=\text{Pr}(T_i=1|n_{i-1,1,}{n}_{i-1,2})(i=2,3,\dots ,n)$$ (3)

SR gives each subject 50% chance for either the treatment or the control group.

$$p_{i1}(\text{SR})=\frac{1}{2}(i=1,2,\dots ,n)$$ (4)

The RAR follows a hypergeometric distribution. Consider a sequence of n (assume even) random draws from a box starting with n/2 balls for each treatment, without replacement, until the box is empty.

$$p_{i1}(\text{RAR})=\frac{n/2-n_{i-1,1}}{n-(i-1)}(i=2,3,\dots ,n)$$ (5)

The TBD uses complete random assignment until one treatment is full. After that, deterministic assignments are used.

$$p_{i1}(\text{TBD})=\{\begin{array}{cc}1/2\hfill & \text{if }{n}_{i-1,1}<n/2\text{ and }{n}_{i-1,2}<n/2\hfill \\ 0\hfill & \text{if }{n}_{i-1,1}=n/2\text{ and }{n}_{i-1,2}<n/2(i=2,3,\dots ,n)\hfill \\ 1\hfill & \text{if }{n}_{i-1,1}<n/2\text{ and }{n}_{i-1,2}=n/2\hfill \end{array}$$ (6)

PBD is the most popular randomization method [20–22]. Rosenberger and Lachin noted that block randomization can be considered as repeated RARs [2]. Therefore, the conditional allocation probability can be obtained by modifying formula (5):

$$p_{i1}(\text{PBD})=\frac{(b/2)(1+\text{int}[(i-1)/b])-n_{i-1,1}}{b(1+\text{int}[(i-1)/b])-(i-1)}(i=2,3,\dots ,n)$$ (7)

Here function int(x) returns the largest integer less than or equal to x.

The VBD is frequently used to reduce the treatment prediction of PBD, although its effectiveness in randomness protection is questionable [2]. With the VBD, each time a block is completed, a new block will be created with a block size randomly picked (with equal or unequal probabilities) from a pre-specified list of block sizes. Let b_k(k = 1, 2, …, c) be the size of the kth block, c be the number of blocks created at the time of randomization for subject i. The conditional allocation probability under the VBD is:

$$p_{i1}(\text{VBD})=\frac{{\displaystyle {\sum }_{k=1}^c}(b_k/2)-n_{i-1,1}}{{\displaystyle {\sum }_{k=1}^c}{b}_k-(i-1)}(i=2,3,\dots ,n)$$ (8)

Efron’s BCD [6] allocates subjects to either treatment arm 1 or arm 2 based on the following rule:

$$p_{i1}(\text{BCD})=\{\begin{array}{cc}{p}_{\text{bias}}\hfill & \text{if }{n}_{i-1,1}<n_{i-1,2}\hfill \\ 0.5\hfill & \text{if }{n}_{i-1,1}=n_{i-1,2}(i=2,3,\dots ,n)\hfill \\ 1-p_{\text{bias}}\hfill & \text{if }{n}_{i-1,1}>n_{i-1,2}\hfill \end{array}$$ (9)

With the biased probability p_bias ∈(0.5, 1), the BCD tends to balance the number of subjects in the two treatment groups. The tendency is weakened to SR if p_bias = 0.5, and is strengthened to PBD with b = 2 when p_bias = 1. Efron suggested p_bias = 2/3.

The ABCD introduced by Wei [23] has a biased coin probability reflecting the current imbalance proportional to the number of subjects currently randomized:

$$p_{\text{bias}}=p_{\text{bias }}\left(\frac{n_{i-1,1}-n_{i-1,2}}{i-1}\right)$$

The function p_bias(x) is chosen to be non-increasing and symmetric about the point (0, 1/2); i.e. p_bias(x) = 1 − p_bias × (−x) for x ∈ [−1, 1]. Obviously, unlimited possibilities for function p_bias(x) exist. For our purpose, we use p_bias(x) = (1 − x)/2, as suggested by Wei.

$$p_{i1}(\text{ABCD})=\frac{1-(n_{i-1,1}-n_{i-12})/(i-1)}{2}=\frac{n_{i-1,2}}{i-1}(i=2,3,\dots ,n)$$ (10)

Soares and Wu’s BSD [8] introduces an imbalance tolerance limit δ into BCD and set p_bias = 1.0.

$$p_{i1}(\text{BSD})=\{\begin{array}{cc}0\hfill & \text{if }{n}_{i-1,1}-n_{i-1,2}=\delta \hfill \\ 0.5\hfill & \text{if }|n_{i-1,1}-n_{i-1,2}|<\delta \hfill \\ 1\hfill & \text{if }{n}_{i-1,1}-n_{i-1,2}=-\delta \hfill \end{array}(i=2,3,\dots ,n)$$ (11)

The GBCD proposed by Smith [9] is characterized by a positive parameter ρ:

$$p_{i1}(\text{GBCD})=\frac{n_{i-1,2}^{\rho }}{n_{i-1,1}^{\rho }+n_{i-1,2}^{\rho }}(i=1,2,\dots ,n)$$ (12)

As ρ approaches to zero, Smith’s design is weakened to SR, and as ρ approaches to infinity, it is becomes the PBD with a block size b = 2.

The BCDWIT method proposed by Chen [10] combines the biased coin probability of the BCD and the imbalance tolerance of the BSD.

$$p_{i1}(\text{BCDWIT})=\{\begin{array}{cc}0\hfill & \text{if }{n}_{i-1,1}-n_{i-1,2}=\delta \hfill \\ 1-p_{\text{bias}}\hfill & \text{if }0<(n_{i-1,1}-n_{i-1,2})<\delta \hfill \\ 0.5\hfill & \text{if }{n}_{i-1,1}-n_{i-1,2}=0\hfill \\ p_{\text{bias}}\hfill & \text{if }0>(n_{i-1,1}-n_{i-1,2})>-\delta \hfill \\ 1\hfill & \text{if }{n}_{i-1,1}-n_{i-1,2}=-\delta \hfill \end{array}(i=2,3,\cdots ,n)$$ (13)

Initially proposed by Wei [7], the UD aims to control the treatment imbalance proportional to the total number of subjects randomized. Initially, w balls for each treatment are placed in the urn. When a subject is ready for randomization, a ball is randomly selected from the urn, and the subject is assigned to the corresponding treatment. Then the ball is returned to the urn and additional α balls for the selected treatment and β balls for the other treatmen will be added to the urn. In this model, we have:

$$p_{i1}(\text{UD})=\frac{w+\alpha n_{i-1,1}+\beta n_{i-1,2}}{2w+(i-1)(\alpha +\beta )}(i=2,3,\dots ,n)$$ (14)

The impact of parameter w diminishes as i increases. For large sample trials, the performance of the UD is determined by the ratio β/α.

Chen proposed an EUD [11], in which the selected ball is given to the opposite treatment after each assignment. The EUD can be considered as a special case of Wei’s UD with α = −1, β = 1.

$$p_{i1}(\text{EU})=\frac{w-(n_{i-1,1}-n_{i-1,2})}{2w}(i=2,3,\dots ,n)$$ (15)

Antognini extended Chen’s EUD to the so-called Sym-EUD and Asym-EUD [12]. In the Sym-EUD, the selected ball is given to the opposite treatment with a biased probability p_bias(0.5, 1). In the Asym-EUD, the selected ball is assigned to either treatment with an equal probability. Let r_i equal 1 if the ball is given to treatment 1 after randomization of subject i, and 0 otherwise. For Sym-EUD, we have:

$$\text{Pr}(r_i=1)=\{\begin{array}{ll}1-p_{\text{bias}}\hfill & \text{if }{T}_i=1\hfill \\ p_{\text{bias}}\hfill & \text{if }{T}_i=2\hfill \end{array}(i=1,2,\dots ,n-1)$$

$$p_{i1}(\text{Sym}-\text{EUD})=\frac{w-n_{i-1,1}+{\displaystyle {\sum }_{k=1}^{i-1}}{r}_k}{2w}(i=2,3,\dots ,n)$$ (16)

For the Asym-EUD, there are:

$$\text{Pr}(r_i=1)=1/2(i=1,2,\dots ,n-1)$$

$$p_{i1}(\text{Asym}-\text{EUD})=\frac{w-n_{i-1,1}+{\displaystyle {\sum }_{k=1}^{i-1}}{r}_k}{2w}(i=2,3,\dots ,n)$$ (17)

4. COMPUTER SIMULATION PLAN

The performance evaluation of randomization designs is affected by three factors: parameters associated with the design, sample size of the trial, and measures used for the evaluation. To obtain a complete assessment of the 14 designs described in Section 3, a total of 260 design-parameter setting scenarios are evaluated under 15 sample sizes, range from 10 to 300, with three measures for treatment imbalance and three measures for allocation imbalance. Table I lists the 260 simulation scenarios.

Table I.

Computer simulation randomization design-parameter scenarios.

Randomization design	Parameter range	Number of scenarios
SR		1
RAR		1
TBD		1
PBD	Block size (2–100)	15
VBD	Maximum block size (4–100)	14
Efron’s BCD	Biased probability (0.5–1.0)	11
Smith’s GBCD	Parameter ρ (0–100)	19
Wei’s ABCD		1
Soares and Wu’s BSD	Imbalance tolerance (0–20)	21
Chen’s BCDWIT	Biased probability (0.5–1.0) & Imbalance tolerance (2–7)	66
Wei’s UD	Initial ball (1–100) & ball for the assigned arm (0–5)	23
Chen’s EUD	Initial ball (1–200)	19
Antognini’s Sym-EUD	Initial ball (1–5) & biased probability (0.5–1.0)	55
Antognini’s Asym-EUD	Initial ball (1–50)	13
Total		260

Six measures are used in the computer simulation:

• EB = the probability of achieving exact balance in the randomization sequence.

• MI = the maximum absolute imbalance in the randomization sequence.

• Dn = the difference in treatment group sizes at the end of the randomization sequence.

• ET = the average entropy of all treatment assignments in the randomization sequence.

• DA = the probability of deterministic assignment in the randomization sequence.

• CG = the probability of correct guess in the randomization sequence.

At the end of the simulation, Dn takes the standard deviation across simulation runs. All other measures take the mean value across simulation runs.

A generic computer simulation program is developed with a structure shown in Figure 1.

Figure 1.

Computer simulation program structure for the evaluation of randomization designs.

Before the treatment assignment for subject i, the system checks the current treatment allocation distribution, n_i−1,1 and n_i−1,2; calculates the treatment imbalance D_i−1 = n_i−1,1 − n_i−1,2; makes a guess for treatment allocation T_i based on n_i−1,1 and n_i−1,2; and calculates the conditional probability p_i1 using the formulas (3)–(17). During the process of randomization, a random number, R, is generated by the system based on a uniform distribution on (0, 1). Subject i is assigned to treatment 1 if R < p_i1, and 2 otherwise. After that, the system calculates the treatment distribution n_i,1 and n_i,2, the treatment imbalance D_i = n_i1 − n_i2, the MI is updated if D_i > MI, the ET is calculated, and the counts for EB, DA, and CG are updated accordingly. At the end of each simulation run, values of the six measures are saved. After the simulations, the mean and standard deviations of these six measures are obtained based on the 5000 replications.

5. PERFORMANCE COMPARISON OF RANDOMIZATION DESIGNS

5.1. Set-up of the evaluation system

To evaluate the performance of different randomization designs based on the trade-off between treatment balance and allocation randomness, we select one primary measure for treatment imbalance and one primary measure for allocation randomness. Table II shows the pairwise Pearson’s correlation coefficients among the six measures.

Table II.

Pearson’s correlation coefficient between measures (Based on 260 design-parameter scenarios and 5,000 simulations per scenario).

Sample size	EB-Dn	EB-MI	EB-ET	EB-DA	EB-CG	Dn-MI	Dn-ET	Dn-DA	Dn-CG	MI-ET	MI-DA	MI-CG	ET-DA	ET-CG	DA-CG
10	−0.928	−0.977	−0.838	0.455	0.988	0.962	0.764	−0.432	−0.968	0.818	−0.459	−0.991	−0.783	−0.809	0.434
20	−0.893	−0.956	−0.778	0.369	0.990	0.951	0.645	−0.326	−0.945	0.742	−0.385	−0.980	−0.764	−0.747	0.353
30	−0.873	−0.941	−0.746	0.338	0.991	0.950	0.580	−0.281	−0.927	0.695	−0.357	−0.969	−0.764	−0.716	0.323
40	−0.856	−0.929	−0.725	0.321	0.993	0.946	0.534	−0.257	−0.911	0.660	−0.341	−0.960	−0.769	−0.695	0.307
50	−0.848	−0.920	−0.709	0.312	0.994	0.949	0.503	−0.235	−0.902	0.632	−0.328	−0.951	−0.774	−0.681	0.298
60	−0.842	−0.912	−0.695	0.304	0.994	0.950	0.482	−0.230	−0.894	0.611	−0.319	−0.944	−0.780	−0.668	0.292
70	−0.839	−0.905	−0.686	0.301	0.995	0.954	0.462	−0.215	−0.888	0.592	−0.311	−0.937	−0.784	−0.660	0.289
80	−0.829	−0.899	−0.676	0.297	0.995	0.950	0.441	−0.206	−0.878	0.575	−0.302	−0.931	−0.789	−0.651	0.285
90	−0.825	−0.894	−0.669	0.295	0.996	0.952	0.427	−0.198	−0.873	0.561	−0.296	−0.926	−0.793	−0.645	0.284
100	−0.816	−0.889	−0.662	0.292	0.996	0.947	0.410	−0.189	−0.864	0.549	−0.291	−0.921	−0.796	−0.638	0.281
120	−0.814	−0.882	−0.651	0.290	0.997	0.951	0.397	−0.186	−0.859	0.530	−0.281	−0.913	−0.802	−0.629	0.280
150	−0.809	−0.873	−0.639	0.287	0.997	0.954	0.372	−0.170	−0.850	0.505	−0.269	−0.903	−0.809	−0.617	0.276
200	−0.793	−0.861	−0.624	0.285	0.998	0.951	0.340	−0.156	−0.833	0.475	−0.255	−0.890	−0.816	−0.605	0.275
250	−0.791	−0.852	−0.615	0.284	0.998	0.958	0.325	−0.148	−0.827	0.453	−0.244	−0.879	−0.820	−0.597	0.274
300	−0.780	−0.844	−0.608	0.283	0.998	0.955	0.307	−0.141	−0.815	0.435	−0.236	−0.870	−0.823	−0.591	0.274
Overall	−0.774	−0.792	−0.667	0.301	0.983	0.948	0.358	−0.165	−0.766	0.422	−0.219	−0.748	−0.790	−0.662	0.300

EB, probability of exact balance; Dn, standard deviation of final treatment imbalance; MI, maximum absolute imbalance; ET, entropy of treatment allocation; DA, probability of deterministic assignment; CG, probability of correct guess.

Among the three imbalance measures, we have:

$$|\text{Correl}(\text{Dn, MI})|>|\text{Correl}(\text{EB, MI})|>|\text{Correl}(\text{Dn, EB})$$

The maximum absolute imbalance (MI) provides the best information on ‘the worst case’, which is one of the most important factors to be taken into account when creating the randomization plan for a trial. MI is particularly important when time-heterogeneous covariates are considered. Unlike Dn, MI applies to all randomization designs. Therefore, we choose MI as the primary measure for treatment imbalance. Among the three measures for allocation randomness, DA and ET depend fully on the current allocation probability, p_i1 and p_i2, whereas CG depends fully on the current treatment imbalance, n_i−1,1 − n_i−1,2. Therefore, it is expected that |Correl(ET, DA)| > |Correl(DA, CG)|. However, when the relationship between imbalance and randomness is assessed, there is |Correl(MI, CG)| > |Correl(MI, ET)|. In clinical trials, CG is directly associated with potential selection bias. In an open-label or single blinded trial, investigators may have information on n_i−1,1 − n_i−1,2, but not necessary on p_i1 and p_i2. Therefore, we choose CG as the primary measure for allocation randomness.

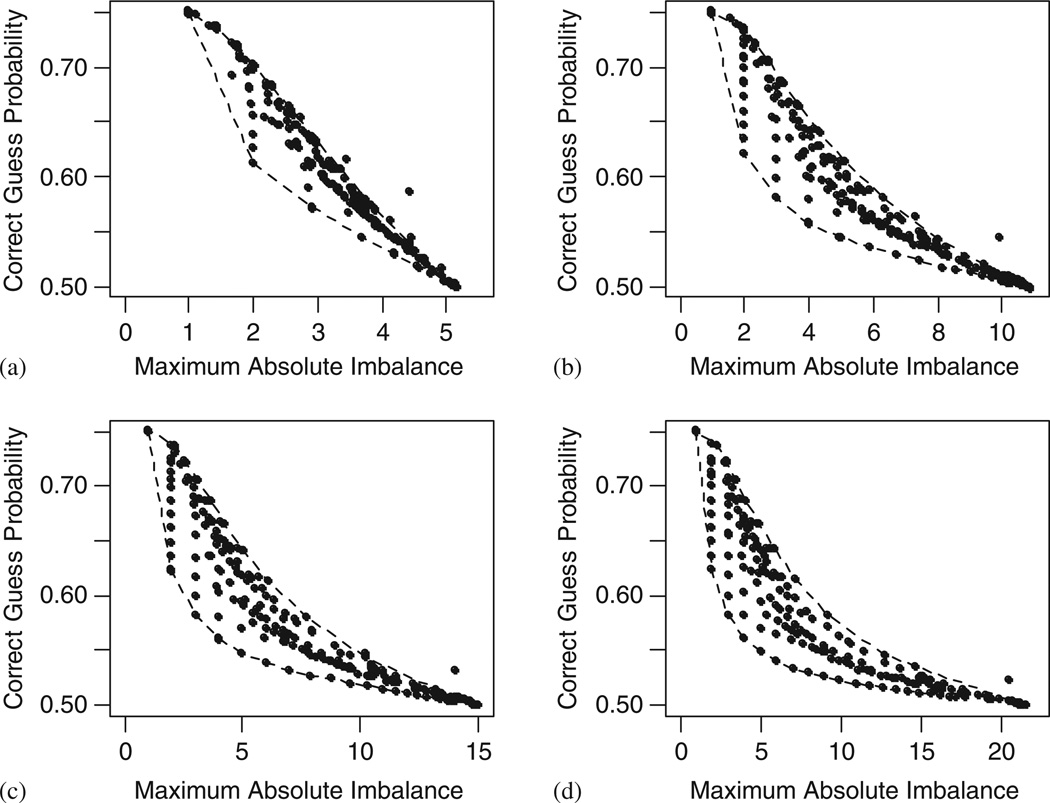
Measured by the maximum imbalance and the CG probability, we found that almost all the 260 simulation scenarios fall in a closed region formed by two boundaries connected at the two extreme points. The upper left extreme point is given by the PBD with a block size of 2, and the lower right extreme point stands for SR. Figure 2 shows that the upper boundary is set by the BCD with the biased probability varying from 0.5 to 1.0. The lower boundary is set by Soares and Wu’s BSD with the imbalance tolerance varying from 1 to 21. This pattern becomes clearer as sample size increases from 20 to 300.

Figure 2.

Performance of 260 randomization design scenarios under different sample sizes. Simulation runs = 5000. Upper boundary: Efron’s biased coin design. Lower boundary: Soares and Wu’s BSD: (a) Sample size = 20; (b) sample size = 80; (c) sample size = 150; and (d) sample size = 300.

5.2. Performances of designs in the biased coin class

Figure 3 plots the performances of 118 scenarios for the five designs in the biased coin class.

Figure 3.

Performance of randomization designs in the biased coin class. Sample size = 80, simulation runs = 5000. BCDWIT: Chen’s biased coin design with imbalance tolerance. GBCD: Smith’s generalized biased coin design. ABCD: Wei’s adaptive biased coin design. Upper boundary: Efron’s biased coin design. Lower boundary: Soares and Wu’s BSD.

Chen’s BCDWIT method connects the upper and lower boundaries. When parameter δ → ∞, BCDWIT is equivalent to BCD. When p_bias = 0.5, it becomes the BSD. Smith’s GBCD has a better performance than BCD but falls far behind the BSD. Wei’s ABCD behaviors the same as GBCD with parameter ρ = 1. This can also be seen from the conditional allocation probabilities (10) and (12),

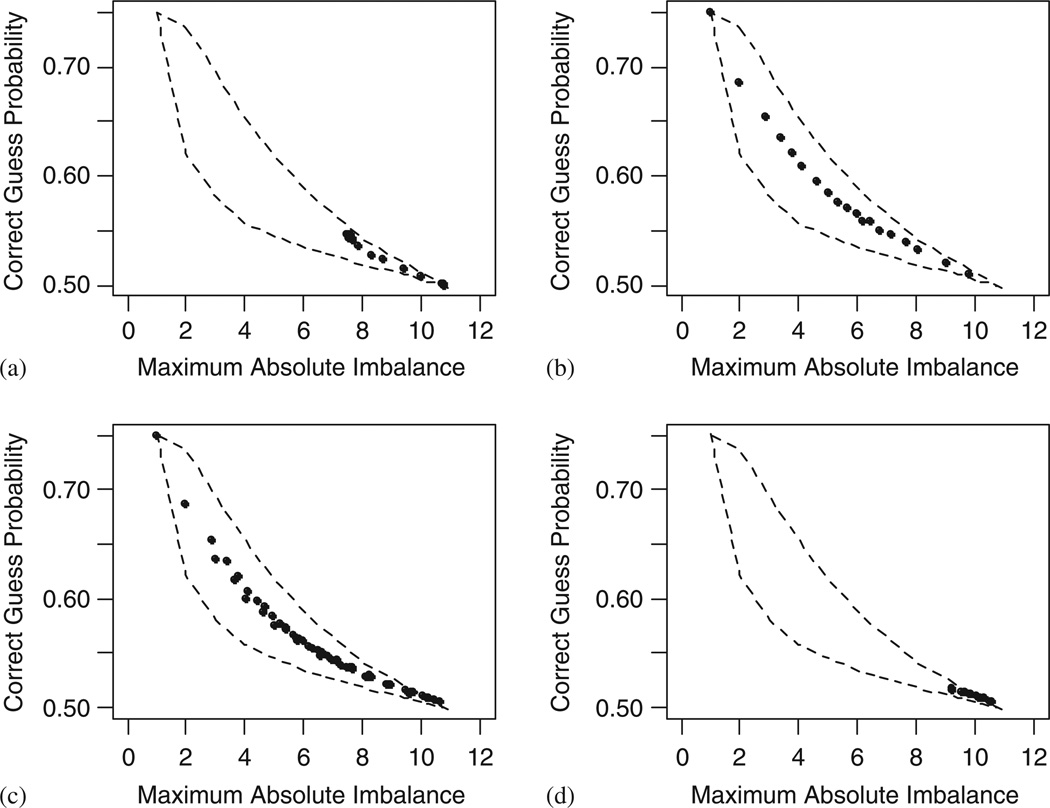
5.3. Performances of designs in the urn class

Figure 4 plots the performances of the four urn type designs with the background of the two boundaries. Parameters in the Wei’s urn design have little effect on its performance. In the conditional allocation probability formula (14), when α = β = 0, or when w > > β, the UD approaches SR as pointed out by Wei and Lachin [24], and Rosenberger and Lachin [2]. The maximum absolute imbalance of the UD decreases as w decreases. It reaches the nadir when w = 1, where the treatment imbalance remains larger than most other designs. Similar to the EBCD and the BSD, Chen’s EUD and Antognini’s Sym-EUD have a wide performance range spanning to the two extremes. Figure 4(b, c) show that with a fixed treatment imbalance, the allocation randomness for EUD and Sym-EUD are about at the middle between the EBCD and the BSD. Antognini’s Asym-EUD does not differ much from SR, and its balancing capacity is very limited.

Figure 4.

Performance plot for randomization designs in the urn class. Sample size = 80. Simulation runs = 5000. Upper boundary: Efron’s biased coin design. Lower boundary: Soares and Wu’s BSD: (a) Wei’s Urn Design; (b) Chen’s Ehrenfest Urn Design; (c) Symmetric Ehrenfest Urn Design; and (d) Asymmetric Ehrenfest Urn Design.

5.4. Which design is better – EUD or BCDWIT?

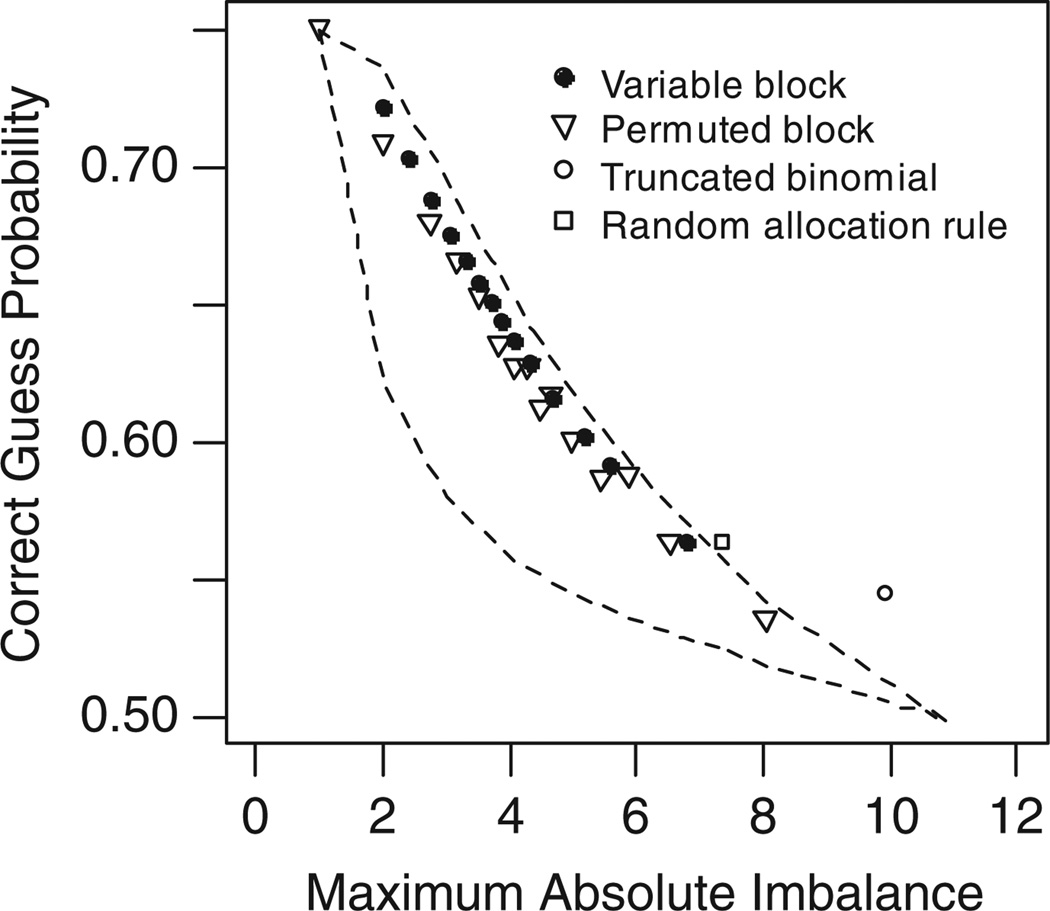
Both the BCDWIT and the EUD are proposed by Chen [10,11]. Chen compared the treatment imbalance and allocation randomness of BCDWIT(δ, p_bias) with EUD(w) under the conditions of δ = w and (1 − 1/2w) > p_bias > 1/2, based on the average treatment imbalance, $(1/n){\displaystyle {\sum }_{i=1}^n}{D}_i$, and the average excess selection bias, $(1/n){\displaystyle {\sum }_{i=1}^n}[\text{max}(p_{i1},p_{i2})-\frac{1}{2}]$. Chen concluded that EUD is more balanced than BCDWIT when both designs own the same level of asymptotic average excess selection bias [11]. Our simulation results shown that this conclusion does not hold in general. EUD has one parameter, w. By scanning w from 1 to 200, we see a line connecting the two extremes. On the other hand, BCDWIT has two parameters, δ and p_bias. For a fixed δ, a curve connecting the BCD and BSD is available by varying p_bias from 0.5 to 1.0. When both EUD and BCDWIT are plotted on the same chart, as shown in Figure 5, we see that BCDWIT provides better performances than EUD when p_bias is close to 0.5. For example, for a sample size of 100, BCDWIT(δ = 3, p_bias = 0.5) has a CG probability CG = 58.1% and a maximum imbalance MI = 3. EUD(w = 3) has a similar MI = 2.94, but its CG probability is CG = 65.5%. On the other hand, with the same CG = 58.5%, EUD(w = 10) has a much larger imbalance, MI = 5.23.

Figure 5.

Performance of the Ehrenfest urn design and the BCDWIT. Sample size = 100. Simulation runs = 5000. Upper boundary: Efron’s biased coin design. Lower boundary: Soares and Wu’s BSD. BCDWIT: Chen’s biased coin design with imbalance tolerance. EUD: Ehrenfest urn design.

5.5. Performances of permuted block and other randomization designs

PBD is the most commonly used randomization method [20,22]. Although its algorithm is different from those in the biased coin class and the urn model class, its performance is very close to Smith’s GBCD and Chen’s EUD. This can be seen by comparing Figure 6 with Figures 2 and 4(b).

Figure 6.

Performance of randomization designs. Sample size = 80, simulation runs = 5000. Upper boundary: Efron’s biased coin design. Lower boundary: Soares and Wu’s BSD.

With PBD, the allocation randomness increases as the block size b increases, at the cost of treatment imbalance. In practice, a block size of 4, 6, or 8 is generally recommended. Block sizes greater than 20 are rarely reported, mainly because of the concern on treatment imbalance, which is believed equal to the half of the block size. However, in a block of size b, among all $\left(\begin{array}{c}\hfill b\hfill \\ \hfill b/2\hfill \end{array}\right)$ equally possible sequences, there are only two sequences with an absolute imbalance of b/2. In other words, the probability that the maximum imbalance b/2 occurs in a block of size b is 2[(b/2)²]/b!. For block size b = 20, this probability is 1.08E-5. It is also found that the performance of PBD (b = 20) is similar to BCD (p_bias = 0.7). Table III lists all the six measures for these two designs at three sample sizes. In practice, BCD (p_bias = 0.7) is much easier to be accepted than PBD (b = 20), mainly because of the lack of quantitative performance analyses of these designs.

Table III.

Performance comparison between PBD(20)^* and BCD(0.7)^† (Simulation runs = 5000).

Sample size	Randomization design	Probability of exact balance	Standard deviation of final imbalance	Maximum imbalance	Entropy	Probability of deterministic allocation	Probability of correct guess
20	Permuted block (size = 20)	0.232	0	3.446	0.607	0.090	0.616
	Biased coin (p-bias = 0.7)	0.298	1.731	2.963	0.637	0	0.633
80	Permuted block (size = 20)	0.234	0	4.655	0.606	0.091	0.617
	Biased coin (p-bias = 0.7)	0.287	1.760	4.374	0.635	0	0.640
300	Permuted block (size = 20)	0.233	0	5.690	0.606	0.091	0.617
	Biased coin (p-bias = 0.7)	0.287	1.783	5.807	0.635	0	0.642

^*Permuted block design with block size b = 20.

^†Efron’s biased coin design with biased coin probability p_bias = 0.7.

The VBD has been widely used with the motivation to reduce the chance of selection bias [1]. Rosenberger and Lachin [2] indicated that, under the Blackwell–Hodges convergence strategy, i.e. guessing the next allocation as the smaller treatment arm [19], use of variable block sizes yields virtually no reduction in selection bias. Our simulation results shown that, with a given maximal block size, the probabilities of deterministic assignment and CG for the VBD is higher than that under the PBD. For example, with a sample size of 80, PBD (b = 8) has DA = 20%, CG = 66.6%, and MI = 3.18 ± 0.54. If VBD (b_max = 8) is used, we have DA = 27%, CG = 68.8%, and MI = 2.77 ± 0.57. The use of VBD may discourage some people attempting making allocation guess based on the block size. Under the Blackwell’s convergence strategy, this benefit disappears.

The RAR and the TBD both require a pre-specified sample (stratum) size, which may not be available when randomization is stratified by baseline covariates. The most significant feature for these two designs is the EB at the end of the randomization sequence. However, their maximum imbalance, which is likely to occur in the middle of the sequence, is close to that under the SR, as shown in Figure 6.

6. DISCUSSION

We define a unified imbalance measure, U_I, and a unified randomness measure, U_R based on the performance relative to the two extremes:

$$\begin{array}{c}{U}_{\mathrm{I}}=\frac{\text{MI}-{\text{MI}}_{\text{PBD}(b=2)}}{{\text{MI}}_{\text{SR}}-{\text{MI}}_{\text{PBD}(b=2)}}\hfill \\ U_{\mathrm{R}}=\frac{\text{CG}-{\text{CG}}_{\text{SR}}}{{\text{CG}}_{\text{PBD}(b=2)}-{\text{CG}}_{\text{SR}}}\hfill \end{array}$$ (18)

where subscript PBD(b = 2) stands for PBD with a block size of 2, and subscript SR stands for SR. Both U_I and U_R vary on [0, 1] depends on the randomization design. For all two-arm parallel trials of any sample size, there are MI_{PBD(b = 2)} = 1, CG_{PBD(b = 2)} = 0.75; and CG_SR = 0.5. MI_SR is affected by the sample size. For a trial with a sample size of 100, MI_SR ≈ 12. An overall performance measure G is defined based on U_I and U_R:

$$G=\sqrt{\frac{{(w_{\mathrm{I}}{U}_{\mathrm{I}})}^2+{(w_{\mathrm{R}}{U}_R)}^2}{w_{\mathrm{I}}^2+w_{\mathrm{R}}^2}}$$ (19)

where weights w_I and w_R represent the importance of balance and randomness for the trial. A lower value of G indicates a better overall performance regarding both balancing and randomness. Using (18) and (19), we are able to select the best randomization designs from different designs. Table IV lists the best scenarios for each of the 14 designs under the condition of w_I = 1 and w_R = 1, with a sample size of 100.

Table IV.

Overall performance ranks of randomization design-scenarios Weight w_I = w_R = 1, Sample size = 100.

Rank*	G†	Design (parameter)	EB‡	Dn§	MI¶	ET‖	DA**	CG††	UI‡‡	UR§§
1	0.253	Big stick(δ = 4)	0.129	2.454	3.999	0.611	0.118	0.558	0.272	0.231
2	0.254	Biased coin with imbalance tolerance (δ = 4, pbias = 0.50)	0.130	2.473	3.999	0.612	0.118	0.559	0.272	0.238
12	0.339	Symmetric extension of Ehrenfest urn design (w = 1, pbias = 0.90)	0.199	3.357	4.458	0.349	0.497	0.590	0.314	0.362
26	0.362	Ehrenfest urn design (w = 10)	0.181	2.221	5.228	0.669	0	0.585	0.384	0.340
46	0.392	Permuted block design (b = 30)	0.196	2.633	5.608	0.635	0.056	0.591	0.418	0.364
85	0.436	Permuted block design (b = 12)	0.285	1.702	3.916	0.574	0.137	0.639	0.265	0.557
103	0.466	Permuted block design (b = 10)	0.307	0	3.620	0.553	0.167	0.654	0.238	0.615
109	0.480	Permuted block design (b = 8)	0.329	1.524	3.272	0.537	0.192	0.662	0.206	0.646
149	0.523	Permuted block design (b = 6)	0.365	1.270	2.830	0.505	0.241	0.680	0.166	0.721
181	0.594	Permuted block design (b = 4)	0.416	0	2	0.448	0.334	0.709	0.091	0.835
255	0.709	Permuted block design (b = 2)	0.500	0	1	0.347	0.5	0.751	0	0.003
57	0.404	Generalized biased coin design (ρ = 5)	0.216	3.040	5.503	0.647	0.010	0.600	0.409	0.399
59	0.407	Variable block design(bmax = 50)	0.199	2.435	5.811	0.631	0.063	0.594	0.437	0.376
79	0.432	Biased coin design (pbias = 0.65)	0.236	2.349	5.490	0.658	0	0.614	0.408	0.455
112	0.490	Random allocation rule	0.116	0	8.207	0.668	0.020	0.558	0.654	0.231
113	0.491	Wei’s UD (w = 1, α = 0, β = 5)	0.122	5.696	8.404	0.684	0	0.543	0.672	0.172
118	0.492	Wei’s adaptive BCD	0.125	5.673	8.415	0.680	0.010	0.544	0.673	0.178
187	0.600	Asymmetric extension of Ehrenfest UD (w = 30)	0.084	7.700	10.317	0.687	0	0.517	0.846	0.066
218	0.658	Truncated binomial design	0.080	0	11.102	0.638	0.079	0.540	0.917	0.162
249	0.707	SR	0.071	10.017	12.019	0.693	0	0.501	1	0.003

Simulation runs = 5000.

^*Only the highest ranking scenario for each design and the most commonly used permuted block designs are listed.

^†Overall performance measure based on maximum absolute imbalance and correct guess probability.

^‡Probability of exact balance.

^§Standard deviation of final treatment imbalance.

^¶Maximum absolute imbalance.

^‖Entropy of treatment assignment.

^**Proportion of deterministic assignment.

^††Probability of correct guess.

^‡‡Unified scale of treatment imbalance.

^§§Unified scale of allocation randomness.

Soares and Wu’s BSD(δ = 4) is the best design for trials with a sample (stratum) size of 100. BCDWIT (δ = 4, p_bias = 0.5) is equivalent to the BSD(δ = 4). Among all scenarios of the BCD, the BCD(p_bias = 0.65) produces the best performance. This is consistent with Efron’s original suggestion of p_bias = 2/3 = 0.666 [6]. The VBD ranks below PBD, suggesting that the use of variable block size does not improve the overall performance. Among all PBD scenarios, PBD(b = 30) gives the best performance, with the maximum imbalance MI < 6. Wei’s urn design falls behind most other designs, indicating that it is not a good design for trials with a sample size of 100. Data listed in Table IV also demonstrate that the two measures we selected as for the overall performance evaluation are consistent with the other measures.

In clinical trial practice, PBDs with block sizes between 2 and 6 are the most commonly used randomization method [25]. Although we have seen people used Wei’s urn design, Efron’s BCD, and SR in clinical trial practice, many randomization designs evaluated in this manuscript have not been reported as being used in real trials. The simplicity in implementation for PBD may be the reason. With the modern computing technology, this advantage is gradually losing its significance. Although the impact of the randomization algorithm on the validity of the conventional statistical analysis strategy remains a topic for all randomization designs except the SR, the potential selection bias associated with the PBD caused by the high CG probability deserves more attention. Berger evaluated the risk of selection bias for PBD under different scenarios of block size, number of treatment groups and allocation ratios, and provided direct evidences of selection bias for 30 trials [26]. Based on our study, PBD with a block size of 6 will have a CG probability of 68%. With the same level of maximum imbalance of 3, the BSD has a CG probability of 58%, much closer to the 50% level associated with the SR.

The performance evaluation presented is affected by the measures selected. One may use (Dn, DA), or (Dn, ET) rather than (MI, CG). People can argue that a 10% deterministic assignments plus 90% pure random assignments is more vulnerable to selection bias compared with a 50% biased assignments with p_bias = 0.65 plus 50% pure random assignments. Based on the convergence strategy proposed by Blackwell and Hodges [19], the CG probability for these two scenarios are 55% and 57.5%, respectively, the one without deterministic assignment is actually more vulnerable to selection bias.

Several randomization designs we choose not to include in this paper. The minimization method proposed by Taves [27], Pocock and Simon [28] aims to balance the distributions of multiple covariates. The maximal procedure proposed by Berger [29] requires a pre-specified sample size and a complex (compared to most randomization designs commonly used) procedure to generate the randomization sequence [30].

The selection of a proper randomization design for a trial may be influenced by many other factors, including the implementation of randomization algorithm and study drug tracking. However, the two primary goals for subject randomization in comparative clinical trials remain the same: to ensure randomness and to control imbalance. Therefore, it is important to evaluate different design options based on the consideration of their performance measured in both imbalance and randomness. With the help of computer simulation, and the conditional allocation probability for each randomization design, this goal can be reached.