Normal Mode Gating Motions of a Ligand-Gated Ion Channel Persist in a Fully Hydrated Lipid Bilayer Model

Abstract

We have previously used molecular modeling and normal-mode analyses combined with experimental data to visualize a plausible model of a transmembrane ligand-gated ion channel. We also postulated how the gating motion of the channel may be affected by the presence of various ligands, especially anesthetics. As is typical for normal-mode analyses, those studies were performed in vacuo to reduce the computational complexity of the problem. While such calculations constitute an efficient way to model the large scale structural flexibility of transmembrane proteins, they can be criticized for neglecting the effects of an explicit phospholipid bilayer or hydrated environment. Here, we show the successful calculation of normal-mode motions for our model of a glycine α-1 receptor, now suspended in a fully hydrated lipid bilayer. Despite the almost uniform atomic density, the introduction of water and lipid does not grossly distort the overall gating motion. Normal-mode analysis revealed that even a fully immersed glycine α-1 receptor continues to demonstrate an iris-like channel gating motion as a low-frequency, high-amplitude natural harmonic vibration consistent with channel gating. Furthermore, the introduction of periodic boundary conditions allows the examination of simultaneous harmonic vibrations of lipid in synchrony with the protein gating motions that are compatible with reasonable lipid bilayer perturbations. While these perturbations tend to influence the overall protein motion, this work provides continued support for the iris-like motion model that characterizes gating within the family of ligand-gated ion channels.

General anesthetics bind to γ-amino butyric acid (GABA) and glycine receptor ion channels and generally increase the open time of these channels. These transmembrane protein complexes are members of the ligand-gated ion channel (LGIC) family of pentameric cysteine-loop receptors. We have previously used molecular modeling techniques combined with experimental data to visualize a plausible model of an anesthetic binding site within a model of the homomeric glycine α-1 receptor (GlyRa1) (1−8). We have also suggested a mechanism, based on normal-mode analysis using an elastic network model, by which these ion channels may open and close and postulated how this motion may be affected by the presence of various ligands (9−11). From this work as well as that of several others (12−15), it has become clear that one of the key fundamental motions in channel gating within this class of ion channel proteins appears to be an “iris-like” motion of the central ion pore that spans the entire length of the protein. This motion is characterized by a twisting of the extracellular ligand binding domain in a circular direction within a plane parallel to the lipid bilayer that is nearly opposite in direction to that of a similar twisting motion within the transmembrane domain. It is associated with movements of pore lining amino acids, as well as alterations in the geometries of both extracellular and transmembrane regions that are thought to be involved in binding a variety of ligands.

Both our previous work and most other normal-mode calculations can rightly be criticized for being conducted in vacuo, completely devoid of proper hydration and suspension within a phospholipid bilayer (16). The main reason for the original approach with normal-mode analysis is that the problem complexity scales as n² or n³ (depending on the algorithm), where n is the number of points that may represent atoms or groups of atoms. Even for an isolated ion channel, this was nontrivial to do on an atomic level with some 26 000 particles.

Since our original calculations were performed though, computational horsepower has become available that now allows similar vibrational calculations via normal-mode analysis on much larger and more realistic systems. Here we show the successful application of the elastic network calculation on our model of a glycine α-1 receptor that has been suspended in a lipid bilayer and water environment, which are all now included as part of a large elastic network. Despite the presence of over 100 000 atoms and the slightly asymmetric placement of the protein ion channel within the lipid bilayer and water, these calculations continue to demonstrate a clearly symmetric motion of the ion channel protein that is consistent with the ion channel gating motion demonstrated in our previous in vacuo works. This result provides new support for both the gating model and the applicability of normal-mode analysis to ever more complex systems.

Results and Discussion

An obvious central weakness of classical in vacuo elastic network normal-mode models of transmembrane protein motion is that they are somewhat artificial. While they can account for the proximity of other atoms that are part of the protein structure, there are no effects from any adjacent lipid bilayer or surrounding water. In particular, one could argue that this will intrinsically lead to normal modes that are mostly rigid motions of the secondary structure elements, regardless of what the true gating transition is. In general, if one only includes the atomic density from the protein (no solvent) and that density is almost cylindrical in shape, there is a clear risk that cylindrical twisting modes would be obtained as an artifact of system symmetry.

In the current manuscript, both water and lipid solvents were included in all of the elastic network calculations, with the GlyRa1 embedded slightly off center to avoid any symmetry bias in the calculation. Despite the size of the system, as well as the fact that the system density is now close to uniform, the calculations involving the GlyRa1 with explicit membrane components as well as water clearly show that the introduction of water and lipids did not grossly distort the overall structure of the GlyRa1 nor the general direction of its gating motion noted in previous works⁹ (Figures 1 and 2). This provides additional support that the functional motion model suggested here is significant and not based on any potential artifact that could be present with the in vacuo approach.

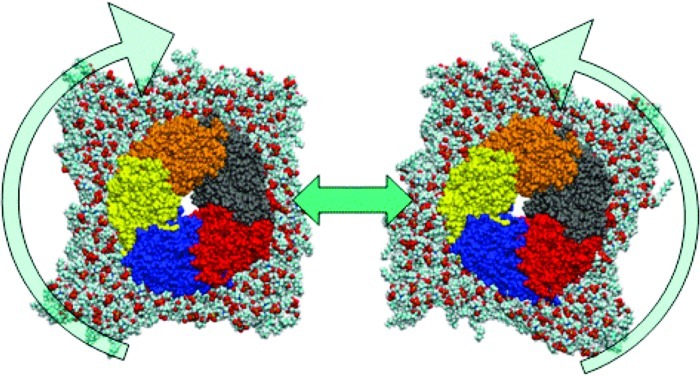
Figure 1.

Van der Waals (VDW) representation of protein as viewed from above (subunits colored) embedded in lipid bilayer (with water box removed for clarity) showing “washing machine-like” motion of protein within lipid bilayer.

Figure 2.

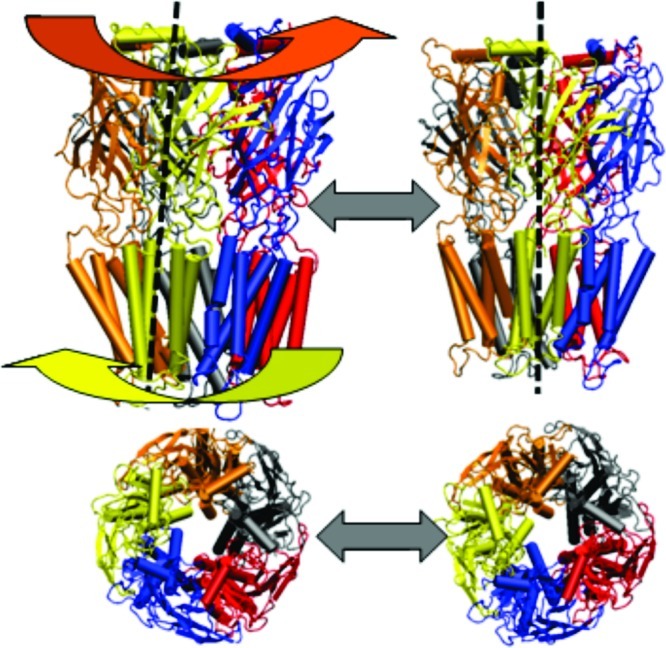
Schematic representation of protein (subunits colored; with water box and lipid bilayer removed for more clear protein visualization) showing “iris-like” motion of protein within lipid bilayer (side and top views).

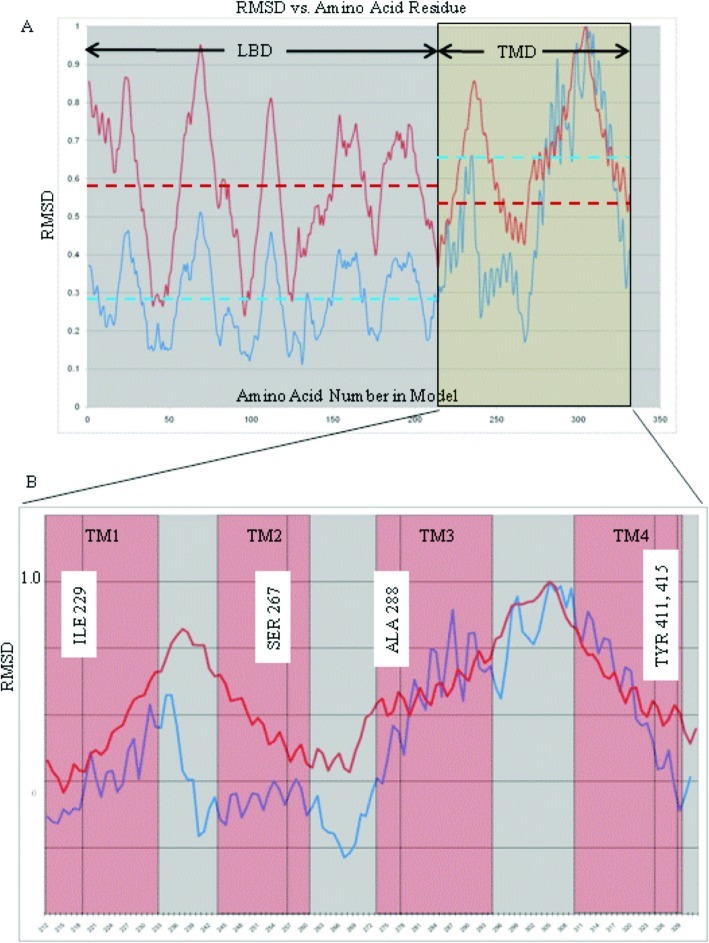
Normal mode analysis revealed that the GlyRa1 in a fully hydrated bilayer environment continues to demonstrate an iris-like gating motion among its low-frequency, high-amplitude natural harmonic vibrations (Figures 1 and 2, also see online videos of view from the extracellular side of the GlyRa1 embedded in lipid with waters removed for clarity and view from the lateral side of the GlyRa1 embedded in lipid with waters removed for clarity). For the particular iris-like mode that has been previously associated with channel gating, a plot of the rmsd of the individual α carbon atoms over the entire GlyRa1 reveals a similar set of deviations from baseline for both the in vacuo and embedded systems (Figure 3). The harmonic motions of both the ligand-binding domain (LBD) and the transmembrane domain (TMD) within the hydrated lipid bilayer system tended to parallel their counterparts in vacuo. However, as can be seen from the rmsd analyses in Figure 3, the presence of the lipid bilayer and waters did influence the overall protein motion compared with that extracted from the in vacuo calculation. In particular, the mean rmsd motions of the LBD (0.28) compared with the TMD (0.53) within the in vacuo complex (blue dotted lines) were quite different and led to significant opposing twists of the LBD relative to the TMD. However, in the fully hydrated lipid bilayer system, the presence of both water and lipid tended to make the mean rmsd motion (red dotted lines) of the LBD (0.58) more uniform about a similar mean with the respect to the TMD (0.66) but produced a similar iris-like twisting motion of channel gating nonetheless. The presence of the lipid bilayer and water tend to influence the motion of the LBD relative to its in vacuo counterpart, producing a motion with less dramatic “wringing-like” activity compared with that of its TMD counterpart. However, the TMD region still seems to maintain a twist that is quite comparable to that seen in vacuo. This may imply that small ligand-induced motions within the LBD relative to the TMD may be all that are required for actual transduction of ligand binding into channel opening.

Figure 3.

Plot of rmsd averaged over all five subunits relative to maximum average rmsd vs amino acid α carbon number: (A) The entire subunit (LBD = ligand binding domain, TMD = transmembrane domain). Dotted lines represent average rmsd over an entire LBD or TMD region (blue = in vacuo model, red = model in fully hydrated lipid bilayer) Note the relative similarity of mean rmsd for TMD and LBD within the fully hydrated lipid based model. (B) Transmembrane domain region magnified with extent of α-helical regions noted in red boxes and residue positions relevant to anesthetic effects labeled.

Those residues associated with alteration of anesthetic effects on GlyRa1 function (Ile229, Ser267, Ala288, Tyr406 and Tyr411, as demonstrated from previous experiments) (4,17−19) lie within the extracellular third of the TMD four-helical bundles. Despite the effects of lipid and water, a plot of the rmsd of these TMD residues during motion demonstrates that the putative anesthetic binding residues seem to be consistently located in a region of intermediate motion (Figure 3), quite similar to that seen with the in vacuo calculations.

Furthermore, the introduction of periodic boundary conditions allowed the illustration of a harmonic vibration of the protein gating motion that is simultaneously accompanied by a locally accommodating lipid bilayer perturbation (see online supplemental movies: view from the extracellular side of the GlyRa1 embedded in lipid with waters removed for clarity; view from the lateral side of the GlyRa1 embedded in lipid with waters removed for clarity; view from the intracellular side of the embedded GlyRa1 with both lipid with waters removed for clarity). The motion of the lipid bilayer with the twisting of the embedded protein is somewhat analogous to the clothes within a washing machine twisting about the central agitator.

Since the natural function of LGICs is the gating motion involved in the transition from the resting to the open state, we had previously postulated that such a natural function should be represented in the harmonic motion of some of the highest amplitude and lowest frequency normal-mode vibrations⁹. While this is, in fact, clearly the case for both the system in vacuo and in the hydrated bilayer, the in vacuo calculations present the gating motion as first and foremost. However, the bilayer-embedded system shows a predominance of lateral swaying motions of the protein within the bilayer among the first four nontrivial normal-mode vibrations, suggesting that bilayer effects may predominate on what could be extremely minute time scales. These first four nontrivial low-frequency modes primarily involved an alternating lateral “hula-like” motion of the hydrated LBD, while the membrane embedded TMD subunits moved in opposite directions, which were simultaneously parallel to the plane of the lipid bilayer. The primary reason for these modes is likely the absence of rotational invariance in a rectangular system when applying periodic boundary conditions (there are only three trivial modes for this setup, compared with six for traditional in vacuo normal modes). Furthermore, the size of the system allows for additional low-frequency modes. The presence of these motions would also seem logical because the continuously undulating lipid bilayer serves as a background within which most of these motions take place.

Unfortunately, it is not possible to derive actual vibrational frequencies from elastic network calculations, because the elastic network model does not take different interaction strengths into account, and only produces motion shapes and approximate relative frequencies within each model.

Additionally, the current analyses for both the hydrated lipid bilayer system and the in vacuo calculations show only minimal pore diameter changes. This is because the native motion being examined is probably occurring on the picosecond time scale but is still in the general direction of channel opening and closing. This implies that these channels are probably always fluttering in the general direction of channel gating. However, it is not until a native ligand binds or a large enough random thermal motion occurs that one sees such small fluctuations transformed into the large motions associated with full ion channel opening and closing. This occurs on the much less likely millisecond time scale.

Ideally, one would like to be able to subject this system to a full molecular mechanics force field treatment for the calculation of normal modes, but the computational requirements for such are virtually intractable. In addition, the rapidly varying potential energy terms used in such calculations would make it hard to approximate large-scale motion from the potential energy shape close to only a local minimum. This, in principle, could be addressed by examining the entire gating cycle for this complex using full-scale molecular dynamics simulations, but again this problem is intractable at this time. This is especially true given current supercomputing hardware capabilities and the fact that most ion channel gating transitions occur on the millisecond time scale. For the immediate future at least, this system should become more amenable to longer scale molecular dynamics simulations over the course of several microseconds (not milliseconds) or perhaps the implementation of other more coarse-grained methods.

While this work is certainly a step forward from our previous in vacuo calculations, criticism could arise because our membrane was only composed of a homogeneous POPC bilayer and contained no cholesterol. Future opportunities for greater realism should present themselves by altering the composition of the lipid bilayer as well as inserting cholesterol moieties, but at that point, it will likely be necessary to go beyond the highly simplified elastic network models. In particular, the inclusion of a variety of methods for better simulating and analyzing membrane fluidity may become very important factors for assessing more subtle membrane and water effects on adjacent protein dynamics (20,21). Furthermore, one may be able to include a myriad of other membrane and protein associated constituents, including the effects of various salt counterions and, in the case of the GlyRa1, zinc (22). However and for the purposes set forth in this manuscript, it is an important step to move from a zero-order to first-order approximation by adding water and lipid in order to at least show that harmonic analyses still result in twisting modes. In no way, though, should one claim that such results can be used for second-order predictions of microenvironment dynamics that would include even more subtle but nonetheless realistic details of the lipid and water microenvironments.

To the best of our knowledge, this is the first description of a normal-mode calculation describing large-scale protein dynamics and ion channel gating that includes the presence of a fully hydrated lipid bilayer complex. This analysis was only possible, given current computer hardware capabilities, using an elastic network approximation due to the large atomic composition of the system. In addition to showing that low-frequency iris-like motions are present in models that are more realistic, these simulations will provide a more accurate means of studying the large-scale motions of this class of ion channel protein in general. In addition, they may provide a means for introducing actual ligands into a water and lipid embedded protein system as well as allow the discernment of ligand binding effects on overall ion channel gating.

Methods

Construction and Embedding of the GlyRa1 Model in a Hydrated Lipid Bilayer

Coordinates of our previously validated homology model of the GlyRa1 were obtained from our previous work (7−9). A 100 molecule × 100 molecule lipid bilayer matrix was constructed from POPC moieties and accompanying water molecules within the VMD 1.86 software package (NCSA, Urbana, IL)²³. Discovery Studio 1.7 (Accelrys, San Diego, CA) molecular modeling software was used to insert and suspend our GlyRa1 model into the lipid bilayer such that the glycine 221 residue was in the locale of the lipid−headgroup boundary. The protein was longitudinally centered in the lipid bilayer but slightly off-center in the remaining two axes to remove any protein center of mass bias in subsequent calculations. All waters within 3.8 Å of the protein were removed, as were all lipid molecules within 2 Å of the protein. Hydrogens were added to the system with subsequent energy minimization of the entire system to remove energetically unfavorable contacts using the CHARMm force field. The bilayer−protein system was subsequently further hydrated in a periodic water box with the GROMACS software suite (24) (Figures 4 and 5). The system was subjected to initial energy minimization followed by 10 ns of equilibration of the lipids and water with position restraints (1000 kJ/(mol·nm²)) on the ion channel. Standard settings were used for the minimization and simulation: 2 fs time step, 1.0 nm cutoff on van der Waals interactions, particle-mesh Ewald electrostatics²⁵, and anisotropic Berendsen pressure coupling²⁶. The ligand-binding domain (LBD) of the GlyRa1 is characterized by its overall β sheet character and the transmembrane domain (TMD) by its primary assembly of four helix bundles. The overall symmetry of the complex remained a pentamer of subunits surrounding a central ion pore. It should be noted that water clearly filled this pore throughout its entire length in the equilibrated and fully hydrated lipid bilayer construct prior to normal-mode analyses.

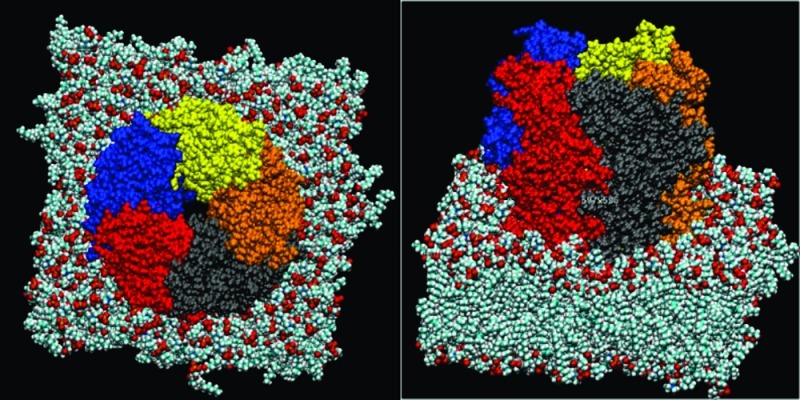
Figure 4.

Van der Waals (VDW) representation of protein (barely visible) embedded in lipid bilayer and water box (red atoms) with periodic boundary conditions.

Figure 5.

VDW representation of protein (subunits colored) embedded in lipid bilayer (with water box removed for clarity).

Normal-Mode Analyses

Normal-mode analysis was performed on the GlyRa1 in vacuo and on the construct embedded into the fully hydrated lipid bilayer system using our previously validated Lindahl all atom based elastic network (LAABEN) method (9) and run locally on a Linux workstation. As previously shown, this approach explicitly retains all atomic coordinates and degrees of freedom in the normal-mode calculation and uses a sparse matrix representation of the Hessian matrix to limit memory requirements compared with some other elastic network algorithms. Input parameters included setting the total number of normal modes to be generated at 11 (including the rigid-body motions of the whole complex), an interaction distance weight parameter of 2 Å, and an interaction cutoff default of 10 Å. The latest version of this software allows the introduction of normal-mode analyses to be carried out in the setting of periodic boundary conditions as well as on system sizes that include a lipid bilayer environment. For the embedded protein system, the entire water, lipid, and protein components were treated as one large elastic network model with the above-noted software parameters. Because the lipid bilayer is allowed to extend to the limits of the periodic box, the lipid bilayer does not interact with any vacuum component but is allowed to interact with itself in the mirrored periodic box as if in the even more realistic extended bilayer configuration.

Root mean square deviations (rmsd) of the α carbon atom for each amino acid residue were calculated over the course of the normal-mode trajectories and tabulated in Microsoft Excel. The rmsd’s for the α carbon atom from the same amino acid within each subunit were then averaged and normalized relative to the maximum average rmsd within the protein. Since amplitudes within normal modes are somewhat arbitrary, the latter normalization within a given protein construct was performed to allow comparison of the in vacuo and hydrated/lipid embedded systems.

Funding Statement

National Institutes of Health, United States