A Calculation Model for Serum Ionized Calcium Based on an Equilibrium Equation for Complexation

Abstract

Measurement of ionized calcium is more important than measurement of total calcium in serum samples. In the present study, equations were derived from complexation and acid dissociation equilibrium equations, and were used to determine the concentration of ionized calcium from the observed serum concentrations of total calcium, albumin, total protein, and inorganic phosphate. The ionized calcium concentration was calculated in 67 serum samples from healthy subjects and 34 outpatients previously identified as having abnormal serum calcium levels. The correlation coefficient between our method (y) and the calcium-ion-selective electrode method (x) was 0.953 and the linear regression equation was y = 0.97x at pH 7.4 with a factor of α = 0.21, which was based on the differences between the concentrations of calcium phosphorus compounds obtained by the electrode method and by calculation. The developed calculation is as useful and accurate as the electrode method, and therefore extremely useful for clinical diagnoses.

Introduction

Blood calcium consists of 39.5% protein-bound calcium, 46.9% ionized calcium and 13.6% diffusible calcium complexes.1 Ionized calcium plays an important physiological role, and determination of ionized calcium in the blood is an important clinical parameter.2

Initial measurements of ionized calcium used an equation developed by McLean and Hastings based on the law of mass action, which used the total protein and albumin concentrations, and the pH.3 However, this calculation was extremely complicated, and required a nomogram. Subsequently, Ross4 developed the calcium-ion-selective electrode method in 1967, which enabled the determination of ionized calcium concentrations in diagnostic laboratories and hospitals.5 However, the electrode method requires special equipment, and the obtained value is greatly influenced by slight variations in the pH. Thus, the electrode method is not routinely used in Japan.

To date, many equations, including a correction equation by Payne, have been proposed to determine ionized calcium concentrations.3,6,7 These equations are essentially empirical equations based on a correlation between a ionized calcium concentration obtained by the electrode method and an observed concentration for albumin or another substance. These equations reportedly fail to yield satisfactory results.2

Total calcium is absorbed and released by the intestines, bones, and kidneys and is biologically regulated by hormones and vitamins. Calcium in the blood consists of free ionized calcium and calcium complexes such as protein-bound calcium, calcium phosphate and organic acid complexes.8 These complexes react reversibly with calcium and remain in equilibrium according to the law of mass action. The blood calcium fraction is influenced by these chemical equilibria. Therefore, we attempted to determine the ionized calcium concentration based on these equilibria.

The aforementioned ligands bind to both calcium and hydrogen ions, and these cations compete for ligand-binding sites. We hypothesized that at pH 7.4, an equilibrium exists between hydrogen ions and the ligands with an acid dissociation constant that can be used to calculate the ionized calcium concentration. We developed equations for calculating the equilibrium constant for calcium to determine the final concentration of ionized calcium. The details of this calculation are described in this study.

Experimental

Serum samples

Serum samples were collected from 67 healthy subjects (14 males, 53 females), and 34 outpatients (10 males, 24 females) with primary hyperparathyroidism, idiopathic hypoparathyroidism, or other conditions that cause abnormal serum calcium levels. The samples were handled anaerobically from blood sampling to determination of ionized calcium by the electrode method, and were handled aerobically during the determination of other parameters.8 The study design was approved by the Ethics Review Committee on Genetic and Genomic Research, Kobe University Graduate School of Medicine. Informed consent was obtained from all healthy subjects and patients.

Analytical Methods

Total serum calcium was determined by the orthocresolphthalein complexone method using a calcium kit (Iatrofine Ca II; Mitsubishi Chemical Medience Corp., Tokyo, Japan)9 with National Institute of Standards and Technology (Gaithersburg, MD) standard reference material 909b as a reference. Total protein was determined by the Biuret test using Aqua-auto kainos TP-II reagent (Kainos Laboratories Inc., Tokyo, Japan), and albumin levels were determined by the bromocresol purple method using Aquaauto kainos albumin reagent (Kainos Laboratories Inc.).10,11 In these analyses, the standard certified reference material 470, which has been approved as The International Reference Preparation for proteins in human serum, was used as a reference. The inorganic phosphate level was determined by the purine nucleoside phosphorylase-xanthine oxidase method by automatic analysis with Determiner L IP (Kyowa Medex Co. Ltd., Tokyo, Japan)12 with a standard serum material (Reference Material Institute for Clinical Chemistry Standards, Kawasaki, Japan) as a reference. Ionized calcium was determined on a RapidPoint 405 (Siemens Healthcare Diagnostics Inc., Deerfield, IL). Reagent cartridges and Quality Control cartridges included with the RapidPoint 405 were used as reagents and standards. The effect of calcium- complex compounds in the electrode method was confirmed using Moore’s method.1 Solutions of calcium carbonate (CaCO₃, Wako Pure Chemical Industries, Ltd., Osaka, Japan), disodium hydrogen phosphate (Na₂HPO₄ · 2H₂O, Wako Pure Chemical Industries, Ltd.), citric acid (C₆H₈O₇, Wako Pure Chemical Industries, Ltd.), lactic acid (dlC₃H₆O₃, Wako Pure Chemical Industries, Ltd.) and sodium hydrogen carbonate (NaHCO₃, Wako Pure Chemical Industries, Ltd.) were prepared in deionized water containing HEPES buffer (Wako Pure Chemical Industries, Ltd.) and aqueous sodium chloride (NaCl, volume fraction 0.85%, Wako Pure Chemical Industries, Ltd.). The solutions were then adjusted to pH 7.4 by addition of sodium hydroxide solution (NaOH, Wako Pure Chemical Industries, Ltd.) (100 mM, M = mol/L) to establish metastable supersaturation. The total concentrations were Ca (as CaCO₃, 1.0 mM), phosphorus (1.0 mM), citrate (0.12 mM), lactate (1.0 mM), and hydrogen carbonate (30 mM).

Development of equation for ionized calcium calculation

Equations for the calcium complexes that formed with each ligand (L_x) were derived based on acid dissociation and complexation equilibrium equations at pH 7.4. The ligands were L₁ = albumin, L₂ = globulin, L₃ = phosphoric acid, L₄ = citric acid, L₅ = lactic acid, and L₆ = hydrogen carbonate. Table 1 shows the acid dissociation constants K_a and stability constants K_s used in these equations.13–18

Table 1.

Acid dissociation constants (K_a), stability constants (K_s), tL_x and tCa_x.

Variable	−log(Ka)	log(Ks)	tLx**(M)	tCax	References
Albumin*	7.55	2.38	Albumin (g/dL) × (1.7 × 10−3)	tCa – Ca2+L2 – Ca2+L3 – Ca2+L4 – Ca2+L5 – Ca2+L6	13,14,15
Globulin+	7.55	2.55	(Total protein-Albumin) (g/dL) × (2.6 × 10−4)	tCa – Ca2+L1 – Ca2+L3 – Ca2+L4 – Ca2+L5 – Ca2+L6	14,15
Phosphorus†	6.43	2.74	iPhosphorus (mg/dL) × (2.6 × 10−4)	tCa – Ca2+L1 – Ca2+L2 – Ca2+L4 – Ca2+L5 – Ca2+L6	16,17
Citrate§	5.69	3.63	1.2 × 10−4	tCa – Ca2+L1 – Ca2+L2 – Ca2+L3 – Ca2+L5 – Ca2+L6	16,18
Lactate¶	3.64	0.48	1.4 × 10−3	tCa – Ca2+L1 – Ca2+L2 – Ca2+L3 – Ca2+L4 – Ca2+L6	16,18
Hydrogen carbonate‡	6.11	1.0	2.3 × 10−2	tCa – Ca2+L1 – Ca2+L2 – Ca2+L3 – Ca2+L4 – Ca2+L5	16,18

Notes:

^*Albumin forms coordinated bonds with up to 12 calcium ions. The molecular weight of albumin is 69 000. tL_x = albumin (g/dL) × 10/69 000 × 12 = albumin (g/dL) × (1.7 × 10⁻³);

⁺The same K_a was used for albumin and globulin. The K_s value of globulin was calculated using K_s = 280 [log(K_s) = 2.45] of total protein and K_s = 241 [log(K_s) = 2.38] of albumin. The maximum concentration of calcium bound to globulin was 0.026 mmol/g using the reported values. In healthy subjects the values were 0.12 mmol/g (total protein) and 0.17 mmol/g (albumin) with a serum A/G ratio of 1.9. tL_x (M) = (total protein − albumin) (g/dL) × 0.026 (mmol/g) = (total protein − albumin) (g/dL) × (2.6 × 10⁻⁴);

^†It has been suggested that 10%–20% of serum inorganic phosphorus binds to proteins with the remaining 82% of phosphate assumed to be present in the free form. Phosphate has K_a and K_s for PO₄³⁻, HPO₄²⁻ and H₂PO₄⁻ at physiological pH. Both HPO₄²⁻ and H₂PO^{4 −} are presumed to bind to calcium at pH 7.4. We calculated the [HPO₄²⁻]/[H₂PO₄⁻] using the Henderson-Hasselbalch equation. [HPO₄²⁻] was deduced to be about ten times greater than [H₂PO₄⁻] from the calculation. Therefore, we only used HPO₄²⁻ as the subject for calculation in our equation. The molecular weight of phosphorus is 3100. tL_x(M) = iPhosphorus (mg/dL) × 10/31/1000 × 0.82 = iPhosphorus (mg/dL) × (2.6 × 10⁻⁴);

^§Citrate average measurement was 2.4 (mg/dL) and the molecular weight is 19300. tL_x (M) = 2.4 (mg/dL) × 10/193/1000 9300 = 1.2 × 10^−4;

^¶Lactate average measurement was 13 (mg/dL) and the molecular weight is 9000. tL_x (M) = 13 (mg/dL) × 10/90/1000 = 1.4 × 10⁻³;

^‡We calculated [HCO₃⁻]/ [H₂CO₃] using the formula of Henderson-Hasselbalch. tL_x (M) = 23 (mM)/1000;

^**tL_x used the measurements from Table 3 and the reported values from references, and the molar concentrations were calculated using each molecular weight.

Acid dissociation equilibrium for each ligand

The acid dissociation equilibrium and acid dissociation constant (K_a) of L_x can be expressed as follows:

$$\begin{array}{c}{\text{H}}^{+}{\text{L}}_{\text{x}}\iff {\text{H}}^{+}+{\text{faL}}_{\text{x}}\\ K_a=\frac{[{\text{H}}^{+}][{\text{faL}}_{\text{x}}]}{[{\text{H}}^{+}{\text{L}}_{\text{x}}]}\end{array}$$ (1)

where [H⁺] is the hydrogen ion concentration at pH 7.4 or actual pH, faL_x is the free site in L_x, and H⁺L_x is the hydrogen ion binding site in L_x.

The total concentration of free, hydrogen ion, and calcium binding sites for L_x (tL_x) can be expressed as follows:

$$\text{tLx}=\text{faLx}+{\text{Ca}}^{2+}{\text{L}}_{\text{x}}+{\text{H}}^{+}{\text{L}}_{\text{x}}$$ (2)

where Ca²⁺L_x is the concentration of calcium bound to L_x.

This equation can be simply transformed to:

$${\text{faL}}_{\text{x}}={\text{tL}}_{\text{x}}-{\text{H}}^{+}{\text{L}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}$$ (3)

When Eq. 3 is substituted into the acid dissociation equilibrium, the following equation is obtained:

$$K_a=\frac{[{\text{H}}^{+}][{\text{tL}}_{\text{x}}-{\text{H}}^{+}{\text{L}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}{[{\text{H}}^{+}{\text{L}}_{\text{x}}]}$$ (4)

The equation can be expressed in terms of H⁺L_x as follows:

$$[{\text{H}}^{+}{\text{L}}_{\text{x}}]=\frac{[{\text{H}}^{+}][{\text{tL}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}{K_a+[{\text{H}}^{+}]}$$ (5)

Complexation equilibrium for the calcium-ligand complexes

Complexation of calcium with L_x and the stability constant (K_s) for L_x can be expressed as follows:

$$\begin{array}{c}{\text{Ca}}^{2+}+{\text{fsL}}_{\text{x}}\iff {\text{Ca}}^{2+}{\text{L}}_{\text{x}}\\ K_S=\frac{[{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}{[{\text{Ca}}^{2+}][{\text{fsL}}_{\text{x}}]}\end{array}$$ (6)

where fsL_x is the free site of L_x.

H⁺L_x is not involved in this equilibrium and must be subtracted from tL_x to give the adjusted value t’L_X. This is expressed in terms of fsL_x and Ca²⁺L_x as follows:

$$\text{t}’{\text{L}}_{\text{x}}={\text{tL}}_{\text{x}}-{\text{H}}^{+}{\text{L}}_{\text{x}}={\text{fsL}}_{\text{x}}+{\text{Ca}}^{2+}{\text{L}}_{\text{x}}$$ (7)

This equation can be simply transformed to:

$${\text{fsL}}_{\text{x}}=\text{t}’{\text{L}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}$$ (8)

When Eq. 8 is substituted into the stability equilibrium, the following equation is obtained:

$$K_S=\frac{[{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}{[{\text{Ca}}^{2+}][\text{t}’{\text{L}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}$$ (9)

The total concentration of calcium (tCa) can be expressed as the sum of the concentration of ionized calcium and total concentration of calcium bound to ligands (albumin, globulin, phosphoric acid, citric acid, lactic acid, and hydrogen carbonate ions) as follows:

$$\text{tCa}={\text{Ca}}^{2+}+{\text{tCa}}^{2+}\text{L}$$ (10)

where tCa²⁺L is the total concentration of ligandbound calcium.

The total concentration of calcium bound to ligands (tCa_x) can be expressed as follows:

$${\text{tCa}}_{\text{x}}={\text{Ca}}^{2+}+{\text{Ca}}^{2+}{\text{L}}_{\text{x}}$$ (11)

where Ca²⁺L_x is the concentration of ligand-bound.

This equation can be simply transformed to:

$${\text{Ca}}^{2+}={\text{tCa}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}$$ (12)

The equilibrium equation can then be expressed as follows:

$$K_S=\frac{[{\text{Ca}}^{2+}\text{Lx}]}{[{\text{tCa}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}][\text{t}’{\text{L}}_{\text{x}}-{\text{Ca}}^{2+}{\text{L}}_{\text{x}}]}$$ (13)

When the equation is expressed in terms of Ca²⁺L_x, the following equation is obtained:

$${\text{Ca}}^{2+}{\text{L}}_{\text{x}}=\frac{-\text{A}-\sqrt{{\text{A}}^2-4K_S\text{B}}}{2K_S}$$ (14)

where A = −K_S × tCa_x − K_S × t’L_x − 1, and B = K_S × tCa_x × t’L_x.

Calculation of calcium complexes formed with each ligand

The concentration of ionized calcium could be calculated by deducting the concentration of each calcium-ligand complex (Ca²⁺L_x) from the total calcium concentration as shown in Eq. 10.

$$\begin{array}{l}{\text{Ca}}^{2+}=\text{tCa}-{\text{tCa}}^{2+}\text{L}\\ =\text{tCa}-{\text{Ca}}^{2+}{\text{L}}_1-{\text{Ca}}^{2+}{\text{L}}_2-{\text{Ca}}^{2+}{\text{L}}_3-{\text{Ca}}^{2+}{\text{L}}_4-{\text{Ca}}^{2+}{\text{L}}_5-{\text{Ca}}^{2+}{\text{L}}_6+\alpha \end{array}$$ (15)

A factor, α, was defined based on the difference between the concentration of calcium bound to each ligand obtained by the calculation and that obtained by the electrode method. We then calculated tCa₁ using Eqs. 11 and 15.

$$\begin{array}{l}{\text{tCa}}_1={\text{Ca}}^{2+}+{\text{Ca}}^{2+}{\text{L}}_1\\ =\text{tCa}-{\text{Ca}}^{2+}{\text{L}}_2-{\text{Ca}}^{2+}{\text{L}}_3-{\text{Ca}}^{2+}{\text{L}}_4-{\text{Ca}}^{2+}{\text{L}}_5-{\text{Ca}}^{2+}{\text{L}}_6\end{array}$$ (16)

First, we assumed that tCa₁ = tCa because we could not calculate the values of Ca²⁺L₂ to Ca²⁺L₆, we calculated H⁺L₁ (Eq. 5) and Ca²⁺L₁ (Eq. 14) using tL₁ and tCa₁ (Table 1). Next, we calculated tCa₁ using the results for Ca²⁺L₂ to Ca²⁺L₆. The values of tCa₂, tCa₃, tCa₄, tCa₅ and tCa₆ were calculated in the same way. Finally, Eq. 15 was used to calculate the ionized calcium concentration (Supplementary Material).

Results

Convergent calculation for calcium complexes

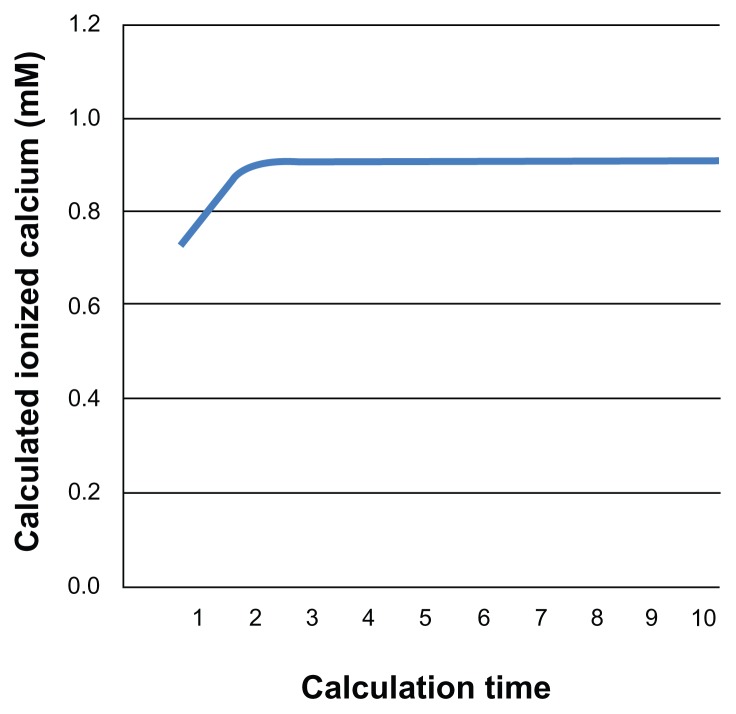
Changes in the concentrations of any of the six complexes affect the concentration of free calcium and the equilibria of the other complexes. To calculate the final concentrations of the calcium complexes in this dynamic equilibrium, the concentrations of the ligands and calcium should be calculated for each change, and the ionized calcium calculation using Eqs. 1–16 should be repeated until the value converges (Fig. 1). Using our equations, the calculations were repeated 10 times. A simulation was performed to confirm the validity of this frequency of repetition, and showed the values converged after four-to-five calculations.

Figure 1.

Convergent calculation for the six calcium complexes. The ionized calcium concentration calculations (Eqs. 1–16) were repeated ten times until the values converged.

Effect of calcium complexes in the electrode method

Table 2 shows the differences between the free calcium and calcium complex (phosphorus, citrate, lactate, and bicarbonate) concentrations obtained with calculation and the electrode method using Moore’s method.1 The electrode method results were almost identical to those obtained with Moore’s method. The largest difference between the electrode method and calculation method results was 0.21 mM for the calcium-phosphorus compounds, and the total difference was 0.32 mM. Thus, we used factors of α = 0.21 and α = 0.32 to calculate the ionized calcium concentration.

Table 2.

Differences between the results from the electrode method and calculation for each ligand.

Variable	Electrode Ca2+ (mean; mM)	Calcium-complex compounds		Difference of measurement and calculation (B-A)	Moore’s calcium-complex compounds
		From measurement* measurement (A)	From calculation (B)
1.0 mM Ca	0.99	–	–	–	–
1.0 mM Ca + 1.0 mM phosphorus	0.97	0.02	0.23	0.21	0.01
1.0 mM Ca + 0.12 mM citrate	0.95	0.05	0.10	0.05	0.08
1.0 mM Ca + 1.0 mM lactate	0.99	0.00	0.00	0.00	0.02
1.0 mM Ca + 30 mM hydrogen carbonate	0.83	0.17	0.23	0.06	0.14
Total difference measurement		0.24	0.56	0.32	0.25

Notes:

^*Moore’s measurements were obtained using the following concentrations: 1.5 mM Ca, 1.0 mM phosphorus, 0.12 mM citrate, 1.0 mM lactate and 25 mM hydrogen carbonate.

Estimation of Ca²⁺ concentration and comparison with Ca²⁺ concentration from the electrode method

Table 3 shows the results for samples obtained from 67 healthy subjects and 34 patients. Table 4 shows the results from electrode measurements and calculations using our equations for the samples at pH 7.4. The total mean concentrations of ionized calcium calculated using our equation were 0.96 ± 0.10 mM (α = 0.00), 1.17 ± 0.10 mM, (α = 0.21), and 1.28 ± 0.11 mM (α = 0.32), while that obtained with the electrode method was 1.20 ± 0.10 mM.

Table 3.

Measured values in healthy subjects and patients.

Variable	Healthy subjects	Patients	Total
	Mean ± SD (n = 67)	Mean ± SD (n = 34)	Mean ± SD (n = 101)
Total calcium (mg/dL)	9.4 ± 0.3	9.9 ± 1.2	9.5 ± 0.8
Albumin (g/dL)	4.8 ± 0.2	4.5 ± 0.3	4.7 ± 0.3
Total protein (g/dL)	7.5 ± 0.4	7.6 ± 0.5	7.5 ± 0.4
iPhosphorus (mg/dL)	3.8 ± 0.4	3.4 ± 1.0	3.7 ± 0.6

Table 4.

Measured and calculated values in healthy subjects and patients at pH 7.4.

Form of calcium (mM)	Electrode	Calculation
	Factor value	0.00	0.21	0.32
	Mean ± SD (n = 101)	Mean ± SD (n = 101)	Mean ± SD (n = 101)	Mean ± SD (n = 101)
Ca2+	1.20 ± 0.10	0.96 ± 0.10	1.17 ± 0.10	1.28 ± 0.11
Albumin Ca	–	0.71 ± 0.07	0.71 ± 0.07	0.71 ± 0.07
Globulin Ca	–	0.09 ± 0.02	0.09 ± 0.02	0.09 ± 0.02
Phosphorus Ca	–	0.31 ± 0.05	0.10 ± 0.05	0.10 ± 0.05
Citrate Ca	–	0.10 ± 0.002	0.10 ± 0.002	0.05 ± 0.002
Lactate Ca	–	0.004 ± 0.0004	0.004 ± 0.0004	0.004 ± 0.0004
Hydrogen carbonate Ca	–	0.22 ± 0.02	0.22 ± 0.02	0.16 ± 0.02

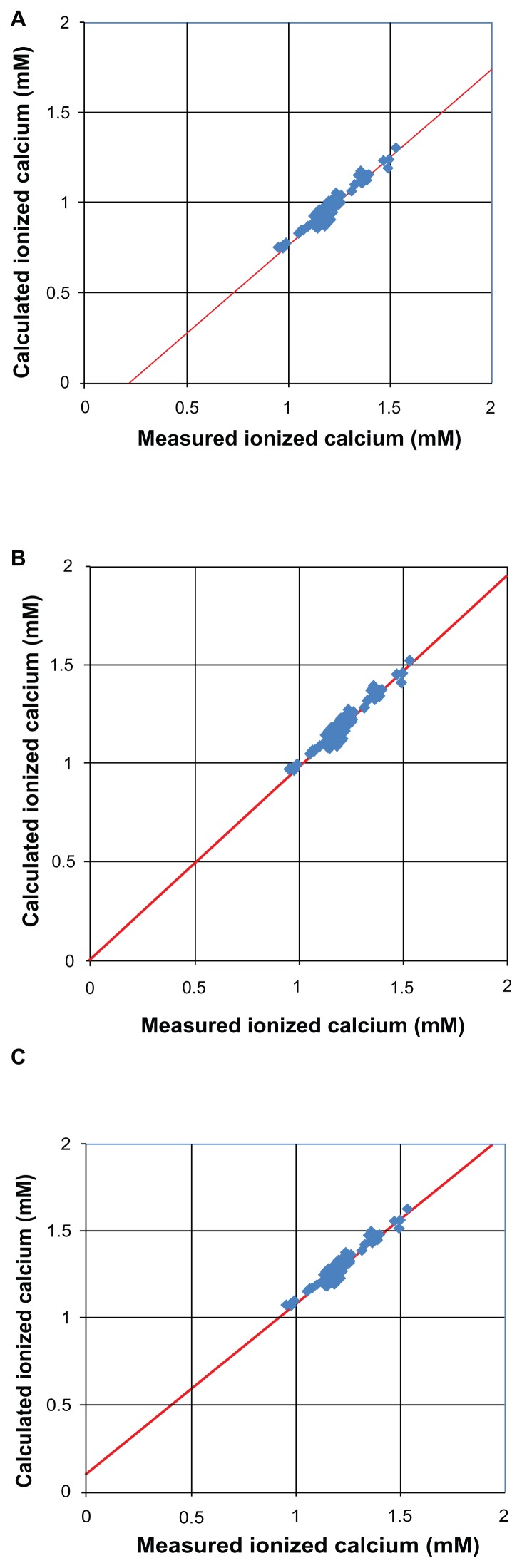
Figure 2 shows the correlations between the values calculated by our equation (y) and those obtained by the electrode method (x) for the healthy subjects and patients. Favorable correlations were observed with α = 0.00 (r = 0.953, y = 0.97x − 0.21), α = 0.21 (r = 0.953, y = 0.97x + 0.00), and α = 0.32 (r = 0.953, y = 0.97x + 0.11) at pH 7.4. These results indicated that among the three factors evaluated, α = 0.21 is the best for the calculation.

Figure 2.

Relationship between the measured and calculated ionized calcium concentrations using α = 0.00 (A), α = 0.21 (B) or α = 0.32 (C) in Eq. (15) at pH 7.4.

Discussion

Equations for calculating ionized calcium were derived based on the acid dissociation constant and the stability constant. The concentration of ionized calcium is greatly influenced by the pH, and it is necessary to maintain the pH at a constant level, even if the measurement is mathematically corrected to pH 7.4. We assumed that the concentrations of ionized calcium fluctuated with the pH because of fluctuations in the concentrations of free ligands. Serum was used for this study because plasma would require the addition of heparin as an anticoagulant. National Committee for Clinical Laboratory Standards/Clinical and Laboratory Standards Institute guidelines recommend against using heparin for measurement of ionized calcium because heparin can bind calcium.19

Magnesium behaves in a similar manner to calcium because it is also an alkaline earth metal. Therefore, we calculated the magnesium concentrations using our equations (data not shown). The effect of magnesium on the ionized calcium concentration was minimal.

The calculation for each healthy serum sample was repeated 10 times, and this confirmed the method was convergence. At α = 0.21, the mean ionized calcium concentration calculated by our method was closer to that obtained with the electrode method than at α = 0.00 or 0.32. There were large differences between the values obtained by the calculation and by the electrode method (Table 2). These differences in the calculation results could be caused by a low concentration of ionized calcium because of high complexation constants for calcium and phosphorus or low acid dissociation equilibrium constants. This also suggests that the Rapid-Point 405 ion-selective electrode contains R₂HPO₄, which is a calcium salt of didecyl phosphoric acid dissolved in didecyl phenylphosphonate. The NOVA CRT ion selective analyzer reportedly gives larger differences between healthy volunteers and patients than the AVL 988-4 ion selective analyzer.20 The range in the calcium levels with the different ion selective analyzers is reportedly 5.86 mg/dL (1.47 mM) or 3.86–5.07 mg/dL (0.97–1.27 mM).21

In our experiment, few samples had abnormal albumin or globulin levels. In particular, globulin, which consists of many proteins, was based on one equilibrium equation of complexation and acid dissociation in our equation. Therefore, if the expression of some proteins increased considerably, the protein levels would potentially influence the results of our calculation. This could occur in patients with cancer.22 The efficacy of our equation may be more clearly demonstrated in samples with marked abnormalities in the serum protein fractions, and samples from patients receiving nutritional support.23

We only used a RapidPoint 405 for analysis of the samples, and not determine conduct measurements with other instruments. A factor of α = 0.21 mM was used to correct for the differences between the calcium concentrations obtained with the RapidPoint 405 and by the calculation. Future research could apply the equation to analysis with other instruments and determine the required factors for these instruments.

In conclusion, with the equations developed in this study, ionized calcium could be routinely calculated from various parameters using a simple program. This method will be useful in clinical diagnostic laboratories.