Efficient Implementation of Hardware-Optimized Gradient Sequences for Real-Time Imaging

Abstract

This work improves the performance of interactive real-time imaging with balanced steady-state free precession. The method employs hardware-optimized gradient pulses, together with a novel phase-encoding strategy that simplifies the design and implementation of the optimized gradient waveforms. In particular, the waveforms for intermediate phase-encode steps are obtained by simple linear combination, rather than separate optimized waveform calculations. Gradient waveforms are redesigned in real time as the scan plane is manipulated, and the resulting sequence operates at the specified limits of the MRI gradient subsystem for each new scan-plane orientation. The implementation provides 14–25% improvement in the sequence pulse repetition time over the vendor-supplied interactive real-time imaging sequence for similar scan parameters on our MRI scanner.

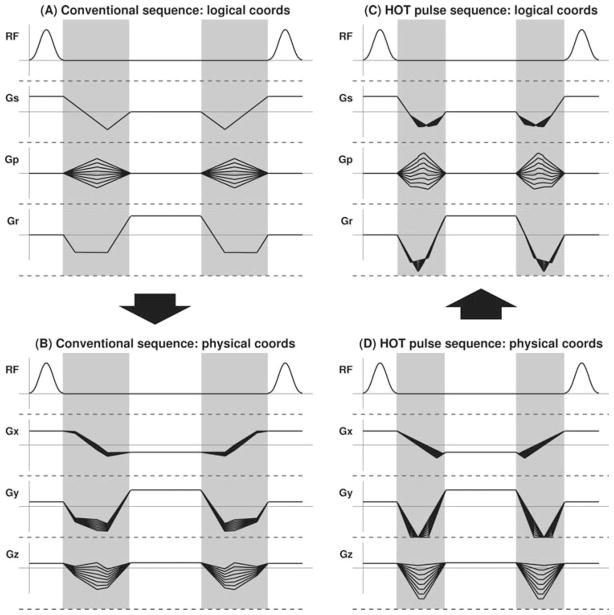
Cardiac and interventional MR applications demand high-frame-rate real-time imaging sequences. The steady-state signal from balanced steady-state free precession (bSSFP), also known as true Fast Imaging with Steady-state Precession (FISP) balanced Fast Field Echo (FFE) or Fast Imaging Employing STeady-state Acquisition (FIESTA), is practically independent of pulse repetition time (TR) (1,2). Frame rates can be increased without Signal to Noise Ratio (SNR) penalty by minimizing TR while maintaining constant acquisition window duration. For bSSFP, the so-called dead times (3) in which k-space is traversed without playing radiofrequency (RF) pulses or acquiring data must be minimized (Fig. 1a). In practice, vendor-supplied interactive imaging sequences use fixed-gradient waveform designs that are applicable in any orientation. To accommodate scan-plane orientations where the resultant of simultaneous pulses in the slice, read, and phase-encoding directions lies along a single physical gradient axis, their waveform design algorithms must employ maximum gradient amplitude and slew rate specifications that are reduced by as much as √3 to avoid overranging.

FIG. 1.

Conventional and HOT pulse-based bSSFP sequences. a: Pulse sequence (top left) shows a bSSFP sequence designed conventionally in logical coordinate system (Gs = slice, Gp = phase, Gr = readout) for an arbitrary oblique scan plane. The gradient specification used for the waveform design was reduced by √3 during design to avoid overranging when the sequence is rotated into the physical coordinate representation (b). The gray regions are dead time where no RF transmission or data acquisition occurs. c,d: A HOT pulse implementation of bSSFP with the same parameters, but optimized for the particular oblique scan-plane orientation and designed in the physical coordinate system (d) to match the full amplitude and slew rate specifications. This approach permits a reduction in dead time and shorter TR. Note that the shapes of the HOT pulse gradient waveforms change from one phase encode to the next on all three axes in both the physical (d) and logical (c) coordinate representations. This observation precludes the use of simple amplitude scaling to implement phase encoding. In effect, the read dephase and slice rephase gradients are modified slightly from one phase encode to the next (without changing their 0th moment) to permit a slight optimization of the phase-encoding pulse.

Hardware-optimized trapezoidal (HOT) pulses (3) are gradient shapes optimized for the particular scan-plane orientation and physical gradient specification (i.e., maximum amplitude and slew rate), which minimize TRs by ensuring at least one of the physical gradient axes is operating at the specified limits during the dead times. The improved performance promised by HOT pulse methods is attractive for real-time imaging, but the need to explicitly redesign the gradient waveform for every phase-encode step whenever the scan plane is reoriented has inhibited their adoption.

In conventional MR sequences, the standard implementation for phase encoding employs constant gradient waveforms in the slice and read directions, with amplitude scaling of a fixed waveform shape on the phase-encoding axis. In contrast, for HOT pulse sequences, the shapes of the gradient pulse waveforms on all three logical gradient axes (read, phase, and slice) generally change from one phase-encoding (and unencoding) step to the next, precluding the use of simple amplitude scaling, as shown in Fig. 1c. Typically, 500–1500 individual gradient waveform shapes (i.e., 2 [encode and unencode] × 3 [axes] × N_pe [phase-encode steps]) are required to image a particular scan-plane orientation with a specific field of view, slice thickness, etc. During interactive scans, reorientation of the scan plane or changes to the imaging prescription parameters require the complete redesign and reloading of all these gradient waveforms. These demands have been considered too computationally burdensome to permit implementation.

Previous Work

In an early implementation of HOT pulse methodology (3), all these waveforms for a single orientation were loaded into waveform memory before the scan was executed. However, because the memory available for storing waveforms was limited, only a single orientation could be scanned, so the sequence was not suitable for real-time interactive scanning. In a more recent implementation (4), the individual gradient waveforms were dynamically loaded into the scanner waveform memory on a TR-by-TR basis while the sequence was running, but the method required unconventional low-level programming techniques such as direct-to-sequencer hardware access, resulting in a platform-dependent sequence that was difficult to maintain and extend.

In this work, we aim to improve the efficiency of interactive real-time imaging sequences through the implementation of a new HOT pulse-based balanced steady-state free precession sequence module that replaces the vendor-supplied sequence in our real-time imaging system. A key technical step is the demonstration that the number of required waveform shapes can be reduced from thousands to just 12 (i.e., two waveforms per phase-encoding and two waveforms per unencoding step, per gradient axis) (5). For each phase-encode step, the sequence plays a linear combination of two pulse shapes simultaneously on each particular gradient axis. The consequent reduction in the computational burden allows a substantial reduction in achievable TR and improvement of scanning efficiency while maintaining completely interactive scanning with real-time control of the scan-plane orientation, field of view, slice thickness, imaging matrix, etc. (6–9).

THEORY

Features of Hardware-Optimized Sequences

HOT gradient pulses are designed by considering the required starting gradient amplitude (e.g., G_slice = [0, 0, G_slice]^T) and ending gradient amplitude (e.g., G_read = [G_read,0,0]^T) and the required time-integrated gradient pulse area (i.e., k-space offsets, Δk = [Δk_read, Δk_phase, Δk_slice]^T) for the read, phase encode and slice (r, p, s) axes simultaneously as three-dimensional vector gradients. These vector design requirements are rotated from logical (r, p, s) (i.e., slice coordinate) gradient space into physical (X, Y, Z) (i.e., magnet coordinate) gradient space where independent, one-dimensional solutions that meet the amplitude and slew-rate specifications for the target scanner can be obtained for each physical gradient axis.

For Cartesian (spin-warp) sequences, HOT pulse design is a two-step process: (i) determine the minimum dead time, and (ii) generate the gradient waveforms. Details of the waveform design algorithm can be found in Atalar and McVeigh (3). Typically, each one-dimensional HOT pulse waveform solution comprises a piecewise linear gradient waveform (PLG) with two or three segments in the physical axis representation, depending on whether the waveform reaches the maximum allowed amplitude.

A full set of gradient waveform solutions (one for each phase-encode step on each physical gradient axis) must be explicitly designed to exactly fit in the minimum dead time. This is in contrast to conventional MR sequences where a single (extreme) phase-encode waveform is calculated and the intermediate phase encodes are generated by amplitude scaling at runtime. This issue arises because the HOT pulse waveforms have fixed, usually nonzero, initial and final amplitudes when expressed in physical gradient coordinates (e.g., consider the physical X-axis component of the slice select and readout gradients in Fig. 1d). In effect, the shape of the required gradient waveform changes from one phase encode to the next, which is not compatible with simple amplitude scaling. A similar problem arises even if the waveforms for a HOT pulse are rotated back into the logical coordinate system because (e.g., see Fig. 1c) the gradient waveform shapes change with phase encode index on the read and slice axes, as well as the conventional phase-encoding axis, and so the problem with constant, nonzero endpoints remains.

A Solution for Phase Encoding

Consider, for example, the HOT pulse waveforms for a full k-space acquisition on the physical X-axis that perform the transition from slice selection to readout, as shown in Fig. 2. Define p_x(t) and n_x(t) to be the PLG waveforms corresponding to the maximally positive and negative phase-encoding steps, respectively, in the X direction. Noting that the linear combination of two PLGs is another PLG (albeit with more vertices), we now define the static s_x(t) and dynamic d_x(t) PLGs:

$$s_x(t)=[P_x(t)+n_x(t)]/2\text{and}{d}_x(t)=[P_x(t)-n_x(t)]/2$$ [1]

FIG. 2.

Construction and implementation of HOT pulses as the linear combination of static and dynamic components. This example demonstrates the design process for the HOT pulse waveform on the physical X-axis gradient between the end of slice selection and the beginning of the readout. Each HOT pulse gradient, designed in physical gradient space, contains portions of the slice rewinder, read dephaser, and phase-encode gradients. The PLG waveforms for the extreme positive and negative phase encodes are decomposed into static portions, s(t), and dynamic portions, d(t). To perform phase encoding, a linear combination g(t) = s(t) + λd(t) is played where −1 ≤ λ < 1 is the phase-encoding factor.

See Fig. 2 to observe that s_x(t) will begin and end at the same constant value as all the PLG steps including p_x(t) and n_x(t). In fact, it can be regarded as the portion of the PLG that is common to all the phase-encoding steps corresponding to the X-component of the read dephaser and slice rephaser gradients. Conversely, d_x(t) begins and ends with zero amplitude and represents the portion of the PLG that varies to perform phase encoding. In general, for an image composed of N phase-encode steps, we can obtain an arbitrary PLG pulse for the rth (−N/2 ≤ r < N/2) phase-encoding step by forming a linear combination:

$$g_x(t)=s_x(t)+\lambda d_x(t)\text{where}:\lambda =2\text{r}/\text{N}\text{such}\text{that}-1\le \lambda <1$$ [2]

By construction, g_x(t) provides the appropriate gradient moment for the X component of the gradient waveform. The method is illustrated in Fig. 2, which shows the physical X-axis gradient waveforms that are to be applied in the dead time between the slice select, and readout gradients in a bSSFP sequence.

By design, the p_x(t) and n_x(t) waveforms do not exceed the original gradient amplitude and slew-rate specifications (G_max and SR_max). It is simple to show that g_x(t) also does not exceed the gradient specifications. Writing g_x(t) in terms of the original p_x(t) and n_x(t), we have:

$$g_x(t)={\alpha p}_x(t)+{\beta n}_x(t)\text{where}\alpha =(1+\lambda )/2\text{and}\beta =(1-\lambda )/2$$ [3]

Note that 0 ≤ α, β ≤ 1 and α + β = 1. Thus, for the maximum gradient specification:

$$\mid g_x(t)\mid =\mid {\alpha p}_x(t)+{\beta n}_x(t)\mid \le \alpha \mid p_x(t)\mid +\beta \mid n_x(t)\mid \le \alpha G_{max}+\beta G_{max}=G_{max}$$ [4]

and, similarly, for slew rate (SR):

$$\mid g_x^{\prime }(t)\mid =\mid {\alpha p}_x^{\prime }(t)+{\beta n}_x^{\prime }(t)\mid \le \alpha \mid p_x^{\prime }(t)\mid +\beta \mid n_x^{\prime }(t)\mid \le \alpha {SR}_{max}+\beta {SR}_{max}={SR}_{max}$$ [5]

Repeating this process for the Y- and Z-axes permits all the phase-encode gradient waveforms to be generated from just two waveforms per axis, s(t) and d(t). This analysis for a full-k-space scan can also be adapted to describe partial Fourier scanning.

MATERIALS AND METHODS

Implementation

A HOT pulse-based bSSFP sequence was implemented on a Siemens Magnetom Espree (Siemens Medical Solutions, Erlangen, Germany) 1.5-T imaging system equipped with a gradient specified for maximum amplitude of 33 mT/m and maximum slew rate of 100 mT/m/ms. Pulse sequence code was written in the Siemens IDEA environment versions for VB12A and VB15A platforms.

A new gradient object class was developed using arbitrary, user-defined gradient waveform shapes to support the preparation and run-time linear combination of the HOT pulse waveforms, as described in the Theory section. These gradient objects were then incorporated into a new bSSFP imaging sequence object. Each bSSFP object contains all the necessary components (e.g., gradient and RF pulses, data acquisition) required to perform bSSFP imaging. Sequence preparation is performed using a simple single method (function call) that designs a self-consistent hardware-optimized bSSFP sequence from a standard scanner protocol derived from the scanner’s user-interface prescription. Other methods provided by the object are available to run a single TR of the sequence, collect a whole image, and also to perform the catalyzation opening and closing (α/2) subsequences.

Support for bSSFP objects was added into the vendor-supplied interactive real-time true FISP sequence on the MR system so that the sequence could be switched in real time between the standard sequence and the new HOT pulse bSSFP module. The interactive scan-plane updates feature provided by the existing implementation was also used to reprepare the bSSFP module (as described above) at the same time as the standard sequence. Since only 12 gradient waveforms need to be generated, the bSSFP object could be rapidly recalculated to provide a new fully optimized sequence for a new prescription.

The default prescription for the new bSSFP object was set to closely match that of the vendor-supplied real-time imaging sequence, including the use of identical RF pulse and data acquisition durations and bandwidths, as well as using the same peak-per-physical-axis gradients and slew rates.

Experimental

The RF (Specific Absorption Rate, SAR) and gradient safety watchdog features of the MR scanner were not disabled during any scans, and the sequence adhered to the MR system SAR and stimulation limits.

An imaging protocol with field of view 360mm × 360mm and slice thickness of 6mm was employed to compare the performance of the sequence with the vendor-supplied sequence. The bSSFP sequence TR was measured at a variety of acquisition matrix sizes (from 128² to 256²) for various scan-plane normal orientation and in-plane rotations and compared to that available for the standard imaging sequence using identical RF pulse (600 us, 2.67 kHz bandwidth) and readout (4.2 μs sampling) and gradient-per-physical-axis performance specifications for the two sequences. In addition to the in-plane rotation, changes to the hardware optimized TR resulting from reversal of the readout and/or slice and/or phase-encode directions were investigated by directly modifying the direction vectors from the imaging protocol. Further investigations were made regarding the optimization of TR for a partial Fourier acquisition by inversion of the read, slice, and phase-encoding gradient polarities.

Cardiac Study

All human studies were approved by and performed in accordance with the Institutional Review Board of the National Heart, Lung and Blood Institute (a part of the National Institutes of Health) and performed on healthy volunteers, with written, informed consent from all subjects. The sequence was tested at a variety of scan-plane orientations, with various image matrix sizes, fields of view, and slice thicknesses to compare image quality with the standard interactive real-time imaging sequence. Six cardiac short-axis and long-axis (four- and two-chamber) views of the heart were prescribed and multiple frames were acquired using the standard and new sequences for comparison of image quality.

RESULTS

The new HOT-pulse enabled sequence functioned as expected within the interactive real-time pulse sequence environment. Images were reconstructed by the scanner’s built-in reconstruction system and displayed in the scanner’s standard real-time viewing window. Image data were also exported from the scanner and were automatically reconstructed using our custom-designed real-time visualization platform (9), without further modification. During interactive scanning, the bSSFP module was able to complete the waveform redesigns when required for scan-plane orientation changes, without the need to introduce any additional delays. The HOT pulse sequence incurred no performance reduction over the vendor-provided sequence. As expected, the resulting sequence provided an orientation- dependent echo time and TR, which adjusted dynamically as the scan-plane orientation was manipulated.

Sequence Performance

Figure 3a shows a typical map of the minimum TR that could be obtained as a function of the scan-plane normal vector obtained by examining 100,000 scan-plane orientations evenly distributed in SO(3). It is immediately apparent that the shortest TRs do not generally occur when the scan plane is in one of the principal orthogonal (transverse/ axial, coronal, or sagittal) configurations. The precise orientation of the best TRs is dependent on the specific geometry (e.g., read, phase resolution, and slice thickness) being scanned. Figure 3b presents performance statistics as a function of the scan-plane resolution. In all cases examined, the TR of the sequence was at least 14% shorter and up to 24% shorter than that of the standard imaging sequence operating with similar scan parameters, RF pulse, and acquisition window durations.

FIG. 3.

Performance of the HOT pulse sequence. The surface plot (a) shows the minimum TR of the HOT pulse sequence as a function of the scan plane normal orientation for a 256² sampling matrix. The TR varies with both scan-plane orientation normal vector and the in-plane rotation. The surface shows the minimum TR over all the in-plane rotations. The upper graph (b) shows the performance of the vendor-supplied interactive real-time true FISP sequence (black) compared with the HOT-pulse sequence as a function of resolution. HOT pulse TRs shown are for the minimum, maximum, and mean obtained from 100,000 scan-plane orientations, with rotation matrices uniformly sampled from the space of all three-dimensional rotation matrices, SO (3). The red plot (“opt”) represents the TR obtained for the same rotation matrices, when sequence optimization by inverting the readout polarity (or, equivalently a 180° in-plane rotation) is permitted. The lower graph (c) shows the variation of the TR of the HOT pulse sequence with in-plane rotation for a cardiac short-axis slice. The preferred slice orientation for imaging (prescribed by the MR system operator) is indicated by the dashed line.

Figure 3a shows the optimized TRs sampled from all possible in-plane rotations for each normal vector orientation. In practice, it is often necessary to adopt a particular in-plane rotation (i.e., set the readout and phase directions) to account for the specific subject anatomy, reduce foldover, minimize flow artifacts, or optimize for parallel imaging. The optimized TR varied continuously with the in-plane rotation. Figure 3c shows the variability of TR as a function of the in-plane rotation for the particular cardiac short-axis slice orientation used in one subject. The figure also indicates the TR that corresponds to the preferred in-plane rotation chosen by the operator to optimize the scan for the subject anatomy.

For a full k-space (i.e., nonpartial Fourier) acquisition, reversing the readout direction (while keeping phase encode constant) yielded a change in TR equal to that obtained by the application of an in-plane rotation of 180°. Inversion of the slice selection direction provided an identical result. However, inversion of the phase-encoding direction had no effect on TR. The TR obtainable for partial k-space (partial Fourier) acquisition was typically shorter (and never longer) than the TR for a full k-space acquisition.

Cardiac scans were performed in three subjects. No adverse effects were observed, such as peripheral nerve stimulation. Figure 4 shows representative real-time cardiac short-axis images obtained using the standard and HOT pulse sequence. Images were obtained that were qualitatively similar to the images obtained with the standard vendor-supplied true FISP sequence. For a 128 × 128 acquisition matrix, the sequence TR was reduced from 2.67 ms to 2.22 ms. For a 192 × 192 acquisition matrix, the sequence TR was reduced from 3.23 ms to 2.78 ms, which is only slightly longer than the standard sequence at the lower resolution. Figure 4e shows an acquisition obtained at 128, but acquired with a lower readout bandwidth in order to maintain the same TR as the standard sequence. We did not observe any image quality penalty (e.g., additional artifacts, SNR degradation) from the use of the HOT pulse sequences.

FIG. 4.

Real-time, cardiac short-axis images. All images were acquired with 360mm square field of view and 6mm slice thickness. Images (a) and (b) were acquired with 192 × 192 matrix using the standard real-time imaging sequence, true FISP (TR = 3.23 ms), and bSSFP with HOT pulses (TR = 2.78 ms), respectively. Images (c–e) are 128 × 128 acquisitions using the standard FISP sequence (TR = 2.67) and the new bSSFP (TR = 2.22 ms and TR = 2.67 ms). Note that the 192-resolution HOT pulse sequence provided TRs only slightly longer than the 128-resolution conventional image. In (e), the bSSFP TR was extended to match the conventional sequence by reducing the acquisition bandwidth (sampling bandwidth).

DISCUSSION

The improved patient accessibility in open-bore systems is generally obtained at the price of a reduced gradient performance, longer TRs, and reduced frame rates. The HOT pulse gradient programming methodology demonstrated here can mitigate these losses by significantly shortening TRs, improving scanning efficiency for bSSFP sequences without apparent penalty.

During interactive scanning, the operator can arbitrarily change the scan-plane orientation and in-plane rotation. This may lead to the resultant of the read, phase, and slice gradient waveform amplitude or slew rates combining onto a single physical gradient axis. Unfortunately, vendor-supplied interactive real-time packages typically adopt a conservative and computationally simple approach to this problem. The gradient performance specifications (i.e., maximum amplitude and slew rates) are derated by √3 (or more) to allow interactive reorientation of the scan plane or resolution and slice thickness changes without having to rebuild the gradient waveforms. The methods described here provide an alternative procedure that obtains the best possible performance with a practically implementable method.

MR Hardware Restrictions

In the method described here, phase encoding is performed by the linear combination of a static gradient waveform, s(t), with a second, amplitude-scaled, dynamic waveform, d(t). In this implementation, we exploited the ability of our scanner hardware to be able to play two waveforms on each gradient axis simultaneously, a feature that may not be available to all systems. In practice, it is likely that the specifics of implementation on various systems will differ according to the details of the scanner’s hardware architecture. For example, our system cannot play more than two gradient pulses simultaneously on the same axis. However, for a different project, we have been able to explicitly calculate the linear combination of three gradient waveforms within the running sequence code and re-synthesize the gradient object during each TR.

TR Optimization for Oblique Scan Plane With Specified Read/Phase-Encoding Direction

For an oblique scan-plane prescription, read-gradient inversion changes the HOT-pulse design problem, providing a complementary sequence that typically has a different minimum dead-time and correspondingly different TR. Slice gradient inversion provides an equivalent complementary sequence. Symmetry arguments show that the TR obtained by slice gradient inversion is always identical to that obtained from read-gradient reversal. For a fully phase-encoded scan, reversal of the phase-encode direction merely reverses phase-encode order and has no effect on TR. However, for a partial Fourier acquisition, phase-encode reversal will typically yield a sequence that has a different TR.

Gradient Moment Nulling, Motion and Flow Encoding

The pulse designs described here were for minimum-time gradient pulses without any constraint on the first moment (M₁) of the gradient. HOT-pulse PLG designs with a specific M₁ (for motion encoding or nulling) have been previously demonstrated (10). The M₁ for a linear combination of gradient waveforms is the corresponding linear combination of their M₁s. Thus, the efficient implementation described here should also be effective for motion nulling and motion encoding with HOT pulses.

CONCLUSIONS

An especially efficient method for the implementation and design of HOT gradient waveforms has been demonstrated. The new method requires that the scanner play a linear combination of two PLG pulses on each of the three gradient waveform generators. The resulting sequences operate at the limit of the specified gradient performance and, correspondingly, provide the shortest possible TRs for the given imaging parameters. For bSSFP imaging, where SNR is essentially independent of TR, reducing TR improves scanning efficiency and reduces off-resonance banding artifacts and increases the available frame rate. In alternative applications, the introduction of HOT gradient waveforms permits either the acquisition of more samples (i.e., higher readout resolution) or acquisitions with reduced sampling rates (i.e., better SNR) without increasing TR.

This new approach to sequence design is particularly well suited for application in sequences supporting real-time, interactive imaging systems. Wider implementation of HOT pulse methods should provide increased SNR efficiency and improved frame rates in interventional real-time imaging. In particular, the approach should prove useful in MR applications that benefit from improved sequence efficiency such as flow imaging.