Abstract
We present a predictive account on adaptive sequential sampling of stimulus-response relations in psychophysical experiments. Our discussion applies to experimental situations with ordinal stimuli when there is only weak structural knowledge available such that parametric modeling is no option. By introducing a certain form of partial exchangeability, we successively develop a hierarchical Bayesian model based on a mixture of Pólya urn processes. Suitable utility measures permit us to optimize the overall experimental sampling process. We provide several measures that are either based on simple count statistics or more elaborate information theoretic quantities. The actual computation of information theoretic utilities often turns out to be infeasible. This is not the case with our sampling method, which relies on an efficient algorithm to compute exact solutions of our posterior predictions and utility measures. Finally, we demonstrate the advantages of our framework on a hypothetical sampling problem.
Keywords: Adaptive Sequential Sampling, Optimal Design, Active Learning, Predictive Inference, Psychophysics, Efficient Statistical Computations
1. Introduction and Motivation
The application of adaptive measurement methods have a long tradition in psychophysics. The need for such methods is mainly due to the limited number of measurements that can be taken during experiments. Most of the classical methods are motivated by their simplicity, both conceptually and computationally. With the advent of modern computers and the continuing progress in statistical theory, the development of more sophisticated adaptive sampling procedures has recently seen much progress.
Especially the consideration of Bayesian experimental designs based on the information theoretic description of experimental objectives and their numerical approximation (cf. MacKay (1992); Chaloner and Verdinelli (1995)) has moved into the focus of contemporary research. Recent developments are, for instance, the Ψ-method introduced in Kontsevich and Tyler (1999), the consideration of multidimensional stimulus spaces in Kujala and Lukka (2006), and the framework of adaptive design optimization (ADO) for model discrimination proposed in Cavagnaro et al. (2010). Another interesting example is given by Kujala (2010) who considers random cost as a further constraint for experimental observations.
Our contribution to the field is twofold. First, we address the case where no particular statistical model in form of parametric curves can be assumed. We present a complete formal description of a suitable framework for such a nonparametric setting. Second, we do not rely on any numerical approximation and the quantities of interest can be computed efficiently and exactly.
Our method applies to the following experimental setting: In a psychophysical experiment, the causal relation X → Y between a physical stimulus X and the psychological response Y of an observer is investigated. Before the experiment, a discrete set of L stimuli
 = {x1, …, xL} and K possible responses
= {x1, …, xL} and K possible responses
 = {y1, …, yK } is determined. The stimuli is considered to be ordinal, i.e. the set of stimuli is assumed to be linearly ordered, for instance by strength or any other property associated with the physical parameters. The actual experiment is then performed in a sequential manner. That is, at the n-th stage of the experiment, a particular stimulus Xn ∈
= {y1, …, yK } is determined. The stimuli is considered to be ordinal, i.e. the set of stimuli is assumed to be linearly ordered, for instance by strength or any other property associated with the physical parameters. The actual experiment is then performed in a sequential manner. That is, at the n-th stage of the experiment, a particular stimulus Xn ∈
 is set and the participant’s response Yn to that stimulus is recorded.
is set and the participant’s response Yn to that stimulus is recorded.
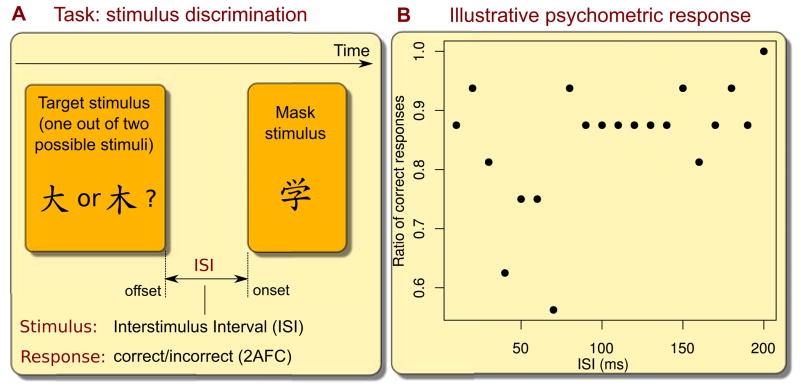
Figure 1 outlines such a experiment for illustrative purposes, taken from Elze et al. (2011), Experiment 2. Figure 1A shows the experimental setup that involves a two-alternative-forced-choice (2AFC) discrimination task: An observer has to report which of two possible target stimuli has been presented on a computer monitor. The discrimination performance was impaired by the presentation of a second stimulus, the so-called mask stimulus, at a position close to the target location. Within this experimental setting, the actual stimulus of interest X is the time interval between the offset of the target and the onset of the mask, the so-called interstimulus interval (ISI) that takes values in
 = {20 ms, 40 ms, …, 200 ms}, whereas the response Y takes values in
= {20 ms, 40 ms, …, 200 ms}, whereas the response Y takes values in
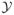 = {correct, incorrect}, depending on whether or not the observer reported the correct target stimulus.
= {correct, incorrect}, depending on whether or not the observer reported the correct target stimulus.
Figure 1.
Illustrative example of a simple psychophysical experiment. A: The observer has to report which of two possible target stimuli were presented on a computer display. The detection of the target stimulus is impaired by a mask stimulus which is presented in close proximity to the position of the target after a variable interstimulus interval (ISI). B: The observed relative frequency of correct responses of a single observer for 20 different discrete ISIs ≤ 200 ms, which have been uniformly sampled. Each ISI occured 16 times.
One of the most often considered approaches to model such an experimental situation is to assume a multinomial sampling law. More specifically, given any stimulus {X = x} the generation of the response Y is thought to be described by multinomial parameters px,
 = (px,y)y∈
= (px,y)y∈
 ∈ Δ
∈ Δ , where
, where
| (1) |
is the probability simplex, such that the conditional probability of the event {Y = y} given {X = x} is
Within this setting, the statistical task is then entirely focused on the estimation of the psychometric rates
. A low-dimensional parametric family of functions
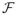 = {fθ| θ ∈ Θ} can be used to introduce dependencies among the psychometric rates, such that
= {fθ| θ ∈ Θ} can be used to introduce dependencies among the psychometric rates, such that
This facilitates the inference task by exploiting structural knowledge about the interlink between the stimuli. The function fθ is commonly termed psychometric function in the particular case of a binary response, e.g. a 2AFC experiment as outlined above. Especially sigmoid curves are a common choice if the stimulus X can be considered to be real-valued. Their geometric parameters such as slope and threshold can serve to actually define relevant psychophysical quantities of interest. There exists a vast literature on the statistical inference of psychometric rates and functions, see for instance Wichmann and Hill (2001); Kuss et al. (2005), which provide a good entry point into the literature.
From a mere statistical point of view, this parametric approach seems to be a reasonable strategy as it allows sharing statistical strength across stimuli. By learning the psychometric rate for a particular stimulus we also learn about all other rates because dependencies are introduced by the parametric family. Hence, the parametric approach allows seemingly good estimates even with few experimental data. Nevertheless, this modeling approach is unsuitable and can even bear the risk of a severe bias if there is no or only vague knowledge about the potential shapes of the functions fθ and no member of the proposed parametric family
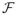 does match with the actual psychometric rates. For instance, in the above example it seems hard to motivate any plausible regular functional form (see Figure 1B).
does match with the actual psychometric rates. For instance, in the above example it seems hard to motivate any plausible regular functional form (see Figure 1B).
This form of bias is of course avoided by allowing the psychometric rates to freely range over , which we refer to as the nonparametric approach1. Clearly, much more data is then needed to draw informative inferences.
In this paper, we use an intermediate approach fairly balancing the advantages and disadvantages of both approaches by exploiting the fact that
 is of ordinal structure. Loosely speaking, we allow neighboring stimuli to share statistical strength by joining their respective psychometric rates. Each possible way of joining neighboring stimuli imposes a particular partition on the stimulus space
is of ordinal structure. Loosely speaking, we allow neighboring stimuli to share statistical strength by joining their respective psychometric rates. Each possible way of joining neighboring stimuli imposes a particular partition on the stimulus space
 , which is then assessed by a suitable Bayesian inference scheme. The resulting model is a variant of the product partition model proposed by Hartigan (1990) and the inhomogeneous Bernoulli process with piecewise constant probabilities described in Endres et al. (2008).
, which is then assessed by a suitable Bayesian inference scheme. The resulting model is a variant of the product partition model proposed by Hartigan (1990) and the inhomogeneous Bernoulli process with piecewise constant probabilities described in Endres et al. (2008).
In our description of the model and the respective adaptive sampling procedures we follow the predictive paradigm as pioneered, for instance, in Roberts (1965); de Finetti (1974); Geisser (1993), by putting special emphasis on the prediction for the observables, which are the stimulus-response outcomes of the sequential experiment. By imposing a particular epistemic condition of partial exchangeability, the psychometric rates naturally emerge as a particular limiting statistic of the data rather than an external quantity. The corresponding Bayesian model matches extensionally with a multinomial sampling model with unknown parameters.
2. A Predictive Perspective on Sequential Experiments
2.1. Sequential Construction of Adaptive Sampling Processes
A reasonable adaptive experimental design requires that we have at least partial control of the sampling process concerning the presentation of stimuli. This experimental controllability can be subject to uncertainty, e.g. the experimental setup might be prone to errors in generating the required stimulus. For simplicity, we shall nonetheless assume that we can adjust the stimulus in the way we want. Our personal action policy, which is the subjective assessment of which stimulus might be best to choose, is then expressed by a probability measure P [X]. By setting a stimulus X w.r.t. P [X], we subsequently observe a respective response Y, where our prediction is described by a conditional measure P [Y |X].
In the following, we shall extend this scenario to sequential sampling schemes. We consider that at any sampling step n ∈ ℕ we can freely choose a stimulus Xn that results in the observation of an instance (Xn, Yn). Let En = (Xn, Yn) denote the n-th experiment, such that we refer to the first n experiments of the overall experimental process
E = (En)n∈ℕ by En = (E1, …, En) = (Xn, Yn), where Xn = (X1, …, Xn) and Yn = (Y1, …, Yn). Two important statistics that summarize the data from the experiments En are given by the total count statistic
n = (nx,
= (nx,
 )x∈
)x∈
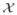 = (nx,y )x∈
= (nx,y )x∈
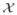 ,y∈
,y∈
 , where nx,y is the (absolute) frequency of the event {X = x, Y = y} in En, and n
, where nx,y is the (absolute) frequency of the event {X = x, Y = y} in En, and n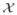 = (nx)x∈
= (nx)x∈
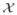 is the related stimulus count statistic, i.e. nx = Σy∈
is the related stimulus count statistic, i.e. nx = Σy∈
 nx,y. We illustrate this notation by the following short example.
nx,y. We illustrate this notation by the following short example.
Example 1
Suppose we run an experiment with a set of stimuli
 = {a, b, c, d} and dichotomous responses
= {a, b, c, d} and dichotomous responses
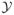 = {0, 1}. If in eight trials we observe that
= {0, 1}. If in eight trials we observe that
| (2) |
then the two statistics just defined are
We now take a sequential and prediction oriented perspective. We fix our expectations about the experimental course E by specifying a sequence of conditional measures in form of kernels πn(En+1 | En), n ∈ ℕ0, where each πn describes our uncertainty about the outcome of the n + 1-th experiment given the experimental data from the previous n sampling steps. Each such sequence of kernels πn(· | ·), n ∈ ℕ0, defines a unique measure π on the space of experimental courses, such that marginally
Thus, we can formally describe the experimental course E as a random process, which we call the adaptive sampling process E distributed with respect to π (i.e E ~ π). This process describes our belief dynamic since it is constructed from our experimental predictions (πn)n∈ℕ0. Each experimental prediction πn can in turn be constructed from two separate kernels
There exists a very natural interpretation for each of these kernels in terms of experimental design and prediction:
The Stimulus Placement Rule: specifies our action policy in the n-th sampling step. It determines which stimulus Xn+1 we select given the n previous experiments En.
The Response Prediction Rule: is our prediction of the response knowing the outcome of the last n experiments En, i.e. which response Yn+1 we expect given the actual stimulus Xn+1.
Given a particular assignment for the prediction rule , we want to learn the stimulus-response relation X → Y in an optimal manner with regard to the inference scheme and external constraints. Thus, we want to derive a placement rule that allows us to adapt the experimental course to our objectives.
In order to understand the logic of adaptive sampling strategies it is worthwhile to first consider the case of a non-adaptive design. Such a conventional design consists of a fixed sequence of stimuli , such that
Clearly, such an action policy does not take any information about the already collected data into account. A more reasonable strategy allows the decision for a stimulus to depend on the outcomes of the n foregoing experiments En, i.e. . More precisely, instead of describing one fixed sequence of stimuli we rather specify a decision rule that determines a stimulus on the basis of the previous experiments En. Many of the classical adaptive procedures for testing psychometric functions, such as PEST (Taylor and Creelman (1967)), QUEST (Watson and Pelli (1983)) and the up-down procedures (Levitt (1971)) can be described that way. A comprehensive review of these methods can be found in Leek (2001).
One principled way to obtain a decision rule is to specify a utility measure Un+1(x, En), which quantifies the utility of a stimulus x based on the outcome of the previous experiments En. Given such a measure, an optimal stimulus is determined by
| (3) |
A proper placement rule in the case of multiple optimal stimuli
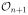 (EN ) ⊆
(EN ) ⊆
 is given by
is given by
Hence, by taking on the utility-oriented perspective, the problem of determining a placement rule becomes a problem of choosing suitable utility measures Un+1, n ∈ ℕ0. Many possible utility measures exist and which one we choose depends solely on our objectives. For instance, if we want to place the stimuli in a random but balanced manner, then we could choose the utility measure
where nx is the stimulus count statistic of x. Clearly, the respective placement rule selects stimuli that have seen the least trials. This random uniform sampling scheme has also been called method of constant stimuli (cf. McKee et al. (1985)) within the context of psychophysical experiments. It is usually considered as a non-adaptive strategy (Watson and Fitzhugh (1990)).
Another common and more sensible strategy to obtain a placement rule is suggested by the theory of optimal sequential decisions under uncertainty (cf. DeGroot (2004); Berger (1993)). In principle we should consider that only a finite number of experiments is performed, say N ∈ ℕ, such that we should formulate our objectives in form of a global utility measure u(EN ) for the outcome of the overall experimental course EN. As a matter of rationality, one should choose a sequence of descision rules , such that the expected global utility
is maximized. This optimization problem is highly non-trivial, but can be solved, at least in principle, with backward induction (Berger (1993); Bernardo and Smith (1995); DeGroot (2004)). For a concise description of the backward induction method see in particular Müller et al. (2007). This procedure leads to a sequence of local utility measures un+1(x, y, En) that are induced from both the global utility u and the predictions πY. The optimal stimulus for the n + 1-th experiment is determined by maximizing the expected local utility, i.e.
| (4) |
The local utility measure un+1(x, y, En) for a particular stimulus-response (x, y) is the expected global utility ū as of the n + 1-th sampling step given that all subsequent decisions are made in the same optimal manner. Although this scheme leads in principle to an optimal design, in most cases, except for trivial settings, the actual computation turns out to be infeasible.
It is primarily for this reason that various approximations to such an optimal design have been developed. One of them is to resort to a myopic adaptive optimal design by directly specifying local utility measures un+1(x, y, En), n = 0, …, N − 1, in an attempt to optimize the global utility. Likewise, the optimal stimulus is determined by (4), such that we optimize the next step, but with the hope that this also maximizes the global utility. We shall discuss particular choices for such measures based on information theoretical considerations in section 3.7.
2.2. Partial Exchangeable Response Processes
Concerning the choice of a proper prediction rule
, we already mentioned in the introduction that the response generation X → Y is usually thought to be governed by a multinomial sample law described by some unknown psychometric rates p ∈ Δ
∈ Δ . From a predictive perspective this amounts to the assumption of a specific form of partial exchangeability, which has been introduced in de Finetti (1980) as a generalization of the concept of exchangeability (de Finetti (1937)). Roughly speaking, we have to assume that particular temporal orderings within any finite sequence of experiments En do not provide relevant information for our predictions.
. From a predictive perspective this amounts to the assumption of a specific form of partial exchangeability, which has been introduced in de Finetti (1980) as a generalization of the concept of exchangeability (de Finetti (1937)). Roughly speaking, we have to assume that particular temporal orderings within any finite sequence of experiments En do not provide relevant information for our predictions.
In order to make this more precise, we need to introduce the following statistics and respective variables. We define the response statistic
, where
. Here
indicates that in the i-th trial in which {X = x} occurred the response outcome was the event {Y = y}. It is crucial to notice that the count statistic n can also be computed from the response statistic. The random variables related to the response statistic are denoted by Y
can also be computed from the response statistic. The random variables related to the response statistic are denoted by Y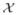 = (Yx)x∈
= (Yx)x∈
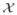 with
, such that
. Since we often need to refer to a particular subset of Y
with
, such that
. Since we often need to refer to a particular subset of Y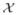 , we also define
, where
, x ∈
, we also define
, where
, x ∈
 , i.e.
.
, i.e.
.
Example 2
In our previous example the response statistic is given by
such that we observed that
We now proceed as follows. Instead of specifying the prediction rule
directly, we rather fix a probability measure P for Y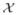 , i.e Y
, i.e Y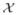 ~ P, such that we treat Y
~ P, such that we treat Y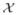 as a random process called the response process. This response process is meant to describe our personal beliefs about the observational part of the experiments irrespective of the actual underlying sequence of stimuli XN, which clearly depends on our action policy. A proper prediction rule is then given by
as a random process called the response process. This response process is meant to describe our personal beliefs about the observational part of the experiments irrespective of the actual underlying sequence of stimuli XN, which clearly depends on our action policy. A proper prediction rule is then given by
| (5) |
Furthermore, and more importantly, the response process Y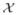 can be utilized to derive an intrinsic statistical model for X → Y by requiring the following form of partial exchangeability (cf. Link (1980); de Finetti (1980)):
can be utilized to derive an intrinsic statistical model for X → Y by requiring the following form of partial exchangeability (cf. Link (1980); de Finetti (1980)):
The response process Y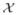 is said to be partial exchangeable iff
is said to be partial exchangeable iff
for every two responses
and
, which share the same count statistic n . This is equivalent to require that the response process Yn
. This is equivalent to require that the response process Yn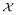 is summarized by the count statistics n
is summarized by the count statistics n (cf. Lauritzen (1974)), i.e. every sequence
with the same count statistic is predicted to be equally likely. We illustrate this notion of exchangeability by the following example.
(cf. Lauritzen (1974)), i.e. every sequence
with the same count statistic is predicted to be equally likely. We illustrate this notion of exchangeability by the following example.
Example 3
Consider we observed the data set in (2), see example 1. The alternative observations
do all preserve the count statistics n , such that we would judge them all to be equally likely under the condition of partial exchangeability. Note that all of these equivalent observations are related by particular permutations, i.e. by exchanging positions within each of the columns
, x ∈
, such that we would judge them all to be equally likely under the condition of partial exchangeability. Note that all of these equivalent observations are related by particular permutations, i.e. by exchanging positions within each of the columns
, x ∈
 , but not across them.
, but not across them.
An import subclass of partially exchangeable response processes is described by the multinomial sampling laws2, where
such that the marginal probability mass function is given by
This class is especially important because for each partial exchangeable random process there exists a mixing measure μ on (Link (1980); Bernardo and Smith (1995)), also called a de Finetti measure, such that
Therefore each partial exchangeable random process is a mixture of the multinomial sampling laws. Within this context, each can be interpreted as a possible limit of the relative frequencies, i.e.
such that the measure μ expresses our prediction for these limits. Hence, under the condition of partial exchangeability we can formally identify these limits as the psychometric rates we are uncertain about, but with the important distinction that the rates are not external quantities but asymptotic statistics of the response process itself. The corresponding Bayesian model can thus be described by
whereas
By conditioning on finite data
, the resulting response process is still partial exchangeable, such that the respective de Finetti measure
describes our posterior belief about the psychometric rates and can be seen to be a Bayesian posterior of p .
.
3. Response Processes with Proximally Related Stimuli
Here, we introduce a particularly useful instance of a partial exchangeable response process, namely the multibin Pólya mixture urn process, which allows a flexible modeling of similarities between stimuli. We first consider the case of only one stimulus and continue with the easiest non-trivial case of two stimuli before we develop the full process with multiple stimuli. Afterwards we shall consider the construction of respective adaptive sampling procedures.
3.1. One stimulus
Let us consider only one stimulus, i.e.
 = {x}, with the following probability assignment for the response process Y
x: We say that Y
x is a Pólya urn process with parameters αx,
= {x}, with the following probability assignment for the response process Y
x: We say that Y
x is a Pólya urn process with parameters αx,
 = (αx,y )y∈
= (αx,y )y∈
 , where αx,y > 0, if
, where αx,y > 0, if
where Beta is the multinomial beta function. The corresponding prediction rule is
where αx = Σy∈
 αx,y, which is commonly known as the (generalized) Bayes-Laplace rule. The parameters αx,
αx,y, which is commonly known as the (generalized) Bayes-Laplace rule. The parameters αx,
 have a natural interpretation as pseudo counts added to the actual counts nx,
have a natural interpretation as pseudo counts added to the actual counts nx,
 . The term Pólya urn stems from the original introduction as an urn model in Eggenberger and Pólya (1923). In this picture, balls are successively drawn from an urn that is initially filled with K balls of different colors. Each color indicates a particular y ∈
. The term Pólya urn stems from the original introduction as an urn model in Eggenberger and Pólya (1923). In this picture, balls are successively drawn from an urn that is initially filled with K balls of different colors. Each color indicates a particular y ∈
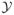 and the respective ball is assigned an initial weight of αx,y. At each sampling step, a ball is thought to be drawn with chance given by its individual mass and put back to the urn with another ball of the same color and mass one. The so generated sequence of colors Y
x is then described by the above Pólya urn process, which is partial exchangeable.
and the respective ball is assigned an initial weight of αx,y. At each sampling step, a ball is thought to be drawn with chance given by its individual mass and put back to the urn with another ball of the same color and mass one. The so generated sequence of colors Y
x is then described by the above Pólya urn process, which is partial exchangeable.
The respective de Finetti measure is given by a Dirichlet distribution with parameters αx,
 , i.e.
, i.e.
where the respective density is
Conditional on finite data , the resulting response process is again a Pólya urn process with parameters given by the update rule
i.e. the observed counts nx,
 are just added to the pseudo counts αx,
are just added to the pseudo counts αx,
 . Hence, assuming a Pólya urn process for describing our personal predictions justifies the formal adoption of the standard Bayesian model of multinomial sampling and a subjective prior in form of the Dirichlet distribution.
. Hence, assuming a Pólya urn process for describing our personal predictions justifies the formal adoption of the standard Bayesian model of multinomial sampling and a subjective prior in form of the Dirichlet distribution.
3.2. Two stimuli
We now consider a stimulus space with two elements, say
 = {x1, x2}. Based on the previously described Pólya urn process we can think of two extremal urn models for the response process Y
= {x1, x2}. Based on the previously described Pólya urn process we can think of two extremal urn models for the response process Y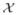 . First, we consider the case where the underlying mechanisms of (X = x1) → Y and (X = x2) → Y are identical. More precisely, we say that x1 and x2 are similar, denoted x1 ~ x2, if we expect that there is no difference in the generation of Y given either x1 or x2. This similarity allows us to define a bin b = {x1, x2}, such that we can exploit the similarity by joining the observations from both stimuli3. We call this binning scheme B1 and conditional on it the response process Y
. First, we consider the case where the underlying mechanisms of (X = x1) → Y and (X = x2) → Y are identical. More precisely, we say that x1 and x2 are similar, denoted x1 ~ x2, if we expect that there is no difference in the generation of Y given either x1 or x2. This similarity allows us to define a bin b = {x1, x2}, such that we can exploit the similarity by joining the observations from both stimuli3. We call this binning scheme B1 and conditional on it the response process Y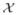 is characterized by
is characterized by
where nb,
 = (nb,y )y∈
= (nb,y )y∈
 is the total count n
is the total count n of observations joined in bin b, i.e. nb,y = nx1,y + nx2,y, y ∈
of observations joined in bin b, i.e. nb,y = nx1,y + nx2,y, y ∈
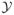 , and αb,
, and αb,
 describes the pseudo counts. The induced prediction rule is
describes the pseudo counts. The induced prediction rule is
where x ∈ b. The so described response process is partial exchangeable and the respective de Finetti measure μ(·|B1) can informally be described by the density
where δ is the Dirac delta function. That is, the measure μ(·|B1) concentrates on the diagonal of the product simplex , which is the set
such that if we identify both psychometric rates px1,
 and px2,
and px2,
 by just one rate pb,
by just one rate pb,
 ∈ Δ
∈ Δ , then this rate is described by a Dirichlet distribution with parameters αb,
, then this rate is described by a Dirichlet distribution with parameters αb,
 . Similar to the case of a single stimulus, the update rule for the parameters is given by
. Similar to the case of a single stimulus, the update rule for the parameters is given by
The second case we have to consider is that both mechanism (X = x1) → Y and (X = x2) → Y are independent. In order to describe a respective response process, consider two independent Pólya urns both filled with the same kind of colored balls, where we mark the two urns x1 respectively x2. In each sampling step we first decide from which urn to sample and then proceed as before. To be consistent with our notation we introduce a binning scheme B2 with two separate bins b1 = {x1} and b2 = {x2}. Instead of assigning weights to the urns directly, we assign them to our bins, i.e. αb1,
 for the first bin and αb2,
for the first bin and αb2,
 for the second one. The respective response is given by the product measure
for the second one. The respective response is given by the product measure
The so induced prediction rule is
| (6) |
where x ∈
 and IB2(x) tells us the bin to which x is assigned. This response process is partially exchangeable and the respective de Finetti measure μ(·|B2) is a product measure on
, where px1,
and IB2(x) tells us the bin to which x is assigned. This response process is partially exchangeable and the respective de Finetti measure μ(·|B2) is a product measure on
, where px1, ~ Dir[αb1,
~ Dir[αb1,
 ] and px2,
] and px2, ~ Dir[αb2,
~ Dir[αb2,
 ] are independently distributed, i.e. the respective density is given by the product density
] are independently distributed, i.e. the respective density is given by the product density
Conditional on finite data , the respectively updated parameters are
We can utilize both schemes B1 and B2 to model our beliefs about the similarity and dissimilarity between the stimuli. If B1 represents the hypothesis that x1 ~ x2, then B2 is the alternative hypothesis that x1 ≁ x2. If we assess our a priori belief in B1 with a probability of P [B1], then our a priori belief for model B2 is P [B2] = 1 − P [B1]. Our overall prediction for the response process is then given by the mixture measure
| (7) |
The induced prediction rule is
which can be rewritten as
| (8) |
where
| (9) |
The latter probability measure
can be interpreted as the Bayesian posterior assessment for each binning scheme Bi. The respective de Finetti measure for p is given by
is given by
which can be seen to be a model average over B1 and B2. One of our major goals is to generalize this mixture to multiple stimuli and responses, for which we want to develop adaptive sequential sampling strategies.
3.3. Multiple stimuli
Here, we briefly discuss the multibin Pólya process on discrete finite stimulus spaces
 = {x1, …, xL}, where we introduce an equivalence relation ~B that describes similarities in
= {x1, …, xL}, where we introduce an equivalence relation ~B that describes similarities in
 . This relation induces a partition B of
. This relation induces a partition B of
 into |B| bins, called a multibin. We then bin the data with respect to the resulting multibin B = {b1, …, b|B|}, such that we get the binned count statistic nB,
into |B| bins, called a multibin. We then bin the data with respect to the resulting multibin B = {b1, …, b|B|}, such that we get the binned count statistic nB,
 = (nb,
= (nb,
 )b∈B. In full analogy to the scenario of two stimuli, we set pseudo counts αB,
)b∈B. In full analogy to the scenario of two stimuli, we set pseudo counts αB,
 = (αb,
= (αb,
 )b∈B and fix the multibin Pólya urn process Y
)b∈B and fix the multibin Pólya urn process Y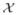 with
with
The induced prediction rule is
where IB (x) denotes the bin of stimulus x given the multibin B, i.e. if x ∈ b then IB (x) = b. Likewise the above case of two separate stimuli, the respective de Finetti measure μ(·|B) can be informally described by the density
such that conditional on some finite data
the relevant parameters αB,
 are simply updated according to
are simply updated according to
3.4. A Hierachical Bayesian Model for Proximally Related Stimuli
We assumed that the stimulus space
 = {x1, x2, …, xL} exhibits some well-ordering, as indicated by the indexing. We need to introduce some suitable terminology. Let
= {x1, x2, …, xL} exhibits some well-ordering, as indicated by the indexing. We need to introduce some suitable terminology. Let
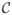 (
(
 ) = {bi,j = {xi, xi+1 …, xj }⊆
) = {bi,j = {xi, xi+1 …, xj }⊆
 | i ≤ j} denote the class of consecutive bins, where we call each partition B of
| i ≤ j} denote the class of consecutive bins, where we call each partition B of
 a proximal multibin if it consists only of consecutive bins. The class of all proximal multibins with m bins is denoted
a proximal multibin if it consists only of consecutive bins. The class of all proximal multibins with m bins is denoted
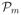 (
(
 ), such that
constitutes the class of all proximal multibins. These definitions are illustrated by the following example.
), such that
constitutes the class of all proximal multibins. These definitions are illustrated by the following example.
Example 4
Consider a set of stimuli
 = {1, 2, 3}, such that
= {1, 2, 3}, such that
Furthermore,
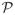 (
(
 ) = {B1, B2, B3, B4}, where
) = {B1, B2, B3, B4}, where
For each consecutive bin b ∈
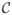 we choose pseudo counts αb,
we choose pseudo counts αb,
 and construct the following response process: By fixing a priori beliefs P [B], B ∈
and construct the following response process: By fixing a priori beliefs P [B], B ∈
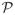 (
(
 ), we can describe the full response process Y
), we can describe the full response process Y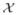 as the mixture
as the mixture
| (10) |
We shall refer to this process as the multibin Pólya mixture process. The induced prediction rule is
| (11) |
which can be rewritten as
| (12) |
where
| (13) |
is the posterior for the multibins B ∈
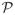 (
(
 ). The Bayesian model that corresponds to the multibin Pólya mixture process is described by the hierarchical model
). The Bayesian model that corresponds to the multibin Pólya mixture process is described by the hierarchical model
| (14) |
There are many ways how to look at the so described hierarchical model. For instance, the model can be seen as a Bayesian regression model for the psychometric rates, where a non-trivial prior in form of
is chosen. This prior assigns probability mass on particular diagonals of the product simplex, such that the psychometric rates become piecewise constant w.r.t. to a particular multibin, which are in turn assumed to be random quantities. From that point of view, the described model can be seen to be a generalization of the inhomogenous Bernoulli process described in Endres et al. (2008). Likewise, the model can be interpreted as a particular clustering model. Observations are clustered with respect to an unknown partition of the data space. From this point of view, the model is related to the so called product partition model as introduced by Hartigan (1990), which requires a particular prior structure for P [B] that will be discussed next.
3.5. Efficient Model Evaluation
The actual computation of the sum-product ΣB∈
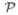 (
(
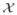 )Πb∈B in equation (10) can become computationally very demanding and infeasible as it may take up to
)Πb∈B in equation (10) can become computationally very demanding and infeasible as it may take up to
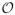 (2L−1 ) steps. This is especially problematic for adaptive sampling where the relevant quantities have to be computed as quickly as possible. However, based on the computational approaches taken by Yao (1984); Barry and Hartigan (1992); Endres and Földiák (2005); Fernhead (2006); Hutter (2007) it can be shown that particular prior structures of P [B] lead to a drastic reduction of the computational effort. In fact, it can be reduced to
(2L−1 ) steps. This is especially problematic for adaptive sampling where the relevant quantities have to be computed as quickly as possible. However, based on the computational approaches taken by Yao (1984); Barry and Hartigan (1992); Endres and Földiák (2005); Fernhead (2006); Hutter (2007) it can be shown that particular prior structures of P [B] lead to a drastic reduction of the computational effort. In fact, it can be reduced to
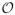 (L3) if
(L3) if
| (15) |
where |B| is the number of bins in B. The respective computational algorithm is given in lemma 1 (see appendix) to which we refer as Proximal
Multi-Bin
Summation (ProMBS). It is an abstracted and generalized version of the algorithm presented in Endres and Földiák (2005). The parameters γ = (γb)b∈
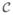 (
(
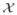 ), with γb ≥ 0, assess the a priori importance of each consecutive bin b ∈
), with γb ≥ 0, assess the a priori importance of each consecutive bin b ∈
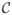 (
(
 ) and have been also called cohesions in Barry and Hartigan (1992), whereas β = (β1, …, βL), with βl ≥ 0, determine a relative weight for each class
) and have been also called cohesions in Barry and Hartigan (1992), whereas β = (β1, …, βL), with βl ≥ 0, determine a relative weight for each class
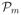 (
(
 ), m = 1, …, L, in
), m = 1, …, L, in
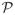 (
(
 ).
).
Given a set of parameters (α, β, γ) a particular multibin Pólya mixture process is fixed that describes our a priori belief about the response process Y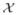 . All relevant posterior quantities are determined by the updated parameters
. All relevant posterior quantities are determined by the updated parameters
where
The ProMBS algorithm can be used to efficiently compute d(α, β, γ, n ), which will reappear in many other relevant expressions. For instance, we can rewrite equation (10) as
), which will reappear in many other relevant expressions. For instance, we can rewrite equation (10) as
whereas the normalization constant in (15) is given by
such that the prediction rule in equation (11) becomes
where
is the count statistic n incremented by one count for the event {X = x, Y = y}. Likewise, given a stimulus x ∈
incremented by one count for the event {X = x, Y = y}. Likewise, given a stimulus x ∈
 , the marginal posterior density of the respective psychometric rate px,
, the marginal posterior density of the respective psychometric rate px,
 is given by
is given by
where
The pointwise evaluation of this density can get computationally very expensive, but is nevertheless possible without Monte Carlo methods. Alternatively, the density can be described by its moments. Here, the k-th raw moment is
where we add k events {X = x, Y = y} to the count statistic n . We can also compute the posterior for the multibins (13)
. We can also compute the posterior for the multibins (13)
and by introducing a variable M ∈ {1, …, L} that restricts the model to multibins from
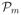 (
(
 ), we can compute
), we can compute
which is the posterior assessment that X → Y is described by a multibin model with m bins. Since neighboring stimuli potentially share strength, it is of interest to quantify to which extent this is happening. Such an informative statistic is the effective count n̄x, which we define as the expectation value
| (16) |
where IB (x) = b if x ∈ b and b ∈ B. An efficient evaluation is possible because
where
3.6. Prior Selection
For the multibin Pólya mixture process we need to select parameters (α, β, γ). With βm we specify the importance of models consisting of exactly m bins. For instance, if we want to fall back to a simpler problem with at most l < L bins we can set βl = 1 and βj = 0 for j ≠ l. A reasonable choice is often given by
The binomial coefficient gives the number of multibin models that constist of m bins. Hence, if for some constant c all γb = c, b ∈
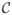 (
(
 ), then the above prior assigns a uniform distribution to P [M = m], the a priori probability of multibins with m bins. In any case, there are only L values that we have to specify for β. However, for αb,
), then the above prior assigns a uniform distribution to P [M = m], the a priori probability of multibins with m bins. In any case, there are only L values that we have to specify for β. However, for αb,
 and γb we need to select values for each b ∈
and γb we need to select values for each b ∈
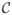 (
(
 ). If we are dealing with many stimuli the assignment of parameters can get a very extensive task. A first and very convenient choice is to set all αb,
). If we are dealing with many stimuli the assignment of parameters can get a very extensive task. A first and very convenient choice is to set all αb,
 and γb to one, which means that we use an uninformative prior for the pseudo counts and we do not have any preference for specific bins. A more elaborate and natural way is to compute αb,
and γb to one, which means that we use an uninformative prior for the pseudo counts and we do not have any preference for specific bins. A more elaborate and natural way is to compute αb,
 in a hierarchical manner, i.e. if we require that
in a hierarchical manner, i.e. if we require that
then we only need to specify αx,
 for each x ∈
for each x ∈
 .
.
3.7. Placement Rules for Adaptive Sampling
We discussed in section 2.1 a utility based approach concerning the choice of a suitable action policy for choosing the placement rule . We shall assume that our objective is to become most informed about the stimulus-response relation modeled by the multibin Pólya mixture process. We present here several proposals for how this might be achieved.
As already mention earlier, a most trivial sampling scheme is to distribute measurements uniformly, where the respective utility is
| (17) |
which guarantees at least some homogeneity in the data, but does not take any properties of the underlying model into account. A more sensible utility is given by
where n̄x is the effective count. The resulting placement rule essentially follows the logic of random uniform sampling, but takes the sharing of strength between neighboring stimuli into account. The attractive feature of this adaptive scheme is of course its conceptual and computational simplicity.
More elaborate adaptive strategies can be obtained by considering utilities based on information-theoretical quantities. The idea of using information theoretic utility measures for experimental designs was probably first considered by Cronbach (1953). A more detailed study of their application in experimental designs was later given by Lindley (1956), whereas explications of Lindley’s ideas within the context of Bayesian experimental design can be found in Bernardo (1979); Chaloner and Verdinelli (1995), but see also the application for optimizing sequential experimental designs in DeGroot (1962).
Consider that we want to learn as much as possible about which multibin model B ∈
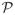 (
(
 ) describes the data best. Our a priori expectation is given by the probability P [B], whereas our a posteriori assessment is expressed by
. The information we would gain about B if we learn that {
} is then quantified by the Kullback-Leiber divergence4
) describes the data best. Our a priori expectation is given by the probability P [B], whereas our a posteriori assessment is expressed by
. The information we would gain about B if we learn that {
} is then quantified by the Kullback-Leiber divergence4
which measures the deviation between both measures. Hence, if we want to learn as much as possible about B then it seems reasonable to adopt the Kullback-Leibler divergence as a global utility measure. This, however, leads to almost intractable computations, as mentioned already in section 2.1. Nonetheless, it motivates the following myopic adaptive sampling strategy with local utility measure
i.e. we try to improve the incremental information in every sampling step. This divergence can be computed with
where
The respective expected local utility is
such that the optimal stimulus is determined by
It is noteworthy that the expected gain can be rewritten in terms of a mutual information5, namely
such that by maximizing the expected local utility we do in fact maximize the mutual information between B and conditional on . The so obtained adaptive sampling scheme, shortly denoted uMB, is fully equivalent to the Bayesian framework of adaptive design optimization (ADO) for model discrimination (cf. Cavagnaro et al. (2010)).
The very same line of reasoning applies to the case where we do have strong evidence for a particular multibin model, say B ∈
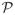 (
(
 ), but want to optimally learn the psychometric rates p
), but want to optimally learn the psychometric rates p . The respective local utility measures are given by
. The respective local utility measures are given by
where
and
are the respective successive posterior measures for the psychometric rates p conditional on B. These utility measures can be computed with
conditional on B. These utility measures can be computed with
where
and ψ is the psigamma function. We expect the resulting adaptive sampling scheme, denoted uΨ|B, to optimize the inferential task for the psychometric rate p given that B is the ‘true’ underlying model.
given that B is the ‘true’ underlying model.
In practice, we usually have only vague knowledge about the underlying multi-bin model. Henceforth, it seems reasonable to consider the local utility measures
where
and
are the respective successive posterior measures for the psychometric rates p . This measure decomposes as
. This measure decomposes as
where
is the model-averaged local utility for optimizing the inference of the psychometric rates given a multibin model. Hence, if we want to learn about p given that B is uncertain, then we also have to make inference about B. That is the uncertainty about B also influences our uncertainty about p
given that B is uncertain, then we also have to make inference about B. That is the uncertainty about B also influences our uncertainty about p . We thus expect this strategy, called uTotal, to optimize the inference of B and p
. We thus expect this strategy, called uTotal, to optimize the inference of B and p . It might also be worthwile to base the sampling process solely on uΨ because it allows us to optimize the inference of the psychometric rates regardless of the underlying multibin model.
. It might also be worthwile to base the sampling process solely on uΨ because it allows us to optimize the inference of the psychometric rates regardless of the underlying multibin model.
The actual effect of the proposed adaptive sampling strategies are difficult to describe and we shall proceed by discussing a simple example. In general, it can be said that there is no such thing as a universal criterium for optimal adaptive sampling as long as we do not clearly formulate what we want to achieve. Whether or not a chosen strategy is appropriate for the experiment at hand must be carefully assessed from case to case, for example with simulation studies or experimental pre-studies.
4. A Practical Demonstration
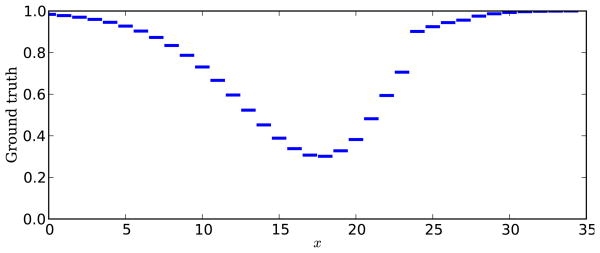
In order to demonstrate our framework we consider a hypothetical 2AFC experiment with 35 stimuli
 = {x1, x2, …, x35} and a dichotomous outcome
= {x1, x2, …, x35} and a dichotomous outcome
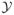 = {s, f }. The stimulus-response relation (ground truth) is given by an asymmetric U-shaped function with a small irregularity on the right side (see Figure 2). We assume that we have no a priori knowledge about the curve, except that proximal stimuli are likely to cause similar responses. In a naïve approach we would simply distribute N measurements random uniformly over
= {s, f }. The stimulus-response relation (ground truth) is given by an asymmetric U-shaped function with a small irregularity on the right side (see Figure 2). We assume that we have no a priori knowledge about the curve, except that proximal stimuli are likely to cause similar responses. In a naïve approach we would simply distribute N measurements random uniformly over
 , see (17), and infer the psychometric rates for each x ∈
, see (17), and infer the psychometric rates for each x ∈
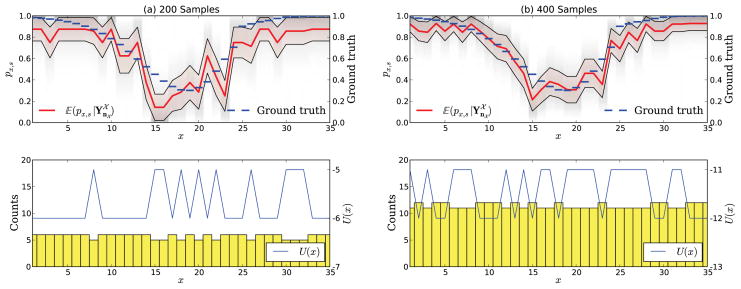
 independently. Figure 3 shows the result of such an experiment with 200 and 400 samples, where we chose pseudo counts αx,
independently. Figure 3 shows the result of such an experiment with 200 and 400 samples, where we chose pseudo counts αx,
 = (1, 1), y ∈
= (1, 1), y ∈
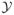 . The variance of the estimate is large because there are only very few samples for each stimulus x. A highly irregular curve as an estimate for the stimulus-response relation is therefore obtained and many measurements are taken at regions that are quite uninformative. This motivates two advantages of our proposed framework: First, we can use samples from neighboring stimuli to share statistical strength. Second, we want to distribute the samples such that we maximize the information that we gain with each measurement.
. The variance of the estimate is large because there are only very few samples for each stimulus x. A highly irregular curve as an estimate for the stimulus-response relation is therefore obtained and many measurements are taken at regions that are quite uninformative. This motivates two advantages of our proposed framework: First, we can use samples from neighboring stimuli to share statistical strength. Second, we want to distribute the samples such that we maximize the information that we gain with each measurement.
Figure 2.
Hypothetical stimulus-response curve used as ground truth for the practical demonstration. The curve shows the probability of the response s (success) for a given stimulus x.
Figure 3.
A hypothetical experiment with (a) 200 and (b) 400 samples uniformly distributed over the stimulus space
 . The stimulus-response relation (ground truth), shown as dashed line, is inferred without taking information from proximal x into account. The thick continuous line shows the first moment
of the stimulus-response function given all outcomes of previous measurements. The standard deviation is shown as a thin continuous line around the expectation. The marginal posterior density
is plotted as shadings in the back of the figure. The number of measurements at each x ∈
. The stimulus-response relation (ground truth), shown as dashed line, is inferred without taking information from proximal x into account. The thick continuous line shows the first moment
of the stimulus-response function given all outcomes of previous measurements. The standard deviation is shown as a thin continuous line around the expectation. The marginal posterior density
is plotted as shadings in the back of the figure. The number of measurements at each x ∈
 is shown as a bar plot in the lower plot with utility U (x) (thin continuous line), which is the negative number of counts, see (17).
is shown as a bar plot in the lower plot with utility U (x) (thin continuous line), which is the negative number of counts, see (17).
With our framework we can optimize the experimental process. We choose the following parameters:
With αx,
 = (1, 1) we assign equal pseudo counts to all stimuli and responses, since we have no a priori knowledge about the shape of the curve. The particular choice of βm and γb assigns a uniform distributions to P [M = m], which is the a priori probability of multibins with m bins (see section 3.6). Finally, we set all γb = 1 since all bins should receive an equal weight.
= (1, 1) we assign equal pseudo counts to all stimuli and responses, since we have no a priori knowledge about the shape of the curve. The particular choice of βm and γb assigns a uniform distributions to P [M = m], which is the a priori probability of multibins with m bins (see section 3.6). Finally, we set all γb = 1 since all bins should receive an equal weight.
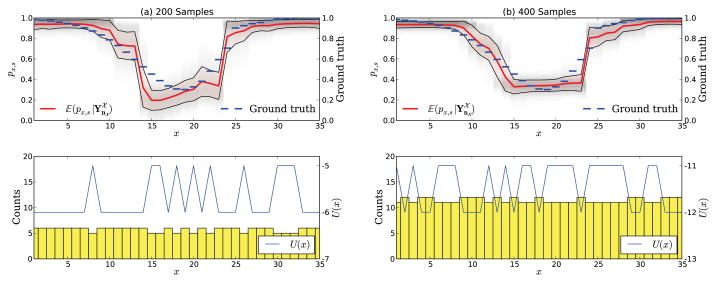
With this prior setting we observe a smoothening of the inferred stimulus-response curve (see Figure 4). However, in contrast to common kernel smoothing approaches, our method does not smear sharp transitions but represents a higher degree of uncertainty whenever necessary.
Figure 4.
A hypothetical experiment with (a) 200 and (b) 400 samples uniformly distributed. The ground truth is inferred by taking information from neighboring x into account. This sharing of statistical strength allows a much more accurate inference of the stimulus-response function as compared to Figure 2.
In order to distribute samples more efficiently, we can utilize the adaptive sampling strategies described in section 3.7. Unfortunately, it is difficult to compare the performance of different strategies since there is no general criterion for optimality. A good intuition can however be gained from the distribution of measurements.
The Figures 5, 6, 7, and 8 show the time course of the experiment for the adaptive sampling schemes uΨ, uMB, uTotal, and the strategy based on the effective count n̄x. All simulations were initialized with the same random seeds for each stimulus x ∈
 , such that results can be better compared. The uninformative parameter setting lead to a uniformly distributed expected local utility for all four strategies before the first experiment. Therefore, the first measurement was always taken at x = 20.
, such that results can be better compared. The uninformative parameter setting lead to a uniformly distributed expected local utility for all four strategies before the first experiment. Therefore, the first measurement was always taken at x = 20.
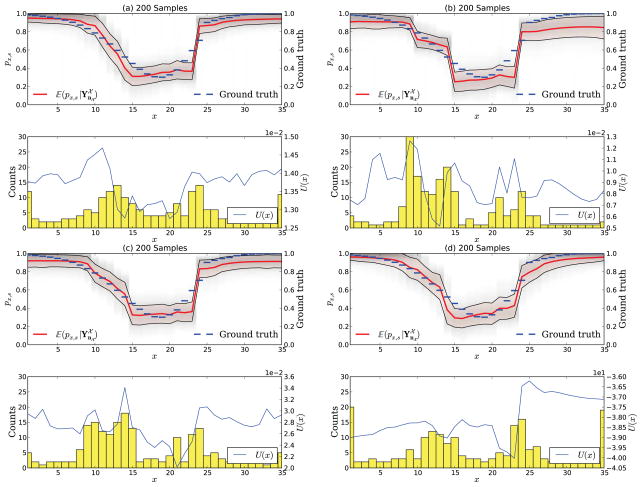
Figure 5.
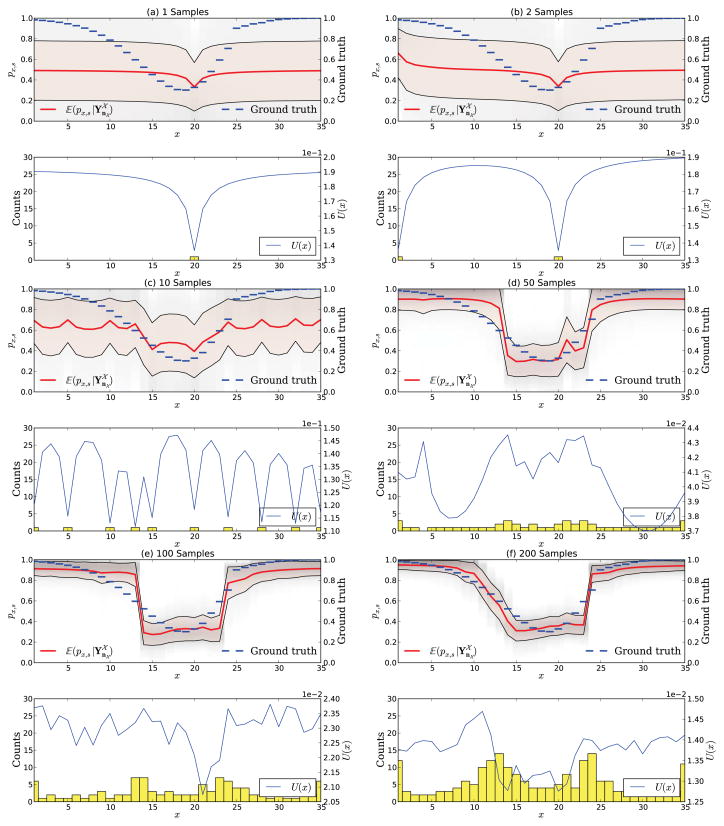
Adaptive sampling in a hypothetical experiment with scheme uΨ. The figure shows the experiment after 1, 2, 10, 50, 100, and 200 samples. At first, samples are uniformly distributed. In (a) only one measurement was taken and the expected utility is largest at the left boundary. (d) shows the experiment after 50 samples where the algorithm starts to locate measurements at sloped regions. The general shape of the stimulus-response function is already well established after 100 samples (e). Many measurements are also taken at x = 1 and x = 35 since those x have only one neighbor.
Figure 6.
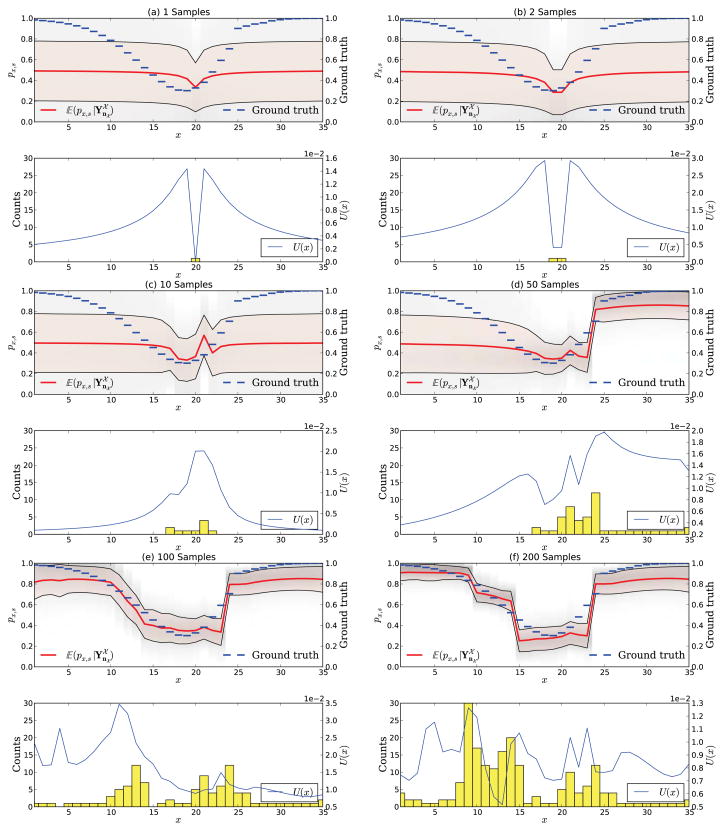
Adaptive sampling in a hypothetical experiment with scheme uMB. The figure shows the experiment after 1, 2, 10, 50, 100, and 200 samples. After the first sample (a) two maxima of the expected utility arise next to the measurement. The first 10 samples (c) are allocated near the initial measurement, whereas afterwards the algorithm starts move further right (d) until almost the full stimulus space has been explored (e–f).
Figure 7.
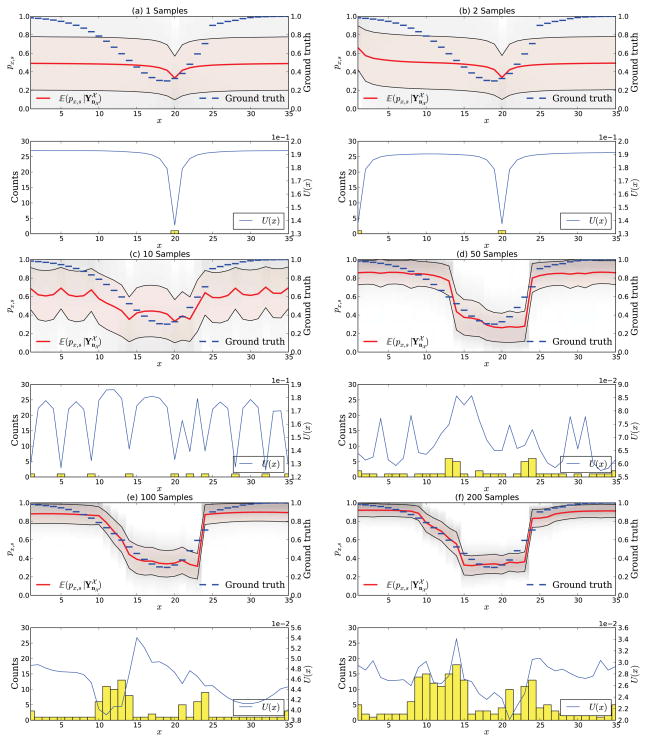
Adaptive sampling in a hypothetical experiment with scheme uTotal. The figure shows the experiment after 1, 2, 10, 50, 100, and 200 samples. The sampling behavior clearly shows a mixture of both schemes uMB and uΨ.
Figure 8.
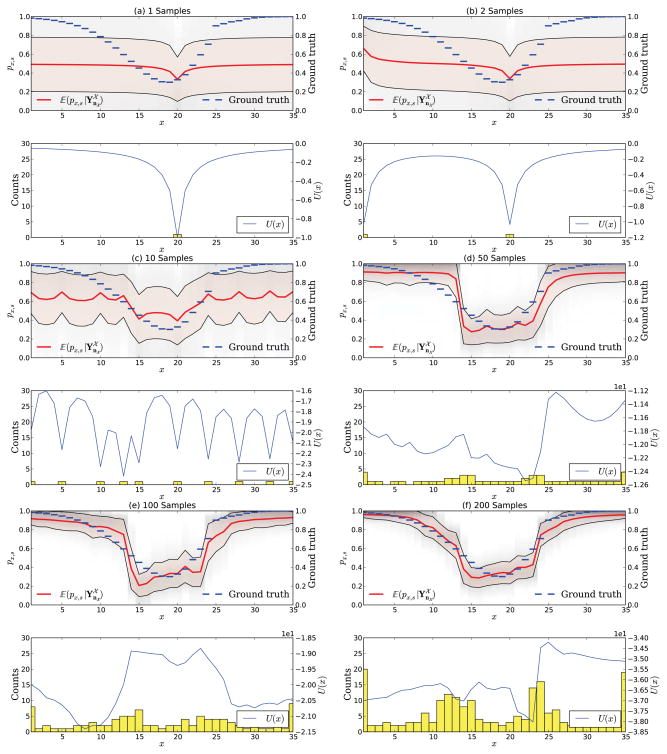
Adaptive sampling in a hypothetical experiment with the strategy based on the effective count n̄x. The figure shows the experiment after 1, 2, 10, 50, 100, and 200 samples. In (a) no measurements are taken and we can see our prior expectation. The respective utility is uniformly distributed on
 . The general shape of the stimulus-response function is already well established after 100 samples. Measurements are mostly allocated at regions where the slope of the stimulus-response function is high. Many measurements are also taken at x = 1 and x = 35 since those x have only one neighbor.
. The general shape of the stimulus-response function is already well established after 100 samples. Measurements are mostly allocated at regions where the slope of the stimulus-response function is high. Many measurements are also taken at x = 1 and x = 35 since those x have only one neighbor.
Already after the first sample one can observe a striking difference between uΨ and uMB. Whereas the expected utility for uΨ is maximal at the very left stimulus x = 1, the expected utility for uMB shows two maxima directly next to the previous measurement at x = 20. This reveals the very distinct properties of both schemes, which are better seen after 10 and 50 samples. uΨ causes a uniform distribution of the first samples on
 . On the other hand, the scheme uMB places all measurements around the initial sample and only gradually moves further away from x = 20. The U-shape of the stimulus-response function is already very well established after 100 samples and after 200 samples one can see that both measures place most samples at positions where the psychometric function is highly sloped. This behavior is expected since those regions allow less sharing of statistical strength. For the scheme uTotal we observe the same initial behavior as for uΨ, but the count statistic after 200 samples shows characteristics of both uΨ and uMB, which is expected from its definition. It is however quite noteworthy that the effective counts show a very similar behavior as uΨ. Figure 9 summarizes the differences between the four adaptive sampling strategies by showing the experiment after 200 samples.
. On the other hand, the scheme uMB places all measurements around the initial sample and only gradually moves further away from x = 20. The U-shape of the stimulus-response function is already very well established after 100 samples and after 200 samples one can see that both measures place most samples at positions where the psychometric function is highly sloped. This behavior is expected since those regions allow less sharing of statistical strength. For the scheme uTotal we observe the same initial behavior as for uΨ, but the count statistic after 200 samples shows characteristics of both uΨ and uMB, which is expected from its definition. It is however quite noteworthy that the effective counts show a very similar behavior as uΨ. Figure 9 summarizes the differences between the four adaptive sampling strategies by showing the experiment after 200 samples.
Figure 9.
Direct comparison of the four adaptive sampling strategies: (a) uΨ, (b) uMB, (c) uTotal, and (d) effective counts. A relatively balanced distributions of measurements is observed with uΨ and the effective counts. On the other hand, uMB and therefore also uTotal lead to a more peaked distribution.
Note also that many measurements are taken at the boundaries. This is because these stimuli have only one neighbor which limits the extent to which statistical strength can be shared. We now assume that we have prior knowledge about the ground truth, i.e. we have a strong belief about its value at x1 and x35. We incorporate this information into our model and thereby optimize the sampling process further. That is, we set α1,
 = α35,
= α35,
 = (100, 1). This parameter setting alters our prior expectation about the stimulus-response relation, i.e. px,s is expected to be close to one at x1 and x35, see Figure 10(a). The expected utility to sample at these points is substantially reduced, since we have a strong belief about the response. Figure 10(b) shows the experiment after 200 samples. One can see that all measurements that were previously allocated at the boundaries are now distributed elsewhere. Further optimizations of the sampling process are possible if more prior knowledge is available.
= (100, 1). This parameter setting alters our prior expectation about the stimulus-response relation, i.e. px,s is expected to be close to one at x1 and x35, see Figure 10(a). The expected utility to sample at these points is substantially reduced, since we have a strong belief about the response. Figure 10(b) shows the experiment after 200 samples. One can see that all measurements that were previously allocated at the boundaries are now distributed elsewhere. Further optimizations of the sampling process are possible if more prior knowledge is available.
Figure 10.
Demonstration of using prior knowledge to limit sampling at the boundaries with scheme uΨ. (a) shows the prior belief before any measurements are made and (b) shows the posterior after 200 samples. The prior setting leads to a strong belief about the response at the boundaries which substantially reduces the expected utility at x1 and x35. The result is that all measurements that were previously allocated at the boundaries are now placed elsewhere.
5. Conclusion
We have introduced a framework for adaptive sequential sampling which helps to optimize the measurement process in a wide range of psychophysical experiments, especially when there is only vague prior knowledge about the relation X → Y. Our framework consists of two major components. The first is a response process that we use to make predictions based on a finite number of observations. We termed it the multibin Pólya mixture process as it consists of a mixture of binned Pólya urns. On top of the response process we defined various adaptive sampling process, which are equipped with utility measures to actively guide the course of an experiment. We also demonstrate the effect of several sampling strategies on a hypothetical experiment and how prior knowledge can be used to further optimize the allocation of measurements. During experiments it is of great importance that decisions for the next stimulus are computed fast. Although our model is computationally demanding, we provide an algorithm that makes it applicable in typical psychophysics experiments.
Supplementary Material
Highlight.
We present a predictive account on adaptive sampling in psychophysical experiments.
Our method applies to situations where there is only weak knowledge available.
We demonstrate the advantages of our framework on a hypothetical sampling problem.
Acknowledgments
All three authors were supported by Max Planck Society. T. E. has been supported by NIH grant R01 EY018664. We thank Claudia Freigang, Pierre-Yves Bourguignon, and Wiktor Mlynarski for most helpful suggestions. We would also like to thank the anonymous reviewers whose suggestions have led to a considerable improvement of the manuscript.
Appendix
In Yao (1984); Barry and Hartigan (1992); Endres and Földiák (2005); Fernhead (2006); Hutter (2007) various algorithms are presented, which in their given context address all the very same computational problem. Within our terminology of proximal multibins the general problem can be described as follows:
Let f: C(
 ) → ℝ be any function from consecutive proximal bins to real numbers and g = (g1, …, gL) ∈ ℝL be any real valued vector. Define the sum-products
) → ℝ be any function from consecutive proximal bins to real numbers and g = (g1, …, gL) ∈ ℝL be any real valued vector. Define the sum-products
and
Each Sm[f ] consists of
terms, whereas the weighted total sum-product S[f, g] consists of 2L−1 terms. For large L a computationally intractable effort of
 (2L−1) is expected. However, the following lemma provides a simple and efficient algorithm, which computes the sum-product in
(2L−1) is expected. However, the following lemma provides a simple and efficient algorithm, which computes the sum-product in
 (L3).
(L3).
Lemma 1 (The Proximal Multibin Summation (ProMBS) Algorithm)
Define the upper triangular matrices , l = 1, …, L, recursively by
and define recursively the matrix-vector product
where the initial vector is v1 = (0, …, 0, 1)T. For every m, l ∈ ℕ with m ≤ l ≤ L it holds that
such that
A simple example might help to illustrate the abstract formulation of the ProMBS algorithm. Consider the case with |
 | = 3 and let us abbreviate f (bi,j ) simply by fij. In the first step we compute
| = 3 and let us abbreviate f (bi,j ) simply by fij. In the first step we compute
Note that . In the next step we compute
where and . In the last step we find that
such that (v4)T = (S1[f ], S2[f ], S3[f ]) and S[f, g] = g1S1[f ]+ g2S2[f ]+ g3S3[f ].
Of course, the real computational power of the ProMBS algorithm becomes only evident when the set
 is large, but the case |
is large, but the case |
 | = 3 shows the general logic behind the ProMBS algorithm sufficiently enough. We should finally mention that numerical imprecisions can occur if the values of f become small. In such cases it is advisable to implement the ProMBS algorithm on a logarithmic number scale.
| = 3 shows the general logic behind the ProMBS algorithm sufficiently enough. We should finally mention that numerical imprecisions can occur if the values of f become small. In such cases it is advisable to implement the ProMBS algorithm on a logarithmic number scale.
Footnotes
There is much ambiguity in the usage of the term nonparametric as different fields of statistics assign different meanings to what is actually meant by nonparametric. Here, we simply mean that no constraint in form of a parametric family is imposed that restricts the topological support for the psychometric rates p in
.
in
.
The multinomial sampling laws described here apply to the categorical process Y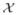 and are not to be confused with the related multinomial distribution for the respective count statistic n
and are not to be confused with the related multinomial distribution for the respective count statistic n .
.
The illustrative metaphor of a bin is taken from Endres and Földiák (2005); Endres et al. (2008), whereas cluster, block or component might serve equally well.
The Kullback-Leibler divergence is formally defined as follows: If μ, ν are two measures on a measurable space [S,
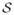 ], such that ν is absolute continuous w.r.t. μ, then
is the Kullback-Leibler divergence from μ to ν, where
is the respective Radon-Nykodým derivate of ν w.r.t. μ.
], such that ν is absolute continuous w.r.t. μ, then
is the Kullback-Leibler divergence from μ to ν, where
is the respective Radon-Nykodým derivate of ν w.r.t. μ.
The mutual information between two variables X and Y conditional on a third variable Z is formally defined as follows: If μY, X | Z is the joint measure of X, Y conditional on Z and μX | Z, μY | Z are the respective conditional marginal measures, such that μX×Y | Z is the product measure constructed from both marginal measures, then the mutual information between X and Y conditional on Z is defined as MI(X: Y |Z):= DKL(μX, Y | Z ||μX×Y | Z ), i.e. the Kullback-Leiber divergence from the conditional product measure to the conditional joint measure.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Stephan Poppe, Email: stephan.poppe@mis.mpg.de.
Philipp Benner, Email: philipp.benner@mis.mpg.de.
Tobias Elze, Email: tobias.elze@schepens.harvard.edu.
References
- Barry D, Hartigan JA. Product partition models for change point problems. The Annals of Statistics. 1992;20 (1):260–279. [Google Scholar]
- Berger JO. Statistical decision theory and Bayesian analysis. 2. Springer-Verlag; New York: 1993. [Google Scholar]
- Bernardo JM. Expected information as expected utility. The Annals of Statistics. 1979;7 (3):686–690. [Google Scholar]
- Bernardo JM, Smith AFM. Bayesian theory. Wiley, Chichester; 1995. [Google Scholar]
- Cavagnaro DR, Myung JI, Pitt MA, Kujala JV. Adaptive design optimization: A mutual information-based approach to model discrimination in cognitive science. Neural Computation. 2010;22:887–905. doi: 10.1162/neco.2009.02-09-959. [DOI] [PubMed] [Google Scholar]
- Chaloner K, Verdinelli I. Bayesian experimental design: A review. Statistical Science. 1995;10 (3):273–304. [Google Scholar]
- Cronbach LJ. Tech Rep. Vol. 1. Illinois University; Urbana: Bureau of Research and Service; 1953. A consideration of information theory and utility theory as tools for psychometric problems. [Google Scholar]
- de Finetti B. La prévision: ses lois logiques, ses sources subjectives. Ann Inst Poincare. 1937;7 (2):1–68. [Google Scholar]
- de Finetti B. Theory of probability: A critical introductory treatment. Vol. 1. Wiley; London;, New York, N.Y: 1974. [Google Scholar]
- de Finetti B. On the condition of partial exchangeability. In: Jeffrey RC, editor. Studies in inductive logic and probability. University of California Press; Berkeley: 1980. pp. 193–205. [Google Scholar]
- DeGroot MH. Uncertainty, information, and sequential experiments. The Annals of Mathematical Statistics. 1962;33 (2):404–419. [Google Scholar]
- DeGroot MH. Optimal statistical decisions, wiley classics library. Wiley-Interscience; Hoboken and N.J: 2004. [Google Scholar]
- Eggenberger F, Pólya G. Über die statistik verketteter vorgänge. ZAMM - Zeitschrift für Angewandte Mathematik und Mechanik. 1923;3 (4):279–289. [Google Scholar]
- Elze T, Song C, Stollhoff R, Jost J. Chinese characters reveal impacts of prior experience on very early stages of perception. BMC Neuroscience. 2011;12:14. doi: 10.1186/1471-2202-12-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endres D, Földiák P. Bayesian bin distribution inference and mutual information. IEEE Transactions on Information Theory. 2005;51 (11):3766–3779. [Google Scholar]
- Endres D, Oram M, Schindelin J, Foldiak P. Bayesian binning beats approximate alternatives: estimating peri-stimulus time histograms. In: Platt J, Koller D, Singer Y, Roweis S, editors. Advances in Neural Information Processing Systems 20. MIT Press; Cambridge, MA: 2008. pp. 393–400. [Google Scholar]
- Fernhead P. Exact and efficient bayesian inference for multiple change-point problems. Statistics and Computing. 2006;16 (2):203–213. [Google Scholar]
- Geisser S. Predictive inference: An introduction. Chapman & Hall; London: 1993. [Google Scholar]
- Hartigan JA. Partition models. Communications in statistics. Theory and methods. 1990;19 (8):2745–2756. [Google Scholar]
- Hutter M. Exact bayesian regression of piecewise constant functions. Bayesian Analysis. 2007;2 (4):635–664. [Google Scholar]
- Kontsevich LL, Tyler CW. Bayesian adaptive estimation of psychometric slope and threshold. Vision Research. 1999;39 (16):2729–2737. doi: 10.1016/s0042-6989(98)00285-5. [DOI] [PubMed] [Google Scholar]
- Kujala JV. Obtaining the best value for money in adaptive sequential estimation. Journal of Mathematical Psychology. 2010;54:475–480. [Google Scholar]
- Kujala JV, Lukka TJ. Bayesian adaptive estimation: The next dimension. Journal of Mathematical Psychology. 2006;50:369–389. [Google Scholar]
- Kuss M, Jakel F, Wichmann FA. Bayesian inference for psychometric functions. Journal of Vision. 2005;5 (5):8. doi: 10.1167/5.5.8. [DOI] [PubMed] [Google Scholar]
- Lauritzen SL. Tech Rep. Vol. 18. Stanford University, Department of Statistics; 1974. On the interrelationships among sufficiency, total sufficiency and some related concepts. [Google Scholar]
- Leek M. Adaptive procedures in psychophysical research. Attention, Perception, Psychophysics. 2001;63:1279–1292. doi: 10.3758/bf03194543. [DOI] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. The Journal of the Acoustical Society of America. 1971;49 (2B):467–477. [PubMed] [Google Scholar]
- Lindley DV. On a measure of the information provided by an experiment. The Annals of Mathematical Statistics. 1956;27 (4):986–1005. [Google Scholar]
- Link G. Representation theorems of the de finetti type for (partially) symmetric probability measures. In: Jeffrey RC, editor. Studies in inductive logic and probability. University of California Press; Berkeley: 1980. pp. 207–231. [Google Scholar]
- MacKay DJC. Information-based objective functions for active data selection. Neural Computation. 1992;4:590–604. [Google Scholar]
- McKee S, Klein S, Teller D. Statistical properties of forced-choice psychometric functions: Implications of probit analysis. Attention, Perception, & Psychophysics. 1985;37 (4):286–298. doi: 10.3758/bf03211350. [DOI] [PubMed] [Google Scholar]
- Müller P, Berry DA, Grieve AP, Smith M, Krams M. Simulation-based sequential bayesian design: Special issue: Bayesian inference for stochastic processes. Journal of Statistical Planning and Inference. 2007;137 (10):3140–3150. [Google Scholar]
- Roberts HV. Probabilistic prediction. Journal of the American Statistical Association. 1965;60 (306):50–62. [Google Scholar]
- Taylor MM, Creelman CD. Pest: Efficient estimates on probability functions. The Journal of the Acoustical Society of America. 1967;41 (4A):782–787. [Google Scholar]
- Watson A, Fitzhugh A. The method of constant stimuli is inefficient. Attention, Perception, & Psychophysics. 1990;47 (1):87–91. doi: 10.3758/bf03208169. [DOI] [PubMed] [Google Scholar]
- Watson A, Pelli D. Quest: A bayesian adaptive psychometric method. Attention, Perception, & Psychophysics. 1983;33:113–120. doi: 10.3758/bf03202828. [DOI] [PubMed] [Google Scholar]
- Wichmann F, Hill N. The psychometric function: I. fitting, sampling, and goodness of fit. Attention, Perception, & Psychophysics. 2001;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]
- Yao YC. Estimation of a noisy discrete-time step function: Bayes and empirical bayes approaches. The Annals of Statistics. 1984;12 (4):1434–1447. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.