Test-retest Stability Analysis of Resting Brain Activity Revealed by BOLD fMRI

Abstract

Purpose

To assess test-retest stability of four fMRI-derived resting brain activity metrics: the seed-region-based functional connectivity (SRFC), independent component analysis (ICA)-derived network-based FC (NTFC), regional homogeneity (ReHo), and the amplitude of low frequency fluctuation (ALFF).

Methods

Simulations were used to assess the sensitivity of SRFC, ReHo, and ALFF to noise interference. Repeat resting blood-oxygen-level-dependent (BOLD) fMRI were acquired from 32 healthy subjects. The intra-class correlation coefficient (ICC) was used to assess the stability of the 4 metrics.

Results

Random noise yielded small random SRFC, small but consistent ReHo and ALFF. A neighborhood size greater than 20 voxels should be used for calculating ReHo in order to reduce the noise interference. Both the anterior cingulate cortex (ACC) and posterior cingulate cortex (PCC)-based SRFC were reproducible in more spatially extended regions than ICA NTFC. The two regional spontaneous brain activity (SBA) measures, ReHo and ALFF, showed test-retest reproducibility in almost the whole grey matter.

Conclusion

SRFC, ReHo, and ALFF are robust to random noise interference. The neighborhood size for calculating ReHo should be larger than 20 voxels. ICC>0.5 and cluster size>11 should be used to assess the ICC maps for ACC/PCC SRFC, ReHo and ALFF. BOLD fMRI-based SBA can be reliably measured using ACC/PCC SRFC, ReHo and ALFF after two months.

INTRODUCTION

Functional neuroimaging has been widely used to assess brain functions using ad hoc cognitive tasks. However the task-related energy consumption increase is usually less than 5% of the baseline energy consumption (1), which can be up to 20% of the whole body’s “energy budget” (2). This striking neurophysiologic phenomenon suggests that the human brain may actually be more involved in the intrinsic spontaneous brain activity (SBA) that presents even if there is no any overt behavior (3). In other words, resting brain activity should be as informative, or even more informative than task- or stimulus-induced brain activity. Stimulated by these prospections, imaging SBA has quickly become an active research topic during the past several years (3,4).

Several metrics have been proposed to characterize SBA based on resting neuroimaging data, which can roughly be divided into two classes: one for characterizing the functional connectivity (FC) and the other for characterizing the regional SBA features. FC is generally assessed using either the seed-region-based FC (SRFC) or the multivariate data-driven method-based network-based FC (NTFC). The local SBA features can be assessed using the regional data coherence-based method (5) or frequency spectrum-based method (6). SRFC is to calculate the data correlation between the seed region and the rest of brain, as first used by Biswal et al in their seminal FC work(7). NTFC is generally explored using independent component analysis (ICA) (8,9). Regional coherence of SBA can be examined using the classical Kendall’s coefficient concordance (KCC, also known as Kendall’s W) (10), which was named by regional homogeneity (ReHo) in Zang et al (5). Another local SBA metric, amplitude of the low frequency fluctuation (ALFF) was proposed by Yang et al (6) to characterize the strength of the low frequency SBA in the resting brain. Consistent SBA patterns using these metrics have been repeatedly identified using BOLD fMRI (1,3,8,11–17). Particularly, SBA differences between normal controls and patients with brain diseases have been demonstrated by many groups (4,14,18–20), and accumulated evidence has been shown in the past years that SBA measured with these 4 metrics could be altered by either functional task (3,8,21) or brain diseases (4,22,23), suggesting SBA as a potential biomarker for brain disease identification or treatment effects.

Stability of these SBA measures has been validated using in-vivo data. Similar FC patterns revealed with SRFC or ICA NTFC have been reported by several independent research groups (8,24). Anderson et al. (25) found reliable estimates of the test-retest reproducibility of single-subject SRFC measurements. But few studies have shown consistent regional SBA patterns measured with either ReHo or ALFF in the normal health brain. Test-retest reproducibility of various SBA measures has also been reported by several groups (26–29). But no one has reported test-retest stability for both types of resting SBA metrics based on the same dataset.

Purely derived from data, these apparent SBA measures might be partially contributed by noise. Noise reduction through smoothing or bandpass filtering are widely used in SRFC or ICA NTFC to suppress the high frequency noise in resting fMRI data, but they could bias ReHo by introducing artificial coherence. Temporal filtering could be completely ineffective for ALFF calculation if the noise is white since white noise contributes equally to the whole spectrum. It is therefore desirable to assess the sensitivity of these SBA metrics, especially the regional measures to noise interference.

Statistical inference for the test-retest stability measures has not yet been addressed. Permutation testing can be used to calculate a probability of the test-retest measures after randomly shuffling the samples (the SBA measures). But it is nearly intractable to do permutation testing for hundreds or thousands of voxels. Simulations with synthetic data provides an easy way to statistically infer the voxel-wise test-retest stability indices by checking the histogram of the test-retest measure obtained during the simulations.

The purposes of this paper are to assess the sensitivity of both kinds of SBA metrics to noise using synthetic data, to estimate a confidence level for choosing a test-retest stability threshold, and to provide a comprehensive test-retest analysis for both kinds of SBA metrics using repeat resting BOLD fMRI acquired from 32 normal healthy controls twice with 2 months apart. Five SBA measures: ACC-FC, PCC-FC, ICA NTFC, ReHo, and ALFF were calculated for each subject at each resting fMRI session. Group level t-test at each session and the test-retest analysis were then performed to assess both the across-subject consistency and the within-subject reproducibility of these measures. Noise data were generated to assess the sensitivity of these metrics to noise interference.

MATERIALS AND METHODS

Synthetic data

Sixty-four series of Rician noise images (30) were generated using Matlab (Mathworks Inc., Natick, MA). Each series contained 220 images and each image had 11 slices. The 64 noise data sets were then randomly assigned to be 32 pairs of test-retest data sets. SRFC, ReHo, ALFF, and the corresponding test-retest reliability measures were calculated using the method as described below. In order to assess the sensitivity to random noise only, no spatial smoothing was applied before calculating these 3 SBA metrics. Bandpass filtering were applied to the synthetic data series to mimic the bandpass filtering due to the convolution of the hemodynamic response function. The bandpass filter was described in the following data analysis section.

Subjects

Thirty two healthy subjects (mean age = 42.97, range = 20 – 81, SD = 19.43, 12 male, 20 female) were scanned with signed written consent form approved by local Institutional Review Board (IRB). All subjects were right-handed without any psychiatric or psychological or neurological disorders.

MRI data acquisition

MR imaging was conducted in a 3-T whole-body scanner (Siemens Medical Systems, Erlangen, Germany). High-resolution structural images were acquired for spatial brain normalization using a 3D MPRAGE sequence (TR/TE/TI = 1620/3/950ms). Gradient-echo echo-planar imaging sequence was used for BOLD fMRI data acquisition with parameters of: TR = 3s, TE = 30 ms, FOV = 220×220 mm², matrix = 64×64×40, slice thickness= 3 mm. Participants were asked to lie still in the scanner at rest and keep eyes open. Two-hundred and twenty images were acquired each time. All the subjects conducted a second scan in 2 months after the first scan.

Data analysis

Data preprocessing

All data preprocessing was performed using SPM (http://www.fil.ion.ucl.ac.uk/spm) based batch scripts (31) with the following steps: motion correction, coregistration, and normalization. A local brain template was generated using the diffeomorphic anatomical registration through exponential Lie algebra (DARTEL) (32) based on each subject’s structural image. This template was subsequently mapped into the MNI standard brain space. The transformation from the MNI space to the local template and the one from the local template to each individual brain were combined into a single transform, which was used to normalize each individual’s images into the standard MNI space. BOLD images were detrended to remove the linear signal drift. Head motion time courses, the whole brain global signal, the mean CSF signal and mean white matter signal were treated as nuisance variables and were regressed out from each voxel’s time series (33) using a multiple regression model. Except for the ALFF analysis, low-pass filtering with a Butterworth filter (cutoff frequency = 0.08Hz), and a high-pass Butterworth filtering (cutoff frequency = 0.01Hz) were applied to the images before calculating the SBA measures. The BOLD images were then spatially smoothed with an isotropic Gaussian kernel with full-width-half-maximum (FWHM) of 6 mm (34). The following 3 measures were calculated from these preprocessed images.

SRFC

Seed regions were defined in ventral anterior cingulate cortex (vACC) and posterior cingulate cortex (PCC) using the Pickatlas utility(35). The mean ROI signal was extracted from each subject’s resting images and was subsequently used as the regressor in a whole brain linear regression analysis. The correlation coefficients of all voxels were collected as the SRFC map. Group level statistical analysis and test-retest stability analyses were then conducted on these individual level SRFC maps. For the synthetic noise data sets, the vACC ROI was chosen as the seed.

ICA-based resting networks analysis

ICA was performed using the probabilistic ICA (9) implemented in MELODIC (Multivariate Exploratory Linear Decomposition into Independent Components) Version 3.09, part of FSL (FMRIB’s Software Library, www.fmrib.ox.ac.uk/fsl). Each subject’s fMRI images at each session were concatenated along time to build a 4D image matrix, which was subsequently analyzed with ICA. The decomposed independent component maps were mapped into the standard MNI space using the structure image-based transformation as described above, and then spatially smoothed using an isotropic 3D Gaussian kernel with FWHM of 6 mm. Although several resting networks have been reported using ICA, we only examined the test-retest stability of the ICA-derived default mode network (DMN) in this work since DMN is the one that has been well established in the literature either using SRFC or ICA. In order to find the DMN component for each subject, all subjects’ 4D image data matrix as mentioned above were further concatenated along subject dimension, which was analyzed using ICA, and the group level DMN component was then identified by checking each component map’s spatial appearance in the DMN regions and the spectrum of its time course after the group level ICA. Using the group level DMN map as a reference, the individual subject’s DMN map was determined by searching for the one that has the highest correlation to the reference map. This map search process was necessary to find the DMN component for all subjects because ICA has an intrinsic order ambiguity. The individual DMN maps were used for a group level statistical analysis and test-retest reliability analysis.

ReHo

ReHo (5) is actually the same as the standard Kendall’s coefficient concordance (KCC, also known as Kendall’s W) (10). With a pre-specified neighborhood (27 neighboring voxels as used in (5)), ReHo was calculated from all the neighboring voxels’ time series. To avoid any artificial coherence due to the spatial smoothing, the non-smoothed motion corrected images rather than the spatially smoothed images were used for calculating ReHo (36).

Suppose there are K voxels in the neighborhood and the time series length is n. The time series of each voxel was converted into a series of rank number, ranging from 1 to n. Denoting r_i,j as the rank of the i-th time point of the j-th voxel, the total rank at the i-th time point was measured by:

$$R_i=\sum _{j=1}^K{r}_{i,j}$$ (1)

Kendall’s W was then calculated as:

$$W=\frac{\sum {(R_i)}^2-n{(\overline{R})}^2}{1/12K^2\left(n^3-n\right)}$$ (2)

where $\overline{R}=\frac{1}{2}K(n+1)$ is the mean value of all voxels’ total ranks.

Kendall’s W ranges from 0 to 1, where 0 means no coherence and 1 means coherent. The collection of all voxels’ Kendall’s W formed the so-called ReHo map. The ReHo maps were smoothed to reduce noise and were used for subsequent group analyses and reliability analyses.

For a fixed K and n, both the denominator and the 2^nd term of the nominator of the right side of Eq. 2 become constant; the only variable part is the 1^st term of the nominator. For random noise, the ranked values r_i,j are uniformly distributed between 1 and n (n is the data length). According to (37), R_i will have a highly complex polynomial probability density function, which changes from a rectangular waveform (the density function of the uniform distribution) when K=1, to a triangular function when K=2, and to a sub-Gaussian function when K>2. Therefore it is possible to calculate the 1^st term of the nominator in Eq. 2, and then calculate W based on the distribution function. However it is difficult to derive an analytic function for W directly from the complicated distribution function of the first term in the nominator. Instead, an empirical W function with regard to the neighborhood size was estimated through a numeric method by varying the neighborhood size from 2 to 100. For each neighborhood size, 50 sets of random noise data (data series length = 400) were generated for all voxels in the neighborhood. Kendal W was then calculated for each dataset and averaged for all 50 calculations. A data fitting process was used to derive an empirical W function. The Monte Carlo (MC) simulations were used here to determine the empirical function. 10000 sets of random noise data of all sizes (2 – 100) of neighborhood were generated. The KCC calculation results for each simulation (where the neighborhood size varied from 2 to 100 was fitted to an empirical function chosen based on the KCC curve shape. The mean and standard deviation of the function parameters were calculated based on the results of all simulations. Similarly, numeric experiments were performed to estimate the curve of W versus data series length by changing the data series length from 2 to 400 while keeping the neighborhood size fixed (27 voxels). For each length, 50 sets of random noise data were generated for all the 27 neighboring points. W was then calculated for all of these 50 datasets and plotted in the figure. Bandpass filtering was applied to all the simulated data series in all of the above simulations.

ALFF

Each voxel’s time series was transformed into the frequency domain using Fourier transform. The mean amplitude of the spectrum over the frequency range of 0.01–0.08Hz was calculated as the ALFF (6). All voxels’ ALFF values were collected to form an ALFF map. In order to reduce the effects of scale variability and across-subject variability, ALFF was further normalized by the global mean ALFF value in the whole-brain mask (6,36). For in-vivo data, ALFF was further smoothed to reduce noise and used for group analyses and test-retest reliability analysis.

As a brief summary, Table 1 lists all the processing steps used for calculating SRFC, ReHo, ALFF and ICA DMN.

Table 1.

Processing steps of SRFC, ReHo, ALFF and ICA DMN for individual data.

SRFC	ReHo	ALFF	ICA DMN
Realign	Realign	Realign	Realign
Registration	Registration	Registration	Registration
			ICA
Normalization	Normalization	Normalization	Normalization
detrend	detrend	detrend
REGRE	REGRE	REGRE
Band pass	Band pass
Smooth	ReHo	Smooth
SRFC	Smooth	ALFF	Find DMN map

[*]The processing steps are ordered from top to bottom as listed. Abbreviations used in the table: SRFC: seed-region-based functional connectivity, ICA DMN: independent component analysis based default mode network, ReHo: regional homogeneity, ALFF: amplitude of low frequency fluctuation, Registration: register functional images to anatomical images. REGRE: Regress out nuisance variables including head motion time courses, the whole brain global signal, the mean CSF signal and mean white matter signal.

Group level patterns of each SBA metric

One sample T tests were conducted for all 4 SBA metrics for each session using the corresponding SBA maps from all subjects, respectively. The statistical results were thresholded at p<0.001 (uncorrected for multiple comparisons) and cluster extent = 30 voxels.

Voxel-wise test-retest reliability

Intra-class correlation (ICC), a common measure of test-retest reliability (38,39), was used to assess the test-retest stability at each voxel for each of the 4 SBA metric maps. ICC was calculated at each voxel using the following equation:

$$\mathit{ICC}=\frac{{MS}_S-{MS}_E}{{MS}_S+(K-1){MS}_E}.$$ (3)

Where MS_S and MS_E are the subject mean square and error mean square, K is the number of sessions (2 here). MS_S and MS_E were estimated using a two-way ANOVA (ANalysis Of VAriance) (38,39) on the 32 subjects’ test-retest (the 2 factors) SBA metrics map values.

The ICC value is between −1.0 to 1.0. An ICC<0.41, from 0.41–0.59, from 0.6–0.75, or >0.75 indicates a poor, fair, good, or excellent reliability, respectively (40). ICC>0.5 was used to threshold the ICC maps in this paper according to the literature (26,40). The cluster wise threshold for assessing the ICC results was chosen to be 0 for the synthetic noise data, and 30 voxels for the in-vivo data.

RESULTS

Resting measures calculated from random noise

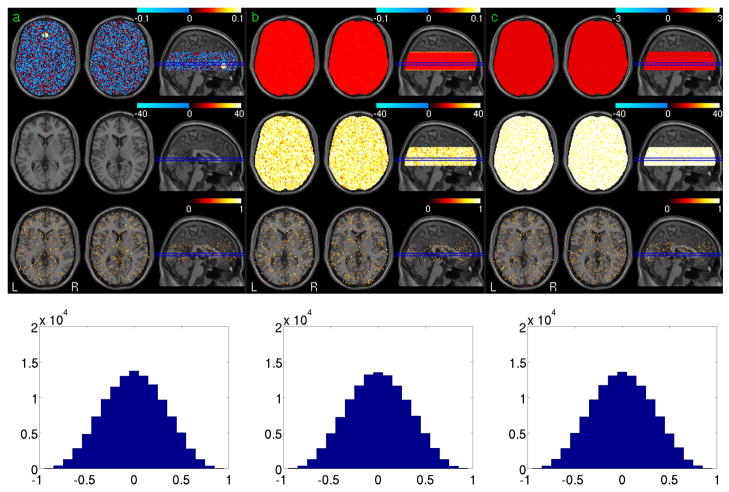
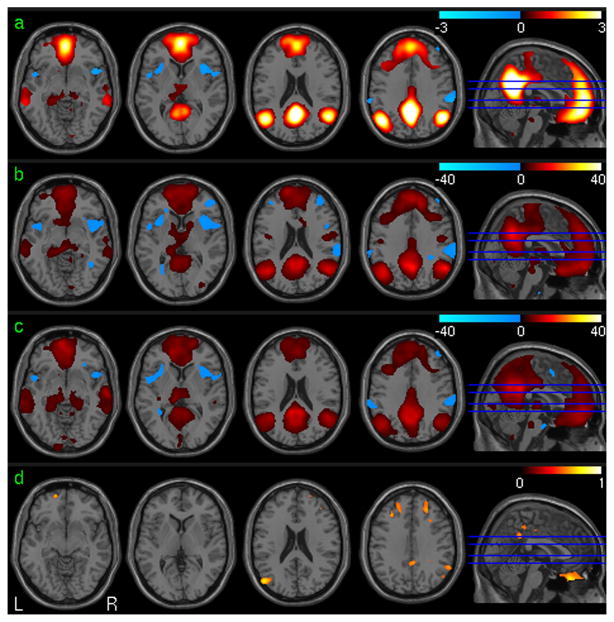
Fig. 1 shows the simulation results based on the synthetic noise data. Fig 1a is the FC calculation and assessment results. The 1^st, 2^nd, 3^rd and 4^th rows are the mean FC map of 32 noise data sets, the group level statistical parametric map (t-map) of one session, the ICC map and the histogram of the ICC values of the synthetic data, respectively. Fig 1b shows the results of ReHo calculation with the mean ReHo map, the group level t-map, and ICC map in the 1^st, 2^nd, and 3^rd rows, respectively. The ALFF calculation results were shown in Fig 1c, and the 1^st, 2^nd, and 3^rd rows are the mean ALFF map, the group level t-map, and ICC map, respectively. Except in the seed region, the FC of random noise is still random noise as shown in Fig. 1a; no voxels showed significant correlation with the mean signal of the seed region (using a threshold of P<0.001 uncorrected). Both ReHo (the 2^nd row in Fig 1b) and ALFF (the 2^nd row in Fig 1c) were consistently small across the whole synthetic brain area. With a threshold of ICC>0.5, test-retest stability of all three measures based on the noise data was found in sporadic regions with the cluster extension less than 11 voxels. The bottom rows of Fig. 1a, 1b, and 1c show the histograms of the ICC of the 3 verified measures, respectively. All three measures presented a similar Gaussian-like ICC distribution pattern. According to these histograms, the probabilities of any ICC value that is no less than 0.5, 0.6, 0.75 are 0.058, 0.025, and 0.004, respectively.

Fig. 1.

Simulation results for FC, ReHo, and ALFF. The 1st, 2nd, 3rd and 4th rows in Fig a/b/c are the mean FC/ReHo/ALFF maps of 32 noise data sets, the group level statistical parametric map (t-map) of one session(p<0.001, FWE corrected), the ICC map (ICC>0.5) and the histogram of the ICC values of the synthetic data, respectively.

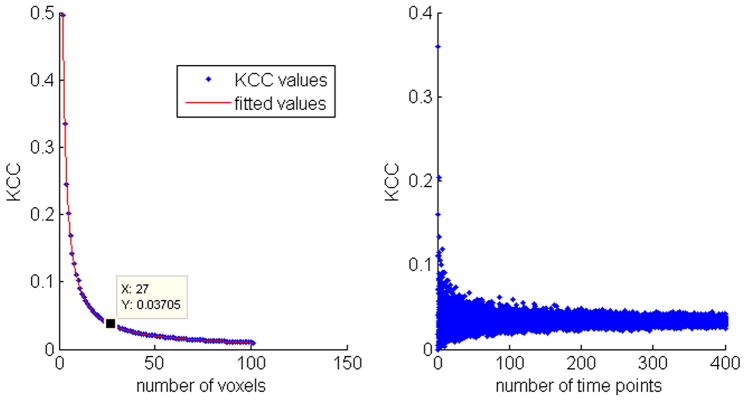
Fig. 2 shows the results of KCC calculations for various random noise data when different neighborhood size (Fig. 2a) or different data length (Fig. 2b) was used. Fig. 2a shows that KCC of noise tended to be more stable when the neighborhood size was larger than 20, and Fig. 2b shows that KCC of noise became more stable after the data length was longer than 100. Through a linear data fitting process, the KCC curve in Fig. 2a can be well approximated by a rational function:

$$f(x)=\frac{a}{\text{x}+b}$$ (4)

Fig. 2.

KCC values estimated from random noise. a) KCC curves versus different neighborhood size, b) KCC values calculated from noise data with different data length (from 2 to 400) and a fixed neighborhood size of 27.

Where x is the number of voxels, and the parameters of the fitted rational function are: a=1.0004±0.0287, b=0.0047±0.1316.

vACC-FC of the resting fMRI

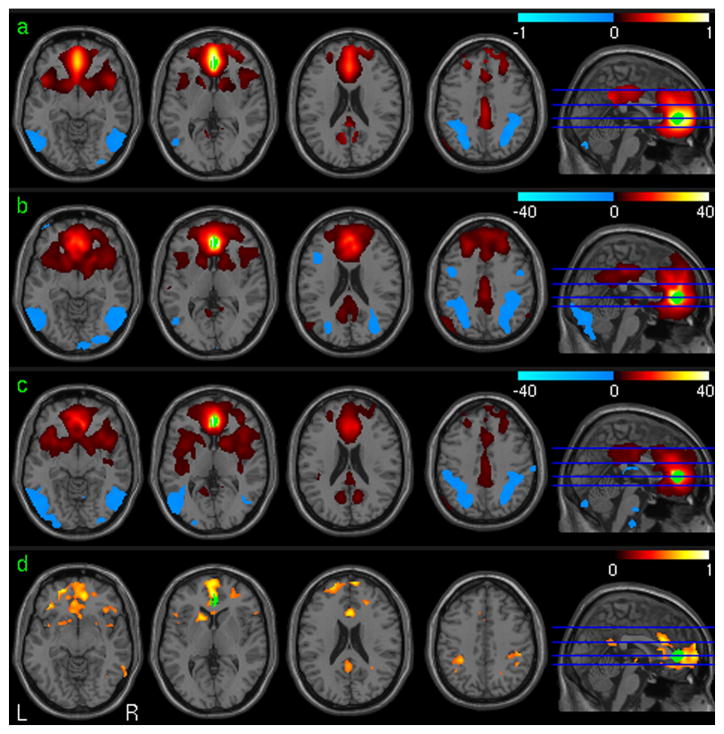
Fig. 3 shows the vACC-FC test-retest analysis results using the in-vivo resting fMRI data. Fig. 3a is the mean vACC-FC of the 1^st session of all subjects in the suprathresholded brain regions as determined by the group level one-sample t-test. Fig. 3b and 3c are the group level T maps of the first session and the second session, respectively. Significant positive vACC-FC was found in PCC, cingulate cortex, bilateral prefrontal cortex (PFC), bilateral medial frontal cortex (MFC), left parietal cortex and bilateral insula. Significant negative vACC-FC was demonstrated in visual cortex, bilateral parietal cortex, and bilateral dorsolateral prefrontal cortex (DLPFC). Fig. 3d is the ICC map of the vACC-FC of the two sessions. High vACC-FC reliability (in terms of high ICC) was found in ACC, PFC, PCC, MFC, ventral striatum, caudate, bilateral frontal cortex, and bilateral parietal cortex.

Fig. 3.

vACC-FC analysis results. a) The mean vACC FC map (32 subjects, session 1). b) and c) Group level one sample T test of vACC-FC maps (32 subjects, p<0.001 (uncorrected)) of session 1 and session 2, respectively. d) ICC of vACC-FC (32 subjects, ICC>0.5). The seed ROI is shown in green.

PCC-FC

The PCC-FC test-retest analysis results using the repeat resting fMRI data were shown in Fig. 4. Fig 4a is the mean PCC-FC map of the 1st session from all subjects in the suprathresholded brain regions determined by the group level one-sample t-test. Fig. 4b and 4c are the group level statistical parametric maps (t-maps) for the first session and the second session, respectively. Significant positive PCC-FC was demonstrated in ACC, bilateral PFC, bilateral parietal cortex, bilateral medial temporal cortex (TC), and MFC. Significant negative PCC-FC was found in bilateral insula cortex, visual cortex, superior TC, and the dorsal ACC. Fig. 4d is the ICC map of the PCC-FC. High PCC-FC reliability (in terms of high ICC) was found in PCC, superior and medial TC, bilateral PFC, parietal cortex.

Fig. 4.

PCC-FC analysis results. a) The mean PCC FC map (32 subjects, session 1). b) and c) Group level one sample T test of PCC FC maps (32 subjects, p<0.001 (uncorrected)) of session 1 and session 2, respectively. d) ICC of PCC FC (32 subjects, ICC>0.5). The seed ROI is shown in green.

ICA-based DMN

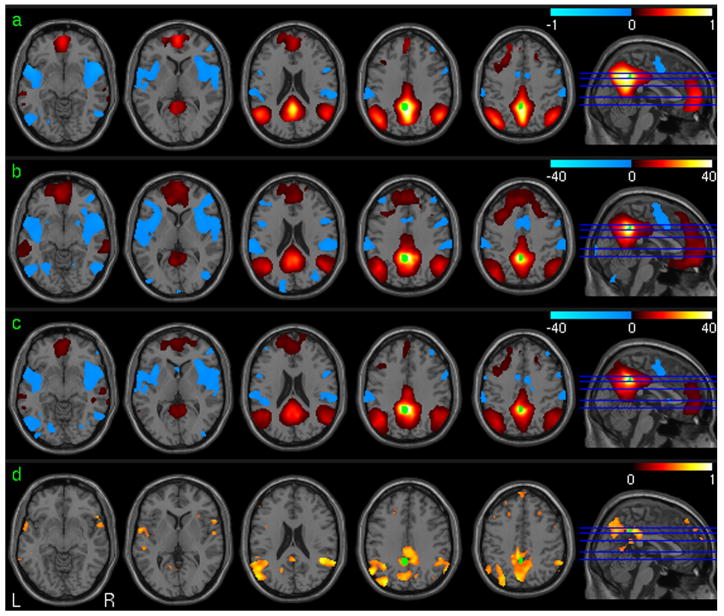
Fig. 5 shows the ICA-based DMN test-retest analysis results using the in-vivo data. Fig. 5a to 5d are the mean DMN map, group level T maps of session 1 and session 2, and the ICC map, respectively. Fig 5b was used to mask Fig. 5a so that only the suprathresholded DMN activity patterns were shown. Significant positive DMN patterns were found in ACC, bilateral PFC, bilateral MFC, bilateral TC, PCC, precuneus, bilateral parietal cortex, amygdala and hippocampus. Negative patterns were found in bilateral insula and part of bilateral parietal cortex. While the DMN patterns of session 1 and session 2 were very similar, high test-retest stability was only demonstrated in a small fraction of these suprathresholded DMN areas including part of PCC, PFC, MFC and parietal cortex (Fig 5d).

Fig. 5.

ICA-DMN analysis results. a) The mean ICA DMN map (32 subjects, session 1). b) and c) Group level one sample T test of ICA DMN maps (32 subjects, p<0.001 (uncorrected)) of session 1 and session 2, respectively. d) ICC of ICA DMN (32 subjects, ICC>0.5).

Test-retest stability of the regional data coherence of resting fMRI

Fig. 6 shows the results of using ReHo to measure the regional SBA. Only the areas having mean KCC greater than the mean KCC value derived from the noise data (the top row of Fig 1b) were displayed. Fig. 6a to 6d are the mean ReHo map of the 1^st session of all subjects, the T map of the 1^st session, T map of the 2^nd session, and the ICC map, respectively. Fig. 6b and 7c were used to spatially threshold Fig 6a. For both sessions, significant ReHo was demonstrated in almost the whole brain (Fig. 6b and 6c). Fig. 6d shows that most of the brain cortex except part of the medial frontal cortex had high ReHo test-retest stability.

Fig. 6.

ReHo analysis results. a) The mean ReHo map (32 subjects, session 1). b) and c) Group level one sample T test of ReHo maps (32 subjects, p<0.001 (uncorrected)) of session 1 and session 2, respectively. d) ICC of ReHo (32 subjects, ICC>0.5).

Fig. 7.

ALFF analysis results. a) The mean ALFF map (32 subjects, session 1). b) and c) Group level one sample T test of ALFF maps (32 subjects, p<0.001 (uncorrected)) of session 1 and session 2, respectively. d) ICC of ALFF (32 subjects, ICC>0.5).

ALFF group analysis

Fig. 7 is the result of ALFF calculation. Only the areas having mean ALFF larger than the mean ALFF value derived from the noise data (as shown in the top row of Fig 1c) were displayed. Fig. 7a to 7d are the mean ALFF map of the 1^st session of all subjects, the T map of the 1^st session, T map of the 2^nd session, and the ICC map, respectively. Fig. 7b and 7c were used to spatially threshold Fig 7a. Fig. 7a shows that most of the brain areas except white matter have greater ALFF than the mean ALFF value derived from random noise. For both sessions, significant ALFF was demonstrated in the whole grey matter (Fig. 7b and 7c). Except parts of the frontal region, high ALFF test-retest stability was shown in most of grey matter as well (Fig. 7d).

The FC maps (Fig 3a, 4a and 5a) were very similar to the group level statistical parametric maps (the 2^nd and 3^rd row of Fig. 3, 4, and 5) in terms of peak location and extension of suprathreshold clusters, while the spatial patterns of both ReHo map (Fig 6a) and ALFF map (Fig. 7a) were very different from those in the group level statistical parametric maps (Fig. 6b and Fig. 7b).

DISCUSSION

We assessed the sensitivity and test-retest stability of several resting fMRI-based SBA metrics using synthetic and in-vivo data. SRFC, ReHo, and ALFF were demonstrated to be stable to noise interference. Standard one-sample t-test was inappropriate for group level ReHo and ALFF inferences since ReHo and ALFF are theoretically greater than 0. Our simulations showed that (Fig. 1b) even if ReHo was small in general, the one-sample t-test results were significant across subjects even after multiple comparison corrections. It is then necessary to consider both the actual KCC values and the statistical parametric map which reflects the mean and the variance to give a valid inference for ReHo analysis. Some guidance can be derived from the results shown in Fig. 2 for choosing an appropriate threshold to assess ReHo in order to exclude the noise-dominated values. Especially, the approximate analytic function given in Eq. 4 can be used to determine a threshold to exclude the purely noise-contributed values when different neighborhood sizes are used during ReHo calculation. For example, the threshold for excluding the noise-dominated KCC for our in-vivo data when a neighborhood size of 27 was used should be no less than 0.03705 based on the approximate equation. The threshold could vary with different data length, but the simulation results (Fig 2b) demonstrated that the fluctuation of KCC of noise decreased quickly when the data length was larger than 150. The ICC maps of all three evaluated measures demonstrated sporadic suprathreshold (ICC>=0.5) spots but with cluster size less than 10 voxels, suggesting using a cluster size of 10 to threshold the ICC map calculated from in-vivo data. It is worth to note that, these results were based on noise data without any of the preprocessing steps that were applied to the in vivo data. But according to additional experiments where the same preprocessing steps as those applied to real fMRI data were applied to the noise data, very similar results were obtained except that the suprathreshold ICC clusters became larger than those without any preprocessing.

Using in-vivo data, both the SRFC (using vACC and PCC as the seed regions) and the ICA methods revealed RSN in DMN, similar to those reported in the literature. Although similar RSN patterns were demonstrated in both scan sessions, resting state brain activity was not stable in some of the identified RSN areas, which might be due to the physiological variations occurred during the long interval (close to 2 months) between the two repeat scans. As compared to SRFC, the ICA-based DMN maps showed test-retest stability only in a small fraction of suprathreshold group level DMN. This instability could be partly induced by the intrinsic scale ambiguity of ICA. Since the magnitude of the output components of ICA is meaningless, the components are usually normalized to be a unit vector in order to compare them across different subjects or different sessions. Even with this normalization, a direct comparison of the spatial ICA component maps might not be valid since the scale for each voxel in the map might still be different across subjects and across different sessions. To still use ICA as a tool to explore RSN, the correlation of each subject’s component maps to a RSN template (can be built up using ICA on a group wise concatenated data) might be a better way to compare the RSN maps across different subjects or different sessions.

To avoid introducing artificial local coherence, no spatial smoothing was performed before running the ReHo analysis on the in-vivo data. The averaged group level ReHo map (Fig 6a) showed higher KCC values than the KCC values calculated from the noise (Fig 1b) in the whole brain area. ReHo of in-vivo data can be enhanced by global fluctuations and movements, but both confounds were excluded in the preprocessing. Therefore, the higher KCC value in resting brain than that of random noise might be a true physiological phenomenon and is required by the brain in order to respond to any potential actions. The higher KCC values in the areas of DMN (e.g., PCC, ACC, frontal cortex, etc.) than the rest of brain (Fig 6abc) suggest that those areas are not just more active but also fluctuating more coherently during the resting state. Significant group level ReHo was demonstrated in nearly the whole brain. High ReHo test-retest stability was demonstrated in most of the grey matter except part of the middle frontal cortex. These results suggest ReHo as a stable metric for measuring resting brain activity. As a local measure based on a priori neighborhood, the stability of ReHo may be affected by the size and shape of the neighborhood. The larger the neighborhood is, the smaller the ReHo will be. Moreover, fMRI data are inherently smoothed due to the T2* decay caused point spread function broadening and the intrinsic brain activity coherence between the neighboring voxels, the selection of neighborhood size should then consider the intrinsic data smoothness as well. However, it is generally difficult to estimate this inherent smoothness even with additional point spread function measuring. The neighborhood size used in this paper was recommended by the authors of the ReHo method. Though determining an optimal neighborhood is out of the topic of this paper, we had calculated ReHo using different neighborhood sizes (7, 19, 27 voxels and spheres of 2, 4, 6mm radius) and performed test-retest analysis, and found that the neighborhood size only introduced minor interference to the test-retest stability of ReHo. Our simulation results showed that 27 voxels are enough to keep the ReHo value small if the data in the neighborhood are random noise. Additional experiments showed that the average ReHo increased from 0.037 to 0.10 after spatially smoothing the synthetic data with a kernel of 3mm, and it increased to 0.5 when the smoothing kernel was 6mm.

For SRFC and ALFF, additional simulations with spatial smoothing increased the suprathreshold cluster size of the group level SRFC and ALFF maps, but only slightly increased the suprathreshold ICC clusters, meaning that the effects of spatial smoothing on the test-retest stability of SRFC and ALFF were minor.

High ALFF values were demonstrated in the ventricles and the tissue boundaries, which is because signal in those areas is mostly composed of low frequency components (e.g., motion, noise and flow signals). Significant group level ALFF (greater than the mean ALFF value determined from noise data) was demonstrated in almost the whole grey matter and most of these areas showed high test-retest ability. Additional analysis showed that ALFF had no test-retest reliability in almost the whole brain without the normalization using the whole brain value, suggesting that the power of the low frequency component of the BOLD signal varies over the time but its ratio to the whole brain mean is consistent.

As time-series based measures, all 4 SBA metrics are sensitive to temporal confounds such as head motions and global signal fluctuations. The contribution of motion to the SBA measures should be assessed using simulated brain data with and without synthetic motions. But in reality, it is difficult to get a gold standard data without any motions, so it is still difficult to estimate the motion contribution to any in-vivo data acquired. Actually, motion correction is a standard process in fMRI. The residual effects after motion corrections should have minimal contributions to FC, ReHo, and ALFF. For ICA, motion could be isolated into an independent component which means motion is less a problem for ICA. Global signal removal has been discussed in the literature for a while. Murphy et al. (41) reported that that global signal regression introduces robust negative correlations.

In a more recent paper (29), Van Dijk et al. reviewed the use of global signal removal and concluded that typical preprocessing procedures (including global signal regression) are sufficient to reduce physiological effects of respiration and other sources of spurious noise. This is the major reason why we used global signal regression in this study. Additional data analyses showed that when global nuisances (the global signal and CSF signal) were not regressed out, FC showed significance and test-retest stability in more brain regions, which might just reflect the contributions of the global nuisances to FC. ALFF is most sensitive to global signal since without spectrum normalization, ALFF showed nearly no test-retest stability. Interestingly, ReHo showed less sensitivity to the global nuisances, meaning that the global nuisances were not affecting each voxel uniformly. We didn’t assess ICA for non-global confounds removed data because ICA is supposed to be able to separate them.

Several limitations exist in this work. First, the test-retest data were acquired with nearly 2 months (1.5 to 2 months) apart, which might introduce large variability to the SBA measures. Second, the sample size is moderate. Nevertheless, the stabilities of the tested SBA measures are consistent with those reported in the literature. Third, we didn’t record the physiological noise so we have no way to assess how much these noises would affect the reproducibility of the 4 SBA measures.

In conclusion, SRFC, ReHo, and ALFF were demonstrated to be robust to random noise interference. The neighborhood size for calculating ReHo should be larger than 20 voxels. ICC>0.5 and cluster size>11 should be used to assess ICC for ACC/PCC SRFC, ReHo and ALFF at each voxel. BOLD fMRI-based SBA can be reliably measured using ACC/PCC SRFC, ReHo and ALFF after two months.