Correlation of Volume Transfer Coefficient K^trans with Histopathologic Grades of Gliomas

Abstract

Purpose

To evaluate the roles of dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) and optimum tracer kinetic parameters in the noninvasive grading of the glial brain tumors with histopathological grades (I–IV).

Materials and Methods

Twenty eight patients with histopathologically graded gliomas were imaged. Images with five flip angles were acquired before injection of gadolinium-DTPA and were processed to calculate the T₁ value of each regions of interest (ROI). All the DCE-MRI data acquired during the injection were processed based on the MRI signal and pharmacokinetic models to establish concentration-time curves in the ROIs drawn within the tumors, counterlateral normal areas, and area of the individual artery input functions (iAIF) of each patient. A nonlinear least square fitting method was used to obtain tracer kinetic parameters. Kruskal-Wallis H-test and Mann-Whitney U-test were applied to these parameters in different histopathological grade groups for statistical differences (P<0.05).

Results

Volume transfer coefficient (K^trans) and extravascular extracellular space volume fraction (V_e) calculated by using iAIFs can be used not only to distinguish the low (i.e., I and II) from the high (i.e., III and IV) grade gliomas (P(_K^trans) <0.001 and P_Ve<0.001), but also grade II from III (P(_K^trans) =0.016 and P_Ve=0.033).

Conclusion

K^trans is the most sensitive and specific parameter in the noninvasive grading, distinguishing the high (III and IV) from the low (I and II) grade and high grade III from low grade II gliomas.

Introduction

Gliomas with a heterogeneous histological spectrum are the most common primary neoplasms of brains. In spite of technical improvements in surgery, radiation therapy, and chemotherapy, prognosis of patients with these tumors, particularly of high-grade, remains poor. An optimal treatment plan to address this aggressive disease depends on accurately determining the tumor grades (1).

Angiogenesis of the tumor plays an important role in staging of origination, progress, infiltration, and metastasis. It also exerts a remarkable influence on the biological activity and prognosis (2,3). Incomplete blood-brain barrier (BBB) tumor neovascularture results in the increment of microvascular permeability, which is a surrogate marker of the degree of malignancy of gliomas (4). The volume transfer constant of contrast agent from a plasma space to an extravascular extracellular space (EES), as defined K^trans, has been used to characterize this microvascular permeability quantitatively (5,6). Another biological significant parameter: fractional extravascular extracellular space (EES) volume (V_e) has been applied to calculate the fraction (%) of a tumor volume occupied by the EES (i.e., the leakage space for contrast agent). Therefore, in determining the histopathological grade of a glioma, evaluation of the tumor vascularity, microvascular permeability and EES could be very valuable.

Recent developments in dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) could provide information on the blood microcirculation of tumors that cannot be acquired from the conventional MR imaging (7–9). DCE-MRI uses T₁-weighted dynamic data points to track leakage information of contrast agents into the surrounding tissue over time. Based on the MRI signal and pharmacokinetic models, the data has permitted the creation of parameters such as K^trans and V_e, leading to qualitative and quantitative evaluation of the angiogenic characteristics of tumors, assessment of tumor grade, and determination of the site of biopsy (10, 11). Quantification of enhancement characteristics of DCE data could be performed using a range of techniques. These include simple measurements of the semi quantitative parameters such as rate of enhancement from the signal intensity-time curve (i.e., the maximum slope of the curve) and complex algorithmic analyses that apply pharmacokinetic models to the contrast agent concentration-time curve to determine K^trans (12–14), which is a surrogate of blood vessel integrity. The integrity in turn has been hypothesized as a marker of glioma grade (11).

Hence, we in the study examined K^trans for gliomas grades I to IV by using a T₁-weighted DCE-MRI technology and MRI and pharmacokinetic models, and also investigated the effect of different tumor grades on K_ep, K_el, V_e, and V_p, obtained from the T₁ perfusion data analyses. For complex algorithmic analyses based on the model, the accuracy of the trace kinetic parameters depends on the accuracy of artery input function (AIF). We discussed the data analysis model and a new approach for using the model by applying an individual artery input function (iAIF) extracting for each patient and the results of Kruskal-Wallis H-test and Mann-Whitney U-tests with P<0.05. The aims of this study were to present the tracer kinetic parameters of glioma and to correlate these parameters with histopathological grades to determine the optimum parameter or parameters for noninvasive differentiation of the grades of gliomas.

Materials and Methods

Patients

Twenty-eight patients (10 females, 18 males; age range, 19–74 years with mean of 47.11±14.18 years) with gliomas were included in this study, and they were part of 82 patients imaged from July 2007 to January 2008 in the Department of Radiology at Xiangya Hospital of School of Medicine, Central South University. This study was approved by the institutional review board (IRB) of the hospital and patients consented prior to the MRI scans. All MR images were acquired before biopsy or neurosurgery for the patients. The histopathologic analyses were performed on 74 patients with “gliomas” after the neurosurgeries. The results revealed that there were 14 low grade gliomas (8 grade I and 6 grade II) and 14 high grade gliomas (6 grade III and 8 grade IV), according to World Health Organization criteria.

MRI acquisition

MRI was performed on a 1.5T Siemens Syngo MR 2002B system with a standard birdcage head coil. All the patients underwent conventional T1-weighted, T2-weighted, and DCE MRI. After a T₁-weighted imaging (TR/TE=450/10ms, slice thickness=5mm, and 10 axial slices), five separate acquisitions using a 2D Turbo FLASH sequence with flip angles of 2, 5, 10, 15 and 20° were acquired to calculate the baseline T₁ value. DCE perfusion imaging dynamic series for the contrast bolus tracking was then performed by using a 3D Turbo FLASH sequence with a 20° flip angle and a 4s temporal resolution over a period of 6 minutes. The major imaging parameters were: TR/TE: 199/1.05 ms, field of view (FOV): 211 mm×260 mm, image acquisition matrix: 256×208, slice numbers: 10 and thickness: 5 mm. During the dynamic image acquiring, the axial slices covered the tumors and the arteries as AIFs were scanned repeatedly 90 times (i.e., 90 volumes). The slice orientation and locations were the same as the ones applied in the above variable flip angle scans. At the beginning of the fifth volume, a 0.1 mmol/kg bolus of Gd-DTPA contrast agent was injected intravenously at the rate of 4mL/s using a power injector. The paramagnetic contrast agent was circulated through the vasculature of the gliomas, which might leak from the damaged BBB over time into the EES where T₁ values were reduced, causing the signal intensity to be increased. The T₁-weighted DCE data recorded the changes in signals within a region of interest (ROI).

Image processing and data analysis

Quantitative analysis of DCE-MRI data requires MRI signal and pharmacokinetics models. The initial step of the quantitative analysis was the conversion of the T₁-weighted signal intensity into contrast agent concentrations based on the MRI model. The quantitative parameters were then calculated from the concentration-time curves (CTCs) based on the pharmacokinetics model.

MRI signal model

The longitudinal relaxation rate of protons in tissue is increased due to increased dipole-dipole interaction between the protons and the unpaired electrons of the contrast agent particles that leaked into EES from plasma space. The vascular leakage is characterized by the enhanced relaxation rate. As equation [1] shows, the relaxation rate enhancement effects could be described as linearly scaling with mean contrast agent concentration in tissue, or C(t), scaled by the longitudinal relaxivity constant of contrast agent r₁ (i.e. the increase in relaxation rate per unit contrast agent concentration or the contrast agent molar relaxivity rate (15)):

$$\mathrm{\Delta }{R}_1(t)=\frac{1}{T_1}-\frac{1}{T_{10}}=r_1·C(t)$$ [1]

Where T₁₀ (=1/R₁₀) is the longitudinal relaxation time before injection of a contrast agent and T₁ (=1/R₁(t)) is the time-dependent longitudinal relaxation time after the injection. In a voxel, the T₁-weighted signal intensity enhancement can be expressed approximately based on a Turbo-FLASH sequence and MR physics by the following equation (16):

$$\mathrm{\Delta }S(t)=\frac{S(t)-S(0)}{S(0)}\approx \frac{e^{-TR/T_{10}}(1-cos\alpha ){\mathit{TRr}}_{1}C(t)}{1-e^{-TR/T_{10}}\left[1+cos\alpha (1-e^{-TR/T_{10}})(1-{\mathit{TRr}}_{1}C(t))\right]}$$ [2]

The above equation was referenced as the MRI signal model. S(0) is the signal intensity before contrast agent arrival (i.e., baseline), ΔS(t) is the signal intensity enhancement normalized to the baseline, TR is the repeat time, and α is the flip angle.

Pharmacokinetic model

The first pharmacokinetic model used for DCE MRI was developed by Tofts (17), and has been one of the most popular methods in the field. In this study, the modified Tofts’ two-compartment model (15), taking into account that the concentration of contrast agent viewed in a voxel depends on the concentrations of contrast agent in both plasma space and EES, was used to measure microvascular permeability according to the equation [3]. This enabled the concentration of contrast agent in tissue to be calculated as a function of time after the contrast agent arrived in the two compartments.

$$C_t(t)=V_e·C_e(t)+V_p·C_p(t)=K^{\mathit{trans}}{\int }_0^t{C}_p(\tau )e^{-K_{ep}(t-\tau )}d\tau +V_p·C_p(t)$$ [3]

Where C_t, C_e, and C_p are contrast agent concentration in tissue, EES, and plasma respectively, V_e is fractional EES volume, V_p is fractional plasma volume, K^trans is volume transfer constant of contrast agent leaked into EES from plasma, and K_ep is rate constant of contrast agent reflux to the plasma.

C_p(t) obtained from the signal of plasma space is the AIF, which was determined from the following section: iAIF determination. One common simplification was to assume C_p(t) to be a mono-exponential ‘step-response’ function: C_p(t)=C_p(0)·exp(−t/T_1/2), where C_p(0) is the initial contrast agent concentration in the plasma and T_1/2 is the elimination half-life of the contrast agent from the plasma. C_p(0) is obtained from the fitting of measured C_p(t) curve by applying the ‘step-response’ function. Using the elimination rate (K_el) instead of T_1/2 (K_el=1/T_1/2), it could then be shown that the solution to equation [3] was given by the tri-exponential function which included a term describing the plasma fraction V_p of the tissue signal:

$$C_t(t)=\frac{K^{\mathit{trans}}·C_p(0)}{K_{el}-K_{ep}}[e^{-K_{ep}(t-t_0)}-e^{-K_{el}(t-t_0)}]+C_p(0)·V_p·e^{-(t-t_0)K_{el}}$$ [4]

There were four independent tracer kinetic parameters in the quantitative model: K^trans, K_ep, K_el, V_p. Fractional EES volume was obtained by V_e = K^trans/k_ep. All data were processed in MATLAB.

Baseline T₁ values

For each patient, data sets with flip angle of 2, 5, 10, 15, and 20° were used to calculate the baseline T₁ values in ROIs by fitting the equation [5] using the algorithm of Levenberg-Marquardt. The mean MR signal intensities of the arteries and tumors’ ROIs determined by the T₁-weighted high resolution images were applied in the equation for calculating the T1 values in the ROIs.

$$S=S_0·sin\alpha ·(\frac{1-e^{-TR/T_{10}}}{1-cos\alpha ·e^{-TR/T_{10}}})$$ [5]

Where TR is the repeat time and α is the flip angle.

iAIF determination

An iAIF was derived from the time courses of the DCE scan within the brain arteries of each patient. The iAIF was extracted based on the distinct features exhibited by the concentration time curve in vascular voxels (18–21), including early bolus arrival time (BAT), high peak height (PH), early arrival of time to peak (TTP), sharp uptake (high initial slope value) of contrast agent, and high concentration of contrast.

First two radiologists (i.e., two coauthors with a MD) determined the imaging slice containing a brain “artery” which supplied blood to the tumor of each patient. Then, 90 dynamic T₁-weighted images with the slice were loaded. The local neighborhood of the artery, utilizing 3*3 voxels as a kernel (i.e., a ROI), was used to calculate the MRI signals, which was then converted to the artery’s concentration-time curves based on the MRI model (i.e., the equations of 1 and 2) and the baseline T₁ value of the artery. A kernel larger than 3*3 voxels was not recommended because it may have involved surrounding tissue voxels. The size of 3*3 voxels was appropriate for our data since the concentration-time curve in the ROI had a good S/N and less partial volume effect for determining an iAIF.

The PH, TTP and initial slope were calculated from the curve in each ROI on the slice. Among all of the curves, the curves with the highest 10 percent initial slopes were first selected, which was for eliminating areas without a sharp mass uptake. Then, within the selected curves, curves with the highest 10 percent PH were selected. The venous voxels showed similar perfusion characteristics (i.e., very high initial slopes and PH), except for delay in TTP when compared to the arterial voxels. Finally the curve with the minimum TTP was extracted from the above filtered curves, and is the needed iAIF.

Estimation of the tracer kinetic parameters

In order to obtain the parameters, DEC images including the tumor and iAIF of each patient were loaded in MATLAB. Motion correction of DCE data and coregistration of the data on the high resolution T1 images were performed with images acquired for each patient before determining ROIs. The ROIs were drawn on the tumors and the counterlateral no affected areas with the same sizes of the corresponding tumors’ by the primary author and verified by all three co-authoring radiologists.

T₁-weighted signals in the ROIs were extracted and normalized to their baselines. The enhanced signal intensity-time curves were converted to contrast agent concentration time curves (CTCs) by applying the MRI model and baseline T₁ values in the ROIs. Trace kinetic parameters of K^trans, K_ep, K_el, V_e, and V_p were calculated when a nonlinear least-squares fitting method using the Levenberg-Marquardt algorithm was performed on the CTCs and the corresponding iAIFs based on the pharmacokinetic model shown in equation [4], in which a square of the goodness-of-fit of more than 0.5 was regarded as the fitting threshold.

Statistical analysis

All the statistical analyses were performed by using commercial software SPSS 11.0 (Chicago, Ill, USA). The mean value with standard deviation (SD) for each parameter was calculated. The relationship between these parameters and grades of gliomas were established by comparing with histopathology results. A paired- t-Test was performed to examine the relationship of the parameters between the tumor and the counterlateral normal ROIs. A Kruskal-Wallis H-test was applied to assess whether the tracer kinetic parameters varied with glioma grades. A Mann-Whitney U-test was used to compare the parameters between any two grades and between the low (i.e., I and II) and high (i.e., III and IV) grades. A value of p<0.05 was regarded as statistically significant. Receiver Operating Characteristic (ROC) Curve was used to calculate the area under curve (AUC) for determining the ideal cutoff points for distinguishing low from high grade and grade II from III. The best cutoff values were determined by considering both highest Sensitivity and Specificity.

Results

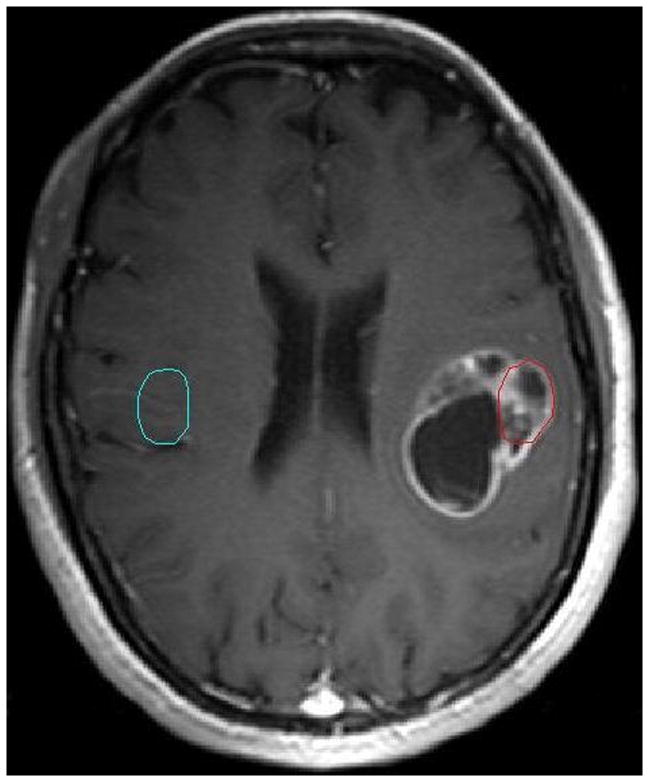
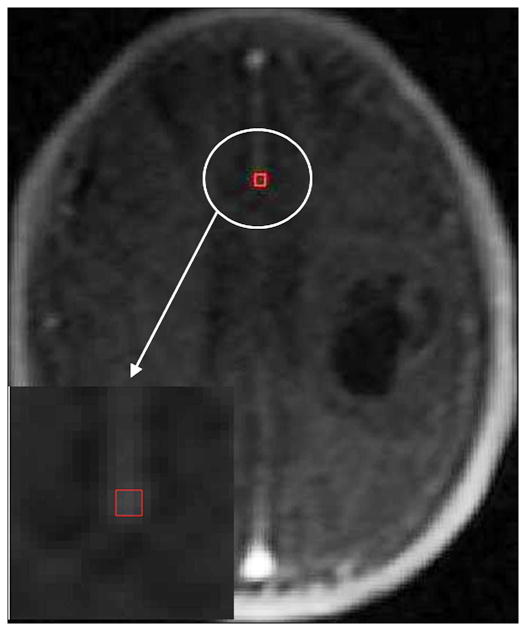
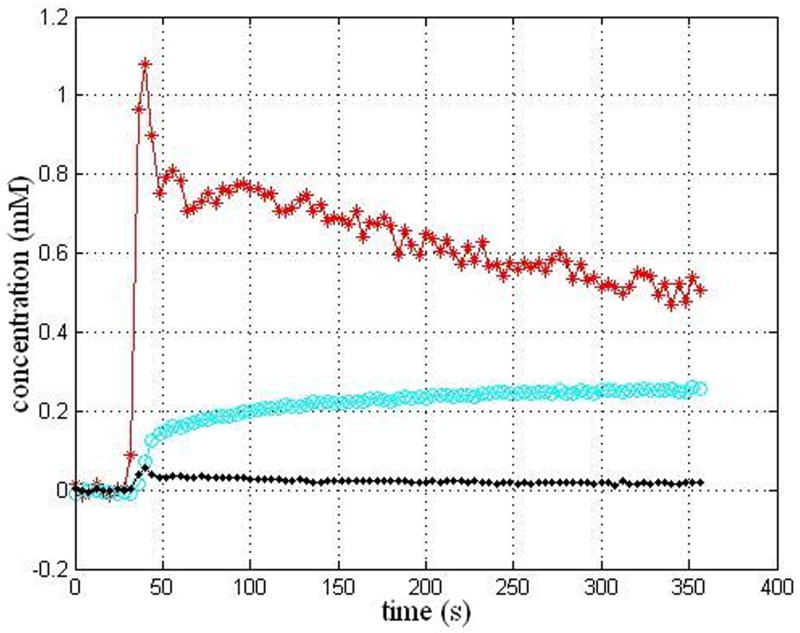
Histopathologic analysis demonstrated there were 14 low grades (8 grade I and 6 grade II) and 14 high grades (6 grade III and 8grade IV). An imaging slice with the ROIs drawn within the tumor and the counterlateral normal areas for a representative patient with a grade III is shown in Figure 1. The artery slice of the patient and the ROI drawn automatically on the arteries is shown in Figure 2. CTCs in the tumor and counterlateral normal ROIs and the iAIF are respectively plotted in Figure 3. The iAIF curve demonstrated sharper wash-in, wash-out, and high concentration characteristics than those in the CTCs.

Figure 1.

An imaging slice of a representative patient with a glioma (III) with the tumor ROI (red circle) and the counterlateral normal ROI (cyan circle).

Figure 2.

The Glioma in the Figure 1 with the iAIF ROI (red box) drawn automatically.

Figure 3.

iAIF determined automatically (red curve) and CTCs within the tumor ROI (cyan curve) and the normal ROI (black curve) for the patient in the Figure 1.

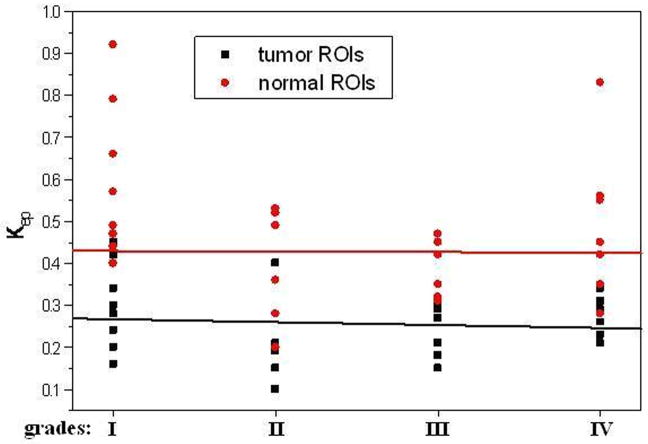
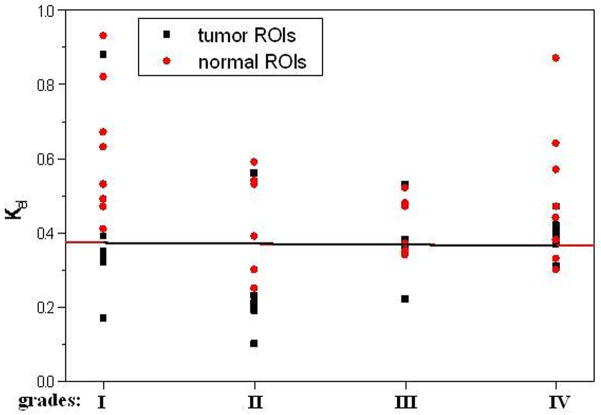
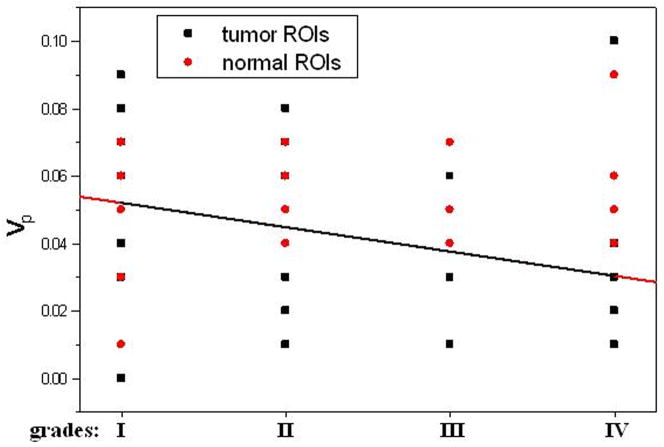
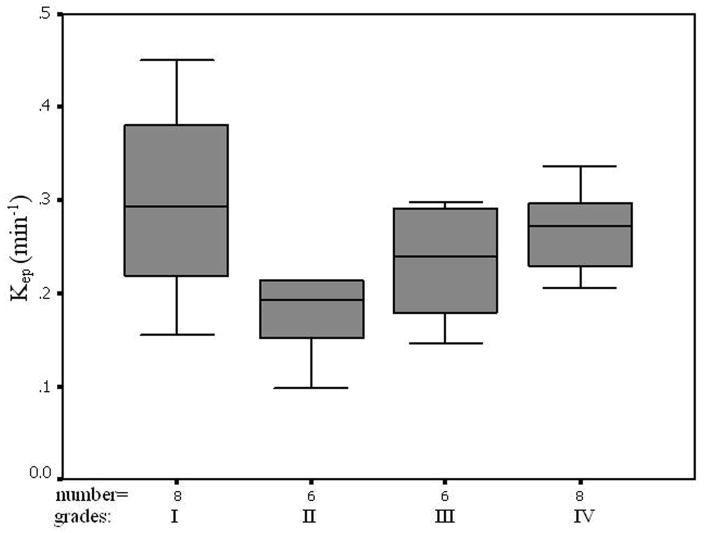
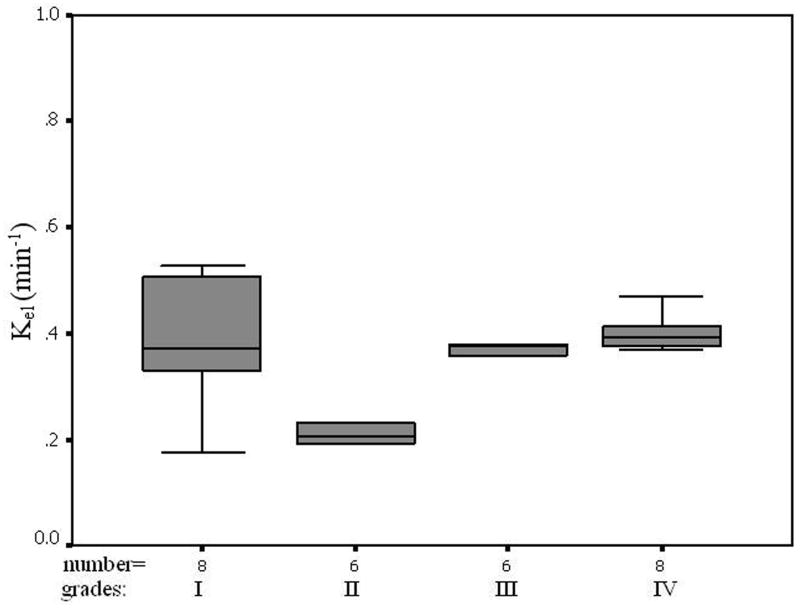
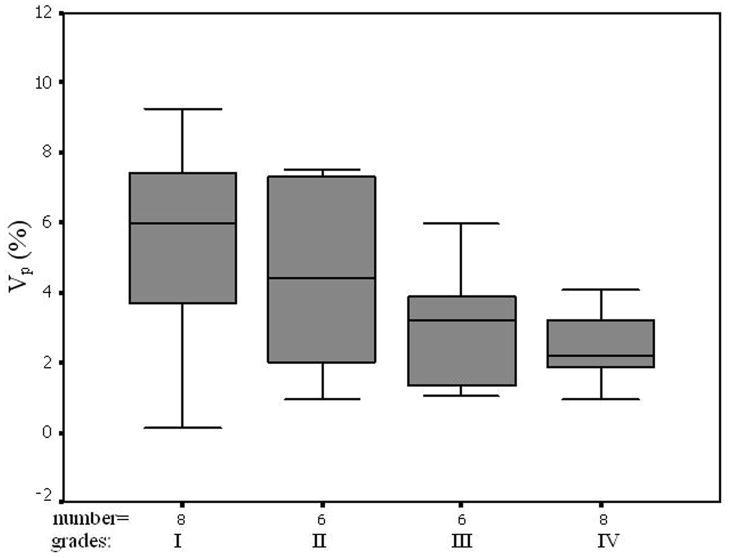
The average pre-contrast T₁ value for the arteries and tumors were 1650 ± 170ms and 1195 ± 220 ms, respectively. The means and standard deviations of K^trans, K_ep, K_el, V_e, and V_p within the tumor and the counterlateral normal ROIs in all patients with four tumor grades are calculated and summarized in Table 1. The results of paired t-test when comparing the tumor with counterlateral normal ROIs are listed in the Table 2. The P values revealed a significant difference between the tumor and the normal ROIs in K^trans, K_ep, and V_e (P <0.05). The parameters K^trans and V_e were significantly higher and K_ep was significantly lower in the tumor ROIs compared to the normal ROIs (Figure 4 and Tables of 1 and 2). K_el and V_p were not significantly different between the tumor and normal ROIs (P>0.05).

Table 1.

Summary of measurement of tumor ROIs and counterlateral normal ROIs (5 parameters) in gliomas of grade I to grade IV (mean± standard deviation)

grades	tumor ROIs					counterlateral normal ROIs
	Ktrans/min−1	Kep/min−1	Kel/min−1	Ve	Vp	Ktrans/min−1	Kep/min−1	Kel/min−1	Ve	Vp
I	0.066±0.02	0.299±0.10	0.434±0.20	0.267±0.17	0.054±0.02	0.003±0.00	0.594±0.18	0.619±0.18	0.006±0.00	0.042±0.01
II	0.093±0.03	0.209±0.10	0.249±0.15	0.426±0.16	0.044±0.02	0.005±0.00	0.398±0.13	0.433±0.13	0.014±0.01	0.056±0.01
III	0.190±0.04	0.232±0.06	0.374±0.09	0.630±0.15	0.016±0.01	0.004±0.00	0.387±0.07	0.422±0.07	0.010±0.01	0.048±0.01
IV	0.214±0.04	0.267±0.04	0.392±0.04	0.722±0.17	0.034±0.02	0.004±0.00	0.464±0.18	0.501±0.18	0.010±0.00	0.061±0.02

Note: K^trans/min⁻¹: volume transfer constant of contrast agent from a plasma space to an extravascular extracellular space;

K_ep/min⁻¹: rate constant of contrast agent reflux to plasma;

K_el/min⁻¹: elimination rate of contrast agent;

Ve: fractional extravascular extracellular space volume;

V_p: fractional plasma volume.

Table 2.

Paired-Samples t Test for the five parameters between the tumor ROIs and the counterlateral normal ROIs

grades	p value (t test)
	Ktrans/min−1	Kep/min−1	Kel/min−1	Ve	Vp
I	0.002	0.002	0.143	0.004	0.166
II	0.006	0.022	0.059	0.001	0.295
III	<0.001	0.011	0.140	0.004	0.241
IV	<0.001	0.030	0.196	<0.001	0.131

Note: K^trans/min⁻¹: volume transfer constant of contrast agent from a plasma space to an extravascular extracellular space;

K_ep/min⁻¹: rate constant of contrast agent reflux to plasma;

K_el/min⁻¹: elimination rate of contrast agent;

Ve: fractional extravascular extracellular space volume;

V_p: fractional plasma volume.

Figure 4.

Trace kinetic parameters of tumor ROIs and counterlateral normal ROIs versus respective glioma grades and the fitting curves.

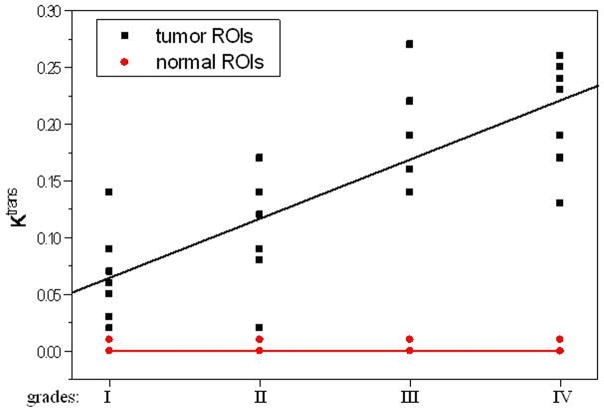
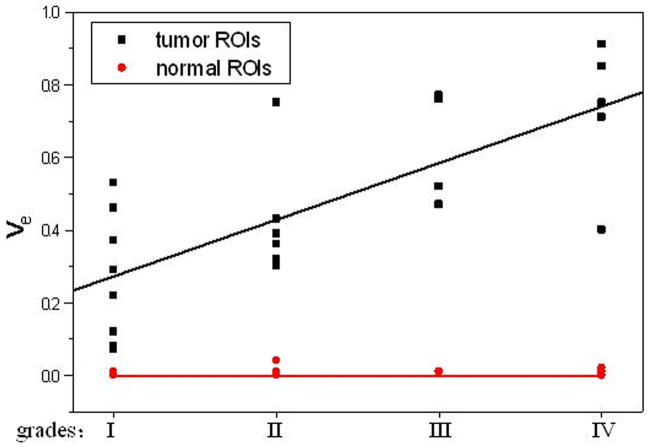
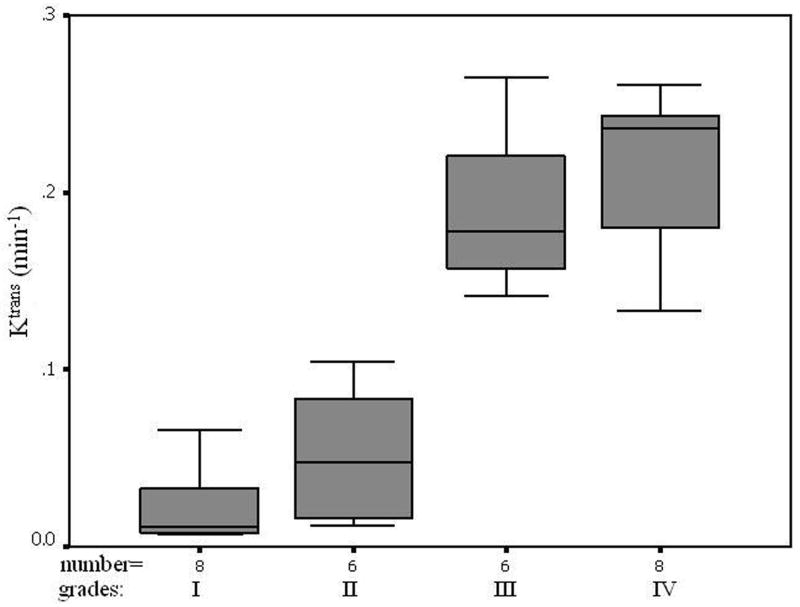
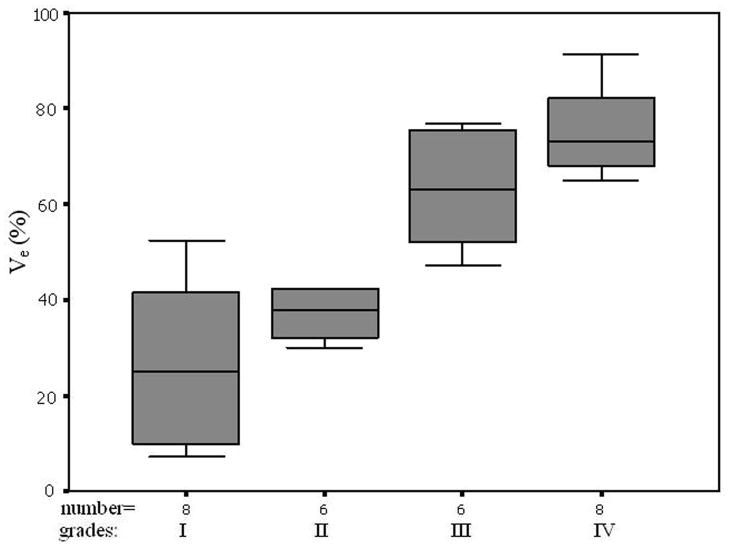
All five parameters from the normal ROIs and K_ep, K_el, and V_p from the tumor ROIs did not vary significantly when the histological grades increased (P>0.05, Table 3). K^trans and V_e from the tumor ROIs increased with an increase in tumor grades (Figures of 4 and 5), and the increases were statistically significant since Kruskal-Wallis H-tests revealed only the K^trans and V_e values have P < 0.05 (Table 3). In the tumor (I–IV) ROIs, K^trans were 0.066, 0.093, 0.190, and 0.214, and V_e were 0.267, 0.426, 0.630, and 0.722. The results from the Mann-Whitney U-tests for comparing the two parameters between any two grades or between low grades (I and II) and high grades (III and IV) are listed in Table 4. Specificity Vs Sensitivity (i.e., receiver operating characteristic (ROC)) curves for K^trans and V_e are drawn in Figure 6.

Table 3.

Kruskal-Wallis H-test deviation for five parameters of tumor ROIs and the counterlateral normal ROIs in four grades

parameters	tumor ROIs		counterlateral normal ROIs
	χ2	p	χ2	p
Ktrans/min−1	18.487	<0.001	2.509	0.474
Kep/min−1	4.921	0.178	5.645	0.130
Kel/min−1	5.384	0.146	5.645	0.130
Ve	12.986	0.005	5.044	0.169
Vp	4.940	0.176	3.864	0.277

Note: K^trans/min⁻¹: volume transfer constant of contrast agent from a plasma space to an extravascular extracellular space;

K_ep/min⁻¹: rate constant of contrast agent reflux to plasma;

K_el/min⁻¹: elimination rate of contrast agent;

V_e: fractional extravascular extracellular space volume;

V_p: fractional plasma volume.

Figure 5.

Values of Trace kinetic parameters in the tumor ROIs. Error bars indicate two standard errors.

Table 4.

Mann-Whitney U-test deviation for five parameters of tumor ROIs in four grades

grades	p value
	Ktrans/min−1	Ve
Ivs II	0.156	0.156
Ivs III	0.003	0.017
Ivs IV	0.001	0.005
IIvs III	0.016	0.033
IIvs IV	0.005	0.037
IIIvs IV	0.366	0.670
Low vs high	<0.001	0.001

Note: K^trans/min⁻¹: volume transfer constant of contrast agent from a plasma space to an extravascular extracellular space;

Ve: fractional extravascular extracellular space volume.

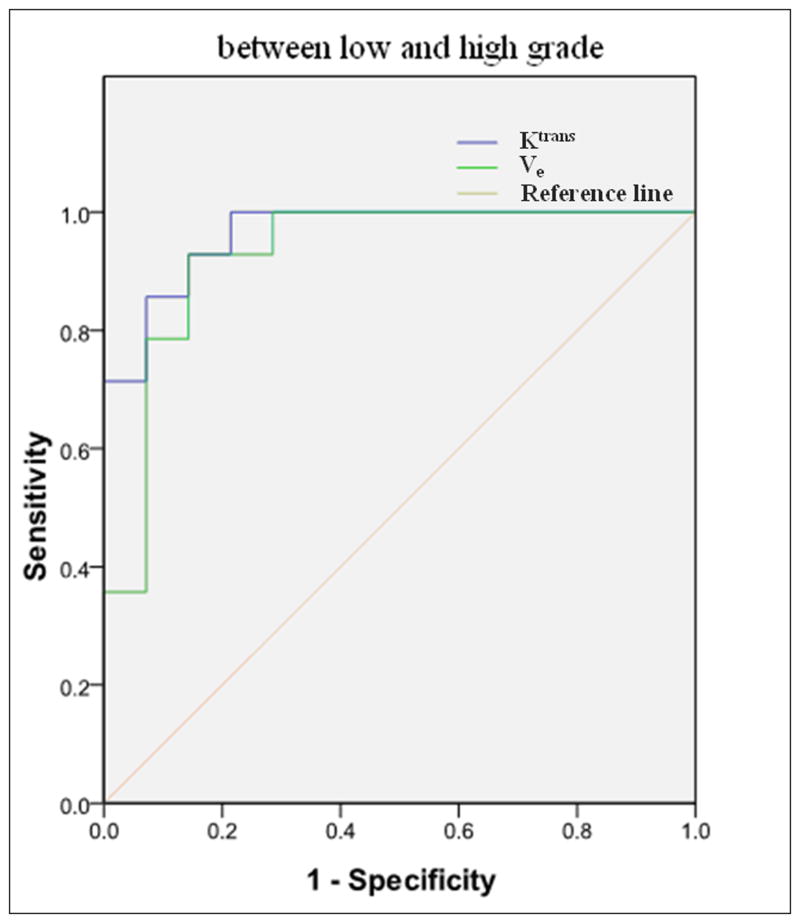
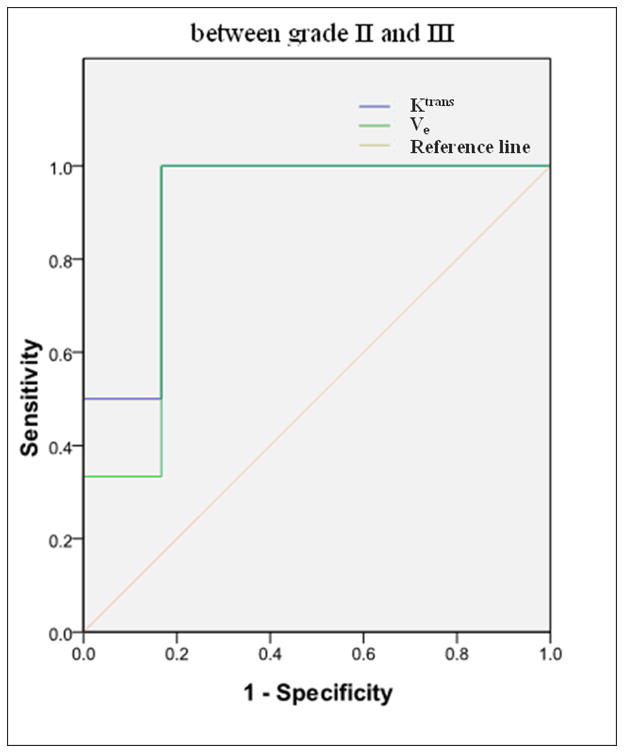
Figure 6.

ROC for discrimination between low (I and II) and high (III and IV) grade glioma (a) (AUC = 0.964 for K^trans and 0.929 for V_e) and between grade II and III (b) (AUC = 0.917 for K^trans and 0.889 for V_e) by K^transand V_e respectively.

Discussion

In the study, tracer kinetic parameters of the twenty-eight gliomas were calculated based on the MRI signal and pharmacokinetic models by using the DCE-MRI data to evaluate the optimum parameters for distinguishing tumor grade. Five flip angle data were used to determine the T₁ values in artery and tumor ROIs. A new approach using the modified Toft’s model by applying an individual artery input function (iAIF) extracting for each patient was performed. The iAIFs were obtained from the artery’s CTCs. The model with an accurately determined iAIF based on each patient (i.e., iAIF) was applied to obtained K^trans, K_ep, K_el, V_e, and V_p. These parameters were compared against the histopathology grades used to seek the optimum parameter to distinguish tumor grades.

As shown in Figure 3, the CTC of the tumor with grade III demonstrated a quick wash-in and slow wash-out pattern, revealing an immediate and persisting leakage of contrast agent into the EES due to the breakdown of the BBB in the high grade glioma. The difference in the CTCs between grade I and the counterlateral normal, which were not shown, was not obvious. It was known that angiogenesis of a tumor occurs as the tumor grade increases, and the process accelerates from the low grade (I and II) to high grade (III and IV). With the tumor angiogenesis, BBB of tumor neovasculature resulted in the increment of microvascular permeability, which led to an increment of wash-in slope of the CTC in tumor.

In this study we did not find significant difference in K_el and V_p between the tumor and the counterlateral normal ROIs. Since K_el describes elimination of contrast from the vasculature, and hence kidney functions, the results suggested no difference for kidney functions of patients with different grades of gliomas. However, the K^trans and V_e in tumor were significantly higher than those in normal brain tissue and K_ep in tumor was significantly lower than those in normal brain tissue (Table 2 and Figure 4). The results suggest an increase in fractional EES in the tumors and blood flow and microvascular permeability (i.e., leakage of the contrast agent into the EES) of the tumors. The data in Table 1 and the fittings in the Figure 4 demonstrated K_ep in tumors was almost a constant with tumor grades, and K^trans and V_e in tumors increased with the grades. Thus, K^trans and V_e may be helpful in noninvasively grading tumor.

The data in Table 3 (the comparison of multi groups) suggested that between any two grades, there were no statistical differences for all five parameters in the normal tissues and K_ep, K_el, and V_p in the tumor ROIs (p>0.05). Only K^trans and V_e in the tumor ROIs had significant differences among the grades (Table 3, p<0.005). A Mann-Whitney U-test, which is for the comparison of two groups, was then applied to determine between which two grades K^trans and V_e were distinct, and the results (Table 4) indicated they were good parameters for distinguishing any two grades except for distinguishing grades I with II and grade III with IV.

In the tumor (I–IV) ROIs the K^trans were found to be 0.066, 0.093, 0.190, and 0.214 in⁻¹, and the V_e were found to be 0.267, 0.426, 0.630, and 0.722, respectively. It was known that K^trans depended on both blood flow and the product of the capillary wall permeability and the surface area, and the parameter of V_e was the ratio of quantity of contrast agent leaked into the EES to that returned to the plasma space (i.e., the fraction (%) of a tumor volume occupied by the EES (i.e., the leakage space for contrast agent)). As shown in Figures 4 and 5, K^trans and V_e increased with the increase of the grades, indicating that the higher the malignant degree was, the higher the contrast agent leakage into EES was. Both K^trans and V_e could be applied to distinguish low (I and II) from high (III and IV) grade gliomas. This finding is in agreement with a prior study (22) which showed a high correlation between K^trans or V_e and the grades of gliomas.

Although K^trans and V_e did not discern well between gliomas of grade III and grade IV (P>0.3) nor between grade I and grade II (P>0.15), there was significant difference of K^trans and V_e between the low (I and II) and the high (III and IV) and between II and III grades (Table 4: Mann-Whitney U-test, P<0.05), which suggested that K^trans and V_e could be applied to distinguish low (I and II) from high (III and IV) grades and grade II from III. There was a remarkable difference between the low (I and II) and high (III and IV) grades (Mann-Whitney U-test, p<0.001). The results showed that analyzing the DCE data by using an AIF from each patient (i.e., iAIF)—instead of applying one common AIF for all patients (19, 20, 23–25)—may lead to more accurate K^trans values for distinguishing tumor grades.

For discrimination between the high (III and IV) and low (I and II) grade gliomas by K^trans and V_e values, the sensitivity and specificity gave two significant numbers: 0.92 and 0.85 respectively by K^trans, and 0.90 and 0.78 by V_e. The area under the ROC curves was 0.964 for K^trans and 0.929 for V_e (Figure 6). Hence, both K^trans and V_e were capable of distinguishing the high grades from the low grades. With smaller P values (Table 4), K^trans seemed to be a better parameter for evaluating the tumor grade, especially for differentiating the high grades from low grades and the grade II from grade III. AUC was 0.964 for K^trans and 0.929 for V_e in distinguish between low and high grade gliomas, and 0.917 for K^trans and 0.889 for V_e in distinguishing between grade II and III glioma, which indicated that K^trans was a better parameter to distinguish not only the low (I and II) from high (III and IV) grade gliomas, but also the grade II and III.

Magnetic resonance spectroscopy (MRS) and dynamic susceptibility contrast (DSC) MRI have also been applied to predict tumor grades. A recent study (26) concluded that the indices of Cho/Cre and Lac/Cre from MRS were good for differentiating grade II from III and III from IV, respectively, whereas the parameter of tumor blood volume from DSC-MRI was only useful for distinguishing II from IV. Compared to the indices and parameter, the results of K^trans in this and previous investigations (6, 11) suggest that K^trans is a better predictive parameter for grading gliomas. The partial volume effect due to the low spatial resolution data of MRS made the indices less sensitive and specific when distinguishing the grades. Also tumor microvascular permeability exposed by K^trans maybe better linked to the tumor grade.

There were limitations in this study. We applied a 2D Turbo FLASH sequence for obtaining the baseline T₁ value and a 3D Turbo FLASH sequence for DCE data. The internal inconsistency in the imaging sequence and alteration in its sensitivity to the tumor blood supply may lead to variations from case to case. The sample size may need to be increased for each group of tumor grade for an effectively statistical comparison including a significant threshold value to distinguish the groups. Also we are working on obtaining the maps of K^trans, K_ep, K_el, V_e, and V_p.

In conclusion, DCE-MRI is a promising technique that can provide a very important trace kinetic parameter: K^trans, which is associated with gliomas’ microvascular permeability—a surrogate for tumor grades. Besides K^trans, V_e can be helpful in grading gliomas; however, K^trans is preferable as K^trans can be utilized not only to differentiate the low (I and II) from high (III and IV) grades, but also to differentiate the grade II from III.