Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Jul 19;2:520. doi: 10.1038/srep00520

Crystal structure of graphite under room-temperature compression and decompression

Yuejian Wang 1,2,a, Joseph E Panzik 1, Boris Kiefer 3, Kanani K M Lee 1,b
PMCID: PMC3400081  PMID: 22816043

Abstract

Recently, sophisticated theoretical computational studies have proposed several new crystal structures of carbon (e.g., bct-C4, H-, M-, R-, S-, W-, and Z-carbon). However, until now, there lacked experimental evidence to verify the predicted high-pressure structures for cold-compressed elemental carbon at least up to 50 GPa. Here we present direct experimental evidence that this enigmatic high-pressure structure is currently only consistent with M-carbon, one of the proposed carbon structures. Furthermore, we show that this phase transition is extremely sluggish, which led to the observed broad x-ray diffraction peaks in previous studies and hindered the proper identification of the post-graphite phase in cold-compressed carbon.

The synthesis of diamond from graphite under high pressures and high temperatures1 has had revolutionary impacts on modern society ranging from industrial applications such as the manufacture of superhard materials, to technological advances in contemporary high-tech applications, and to scientific exploration of materials' behavior under extreme conditions2,3,4. Since then, the high-pressure behavior of graphite has been extensively studied for the purpose of understanding the mechanisms and pathways of its structural transformation as well as the discovery of new superhard materials which may be harder than diamond5,6,7,8,9,10,11,12,13,14,15,16,17. Unlike the direct transition from graphite to cubic diamond under simultaneously high pressures and high temperatures, the phase transition of cold-compressed graphite has been an enigma for over fifty years. The first indication of a post-graphite phase was based on a remarkable increase in the electrical resistance when it was compressed to pressures above ~15 GPa18,19 at room temperature. This new carbon phase was initially indexed as a cubic, non-diamond structure18 and alternatively as hexagonal diamond6,19. However, the lack of the characteristic Raman band of the post-graphite phase near the ~1332 cm−1 spectral region20 shed doubt on the validity of hexagonal diamond for this post-graphite phase. Although the occurrence of a phase transformation of graphite at ~15 GPa was further confirmed by a series of observations: a rapid drop in optical reflectivity10,21,22, the broadening of Raman spectra in the high-frequency region near 1580 cm−1 10,22 and the onset of transparency14,23, the nature of the post-graphite phase remains poorly understood, and even its crystal structure is not well-determined. Recently, theoretical computations have proposed many possible structures for the high-pressure, room-temperature graphite phase. Oganov & Glass predicted, for the first time, that this post-graphite phase has a monoclinic C2/m structure24, later dubbed M-carbon and identified as superhard25. The estimated hardness and computed bulk modulus suggest that M-carbon is comparable in strength to cubic diamond25, consistent with observations of surface damage on the diamond anvils by the post-graphite phase under high pressure5. However, several other crystal structures have also been proposed by first-principles computations. A body-centered tetragonal structure (bct-C4), together with M-carbon may better explain the x-ray diffraction (XRD) pattern of post-graphite26. Other studies have predicted that under high pressure, graphite may adopt structures such as a metallic carbon structure (K4)27, orthorhombic polymorphs (e.g., C-, H-, R-, S-, W-, Z-, Z-ACA, Z-CACB, Z4-A3B1 and A4-A2B2 carbon)28,29,30,31,32,33,34, or a carbon allotrope derived by substituting each atom in diamond with a carbon tetrahedron (T-carbon)35. The K4 structure has since been determined to be dynamically unstable36, and T-carbon is only energetically favorable for expanded volumes (rather than compressed volumes)35, thus we do not discuss these structures further. To date, there lacks definitive experimental data to verify and evaluate the computational structure predictions. Furthermore, previous experimental studies were performed at pressures below 30 GPa with a focus on the compressional behavior of the low-pressure H-graphite phase6,8,10,14. Additionally, the evolution of optical properties23 as well as electrical resistance of graphite37 at constant loading has been reported to be sluggish. In this study, we investigate the behavior of highly-ordered pyrolitic graphite (HOPG) up to ~50 GPa at room temperature using a variety of techniques including in-situ synchrotron XRD, optical microscopy and Raman spectroscopy in a diamond-anvil cell (DAC) and scanning electron microscopy (SEM) on quenched samples. XRD patterns were collected during compression and decompression as well as with long relaxation times (6+ hours) between pressure changes near the phase transition to explore the kinetics of the graphite phase transformation at high pressures and room temperature.

Results

High-Pressure Diamond-Anvil Cell Experiments X-ray Diffraction

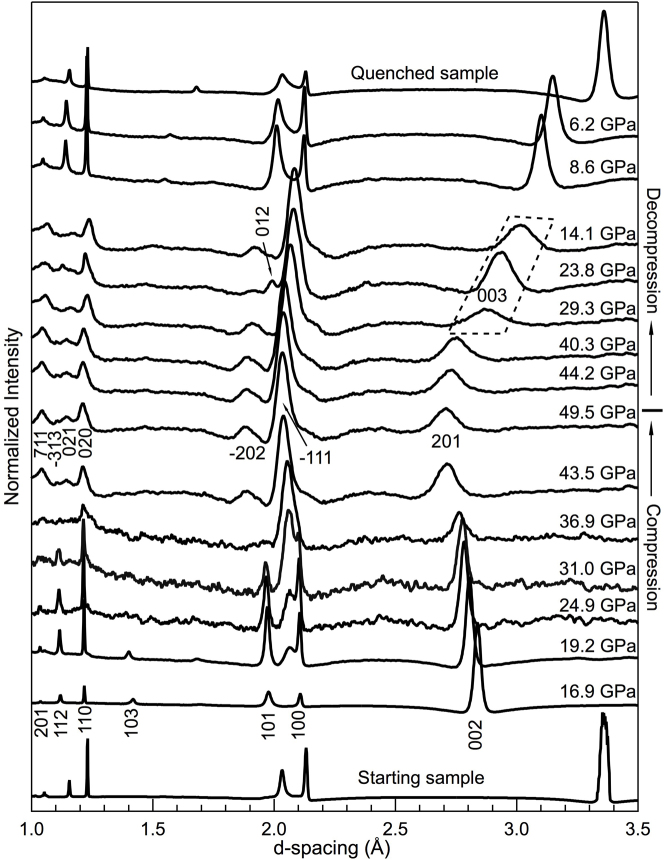
The compression behavior of graphite was investigated by synchrotron XRD (Fig. 1). At pressures up to ~19 GPa, the (002) peak of H-graphite shifts more rapidly toward smaller d-spacing than the other H-graphite peaks, confirming that the compressibility of H-graphite is highly anisotropic with the c-axis much more compressible than the a-axis8,10 (Fig. 2a, Table 1). At a pressure of ~19.2 GPa, a new diffraction line between the (100) and (101) peaks of H-graphite appeared after 100+ hours at this loading (Fig. 1), and its intensity increased with experiment duration and applied pressure.

Figure 1. Synchrotron XRD patterns of H-graphite and its successive phases under cold compression.

Figure 1

Open in a new tab

The bottom portion of the figure shows XRD patterns obtained on compression, whereas the upper portion contains XRD patterns acquired on decompression. The hkl indices for H-graphite, M-carbon and R-graphite are marked on the patterns acquired at 16.9, 49.5, 29.3, and 23.8 GPa, respectively. Among them, peaks (003) and (012) belong to R-graphite. At 19.2 GPa, the first evidence of M-carbon, the (−111) peak (the most intense peak predicted), appears between the (100) and (101) peaks of H-graphite. On compression and below 36.9 GPa, all of the XRD patterns are collected after at least 6–9 hours relaxation. Above 36.9 GPa and on decompression, we collect XRD data immediately upon pressure change.

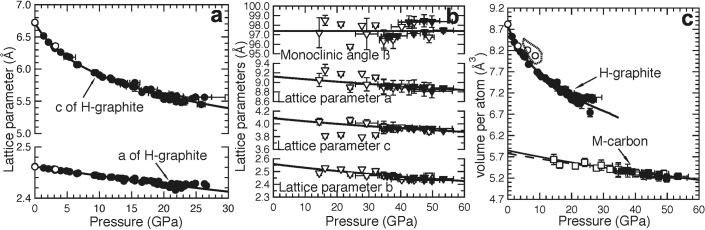
Figure 2. Unit-cell volume as well as lattice parameters as function of pressure for H-graphite and M-carbon, respectively.

Figure 2

Open in a new tab

(a) Lattice parameters a and c of H-graphite versus pressure. As the lattice parameters of H-graphite have very different compressibilities, we also fit lattice parameters a and c to a Birch-Murnaghan-like formulism. (b) Lattice parameters a, b, c, and monoclinic angle β of M-carbon versus pressure. (c) Measured unit-cell volume versus pressure for H-graphite (circles), and M-carbon (squares) with corresponding Birch-Murnaghan EOSs. The solid lines represent the Birch-Murnaghan EOS fits (Table 1). The dashed line represents the predicted results by Li et al.25. The two data points at 8.6 and 6.2 GPa lay slightly off the P-V curves of H-graphite suggest that at these pressures R-graphite may coexist with H-graphite. Data collected on compression (filled symbols) and decompression (open symbols) are shown.

Table 1. The lattice parameters and volume per atom in H-graphite and M-carbon, as well as the corresponding Birch-Murnaghan EOS parameters, assuming K0x' = 4. Uncertainties are given in parentheses. V0 represents the volume occupied by each atom. Note that for H-graphite, K0a ≫ K0c, indicative of the highly anisotropic nature of graphite. For M-carbon, the monoclinic angle β is measured and fluctuates with pressure (Fig. 2), thus we assume an average value of 97.38° (0.79°). The Birch-Murnaghan-like EOS fit for the lattice parameters is for data collected on compression, whereas all of the volume data is used to fit the complete Birch-Murnaghan EOS. Where values are not available or given, NA is noted.

  a0 (Å) K0a (GPa) b0 (Å) K0b (GPa) c0 (Å) K0c (GPa) β (deg) V0a (Å3) V0b (Å3) K0b (GPa) Ref
H-graphite 2.462 (0.001) 442 (6)     6.721 (0.002) 12.0 (0.1)     8.817 (0.011) 57.3 (0.8) Present work
  2.461 (NA) 516 (41)     6.708 (NA) 14.9 (0.5)     8.797 (NA) 67.4 (3.8) 9
  2.459 (0.004) 481 (32)     6.706 (0.003) 11.9 (0.1)     8.78 (0.01) 51.2 (1.4) 10
M-carbon 9.123 (0.001) 527 (2) 2.559 (0.001) 271 (1) 4.088 (0.001) 267 (1) 97.38 (0.79) 5.91 (0.05) 5.84 (0.05) 365 (38) Present work
  9.089 (NA) NA 2.496 (NA) NA 4.104 (NA) NA 96.96 (NA)   5.78 (NA) 431.2 (NA) 25
Open in a new tab

aV0 as calculated by zero pressure lattice parameters determined by linear Birch-Murnaghan-like fit.

bV0 and K0 as determined by Birch-Murnaghan EOS fit.

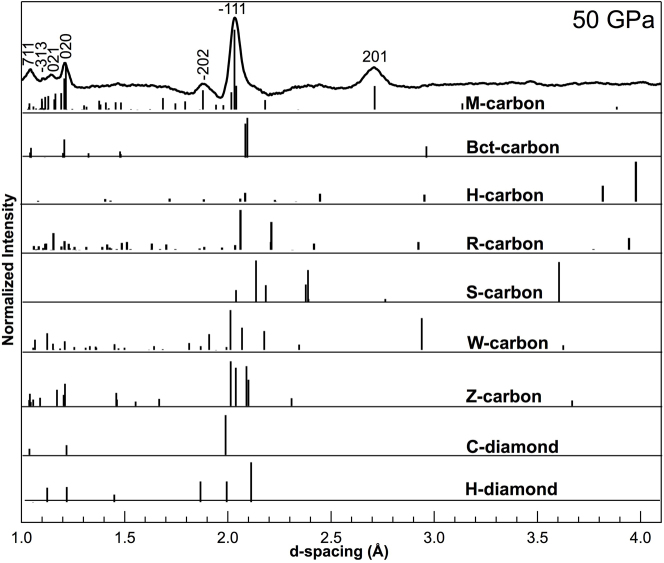
The observed phase transition pressure is higher than previously reported, 11–18.4 GPa, which may be attributed either to the differences of the starting materials5,6,8,10,20,23 used in the experiments or to the level of hydrostaticity in the sample chamber5. At a pressure of ~37 GPa, H-graphite has completely transformed into the post-graphite phase, which can be indexed as M-carbon25. However, because of the low scattering power (low-Z) of carbon and preferred orientation developed under high pressure, many of the theoretically predicted M-carbon peaks are not observed in the XRD patterns. The predicted peak positions of diamond, hexagonal diamond6,19, bct-C426, H-33, R-31, S-33, W-32, Z-30, Z-ACA34,Z-CACB34, Z4-A3B134 and A4-A2B234 carbon structures were also tested against the XRD measurements, however the predicted x-ray peaks for the monoclinic M-carbon structure fit all observed peaks whereas the other structures do not, primarily the high d-spacing peak at ~2.7 Å is lacking in all other structures (Fig. 3).

Figure 3.

Figure 3

Open in a new tab

XRD pattern at ~50 GPa and corresponding predicted XRD peaks for M-carbon (hkl's used to determine volume are labeled), bct-C4, H-carbon, R-carbon, S-carbon, W-carbon, Z-carbon, cubic diamond (C-diamond) and hexagonal diamond (H-diamond) are shown as vertical lines.

The XRD peaks are observed to broaden with increasing pressures above 19.2 GPa (Fig. 1), consistent with peak broadening observed in a previous study that used helium as a pressure medium5. The broad diffraction peaks indicate that the M-carbon phase has a small grain size (~100 nm), as evidenced by SEM images and Raman spectroscopy taken on quench (Fig. 4). Additionally, the minimal XRD peak shift over a pressure range of 19.2–49.8 GPa suggests that M-carbon is highly incompressible (Figs. 1 and 2b). Because H-graphite is soft, at least along the c-axis, the measured pressure uncertainties before the phase transition are small, <0.2%. In contrast, at pressures above the phase transition (P ≥ 19.2 GPa), the pressure uncertainties monotonically increase suggesting that large stress gradients develop across the sample chamber after the onset of the phase transformation corroborating the highly incompressible nature for M-carbon. Even with peak broadening, the XRD peaks in the present study are better resolved, without the use of a pressure medium, and provide good constraints for the crystal structure of the post-graphite phase. The better-resolved XRD peaks can be attributed to significantly longer relaxation times in the present study while the remaining large width of the XRD peaks can be ascribed to the small grain size and non-hydrostatic stress conditions across the sample.

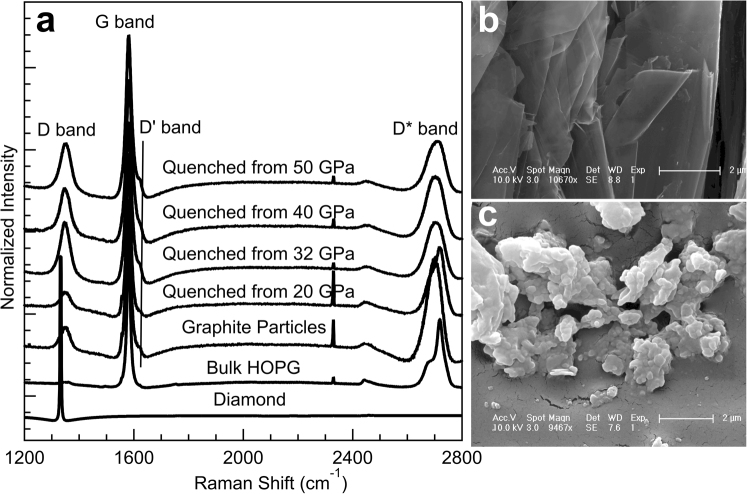
Figure 4. Raman spectra and SEM images of the recovered samples and starting HOPG at ambient conditions.

Figure 4

Open in a new tab

(a) Raman spectra of graphite samples quenched from various high pressures. For comparison, Raman spectra of diamond, bulk HOPG starting material, and powdered graphite are also shown. The D, G, D' and D* bands are labeled. (b) SEM image of bulk HOPG starting material. (c) SEM image of sample recovered from cold-compression to 50 GPa. The scale bars represent 2 μm.

On decompression, beginning at ~29.3 GPa (Fig. 1), the diffraction line near ~3 Å becomes significantly more broad and also shows an abrupt shift to higher d-spacing, indicating that carbon experiences another phase change. The rapid peak shift excludes the possibility that the new phase is cubic diamond or hexagonal diamond or any other highly-incompressible form of carbon. Among all of the known carbon phases, only hexagonal and rhombohedral graphite (R-graphite) exhibit the anisotropic compressibility along different crystallographic axes8. Additionally, the measured d-spacing values at 29.3 GPa are larger than those at 16.9 GPa during compression, ruling out the possibility that the decompression phase is H-graphite. The only known carbon phase with this characteristic is R-graphite. This is also consistent with a previous study that also observed R-graphite on decompression8. Here, M-carbon coexists with R-graphite as evidenced by two R-graphite peaks: (003) as shown by the dashed outline in Fig. 1 and (012) at a pressure of 23.8 GPa in addition to the M-carbon peaks. On further decompression, the sample reverts completely back to H-graphite.

Raman Spectroscopy

The XRD results are consistent with Raman spectra taken of graphite collected under compression (Fig. 5). From the spectra, we can clearly see that starting at ~20 GPa, the G band of graphite broadens with pressure. At higher pressures, the peak widens and its intensity decreases. As Raman spectra reflect bonding rather than the atom arrangement in lattice planes as measured by x-rays, the change in Raman bands also suggests that at ~20 GPa, graphite transforms into a new phase, consistent with our XRD measurements. However, in the present study we are unfortunately unable to verify sp3 bond formation because of the strong overlapping D band of the diamond anvil. Previous synchrotron x-ray inelastic scattering measurements have suggested that graphite at these high-pressure conditions changes from π-bonds to σ-bonds5 which is not inconsistent with our measurements.

Figure 5.

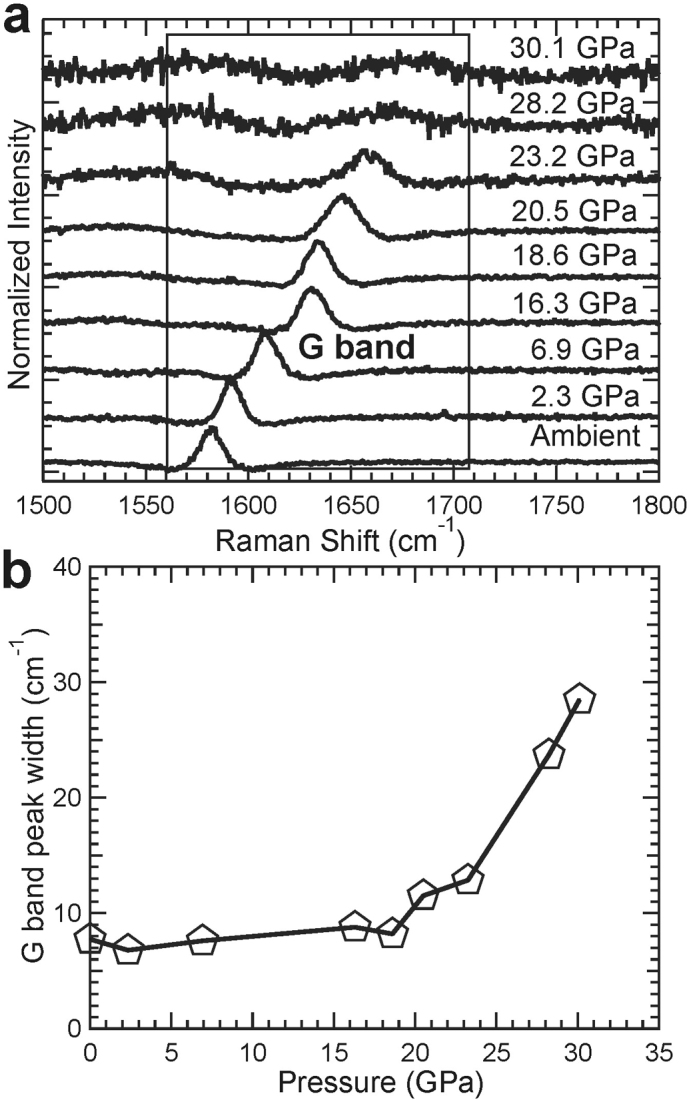
Figure 5

Open in a new tab

(a) Raman spectra of HOPG collected under room temperature and high pressure up to 30 GPa.The G peak from the HOPG sample is labeled and boxed. (b) Full-width at half-maximum (FWHM) of the G peak of HOPG under compression. At pressures above ~20 GPa, the FWHM increases, showing the disappearance of H-graphite and appearance of the new high-pressure phase.

Quenched Measurements

As compared to the bulk HOPG starting material, the wide peak shape of the pressure-quenched H-graphite suggests that the microstructure of H-graphite in the quenched samples is distinct from the starting material, as illustrated at the top of Fig. 1. We also collected Raman spectra on samples quenched from different pressures and on starting HOPG, powdered graphite, as well as diamond at ambient conditions (Fig. 4a). Like H-graphite particles, the Raman spectra of recovered samples show D, G, D', and D* bands at 1348, 1581, 1623, and 2699 cm−1, respectively38. A weak D-band signal is also detected in the bulk HOPG starting material. The recovered sample is not cubic diamond as its D band deviates from the characteristic Raman mode for sp3-bonded diamond, centered at 1332 cm−1. The intense and broad Raman D bands for the recovered samples are consistent with the observations reported for sub-micron sized graphite38,39. The intensity ratio between D and G bands in Raman spectra can be correlated with the grain size of graphite40. At the onset of the phase transition to M-carbon, ~19.2 GPa, the intensity of the D band starts increasing relative to that of the starting HOPG material, suggesting that the well-aligned layered structure of HOPG begins to disorder and fragment into smaller crystallites. After higher-pressure treatments (32–50 GPa), the similar intensities of normalized D bands in the recovered samples suggest that the grain size of quenched samples may be determined by that of M-carbon if the sample is quenched from pressures where the phase transition is complete. Furthermore, the microstructure of the HOPG starting material and recovered samples were investigated by SEM, as shown in Figs. 4b and 4c. To facilitate morphologic observations of the HOPG starting material, we gently cut the surface parallel to the c axis to expose the inner structure. Bulk HOPG shows a well-aligned, layered structure with micron-sized grains (≫1 μm). In contrast, the recovered sample is nanocrystalline with grain sizes of 100-200 nm, consistent with the observed broad XRD peaks, Raman spectroscopic measurements on quenched samples, and TEM.

Kinetics of the Phase Transition

In the present study, we explore the sluggishness of the phase transition from H-graphite to M-carbon at selected pressures using synchrotron XRD, Raman spectroscopy, and optical microscopy. As revealed in Fig. 6a, the photomicrographs taken immediately after reaching 6.9 and 19.8 GPa show no visual difference. At 19.8 GPa, a few dark spots appeared after a relaxation time of 1 hour and their abundance increased with longer relaxation times (Fig. 6c–e). After a relaxation time of 93 hours, the sample surface appears dark. This drop in optical reflectivity marks the onset of the phase transition which is consistent with previous observations and suggests that the high-pressure phase is less conductive than graphite, likely insulating21,22. Subsequently, at constant loading (with a pressure drop from the initial 19.8 to 19.2 GPa due to relaxation) we collected XRD patterns (Fig. 1) to corroborate the presence of the new phase. The measured pressure decrease during relaxation is consistent with a smaller unit-cell volume of M-carbon as compared to H-graphite (Fig. 2c). We monitored the phase transition by XRD at pressures of 24.9 and 26.3 GPa with relaxation times of 9 and 6.3 hours, respectively. In both cases, the intensity of (−111) peak, the most intense line of M-carbon, increases with time, indicating that the volumetric abundance of M-carbon relative to H-graphite increases (Fig. 6f). Our further synchrotron XRD study suggests that M-carbon is stable under high pressure (~50 GPa) and does not transform into another phase even over the course of nearly one year.

Figure 6. Photomicrographs (reflected light) and XRD patterns show the evolution of compressed sample as a function of relaxation time.

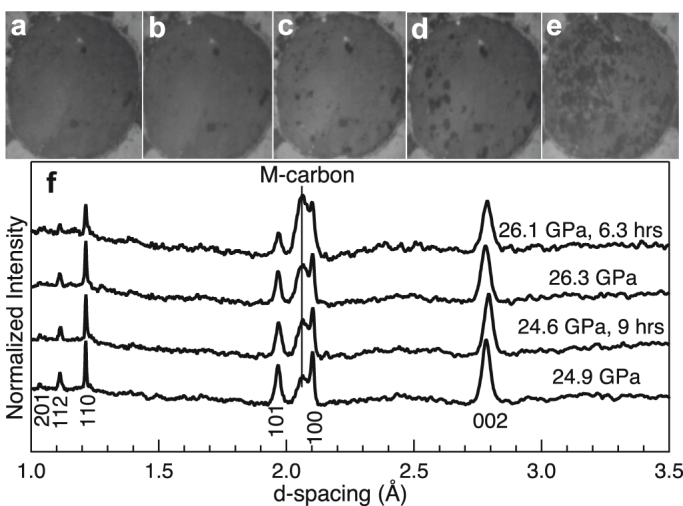
Figure 6

Open in a new tab

Images taken at pressures of (a) 6.9 and (b) 19.8 GPa, respectively, in which the dark spots come from ruby chips. Images obtained at a nominal pressure of 19.8 GPa after relaxation times of (c) 1, (d) 51, and (e) 93 hours, respectively. (f) XRD patterns immediately obtained at pressures of 24.9 and 26.3 GPa and after 9 and 6.3 hours of relaxation time, respectively.

Equations of State

The equations of state of M-carbon and H-graphite are determined by fitting the pressure-volume data sets to a second-order Birch-Murnaghan EOS41,42, as shown in Fig. 2c. The obtained bulk moduli for M-carbon and H-graphite are in good agreement with previous experimental and computational results8,9,10,25,43 (Table 1). We find the bulk modulus of M-carbon to be 365±38 GPa, thus is one of the stiffest materials known comparable to that of cubic-BN (387±4 GPa)44 and wurtzitic BN (375±9 GPa)45. The compressibility along each lattice axis of H-graphite and M-carbon are calculated by a Birch-Murnaghan-like formulism fitting, as shown in the Figs. 2a & 2b and Table 1. The highly anisotropic compressibility within atomic layers and between layers in H-graphite are consistent with previously reported values9,10. M-carbon also shows anisotropic compressibilities along lattice axes: the a axis is stiffest and the b and c axes are roughly equivalent (Table 1).

Mechanical Strength

Upon releasing pressure to ambient conditions, we observed cracks on the culets of the diamond anvils, which follow the sample boundary in the gasket hole (Fig. 7) similar to anvil damage observed previously5. This observation suggests the presence of a carbon phase with similar mechanical properties to diamond and a similar sp3 carbon bond topology, consistent with most of the predicted high-pressure carbon phases. However, the XRD data (Fig. 3) supports M-carbon as this phase and the damage to the diamond culets provides additional evidence that the mechanical strength of M-carbon rivals that of diamond as estimated previously25. The severity of the anvil's damage depends on the highest pressure achieved during compression. At 32 GPa, only a microcrack emerged on the anvil's surface following the sample's boundary (Fig. 7b). However, at 50 GPa, M-carbon fractured the diamond anvils following the sample's boundary, deforming and indenting the central portion of diamond such that the exertion of highly-concentrated stress on the gasket-diamond contact area lead to severe damage on the outer portion of the culet (Fig. 7c). This is consistent with previous observations of culet damage due to room-temperature compression of graphite5.

Figure 7. Photomicrographs showing the damaged diamond anvils after high-pressure experiments.

Figure 7

Open in a new tab

(a) Photomicrograph of graphite loaded in a DAC at ambient pressure. (b) Minor scratch on the anvil surface by M-carbon after reaching a maximum pressure of 32 GPa. The photo was taken after the experiment with reflected light. (c) Severely damaged anvil surface by M-carbon after reaching a maximum pressure of 50 GPa. The photo was taken after the experiment with transmitted light. All culets are 300 μm in diameter.

Discussion

We have studied the phase transition of graphite under compression and decompression at room temperature. Under compression, graphite transforms directly, albeit sluggishly, into M-carbon accompanied by a decrease in grain size, which is induced by disordering and buckling of the graphite layers as well as the formation of σ-bonds and the removal of π-bonds5. On decompression, M-carbon first partially transforms into R-graphite and eventually back into H-graphite. The high bulk modulus, measured in the present study and predicted by previous ab-initio computations, along with the experimental evidence that M-carbon has the ability to indent diamond anvils, indicates that this new carbon phase has mechanical properties similar to diamond. Furthermore, our observations of the phase transformation kinetics are in good agreement with optical23 and electrical resistance measurements37. Additionally, the kinetics of the cold-compressed transition of graphite to M-carbon has been recently found to be energetically more favorable than the same transition of graphite to either bct-C4 or W-carbon structures or any other sp3 forms of carbon46, consistent with our observations of M-carbon formation. Our results provide strong evidence that only the M-carbon structure is consistent with the observed x-ray diffraction patterns.

Methods

High-Pressure Diamond-Anvil Cell Experiments

In the current investigation, a sample of “calibration SPI-1 grade” HOPG commercially obtained from SPI Supplies was used as the starting material in our DAC experiments. A rhenium foil was used as the gasket material and was pre-indented to a thickness of 35 μm with a 120 μm hole drilled in the center for the sample chamber. The polycrystalline sample was carefully cleaved from the HOPG sheet and loaded into the gasket hole. We also placed a few ruby spheres into the gasket hole for pressure determination. A mixture of methanol, ethanol and water (MEW, 16:3:1 volume ratio) served as a pressure-transmitting medium in some of the experiments. When used, MEW provided a quasi-hydrostatic sample environment at least before MEW becomes a glass at a pressure of ~11 GPa47. Even so, graphite is soft, at least initially along the c-axis (the axis of compression)9,10 so that it acts as its own pressure medium. In either type of loading, the XRD patterns were not contaminated with the diffraction from typical pressure media used in DAC experiments (e.g., Ar, Ne or NaCl), which would have led to overlap of XRD peaks and further difficulty in observing the already weak peaks from carbon. Within our experimental uncertainties, the volumes obtained with and without the MEW pressure medium are indistinguishable. Additionally, the XRD peak widths at the highest pressures, although broad, are no broader than XRD peaks collected on high-pressure graphite using helium as a pressure medium5, suggesting that peak broadness is not only due to non-hydrostaticity but also due to grain size and relaxation times. The high-pressure synchrotron XRD experiments were performed at sectors 16-IDB, 16-BMD and 13-BMD of Advanced Photon Source (APS) at the Argonne National Laboratory as well as at CALIPSO of Advanced Light Source (ALS) at the Lawrence Berkeley National Laboratory. The incident monochromatic x-ray beams (λ = 0.414671 Å at 16-IDB, 0.413280 Å at 16-BMD and CALIPSO, 0.3344 Å at 13-BMD) were focused down to 5−10 μm in diameter, and the XRD patterns were collected on a MAR345 image plate and integrated with the software package FIT2D48. Raman spectra were obtained by using a Horiba Jobin Yvon Labram HR800 equipped with a 532 nm laser and 1800 g/mm grating.

Birch-Murnaghan Equation of State

The Birch-Murnaghan equation of state (EOS) was used to determine the bulk moduli of the observed carbon phases during compression and decompression. The third-order Birch-Murnaghan EOS41,42 is given by:

graphic file with name srep00520-m1.jpg

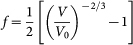where Inline graphic.

V0 and V are the unit-cell volumes at ambient and high-pressure conditions, respectively, and K0 and K0' are ambient isothermal bulk modulus and its pressure derivative, respectively. We also fit the lattice parameters to a Birch-Murnaghan-like formulism by replacing V and V0 with a3 and a03, b3 and b03, and c3 and c03 respectively, yielding each a linear modulus K0a, K0b and K0c, with corresponding pressure derivatives K0a', K0b' and K0c' 49.

Author Contributions

YW, BK and KKML wrote the main manuscript text. YW and JEP conducted the experiments. YW, JEP and KKML analyzed the data. All authors reviewed the manuscript.

Acknowledgments

Portions of this work were financially supported by the Carnegie/DOE Alliance Center (CDAC). Parts of the experiments were performed at HPCAT and GESCARS, Advanced Photon Source (APS), Argonne National Laboratory; and at CALIPSO, Advanced Light Source (ALS), Lawrence Berkeley National Laboratory. HPCAT is supported by DOE-BES, DOE-NNSA, NSF, and the W.M. Keck Foundation. APS and ALS are supported by DOE. We are grateful to, in particular, Yue Meng, Simon Clark, Jinyuan Yan, Changyong Park, Dmitry Popov and Przemyslaw Dera. We thank Jeffrey M. Montgomery, Maik Lang, Xiaohui Yu, Jinlong Zhu, Fuxiang Zhang, Jiaming Zhang, Jianzhong Zhang and Lowell Miyagi for helpful discussion.

References

  1. Bovenkerk H. P., Bundy F. P., Hall H. T., Strong H. M. & Wentorf R. H. Preparation of Diamond. Nature 184, 1094–1098 (1959). [Google Scholar]
  2. Hall D. R., Russell M. E. & Hall H. T. J. Composite polycrystalline diamond cmpact. USA patent 4604106 (1986).
  3. Irifune T., Ohnishi T., Shinmei T., Ohfuji H. & Sumiya H. in International Workshop on Synchrotron High-Pressure Mineral Physics and Materials Science. [Google Scholar]
  4. Lai A. J. D. Diamond compact abrasive. USA patent 3141746 (1964).
  5. Mao W. L. et al. Bonding Changes in Compressed Superhard Graphite. Science 302, 425–427 (2003). [DOI] [PubMed] [Google Scholar]
  6. Yagi T., Utsumi W., Yamakata M., Kikegawa T. & Shimomura O. High-pressure in situ x-ray-diffraction study of the phase transfromation from graphite to hexagonal diamond at room temperature. Phys. Rev. B 46, 6031–6039 (1992). [DOI] [PubMed] [Google Scholar]
  7. Kim Y. & Na K. High pressure X-ray diffraction study on a graphite using Synchrotron Radiation. J. Petrol. Soc. Korea 3, 34–40 (1994). [Google Scholar]
  8. Zhao Y. X. & Spain I. L. X-ray diffraction data for graphite to 20 GPa. Phys. Rev. B 40, 993–997 (1989). [DOI] [PubMed] [Google Scholar]
  9. Lynch R. W. & Drickamer H. G. Effect of high pressure on the lattice parameters of diamond, graphite, and hexagonal boron nitride. J. Chem. Phys. 44, 181–184 (1966). [DOI] [PubMed] [Google Scholar]
  10. Hanfland M., Beister H. & Syassen K. Graphite under pressure: Equation of state and first-order Raman modes. Phys. Rev. B 39, 12598–12603 (1989). [DOI] [PubMed] [Google Scholar]
  11. Goncharov A. F., Makarenko I. N. & Stishov S. M. Graphite at pressures up to 55 GPa: Optical properties and raman spectra. High Press. Res. 4, 345–347 (1990). [Google Scholar]
  12. Liu Z., Wang L., Zhao Y., Cui Q. & Zou G. High-pressure Raman studies of graphite and ferric chloride-graphite. J. Phys.: Condens. Matter 2, 8083–8088 (1990). [Google Scholar]
  13. Schindler T. & Vohra Y. K. A micro-Raman investigation of high-pressure quenched graphite. I. Phys.: Condens. Matter 7, L637–L642 (1995). [Google Scholar]
  14. Miller E. D., Nesting D. C. & Badding J. V. Quenchable Transparent Phase of Carbon. Chem. Mater. 9, 18–22 (1997). [Google Scholar]
  15. Fayos J. Possible 3D Carbon Structures as Progressive Intermediates in Graphite to Diamond Phase Transition. J. Solid State Chem. 148, 278–285 (1999). [Google Scholar]
  16. Nakayama A. et al. Compression of polyhedral graphite up to 43 GPa and x-ray diffraction study on elasticity and stability of the graphite phase. Appl. Phys. Lett. 84, 5112–5114 (2004). [Google Scholar]
  17. Reich S. & Thomsen C. Raman spectroscopy of graphite. Phil. Trans. R. Soc. Lond. A 362, 2271–2288 (2004). [DOI] [PubMed] [Google Scholar]
  18. Aust R. B. & Drickamer H. G. Carbon: A New Crystalline Phase. Science 140, 817–819 (1963). [DOI] [PubMed] [Google Scholar]
  19. Bundy F. P. & Kasper J. S. Hexagonal diamond -A new form of carbon. J. Chem. Phys. 46, 3437–3446 (1967). [Google Scholar]
  20. Xu J., Mao H. & Hemley R. The gem anvil cell: high-pressure behavior of diamond and related materials. J. Phys: Condens. Matter 14, 11549–11552 (2002). [Google Scholar]
  21. Hanfland M., Syassen K. & Sonnenschein R. Optical reflectivity of graphite under pressure. Phys. Rev. B 40, 1951–1954 (1989). [DOI] [PubMed] [Google Scholar]
  22. Goncharov A. F., Makarenko I. N. & Stishov S. M. Sov. Phys. JETP 69, 380 (1989). [Google Scholar]
  23. Utsumi W. & Yagi T. Light-Transparent Phase Formed by Room-Temperature Compression of Graphite. Science 252, 1542 (1991). [Google Scholar]
  24. Oganov A. R. & Glass C. W. Crystal structure prediction using ab initio evolutionary techniques: Principles and applications. J. Chem. Phys. 124, 244704 (2006). [DOI] [PubMed] [Google Scholar]
  25. Li Q. et al. Superhard Monoclinic Ploymorph of Carbon. Phys. Rev. Lett. 102, 175506–175509 (2009). [DOI] [PubMed] [Google Scholar]
  26. Umemoto K., Wentzcovitch R. M., Saito S. & Miyake T. Body-Centered Tetragonal C4 : A Viable sp3 Carbon Allotrope. Phys. Rev. Lett. 104, 125504 (2010). [DOI] [PubMed] [Google Scholar]
  27. Itoh M. et al. New Metallic Carbon Crystal. Phys. Rev. Lett. 102, 055703 (2009). [DOI] [PubMed] [Google Scholar]
  28. Zhou R. & Zeng X. Polymorphic Phases of sp3-Hybridized Carbon under Cold Compression. J. Am. Chem. Soc. 134, 7530–7538 (2012). [DOI] [PubMed] [Google Scholar]
  29. Li D. et al. Lowest enthalpy polymorph of cold-compressed graphite phase. Phys. Chem. Chem. Phys. 14, 4347–4350 (2012). [DOI] [PubMed] [Google Scholar]
  30. Amsler M. et al. Crystal Structure of Cold Compressed Graphite. Physical Review Letters 108, 065501, 10.1103/PhysRevLett.108.065501 (2012). [DOI] [PubMed] [Google Scholar]
  31. Niu H. et al. Families of Superhard Crystalline Carbon Allotropes Constructed via Cold Compression of Graphite and Nanotubes. Physical Review Letters 108, 135501, doi:10.1103/PhysRevLett.108.135501 (2012). [DOI] [PubMed] [Google Scholar]
  32. Wang J. T., Chen C. & Kawazoe Y. Low-Temperature Phase Transformation from Graphite to sp3 Orthorhombic Carbon. Phys. Rev. Lett. 106, 075501 (2011). [DOI] [PubMed] [Google Scholar]
  33. He C. et al. New Superhard Carbon Phases Between Graphite and Diamond. Solid State Comm. In press (2012). [Google Scholar]
  34. He C. et al. Four superhard carbon allotropes: a first-principles study. Phys. Chem. Chem. Phys. 14, 8410–8414 (2012). [DOI] [PubMed] [Google Scholar]
  35. Sheng X. L., Yan Q. B., Ye F., Zheng Q. R. & Su G. T-Carbon: A Novel Carbon Allotrope. Phys. Rev. Lett. 106, 155703 (2011). [DOI] [PubMed] [Google Scholar]
  36. Yao Y. et al. Comment on “New Metallic Carbon Crystal”. Phy. Rev. Lett. 102, 229601 (2009). [DOI] [PubMed] [Google Scholar]
  37. Montgomery J. M., Kiefer B. & Lee K. K. M. Determining the high-pressure phase transition in highly-ordered pyrolitic graphite with time-dependent resistance measurements. J. Appl. Phys. 110, 043725 (2011). [Google Scholar]
  38. Loa I. et al. Novel Graphitic Spheres : Raman Spectroscopy at High Pressures. Phys. Stat. Sol. (b) 223, 293–298 (2001). [Google Scholar]
  39. Pocsik I., Hundhausen M., Koos M. & Ley L. Origin of the D peak in the Raman spectrum of microcrystalline graphite. J. non-cryst. solids 227–230, 1083–1086 (1998). [Google Scholar]
  40. Patterson J. R., Kudryavtsev A. & Vohra Y. K. X-ray diffraction and nanoindentation studies of nanocrystalline graphite at high pressures. Appl. Phys. Lett. 81, 2073–2075 (2002). [Google Scholar]
  41. Birch F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaC1 at high pressures and 300K. J. Geophys. Res. 83, 1257–1268 (1978). [Google Scholar]
  42. Jeanloz R. Finite-strain equation of state for high-pressure phases. Geophys. Res. Lett. 8, 1219–1222 (1981). [Google Scholar]
  43. Liang Y., Zhang W. & Chen L. Phase stabilities and mechanical properties of two new carbon crystals. EPL 87, 56003–56008 (2009). [Google Scholar]
  44. Goncharov A. F. et al. Thermal equation of state of cubic boron nitride: Implications for a high-temperature pressure scale. Phys. Rev. B 75, 224114 (2007). [Google Scholar]
  45. Solozhenko V. L., Häusermann D., Mezouar M. & Kunz M. Equation of state of wurtzitic boron nitride to 66 GPa. Appl. Phys. Lett. 72, 1691 (1998). [Google Scholar]
  46. Boulfelfel S. E., Oganov A. R. & Leoni S. Understanding the nature of “superhard graphite”. Scientific Reports in press (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Angel R. J., Bujak M., Zhao J., Gatta G. D. & Jacobsen S. D. Effective hydrostatic limits of pressure media for high-pressure crystallographic studies. Journal of Applied Crystallography 40, 26–32, 10.1107/S0021889806045523 (2007). [Google Scholar]
  48. Hammersley A. P., Svensson S. O., Hanfland M. & Fitch A. N. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press. Res. 14, 235 (1996). [Google Scholar]
  49. Xu H. et al. Anisotropic elasticity of jarosite: A high-P synchrotron XRD study. American Mineralogist 95, 19–23 (2010). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES