Machine learning algorithms to classify spinal muscular atrophy subtypes

Abstract

Objectives:

The development of better biomarkers for disease assessment remains an ongoing effort across the spectrum of neurologic illnesses. One approach for refining biomarkers is based on the concept of machine learning, in which individual, unrelated biomarkers are simultaneously evaluated. In this cross-sectional study, we assess the possibility of using machine learning, incorporating both quantitative muscle ultrasound (QMU) and electrical impedance myography (EIM) data, for classification of muscles affected by spinal muscular atrophy (SMA).

Methods:

Twenty-one normal subjects, 15 subjects with SMA type 2, and 10 subjects with SMA type 3 underwent EIM and QMU measurements of unilateral biceps, wrist extensors, quadriceps, and tibialis anterior. EIM and QMU parameters were then applied in combination using a support vector machine (SVM), a type of machine learning, in an attempt to accurately categorize 165 individual muscles.

Results:

For all 3 classification problems, normal vs SMA, normal vs SMA 3, and SMA 2 vs SMA 3, use of SVM provided the greatest accuracy in discrimination, surpassing both EIM and QMU individually. For example, the accuracy, as measured by the receiver operating characteristic area under the curve (ROC-AUC) for the SVM discriminating SMA 2 muscles from SMA 3 muscles was 0.928; in comparison, the ROC-AUCs for EIM and QMU parameters alone were only 0.877 (p < 0.05) and 0.627 (p < 0.05), respectively.

Conclusions:

Combining EIM and QMU data categorizes individual SMA-affected muscles with very high accuracy. Further investigation of this approach for classifying and for following the progression of neuromuscular illness is warranted.

In recent years, there has been an effort to identify biomarkers to improve the efficiency of neurologic disease clinical trials.¹ Whereas early biomarker studies focused mainly on identifying molecular tools to assess disease diagnosis and status, a variety of nonmolecular biomarkers are now being considered, including electrophysiologically and radiologically based ones.²

Each biomarker is typically viewed as an independent test for assessing disease. However, there is no constraint that demands biomarkers be evaluated individually. Indeed, computational tools already exist to combine biomarkers into new, more powerful indices of disease status.^3–6 In oncology, such an approach has been used to stratify tumor type and to assess disease status and response to therapy.^7,8

One method for combining biomarkers is through machine learning algorithms in which unrelated variables are integrated by a computer program that is first taught to associate one specific clinical value with a combination of data sets.⁹ The learned algorithm is then applied to new data sets. Support vector machines (SVMs) are one method for doing this. SVMs, in fact, have already been explored in Alzheimer disease,³ Parkinson disease,⁴ and Huntington disease⁵ to assist with the identification of disease onset.

In this study, we take this approach for the first time in neuromuscular disease, by combining features from 2 unrelated technologies, quantitative muscle ultrasound (QMU)^10–16 and electrical impedance myography (EIM)^17,18 to determine whether SVM algorithms can more accurately classify normal muscles and those affected by type 2 and type 3 spinal muscular atrophy (SMA) than either method alone.

METHODS

Standard protocol approvals, registrations, and patient consents.

All procedures were approved by the institutional review board at Children's Hospital Boston, and signed consent was obtained from patients older than 18 years or from parents with verbal or written assent obtained from individuals younger than 18 years.

Subjects.

Normal subjects were recruited through the Department of Neurology at Children's Hospital Boston. Normal subjects were required to be younger than 30 years, to have no history of neuromuscular or other neurologic disease, and to be in otherwise good health. Patients with SMA were identified through the Neuromuscular and SMA Clinics at Children's Hospital Boston and through the Pediatric Neuromuscular Clinical Research network. Patients with SMA were required to have a positive genetic test for SMA or have a sibling with a known positive SMN gene mutation and the appropriate clinical phenotype. Patients with SMA were differentiated into those with type 2 and type 3 based on the standard clinical criterion of their maximum level of motor function achieved at any point, including whether the patient was able to walk (type 3) or only sit (type 2). No patients with SMA type 0, 1, or 4 were included in this study. No formal sample size estimation was performed before initiation of the study, given its preliminary nature; the goal was simply to recruit as many patients with SMA as possible in the time allotted.

QMU.

QMU is a technique in which muscle and subcutaneous fat echo intensity is quantified using computer-assisted gray scale analysis. Using a histogram function on ultrasound images, luminosity values that can be compared across patients and within the same patient over time can be generated for muscle and subcutaneous fat. This technique has been shown to be useful in assessing muscle deterioration in neuromuscular disease in children.^10–14 In particular, patients with neuromuscular disorders have elevated muscle echo intensity levels caused by infiltration of muscle architecture by fat and connective tissue.¹⁵ Through methods of quantification of muscle echo intensity, QMU can serve as a biomarker for SMA severity.¹⁶

In this study, ultrasound measurements were taken on the Terason 2000 Handheld Ultrasound System (Terason, Burlington, MA), and analysis was performed on the transverse images that were exported to Adobe Photoshop. Tissue luminosity was then quantified as described previously.¹⁶ Statistics of muscle and fat luminosity (mean, median, and SD) were also available. The ratios of mean muscle to fat luminosities and median muscle to fat luminosities were also calculated for analysis.

EIM.

The second technique, EIM, is a newer, also noninvasive, painless technique.^17,19 In EIM, a high-frequency, low-power electrical current is passed through a local volume of body tissue, and the surface voltages on the skin resulting from the current are measured. EIM has shown high accuracy in its ability to correctly distinguish patients with SMA from normal patients, as well as to distinguish patients with type 2 SMA from patients with type 3 SMA¹⁸ and to follow patients with SMA over time.²⁰

EIM measurements were performed with an Imp SFB7 device (Impedimed, Inc., San Diego, CA) over a frequency range of 2 to 500 kHz using the approach described previously.¹⁸ Biceps, wrist extensors, quadriceps, and tibialis anterior muscles were studied unilaterally in each subject. Although all subjects were part of a longitudinal study, for the purposes of this cross-sectional analysis, only data from the last visit were used. In addition to 50 kHz resistance, reactance, and phase data, a variety of multifrequency collapsed parameters were also incorporated as described previously²¹ and included the 10–30 kHz phase and reactance slopes, the 100–500 kHz phase and reactance slopes, and, for resistance, the log resistance 10–30 and 10–500 kHz slopes.

SVMs.

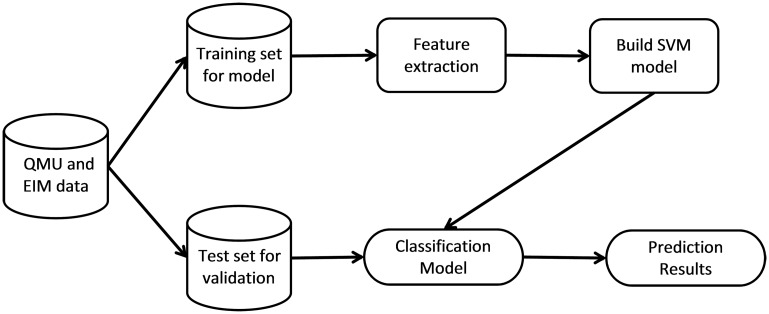
SVMs were trained to classify the data described above as normal, type 2 SMA, or type 3 SMA. SVMs are learning and pattern recognition algorithms that are developed with the goal of separating classes by a function that is computed from available examples.²² The general algorithm for developing and using SVMs is shown in figure 1. The first step in classification is to separate randomly the data into training and test sets. The training set contains the class label and several attributes or features. The model is trained on this training set such that it is able to predict the class label from unseen sets of attributes in the test set.²³

Figure 1. Generalized support vector machine (SVM) algorithm for neurologic disease classification.

The data are partitioned by random sampling into a training set and test set. The training set is used to extract the relevant features and build a SVM classification model. The test set is inputted to the classification model to obtain the results. This process is repeated multiple times, and the average accuracy is reported as the cross-validation accuracy. EIM = electrical impedance myography; QMU = quantitative muscle ultrasound.

Training sets consist of a group of vectors with known class labels, in which each vector corresponds to a subject and the elements of the vector correspond to the different features of the subjects. The goal is then to find a plane or higher dimensional hyperplane that separates the 2 classes and maximizes the distance to the closest point from either class. In other words, the goal is to find the hyperplane that maximizes the separation (or margin) between the classes.^3,22 This is known as the optimal separating hyperplane. If the data are not linearly separable, a mathematical kernel function may be used to nonlinearly transform the data into a higher dimensional space where they may be easier to separate. Once the model has been trained by finding the optimal separating hyperplane, the test data set is input, and the predicted class labels are compared with the known values to assess accuracy. A more detailed description of these algorithms can be found elsewhere.^22,24,25

In our model, several EIM and ultrasound features were entered for each individual muscle (attributes or features), and the model was trained to combine these features in a way such that it was able to efficiently distinguish among normal, type 2 SMA, and type 3 SMA muscles. Importantly, given our limited number of subjects, we applied the data separately to each muscle rather than applying these methods to each patient. The first iteration of model creation included all the parameters described above for both ultrasound and EIM through linear mapping to a higher dimensional space or linear kernel. The weighting of each parameter was analyzed to identify the relative importance of each parameter to the learning algorithm. The SVM model was then remodeled, incorporating only the most important parameters analyzed in the previous step, and recursive feature elimination⁶ was performed to find the optimal number of parameters. Furthermore, several different kernels were tested to find the best performing SVM model. All SVM classification models were developed and tested with the statistical programming software R (R Development Core Team) using the e1071, caret, and ROCR packages.

For EIM, the features included single frequency phase, resistance and reactance and multifrequency phase, and resistance and reactance slopes over high and low frequencies. For QMU, the features that were included were the mean, median, and SD of fat and muscle luminosities, and the ratios of mean and median muscle to fat luminosities.

Analysis of resulting models.

We used receiver operator characteristic (ROC) curve analysis²⁶ to assess and compare the performances of the individual EIM and ultrasound measures and the SVM models to discriminate between the different groups of disease states, using only an analysis from the test data set. The method of DeLong et al.²⁷ was used to assess significant differences between performances. Furthermore, 10 cross-validations of each SVM were also performed to assess how well the model would generalize to an independent data set. The cross-validation or bootstrapping was performed by partitioning the training set into 10 subsamples. One of the 10 subsamples is retained as the validation data and the remaining 9 are used as training data. This process was then repeated 9 more times with each subsample being retained as the validation data. The average accuracy of the 10 iterations is reported as the cross-validation accuracy.

RESULTS

Subject demographics.

A total of 46 subjects were recruited, and data from 165 individual muscles were analyzed; the demographic data are provided in table 1. No subject who enrolled was excluded from the analysis.

Table 1.

Subject demographics

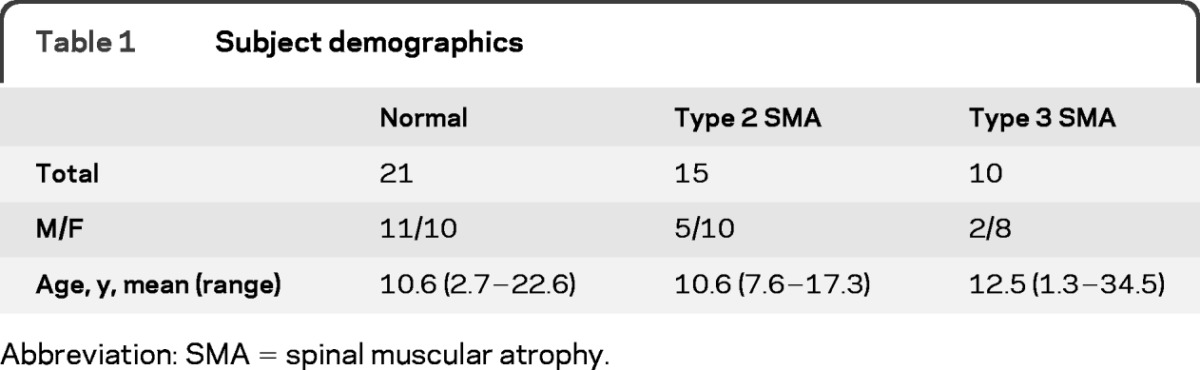
Abbreviation: SMA = spinal muscular atrophy.

Classification performance

SVM models were developed for 3 different classifications: normal subjects vs subjects with SMA (type 2 and type 3), normal subjects vs subjects with type 3 SMA, and subjects with type 2 SMA vs subjects with type 3 SMA. Differentiation of normal subjects from subjects with type 2 SMA alone was trivial and not included in this analysis. The breakdown of the training and test sets for each of these classifications is shown in table 2.

Table 2.

Summary and breakdown of training and test sets for SVM models^a

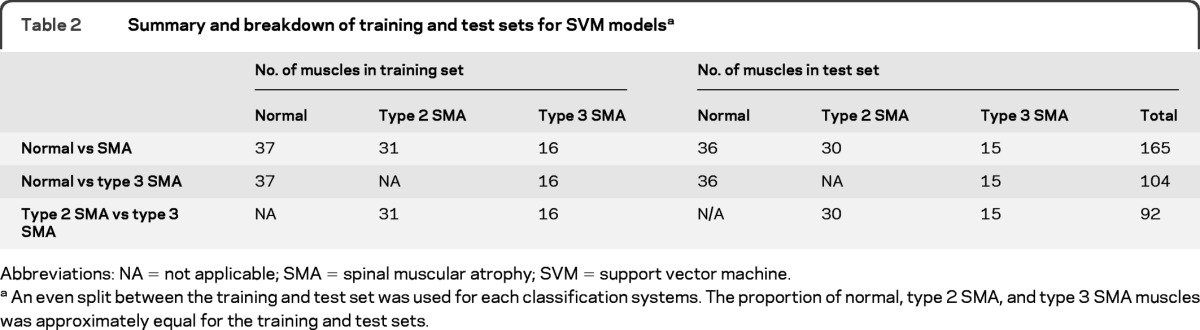
Abbreviations: NA = not applicable; SMA = spinal muscular atrophy; SVM = support vector machine.

^aAn even split between the training and test set was used for each classification systems. The proportion of normal, type 2 SMA, and type 3 SMA muscles was approximately equal for the training and test sets.

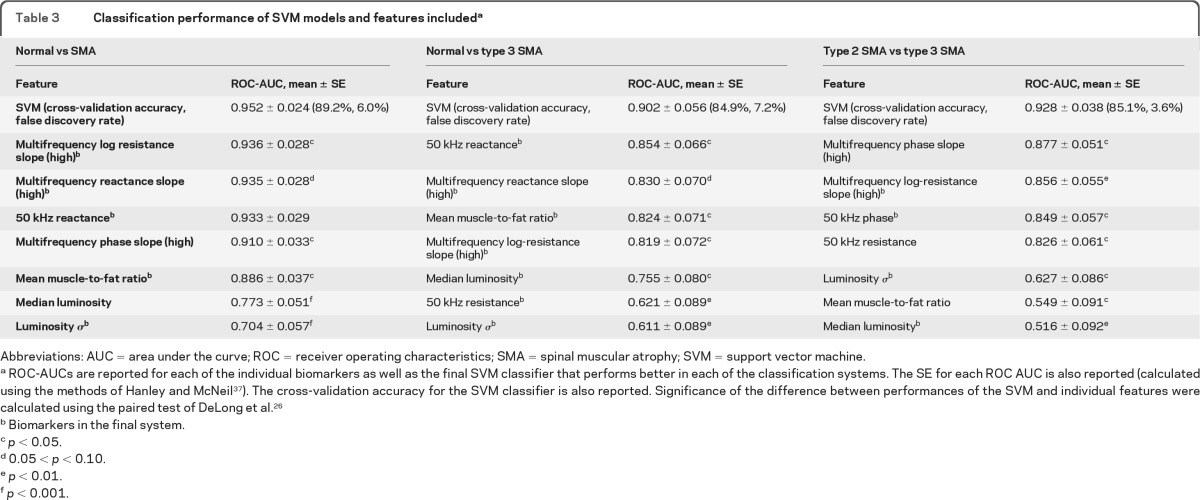
For each initial classification system, all the EIM and QMU features were included in a model run with a linear kernel. The 7 most important features for each classification system as ranked by the initial models are shown in table 3. Next, we performed recursive feature elimination to determine the optimal number of features for each system. For classifying normal subjects vs subjects with SMA (type 2 and type 3), use of a combination of 5 features yielded the best classification results; for normal subjects vs subjects with type 3 SMA, 6 features worked best; and for type 2 SMA vs type 3 SMA, a combination of 4 features was most successful. The ROC areas under the curve (AUCs) of the top-ranked measures that were included in the initial SVM model are also shown in table 3. The features used in the final SVM models are indicated (footnote b).

Table 3.

Classification performance of SVM models and features included^a

Abbreviations: AUC = area under the curve; ROC = receiver operating characteristics; SMA = spinal muscular atrophy; SVM = support vector machine.

^aROC-AUCs are reported for each of the individual biomarkers as well as the final SVM classifier that performs better in each of the classification systems. The SE for each ROC AUC is also reported (calculated using the methods of Hanley and McNeil³⁷). The cross-validation accuracy for the SVM classifier is also reported. Significance of the difference between performances of the SVM and individual features were calculated using the paired test of DeLong et al.²⁶

^bBiomarkers in the final system.

^cp < 0.05.

^d0.05 < p < 0.10.

^ep < 0.01.

^fp < 0.001.

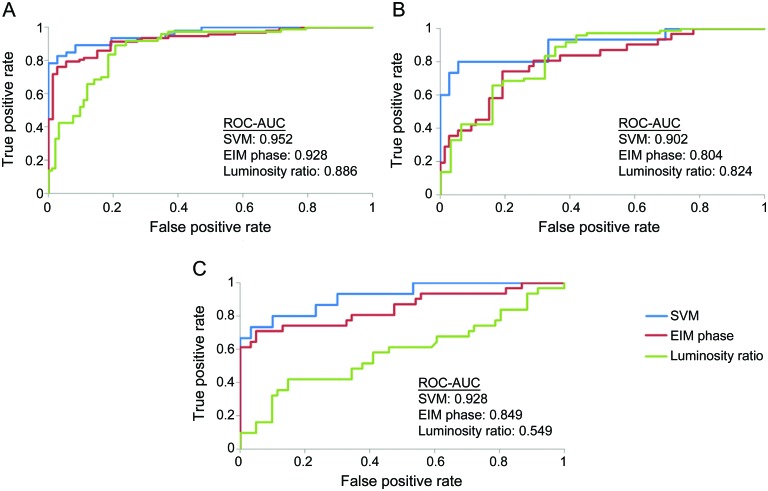
As shown in table 3, the combined classifiers obtained from the SVMs produced greater AUC values than any of the individual EIM or ultrasound measures for each of 3 muscle classification problems, the differences reaching significance in most cases. Given the relatively small sample size, p values between 0.05 and 0.10 are also included. In particular, the combined classifier fared better than the 50 kHz phase and mean muscle/fat luminosity ratio, which have both been shown to have significant power in discriminating between subjects with type 2 SMA, subjects with type 3 SMA, and normal subjects.^16,18 Figure 2 shows the ROC curves for the SVM classifiers, 50 kHz phase and mean muscle/fat luminosity ratio for each of the 3 muscle classification problems. The cross-validation accuracies, also shown in table 3, are also high, indicating that the training data set was not overfitting the data.

Figure 2. Receiver operating characteristic (ROC) curves for support vector machine (SVM) model.

ROC curves show the classification performance of the SVM model in comparison with the performance of key electrical impedance myography (EIM) and ultrasound measures for (A) normal vs spinal muscular atrophy (SMA) classification, (B) normal vs type 3 SMA classification, and (C) type 2 SMA vs type 3 SMA classification. AUC = area under the curve.

DISCUSSION

In this study, we show that by combining EIM and QMU through machine learning, we are able to discriminate between individual normal muscles and muscles affected by type 2 and type 3 SMA with greater accuracy than with either EIM or QMU alone. In general, the features that were identified as most important by the algorithm had the greatest discriminating power individually. The successful use of this algorithm in combining electrophysiologic and imaging markers is, to our knowledge, the first reported effort to combine these data types and serves as a specific example of a potential broader application of machine learning to the classification problems in neuromuscular disease.

Machine learning techniques have been used in other medical disciplines for diagnosis and prognosis, incorporating for the most part molecular biomarkers. For example, DNA microarray expression data have been used with various machine learning techniques to classify and validate cancer tissue samples.^7,28 In another study, electrophysiologic markers were used with SVMs for arrhythmia discrimination.²⁹ SVMs have also been used in neurology with brain imaging metrics such as MRI, fluorodeoxyglucose-PET, and CSF to classify Alzheimer disease³ and to track neurodegeneration in Huntington disease.⁵

As is evident from the results outlined in table 3, the individual EIM and QMU biomarkers varied considerably in their ability to discriminate individual muscles affected by type 2 and type 3 SMA. Conversely, the combined biomarker uniformly performed quite well. Clinically, this discrimination is usually straightforward for a physician, and such sophisticated techniques are not required. However, this study provides an example of the power of using machine learning to combine individual neuromuscular biomarkers into more powerful indices of disease. For example, such measurements could be used to improve the early diagnosis of acquired diseases such as amyotrophic lateral sclerosis or even in the automated interpretation of electrophysiologic or imaging studies. Perhaps more importantly, an improved ability to monitor disease status may also be developed through the use of these biomarkers. Machine learning can be used to assist in combining multiple biomarkers of progression to provide new surrogate measures of disease status and the effects of therapy. One approach for doing this is through support vector regression^30,31 or the more recently described relevance vector machines.³²

The enhanced power of the applied algorithm is probably due to the different muscle characteristics extracted by the 2 modalities being used (QMU and EIM). Although elements of these modalities are somewhat correlated, with a coefficient of determination (R²) of 0.36, the differences in underlying principles ensure that each modality brings new information to the classification process. Thus, when SVM algorithms are applied to other neurologic classification and regression problems, it will be important to use variables that are individually correlated with the outcome yet share limited information. This will help to ensure that there is sufficient information present for the algorithm to act upon.

Importantly, clinical rating scores could also be incorporated into future analyses. These scores could be used as features to provide a better classification by extracting information about patient function not captured by measures such as EIM or QMU. Alternatively, the clinical rating scores could be used as classes or outcomes that are predicted by these measures in a classification or regression problem.

There are several factors that limit our analysis here and others that need to be considered more generally when SVMs are used. First, there were relatively few patients in the study. Although this issue was countered by classifying individual muscles rather than the actual patients, an ideal machine would have more observations or more features because error is minimized as the number of features and observations increases for linear and polynomial SVMs. Furthermore, although the SVM performance was, for the most part, significantly better than that for the best individual EIM and QMU feature classifiers for each of the problems, there were a few features for which significance at p < 0.05 was not reached. A major contributor to this lack of significance was probably the relatively small sample size, and for this reason we specifically identified p values between 0.05 and 0.10. There was only a single feature, 50 kHz reactance for the SMA vs normal problem, for which the p value was greater than 0.1 (0.11, specifically). Second, the accuracy and precision of the analysis will be limited by the quality of the raw data. In this case, ultrasound data could be affected by device limitations and the quantification process.¹⁶ Quality problems in the EIM data arise from the dependence on position and electrode placement³³ as well as technical limitations of the currently available devices, including the one used here.¹⁷ Last, a complex data set can lead to the SVM algorithm being computationally expensive to perform and slow.³⁴ In the classification problems considered, there were relatively few features and observations. However, when a large number of features or observations are included, other machine learning methods may be more desirable than SVMs.^35,36

Other feature selection methods could also be used to rank the features and identify the optimal set of features for the classification. One well-known technique is principal component analysis (PCA), which is a dimensionality reduction method that combines features to transform a set of observations of possibly intercorrelated variables into a set of values of uncorrelated variables that maximally account for the variance in the original data set. To evaluate how PCA performed compared with SVM for this problem, we applied PCA to the 3 data sets and found that the relative weightings of the features in the computed principal components were roughly equivalent to the feature ranking obtained by the recursive feature elimination in the original SVM algorithm. The major difference between PCA and SVM, however, is that PCA cannot be used to accurately classify individual new cases, which was the impetus for our pursuing this study in the first place, but rather can only deconstruct sets of already obtained data.

We have shown that machine learning techniques can be used to develop stronger, more robust biomarkers for classification of SMA by combining data from unrelated testing modalities. A next step would be to explore the use of these techniques in performing neuromuscular disease classifications that are clinically difficult for physicians in larger data sets and with more features. Such studies will help determine whether machine learning techniques ultimately can effectively assist physicians in the diagnosis and in monitoring the status of neuromuscular disease.

GLOSSARY

AUC

area under the curve

EIM

electrical impedance myography

PCA

principal component analysis

QMU

quantitative muscle ultrasound

ROC

receiver operating characteristic

SMA

spinal muscular atrophy

SVM

support vector machine

AUTHOR CONTRIBUTIONS

T. Srivastava analyzed and interpreted data acquired from the study, completed statistical analysis, and drafted and revised the manuscript for content. B. Darras supervised the study, participated in the acquisition of data for the study, and assisted with manuscript preparation. J. Wu analyzed and interpreted data acquired from the study and assisted with manuscript preparation. S. Rutkove designed and supervised the study, drafted and revised the manuscript for content, and obtained funding for the study.

DISCLOSURE

T. Srivastava reports no disclosures. B. Darras has served as a consultant for ISIS Pharmaceuticals and Quest Diagnostics, Inc.; receives research support from the NIH (NIAMS 2P01-NS040828–6A11 [co-PI], NINDS 1U10-NS077269 [site PI/PD], and NIAMS R01-AR060850 [co-PI]), the SMA Foundation, the Muscular Dystrophy Association, and the Slaney Family Fund for SMA. J. Wu reports no disclosures., S. Rutkove has a patent pending re: Electrical impedance myography; serves as a consultant for and holds stock in Convergence Medical Devices, Inc.; and receives research support from the NIH (NINDS R01-NS055099 [PI] and NINDS K24-NS060951–01A1 [PI]), R01-AR060850 (co-PI), the SMA Foundation, the ALS Association, and the Center for Integration of Medicine and Innovative Technology. Go to Neurology.org for full disclosures.