Extremely low-coverage sequencing and imputation increases power for genome-wide association studies

Abstract

Genome wide association studies (GWAS) have proven a powerful method to identify common genetic variants contributing to susceptibility to common diseases. Here we show that extremely low-coverage sequencing (0.1–0.5x) captures almost as much of the common (>5%) and low-frequency (1–5%) variation across the genome as SNP arrays. As an empirical demonstration, we show that genome-wide SNP genotypes can be inferred at a mean r² of 0.71 using off-target data (0.24x average coverage) in a whole-exome study of 909 samples. Using both simulated and real exome sequencing datasets we show that association statistics obtained using ultra low-coverage sequencing data attain similar P-values at known associated variants as genotyping arrays, without an excess of false positives. Within the context of reductions in sample preparation and sequencing costs, funds invested in ultra low-coverage sequencing can yield several times the effective sample size of SNP-array GWAS, and a commensurate increase in statistical power.

Genome-wide association studies (GWAS) have identified over a thousand SNPs associated to complex traits¹. To date, these studies have been carried out using SNP arrays that assay up to 2.5 million polymorphisms at a cost of hundreds of dollars per sample, often augmented by imputation of untyped variants using HapMap or 1000 Genomes reference panels^2–5. At the same time, DNA sequencing has emerged as a powerful new technology^3,6,7, with the first major applications to disease gene discovery arising in the course of exome sequencing⁸. Recent cost reductions raise the question of whether sequencing might be a viable alternative for GWAS, analogous to RNA sequencing (RNA-seq) in gene expression studies^3,9,10. One limitation to using sequencing for GWAS has been the cost of preparing each DNA sample, which historically has been at least as large as the cost of SNP array genotyping. However, this is no longer the case; for example Epicentre offers a high throughput sample preparation for roughly $100 per sample (see URLs), and we have recently demonstrated that sequencing libraries appropriate for whole-genome sequencing can be produced for approximately $15 per sample on a scale of thousands of samples¹¹. Below, we show that by sequencing such libraries at ultra-low coverage (0.1–0.5x, at an effective sequencing cost of $10–$100 per sample) followed by genotype calling using 1000 Genomes Project reference panels², the effective sample size per unit cost of this approach is several times greater than for the standard GWAS study design using SNP arrays. This gap will increase if sequencing costs continue to drop more quickly than genotyping costs.

Results

To explore the effectiveness of GWAS based on low coverage sequencing, we simulated sequencing data at various coverage levels, accounting for sequencing errors as well as variation in average coverage across samples and loci. We used the 762 haplotypes inferred from the 381 European samples of the 1000 Genomes Project (phase 1, June 2011 release), and restricted the analysis to 10 distinct 5Mb regions (total of 50 Mb, containing 150,261 SNPs) that were randomly chosen to represent the average genome-wide recombination rate and SNP density (Supplementary Note, Supplementary Table 1). One-half of the haplotypes were used to build simulated data, and the other half were used as an imputation reference panel. Simulated data were used to infer genotype dosages at known SNPs using Beagle¹², an imputation engine appropriate for analysis of sequencing data. To assess the accuracy of imputation, we used the squared correlation (r²) between imputed dosages and true genotypes, which quantifies the reduction in effective sample size in GWAS due to imperfect imputation¹³ (Online Methods).

Figure 1 shows the accuracy of imputation either using just the sequencing reads to impute genotypes or using the reads coupled with the 1000 Genomes Project reference panels² (Online Methods). We observe high accuracies at ultra low-coverage (0.1–0.5x) when reference panels are used (Figure 1, Supplementary Note, Supplementary Figure 1). Sequencing at 0.2x coverage yields more than 90% of the effective sample size than is achieved by Illumina Human-1M-duo array plus conventional imputation, as assessed by average r² to SNPs in the 1000 Genomes Project dataset for both common (>5% minor allele frequency) as well as low-frequency variants (1 to 5% minor allele frequency) (Figure 1). These simulations results suggest that sequencing at 0.1–0.5x coverage with imputation using the 1000 Genomes Project datasets can in principle achieve power comparable to high-density SNP arrays. These simulation results are robust to model assumptions and parameter values (Supplementary Note, Supplementary Tables 1,2,3).

Figure 1.

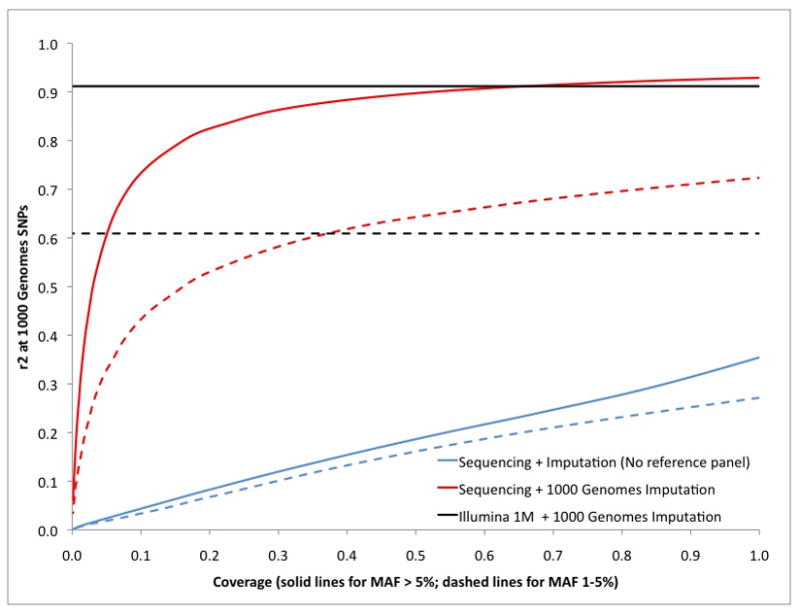
Genotype imputation accuracy as function of coverage in 1000 Genomes Project simulations. Accuracy as function of coverage is displayed using solid lines for common SNPs (MAF >5%) and dashed lines for low-frequency SNPs (MAF<5%).

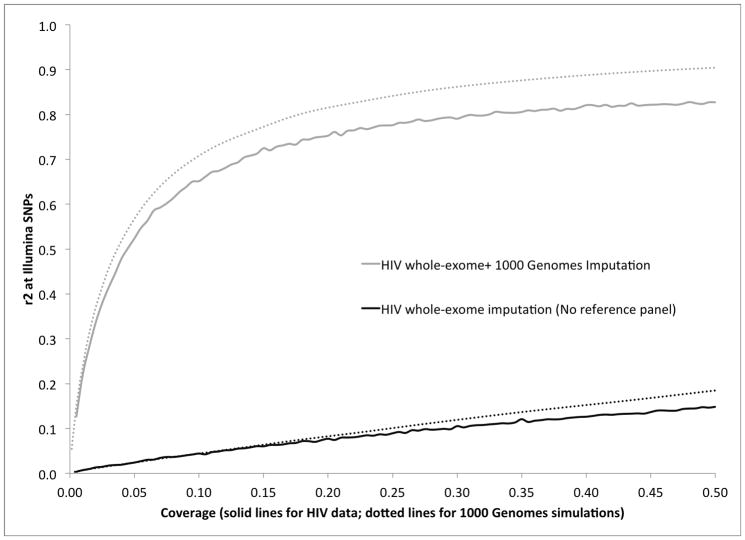
We investigated whether similar results could be achieved with real data by analyzing whole exome sequencing data from 909 individuals of European ancestry, combining samples from the International HIV Controllers Study (IHCS) (84), Swedish Schizophrenia Study (SCZ) (503) and Autism NIHM Controls Study (AUT) (322) (Online Methods)^14–18. Whole-exome studies enrich the sample DNA for genic content prior to sequencing^3,19,20 and usually discard data from non-exonic regions. However, current DNA capture technologies do not yield perfect enrichment and the “off-target” data can often be substantial given the high coverage of many exome-sequencing studies. For example, in the 909 exomes, the average coverage is 0.24x for non-exonic regions and more than 60x for exons (Supplementary Note, Supplementary Figure 2). We explored whether the whole-exome data, coupled with imputation based on the 1000 Genomes Project reference dataset, could support a GWAS. We imputed genotypes at all polymorphic sites indentified in the European samples of the 1000 Genomes Project, using sequencing data together with the 762 haplotypes inferred from the European samples of the 1000 Genomes Project phase 1 (Online Methods), and quantified accuracy by comparing imputed calls with Illumina array genotyping calls (Online Methods). To remove effects of high coverage at or near exons we removed data at all SNPs covered at more than 4x (Supplementary Figure 2). At 0.24x coverage we observe an average r²=0.71 (s.d. 0.15) to the genotype calls assayed by genome-wide SNP arrays, roughly similar in average expected power to a conventional GWAS with 71% of the sample size (see Supplementary Note, Supplementary Figure 3, Supplementary Table 4 for results averaged by chromosome, minor allele frequency and coverage). We also quantified the genome-wide accuracy achieved by using all data from the whole exome scan (off-target and on-target); the average r² increased to 0.77 when all data from the whole-exome study was used.

To illustrate how this approach might be used in practice to carry out a GWAS, we used the off-target exome data to compute association statistics at 103,977 SNPs across the genome using simulated phenotypes starting from the genotype calls from the arrays (Online Methods). We observed similar association statistics when imputed dosages were used as compared to SNP arrays under both null (phenotype uncorrelated to the genotype) and true nonzero effect sizes (Figure 2, Supplementary Figure 4,5,6, Supplementary Table 5), indicating that our approach is robust to false positives while accurately recovering the association signal when present. In addition, we also performed a case-control scan in which the AUT samples were treated as “controls” and SCZ as “cases”. After adjusting for differences in genetic ancestry between SCZ and AUT samples, we observed no genome-wide significant association, thus further emphasizing the robustness of our approach (Supplementary Note, Supplementary Figure 7). To assess the power of detecting true positives, in addition to simulated phenotypes, we also carried out a case-control study comparing HIV-1 controllers (61) and progressors (23) from the IHCS data set (Online Methods). The higher off-target coverage (0.5x) in the IHCS data leads to an average of r²=0.82 to the genotype calls at the 398,098 SNPs assayed by arrays in the IHCS data¹⁴. A similar λ_GC (genomic control)²¹ value of 1.05 for imputed data as compared to 1.04 for typed data was observed (Supplementary Note, Supplementary Figure 4). We specifically looked at SNPs previously reported to be significantly associated with HIV-1 controller status¹⁴ and observed similar association statistics and effect sizes as compared to SNP arrays, both for the entire set of 47 previously associated SNPs (Supplementary Note, Supplementary Table 5) and for the subset of 10 SNPs with nominal P<0.05 in the SNP array data (Table 1). The association statistics obtained using extremely low-coverage sequencing did not exhibit the 9% drop that might have been expected given r²=0.91 imputation accuracy at these SNPs (ratio between the average −log 10 p-values at imputed versus typed data of 1.04), but this can be explained by statistical fluctuation (Table 1 and Supplementary Note).

Figure 2.

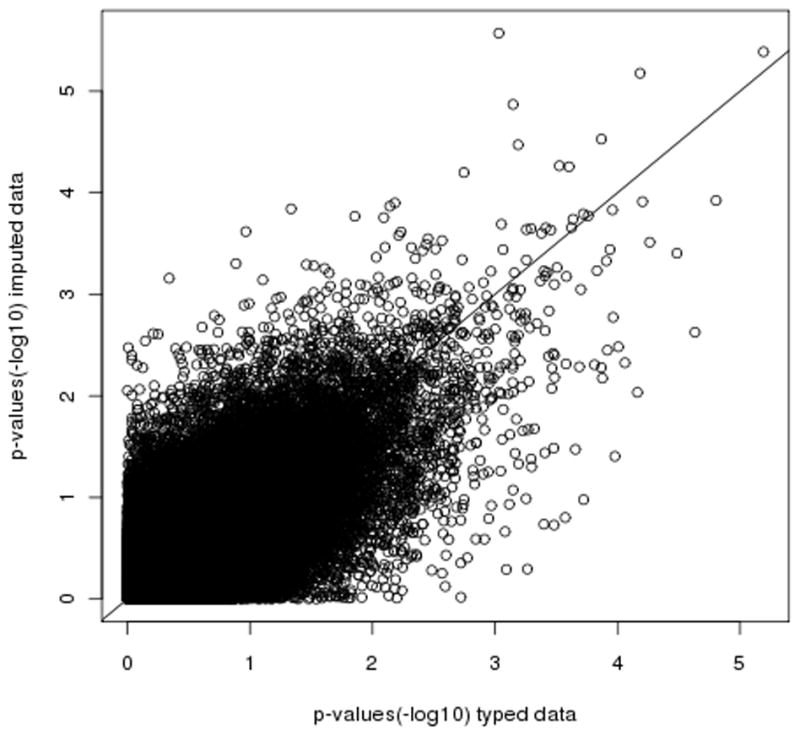
Observed versus expected association minus log 10 p-values at 103,977 SNPs across the genome in simulated null data sets over 909 samples of the combined data set. We observe r² of 0.64 between p-values computed in typed versus imputed data, similar to simulations of association statistics at imputed versus genotyping calls (Supplementary Note). Results for alternate hypothesis of association can be found in Supplementary Note.

Table 1.

Statistics attained at known associated SNPs in the International HIV Controllers Study computed over typed or imputed genotypes (only SNPs with nominal p-value < 0.05 in the typed data are shown).

RsID	Chr	Position	Coverage	r2	Association p-value (−log10) typed data	Association p-value (−log10) imputed data	Ratio	Effect typed [confidence interval]	Effect imputed [confidence interval]
rs7756521	6	30848253	0.33	0.96	1.38	1.12	0.81	0.19 [0.01 0.38]	0.17 [−0.02 0.36]
rs3094212	6	31085770	0.73	0.96	1.37	1.42	1.03	0.15 [0.01 0.29]	0.15 [0.01 0.29]
rs2395471	6	31240692	0.27	0.96	1.38	1.41	1.02	0.14 [0.01 0.28]	0.14 [0.01 0.27]
rs9366778	6	31269173	0.43	0.84	1.34	1.87	1.4	0.15 [0.00 0.29]	0.18 [0.04 0.31]
rs9264942	6	31274380	0.26	0.69	1.77	2.35	1.33	0.19 [0.04 0.34]	0.24 [0.08 0.40]
rs2156875	6	31317347	0.31	0.94	1.56	1.16	0.74	0.17 [0.02 0.31]	0.13 [−0.01 0.28]
rs2844529	6	31353593	0.94	0.92	2.53	3.02	1.19	0.21 [0.08 0.35]	0.23 [0.10 0.37]
rs2523467	6	31362930	0.63	0.93	2.53	2.39	0.94	0.21 [0.08 0.35]	0.21 [0.07 0.34]
rs2596531	6	31387557	0.55	0.94	1.31	1.38	1.05	0.15 [0.00 0.30]	0.16 [0.01 0.31]
rs2516513	6	31447588	0.36	0.86	1.53	1.25	0.82	0.18 [0.02 0.34]	0.15 [−0.00 0.31]
Average			0.48	0.90	1.67	1.74	1.04*	-

^*Average ratio is computed as the ratio of the sum of association p-values. Effect is computed assuming a linear additive model associating genotype to phenotype.

We also evaluated empirical results at lower coverage (0.005x to 0.5x) by sub-sampling reads with corresponding probability. Due to the large number of experiments and the higher non-exome coverage of the IHCS data as compared to all the 909 samples, we restricted this analysis to the 10 distinct 5Mb regions (total of 50Mb) described above in the IHCS data set (84 samples). As coverage decreases, we observe a reduction in accuracy, analogous to our simulations based on the 1000 Genomes Project dataset, restricted to the same set of 6,070 SNPs from the array (Figure 3). At 0.5x coverage we observe a mean r² of 0.82, standard deviation of 0.03 and standard error of 0.01 across the 10 regions. However, the accuracy of imputation in the IHCS sequencing data is lower than in simulations for any level of coverage (Figure 3). The discrepancy between simulations and real data could be an effect of increased similarity across haplotypes inferred from the 1000 Genomes Project phase 1 data due to the genotype calling and phasing procedure from 4x sequencing data that aggregated information across samples (Supplementary Note, Supplementary Table 6). Other possible explanations include nonuniform error rates in base-calling and alignment of reads across the genome or simulation parameters that do not perfectly model aspects of the empirical data such as variance in coverage across samples and loci, although our experiments suggest that these are unlikely to be the primary explanation (Supplementary Note).

Figure 3.

Genotype imputation accuracy in IHCS whole-exome data as a function of coverage. Illumina 1M genotype calls were used as a gold standard, restricting to 6070 SNPs in 10 distinct 5Mb regions (total of 50Mb) of the genome (see main text). Dotted lines denote results attained in 1000 Genomes simulations on the same SNP set.

Discussion

To explore the economic ramifications of sequencing-based GWAS, we considered the trade-off between the number of samples sequenced and the average coverage (which affects accuracy). We evaluated the expected effective sample size attained with different strategies and compared this with the effective sample size that would be obtained by genotyping using standard genotyping arrays (e.g. Illumina Human-1M-duo). We derived all results from empirical accuracies using sequencing data sets sub-sampled from the IHCS data, so that results do not rely on any simulation assumptions. We compared accuracies only at SNPs typed on the array, a conservative computation that ignores the potentially greater benefit at SNPs not present on the array. We assumed a fixed total budget of $300,000, an arbitrarily large number of samples available, a sample preparation cost of $30 (conservatively double the cost that we have recently demonstrated¹¹), and DNA sequencing cost of $133 per 1x sequencing (based on the Illumina Network cost of $4,000 for 30x sequencing of 50 samples or more, which scales linearly with lower coverage). We calculated the effective sample size of a sequencing-based GWAS as a function of average coverage, which determines the number of samples sequenced under a fixed budget (Online Methods). Under zero sample preparation cost and ignoring the benefit of imputation, the optimal study design involves sequencing a maximal number of samples at minimal coverage^22,23. However, when sample preparation cost and imputation are taken into account, there exists an optimal number of samples to sequence for any budget. For a fixed budget of $300,000, the highest effective sample size (roughly equivalent to more than 4,600 typed individuals) is achieved at an average coverage of 0.1x (6,800 samples sequenced at $45 total cost per sample, r²=0.65) (Figure 4a). The optimal value of average coverage varies as function of sample preparation and sequencing costs, but we obtained qualitatively similar results for other cost assumptions (Supplementary Note). We note that a sequencing-based approach can attain a higher effective sample size than SNP arrays even when constraints on sample availability limit the space of available study designs (Figure 4a).

Figure 4.

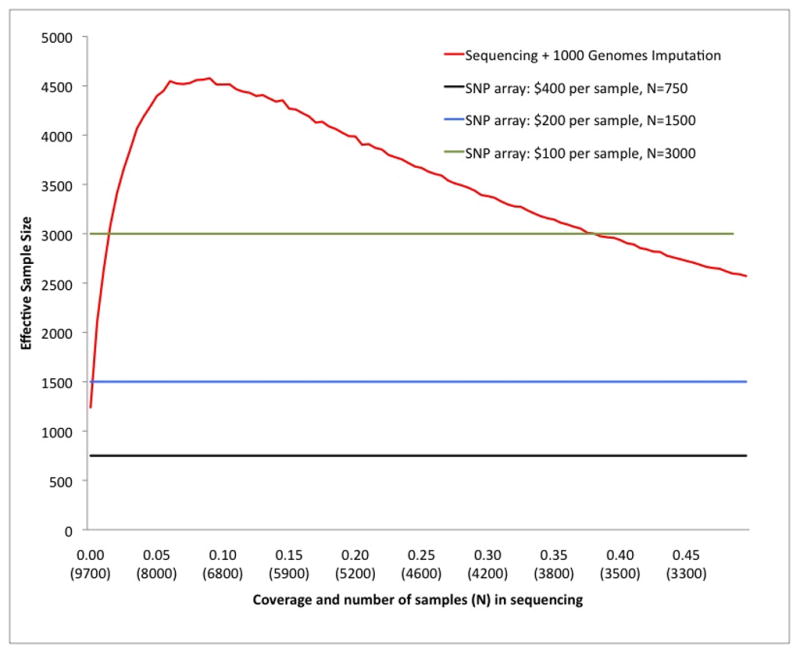
Coverage (and corresponding number of samples) for fixed budget of $300,000. (a) Effective sample size in sequencing-based GWAS as function of number of samples and resulting coverage. Cost assumptions: $30 per sample preparation cost, $133 per 1x sequencing cost (see main text).

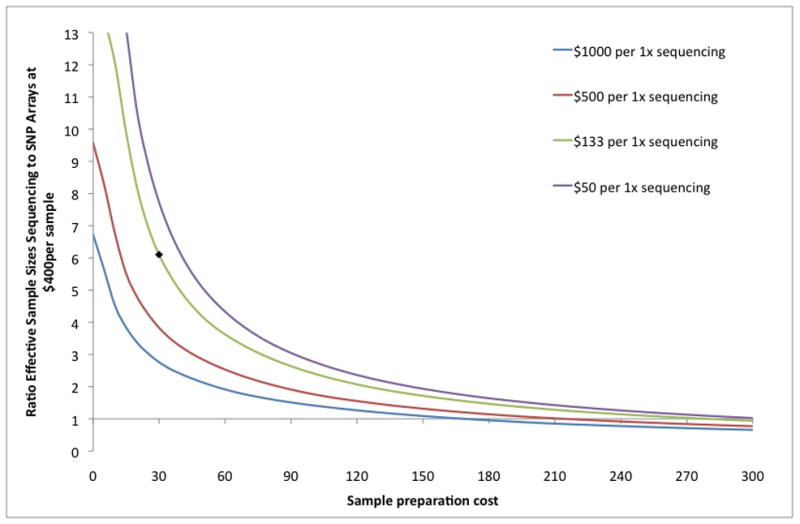
(b) Ratio of expected association statistic (effective sample size) in sequencing-based GWAS vs. array-based GWAS at $400/sample, as a function of sample preparation and sequencing costs. Expected association statistics for sequencing-based GWAS are based on optimum coverage and number of samples (assuming arbitrarily large number of samples available) subject to budget constraint. The optimum coverage and number of samples varies at different points on the graph (not shown). Black dot denotes $30 sample preparation cost and $133 per 1x.

A striking finding is that the effective sample size achieved using sequencing-based GWAS with current costs¹¹ is more than six times higher than SNP-array genotyping at $400/sample, corresponding to a large increase in power (Figure 4b, Supplementary Note, Supplementary Figure 8). Only if SNP array typing is less than $70 per sample, or if sample preparation and sequencing costs are much higher (e.g. greater than $120 per sample for sample preparation or $1,000 for 1x sequencing) does sequencing-based GWAS lose its advantage in terms of statistical power to associate variants. If sequencing technology—both in the efficiency of library preparation and the cost of sequencing—continues to improve more quickly than genotyping technology, the advantage of sequencing-based GWAS will increase. We note that a critical ingredient for attaining high accuracy at ultra low-coverage is the availability of large panels of reference haplotypes. As additional reference haplotypes over larger numbers of SNPs become available from 1000 Genomes Project and other projects, we expect the accuracy attained by ultra low-coverage sequencing to further increase.

We conclude with several caveats. First, computational methods for sequencing-based GWAS are still under development^3,7,22,24, whereas SNP-array based GWAS is a proven method that produces high quality data that can be analyzed using readily available computational tools. Second, sequencing data requires additional computational resources beyond what is necessary to analyze conventional GWAS as the analysis pipeline of sequencing data is typically more demanding than for genotyping data. Third, sequencing-based GWAS of the type described here does not involve sufficient coverage to discover rare variants and to associate them with disease; thus, as with SNP arrays, the power of this approach is limited to common and (to a lesser extent) low-frequency variants. Fourth, although results from our empirical IHCS sequencing data are encouraging, no study to date has used sequencing-based GWAS to identify new disease risk variants. A priority for future work should be to carry out studies that demonstrate that this approach can discover new associations between genetic variants and common diseases.

Online Methods

Simulation of sequencing data based on 1000 Genomes Project dataset

For our simulations we used the 381 diploid European individuals from the phase 1 release of the 1000 Genomes Project (June 2011)². The 381 individuals include 87 CEPH individuals of North European ancestry (CEU), 93 Finnish individuals from Finland (FIN), 89 British individuals from England and Scotland (GBR), 98 Tuscan individuals (TSI), and 14 individuals from the Iberian peninsula (IBS). Genotype calls and haplotypic phase was inferred from low-coverage sequencing (4x) using an imputation strategy that borrowed information across samples and loci. The 762 haplotypes were split at random between two panels of 381 haplotypes; one panel was used to build simulated data, and the other was used as an imputation reference panel. We simulated data for 100 samples by randomly sampling (without replacement) pairs of haplotypes from the simulation panel. All simulation results were generated over 10 distinct 5Mb regions (total of 50Mb) across the genome, randomly chosen to represent the average genome-wide recombination rate and SNP density (Supplementary Note). Reads spanning polymorphic sites identified in the 1000 Genomes Project were simulated assuming a fixed error rate of 1%, per-locus coverage multipliers were drawn from a Gamma distribution Γ(α,β) with shape parameters α = 4 and β =1/α and mean 1²⁵ and per-sample coverage multipliers were drawn from a normal distribution N(1,0.2) (matching the empirical IHCS sequencing data) with negative values set to 0. Reads were sampled assuming a Poisson distribution with mean equal to the average coverage times per-locus multiplier times per-sample multiplier. Results were generally insensitive to the choice of simulation parameters (with the exception of average coverage per sample) (Supplementary Note).

Imputing genotypes from sequencing data

Genotypes can be inferred from sequencing data by either (1) inferring genotypes independently at each SNP in each individual, (2) making use of allele frequencies inferred from all sequenced individuals, (3) making use of linkage disequilibrium (LD) patterns inferred from sequenced individuals, or (4) making use of LD patterns inferred from sequenced individuals as well as reference panels of haplotypes^7,22,24,26. Here we focus on (3) and (4), using a two-step imputation approach (see Supplementary Note for details and results of other approaches). In the first step, we computed genotype likelihoods at all polymorphic loci identified in the 1000 Genomes Project dataset independently for each individual. We disregarded all observed alleles that did not match either the reference or alternate allele identified in the 1000 Genomes Project dataset and computed likelihoods of 0,1,2 copies of the 1000 Genomes Project dataset “reference” allele at all SNPs identified in the phase 1 release of the 1000 Genomes Project. Reads that did not overlap any polymorphic sites were discarded. In the second step, the genotype likelihoods for all loci in all samples (with or without the reference panel of haplotypes, 381 in total for simulations) were passed to the Beagle imputation software¹² with default parameters (i.e. “like” for the genotype likelihoods and “phased” for the reference haplotypes).

Imputing genotypes from GWAS arrays

Imputation from the Illumina Human-1M-duo array was simulated by masking all genotypes at SNPs (in the 50Mb simulated region) not present on the array followed by imputation at all polymorphic loci identified in the European samples of the 1000 Genomes Project phase 1 dataset using the remaining reference panel of haplotypes (381 in total). We used the MaCH²⁷ imputation software with default parameters “--rounds 40 --greedy --mle --mldetails”.

Metric for imputation accuracy

Imputation accuracy was measured using the r² (squared Pearson correlation coefficient) between imputed dosages and typed genotypes.

Simulated phenotypes

Starting from the typed genotype calls, we simulated continuous randomly ascertained phenotypes Y ~ gβ + ε, with ε ~ N(0,1). β = 0 represents the null model of no association between genotype and phenotype.

IHCS whole-exome data set

Genome-wide SNP genotyping and whole-exome sequencing data for 84 samples were obtained from the International HIV Controllers Study¹⁴, of which 43 were genotyped on the Illumina HumanHap 650Y and 41 on the Human-1M-duo array. Of the 84 samples, 61 are HIV-1 controllers enrolled by the IHCS and 23 enrolled by the AIDS Clinical Trials Group. Only unrelated samples of European ancestry with high genotyping rates (>95%) were included, after filtering out SNPs with low minor allele frequency (MAF < 1%), >2% missing data, or departure from Hardy-Weinberg equilibrium (P < 10⁻⁶). The SNP sets were intersected to obtain 398,098 SNPs genotyped in all samples. Imputation was performed using all the 762 available 1000 Genomes phase 1 haplotypes as opposed to 381 for simulations using non-overlapping regions of size 2.5Mb with 250Kb flanking regions on either side.

Combined whole-exome dataset

Exome sequencing of the Autism NIMH Controls (AUT, 322 samples), for the Swedish Schizophrenia control data (SCZ, 503 samples) and IHCS data (IHCS, 84 samples) was carried out at the Broad Institute^14–18. We only used samples ascertained as controls in the AUT and SCZ data (i.e. no presence of disease). Exons were captured using the Agilent 38Mb SureSelect v2 Libraries and sequenced using either an Illumina HiSeq2000 or Illumina GenomeAnalyzerII instrument. All samples met the criterion of >90% of targeted bases having >10x coverage and >80% of targeted bases having >20x coverage. Reads were mapped to hg19 using BWA and processed with Picard and GATK (see URLs). The SCZ samples were genotyped on the Affy 5.0 or 6.0 platforms. Genotype data across all samples (SCZ, AUT and IHCS, 909 in total) was merged with SNPs filtered by missing data and departure from Hardy-Weinberg equilibrium. Genotype likelihoods obtained using GATK²⁸ software were passed to Beagle in windows of 1Mb with 250Kb to impute all SNPs identified as polymorphic in the haplotypes of the European 1000 Genomes Project phase 1 data. 103,977 genome-wide SNPs both genotyped and imputed from sequencing across all 909 samples were used in all experiments over combined data (Supplementary Note). To remove effects of high coverage at or near exons we removed data at all SNPs covered at more than 4x.

Association statistic for GWAS

A standard test for association in GWAS is the Armitage trend test^21,29, equal to N times the squared correlation between genotypes G (0, 1 or 2) and phenotypes Φ (0 or 1), where N is the number of samples. This statistic extends to imputed data by using genotype dosages. The value of the statistic decreases by a factor of r² if computed at a genotyped or imputed SNP in partial LD with the causal SNP¹³. To estimate the expected association statistic in a GWAS over a set of N samples sequenced at average coverage c, we first estimate the accuracy r²(c) attained at coverage c by sub-sampling IHCS data. We then estimate the expected association statistic as Nρ²(G, Φ) r²(c).

Data access

The analyses presented here make use of genetic data from Autism NIMH Controls (AUT, 322 samples), the Swedish Schizophrenia control data (SCZ, 503 samples) and the International HIV Controllers Study (IHCS, 84 samples). AUT and SCZ datasets are available from dbGaP under accession numbers phs000298.v1.p1 and phs000473.v1.p1. The IHCS data is available by direct request from Pamela Richtmyer (prichtmyer@partners.org); investigators can submit a concept sheet detailing their study design, research questions and other needs in order to request access to IHCS genetic data. The concept sheet with detailed instructions can be downloaded from: http://cfar.globalhealth.harvard.edu/fs/docs/icb.topic938249.files/Harvard%20CFAR%20Concept%20Sheet%20Template%20.docx. Requests will be reviewed on the basis of scientific merit, feasibility and potential overlap with accepted concept sheets or ongoing investigations.