Contributions of leaf photosynthetic capacity, leaf angle and self-shading to the maximization of net photosynthesis in Acer saccharum: a modelling assessment

Abstract

Background and Aims

Plants are expected to maximize their net photosynthetic gains and efficiently use available resources, but the fundamental principles governing trade-offs in suites of traits related to resource-use optimization remain uncertain. This study investigated whether Acer saccharum (sugar maple) saplings could maximize their net photosynthetic gains through a combination of crown structure and foliar characteristics that let all leaves maximize their photosynthetic light-use efficiency (ɛ).

Methods

A functional–structural model, LIGNUM, was used to simulate individuals of different leaf area index (LAI_ind) together with a genetic algorithm to find distributions of leaf angle (L_A) and leaf photosynthetic capacity (A_max) that maximized net carbon gain at the whole-plant level. Saplings grown in either the open or in a forest gap were simulated with A_max either unconstrained or constrained to an upper value consistent with reported values for A_max in A. saccharum.

Key Results

It was found that total net photosynthetic gain was highest when whole-plant PPFD absorption and leaf ɛ were simultaneously maximized. Maximization of ɛ required simultaneous adjustments in L_A and A_max along gradients of PPFD in the plants. When A_max was constrained to a maximum, plants growing in the open maximized their PPFD absorption but not ɛ because PPFD incident on leaves was higher than the PPFD at which ɛ_max was attainable. Average leaf ɛ in constrained plants nonetheless improved with increasing LAI_ind because of an increase in self-shading.

Conclusions

It is concluded that there are selective pressures for plants to simultaneously maximize both PPFD absorption at the scale of the whole individual and ɛ at the scale of leaves, which requires a highly integrated response between L_A, A_max and LAI_ind. The results also suggest that to maximize ɛ plants have evolved mechanisms that co-ordinate the L_A and A_max of individual leaves with PPFD availability.

INTRODUCTION

Since net available carbohydrates can be allocated to key fitness components that improve growth, survival and reproduction (Givnish, 1988; Reich et al., 2003), maximizing plant net photosynthetic gain is expected to be favoured by natural selection. Although plants exploit light, photosynthetic photon flux density (PPFD), as their source of energy, they also require ancillary resources (e.g. water, nitrogen, phosphorus, etc.) to build and maintain their photosynthetic machinery. Acquiring and retaining these additional resources comes at a cost, and to maximize their net gain in principle plants should minimize these costs while maximizing their gross photosynthetic gains. Various studies suggest net photosynthetic gain can be maximized if plants maximize the efficiency with which they use available resources (Tooming, 1970; Mooney and Gulmon, 1979; Field, 1983; Bloom et al., 1985; Chapin et al., 1987; Nikinmaa, 1992), but there are discrepancies between theoretical predictions and observed resource-use efficiencies (reviews by Kull, 2002; Niinemets and Anten, 2009).

Since nitrogen (N) is a key component of both chlorophyll and photosynthetic enzymes (Evans, 1989) and N frequently limits productivity at higher latitudes (Chapin et al., 1987; Martinelli et al., 1999), attention has focused especially on optimizing photosynthetic N-use efficiency (PNUE), the ratio of photosynthesis to leaf N content. Yet, observed N allocation to leaves typically deviates from theoretical expectations (Field, 1983; Hirose and Werger, 1987; Evans, 1993; Hollinger, 1996; Kull, 2002; Meir et al., 2002; Wright et al., 2006; Niinemets and Anten, 2009), based on the idea that PNUE should be maximal and the same for all leaves independently of their position in the canopy (Mooney and Gulmon, 1979; Field, 1983). These discrepancies can arise because there is co-limitation between multiple resources (Chapin et al., 1987; Wright et al., 2006; Kaspari et al., 2008), incomplete estimates of costs (Field, 1983; Hollinger, 1996), competitive interactions among neighbouring plants (Anten, 2005), and trade-offs in the efficient use of different resources (Hirose and Bazzaz, 1998; Hikosaka et al., 1999). This latter point is particularly relevant since it suggests that plants may not be able to optimize the use of several resources simultaneously. For instance, it has been shown that leaves that maximize PNUE should have lower N content than leaves that maximize PPFD-use efficiency (Hikosaka et al., 1999). Given the importance of PPFD for plant fitness, an alternative to the PNUE hypothesis would be that plants have evolved to optimize PPFD use instead.

In theory, a plant could maximize its net photosynthetic gains if all its leaves attain maximal net photosynthetic PPFD use efficiency (ε_max; i.e. the ratio of net photosynthesis to PPFD) independently of their position in the canopy (Fig. 1; e.g. Tooming, 1970). Instantaneous ɛ_max occurs on the ascending part of a leaf photosynthetic light-response curve, at the point where a tangent drawn from the origin intercepts the curve (Tooming, 1970; Kadaja and Tooming, 2004). Typically, ɛ_max occurs at low to medium PPFD and well below photosynthetic saturation (A_max) (Fig. 1). Note that the apparent quantum yield (ϕ) on a photosynthetic light-response curve is a different measure of efficiency because ϕ occurs on the initial section of the curve where net carbon gain is negative. In contrast, ɛ_max is the point of maximum net positive photosynthetic PPFD-use efficiency, i.e. the point where the marginal net gain in PPFD is highest. Despite its potentially important role in the evolution of plant form and function, the functional basis for attaining ɛ_max remains poorly studied.

Fig. 1.

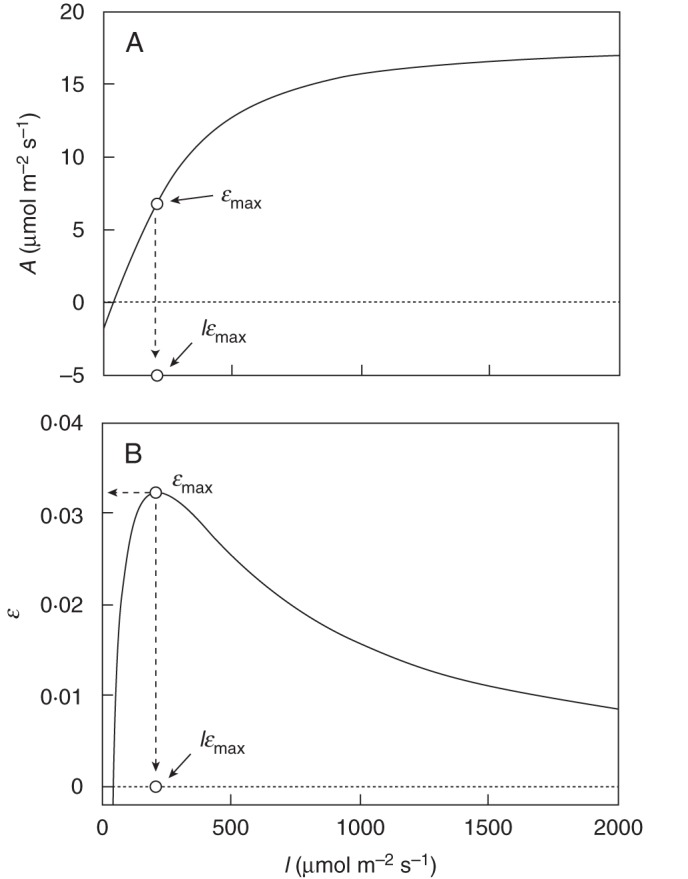
(A) Representative photosynthetic PPFD-response curve of a leaf; I is PPFD incident on the leaf surface. The curve was obtained using the equation for a non rectangular hyperbola (Thornley, 1976) with parameter values A_max = 20·0 µmol m⁻² s⁻¹, ϕ = 0·05, θ = 0·75 and R_d = 2·0 µmol m⁻² s⁻¹. (B) Corresponding photosynthetic light-use efficiency (ɛ) curve where ɛ = A/I. Instantaneous ɛ_max is the point of maximum ɛ while Iɛ_max is the PPFD at which ɛ_max was attained.

To reach ɛ_max at the whole-plant level, the PPFD incident on each leaf (I) should be equal to Iɛ_max (cf. Fig. 1), which suggests ɛ_max could be attained either by changing I incident on a leaf or by changing the value of Iɛ_max through physiological adjustments (e.g. by increasing A_max). Plants can readily change PPFD on leaves within their canopy through changes in leaf inclination (Monsi and Saeki, 1953; Ehleringer and Forseth, 1980; Kao and Forseth, 1992; Terashima and Hikosaka, 1995; Terashima et al., 2005). Similarly, leaves acclimate their physiology to the availability of PPFD (Boardman, 1977; Björkman, 1981), which rescale the photosynthetic light-response curve (Koyama and Kikuzawa, 2010), affecting the value of Iɛ_max. Furthermore, several studies suggest that leaves concentrate their photosynthetic activity on the ascending part of the photosynthetic PPFD-response curve (Rosati and DeJong, 2003; Rosati et al., 2004; Posada et al., 2009; Koyama and Kikuzawa, 2010). Since ɛ_max is about half way on the ascending portion of the curves (Fig. 1), this indirectly support the idea that plants are attaining ɛ_max in nature.

Posada et al. (2009) showed that leaves of tropical canopy trees maintained constant light-use efficiency along PPFD gradients and proposed that this efficiency was maintained by simultaneous acclimation in leaf angle (L_A) and leaf A_max. Here we investigated through a model, using some simple plasticity rules acting at the scale of individual leaves, whether distributions of L_A and A_max within crowns exist that maximize whole-plant net carbon gain. We tested the hypothesis that maximization of plant net carbon gain occurred when all individual leaves attained ɛ_max. We approached the problem of maximizing plant net photosynthesis computationally using the spatially explicit functional–structural tree model LIGNUM (Perttunen et al., 2001) to generate simulated saplings of Acer saccharum. Plants had the capacity to change both the A_max and L_A of individual leaves within their crown as a function of PPFD availability, but no optimization criteria was imposed a priori at the leaf level, i.e. any optimal leaf-level resource use would be a consequence of plants maximizing their net photosynthesis. Simulations were carried out for saplings of four different sizes (Table 1) that were either in an open field or in a large forest gap, with leaf A_max either unconstrained or constrained to a maximum upper value.

Table 1.

General characteristics of A. saccharum saplings used in the simulations

Age (years)	LAIind	Height (m)	No. of leaves	Total leaf surface area (m2)	Self shading (% max reduction)
1	0·443	0·506	8	0·063	7·6
2	0·837	1·054	38	0·314	42·3
3	0·973	1·559	72	0·574	51·8
4	2·562	2·232	481	3·337	96·8

The data are for saplings in an open environment with all leaves horizontal. Potential self-shading was calculated as the ratio between PPFD incident on the least-exposed leaf to PPFD incident on the most-exposed leaf in the plant.

MATERIALS AND METHODS

Functional–structural tree model

LIGNUM (Perttunen et al., 1998, 2001; Sievänen et al., 2008) is a spatially explicit tree growth model that reiteratively utilizes a few basic structural units as a framework to integrate both physiology and architecture. Accurate methods are used to calculate radiation conditions (Perttunen et al., 1998, 2001) and the photosynthetic rate in the crown depends on local light conditions. To account for incoming radiation the upper sky hemisphere is divided into sectors and their number and brightness are given as input to the model. LIGNUM has successfully simulated both coniferous and deciduous trees (Perttunen et al., 2001; Sievänen et al., 2008).

Template saplings

We first simulated open-grown Acer saccharum saplings aged between 1 and 4 years (Table 1), and used each one of them as architectural ‘templates’ for the optimization calculations (see below). The simulation was carried out with a version of LIGNUM that has been adapted to A. saccharum (Perttunen et al., 2001). In the simulation, the incoming photosynthetic active radiation (PAR) during the entire growing season was kept constant at a 1450 MJ m⁻² with a hemispherical distribution of radiation corresponding to that of standard overcast conditions (Ross, 1981). The area of individual leaves varied between 30 cm² and 97 cm² in relation to light availability and relative position on a branch. Template saplings varied in size between 0·51 m and 2·23 m, with large differences in individual leaf area index (LAI_ind) and in the degree of potential self-shading (Table 1). Sapling LAI_ind was calculated as plant total leaf area divided by the area of the sapling crown silhouette projected on a horizontal plane.

OptimalTree

We then developed a modified version of LIGNUM called ‘OptimalTree’ that used the four sapling architectural templates to find the distributions of L_A and A_max in the crown that maximized instantaneous whole-plant net photosynthesis. OptimalTree used the tridimensional information of each template sapling (e.g. trunk and branch dimension, position and angle, individual leaf areas and bud positions), changing only L_A and A_max of individual leaves along gradients of PPFD in the crown. Calculations were done from top to bottom. First, the program calculated PPFD incident on a horizontal plane (I_h; see Table 2 for a list of abbreviations) next to the point of emergence of the uppermost leaf and assigned values of A_max and leaf angle (L_A) using eqns (1) and (2), below. Second, I_h, A_max and L_A were determined for the second highest leaf considering the shade cast by the uppermost leaf, which was influenced by its leaf angle. This calculation was repeated down to the lowest leaf considering the shading caused by leaves above. In addition, leaves that would produce negative net photosynthetic rate were excluded from the calculations (i.e. areas were set equal to zero).

Table 2.

Summary of abbreviations used in the study

Abbreviation	Description
PPFD	Photosynthetic photon flux density (μmol m−2 s−1)
I	PPFD incident on a leaf surface (μmol m−2 s−1)
Ih	PPFD incident on a horizontal plane (μmol m−2 s−1)
A	Leaf net CO2 assimilation (μmol m−2 s−1)
Aplant	Plant net photosynthesis (μmol s−1)
Amax	Leaf maximum gross CO2 assimilation (μmol m−2 s−1)
Rd	Leaf dark respiration (μmol m−2 s−1)
ϕ	Apparent quantum yield (unitless)
θ	Convexity (unitless)
ɛ	Photosynthetic light-use efficiency (unitless)
ɛmax	Maximum photosynthetic light-use efficiency (unitless)
Iɛmax	I at which ɛmax is attained (μmol m−2 s−1)
LA	Leaf angle (°)

Leaf A_max and L_A were a function of I_h next to the point of emergence of leaves. Leaf A_max was subject to a simple hyperbolic function given by

(1)

where a is the asymptote and b is a parameter that determines the ‘rate’ of change of A_max along gradients of I_h in the sapling canopies. Various studies have shown that leaf A_max, or other traits functionally related to A_max, are distributed non-linearly along PPFD gradients in the canopy (e.g. Evans, 1993; Hollinger, 1996; Dang et al., 1997; Kull, 2002; Posada et al., 2009). Variation in A_max with PPFD regime has also been described with simple linear equations (for a review, see Kull, 2002) but non-linear functions appear to be more appropriate to describe changes in leaf functional traits when gradients of PPFD in the canopy of plants are pronounced (e.g. Evans, 1993; Hollinger, 1996; Posada et al., 2009). Leaf angle (degrees) was set by a linear equation

(2)

where c is the slope and d the intercept. An angle of 90 ° corresponded to a horizontal leaf and 0 ° to a vertical-up leaf. Leaf azimuth, i.e. the compass direction of the leaf lamina, was assigned according to the morphological rules of the A. saccharum version of LIGNUM (Perttunen et al., 2001) in the generation of the template saplings; leaf blade rotational angle was equal to 0 °.

The rate of leaf dark respiration (R_d, μmol m⁻² s⁻¹) was related to A_max using the simple relationship

(3)

This function defined the respiratory cost of increasing A_max. Leaf A_max and R_d are generally strongly correlated (Niinemets and Tenhunen, 1997) and R_d is approx. 10 % of A_max (Zotz and Winter, 1993; Hollinger, 1996; Posada et al., 2009). For simplicity, we assumed a zero intercept due to statistical uncertainty in estimates of the intercept of R_d–A_max regressions for A. saccharum (Ellsworth and Reich, 1993; Raulier et al., 1999).

Leaf net assimilation (A; μmol m⁻² s⁻¹) was subject to a photosynthetic light-response curve given by a non-rectangular equation (Thornley, 1976)

(4)

where I is instantaneous PPFD (μmol m⁻² s⁻¹) incident on the adaxial surface of the leaf, ϕ is apparent quantum yield (unitless) and θ is the curvature parameter (unitless). We assumed that both ϕ and θ were constant and equal to 0·05 and 0·75, respectively. These constant values of ϕ and θ result in photosynthetic light-response curves with the same shape irrespective of the value of A_max (Koyama and Kikuzawa, 2010). This assumption was supported by studies that have indicated that these two parameters are commonly not related to PPFD gradients in the canopy (e.g. Posada et al., 2009) and, even in cases where they are, their effect on the shape of the photosynthetic light curves is small (Koyama and Kikuzawa, 2010). Other theoretical studies have taken similar approaches to simulate leaf and canopy photosynthesis (e.g. Sands, 1995; Niinemets and Tenhunen, 1997).

Leaf mass per area (LMA; g m⁻²) generally varies with PPFD regime and A_max within plant canopies (Gutschick and Wiegel, 1988; Reich et al., 1991; Ellsworth and Reich, 1993; Niinemets and Tenhunen, 1997). In our initial simulations we used a linear relationship between LMA and A_max based on empirical parameters for A. saccharum, which allowed us to increase leaf size with decreasing A_max (assuming constant leaf mass). However, there was uncertainty in the intercepts of the LMA–A_max regression for A. saccharum (Reich et al., 1991), which caused some of our initial ‘optimal’ saplings to have biologically unrealistic leaf sizes (e.g. 16 m²). Thus, we took a more conservative approach and used the leaf sizes of the template saplings in the calculations.

Instantaneous plant net photosynthesis (A_plant; μmol s⁻¹) was calculated as the sum of the leaf area-weighted net photosynthetic rate of individual leaves 1, …, N

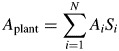(5)

where A (μmol m⁻² s⁻¹) is leaf net photosynthesis and S is leaf area (m²).

Light environments

Optimal distributions of A_max and L_A were estimated with a light distribution for an open site and for a site equivalent to a large forest gap. In the open environment the distribution of PPFD in the hemisphere followed that of a standard overcast sky (Ross, 1981). The brightest PPFD was at the zenith but a large fraction of radiation still came from lateral sectors of the sky. Saplings in the open were exposed to a constant PPFD of 500 µmol m⁻² s⁻¹ on a horizontal surface, corresponding to a daily (12 h) exposure of 21·6 mol m⁻² d⁻¹. The gap environment was created by blocking 95 % of the PPFD between 90 ° (the horizon) and 20 °, leaving a circular opening of 40 ° centred at the zenith. PPFD incident on a horizontal plane in the gap was 83·3 µmol m⁻² s⁻¹, which corresponded to a daily exposure of 3·6 mol m⁻² d⁻¹. In each light environment, we subdivided the sky into 100 sectors of equal area and obtained an integral value of PPFD per sector. LIGNUM traced PPFD rays coming from the centre of each sky sector and determined if leaves intercepted them and assumed that PPFD transmission was equal to 0·06 (Ross, 1981); reflection of light was not considered. Light incident on an individual leaf was ultimately obtained by summing PPFD rays coming from all 100 sectors. For computational efficiency in radiation calculations leaves were simplified as ellipses with an eccentricity of 0·42 and it was assumed that 80 % of the area was covered by the leaf blade (see eqn 4 in Perttunen et al., 2001).

Genetic algorithm

We used a genetic algorithm (GA) to explore the search space of the four parameters a, b, c and d (eqns (1) and (2)) and find the combination(s) of A_max and L_A distributions along I_h gradient in the sapling canopies that maximized A_plant (e.g. Fig 2). A GA is a search heuristic based on principles inspired from evolutionary biology that is commonly used to find solutions to optimization problems (Lucasius and Kateman, 1993, 1994). We utilized a GA with floating point chromosome in the package genalg and the function rbga in R (R Development Core Team, 2008).

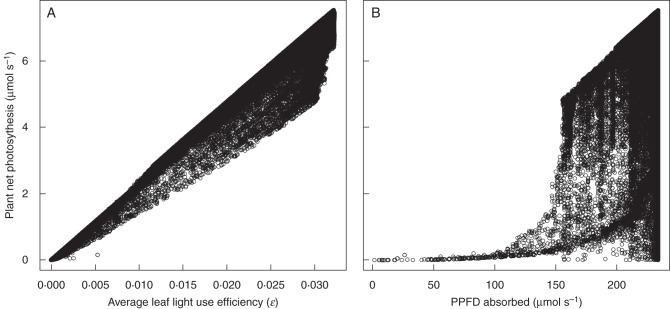
Fig. 2.

(A) Net plant photosynthesis (A_plant) versus average photosynthetic PPFD-use efficiency (ɛ) and (B) net plant photosynthesis versus PPFD absorbed by the plant for a 3-year-old sapling growing in the open with an unconstrained A_max (OU condition). In these figures, each point represents an individual plant with a certain combinations of parameters a, b, c and d generated during the genetic algorithm search (n = 165467; see Materials and Methods).

We ran detailed preliminary tests to tune the GA conditions to find reasonable limits for the optimization search space. The A_max distribution given by parameters a and b (eqn 1) varied within a broad search space of positive numbers. Parameters c and d varied in both positive and negative values, although we limited the range of L_A to between 180 ° (leaf vertically down) and 0 ° (leaf vertically up). The search space for parameters a and b was relatively ‘smooth’ while parameters c and d had a rugged space with several local optima, which required a more detailed search. We ran the GA for 400–600 generations with a constant population size of 2000 saplings; given the small number of parameters relatively few generations were necessary to converge to a solution. During the optimization, 20 % of the saplings with the best A_plant values were allowed to pass unchanged to the next generation; the mutation rate (random changes in the parameter values) was set to a constant value of 10 %. The largest saplings (Table 1) required considerable computational time and, to increase efficiency, we ran the GA a first time to determine the overall structure of the search space and then reran the GA within a narrower parameter space (i.e. local optimization) for 200 generations.

Analyses

We evaluated how the optimal distributions of A_max and L_A changed depending on whether saplings were in an open environment or in a gap. We also determined the effect of constraining leaf A_max to an upper value or letting it be unconstrained. Constrained A_max was set to a maximum value of 12·0 µmol m⁻² s⁻¹, which is within the upper range of naturally occurring A_{max, net} values reported for A. saccharum (Ellsworth and Reich, 1993; Raulier et al., 1999; Jones and Thomas, 2007). For each sapling size (Table 1), we evaluated four conditions: open/unconstrained (OU), open/constrained (OC), gap/unconstrained (GU) and gap/constrained (GC). Note that given the positive relationship between A_max and leaf N_area in A. saccharum (Ellsworth and Reich, 1993; Niinemets and Tenhunen, 1997), the two cases where A_max was unconstrained were equivalent to assuming that soil N availability relative to other resources was unlimited for a given leaf area and N_area could potentially take any value. Our constrained maximum leaf A_max was equivalent to limiting individual leaf N_area to a maximum and allowing optimal plants to have a lower total N than the maximum potential total N. Yet, both constrained and unconstrained cases differed from studies that have looked at the optimal allocation of a fix amount of N in the canopy (e.g. Field, 1983; Hirose and Werger, 1987).

Leaf photosynthetic PPFD-use efficiency (ɛ), the efficiency of CO₂ assimilation per unit PPFD, was calculated as

(6)

For any photosynthetic light-response curve (eqn 4) the value of I that maximized ɛ (Iɛ_max) was calculated as

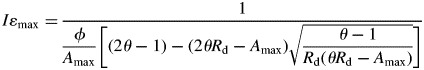(7)

We calculated maximal ɛ (ɛ_max) as A(Iɛ_max)/Iɛ_max using eqns (4) and (6).

RESULTS

Optimal solutions

We identified two key functional characteristics in the genetic algorithm search that were simultaneously optimized. To maximize net photosynthesis, plants had to maximize both instantaneous leaf ɛ across gradients of PPFD in their crowns and PPFD absorption by the whole plant (Fig. 2). In Fig. 2 each point corresponds to one simulated plant with a particular combination of parameters a, b, c and d, which define the distribution of leaf A_max and L_A along PPFD gradients in the plant (eqns 1 and 2). The genetic algorithm generated many saplings in which average ɛ or PPFD absorption were maximal but with A_plant below the maximum. Only when both ɛ and PPFD absorption where maximized did the plants attain maximum A_plant.

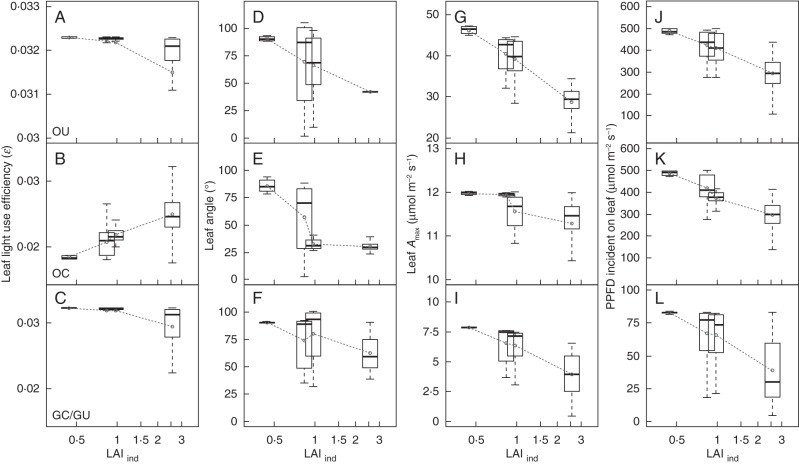
This response was observed for plants in the open with an unconstrained A_max (OU) and for plants in a gap with either constrained (GC) or unconstrained A_max (GU). Small OU seedlings (LAI_ind = 0·4) had an average ɛ that reached the maximum ɛ_max of 0·0323 (i.e. when average ɛ was exactly equal to maximum ɛ_max in all leaves; Fig. 3A). Yet, average ɛ declined slightly with increasing LAI_ind and was 99·8, 99·6 and 97·5 % of maximum ɛ_max for 2-, 3- and 4-year-old individuals, respectively; there was some variability in ɛ between leaves in the 4-year-old saplings, albeit small. In contrast, OC plants had significantly lower average ɛ than OU or GC/GU individuals (Fig. 3B). In OC seedlings, average ɛ was only 56·9 % of ɛ_max, although ɛ increased with LAI_ind reaching 77·1 % of ɛ_max in the largest individuals. Plants in a gap (GC and GU) behaved similarly to the OU individuals, yet their decline in average ɛ at the highest LAI_ind was more pronounced than for OU individuals (average ɛ for 4-year-old saplings was 90·8 % of ɛ_max) and between leaves variability in ɛ increased with size (Fig. 3C).

Fig. 3.

(A–C) Box plots showing the distribution of leaf photosynthetic light-use efficiency (ɛ) as a function of plant leaf area index (LAI_ind). All upper panels correspond to plants in the open with unconstrained A_max (OU), middle panels correspond to plants in the open with constrained maximum A_max (OC), and lower panels to plants in a gap with constrained A_max (GC) and unconstrained A_max (GU); since there were no differences between GC and GU plants, only GC individuals were plotted in the bottom panels. (D–F) Distributions of leaf angle (°; where 90 ° corresponds to a horizontal leaf) as a function of LAI_ind for OU (D), OC (E) and GC/GU plants (F). (G–I) Box plots of leaf A_max as a function of LAI_ind for OU (G), OC (H) and GC/GU plants (I). (J–L) Box plots of PPFD incident on individual leaves as a function of LAI_ind for OU (J), OC (K) and GC/GU plants (L). The dashed lines connect the means of each variable. The horizontal line in each box plot correspond to the median while the boxes are the upper and lower quartile (50 % of the data) and the whiskers encompass the data with values that extend to 1·5 times the interquartile range.

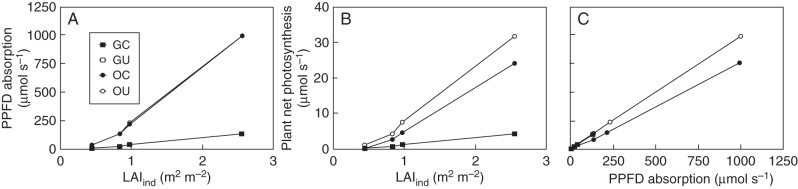
Not surprisingly, plant PPFD absorption increased with LAI_ind and was higher in the open than in a gap (Fig. 4A). Interestingly, however, and, in contrast, with average leaf ɛ, there were no marked differences in PPFD absorption when comparing OC and OU plants. This suggests that the optimal solution prioritized the maximization of PPFD absorption over the maximization of leaf ɛ when A_max was constrained. There was no difference between PPFD absorption in GC and GU saplings. Values of A_plant mirrored PPFD absorption in OU, GC and GU plants, yet carbon gain was lower in OC individuals (Fig. 4B). Since OU and OC plants had the same PPFD absorption, lower photosynthesis of OC plants was attributed to their lower average leaf ɛ. In addition, we found strong linear relationships between plant photosynthesis and PPFD absorption in all plants (Fig. 4C). These relationships for OU and GU/GC had comparable slopes, with values close to the maximum ɛ_max of 0·0323 (slopes: OU = 0·0317; GU/GC = 0·0304), and fell along one line. In contrast, OC plants had lower photosynthesis than OU individuals and a considerably lower slope (0·0247). All regression lines had intercepts close to zero (not shown).

Fig. 4.

(A) Relationship between PPFD absorbed by the plants and LAI_ind, (B) between plant net photosynthesis and LAI_ind and (C) between plant net photosynthesis and PPFD absorption. In each plot, the relationships for plants in the open with unconstrained (OU) and constrained A_max (OC) and for plants in gaps with constrained (GC) and unconstrained A_max (GU) are shown. The results for GC and GU plants were identical and only the points for GC are visible.

Role of leaf A_max and L_A in the optimization

Since individual leaf area and plant architecture did not change during the GA parameter-search, PPFD absorption was almost exclusively determined by L_A. The leaves that were excluded due to their negative carbon gain played a minor role as only two out of 481 leaves in the 4-year-old GC and GU saplings (0·37 % of the total leaf surface) were such; all other plants maintained the maximum number of leaves independently of age, light environment or constraints on A_max. While plant PPFD absorption was determined by L_A, maximization of ɛ was more complex and required co-ordinated adjustments in both A_max and L_A.

In order to attain ɛ_max, I (PPFD incident on a leaf) should be equal to Iɛ_max (Fig. 1), a condition which could be satisfied in two ways. Since leaf A_max and Iɛ_max were linearly related, a leaf could change its Iɛ_max by changing A_max (Fig. 5A) or a leaf could modulate I through changes in its angle of inclination to attain Iɛ_max (Fig. 5B). The change in I with angle was small in the open environment, reflecting the relatively homogeneous PPFD distribution for a standard overcast sky but was more pronounced in the gap. A completely upward oriented leaf in the open environment received 77 % of PPFD incident on a horizontal plane because there was considerable PPFD available in lower positions in the sky hemisphere. In the gap environment, most PPFD came from the upper part of the sky and, as a result, PPFD declined more steeply with increasing leaf inclination than in the open (Fig 5B). For reference, we also plotted changes in I predicted by the cosine law, which corresponded to the case where all PPFD would come from a single point source of beam radiation in the zenith. These curves show that the role of L_A in the optimization of ɛ is modest under cloudy conditions, but can be significant in gaps or under clear sunny skies.

Fig. 5.

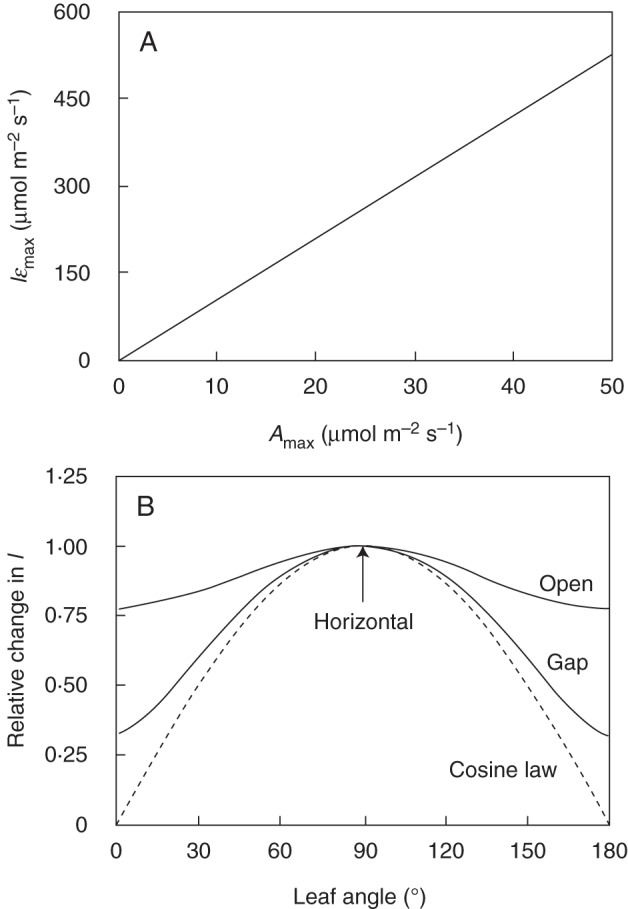
(A) Relationship between PPFD at which a leaf attains maximum photosynthetic light-use efficiency (Iɛ_max; eqn 7) and leaf A_max. (B) Relative change in PPFD incident on a leaf (I) as a function of leaf angle in the open and gap environments simulated in this study. For comparison, relative changes in I that would follow the cosine law (Campbell and Norman, 1998) are also plotted as a dotted line.

The distributions of L_A and A_max (Fig. 3D–I) were a consequence of the simultaneous maximization of plant PPFD absorption and ɛ. Seedlings had leaves with mostly horizontal orientation (90 °), but as LAI_ind increased self-shading also increased, suggesting that larger individuals increased leaf inclination to better distribute PPFD to more shaded leaves (Fig. 3D, E). The OU plants decreased average L_A from 91 ° to 42 °, while OC individuals showed a more pronounced decrease from 86 ° to 30 °, particularly in the transition between an LAI_ind of 0·85 and 0·97 (Fig. 3E). Similar to previous results, there were no differences between GU and GC plants, yet plants in the gap maintained their leaves more horizontal than plants in the open, even when LAI_ind was at its highest. Except for seedlings that had mostly horizontal leaves, average L_A of saplings was below 90 °, and most leaf blades were pointing upward despite having a potential range of variation between 0 ° and 180 °.

Average leaf A_max of OU seedlings was 46·3 µmol m⁻² s⁻¹ which illustrated how A_max and L_A were ‘co-ordinated’ to maximize ɛ (Fig. 3G). If PPFD incident on a leaf would be 500 µmol m⁻² s⁻¹ (which was the PPFD incident on a horizontal plane in the open environments) then leaf A_max had to be equal to 47·4 µmol m⁻² s⁻¹ to have Iɛ_max at 500 µmol m⁻² s⁻¹ (Fig. 5A). The OU seedlings had a maximum A_max of 47·1 µmol m⁻² s⁻¹ and mostly horizontal leaves, meaning that these plants basically attained ɛ_max by increasing A_max and Iɛ_max to very high values (Fig. 3D, G). Similarly, the greatest A_max of GC/GU seedlings was 7·9 µmol m⁻² s⁻¹, which corresponded to an Iɛ_max of 83. 3 µmol m⁻² s⁻¹ – exactly equal to the PPFD of 83·3 µmol m⁻² s⁻¹ incident on a horizontal plane in the gap. The A_max of OC seedling attained the maximum of 12·0 µmol m⁻² s⁻¹ but was particular in that the plant maintained its leaves horizontal, suggesting that the benefits of maximizing PPFD absorption outweighed the cost of having an ε well below ɛ_max.

Role of self-shading and LAI_ind in the optimization

As LAI_ind increased, the proportion of leaves in the sapling crowns exposed to low PPFD also increased (Fig. 3J–L). Average PPFD incident on leaves declined from 488 to 296 µmol m⁻² s⁻¹ in OU plants and from 487 to 295 in μmol m⁻² s⁻¹ in OC plants. The largest difference between OU and OC plants was for 3-year-old saplings, which had an average PPFD of 411 and 372 µmol m⁻² s⁻¹, respectively. This difference was due to the more erect leaves in OC plants (Fig. 3D, E). Average PPFD for GC/GU changed from 83 to 39 µmol m⁻² s⁻¹ (Fig. 3K). This general increase in self-shading helped explain the decrease in A_max with LAI_ind. In OU plants, average A_max declined from 46·3 to 28·7 µmol m⁻² s⁻¹ with increasing LAI_ind, and in GC/GU plants A_max declined from 7·9 to 4·0 µmol m⁻² s⁻¹ (Fig. 3G–I). Since A_max is linearly related to Iɛ_max, the decline in A_max can be attributed to the decrease in average I, i.e. leaves exposed to a lower PPFD attain ɛ_max with a lower A_max than leaves exposed to a higher PPFD. Average A_max of OC saplings also declined slightly (12·0 to 11·3 µmol m⁻² s⁻¹), reflecting the increase in the proportion of leaves that were exposed to low I with increasing LAI_ind.

DISCUSSION

Our results showed that whole-plant net photosynthesis was maximal when average leaf ɛ and whole-plant PPFD absorption were maximized. This suggests that there are selection pressures to simultaneously absorb the maximum amount of PPFD available and use it as efficiently as possible. Many observations show that vegetation commonly absorbs almost all incident radiation. For instance, average PPFD transmittance measured below the crown of mature trees in temperate forest biomes varies between 2·5 % and 7·7 % (Messier et al., 2009) and, in the case of forest canopies dominated by A. saccharum, transmittance is 7·7 % (Beaudet et al., 2004). Understorey tropical species also converge towards high PPFD capture ratios (Valladares et al., 2002), suggesting selection favouring maximal PPFD capture. These results are consistent with the self-limiting development of plant canopies to the point where shade leaves can maintain a positive carbon balance, provided no other resources than PPFD are limiting (Saeki, 1960; Oikawa et al., 2006). If the availability of resources other than light allows, we can expect that plants have evolved to maximize absorption of available PPFD.

By comparison to PPFD capture, maximization of leaf ɛ remains poorly studied. Theoretical analyses suggest that plant photosynthesis is maximized if all leaves in a plant are exposed to their Iɛ_max (Tooming, 1970; Kadaja and Tooming, 2004)_, which is indirectly supported by field studies indicating that leaves concentrate their photosynthetic activity on the ascending part of their photosynthetic light-response curves (Monteith, 1994; Rosati and DeJong, 2003; Rosati et al., 2004; Posada et al., 2009; Koyama and Kikuzawa, 2010) where ɛ is highest. Our results further support this prediction, showing that there should be selection pressure for both maximizing ɛ and for leaf acclimatory responses to PPFD availability that lead to PPFD incident on a leaf coincident with Iɛ_max.

We found, however, that there are limits to maximizing ɛ because of trade-offs associated with a decrease in PPFD absorption at the leaf level. This occurred in individuals with a constrained A_max growing in the open, which had an average ɛ well below ɛ_max but still maintained maximum PPFD absorption at the whole-plant level (i.e. absorption was nearly equal to that of saplings growing in the open with an unconstrained A_max). This hierarchical response suggests that the benefits of maximizing absorption were higher than the costs of a decrease in average leaf ɛ; plants could have improved ɛ to some extent by increasing their angle of inclination, but the costs in terms of a decrease in PPFD absorption by the whole plant were higher than the benefits. In contrast, however, constrained saplings in a gap attained ɛ_max, indicating that optimization of ɛ was possible in environments with lower PPFD availability. Thus, the prediction that plants should maximize ɛ was supported in our study, although when A_max was constrained to an upper value and PPFD availability was high optimization of ɛ was not possible.

In addition to showing that plants are under selection pressure to simultaneously maximize both ɛ and PPFD absorption, our simulations illustrated that maximization of net photosynthesis required strongly integrated adjustments between the angle and A_max of leaves, and LAI_ind. Maximization of plant PPFD absorption was basically controlled in concert by LAI_ind and the distribution of leaf angles because sapling branch architecture and leaf size could not change. Attaining ɛ_max involved co-ordinated leaf-level adjustments between leaf angle and A_max, but also plant-level adjustments in the PPFD gradients within the crowns related to leaf angle and LAI_ind. LAI_ind played an important role in the optimization because it influenced PPFD absorption, the degree of self-shading and the optimal distribution of leaf angle and A_max. When saplings were small, maximizing PPFD absorption was attained by placing leaves horizontally and matching PPFD incident on leaves with Iɛ_max, which, in the case of open-unconstrained plants, required a very high A_max. With increasing LAI_ind, self-shading increased, leaves became more inclined and average A_max declined due to a lower average PPFD incident on leaves. Thus, our results suggest that the well-documented relationships among leaf angle, leaf A_max, LAI and PPFD gradients in the canopy (Monsi and Saeki, 1953; Terashima and Hikosaka, 1995; Kull, 2002; Kitajima et al., 2005; Terashima et al., 2005) are an emergent property of the co-ordinated maximization of canopy PPFD absorption and maximization of ɛ at the leaf level.

An important aspect of our study was to evaluate how constraining maximum A_max to an upper value consistent with field measurements for A. saccharum trees (Ellsworth and Reich, 1993; Raulier et al., 1999; Jones and Thomas, 2007) influenced this dual maximization. At an A_max of 12·0 µmol m⁻² s⁻¹, the PPFD at which photosynthetic efficiency was maximal (i.e. Iɛ_max) was only 126·5 µmol m⁻² s⁻¹; leaves will have lower efficiency if PPFD incident on their surface is above this value. There were two noteworthy effects of constraining A_max in the simulations. First, there was a decrease in average ɛ in the open environment where the PPFD on a horizontal plane of 500 µmol m⁻² s⁻¹ was well above the maximum Iɛ_max. An increase in leaf inclination in these constrained individuals could have brought the PPFD incident on leaves closer to Iɛ_max, but the potential role of leaf inclination was limited by the relatively homogenous distribution of PPFD in the open and costs associated with a reduction in PPFD absorption. A second important aspect of constraining A_max was that, despite limitations in Iɛ_max, average ɛ improved considerably with LAI_ind. Self-shading increased with increasing LAI_ind; hence the constraint on A_max was gradually released because more leaves were exposed to I values closer to Iɛ_max. This suggests that in large A. saccharum individuals with an LAI of 5·7–6·1 (Ellsworth and Reich, 1993), most leaves in the crown should attain ɛ_max because self-shading will be higher. Several studies have reported that self-shading can favour plants because it can reduce photoinhibition (e.g. Howell et al., 2002; Kern et al., 2004). Our results show that, in addition, self-shading can be crucial for plants because it improves average marginal returns in PPFD (i.e. ɛ).

Despite the consequences of a constrained A_max on ɛ, our results appear consistent with the evolution of A. saccharum as a shade-tolerant species and suggest that optimization of ɛ should take place during most life stages in A saccharum. In gap conditions, seedlings were not influenced by constraints on A_max because the PPFD incident above the plants was 83·3 µmol m⁻² s⁻¹ and the maximum A_max of the most exposed leaves was optimized at 7·9 µmol m⁻² s⁻¹, which is below the maximum A_max of 12·0 µmol m⁻² s⁻¹ reported for A. saccharum. In forests were A. saccharum grows, PPFD in gaps varies between approx. 5·6 and 6·5 mol m⁻² d⁻¹ with an average instantaneous PPFD of only 122 µmol m⁻² s⁻¹ (Ellsworth and Reich, 1992; Beaudet et al., 2004). Thus, under gap conditions, or in understorey conditions with lower PPFD availability, A. saccharum saplings should be able to maximize leaf ɛ. However, under the relatively high PPFD of open environments simulated in this study (500 µmol m⁻² s⁻¹) or measured in the field (932 µmol m⁻² s⁻¹; Ellsworth and Reich, 1992), seedlings and saplings of A. saccharum will not attain ɛ_max in all leaves. Nonetheless, since the LAI_ind of 2·6 for the largest individuals that we simulated was well below the 5·7–6·1 LAI in mature A. saccharum (Ellsworth and Reich, 1993), adult trees should be able to maximize ɛ in leaves under high PPFD conditions because most leaves in the trees will be exposed to a lower PPFD due to self-shading. Thus, if we suppose that A. saccharum spends most of its juvenile stages in the shade or in small to medium gaps and only reaches the sunlit canopy as an adult with a large LAI_ind, then maximization of ɛ should occur during most life stages.

Another consideration is that optimization of ɛ will also be influenced by the temporal distribution of PPFD. In this study, we applied two static distributions of incoming light (standard overcast distribution in the open and within a forest gap). Yet, under natural conditions, instantaneous PPFD will often be highly variable in time due to both broken cloud cover and the effects of fine-scale canopy heterogeneity on insolation regime (e.g. sunflecks). Consequently leaves should have a lower ɛ than the one we estimated. Acclimation of the photosynthetic apparatus to PPFD availability is also a relatively slow process that can take days or weeks (Turnbull et al., 1993; Oguchi et al., 2003, 2006; Niinemets and Anten, 2009). Therefore, under natural conditions leaves will not be able to adjust to rapid (minutes/hours) changes in instantaneous PPFD and will only attain Iɛ_max during a fraction of the day. Here, average instantaneous leaf ɛ estimates were close to the maximum possible value (ɛ_max = 0·032) except for open-constrained plants which had values that varied between 0·018 and 0·025 (Fig. 2A). In contrast, field measurements of leaf ɛ measured over a time scale of days/weeks vary between approx. 0·07 and 0·026 depending on light conditions (e.g. cloudy/sunny) and the time scale (day/weeks) over which ɛ is integrated (Rosati and DeJong, 2003; Rosati et al., 2004; Posada et al., 2009; Koyama and Kikuzawa, 2010). These results suggest that in natural conditions leaves should acclimate so that PPFD incident on their surface remains as close as possible to Iɛ_max, but that deviations from Iɛ_max are unavoidable during parts of the day due to rapid changes in instantaneous PPFD.

An important outcome of the maximization of PPFD absorption and ɛ was the linear relationship observed between plant net photosynthesis and PPFD absorbed by the saplings (Fig 5). In all but open-constrained plants, leaf ɛ did not vary to a large extent: leaves used PPFD with similar efficiency regardless of their position in the plant crown. If all leaves converted PPFD into photosynthate with similar efficiency then, by extension, plant photosynthesis was proportional to the amount of PPFD absorbed by the crown. These results agree with studies that have shown that leaf ɛ stays constant along canopy PPFD gradients and could be used to scale photosynthesis from leaves to canopy (Rosati and DeJong, 2003; Rosati et al., 2004; Posada et al., 2009; Koyama and Kikuzawa, 2010). Our results are also consistent with the general observation that plant biomass production is linearly related to PAR absorbed by the canopy (Monteith, 1977). Thus, these biomass-absorbed PAR relationships should be functionally related to leaves concentrating their photosynthetic activity on the ascending portion of the photosynthetic light-response curves, where ɛ is highest (Monteith, 1994).

In summary, to maximize net photosynthesis, plants had to simultaneously maximize PPFD absorption at the plant level and maximize ɛ at the leaf level. Given the importance of net carbon gain for plant fitness (Givnish, 1988; Reich et al., 2003) we expect that plants have been under continuous selection pressure to attain these two conditions through adjustments in leaf angle, A_max and LAI_ind. Optimization of ɛ required adjustments at the level of individual leaves, which suggests that plants should have evolved a co-ordinating a mechanism between leaf angle and A_max that exposes a leaf to Iɛ_max. The existence of such mechanism, however, remains hypothetical and will have to be demonstrated experimentally. We also found that imposing constraints on A_max limited the range of PPFD environments where saplings could maximize their marginal returns on PPFD. Nevertheless, A_max of A. saccharum was relatively low compared with other species (Wright et al., 2004), suggesting that species with higher A_max could attain ɛ_max in a broader range of light environments. Lastly, our results support previous findings that have indicated that leaf ɛ should be a key functional trait behind the linear relationship between canopy photosynthesis and absorbed PPFD (Rosati and DeJong, 2003; Posada et al., 2009). We note, however, that our model was static (Anten and During, 2011) and mostly applicable to deciduous tree species that flush their leaves once in the season. Further studies should explore the extent to which these results will be influenced by changes in edaphic resource availability and nutrient resorption from senescent leaves (Franklin and Ågren, 2002; Hikosaka, 2003). It will also be important to evaluate the effect of covariation between leaf mass per area along PPFD gradients, interspecific interactions (e.g. Anten, 2005) and variability in spatial and temporal availability of PPFD on the optimal functional organization of plants at leaf and crown levels. These modelling exercises, combined with field experimentations, will keep strengthening our understanding of the key functional traits that determine the functional organization of plants.