Computational and experimental studies of the interaction between phosphopeptides and the C-terminal domain of BRCA1

Abstract

The C-terminal domain of BRCA1 (BRCT) is involved in the DNA repair pathway by recognizing the pSXXF motif in interacting proteins. It has been reported that short peptides containing this motif bind to BRCA1(BRCT) in the micromolar range with high specificity. In this work, the binding of pSXXF peptides has been studied computationally and experimentally in order to characterize their interaction with BRCA1(BRCT). Elucidation of the contacts that drive the protein-ligand interactions is critical for the development of high affinity small-molecule BRCA1 inhibitors. Molecular dynamics simulations revealed the key role of threonine at the peptide P+2 position in providing structural rigidity to the ligand in the bound state. The mutation at P+1 had minor effects. Peptide extension at the N-terminal position with the naphthyl amino acid exhibited a modest increase in binding affinity, what could be explained by the dispersion interaction of the naphthyl side-chain with a hydrophobic patch. Three in silico end-point methods were considered for the calculation of binding free energy. The Molecular Mechanics Poisson-Boltzmann Surface Area (MM/PB-SA) and the Solvated Interaction Energy (SIE) gave reasonable agreement with experimental data, exhibiting a Pearlman predictive index of 0.71 and 0.78, respectively. The MM-Quantum Mechanics-Surface Area (MM-QMSA) method yielded improved results, which was characterized by a Pearlman index of 0.78. The correlation coefficients were 0.59, 0.61 and 0.69, respectively. The ability to apply a QM level of theory within an end-point binding free energy protocol may provide a way for a consistent improvement of accuracy in computer-aided drug design.

Introduction

Mutations in the breast cancer susceptibility gene 1 (BRCA1) predispose women to breast and ovarian cancers. The BRCA1 gene product is a 220-Kda protein that has functional domains at its N and C termini [1]. Protein-protein interactions mediated by the C-terminus domains of BRCA1 (BRCT) regulate a number of DNA damage response functions. In response to DNA damage, proteins CCDC98/Abraxas, BACH1 and CtIP recognize and bind the BRCT(BRCA1) to regulate cell cycle checkpoints and activate DNA repair [2–7]. Preclinical studies suggest that cells with mutations in BRCT(BRCA1) are sensitive to DNA damage based therapeutics [8]. Therefore, use of small molecule inhibitors that functionally mimic these chemosensitizing mutations may be an attractive therapeutic strategy. Towards this goal we have identified short phosphoserine peptides (pSXXF) that bind BRCT(BRCA1) with low-micromolar affinities [9]. Structural and biochemical studies have shown that the peptides bind BRCT(BRCA1) in a two-point binding mode. The phosphate group on the serine residues makes hydrophilic contact with the backbone and side chain residues on the BRCT(BRCA1). The phenyl ring at the P+3 position resides in a hydrophobic pocket ~15Å away from the hydrophilic contact [10–17].

Structural studies show that (1) the oxygen atoms on the phosphate group makes three hydrogen bonds with the backbone nitrogen of G1655, the side chain oxygen of S1656 and the ε-nitrogen of K1702 and (2) the P+3 phenyl alanine sits in a hydrophobic pocket made by F1704, M1775 and N1774 [10–17] (cfr. Figure 1). To further dissect this interface we recently generated a library of tetrapeptides and evaluated their binding ability to BRCT(BRCA1) using a set of biochemical techniques. The results from this study suggests that all four residues contribute to BRCT(BRCA1) with the phosphoserine and phenylalanine (P+3) residue being the major contributors. More importantly even small changes to the tetrapeptide results in a loss of activity which is an indication of binding specificity [18]. A recent report also showed that BRCT(BRCA1) is the more selective for a phosphoserine as opposed to a phosphotheronine by more than 2 orders of magnitude, while the BRCT domains of TopBP1 shows no such selectivity [19].

Fig. 1.

Interactions of T1 (Ac-pSPTF-CONH₂) with BRCT(BRCA1) (From PDB 1T29)

Analysis of the BRCT(BRCA1)-phosphopeptide structures show several hydrophobic patches/crevices around the pSXXF binding site. These additional binding sites can be effectively exploited to improve the binding affinity for the target protein. One such binding site on BRCT(BRCA1) is found at the N-terminus of the pSXXF binding site formed by P1659, V1654, L1657 and F1662 (PVLF) residues. We hypothesize that conjugating a hydrophobic moiety (that occupies the PVLF cluster) to the N-terminus of the parent peptide pSPTF will lead to increased binding affinity for BRCT(BRCA1). In the first part of this study, we synthesized pentapeptide P7 (Ac-Nap-pSPTF-CONH₂), which includes a hydrophobic naphthyl functional group that could potentially occupy the PVLF cluster. In the second part of this study we performed molecular dynamics (MD) simulations to further characterize the interaction of BRCA1(BRCT) with a family of pSXXF phosphopeptides and P7, in order to assess the impact of point mutations in binding affinity and the dynamics of the system; the importance of properly accounting for flexibility in studying protein-ligand interaction is already solidly documented [20,21].

In the third part of the study, the binding free energy between the phosphopeptides and BRCA1(BRCT) was calculated in silico with three end-point methods. We were seeking to obtain an adequate balance of accuracy and computational speed. End-point methods are much more computationally affordable than Thermodynamic Integration [22] (TI) and Free Energy Perturbation [23] (FEP) method. We considered two classical-mechanics based methods, the Molecular Mechanics/Poisson Boltzmann-Surface Area [24,25] (MM/PB-SA), and the MM/PB-SA-derived Solvated Interaction Energy [26] (SIE) method. Completing the list of simulation methods, we used the recently developed Molecular Mechanics/Quantum Mechanics-COnductor-like Screening Model [27] (MM/QM-COSMO) in which rescoring of the classical MD trajectories is performed using a QM representation of the complete system and a continuum solvent model; an enhanced method to calculate entropic change based on configurational integrals is also used. For the sake of simplicity, we will refer from now on to this method as MM-QMSA. The MM-QMSA method was recently successfully applied to calculate binding free energies of phosphopeptides to the SH2 domain of human Lck p56 tyrosine kinase, adding to the list of recent applications of QM methods to study ligand binding [28–32].

Semiempirical methods have the advantage that they explicitly describe the effects of charge transfer and polarization, and which are the essential part of protein-ligand interaction [33,34]. Electronic polarization is responsible for the deformation of charge distribution due to an external electric field. Being formulated on the quantum mechanical framework, semiempirical methods provide a greater degree of parameter transferability than it is possible with classical force fields. Due to the significant progress in linear scaling quantum chemistry and computer hardware semiempirical QM calculations of biological systems are routinely affordable now. In this contribution continue the series of publications in which we utilize the advantage of using semiempirical methods to improve the accuracy of protein-ligand binding free energy prediction [27].

Materials and Methods

The phosphorylated peptides used in the current study were Ac-pSPTF-CONH₂ (T1), Ac-pSATF-CONH₂ (T2), Ac-pSPAF-CONH₂ (T3), Ac-EPTF-CONH₂ (T4), Ac-pSPVF-CONH₂ (T5), and Ac-Nap-pSPTF-CONH₂ (P7), where pS stands for phosphorylated amino acid serine, and Nap for the non-natural 2-naphthyl amino acid (Fig. 2). A list of these peptides is shown in Table 1.

Fig. 2.

Structure of the non-natural naphthyl amino acid (Nap)

Table 1.

Composition and binding free energy of T1–T5 and P7 peptides

Peptide	ID	ΔGexp (kcal/mol)	Ref.
Ac-pSPTF-CONH2	T1	−7.5	[9]
Ac-pSATF-CONH2	T2	−6.7	[9]
Ac-pSPAF-CONH2	T3	−5.9	[9]
Ac-EPTF-CONH2	T4	No binding	[9]
Ac-pSPVF-CONH2	T5	−7.8	[18]
Ac-Nap-pSPTF-CONH2	P7	−7.8	This work

Sample preparation

The plasmid construct (pAM15, gift from Luc Gadraeu, University De Sherbrook) encoding six his-tagged BRCA1(BRCT) domains of BRCA-1 (amino acids 1646–1859) was used to transform BL21(DE3) RIL (Stratagene). Protein expression was induced by 1mM IPTG and the recombinant protein was purified by nickel affinity chromatography (Qiagen). The protein was concentrated 10 fold using a molecular weight cut-off centricon filter (Millipore) at 4°C. The concentrated protein sample was then filtered using a 2 micron filter (Millipore). Homogeneity of the purified protein preparation was assessed by SDS-PAGE. The filtered samples were dialyzed 3 times, for 2 hours each, against phosphate buffer (50 mM KH₂PO₄ pH = 7.2) at room temperature. The concentration of the protein sample was determined by the BCA method using a Thermo-Pierce kit (Thermo Scientific Pierce BCA protein assay). All peptides used in this study were synthesized and purified by the Tufts core facility. The solid peptides were reconstituted in water and amino acid analysis was done to determine concentrations. Peptide solutions for the ITC study were made by freeze-drying the aqueous solutions and reconstituting the resulting solid in 50 mM KH₂PO₄ pH = 7.2.

Free energy measurements

A MicroCal VP-ITC instrument was used to study the thermodynamic factors arising from the protein-peptide interaction. All experiments were carried out at 25°C. The reference cell was filled with buffer (50 mM KH₂PO₄ pH = 7.2) remaining after the third dialysis. The reference power supplied to the cells was 15 µcal/sec. Varying concentrations of the peptide were loaded in the syringe (100 – 900 µM) and 10 – 30 µM of His-BRCT was loaded in the cell. All solutions were filtered through a 2 micron filter before loading into syringe or cell. Samples were also degassed with stirring for 10 min at 25°C using the Thermovac.

The first injection of 3µL of peptide into protein was followed by 29 – 10 µL injections spaced every 3 minutes apart. The solution was constantly stirred at 307 rpm. Heats in the range of 0.2 to 0.5µcal/sec were seen for most peptides. Peptide dilution curves were obtained by titrating the peptide into buffer under similar conditions. This curve was subtracted from the sample curve to get the corrected heats obtained for the reaction. The data obtained was integrated using Origin 7 software supplied with the MicroCal VP-ITC.

Molecular dynamics

MD simulations were performed on the C-terminal domain of the BRCA1 protein (PDB code 1T29). The protonation state of His, as well as flips of Gln and Asn amino acids, were visually inspected. Hydrogen atoms were added at physiological condition by using AMBER package leap module. After that, the protein acquired a net charge of −5 electron units. The crystallographic bound decapeptide was used as a template to prepare the starting geometries of the T1–T5 and P7 phosphorylated peptides. The peptides were terminated by acetyl and N-methyl groups, as standard in AMBER. This resulted in replacing the C-terminal amide by a N-methyl amide, what has a negligible effect on the outcome. The peptides carried a net charge of −2 electron units due to the phosphate group. The peptide T4 carried a charge of −1. Three distinct manually docked conformations of P7 were examined. In the first conformation the side chain of Nap was positioned toward amino acids L1657, T1658, P1659. In the second conformation the Nap side chain was arranged in a small pocket formed by amino acids M1689, K1690, T1691, C1697, and E1698. The third examined conformation had the naphthyl group directed toward the solvent; however during the MD simulation it spontaneously converged to the first conformation. Out of the two stable conformations the first one showed more favorable binding free energy, therefore it was retained, and the second and third conformations of P7 were excluded from the analysis.

MD simulations of the complexes were performed using AMBER ff99SB force field [35]. The missing parameters for Nap were derived using REDDB parameter development tool [36] (The AMBER parameter file for P7 is displayed in Supplementary Material). The AMBER parameters for pS were obtained from the work of Homeyer et al. [37]. Simulations were performed using the NAMD 2.6 [38] program, and an isothermal-isobaric NPT ensemble under periodic boundary condition. The protein-ligand complex was placed in cubic box of TIP3P water molecules [39] with a minimum of 13 Å solvent padding on each side and neutralized by adding sodium counterions by using the AMBER leap utility. A non-bonded cutoff of 12 Å was used, and the non-bonding interactions were switched on starting at 10 Å. The SHAKE algorithm [40] was applied to constrain bonds involving hydrogen atoms. The system geometry was minimized for 1000 steps under a harmonic restraint of 10 kcal/(mol/Ų) placed on the coordinates of the complex backbone atoms. Holding the restraints, the system was gradually heated to 300K within 30 ps and then equilibrated for another 50 ps after removing the restrains. Constant temperature was maintained by using a stochastic Langevin thermostat with a collision frequency of 1 ps⁻¹. A constant pressure of 1 atm was maintained by using the Langevin piston method with a period of 200 fs and a damping timescale of 100 fs. Long-range electrostatics was treated by the particle-mesh Ewald method using grid density of about 1 Å⁻¹. The integration time step was set to 2 fs and the dynamics trajectory was saved with 1 ps interval. Each complex was simulated for 10 ns. The NAMD generated trajectories were converted to AMBER format by using ptraj utility [41]. The first 5 ns of the NPT simulation were treated as equilibration part and the remaining 5 ns were considered as production trajectory.

MM/PB-SA free energy calculations

Protein-ligand binding affinities ΔG_bind were computed using the Molecular Mechanics Poisson Bolztmann Surface Area (MM/PB-SA) method, where the binding free energy is calculated as the difference between the bound and unbound states of protein and ligand, according to [24,25,42,43,27]

$$\mathrm{\Delta }{G}_{\mathit{\text{bind}}}=\mathrm{\Delta }\langle E_{\mathit{\text{MM}}}\rangle +\mathrm{\Delta }{G}_{\mathit{\text{solv}}}-T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}$$ (1)

where 〈…〉 is the ensemble average, E_MM is the gas-phase potential energy, ΔG_solv = Δ〈W〉 (W is the effective solvation energy which incorporates the solvent degrees of freedom [DOF]), and the third term accounts for the entropy change of the solute. The entropy change of the solvent is implicitly taken into account in ΔG_solv.

Binding free energy calculations were performed averaging over 1000 snapshots extracted from the production trajectory with 5 ps interval, after water, ions, and periodicity were removed. This separation is enough to consider uncorrelated motions and thus to report errors as the variance of energy averages [44]. Calculations were performed using a single-trajectory approach where unbound protein and ligand conformations are extracted from the complex trajectory. The single-trajectory approach has been shown to reduce noise in end-point calculations [45]. The gas-phase molecular mechanics energy term (E_MM) was calculated using the AMBER sander module [41] treating all non-bonded interactions explicitly, and with an internal dielectric constant of 1. There were no conserved water molecules in the protein-ligand area observed during the MD simulation, and therefore all water molecules were deleted for the purpose of free energy calculation.

The solvation free energy ΔG_solv was separated into polar and non-polar contributions as

$$\mathrm{\Delta }{G}_{\mathit{\text{solv}}}=\mathrm{\Delta }{G}_{\mathit{\text{solv}}}^{\mathit{\text{pol}}}+\mathrm{\Delta }{G}_{\mathit{\text{solv}}}^{\mathit{\text{np}}}$$ (2)

The polar contribution was calculated according to the PBSA method using the pbsa utility in AMBER [41]. The dielectric constant for water was taken as 80. The calculations were performed using atomic radii specifically optimized for Poisson-Boltzmann implicit solvent model by Swanson et al. [46]. The missing radii were derived by analogy with the published atom types given in the form of AMBER atom names, and were assigned the following values (in Å): CH3(Ace) = 2.595; CZ*(Trp) = 1.651; CH2(Trp) = 1.651; CD(Glu) = 1.942; OXT(C-terminal) = 1.516; H4, H5(His, Trp) = 0.840, CB(Nap) = 2.087, CG(Nap) = 1.651, C*(Nap) = 1.837, where the amino acid name is shown in brackets and “*” indicates wildcard in the atom name. The following radii for the phosphate group were taken from the work of Tsui et al. [47] (in Å): OG = 1.500, P = 1.850, O1P = 1.500, O2P = 1.500, and O3P = 1.500.

The non-polar contribution, which accounts for the energy to build the cavity and the dispersion interaction, was determined using the solvent-accessible-surface-area (SASA) approach,

$$G_{\mathit{\text{nonp}}}=\gamma \text{ SASA}$$ (3)

where the default value of the surface tension coefficient γ was used [0.0072 kcal/(mol * Ų)]. The surface area was computed with the molsurf program in AMBER, using a solvent probe radius of 1.4 Å.

The entropic contribution ΔS_bind to protein-ligand binding free energy was computed as a sum of rigid-body rotational ΔS_rot and translational ΔS_tran, and vibrational ΔS_vib terms according to

$$\mathrm{\Delta }{S}_{\mathit{\text{bind}}}=\mathrm{\Delta }{S}_{\mathit{\text{rot}}}+\mathrm{\Delta }{S}_{\mathit{\text{tran}}}+\mathrm{\Delta }{S}_{\mathit{\text{vib}}}$$ (4)

Assuming that the ligand rotational and translational DOF are uncorrelated and decoupled from the protein motion, the rotational and translational entropy terms are computed using the following equations [48,49,27]

$$\mathrm{\Delta }{S}_{\mathit{\text{rot}}}=\frac{3}{2}R+R\text{ ln}\left[\frac{1}{8{\pi }^2}{(2\pi )}^{3/2}\sqrt{\langle \mathrm{\Delta }{\alpha }^2\rangle \langle \mathrm{\Delta }{\beta }^2\rangle \langle \mathrm{\Delta }{\gamma }^2\rangle }\right]$$ (5)

$$\mathrm{\Delta }{S}_{\mathit{\text{tran}}}=\frac{3}{2}R+R\text{ ln}\left[C^0{(2\pi )}^{3/2}\sqrt{\langle \mathrm{\Delta }{x}^2\rangle \langle \mathrm{\Delta }{y}^2\rangle \langle \mathrm{\Delta }{z}^2\rangle }\right]$$ (6)

where R is universal gas constant, C° is the standard concentration of 1M or 1 molecule per 1660 ų, Δx², Δy², Δz² are the variances of the ligand center of mass from its average position when the complex snapshots are aligned by protein atoms, and Δα², Δβ², Δγ² are the variances of ligand rotation angles around the x, y, and z axes in the protein frame. The rigid-body entropy loss of the ligand was computed for 5 independent windows each containing 200 snapshots along the MD trajectory using the algorithm described by Swanson et al. [48], and block-averaging the computed values. The vibrational entropy change ΔS_vib upon complex formation was computed using AMBER’s nmode utility as the difference in vibrational entropy of complex and its constituents within the harmonic oscillator approximation.

$$\mathrm{\Delta }{S}_{\mathit{\text{vib}}}=S_{\mathit{\text{vib}}}^{\mathit{\text{cpx}}}-S_{\mathit{\text{vib}}}^{\mathit{\text{pro}}}-S_{\mathit{\text{vib}}}^{\mathit{\text{lig}}}$$ (7)

The snapshot geometry for the purpose of normal mode analysis was minimized to meet a RMS gradient of 0.0001 kcal/(mol*Å) using a distance-dependent dielectric constant of 4r. The vibrational entropy was averaged over 1000 snapshots. The conformational entropy change corresponding to the loss of dihedral DOF upon complexation was not considered due to its lesser significance, especially for the calculation of relative binding free energy of series of congeneric ligands [27]. This was confirmed by a Monte Carlo simulation with minimization [50] of T1 using a continuum solvation model, similar to what has been presented recently [27] (see Refs. [51–53] for computational details). An upper bound for the conformational entropy change could be obtained assuming that the low energy conformations within 5 kcal/mol were equally visited, and that the bound state were characterized by a single conformation, thus obtaining RTlnN_conf ~ 2.3 kcal/mol. This value is smaller than the rigid body and vibrational entropies (cfr. Table 2). However, only the lowest energy states will be heavily populated –thus reducing the actual number of distinct accessible conformational states, and the bound ligand might keep some residual entropy. So, the actual change in conformational entropy would be smaller than 2.3 kcal/mol.

Table 2.

Calculated protein-ligand binding free energies and their components^a,^b

Ligand	TΔSc	ΔH (PB)d	ΔH (QM)e	ΔG (PB)f	ΔG (SIE)g	ΔG (QM)h	ΔG (Exp)
T1	−9.0 (0.2)	−40.7 (0.2)	−15.9 (0.2)	−31.7 (0.3)	−7.8 (0.01)	−6.9 (0.3)	−7.5 (0.2)
T2	−9.5 (0.4)	−38.0 (0.3)	−12.6 (0.2)	−28.4 (0.5)	−7.3 (0.02)	−3.1 (0.5)	−6.7 (0.3)
T3	−10.1 (0.2)	−37.2 (0.2)	−13.7 (0.2)	−27.0 (0.3)	−7.4 (0.01)	−3.6 (0.3)	−5.9 (0.2)
T4	no binding
T5	−8.8 (0.4)	−36.4 (0.2)	−16.5 (0.2)	−27.6 (0.4)	−7.5 (0.01)	−7.7 (0.5)	−7.8 (0.1)
P7	−12.9 (0.2)	−47.8 (0.2)	−17.3 (0.3)	−34.9 (0.2)	−8.7 (0.01)	−4.4 (0.3)	−7.8 (0.1)
PIi	n/a	n/a	n/a	0.71	0.78	0.78	n/a

^aValues of energies in kcal/mol

^bThe values in brackets represent the error of the mean.

^cEntropic contribution calculated according to eq 4.

^dEnthalpic part from MM/PB-SA calculation including internal and solvation free energy.

^eEnthalpic part from MM-QMSA calculation including internal energy and solvation free energy.

^fBinding free energy from MM/PB-SA calculation (eq 1)

^gBinding free energy from SIE calculation (eq 8)

^hBinding free energy from MM-QMSA calculation (eq 9).

ⁱPearlman’s predictive index.

SIE scoring calculations

The binding affinity was also computed using the SIE empirical scoring function with its parameters being fitted to experimental binding affinity of 99 protein-ligand complexes [26],

$$\mathrm{\Delta }{G}_{\mathit{\text{bind}}}(\alpha ,{\epsilon }_{\mathit{\text{in}}},\rho ,\gamma ,C)=\alpha [E_{\mathit{\text{vdw}}}+E_{\mathit{\text{coul}}}({\epsilon }_{\mathit{\text{in}}})+\mathrm{\Delta }{E}_{\mathit{\text{rf}}}(\rho ,{\epsilon }_{\mathit{\text{in}}})+\gamma \mathrm{\Delta }\mathit{\text{MSA}}(\rho )]+C$$ (8)

The SIE function is internally based on the standard MM/PB-SA approach with additional empirical scaling applied to the energy terms. The computations were performed using the sietraj utility in the SIE program package with default parameters [54] by postprocessing 1000 snapshots of protein-ligand complexes written in the format of AMBER trajectory file after water, ions, and periodicity were removed. The reaction field contribution (ΔE_rf) was obtained by solving the Poisson-Boltzman equation by an integrated solver employing the AMBER force field ff03 [55,56] parameters with atomic radii scaled by factor ρ = 1.1, and using an internal dielectric constant ε_in = 2.25, and an external dielectric constant ε_out = 78.5. The non-polar contribution was computed on molecular surface area (MSA) by sietraj tool and using surface tension coefficient γ = 0.012894 kcal/(mol*Ų). The computed sum of internal energy (E_vdw+E_coul), the reaction field (ΔE_rf), and the non-polar contribution (γΔMSA) were scaled by a factor α = 0.104758. The result was augmented by a constant C=−2.89 kcal/mol, thus producing the final value of the binding free energy. No explicit entropy term is included in the SIE formalism which relies on enthalpy-entropy cancellation.

MM-QMSA calculations of binding free energy

QM calculations were performed according to the MM-QMSA approach [27], where the binding free energy is calculated in an analogue way to eq 1 as

$$\mathrm{\Delta }{G}_{\mathit{\text{bind}}}=\langle \mathrm{\Delta }{H}^{\mathit{\text{COSMO}}}\rangle -T\mathrm{\Delta }{S}_{\mathit{\text{bind}}}$$ (9)

where H^COSMO includes the QM energy of solute in solvated state (calculated using the COSMO continuum solvent model [57], E^COSMO) and the non-polar contribution to the solvation energy according to

$$H^{\mathit{\text{COSMO}}}=E^{\mathit{\text{COSMO}}}+G_{\mathit{\text{solv}}}^{\mathit{\text{np}}}$$ (10)

The term ΔH^COSMO represents the enthalpy difference between the complex and its constituents, and it also accounts for the entropic change of the solvent. The entropy term TΔS_bind in eq (9) was computed as described above for MM/PB-SA.

The QM-COSMO calculations were performed on the same structures which were used in MM/PB-SA and SIE calculations. Complex, protein, and ligand were subjected each to 100 steps of geometry relaxation using the continuum solvent model COSMO while treating the entire system at quantum mechanical level. Performing a longer relaxation may lead to structure deviation from the experimental geometry [58,59], which is related to insufficient optimization of semiempirical Hamiltonians for condensed phase. This is not surprising considering the novelty of the application of semiempirical methods to macromolecular systems. Hence, in order to only relieve the structural strain we performed a limited geometry optimization as was previously done by us [27] and others [60].

QM calculations were performed by using the LocalSCF program package [61] with implicit solvent model COSMO and the PM3 Hamiltonian [62] (cfr. Refs. [27,63] for details). The COSMO cavity surface was constructed as a union of atomic van der Waals radii which were previously optimized to fit hydration free energy of 98 small molecules [27]. The surface charges were generated utilizing 32 triangular segments assigned to non-hydrogen atoms and 12 segments assigned to hydrogen atoms. The non-polar contribution to hydration free energy was computed for solvent accessible surface using a solvent probe radius of 1.3 Å, and a surface tension coefficient set to 0.0020 kcal/(mol*Ų) as previously described [27]. The exchange interactions and the product of Fock matrix with localized molecular orbital vectors were computed using a 6 Å cutoff. Empirical corrections were applied to maintain the planarity of peptide group (keyword MMOK) and to correct the geometry of 5- and 6-membered saturated rings (keyword MMCCROK). Long-range electrostatics was treated via the fast multipole method under default program settings.

In semiempirical QM theory electron-repulsion integrals implicitly include the effect of dispersion interactions via model parameters [64]. Nevertheless, the traditional semiempirical Hamiltonians underestimate the strength of mid-range dispersion interactions [65]. Improving this term would require a complete a reparameterization of the Hamiltonians. A simpler but still efficient approach to account for dispersion interactions is via an empirical Lennard-Jones (LJ) potential which is optimized for condensed phase and actively employed in classical force fields (similar approaches can be found elsewhere [66,67,65]). Despite the successes of adding a LJ dispersion term to the QM energy on small molecules [68], no rigorous tests have been performed in the literature on real macromolecules. Our QM MD simulations [69] with full LJ potential resulted in structure collapse. This suggests that the classical LJ contribution has to be scaled down, in agreement with others [67]. Indeed, part of the dispersion contribution is already incorporated into semiempirical Hamiltonians via parametrization. In the present QM calculation, the lack of dispersion interactions in the PM3 Hamiltonian was compensated by adding 50% of LJ interaction energy computed using CHARMM22 parameters [70]. This improved the ability of the model to better account for dispersion interactions while avoiding double counting of close-range dispersion interactions which are already partially included in the semiempirical methods. The LJ interactions were applied to all atoms of the BRCA1(BRCT) complexes and their constituents including the step of geometry optimization, and switched on the interval from 8 to 10 Å using CHARMM switching function [71].

Results and Discussion

The P7 pentapeptide was synthetized and its binding free energy measured by ITC (cfr. Materials and Methods section, and Table 1). We observed a modest increase (ΔΔG = 0.3 kcal/mol) in the binding affinity of P7 when compared to T1. This result is consistent with our hypothesis that the Nap side chain occupies a hydrophobic cluster on the N-terminus of the pSXXF binding site and results in a slightly tighter binding ligand.

MD simulations were performed on the series T1–T5 and P7 phosphopeptides complexed with BRCA1(BRCT). The root mean square difference (RMSD) of the protein backbone non-hydrogen atoms compared to the crystallographic geometry of the BRCA1(BRCT) protein is displayed in Fig. 3. BRCA1(BRCT) in complex with pSPVF (T5) showed the lowest RMSD of 1.2 Å among the series. The protein in other complexes is characterized with average RMSD of 1.5 Å. To test the feasibility of the replacement of pS by another negatively charged group, we tried the commonly used Glu substitution of pS in ligand T4. Unlike other studied peptides, T4 peptide did not form a stable complex with BRCA1(BRCT). After a few nanoseconds, T4 started separating from BRCA1(BRCT) and eventually left it. It has been recently found experimentally that T4 does not bind BRCA1(BRCT), and thus our MD simulation is consistent with the experimental data [9]. This result confirms that pS plays a key role in high affinity peptide binding to BRCA1(BRCT).

Fig. 3.

RMSD of protein backbone atoms of BRCA1(BRCT) complexes along MD simulations using the crystallographic structure as a reference.

Characterization of Ac-pSPTF-CONH (T1) binding to BRCA1(BRCT)

During the MD simulations of T1 bound to BRCA1(BRCT), it was observed that the pS group of T1 forms a salt bridge with the side chain of K1702, and two hydrogen bonds with the side chain of S1655 and the peptide hydrogen of G1656 in the hydrophilic pocket of the receptor. These three interactions are stable throughout the MD simulation with average interatomic distances OP(pS)…N_z(K1702) = 2.8 ± 0.1 Å, OP(pS)…O_γ(S1655) = 2.6 ± 0.1 Å, and OP(pS)…N(G1656) = 3.1 ± 0.2 Å The pattern of hydrogen bonds established between pS and the receptor is illustrated on Fig. 4. It was also observed that these interactions were preserved among the other studied peptides (T2, T3, T5, P7). The MD simulations show no direct interaction between T1 and the side-chain of T1700, which contributes to delineate the pS pocket.

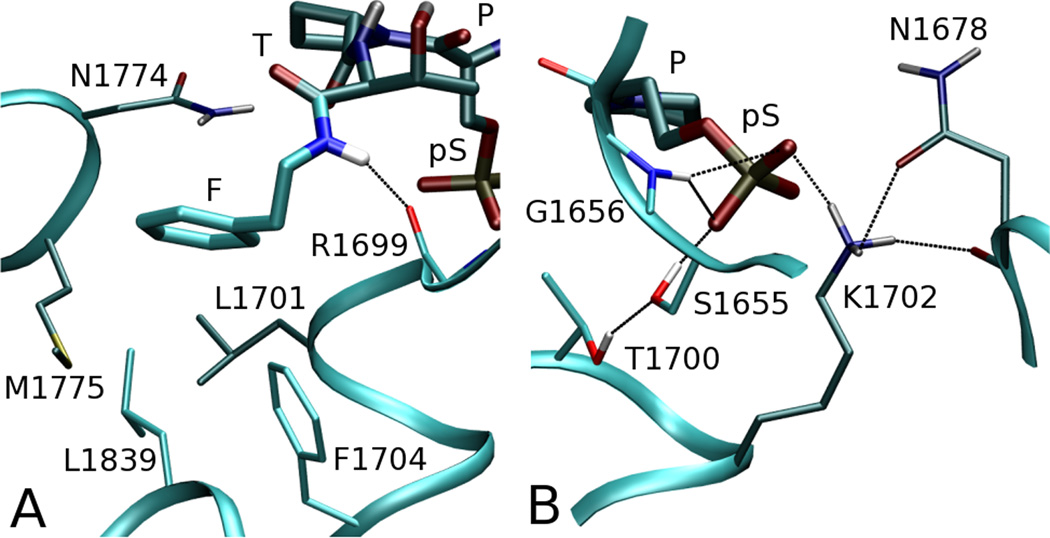
Fig. 4.

T1-BRCA1(BRCT) interactions. Peptide T1 and receptor amino acids involved in the interaction are shown in licorice mode; distant amino acids are displayed in darker color. Color code for T1: H, white; C, green; N, blue; O, red. A. T1(F)-BRCA1(BRCT) interactions. The receptor hydrophobic pocket is formed by L1701, F1704, N1774, M1775, and L1839. The peptide hydrogen of F makes a hydrogen bond with the carbonyl oxygen of R1699. B. T1(pS)-BRCA1(BRCT) interactions via hydrogen-bonds OP(pS)…O_γ(S1655), OP(pS)…N(G1656), OP(pS)…N_z(K1702). The hydrophylic pocket of the receptor is additionally preconditioned for these interactions by hydrogen bonds S1655…T1700 and N1678…K1702. Figure was generated with VMD [72] and Pov-Ray.

A second point of contact between T1 and BRCA1(BRCT) is at the P+3 (F) position (Fig.4A). The phenyl ring of Phe is anchored in a hydrophobic pocket formed by amino acids L1701, F1704, N1774, M1775, and L1839. There is also a hydrogen bond between the backbone HN of Phe and the carbonyl oxygen of R1699, characterized by N(F)…O(R1699) = 3.0 ± 0.2 Å.

The above described interactions of pS and P+3 with the receptor are qualitatively observed in the trajectories of all studied complexes, and constitute the primary mode of peptide-BRCA1(BRCT) interaction. These data are consistent with previous experimental finding of primary role of pS and Phe in binding to BRCA1(BRCT) [9]. From the tight fit of Phe(P+3) side-chain within the hydrophobic pocket of the receptor, maintained throughout the simulation (Fig 3), it is apparent that this pocket would not tolerate larger side-chains (cfr. Fig. 4), in agreement with recent experimental data [18].

The role of mutation at the P+2 position in protein-ligand binding

The role of Thr(P+2) in T1 (pSPTF) was studied by mutating Thr to Ala (T3), and to valine (T5). According to isothermal calorimetric data, the Ala mutation caused a loss of 1.6 kcal/mol in binding affinity, whereas the Val mutation slightly enhanced binding by 0.3 kcal/mol [9]. These data confirm the important role that the P+2 position plays in protein-ligand binding. To show the impact of mutations at the P+2 site, the Thr→ Ala mutation (T3) is analyzed relative to T1. The interaction of pS with the receptor remains unchanged; in the T3 complex, the average interatomic distances between phosphate oxygen atoms and the receptor amino acids are practically the same as in T1 complex (data not shown). Indeed, considering the strength of the electrostatic interaction between the charged phosphate group with three polar amino acids of the receptor it is hardly reasonable to expect significant perturbations at this site (Fig. 4). However, the analysis of the averaged trajectories of peptides T1, T3, and T5 bound to BRCA1(BRCT) shows important structural differences (Fig. 5).

Fig. 5.

Superimposed averaged structures of the bound conformation of T1, T3, and T5. In T1, H is white, C is green, N is blue, O is red; T3 is in orange, and T5 is in gray. P+2 is Thr, Ala, and Val in T1, T3 and T5, respectively. The alignment was performed using the backbone atoms of residues R1649 – R1751, which represent half of the receptor size, and include the hydrophilic pocket of BRCA1(BRCT) which strongly interacts with pS, and which is structurally unaffected by the mutation at the P+2 position. Figure was generated with VMD [72] and Pov-Ray.

It is readily seen that backbone atoms from pS to the P+2 residue show nearly a perfect structural alignment. Changes in the bound conformation start showing up right after the mutation at the P+2 position (Fig. 5). In the Thr→Ala mutation in T3, Phe bends from its position in T1. This could happen due to Ala offering less steric hindrance to dihedral rotation at the P+2 position than that of Thr (T1) or Val (T5). Moreover, a Monte Carlo-based conformational search on free ligands T1 and T3 using generalized-Born implicit solvent model showed that T3 had 50% more accessible rotameric states than T1 or T5 (see Refs. [51–53] for computational details). This shows that T3 ligand is intrinsically more flexible than T1. Thus, T3 can interact with the receptor in different ways than T1. The superposition of complexes based on protein backbone atoms of amino acids R1649 – R1751 is shown in Fig. 6.

Fig. 6.

Superimposed averaged complexes of T1, T3, and T5 with BRCA1(BRCT). In T1, H is white, C is green, N is blue, O is red; T3 is in orange, and T5 is in gray. In T1 and T5, the side chain of R1699 makes salt-bridge interactions with D1840 and D1739. In T3, the hydrogen bond with D1840 is lost. The amide hydrogen at the P+3 position (F) makes a hydrogen bond with the carbonyl oxygen of R1699. Figure was generated with VMD [72] and Pov-Ray.

Compared to T1 and T5, the Ala substitution in T3 increases the average distance between the N of Phe(P+3) and the C_α of E1698 from 6.9 ± 0.3 and 6.7 ± 0.5 Å in T1 and T5, respectively, to 7.5 ± 0.4 Å in T3 (see Fig. 6). Thus, the hydrogen bond between the backbone HN of Phe and the carbonyl O of R1699 is geometrically shifted in T3 compared to T1 and T5 (see Fig. 6). In T1 and T5, the side chain of R1699 establishes salt-bridges with the side chains of D1840 and D1739, which are stable throughout the simulation (average distances in T1 are NH(R1699)…O_δ(D1840) = 1.9 ± 0.3 Å, NH(R1699)…O_δ(D1739) = 1.9 ± 0.1 Å, and 1.9 ± 0.4 and 2.0 ± 0.2 Å in T5, respectively). In T3, the salt bridge between R1699 and D1840 is disrupted, and only the salt bridge between R1699 and D1739 is retained (average distance NH(R1699)…O_δ (D1739) = 1.9 ± 0.2 Å). Another significant difference in T3 compared to T1 and T5 occurs at the P+3 position. In T1 and T5, the angle χ_{N−Cα−Cβ−Cγ} is 72 ± 9° and 60 ± 10°, respectively. In T3, this angle is 169 ± 12° (Fig. 6), meaning that the Phe side chain is oriented quite differently than that in T1 and T5.

To expand our analysis, we considered the two arms of the receptor characterized by residues R1753 – P1859 (right arm, which contains the hydrophilic pocket interacting with pS), and R1649 – R1751 (left arm, which contains the hydrophobic pocket interacting with Phe, P+3) connected by a hinge at A1752. The relative position of the arms can be characterized by the angles defined by the C_α atoms of E1698–A1752–E1836 and S1655–A1752–N1774 (see Fig. 7). When T1 is bound, these angles are 49 ± 2° and 37 ± 1°, respectively, with similar angles for T5 (47 ± 2° and 41 ± 2°, respectively). In T3, however, the values are 55 ± 3° and 47 ± 3°, respectively. This means that in T3 the arms moved apart relative to their position in T1 and T5. Due to this opening, the average distance between the C_α atoms of E1698…E1836 and S1655…N1774 in T3 increased by 1.5 and 3.0 Å, respectively, compared to those in T1. If the backbone atomic coordinates of the left and right arms were treated separately, they would align nearly perfectly for T1, T3, and T5 complexes, what supports our division of BRCA1(BRCT) in two quasi-rigid arms.

Fig. 7.

Representation of the T1-BRCA1(BRCT) complex as consisting of left and right arms connected by a hinge around A1752. T1 is shown in licorice mode; H is white, C is green, N is blue, O is red. Upon T1 or T5 binding, the two arms stay closer than when T3 binds. Figure was generated with VMD [72] and Pov-Ray.

Two factors could be identified related to the widening upon T3 binding. The Ala mutation at the P+2 position in T3 induces a change in the Phe(P+3) side-chain orientation, and a disruption of the salt-bridge between the side-chains of R1699…D1840. The new orientation of Phe requires more room to accommodate the ligand conformation, while the broken salt-bridge no longer contributes to holding arms together. Both these factors may originate in the increased flexibility of T3 compared to T1 and T5. It is not possible, however, to state which of these two factors is dominant. Additional studies will be necessary to decipher the mechanism of receptor widening.

The residual flexibility of T3 is further propagated to increase the rotational freedom of the NMe group, which terminates the peptide at the P+3 position. According to MD data, the standard deviation of the NMe group torsion angle as a measure of fluctuation is 17° in the T1 complex, whereas it increases to 50° in the T3 complex.

Our MD simulations confirmed that the Thr side-chain indeed makes no contacts with the receptor, as was previously postulated based on the analysis of X-ray structure of complex of BACH1 dodecapeptide with BRCA1(BRCT) [9]. Indeed, the average distance O_γ(T)…O_ε(E1698) for T1 is 4.3 ± 1.0 Å. Moreover, we could not observe any intra-molecular hydrogen bonds involving Thr at P+2 in T1, either O_γ(T)…H(P+4) or H_γ(T)…O(pS), what indirectly supports the relative insensitivity to the Thr→Val mutation (see below).

The role of Thr in peptide binding to BRCA1(BRCT) was additionally studied via the Thr→Val mutation (T5). The isothermal calorimetric study showed practically the same binding affinity for T5 as that of T1. Our structural analysis of the T1 and T5 complexes also shows overwhelming similarity between these two systems, while the Monte Carlo conformational search exhibited very similar number of accessible rotamers compared to T1. Therefore we conclude that this mutation makes practically no difference over T1. These results are in agreement with the experimental studies showing a minor role of the hydroxyl group of Thr on binding affinity [18].

The role of proline at the P+1 site

We also studied the Pro→Ala mutation at the P+1 position (T2). The complex of T2 with BRCA1(BRCT) shows the same structural characteristics discussed above for T1. This is consistent with the experimentally observed minimal impact that this mutation has on binding free energy. The observation that the Pro→Ala mutation (T2) brings less structural changes in the complex than the Thr→Ala one (T3), agrees with the previously made conclusion about the minor role of Pro in the ligand structure [9]. The Pro→Ala makes the ligand intrinsically more mobile which may explain the slight loss in the binding affinity of T2 over T1. This is consistent with an earlier conclusion based on the analysis of experimental data that Pro(P+1) and Thr(P+2) serve primarily as spacers between pS and Phe, thus providing optimal peptide backbone conformation to maximize the interaction of pS and Phe with the receptor [13]. The results of our binding free energy calculation for T1, T2, and T3 (Table 2) are also in agreement with experimental data [13] showing that the loss in binding affinity due to mutations at P+1 and P+2 positions is accompanied with an increase of entropy compared to T1.

Probing the hydrophobic pocket near the phosphate binding site

In earlier docking studies on BRCA1(BRCT) it was hypothesized that the BRCA1(BRCT) hydrophobic site constituted by V1654, L1657, and F1662 could be used to enhance protein-ligand binding affinity, by designing a ligand occupying this pocket [9]. To explore this possibility we extended the ligand at pS by adding a hydrophobic non-standard amino acid containing a naphthyl side chain (pentapeptide P7). The average MD structure of the P7 complex shows that the naphthyl group cannot reach that cleft due to geometric constraints stemming from the ligand anchored in two places (by the pS phosphate, and by the Phe(P+3)). Forcing the naphthyl fragment to stay in that hydrophobic pocket would require displacing the phosphate group away from the electrophilic pocket, which is energetically unfavorable. Therefore, the naphthyl fragment adopts a conformation in which it makes favorable dispersion interactions with L1657, T1658, and P1659 of BRCA1(BRCT), what could explain some improvement in the binding affinity of P7 over that of T1. A longer and more flexible side chain than naphthyl would be necessary to reach the hydrophobic pocket lined up by V1654, L1657, and F1662 (cfr. Fig. 8).

Fig. 8.

Averaged structure of P7-BRCA1(BRCT) complex showing the solvent accessible surface of the receptor, and P7 in licorice mode. The positively charged amino acids are shown in blue on the surface, negatively charged in red, polar in green, and hydrophobic in white. In P7, C is green, N is blue, O is red. Geometrical restraints of the ligand backbone prevent the Nap side chain to reach the hydrophobic pocket defined by V1654, L1657, and F1662. Nap side-chain makes hydrophobic interactions with T1658 and P1659. Figure was generated with VMD [72] and Pov-Ray.

Protein-ligand binding free energy calculation

Computational data on binding free energy are presented in Table 2. MM/PB-SA predicts too favorable energies in the range of −30 kcal/mol, which exceeds the range of experimental values by an average factor of four. To estimate the quality of the prediction of relative energies we employed Pearlman’s predictive index (PI) [73]. This index assumes continuous values in the [−1, 1] range, where a value of −1 corresponds to systematically wrong predictions, zero corresponds to random, and a value of +1 corresponds to the ideal agreement in relative binding free energies between computational and experimental data. The PI associated with MM/PB-SA calculations is 0.71, representing a satisfactory performance.

The tendency to overestimate binding affinities is a known deficiency of the MM/PB-SA method [26,74]. In an attempt to improve its predictability, Swanson et al. [46] performed an optimization of the atomic radii on a series of 14 polyalanine peptides using computed hydration free energies from TI simulations, given the absence of direct experimental data for such complex systems. These atomic radii were used in the present MM/PB-SA calculations showing a reasonable outcome in terms of relative binding free energy.

An alternative approach to improve the agreement between computational and experimental data was suggested by Purisima and co-workers [54,26], scaling down the MM/PB-SA computed values, resulting in the empirical scoring function SIE. The corresponding binding free energies are presented in Table 2. There is an improvement in the absolute values of the computed binding free energies in closer agreement with experimental data. SIE predictions are characterized by a Pearlman index of 0.78. On the technical side, SIE calculation involves exactly the same steps as the standard MM/PB-SA calculation, which is evident from eq 8. Given its better accuracy, the SIE method may serve as a practical alternative to the standard MM/PB-SA method in computer-aided drug design [54]. However, a limiting factor of the SIE method is its explicit reliance on enthalpy-entropy compensation, which may not be complete. Besides, scaling down the Poisson-Boltzmann reaction field by a factor of ~10 (α = 0.104758 in eq 8) masks the potential deficiencies of the used electrostatic model. This is why it is important to search for first-principle methods which offer a better computational efficiency and a wider range of applicability than FEP and TI.

One alternative approach is the QM description of the electrostatic interactions in protein-ligand systems. With the advent of modern computer hardware it is technically feasible to perform MM/PB-SA-like calculations on protein-ligand complexes using QM and a continuum solvent model. Such computations were previously reported by us on a series of phosphopeptide inhibitors of p56 LCK SH2 domain using 1000 snapshots generated by MD with AMBER force field, followed by geometry optimization of the snapshots with the semiempirical PM3 Hamiltonian coupled with the implicit solvent model COSMO [27]. In this work we applied a similar strategy to calculate the binding free energy of peptides to the BRCA1(BRCT) system using QM.

The results of the MM-QMSA binding free energy calculations on BRCA1(BRCT) complexes are presented in Table 2, showing good agreement with experimental data. Similar to SIE, the QM predictions are characterized by an improved Pearlman index of 0.78 relative to the standard MM/PB-SA calculation (Pearlman index of 0.71). However, unlike SIE, the improvement in accuracy of prediction is obtained from a first-principle calculation method. This is a significant result because no other first-principle method (FEP or TI) may be applied to BRCA1(BRCT) and phosphopeptide ligands due to large net charge carried by the protein and ligands. The correlation coefficients for MM/PB-SA, SIE and MM-QMSA are 0.59, 0.61 and 0.69, respectively. Although the number of points is small to draw conclusions with statistical meaning, it shows an improvement in going towards QM. In this work, the LJ contribution scaled by 50% was found to provide the best performance across the set of peptides. However, the difference in calculated and experimental binding free energies, especially for T2 and P7 (~3 kcal/mol), shows that additional improvement could be achieved by improving the balance between the QM term and the dispersion contribution.

First-principle computation of protein-ligand binding affinity is particularly challenging in the present case of phosphopeptides binding to BRCA1(BRCT) due to the strong electrostatic interactions; simulations in such systems might require accounting for the effects of electronic polarization in protein-ligand and solute-solvent interactions, what is directly accounted for in the QM framework due to the treatment of electrostatic interactions via charge density which self-consistently adjusts to the electric field of the environment. Moreover, it is well-known that the description of biological systems can be improved by accounting for polarization effects [75,76].

In fact, the success of a QM treatment of electrostatic interactions as part of the MM/PB-SA-like computational protocol also suggests that electrostatic properties of protein and ligand in the free state are different from their state in the protein-ligand complex. This could explain the sensitivity of MM/PB-SA to insufficient charge transferability, displaying in some cases an improper balance between the intermolecular electrostatic interaction and the electrostatic contribution of the solvent calculated via a continuum solvent model. The importance of ad hoc derived charges has been already shown [77].

While the application of polarizable force fields in binding free-energy calculation is still an area of ongoing development, it is already feasible to account for electrostatic polarization in protein-ligand complexes by means of semiempirical QM methods.

Conclusions

The computational study of inhibitor binding to BRCA1(BRCT) confirms that the studied peptides are anchored by a two-point interaction involving the phosphate group of pS and the Phe residue at the P+3 position. It was observed that mutation at the P+2 position controls structural flexibility of the peptide, which is less affected by mutations at the P+1 position. We also observed that A1752 could be considered a hinge between the left and right arms of the receptor: upon binding of peptides T1 and T5, which are characterized by a lesser backbone flexibility, these arms stay closer together. The Thr→Ala mutation at the P+2 position in T3 leads to receptor opening. No intra-peptide hydrogen bond was observed throughout the simulation involving Thr(P+2) in T1. Thus, it is not surprising that the Thr→Val mutation (T5) had very similar experimental binding energy, and that the simulation of T5 bound to BRCA1(BRCT) exhibited a very similar behavior to that of T1. From ITC measurements, it was determined that P7 displayed a modest increase in binding free energy compared to T1, and the dispersion interactions of the Nap side chain of P7 within the hydrophobic patch observed during the MD simulations correlate well with experiments. The pSPTF and pSVTF signatures exhibited the highest affinities, and showed conserved interactions with the protein during the simulations. This, coupled with the fact that to reach the hydrophobic pocket lined up by V1654, L1657, and F1662 (cfr. Fig. 8) a longer side chain than naphthyl would be necessary, led to the synthesis of a small library of peptidemimics with varied hydrophobic groups and longer linkers attached to the N-terminus of the phosphoserine residue on pSPTF and pSVTF scaffolds. Evaluation of this library may lead to the identification of a high affinity BRCT(BRCA1) binding peptide mimic (in progress).

Calculations with the MM/PB-SA protocol using optimized atomic radii resulted in relative binding free energy calculations showed a reasonable agreement with experimental results, though it resulted in too favorable absolute binding free energies by an average factor of four. The SIE method exhibited a better performance, though its empirical character poses uncertainties regarding its general applicability. The MM-QMSA method [27], a QM-based end-point method in which the fixed-charge electrostatic model is replaced by a QM treatment of electrostatic interactions using the semiempirical PM3 Hamiltonian, and the continuum solvent model COSMO, predicted binding free energies in better agreement with experimental values. The insufficiently favorable binding free energy prediction for P7 in QM calculation suggests there is room for additional improvement in reaching a better balance between the QM calculation and the treatment of dispersion interactions via a LJ term, for example, by integrating the dispersion interactions into semiempirical parameters.

The present study demonstrates that too favorable binding affinity predictions of the classical MM/PB-SA method persist despite using an optimized set of atomic radii directly optimized to reproduce hydration free energies of biomolecules using the Poisson-Boltzmann implicit solvent model. This may also suggest that when using a continuum solvent model in the classical mechanics approach, it remains questionable whether fixed charges would provide equally good representation of the bound and free states of the biomolecules, since ligand and protein would experience very different environments in each case, and different sets of charges would be necessary to account for this effect. This balance appears to be better accounted for by the QM treatment of electrostatic interactions in the MM-QMSA method, what provides further motivation to continue developing of QM-based first-principle end-point methods.

In summary, the interactions of the C-terminus domains of BRCA1 (BRCT) protein with phosphopeptide inhibitors have been studied by experimental and computational methods in order to characterize those interactions at an atomic level. As a complement, binding free energy was evaluated by three different methods, namely MM/PB-SA, SIE and the QM-based MM-QMSA. Although further systematic validation on other systems is necessary, it is encouraging that QM binding free energy calculations can be performed with an adequate balance of accuracy and computational efficiency.