Pharmacokinetic similarity of biologics: analysis using nonlinear mixed-effects modeling

Abstract

Our objective was to show with two examples that a pharmacokinetic (PK) similarity analysis can be performed with nonlinear mixed effects models (NLMEM). We used two studies comparing different biosimilars: a three-way crossover trial on somatropin and a parallel group trial on epoetin alpha. For both datasets, NLMEM-based analysis was compared to non-compartmental analysis (NCA). As for NCA, we performed NLMEM-based equivalence Wald test on secondary parameters of the model: the area under the curve and the maximal concentration. Somatropin PK was described by a one-compartment model, epoetin alpha PK by a two-compartment model with linear and Michaelis-Menten elimination. For both studies, PK similarity was demonstrated by NCA and NLMEM. Both approaches led to similar results. Therefore, PK similarity data can be analyzed by both methods. NCA is an easier approach as it does not require data modelling but NLMEM leads to a better understanding of the underlying biological system.

INTRODUCTION

During the past two decades, an increasing fraction of pharmaceutical research and development (R&D) effort has been devoted to biologic drugs [1]. This is driven by evidence that biologics are bringing significant patient benefit in difficult-to-treat diseases such as rheumatoid arthritis and various cancers, and often changing the practice of medicine in these conditions. Biologics are typically expensive and place a large burden on shrinking health-care budgets. Follow-on biologics or biosimilars are new biological medicinal products that are similar or comparable to the originator’s compound and that may be lower in price, and hence offer the promise of reduced healthcare expenditure [2]. However, biologics are more complex, containing mixtures of proteins with variations in molecular structure, versus the more homogeneous small molecule drugs. Generic versions of the latter can be easily characterized by standard analytical techniques since they are chemically identical. Consequently, assessing the similarity between different formulations of biologics is more complex than assessing the equivalence between different formulations of chemical drugs [3]. It is not surprising therefore that the regulatory approval procedures vary from country to country regarding biosimilars. Currently, there is no guideline for an abbreviated approval pathway of biosimilars from the Food and Drug Administration (FDA). The actual policy is decided on a “case-by-case” principle [4]. The European Medicines Agency (EMA) has more stringent approval requirements for biosimilars than for typical generic drugs [2]. As part of the required information, a pharmacokinetic (PK) bioequivalence study is usually performed as traditionally done for chemical drugs [5, 6], even if the study design is less straightforward. For example, a parallel group design may be necessary for biologics with long half-life, as monoclonal antibodies [7]. Also, biosimilarity studies are often performed in patients, which raises several design challenges such as the selection of the study population, the number of doses or the treatment regimen.

Generally, to analyze bioequivalence study data, the area under the curve (AUC) and the maximal concentration (C_max) are estimated by non-compartmental analysis (NCA) and pharmacokinetic bioequivalence is assessed using these NCA estimates [6, 8]. Although nonlinear mixed effects models (NLMEM) are increasingly used in drug development for analyzing PK data (especially in sparse sampling design phase III trials) [9], there are only few published studies which use NLMEM to analyze bioequivalence trial data [10–17]. These authors used various statistical approaches to test bioequivalence with NLMEM but did not propose a general methodology. Model-based bioequivalence tests were studied through simulation for crossover trials [18–21]. Recently, we proposed a NLMEM-based bioequivalence analysis with a statistical approach similar to that recommended for NCA [21]. We showed that NLMEM-based Wald tests have good properties except for very sparse designs and/or drugs with highly variable PK. NCA requires a large enough number of samples per subject to accurately determine AUC and C_max and suffers from some caveats such as an inability to take into account nonlinear pharmacokinetics which is often exhibited by biologics [22]. NLMEM-based bioequivalence analysis would be more appropriate for such cases.

In this paper, we describe the methodology to perform PK similarity analysis using NLMEM and illustrate this with data from two trials studying PK similarity of different biosimilars. Omnitrope (Sandoz GmbH, Kundl, Austria) was the first biosimilar recombinant growth hormone (or somatropin) approved in Europe, Japan, and Canada as well as in the US⁽¹⁾ and is the first of our examples. Somatropins are used to treat growth hormone deficiency, mainly in pituitary dwarfism. In the dataset we used, two formulations of this biosimilar, 3.3 mg/ml solution (formulation T₁) and 5 mg/ml powder (formulation T₂), were compared to the reference formulation, Genotropin (Pfizer Pharma GmbH, Karlsruhe, Germany). The second biologic is a recombinant human erythropoietin, or epoetin alpha. Epoetins alpha are used to treat, amongst others, anaemia in chronic renal failure patients as it regulates the maturation of erythroid-progenitor cells into red-blood cells. In the dataset we used, the test formulation Binocrit (Sandoz GmbH, Kundl, Austria) was compared to the reference formulation Erypo/Eprex (Janssen-Cilag GmbH, Neuss, Germany). The single dose, three-way crossover trial on somatropin was chosen to illustrate the NLMEM-based PK similarity analysis for “simple pharmacokinetics” and its utility for designs with fewer sampling times than usually done in NCA. The multiple dose parallel group trial on epoetin alpha was chosen to illustrate NLMEM-based PK similarity for “complex pharmacokinetics”.

RESULTS

Somatropin

Data

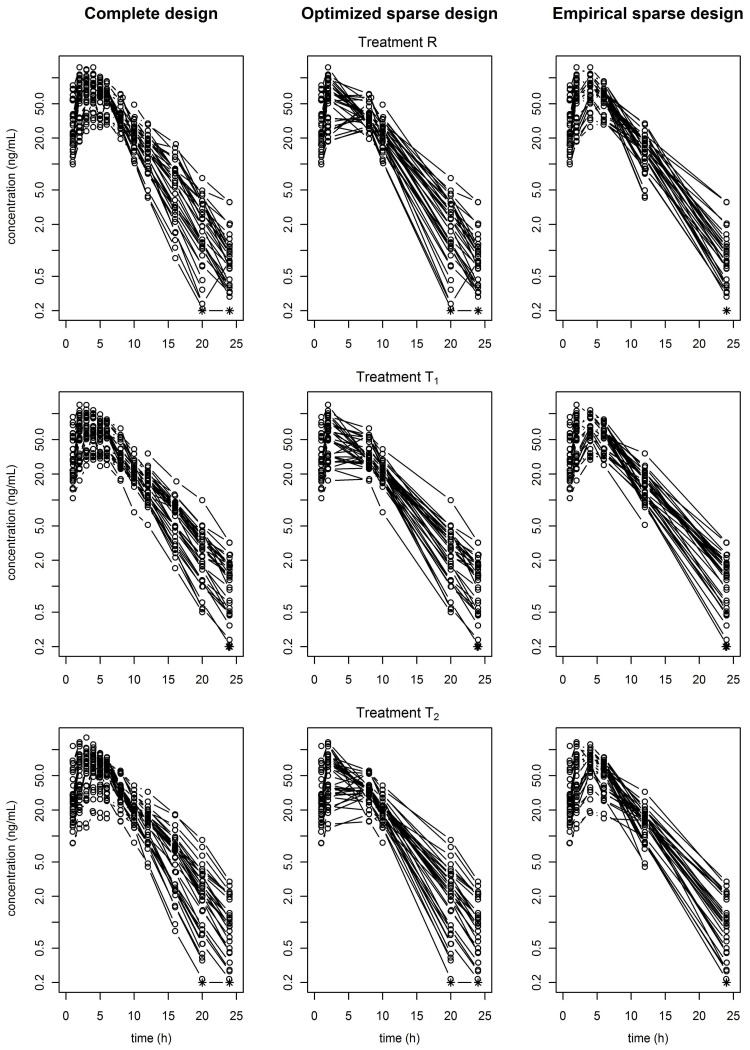
36 subjects were randomized, but one was prematurely withdrawn from the study as s/he did not present for the second treatment period. Thus, 35 subjects were included in the PK analysis. Overall measurements, 18 concentrations (1.4%) are below the limit of quantification (LOQ). These concentrations were measured at one of the two last sampling times. Based on pre and post-dose syringe weights, differences between the intended and actually administered dose were observed, possibly caused by slight variations in drug reconstitution and administration technique. Individual concentrations versus time profiles plotted for each formulation with a semi-logarithmic scale are displayed in the first column of Figure 1 for the complete dataset.

Figure 1.

Somatropin concentration versus time (N=35) from the three-way crossover study for each formulation and the three datasets: the complete (left), the optimized design (middle) and the empirical design (right). Data from the same formulation but different periods are pooled.

PK modelling

Administered doses were used for the population PK analysis and the plasma concentrations below LOQ were taken into account in the parameter estimation by the SAEM algorithm implemented in MONOLIX software [23] which considers those data as left censored [24]. A one-compartment model with first-order absorption with a lag time, and first-order elimination best described the somatropin data of the reference formulation. The best statistical model included between-subject variability (BSV) for all PK parameters with a correlation between the clearance and the volume of distribution, and a combined (additive plus proportional) error model. Parameter estimates (except period and sequence effects) of the final model used for PK similarity analysis are displayed in Table 1 with their standard errors (SE). Precision of estimation was judged satisfactory for all parameters. Model evaluation plots are displayed in supplementary Figure S1 online and are satisfactory.

Table 1.

Pharmacokinetic parameter estimates of somatropin (standard errors) from the three-way crossover trial (complete dataset)

	tlag (h)	ka (h−1)	V/F (L)	CL/F (L/h)	corrCL-V
μR	0.49 (0.07)	0.32 (0.07)	26.22 (0.1)	8.63 (0.03)
βT1	−0.22 (0.07)	−0.2 (0.07)	−0.12 (0.1)	0.01 (0.03)
βT2	−0.07 (0.06)	−0.06 (0.08)	0.07 (0.11)	0.05 (0.03)
BSV	0.33 (0.05)	0.18 (0.04)	0.44 (0.04)	0.23 (0.02)	0.81
WSV	0.09 (0.04)	0.19 (0.03)	0.26 (0.03)	0.1 (0.01)	0.49
a (ng/mL)	0.11 (0.02)
b	0.14 (0.004)

Period and sequence effects are not reported. a, additive error model parameter; b, proportional error model parameter; BSV, standard deviation for between-subject variability; β_T1, formulation effect for the test formulation T₁; β_T2, formulation effect for the test formulation T₂; corr_CL-V, correlation between CL/F and V/F; μ_R, fixed effects for the formulation of reference; WSV, standard deviation for within-subject variability.

We used the reference formulation estimates in the PFIM software [25] to determine the six sampling times per subject and per period of the optimized design (OD). The optimized sampling times were: 1, 2, 8, 10, 20, and 24 h. For the empirical design (ED), the PK modeller chose the following sampling times: 1, 2, 4, 6, 12, and 24 h. Individual concentrations versus time profiles plotted for each formulation with a semi-logarithmic scale are displayed in the second and third columns of Figure 1 for the OD and ED datasets. For both sparse datasets, the additive parameter of the error model was fixed to 0.1, the estimated value for the complete dataset. Parameter estimates are displayed in supplementary Table S1 online. Precision of estimation was judged satisfactory for all parameters and both sparse datasets.

PK similarity analysis

Table 2 summarizes the PK similarity analysis using NLMEM and NCA for the complete dataset and both sparse datasets (OD and ED). For AUC and C_max, and the three datasets, the 90% confidence interval (CI) ratio of AUC and C_max for both formulations are within the equivalence interval 80–125%. Thus, PK similarity was demonstrated using both methodologies, for both formulations, and the three datasets. For both parameters and each dataset, the ratios and their 90% CI obtained by NCA or NLMEM are similar. For NLMEM estimates, the geometric means of AUC and C_max are rather similar for the three datasets. For NCA estimates, the geometric means of AUC and C_max are lower for OD dataset compared to complete and ED datasets.

Table 2.

Pharmacokinetic similarity analysis for the somatropin data

			Formulation R		Formulation T1		Formulation T2		T1/R		T2/R
Dataset	PK parameter	Method	Geometric mean	CV (%)	Geometric mean	CV (%)	Geometric mean	CV (%)	Ratio (%)	90% CI (%)	Ratio (%)	90% CI (%)
C	AUC0-∞ (h.ng/mL)	NLMEM	579.1	25.0	574	25.0	550.1	25.0	99.1	[95.0; 103.4]	95.0	[91.0; 99.1]
		NCA	574.5	21.6	565.7	26.2	544	24.9	98.5	[94.1;103.1]	94.6	[90.4; 99.1]
	Cmax (ng/mL)	NLMEM	69.5	38.1	66.0	38.1	63.5	38.1	95.0	[87.5; 103.0]	91.4	[84.5; 98.8]
		NCA	73.7	34.5	70.0	31.9	68.6	37.9	95.3	[87.8;103. 3]	93.1	[85.9; 101.0]
OD	AUC0-∞ (h.ng/mL)	NLMEM	559.2	25.9	550.2	25.9	524.1	25.9	98.4	[94.1; 102.9]	93.7	[89.6; 98.0]
		NCA	491.3	23.2	491.6	29.3	464.2	26.4	100.1	[95.6; 104.9]	94.4	[90.1; 98.9]
	Cmax (ng/mL)	NLMEM	68.6	38.8	63.7	38.8	60.7	38.8	92.9	[85.2; 101.3]	88.5	[81.4; 96.2]
		NCA	59.7	42.2	55.1	45.3	54.0	47.8	92.6	[83.4; 102.8]	90.4	[81.4; 100.4]
ED	AUC0-∞ (h.ng/mL)	NLMEM	586.4	23.2	597.0	23.2	565.1	23.2	101.8	[97.8; 106]	96.4	[92.5; 100.4]
		NCA	566.4	21.6	570	26	541.9	25.6	100.7	[96.1; 105.6]	95.6	[91.2; 100.2]
	Cmax (ng/mL)	NLMEM	70.8	38.2	68.1	38.2	65.2	38.2	96.2	[88.8; 104.1]	92.0	[85.0; 99.7]
		NCA	72.4	34.3	68.6	32.4	67.5	37.0	95.0	[87.5; 103.2]	93.3	[86.0; 101.3]

AUC_0-∞, area under the curve between the time of dose and infinity; C, complete dataset; C_max, maximal concentration; CV, coefficient of variation; CI, confidence interval; ED, empirical design dataset; NCA, non-compartmental analysis; NLMEM, nonlinear mixed effects model; OD, optimized design dataset; PK, pharmacokinetic.

Epoetin alpha

Data

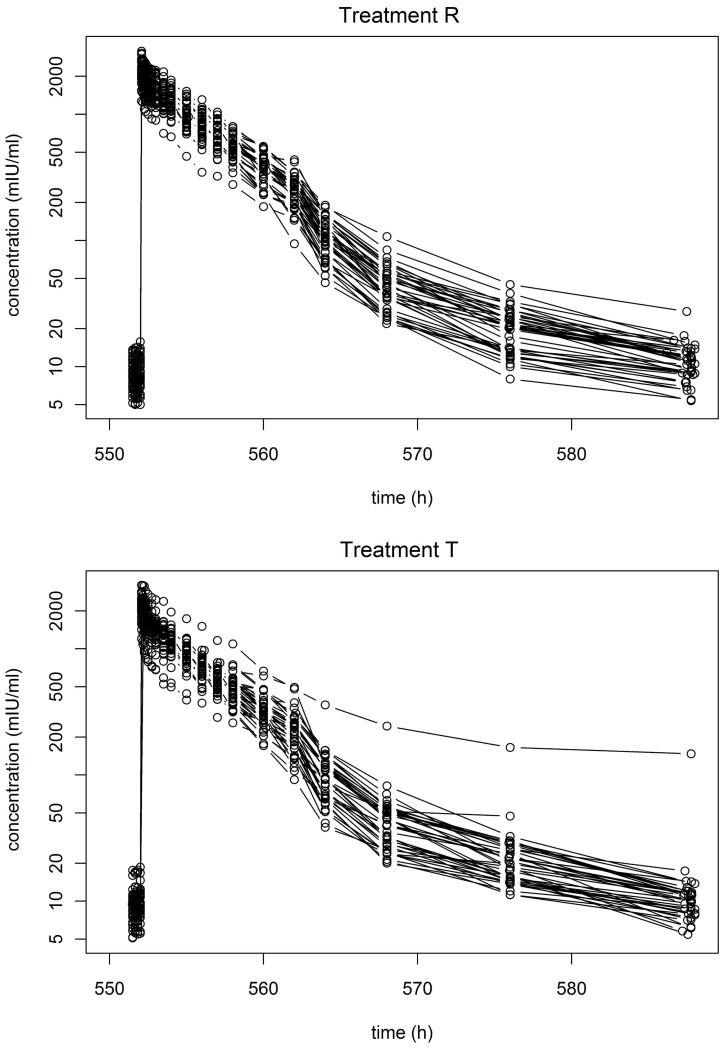
Of the 80 subjects, 76 completed the study according to the protocol; 39 subjects received the reference formulation and 37 received the test. Due to subject bodyweight, the administered doses were between 5900 and 10,000 IU. There are no concentrations below LOQ. As expected, the epoetin alpha concentration versus time plotted for each formulation with a semi-logarithmic scale showed a behaviour that is characteristic of a non-linear (capacity limited) elimination process [22] (Figure 2).

Figure 2.

Epoetin alpha concentration versus time for each formulation (N=39 for the reference and N=37 for the test formulation) from the parallel group study

PK modelling

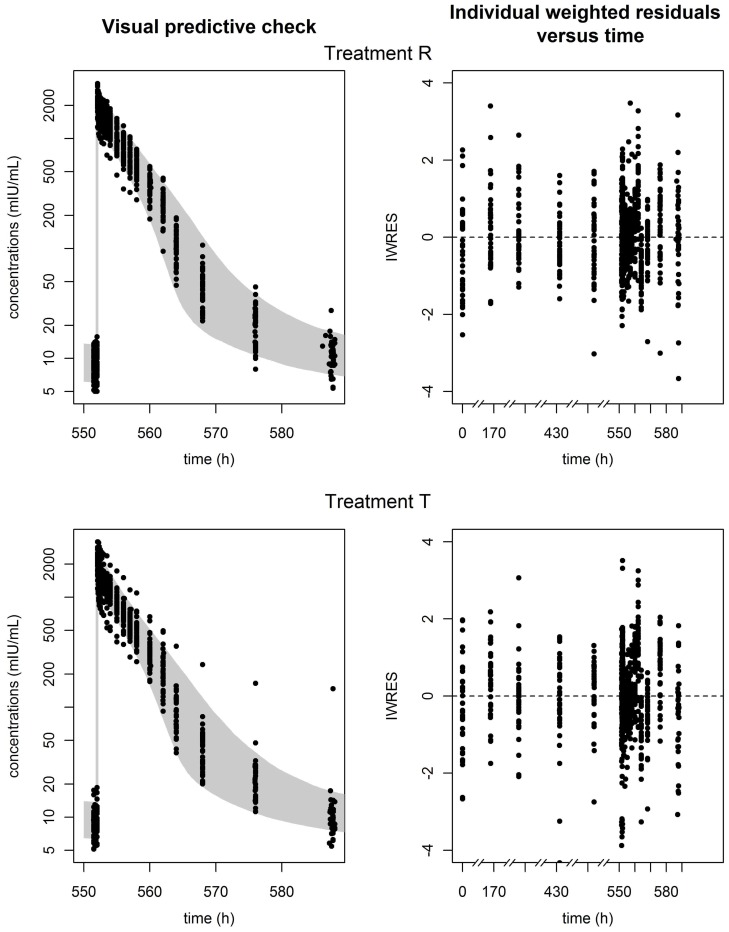
A two-compartment model with linear and Michaelis-Menten elimination best described the epoetin alpha data of the reference formulation. To check our hypothesis on the elimination pathway, we compared the Bayesian Information Criteria (BIC) for this model versus the corresponding models with only linear (ΔBIC=221) or Michaelis-Menten (ΔBIC=11) elimination and confirmed that the mixed elimination pathway better described the data. The best statistical model included BSV for all PK parameters, with a correlation between the clearance and the volume of central compartment, and a proportional error model. Parameter estimates of the final model used for PK similarity analysis are displayed in Table 3 with their SE. Precision of estimation was judged satisfactory for all parameters. Figure 3 displays the visual predictive check (left) and the individual weighted residuals (IWRES) versus time (right) for each formulation group. Most of the observations are in the 90% prediction interval, and there are no major biases or trends in the IWRES plot.

Table 3.

Pharmacokinetic parameter estimates of epoetin alpha (standard errors) from the parallel group trial

	Vc (L)	Vp (L)	CLlin (L/h)	Q (L/h)	Vmax (IU/h)	Km (IU/L)	C0 (IU/L)	corr CLlin− Vc
μR	4.05 (0.14)	2.58 (0.46)	0.36 (0.06)	0.34 (0.06)	341.22 (38.09)	90.83 (17.74)	8.26 (0.34)
βT	0.06 (0.05)	0.17 (0.23)	0.17 (0.23)	0.20 (0.21)	−0.07 (0.16)	−0.16 (0.28)	0.06 (0.06)
BSV	0.21 (0.01)	0.16 (0.04)	0.34 (0.02)	0.13 (0.05)	0.13 (0.03)	0.39 (0.05)	0.25 (0.02)	0.9 (/)
b	0.15 (0.003)

b, proportional error model parameter; BSV, standard deviation for the between-subject variability; β_T, formulation effect for the test formulation; corr_CLlin−Vc, correlation between CL_lin and V_c; μ_R, fixed effects for the formulation of reference

Figure 3.

Observed concentrations of epoetin alpha versus time with their 90% prediction interval (left), and individual weighted residuals (IWRES) versus time (right) for each formulation, reference (top), and test (bottom).

PK similarity analysis

Table 4 summarizes the PK similarity analysis using NLMEM and NCA. The 90% CI ratio of AUC and C_max at steady state are within the equivalence interval 80–125%, using NCA and NLMEM. For both parameters, the ratios and their 90% CI obtained by NCA or NLMEM are similar. The geometric means of C_max are higher by NCA compared to NLMEM. The geometric means of AUC are lower by NCA compared to NLMEM. We estimated the formulation effect on the proportion of the dose nonlinearly eliminated (PDNE) by NLMEM-based analysis. The PDNE test/reference ratio was estimated as 94.6 with a 90% CI of [72.2; 123.9].

Table 4.

Pharmacokinetic similarity analysis for the epoetin alpha data

		Formulation R		Formulation T		T/R
PK parameter	Method	Geometric mean	CV (%)	Geometric mean	CV (%)	Ratio (%)	90% CI (%)
AUCss (h.mIU/mL)	NLMEM	9,522.4	21.4	8,643.5	21.5	91.1	[83.6; 99.3]
	NCA	8,651.5	20.5	7,755.3	29.7	89.6	[85.7; 93.8]
Cmax (mIU/mL)	NLMEM	2,024.4	20.3	1,916.9	20.3	94.7	[87.5; 102.6]
	NCA	2,213.7	18.7	2,143.9	18.0	96.8	[93.3; 100.5]

AUC_ss, area under the curve between for the 11^th dose; C_max, maximal concentration for the 11^th dose; CV, coefficient of variation; CI, confidence interval; NCA, non-compartmental analysis; NLMEM, nonlinear mixed effects model; PK, pharmacokinetic.

DISCUSSION

In this study, we presented the results of a pharmacokinetic similarity analysis using NLMEM for two biologics: somatropin and epoetin alpha. Such analysis requires the collaboration of statisticians and pharmacokineticists [26]. We proposed a general methodology to perform such analysis for crossover and parallel designs and we compared the results to those obtained using traditional NCA. NLMEM-based equivalence tests were performed on secondary parameters of the models using the delta method or simulation to estimate the standard error of formulation effects. PK bioequivalence results from NCA and NLMEM are similar thereby demonstrating that NLMEM can be used for equivalence testing.

For somatropin where the PK is simple, we also performed the analysis on two sparse datasets showing the importance of the design, especially for NCA. Indeed, NCA is highly sensitive to design, especially for the determination of C_max and the computation of the terminal slope of the PK profile. The currently available tools to optimize the PK sampling times cannot take into account that equivalence test would be performed on C_max. Indeed, optimisation using the Fisher information matrix gives sampling times providing information on PK parameters of the model. This explains the difference in the NCA estimation of C_max between OD dataset and the two other datasets. As shown in Dubois et al [27], with few samples per subject, NCA estimates can be biased, even if the PK similarity is still demonstrated. For somatropin, we adjusted the dose to estimate comparable AUC. This adjustment assumed a linear relation between dose and concentration which is wrong for nonlinear PK [22]. The dose adjustment is not necessary for the analysis by NLMEM as the dose is taken into account in the model.

For epoetin alpha where the PK is complex, we estimated by NLMEM PDNE, a PK parameter that cannot be obtained by NCA. For nonlinear PK, clearance is not proportional to AUC and NCA parameters are not very physiologically meaningful. Only the use of models allowed us to adequately study the nonlinear PK of the drug and its properties. We would like to propose that parameters such as PDNE (or others perhaps linked to receptor occupancy) might be useful metrics particularly if they can be linked to clinically meaningful readouts of efficacy and safety [28].

The estimation of parameters through NCA does not require the assumptions inherent in model-based approaches and tends to be more acceptable and familiar to Health Authorities. Despite claims that NCA is an “assumption-free” approach, it assumes linear pharmacokinetics. It was already shown that, in case of nonlinear pharmacokinetics, NCA can bias the comparability analysis of a biologic and that a model-based approach can correct it [29, 30]. Even for linear PK, the interpolation of the AUC between last sampling time and infinity could be problematic for atypical concentrations profiles [20]. Furthermore, NCA estimates are sensitive to data below LOQ. In standard analysis, pharmacokineticists usually omit these data. When analyzing data below LOQ in a model-based paradigm, various innovative approaches have been proposed [31, 32]. In this study, we used the SAEM algorithm implemented in MONOLIX [33] which takes into account data below LOQ [24]. Though the percentage of these data is small in our examples, it can be important such as their consideration impacts the parameter estimates. So, in circumstances as outlined above, NLMEM-based bioequivalence analysis might be more appropriate than NCA.

In this paper, we proposed a PK similarity analysis using NLMEM in agreement with the guidelines recommendations for bioequivalence [5, 6]. For crossover trials, treatment, period and sequence effects were taken into account. For parallel and crossover trials, equivalence tests were performed on the treatment effect estimate. This latter type of PK similarity analysis requires the use of a robust algorithm such as SAEM because many parameters are estimated in these complex models. NLMEM take into account the knowledge accumulated on the drug. Appropriately parameterised, such mathematical models can lead to a better understanding of the underlying biological system than the fully empirical NCA approach, especially for drugs with complex PK such as often biosimilars.

METHODS

Data

Both studies were conducted according to the revised Helsinki Declaration and GCP guidelines. Data were described previously [34, 35].

Somatropin

The trial was a randomized, double-blind, single-dose, three-way crossover trial designed to demonstrate the bioequivalence of two novel somatropin formulations compared to a reference in healthy subjects. Thirty-six caucasian adults received octreotide for endogenous growth hormone suppression before somatropin administration. A single subcutaneous dose of 5 mg was administered at the beginning of each treatment period separated by a seven day wash-out period. Subjects were randomly allocated to one of the six sequences of treatment (R-T₁-T₂, R-T₂-T₁, T₁-T₂-R, T₁-R-T₂, T₂-T₁-R, T₂-R-T₁) knowing that there were six subjects by sequence. Blood samples for pharmacokinetic assessments were collected after each drug administration at 1, 2, 3, 4, 5, 6, 8, 10, 12, 16, 20, and 24 h after dosing. Concentrations were measured by a chemiluminescent immunometric assay with a LOQ of 0.2 ng/mL.

Epoetin alpha

The trial was a randomized, double-blind, multiple doses, parallel group trial designed to assess biosimilarity of epoetin alpha T compared to epoetin alpha R at steady state (after eleven doses). Eighty healthy caucasian males (forty by formulation) received intravenous doses of 100 IU/kg three times a week for four weeks. Blood samples for pharmacokinetic assessments were collected at the following sampling times: day 1, at 0.01 h before dosing; days 8, 15, 19, 22 at the time of dose; day 24, at 0.5, 0.33, 0.17, and 0 h before dosing; and 0.08, 0.17, 0.25, 0.33, 0.5, 0.75, 1, 1.5, 2, 3, 4, 5, 6, 8, 10, 12, 16, 24, and 36 h after dosing. Concentrations were determined using an enzyme immunoassay kit (EPO-ELISA, Medac GmbH, Hamburg, Germany) with a LOQ of 2.5 mIU/mL.

Nonlinear mixed effects modelling

Model building using the reference data

Before performing the model-based PK similarity assessment, a population PK model was defined. To determine the structural and the statistical model (random effect matrices and residual error model), data from the reference formulation and information on the drug were used. We assumed exponential random effects for all PK profiles. Diagonal, block diagonal, and complete matrices were tested during model building. Regarding the error model, additive, proportional, and combined error models were tested. Models were compared by the Bayesian Information Criteria [36], standard goodness of fit plots and visual predictive checks.

The final model was then used to fit all the data (reference and test formulations) and to perform the PK similarity analysis. For crossover trial, the structure of the within-subject variability (WSV) matrix was chosen to be identical to the structure of the BSV matrix. Population PK analyses were performed using the SAEM algorithm [37, 38] implemented in the MONOLIX software version 3.1R2 [33] (Monolix Software Project Group, Orsay, France) with log-likelihoods estimated by importance sampling.

For somatropin, a one-compartment model with first order absorption and first order elimination was used with or without a lag time for the absorption [39]. The estimated PK parameters were CL/F (L/h), the apparent clearance of elimination, V/F (L), the apparent volume of distribution, k_a (h⁻¹), the absorption rate constant, t_lag (h), the absorption lag time. Epoetin alpha is a drug showing target-mediated drug disposition (TMDD) properties due to its specific and saturable internalization in erythroid progenitor cells [40, 41]. Fitting the TMDD PK model requires to assign some of the receptor-binding parameter values using results of in vitro receptor binding studies. When such data are not available, a Michaelis-Menten approximation can be made [42–44]. The first considered structural model was a two-compartment model with linear and Michaelis-Menten elimination. The corresponding differential equation system is defined in Equation 1 and 2:

$$\frac{{dC}_c(t)}{dt}=\frac{Q}{V_c}{C}_p(t)-\frac{Q}{V_c}{C}_c(t)-\frac{{CL}_{\mathit{lin}}}{V_c}{C}_c(t)-\frac{V_{max}{C}_c(t)}{V_c(K_m+C_c(t))}$$ (1)

$$\frac{{dC}_p(t)}{dt}=\frac{Q}{V_p}{C}_c(t)-\frac{Q}{V_p}{C}_p(t)$$ (2)

With C_c: the drug concentration in the central compartment, C_p: the drug concentration in the peripheral compartment, C_c (0) = C_p (0) = 0, and for each dosing time

$$C_c(t^{+})=C_c(t^{-})+\frac{\mathit{Dose}}{V_c}.$$

Modelling endogenous epoetin alpha production is complex and requires much more information on endogenous concentration than those available [44]. As in Ramakrishnan et al [45], we assumed this production was not altered by the administration of recombinant human epoetin alpha. The endogenous baseline concentrations (C₀) measured before any drug administration were taken into account considering that: C(t) = C₀ + C_c (t), with C(t) the measured concentration. The estimated PK parameters were CL_lin (L/h), the clearance of elimination, Q (L/h), the inter-compartmental clearance, V_c (L), the volume of distribution of the central compartment, V_p (L), the volume of distribution of the peripheral compartment, V_max (IU/h), the maximum elimination rate from plasma, K_m (IU/L), the plasma concentration at V_max/2, C₀ (IU/L), the endogenous baseline concentration. K_m is equal to the equilibrium dissociation constant (K_D) of the TMDD model and V_max is proportional to the total receptor concentration [42, 43]. We computed the proportion of the dose nonlinearly eliminated at steady state for each formulation. Since $\mathit{Dose}={CL}_{\mathit{lin}}\times \mathit{AUC}+\int \frac{V_{max}(t)}{K_m+C_c(t)}\times C_c(t)dt$, we deduced $1=\frac{{CL}_{\mathit{lin}}\times \mathit{AUC}}{\mathit{Dose}}+\frac{1}{\mathit{Dose}}\int \frac{V_{max}(t)}{K_m+C_c(t)}\times C_c(t)dt=\frac{{CL}_{\mathit{lin}}\times \mathit{AUC}}{\mathit{Dose}}+\mathit{PDNE}$ and $\mathit{PDNE}=1-\frac{{CL}_{\mathit{lin}}\times \mathit{AUC}}{\mathit{Dose}}$.

Sparse data for somatropin

From the somatropin dataset with twelve sampling times per subject and period, two “sparse” datasets were produced: the optimized and empirical design datasets. For both datasets, we fixed the number of samples to be half of the original design, i.e. six per subject and period, and the sampling times were chosen among those of the complete dataset. To optimize the OD dataset sampling times, we used the PFIM software version 3.2 [25, 46] (Paris, France) with the parameter estimation of the reference formulation [47]. The Fedorov-Wynn algorithm was used to define the six sampling times for which the determinant of Fisher information matrix is maximum [48]. The ED dataset sampling times were determined by an experienced PK modeller before any knowledge on the data analysis, using the somatropin concentration versus time profiles for each formulation (see Figure 1), and knowing that we would estimate AUC and C_max.

PK similarity analysis

NLMEM based approach

We show here how to perform a model-based equivalence analysis with a statistical approach similar to NCA but using NLMEM. For crossover trial (somatropin data), the statistical model included formulation, period, and sequence effects for all PK parameters. We considered that the reference formulation, the first period, and the first sequence (R-T₁-T₂) were the reference classes. For details on the statistical model, see Dubois et al [27]. For parallel group trial (epoetin alpha data), formulation effects were added to all PK parameters.

We assumed additive formulation, period and sequence effects on log parameters. We defined β_T the formulation effect for a PK parameter. We performed equivalence tests on the estimate of β_T using its SE and the Schuirman’s two one-sided tests procedure [49]. As we performed equivalence tests on secondary parameters of the structural model, we estimated the formulation effects from the fixed effects estimates or using simulation. The corresponding SE was computed by the delta method [50] or via simulation using the fixed effects estimates, and the Fisher information matrix estimate of the fixed effects. We also estimated the 90% confidence interval of exp(β_T) which corresponds to the 90% CI of the test/reference ratio for average considered parameter. Furthermore, as recommended in the guidelines, we reported the geometric mean and coefficient of variation (CV) of AUC and C_max for each formulation.

For somatropin, equivalence tests were performed on the formulation effects of AUC_0-∞ and C_max for each test formulation, with respect to the reference formulation. Formulation effects of AUC_0-∞ and their SE were obtained directly from the formulation effects of the clearance and their SE. The formulation effects on C_max were computing from the fixed effects estimates; their SE were computing by the delta method, as described in Dubois et al [27].

For epoetin alpha, equivalence tests were performed on the formulation effects of AUC and C_max at steady state. AUC were computed between the time of dose and the last sampling time of the dose (AUC_0-36). Because of the Michaelis-Menten elimination, the structural PK model of epoetin alpha is written with ordinary differential equations. So, the formulation effects and their SE for these secondary parameters were estimated through simulations of concentration profiles. See supplementary information online for details on the simulation process.

For somatropin, AUC_0-∞ and C_max were also the estimates of the geometric means, and the corresponding CV were estimated by the total variability, i.e. by the sum of the BSV and WSV. For epoetin alpha, we computed by simulation the NLMEM-based geometric mean of AUC_0-36 and C_max for each formulation and their CV were obtained from their BSV (see supplementary information online). We also estimated the formulation effect on PDNE at steady state and the corresponding 90% CI. All simulations were performed using the R software version 2.11.0 (R foundation for Statistical Computing).

Comparison to non-compartmental analysis

AUC and C_max were calculated from the concentrations versus sampling time profiles by standard NCA using the R software. A combination of the linear and log-linear trapezoidal method was used, data below LOQ were omitted, three to six sampling times were used to compute the terminal slope [22]. When the administered dose differed from the intended dose, concentrations were divided by the ratio administered/intended dose before NCA estimation. For somatropin, AUC were computed from the time of dose to infinity (AUC_0-∞). For epoetin alpha, AUC and C_max were calculated at steady state, subtracting the endogenous baseline concentrations. AUC were calculated between the time of dose and the last sampling time (AUC_0-36) which corresponds to the AUC at steady state (AUC_ss ).

Equivalence testing was performed on log-transformed parameters. For crossover trial (somatropin data), a linear mixed effects model including formulation, period, sequence as fixed effects, and subject as random effect, was used. For parallel group trial (epoetin alpha data), a linear model with formulation effect was used. 90% CI of formulation effects were computed using a Student distribution with N-2 degrees of freedom (N: total number of subjects). Equivalence analyses were performed using the R software.