Skip to main content
PMC home page
European Journal of Human Genetics logoLink to European Journal of Human Genetics
. 2012 Feb 15;20(8):831–836. doi: 10.1038/ejhg.2012.15

Estimating the contribution of genetic variants to difference in incidence of disease between population groups

Ramal Moonesinghe 1,*, John PA Ioannidis 2,3,4, W Dana Flanders 5, Quanhe Yang 6, Benedict I Truman 1, Muin J Khoury 6
PMCID: PMC3400729  PMID: 22333905

Abstract

Genome-wide association studies have identified multiple genetic susceptibility variants to several complex human diseases. However, risk-genotype frequency at loci showing robust associations might differ substantially among different populations. In this paper, we present methods to assess the contribution of genetic variants to the difference in the incidence of disease between different population groups for different scenarios. We derive expressions for the contribution of a single genetic variant, multiple genetic variants, and the contribution of the joint effect of a genetic variant and an environmental factor to the difference in the incidence of disease. The contribution of genetic variants to the difference in incidence increases with increasing difference in risk-genotype frequency, but declines with increasing difference in incidence between the two populations. The contribution of genetic variants also increases with increasing relative risk and the contribution of joint effect of genetic and environmental factors increases with increasing relative risk of the gene–environmental interaction. The contribution of genetic variants to the difference in incidence between two populations can be expressed as a function of the population attributable risks of the genetic variants in the two populations. The contribution of a group of genetic variants to the disparity in incidence of disease could change considerably by adding one more genetic variant to the group. Any estimate of genetic contribution to the disparity in incidence of disease between two populations at this stage seems to be an elusive goal.

Keywords: difference in incidence, genetic variants, gene–environmental interaction, population attributable risks

Introduction

Differences in allele frequencies between geographic populations have well-known effects on the incidence of uncommon single gene disorders such as cystic fibrosis and sickle cell anemia.1, 2 Recent genome-wide association studies (GWAS) have successfully identified multiple susceptible genetic variants associated with increased risks for common complex diseases. Most of these GWAS have been conducted in populations of European ancestry.3 Allele frequencies at loci showing strong and consistent association from GWAS with any of five common complex human conditions – type 2 diabetes, obesity, Crohn's disease, prostate cancer and breast cancer have shown wide variation across the 11 populations in the phase III of the International HapMap Project.3 Another study of 25 single-nucleotide polymorphisms (SNPs), which show robust GWAS-derived associations with six complex human diseases (Crohn's disease, type 1 diabetes, type 2 diabetes, rheumatoid arthritis, coronary artery disease and obesity) using individuals from 53 populations worldwide resulted in substantial variation in risk allele frequencies among populations.4 The authors of the study speculated that although the differences in risk allele frequencies between human populations are not larger on average than what one would expect for random SNPs, the variation in risk allele frequencies may account for differences in disease prevalence between human populations.4 Recently, a collaborative study between the Centers for Disease Control and Prevention and the National Cancer Institute examined racial/ethnic variations in prevalence of allele and genotype frequencies in a large nationally representative sample of the US population using the Third National Health and Nutrition Examination Survey and focusing on three ethnic-racial groups: non-Hispanic whites, non-Hispanic blacks and Mexican Americans. The authors found significant differences in allele frequency (in 88 of 90 genetic variants) and genotype prevalence (in 87 of 90 genetic variants).5 Non-Hispanic blacks had considerable differences in minor allele frequency compared with non-Hispanic whites, with almost one-quarter of variants differing by at least 20% (absolute difference).5

Ioannidis et al6 assessed 43 meta-analyses of gene–disease associations from the candidate gene era across 697 study populations of various ethnicities and found that frequencies of polymorphisms in seven cardiovascular disease genes varied significantly between ethnicities. However, they observed large heterogeneity in the genetic effects (odds ratios) between ethnicities in only 14% of the cases indicating that their biological impact on the risk for common diseases may usually be consistent across traditional ‘racial' boundaries.6 In GWAS, the variants involved in discovered associations are tag SNPs rather than causal variants. The linkage disequilibrium pattern of these tag SNPs with the real culprits might differ in different populations and this could result in discrepancies in the odds ratios. Preliminary data from GWAS-discovered SNPs does not suggest markedly different odds ratios in different ancestry groups, but it should be acknowledged that the magnitude of the GWAS-discovered effects is very modest and the ability to discern different effects would require very large studies.7, 8 In a recent empirical evaluation of 108 GWAS-discovered associations, the genetic effect (odds ratio) point estimates between European, African and Asian ancestry groups correlated only modestly (pair-wise comparisons' correlation coefficients: 0.20–0.33) and point estimates of risks were opposite in direction or differed more than twofold in 57%, 79% and 89% of the European versus Asian, European versus African and Asian versus African comparisons, respectively.9

Gene–gene and gene–environmental interactions may have contributed to many of the reported differences in gene–disease associations between different racial or ethnic groups. The greater the environmental contribution, the more genetic factors and the more complex interactions, the more difficult it is to separate group differences in terms of genetic and environmental contributions.10 Common diseases have strong environmental components such as diet, smoking, physical activity, and environmental and occupational exposures (which may also have joint effects with genes) also vary across populations.

Given the genetic variants identified in recent GWAS, we do not know whether or not and how much these genetic variants contribute to differences in incidence of disease among population groups. Genes undoubtedly make some contribution to disparities in aggregate group health status, but the potential genetic contribution is unknown.11 What is the contribution of genetic variants to the difference in incidence between different groups? To address this question, we develop methods to assess the contribution of genetic variants to group-specific disease incidence for different scenarios in this paper.

Materials and methods

Let Pi, i=1,2, be the incidence of disease and Ii be the background risk or the risk of individuals not carrying the risk-genotype in the ith population. We express the contribution of a risk-genotype to the difference in incidence between two populations 1 and 2 as a proportion of the difference in incidence:

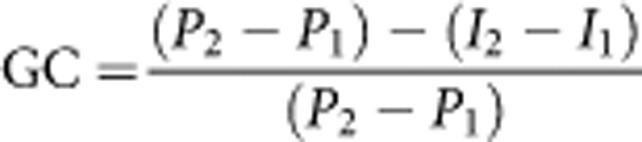graphic file with name ejhg201215e1.jpg

Note that (I2–I1) represents difference in incidence of disease in the two populations if the risk due to the high risk-genotype in both populations were changed, that is, reduced, to that among those with the low risk-genotype. Therefore, GC measures the change in disparity in incidence in the two populations due to the high risk-genotype as a proportion of the difference in incidence. When P2>P1 and I2<I1, the change in disparity in incidence in the two populations is >(P2–P1), which results in a GC of >100%. Also, if P2>P1 and I2>I1 but (P2–P1) is <(I2–I1), the change in disparity in incidence in the two populations is negative, which results in a negative value for GC. A negative value for GC indicates that the high risk-genotype contributes to a reduction in disparity in incidence in the two populations.

As the simplest case scenario, we first consider the genetic contribution to the difference in incidence of a disease between two groups due to a single genetic variant associated with the disease when risk-genotype frequency is varied. Assuming dominant or recessive models, let Gi, i=1, 2, be the risk-genotype frequency of the genetic variant for the ith population and R be the relative risk associated with the genetic variant. Let D denotes the disease (one or zero depending on the presence or absence of the disease) and G denotes the risk-genotype (one or zero depending on the presence or absence of the risk-genotype). Then,

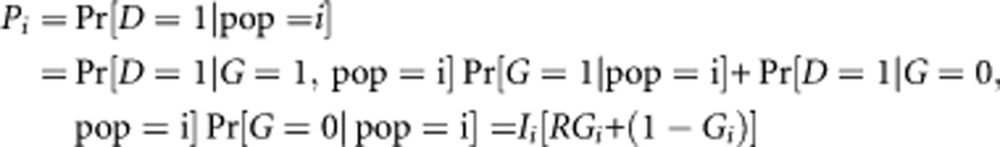graphic file with name ejhg201215e2.jpg

Note that Ii = Pr[ D = 1 ∣G = 0, pop=i] and R = Pr[D = 1∣G = 1, pop=i] / Pr[D = 1∣ G=0,pop=i]. The background risk for the ith group is then given by:

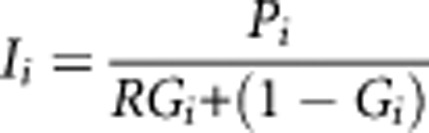graphic file with name ejhg201215e3.jpg

It is interesting to note that even when two populations have the same risk-genotype frequencies and the risk- genotype carries the same relative risk in both of them, if there is a difference in incidence of the disease in the two populations (ie, Ii), the risk-genotype would be calculated to have a contribution to this difference in incidence. The reason that this somewhat counter-intuitive situation can arise even when the risk ratio is the same in the two populations can be understood as follows: a difference between I1 and I2 implies that, for an individual with the high risk-genotype, the increase risk attributable to his/her genotype is: (R-1)I1 in population 1 and (R-1)I2 in population 2 – these attributable risks differ under the non-null, if I1 and I2 differ. Note we could also express Pi as Ii+RDGi, using the risk difference RD and that this seemingly counter-intuitive situation does not arise if the risk-genotype has the same causal risk difference in two populations with the same risk-genotype frequencies. That is, GC=0 under these conditions.

Next, we extend this result to joint multiplicative effects of independent multiple genetic variants. For k genetic variants with relative risk Rj and risk-genotype frequency Gji for the jth genetic variant in the ith population, it can be shown that the incidence of disease, Pi, in the ith population is given by:

graphic file with name ejhg201215e4.jpg

Substituting the values of background risks for the two populations obtained from this equation in equation (1), gives us the genetic contribution of the k genetic variants to the difference in incidence of disease between the two populations. To simplify the presentation of our results, we assume k risk-genotypes with identical relative risk R and risk-genotype frequency Gi for the ith population. The above equation then simplifies to:

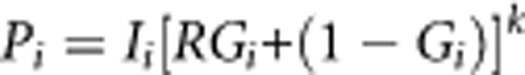graphic file with name ejhg201215e5.jpg

These results can be extended to risk alleles. When all the risk alleles have identical risk allele frequency, p, and relative risk λ, assuming Hardy–Weinberg equilibrium, Wray et al12 showed that the total number of risk alleles across n loci is distributed binomial (2n, p), and the incidence of disease can be expressed as Pi=Ii[λpi+(1−pi)]2n for the multiplicative risk model. Under the same assumptions, the incidence of disease for the additive model can be expressed as Pi=Ii[2npi(λ−1)+1].

Finally, we consider the difference in incidence between groups because of the joint effect of a genetic variant and an environmental factor. Let E denotes the environmental factor (one or zero depending on the presence or absence of the environmental factor) and let Ei, i=1, 2, be the prevalence of the environmental factor for the two groups. Let RG, RE and RGE be the relative risks of the genotype, the environmental factor and the interaction between the genotype and the environmental factor, respectively. We assume that the genotype and the environmental factor are independent in the population. Also, we assume a multiplicative model to estimate the joint effect of the genotype and the environmental factor. For this scenario, the incidence of disease, Pi, is given by:

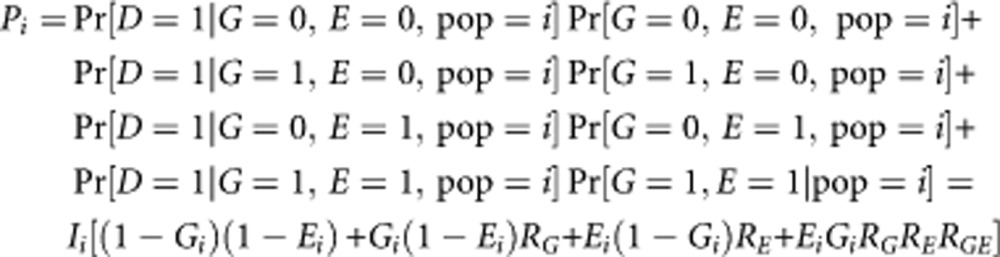graphic file with name ejhg201215e6.jpg

Estimating the background risks from this formula for the two populations leads to the calculation of the contribution of the joint effect of the genotype and the environmental factor to the difference in incidence of the disease. This formula can be extended for multiple risk-genotypes and binary environmental factors under the assumption that these risk factors are independent from each other. As the marginal relative risk, R′G, is given by

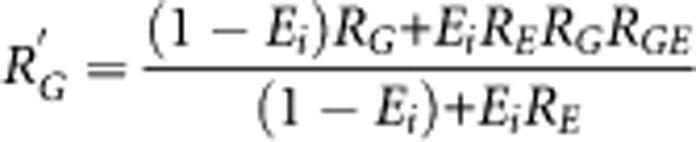graphic file with name ejhg201215e7.jpg

one could express the above equation as Pi=Ii[(1−Gi)+R′GGi][(1−Ei)+REEi], which shows that GC only depends on the marginal genetic effect.13

The approach we took to define the contribution of a genetic variant to the difference in incidence of disease between two populations is similar to the definition of population attributable risk (PAR), which has been described as the reduction in incidence that would be observed if the population were entirely unexposed compared with its current (actual) exposure pattern.14 For a risk factor with relative risk R and frequency G, PAR is given by PAR=(P−I)/P, where P is the incidence, and I is the background risk. PAR is a population-specific measure whereas GC is used to compare two populations. Similar to PAR, the interpretation of GC for two populations requires the assumption that the removal of risk factor alters neither the distribution of other risk factors nor their effects on the incidence of disease in each population. We should acknowledge that these assumptions may not necessarily always hold true. We can also express GC as a linear function of the two PARs, PAR1 and PAR2, for the two populations:

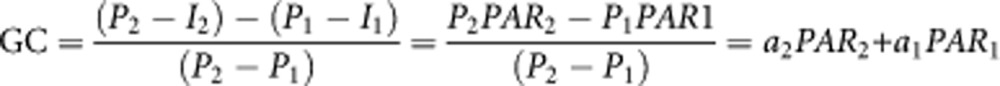graphic file with name ejhg201215e8.jpg

where a2=P2/(P2−P1), a1=−P1/(P2−P1) and a1+a2=1. GC can also be expressed as GC=PAR2+w(PAR2−PAR1), where w=P2/(P2–P1).

All analyses were performed using the R programming language version 2.12.0.15

Results

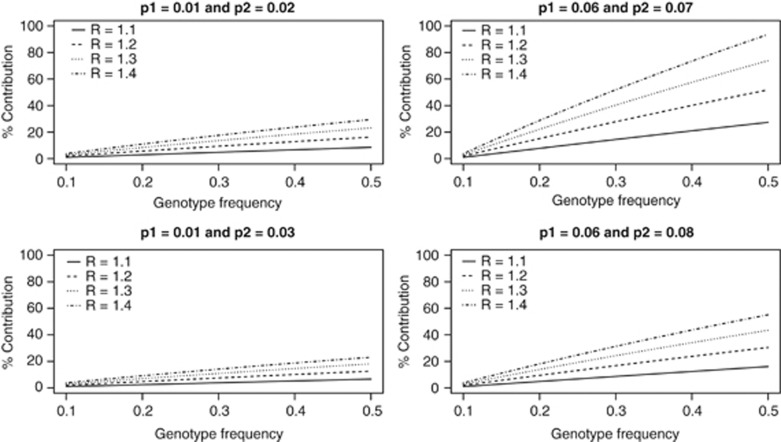
For a single genetic variant, we assumed a risk-genotype frequency of 10% for the first population. For relative risks of 1.1, 1.2, 1.3 and 1.4, we varied the risk-genotype frequency from 10 to 50% for the second population. Figure 1 shows the genetic contribution to the difference in incidence of disease when the incidence of disease for the two populations are given by 1% and 2% 6% and 7% 1% and 3% and 6% and 8%, respectively. As expected, the genetic contribution to the difference in incidence of disease is almost negligible (<4%) when the risk-genotype frequency for the second population is also 10% for all the relative risks considered and the genetic contribution to the difference in incidence increases for higher relative risks and higher risk-genotype frequency for the second population and it is smaller when the overall difference in incidence between the two populations is larger. Whatever the overall difference in incidence, when relative risk and risk-genotype frequency are identical in the two populations, the contribution of the genetic variant to the difference in incidence remains the same.

Figure 1.

Figure 1

Open in a new tab

Genetic contribution of a single genetic variant to the difference in incidence of disease between two groups when risk-genotype frequency is 0.1 in the first group, and varied from 0.1 to 0.5 in the second group for different values of relative risks and incidence of disease.

When the disease incidences for the two populations are 1% and 2%, respectively, and the relative risk is 1.1, the genetic contribution is 1% for risk-genotype frequency of 10% for the second population. When risk-genotype frequency for the second population is increased to 50%, genetic contribution increases to 9%. When the relative risk is also increased to 1.4, the genetic contribution is 30%.

Increase in incidence of disease for both populations lead to higher genetic contributions. For example, when disease incidence for the two populations are 6% and 7%, respectively, and the relative risk is 1.1, the genetic contribution is 27% for risk-genotype frequency of 50% for the second population; when the relative risk is 1.4, the genetic contribution increases to 94%. On the other hand, an increase in the difference of incidence seems to reduce the genetic contribution. For example, when the incidence of disease is 6% in the first population, increasing the incidence of disease from 7 to 8% for the second population reduces the genetic contribution from 21 to 16% for a risk-genotype frequency of 50% and relative risk of 1.1, and reduces the genetic contribution from 94 to 55% for a relative risk of 1.4. Note that an increase in the difference of incidence increases the numerator of GC, but GC declines because of the increase in the denominator.

Throughout this analysis, we have assumed that the incidence of disease in the first population is less than the incidence of disease in the second population and the estimated background risks for the two populations followed the same trend. However, in some situations, the absence of the genetic variant could reverse this trend and result in a genetic contribution estimate of >100%. For example, let the incidence of disease for the first and second populations be 6% and 7%, respectively. Consider a genetic variant with a relative risk of 1.5 and risk-genotype frequency of 10% and 50% for the first and second populations, respectively. If this genetic variant was not present in the two populations, the incidence of disease (background risks) would have been 4.7% and 2.3% for the first and second populations, respectively. As the risk-genotype frequency in the second population is higher (50% compared with 10% in the first population), the presence of the genetic variant in the two populations leads to a higher disease risk in the second population (7%) compared with the first population (6%). The higher risk of disease but lower background risk in the second population compared with the first population results in a genetic contribution estimate of ((0.07–0.06)−(0.023–0.047))/(0.07–0.06)=341%. These higher genetic contributions are possible because of the small difference (1%) in incidence in the two populations.

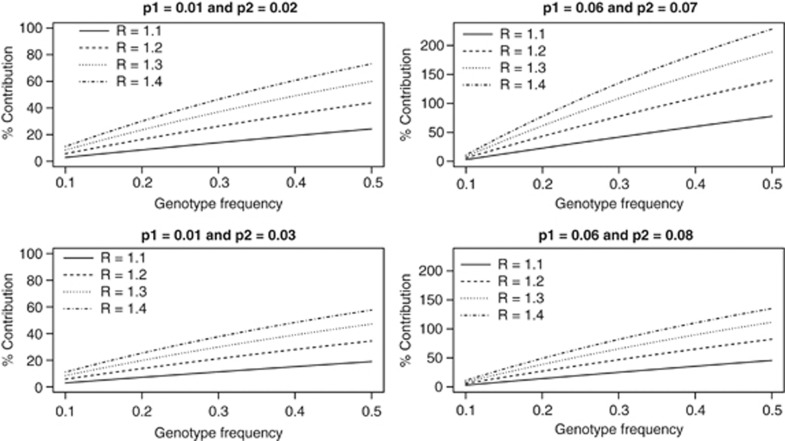
For multiple genetic variants, we assumed three risk-genotypes with identical relative risks of 1.1, 1.2, 1.3 and 1.4, risk-genotype frequency of 10% for the first population and varied the risk-genotype frequency from 10 to 50% for the second population. Figure 2 gives the genetic contribution to the difference in incidence of disease because of these three risk-genotypes for the same scenarios of incidence of disease considered in Figure 1. Even with three genetic variants, the genetic contribution to the difference in incidence is <11% for all the relative risks considered when genotype frequencies for the three risk-genotypes are identical (10%) in the two populations. The trends in genetic contribution to the difference in incidence are similar to the trends for a single genetic variant for the different scenarios of incidence considered but as expected the genetic contribution for three genetic variants is much higher than that of a single genetic variant. For example, when the incidence of disease are 1 and 2% for the two populations and the relative risk is 1.2 for a single genetic variant, the genetic contribution increased from 2 to 16% when risk-genotype frequency in the second population varied from 10 to 50% for three genetic variants with each variant having the same relative risk of 1.2, the genetic contribution increased from 6 to 36%.

Figure 2.

Figure 2

Open in a new tab

Genetic contribution of three genetic variants to the difference in incidence of disease between two groups when risk-genotype frequency is 0.1 in the first group, and varied from 0.1 to 0.5 in the second group for different values of relative risks and incidence of disease.

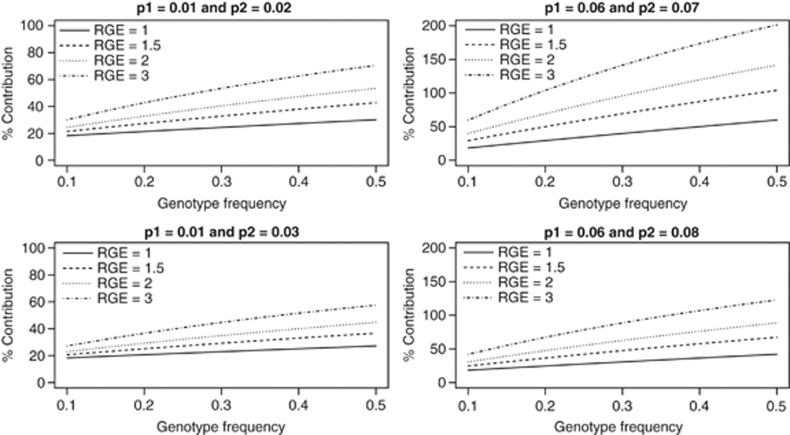
To evaluate the contribution of the joint effect of a genetic variant and an environmental factor to the difference in incidence for two populations, we consider a genetic variant with relative risk of 1.2 and an environmental factor with relative risk of 2 and frequency 20% in both populations. As before, the risk-genotype frequency in the first population is 10% and the risk-genotype frequency for the second population is varied from 10 to 50%. We assume no gene–environmental interaction in the first population (RGE=1). Figure 3 gives the contribution of the joint effect of the genetic variant and the environmental factor when the relative risks of the interaction of the genetic variant and environmental factor are 1, 1.5, 2 and 3 in the second population. With no gene–environmental interaction in both populations, the contribution of the joint effect of gene and environmental factor increases from 18% to 30% when risk-genotype frequency in the second population is increased from 10% to 50% for incidence of disease 1% and 2% for the first and second populations, respectively. As expected, the contribution of the joint effect of genetic variant and the environmental factor to the difference in incidence of disease increases with increasing relative risk of the gene environmental interaction. When the relative risk of the interaction of the genetic variant and the environmental factor is 1.5 in the second population, the contribution of the joint effect varied from 21% to 41% when risk-genotype frequency varied from 10% to 50% in the second population; when the relative risk of the interaction is 3 in the second population, the contribution of the joint effect varied from 30% to 71%.

Figure 3.

Figure 3

Open in a new tab

Contribution of joint effect of a genetic variant and an environmental factor to the difference in incidence of disease between two groups when risk-genotype frequency is 0.1 in the first group and varied from 0.1 to 0.5 in the second group for different values of relative risks of the interaction (RGE) between the genetic variant and the environmental factor and incidence of disease. The frequency of the environmental factor is 20% with a relative risk of 2 for both populations.

Example

Several GWA studies on type 2 diabetes have been conducted in large scale case–control samples. Ng et al16 conducted a large scale case–control replication study of 6719 Asians to test the association of six novel genes from GWA studies and TCF7L2, which had the largest effect in Europeans, and their joint effects on type 2 diabetes risk. Table 1 presents their meta-analysis of seven genes for type 2 diabetes association, control frequency and PAR for each gene in European and Asian populations using their data and published studies. There is not much difference between their risk allele frequency in controls and risk allele frequency in the combined phase I, phase II and phase III International HapMap data.17 As only the odds ratio for risk alleles are provided, we use an approximate method given by Wray et al12 to calculate the incidence of disease for each population:

Table 1. Meta-analysis of seven genes for type 2 diabetes association in European and Asian populations.

    Caucasians Asians
Gene SNP Control risk allele frequency % OR PAR % Control risk allele frequency % OR PAR %
IGF2BP2 rs4402960 30 1.14 8.2 27 1.12 6.5
CDKAL1 rs7756992 29 1.14 7.9 50 1.26 21.6
SLC30A8 rs13266634 67 1.16 18.6 56 1.13 13.5
CDKN2A/B rs10811661 84 1.19 25.8 55 1.27 24.5
HHEX rs7923837 60 1.23 22.5 20 1.25 9.2
TCF7L2 rs7903146 27 1.44 20.2 3 1.44 2.2
FTO rs8050136 39 1.11 8.3 14 1.16 4.4
Open in a new tab
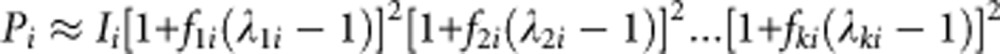graphic file with name ejhg201215e9.jpg

where fji and λjiare the frequency and the relative risk of the risk allele in the jth SNP in the ith population.

After adjusting for age differences, the estimated incidence rates of diabetes for non-Hispanic whites and Asian Americans aged 67 years or older in 2001 were 34.3/1000 and 49.4/1000, respectively, based on a sample of Medicare elderly fee-for-service beneficiaries.18 Table 1 also gives PAR for each SNP for the two populations. The PARs of the joint effect of the seven SNPs for Caucasians and Asians are 71% and 59.4%, respectively. The GC for these seven SNPs is 33%, which indicates that the seven SNPs contributed to an increase in disparity in incidence between non-Hispanic whites and American Asians. The PARs for all the SNPs except for rs7756992 are higher in Caucasians than Asians (Table 1). If we consider the joint effect of only these six SNPs, the GC is only 1.1% whereas the GC for rs7756992 alone is 53.6%, which shows a large contribution of this SNP to the disparity in incidence between the two populations. On the other hand, the contribution of each SNP of the last three SNPs in the Table has a negative contribution to the difference in incidence indicating that these three SNPs contributed to a reduction in the difference in incidence. For example, the GC for rs7903146 is −37.2%. These results show that just adding one genetic variant to a combination of genetic variants could change GC considerably and these changes are related to the PARs in the two populations.

Discussion

We provide a method to evaluate the contribution of the joint effect of genetic variants to the difference in incidence between two populations when risk-genotype frequency and relative risk for each variant is known. We showed that the contribution of genetic variants to the difference in incidence increases with increasing difference in risk-genotype frequency, but declines with increasing difference in incidence between the two populations. The contribution of genetic variants also increases with increasing relative risk and the contribution of joint effect of genetic and environmental factors increases with increasing relative risk of the gene–environmental interaction.

Our results show that the contribution of a genetic variant to the difference in incidence of disease is not zero even when the risk-genotype frequency and relative risks are identical in the two populations. Initially, this result seems to be counterintuitive, but we calculate the contribution of the genetic variant to the difference in incidence of disease in the two populations and not the difference between contributions of the genetic variant to the incidence of disease or PAR in each population. For example, let P be the incidence of disease in the first population, kP, be the incidence of disease in the second population and I be the background risk in the first population. If the risk-genotype frequency and relative risk of a risk-genotype is identical in both populations, it can be easily shown that the background risk in the second population is kI, PAR1=(P−I)/P, and PAR2=k(P−I)/kP=PAR1=PAR. The difference between contributions of the genetic variant to the incidence of disease in each population is given by PAR2−PAR1=0; however, GC=a2PAR+a1PAR=PAR or the contribution of the genetic variant to the difference in incidence is the PAR in each population. When the risk-genotype frequency, G, and relative risks, R, are identical in the two populations, GC=G(R−1)/(1+G(R−1)), and the value of GC remains the same whatever the difference in incidence between the two populations. GC can be zero only if the genetic variant is not a risk factor for both populations or the product of risk-genotype frequency, relative risk –1, and background risk is identical in both populations. When risk-genotype frequency and relative risks are identical in both populations, as long as there is a difference in incidence of disease, the background risks for the two populations would differ and GC cannot be zero. It is also possible to have identical incidence of disease in both populations but have different PARs for the two populations. The GC is not defined in this situation.

When a group of risk variants are associated with a disease for one population but a different group of risk variants are associated with the disease for the second population, the contribution of both groups of risk variants to the difference in incidence can still be calculated using GC formula by keeping relative risk equal to 1 for the variants not associated with the respective populations.

A limitation in our study is not having the causal variants associated with disease in different populations. The prevalence of obesity in African Americans is 50% more than the prevalence in European Americans. Recent GWAS have shown that the variants in the obesity-related gene, FTO, is significantly associated with obesity in populations of European origin.19 The SNP rs9939609, is significantly associated with obesity in populations of European descent. This association was not observed in African Americans.20 However, there is evidence that another SNP, rs3751812, affects the risk of obesity in African Americans.21 These results suggest that the genetic factors predisposing to obesity in African Americans at FTO may be different from that in other populations, although an alternative explanation for these observations is that the causal variant has not been identified, and the linkage disequilibrium patterns to the causal variant are different in African and non-African populations.22

GC can be used not only for genetic variants but an equivalent expression can be used also for environmental factors. The same concept can be used to compare contributions from genetic variants, environmental factors and joint effects of gene and environment to the difference in incidence between populations for a given disease. By identifying the relative contributions of these environmental risk factors and genetic variants to the difference in incidence of disease, public health interventions can be tailored to reduce these differences between populations. Finally, we should make clear that GC estimates should not be confused with the proportion of risk variance explained in each population. The proportion of risk variance explained for most common variants associated with complex diseases is very small, even when many such variants are considered. Conversely, the PAR estimates can be large and this applies also to GC, which is conceptually more akin to PAR, as we discussed above.

Currently, only few genetic variants are known to be associated with a given disease in different populations. We have shown that the contribution of a group of genetic variants to the disparity in incidence of disease could change considerably by adding one more genetic variant to the group. Although many more genetic variants associated with disease remain to be discovered, any estimate of genetic contribution to the disparity in incidence of disease between two populations at this stage seems to be an elusive goal. This is both a result of not knowing the genetic architecture and of complexity in interpreting the GC measure. In the current status of knowledge, statements about specific variants or clusters thereof explaining the difference in disease incidence and prevalence in different populations and thus having clinical or public health consequences are precarious.

The authors declare no conflict of interest.

Disclaimer

The findings and conclusions in this report are those of the authors and do not necessarily represent the official position of the Centers for Disease Control and Prevention.

References

  1. Richard D, Collins J. Disparities in infant mortality: what's genetics got to do with it. Am J Public Health. 2007;97:1191–1197. doi: 10.2105/AJPH.2005.068387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Drayna D. Founder mutations. Sci Am. 2005;293:78–85. doi: 10.1038/scientificamerican1005-78. [DOI] [PubMed] [Google Scholar]
  3. Adeyomo A, Rotmi C. Genetic variations associated with complex human diseases show wide variation across multiple populations. Public Health Genomics. 2010;13:72–79. doi: 10.1159/000218711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Myles S, Davison D, Barret J, Stoneking M, Timpson N. Worldwide population differentiation at disease associated SNPs. BMC Med Genomics. 2008;1:22. doi: 10.1186/1755-8794-1-22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Chang MH, Lindegren ML, Butler MA, et al. Prevalence in the United States of selected candidate gene variants: third National Health and Nutrition Examination Survey (NHANES III), 1991-1994. Am J Epidemiol. 2009;169:54–66. doi: 10.1093/aje/kwn286. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Ioannidis JPA, Ntzani EE, Trikalinos TA. ‘Racial' differences in genetic effects for complex diseases. Nat Genet. 2004;36:1312–1318. doi: 10.1038/ng1474. [DOI] [PubMed] [Google Scholar]
  7. Ioannidis JPA, Thomas G, Daly MJ. Validating, augmenting and refining genome-wide association signals. Nat Rev Genet. 2009;10:318–329. doi: 10.1038/nrg2544. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Ioannidis JPA. Population-wide generalizability of genome-wide discovered associations. J Natl Cancer Inst. 2009;101:1297–1299. doi: 10.1093/jnci/djp298. [DOI] [PubMed] [Google Scholar]
  9. Ntzani E, Liberopoulos G, Manolio T, Ioannidis JP.Consistency of genome-wide associations across major ancestry groups Hum Genet 2011. e-pub ahead of print 20 December 2011; doi: 10.1007/s00439-011-1124-4 [DOI] [PubMed]
  10. Mountain JL, Risch N. Assessing genetic contributions to phenotypic differences among ‘racial' and ‘ethnic' groups. Nat Genet. 2004;36:S48–S53. doi: 10.1038/ng1456. [DOI] [PubMed] [Google Scholar]
  11. Sankar P, Cho MK, Condit CM, et al. Genetic research and health disparities. JAMA. 2004;291:2985–2989. doi: 10.1001/jama.291.24.2985. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Wray NR, Goddard ME, Visscher PM. Prediction of individual genetic risk to disease from genome-wide association studies. Genome Res. 2007;17:1520–1528. doi: 10.1101/gr.6665407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Khoury MJ, Beaty TH, Hwang S. Detection of genotype-environment interaction in case-control studies of birth defects: how big a sample size. Teratalogy. 1995;51:336–343. doi: 10.1002/tera.1420510510. [DOI] [PubMed] [Google Scholar]
  14. Rothman K, Greenland S.Modern Epidemiology2nd edn. Philadelphia: Lippincott Williams & Wilkins; 1998 [Google Scholar]
  15. The R Project for Statistical Computing . www.R-project.org .
  16. Ng MC, Park KS, Oh B, et al. Implication of genetic variants near TCF7L2, SLC30A8, HHEX, CDKAL1, CDKN2A/B, IGF2BP2, and FTO in type 2 diabetes and obesity in 6,719 Asians. Diabetes. 2008;57:2226–2233. doi: 10.2337/db07-1583. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. International HapMap Project . http://hapmap.ncbi.nlm.nih.gov .
  18. McBean AM, Li S, Gilbertson DT, et al. Differences in diabetes prevalence, incidence, and mortality among the elderly of four racial/ethnic groups: Whites, Blacks, Hispanics, and Asians. Diabetes Care. 2004;27:2317–2324. doi: 10.2337/diacare.27.10.2317. [DOI] [PubMed] [Google Scholar]
  19. Fraling TM, Timpson NJ, Weedon MN, et al. A common variant in the FTO gene is associated with body mass index and predisposes to childhood and adult obesity. Science. 2007;316:889–894. doi: 10.1126/science.1141634. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Scuteri A, Sanna S, Chen WM, et al. Genome-wide association scan shows genetic variants in the FTO gene are associated with obesity related traits. PLoS Genet. 2007;3:e115. doi: 10.1371/journal.pgen.0030115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Grant SF, Li M, Bradfield JP, et al. Association analysis of the FTO gene with obesity in children of Caucasian and African ancestry reveals a common tagging SNP. PLoS One. 2008;3:e1746. doi: 10.1371/journal.pone.0001746. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Cheng CY, Kao WH, Patterson N, et al. Admixture mapping of 15,280 African Americans identifies obesity susceptibility loci on chromosome 5 and X. PLoS Genet. 2009;5:e1000490. doi: 10.1371/journal.pgen.1000490. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from European Journal of Human Genetics are provided here courtesy of Nature Publishing Group

RESOURCES