Synchronization of Early Afterdepolarizations and Arrhythmogenesis in Heterogeneous Cardiac Tissue Models

Abstract

Early afterdepolarizations (EADs) are linked to both triggered arrhythmias and reentrant arrhythmias by causing premature ventricular complexes (PVCs), focal excitations, or heterogeneous tissue substrates for reentry formation. However, a critical number of cells that synchronously exhibit EADs are needed to result in arrhythmia triggers and substrates in tissue. In this study, we use mathematical modeling and computer simulations to investigate EAD synchronization and arrhythmia induction in tissue models with random cell-to-cell variations. Our major observations are as follows. Random cell-to-cell variations in action potential duration without EAD presence do not cause large dispersion of refractoriness in well-coupled tissue. In the presence of phase-2 EADs, the cells may synchronously exhibit the same number of EADs or no EADs with a very small dispersion of refractoriness, or synchronize regionally to result in large dispersion of refractoriness. In the presence of phase-3 EADs, regional synchronization leads to propagating EADs, forming PVCs in tissue. Interestingly, even though the uncoupled cells exhibit either no EAD or only a single EAD, when these cells are coupled to form a tissue, more than one PVC can occur. When the PVCs occur at different locations and time, multifocal arrhythmias are triggered, with the foci shifting in space and time in an irregular manner. The focal arrhythmias either spontaneously terminate or degenerate into reentrant arrhythmias due to heterogeneities and spatiotemporal chaotic dynamics of the foci.

Introduction

Early afterdepolarizations (EADs) are secondary depolarizations of an action potential, which are associated with arrhythmogenesis in many cardiac diseases, such as long-QT syndrome (1–7) and heart failure (8,9). EADs have historically been linked to triggered arrhythmias maintained by focal excitations (10,11), but exactly how they trigger focal arrhythmias in cardiac tissue is not well understood. Later studies (2–4,12,13) have also proposed that EADs may cause reentrant arrhythmias by forming premature ventricular complexes (PVCs), or by regionally lengthening the action potential duration (APD) to increase dispersion of refractoriness, forming reentry substrates. However, EADs tend to occur irregularly from beat to beat in a given cell (8,14–16) due to dynamical chaos (17,18) or random ion channel fluctuations (19,20). They may occur randomly from cell to cell in a given beat due to random cell-to-cell variations (21,22), such as variations in ion channel conductance or kinetics, cell size and geometry, etc. How the irregularly occurring EADs synchronize in tissue to reach a critical size to form PVCs or reentry substrates remains incompletely understood.

In previous studies (17,18,23), we showed that irregularly occurring EADs could be explained by dynamical chaos. Due to the chaotic behavior of EADs, regional synchronization of EADs occurs in homogeneous tissue, with regions exhibiting EADs bordering to regions without EADs. This forms both PVCs and regionally lengthened APD, which gives rise to both triggers and substrates of arrhythmias, including reentrant and multiple shifting focal arrhythmias. However, real tissue is not homogeneous, but has random cell-to-cell fluctuations in cell parameters, such as the number of ion channels and regional heterogeneities. Because the properties of the cells in heterogeneous tissue are intrinsically different from each other, the way that EADs synchronize differs from that in the homogeneous tissue.

The essential difference is that in homogeneous tissue, because the cells are identical, synchronization means to maintain the cells in the same phase by gap junction coupling. The gap junction current is almost negligible after synchronization is achieved. In heterogeneous tissue, however, some cells are more prone to EADs than others. The ones more prone to EADs tend to promote EADs in the ones without EADs, and the ones without EADs tend to suppress EADs. Synchronization of EADs requires large gap junction currents to smooth out the intrinsic difference between cells. Therefore, understanding the roles of cellular heterogeneities and their interactions with dynamical instabilities in PVC formation, regional APD lengthening, and in maintaining multifocal arrhythmias (5,6) is important for understanding EAD-mediated arrhythmogenesis in cardiac tissue.

In this study, we use computer simulation to address the question of how EADs are regionally synchronized and cause arrhythmias in heterogeneous tissue. We focus on the heterogeneities caused by cell-to-cell fluctuations in ionic conductance. Simulations were carried out in one-dimensional cable and two-dimensional tissue models to study regional synchronization of EADs and EAD-mediated triggered and reentrant arrhythmias. To avoid the confluent effects of dynamical chaos on EAD synchronization, we only gave one pacing stimulus to all cells in the tissue models at the beginning of the simulation and studied the behaviors of the system after the stimulus. This is also similar to the condition of a single long pause in the heartbeat, which has been shown to be responsible for arrhythmogenesis in long-QT syndrome (4,24–26). We studied the effects of the spatial distribution of the cell properties and gap junction coupling on EAD synchronization, PVC formation, and multiple focal arrhythmia induction.

Methods

We used the rabbit ventricular action potential model by Mahajan et al. (27) to generate phase-2 EADs following the modifications in Sato et al. (17,18). We modified this model as in Xie et al. (28) to generate phase-3 EADs that can propagate in tissue.

The one-dimensional cable and two-dimensional tissue are monodomain models. The one-dimensional cable was simulated by solving the following partial differential equation of voltage,

$$\frac{\partial V}{\partial t}=-\frac{I_{ion}}{C_m}+D\frac{{\partial }^{2}V}{\partial x^2},$$ (1)

where V is the membrane potential (in mV), C_m = 1 μF/cm² is the membrane capacitance, and D is the diffusion constant (in cm²/ms), which was computed as D = 250g_gapl_c/πr_c/C_m, with g_gap the gap junction conductance in Siemens (250 nS, unless specified otherwise), l_c = 0.015 cm the cell length, and r_c = 0.001 cm the cell radius. The two-dimensional tissue was simulated by solving the partial differential equation,

$$\frac{\partial V}{\partial t}=-\frac{I_{ion}}{C_m}+D\left(\frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}\right),$$ (2)

where we chose D = 0.0005 cm²/ms, which results in a conduction velocity of ∼50 cm/s. No-flux boundary conditions and a spatial discretization of Δx = Δy = 0.015 cm were used. Heterogeneities were modeled in one-dimensional cable and two-dimensional tissue by randomly varying the maximum conductance of the L-type Ca current (I_Ca,L) from cell to cell following a Gaussian distribution.

In all simulations, the entire cable or tissue was stimulated once at the beginning of the simulation with a current pulse of strength of 40 μA/cm² and duration of 1 ms. Equations 1 and 2 were solved using the Euler method with an adaptive time step varying from 0.001 to 0.1 ms, using operator splitting as described previously (29). APD was defined as the time duration in which V > −70 mV in an action potential. Simulations were carried out on graphic processing units as described in Sato et al. (30). The graphic-processing-unit cards used were NVIDIA Tesla C2050 cards (NVIDIA, Santa Clara, CA).

Results

EAD synchronization in a one-dimensional cable model with phase-2 EADs

The original rabbit ventricular myocyte model was modified to exhibit phase-2 EADs following the study by Sato et al. (17). We altered the strength of the I_Ca,L flux (g_Ca) to simulate different cellular action-potential properties. As shown in Fig. 1 A, when g_Ca is increased from the default value, APD increases. When g_Ca is increased to 520 mmol/(cm C), a single EAD appears in the action potential. As g_Ca is increased further, a second EAD appears at another critical g_Ca, and so on, resulting in a staircase in APD.

Figure 1.

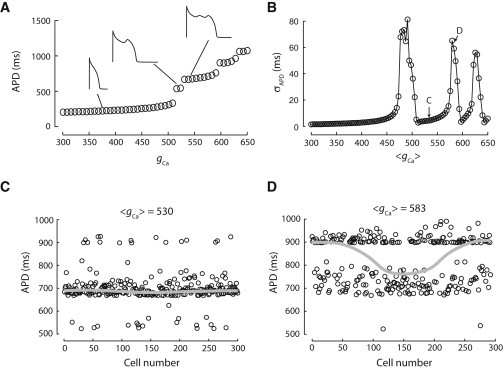
Synchronization of phase-2 EADs in a one-dimensional cable with random cell-to-cell variations. (A) APD of a single rabbit ventricular cell as a function of g_Ca. (B) σ_APD in a cable of 300 cells versus 〈g_Ca〉 with random g_Ca drawn from a Gaussian distribution and standard deviation σ_gCa = 35 mmol/(cm C). (C) APD distribution with 〈g_Ca〉 = 530 mmol/(cm C) when uncoupled (open circles) and coupled (shaded line). (D) Same as panel C but for 〈g_Ca〉 = 583 mmol/(cm C).

We placed the model cells in a one-dimensional cable in which g_Ca was varied randomly along the cable following a Gaussian distribution. When the cells are uncoupled, the random variations in APD are very large (large standard deviation σ_APD). When no (or a few) cells exhibit EADs, electrotonic coupling smoothes out these fluctuations and APD varies slightly across the cable. However, as 〈g_Ca〉 increases to include more cells exhibiting EADs, both small and large heterogeneities in APD distribution can develop in the cable, showing an oscillating pattern as g_Ca increases (Fig. 1 B). For example, Fig. 1 C shows a simulation with g_Ca = 530 mmol/(cm C). When the cells are uncoupled, APD varies largely. But when the cells are coupled, the APDs are almost the same in all cells and all cells have a single EAD, exhibiting a small variation. Fig. 1 D shows another simulation with g_Ca = 585 mmol/(cm C). The cell-to-cell APD variation in the uncoupled cells is similar to that in Fig. 1 C, but when the cells are coupled, APD distribution in the cable shows large gradients with cells exhibiting different numbers of EADs.

The observations above can be understood as follows. As shown in Fig. 1 A, as g_Ca increases, the action potential suddenly gains one EAD at certain g_Ca values, exhibiting an “all-or-none” behavior. When 〈g_Ca〉 is close to these critical g_Ca values, the cells have to choose which number of EADs to have due to the all-or-none competition between these cells. As a result of the competition, one type of action potential dominates in one region and the other type dominates in another region. When 〈g_Ca〉 is further away from these critical g_Ca values, one type of action potential wins across the whole cable, resulting in a synchronous distribution. This gives rise to the oscillation pattern shown in Fig. 1 B. It is well known that gap junction coupling affects EAD formation and propagation (28,31–33) in tissue, i.e., EADs are suppressed by stronger gap junction coupling. The APD dispersion shown in Fig. 1 can be suppressed by stronger coupling or enhanced by weaker coupling.

EAD synchronization in a one-dimensional cable model with phase-3 EADs

Because phase-2 EADs cannot propagate in our tissue models (which agrees with the experimental observations by Damiano and Rosen (34)), we used another action-potential model in which phase-3 EADs are generated (Fig. 2 A) to study EAD propagation (28). We simulated a one-dimensional cable with random cell-to-cell variations in g_Ca following a Gaussian distribution. When the cells are uncoupled, they may exhibit no EADs or a single phase-3 EAD (Fig. 2 A). Depending on the exact realization of the random g_Ca distribution, for the same mean value of g_Ca (〈g_Ca〉), EADs may either be suppressed altogether in a cable, or may be able to exist in one or more regions of the cable and form PVCs. Fig. 2 B shows the action potentials from 45 out of the 300 cells when they are uncoupled. The values of g_Ca for each cell were drawn from a Gaussian distribution with 〈g_Ca〉 = 870 mmol/(cm C) and standard deviation σ_gCa = 35 mmol/(cm C). Fig. 2 C shows time-space plots for two randomizations of the same 300 cells when they are coupled. A PVC forms in one of the two randomizations.

Figure 2.

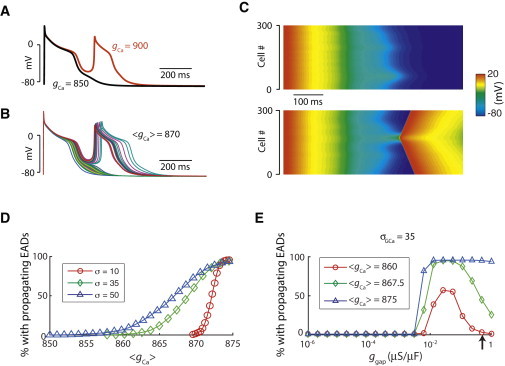
PVC formation in a one-dimensional cable of coupled phase-3 EAD cells. (A) Examples of action potentials of the phase-3 EAD model for two different values of g_Ca. (B) Action potentials of 45 out of 300 uncoupled cells with 〈g_Ca〉 = 870 mmol/(cm C) and σ_gCa= 35 mmol/(cm C). (C) Space-time plots of two simulations of a cable of 300 cells. Both simulations were done with the same set of g_Ca as in panel B, but reshuffled randomly across the cable. A single stimulus was given to all cells at t = 0. (D) Percentage of simulations exhibiting PVCs versus 〈g_Ca〉 for different σ_gCa. For each 〈g_Ca〉, 1000 trials (random reshuffles) were done from the same set of g_Ca. A propagating EAD was defined as the second activation after the initial stimulus reaching the end of the cable. (E) Same as panel D, but for varying gap junction conductance and different 〈g_Ca〉 with σ_gCa = 35 mmol/(cm C). (Arrow) Normal gap junction coupling.

We then studied the statistics of PVC occurrence as a function of 〈g_Ca〉. Fig. 2 D shows the percentage of simulated random trails that have one or more PVCs as a function of 〈g_Ca〉 for different values of the standard deviation, σ_gCa. As expected, the probability of having a PVC in a cable increases monotonically with 〈g_Ca〉, because for higher values of 〈g_Ca〉, more cells “want” to have an EAD and thus the chance for a PVC to occur is higher. When σ_GCa is increased, not only does the range of 〈g_Ca〉 for which PVCs can occur become larger, but the entire curve is shifted to lower values of 〈g_Ca〉. Therefore, when the cell-to-cell fluctuations in g_Ca are higher, the chance to have a PVC is higher.

When the gap junction coupling strength is reduced, the probability for PVCs increases (Fig. 2 E). This agrees with the observations that when gap junction coupling is reduced, the critical number of EAD cells required for a PVC to form is reduced (28), or with the increased occurrence of focal arrhythmias under fibrosis (35). When the gap junction conductance is reduced below a certain critical value (∼10 nS), propagation failure occurs, and the probability for PVCs drops to zero.

EAD-triggered arrhythmias in a two-dimensional tissue model with random cell-to-cell variations

To study how phase-3 EADs cause arrhythmias in tissue, we carried out simulations in a square tissue with the phase-3 EAD model cells. The values of g_Ca for different cells were drawn from a Gaussian distribution. The entire tissue was stimulated once at the beginning. Depending on 〈g_Ca〉 and the distribution of the cells, different behaviors occurred in the tissue simulations. The different outcomes are shown in Fig. 3, and detailed as follows:

Figure 3.

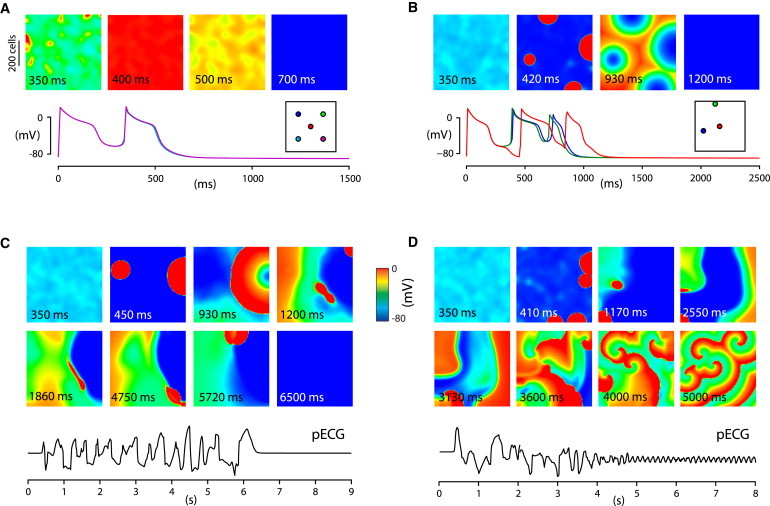
PVCs and arrhythmias triggered phase-3 EADs in two-dimensional tissue. Simulations of 600 × 600 cell tissue of phase-3 EAD model cells with σ_gCa = 35 mmol/(cm C) and 〈g_Ca〉 = 867 mmol/(cm C) (B–D) and 〈g_Ca〉 = 870 mmol/(cm C) (A). The entire tissue was stimulated once at t = 0. Membrane potential time series in panels A and B correspond to locations in the tissue (highlighted by circles of the same color in the inset). Pseudo- electrocardiograms are shown for panels C and D.

When 〈g_Ca〉 is small, the majority of the cells exhibits no EADs when they are uncoupled. When the cells are coupled via gap junction conductance, the sink effect of non-EAD cells overcomes the source effect of the cells prone to EADs, suppressing the EADs in the coupled tissue. Therefore, as expected, no PVCs or arrhythmias occur.

When 〈g_Ca〉 is large, the majority of the cells exhibits EADs when they are uncoupled. When they are coupled in tissue, a synchronous whole-tissue PVC occurs (Fig. 3 A, and see Movie S1 in the Supporting Material). The source effect of the cells prone to EADs overcomes the sink effect from the non-EAD cells, synchronizing the whole tissue to exhibit an EAD. The mechanism of EAD synchronization is the same as that in the case of phase-2 EADs shown in Fig. 1 C.

More interesting scenarios occur when 〈g_Ca〉 is in the intermediate range. In this case, different arrhythmias can occur for identical 〈g_Ca〉, depending on the exact distributions. Fig. 3, B–D, shows three examples with the same 〈g_Ca〉 and the same standard deviation σ_GCa but different random distributions of the cells. Fig. 3 B (see Movie S2) shows that the competition between the cells prone to EADs and non-EAD cells results in regionally synchronized EADs in multiple sites of the tissue (four sites as seen in the second panel of Fig. 3 B), which occur in roughly the same time. These regionally synchronized EADs then propagate in tissue as target waves to give rise to a PVC. Interestingly, the uncoupled cells can only exhibit a single EAD, but two PVCs (two EADs occur after the stimulated beat, see bottom panel in Fig. 3 B) occur in the coupled tissue. The second PVC originates at the same four sites. This indicates that the heterogeneous cellular properties promote EADs, a tissue-scale phenomenon that cannot be seen in single uncoupled cells or homogeneous tissue. The exact mechanism is not clear to us, but it agrees with the observations in our previous study in which we showed that phase-3 EADs occur as a result of electrical heterogeneities (36).

Fig. 3 C (see Movie S3) shows another case in which multifocal arrhythmias occur, which then terminate spontaneously after many revolutions. In this case, the competition between different types of cells causes regionally synchronized EADs. After the first PVC (second panel), regional synchronized EADs occur at locations different from the first PVC (fourth panel), differing from the case in Fig. 3 B. As this process repeats in the tissue, it results in multiple shifting focal arrhythmias. These arrhythmias last for several seconds and then terminate spontaneously. This behavior is a type of spatiotemporal chaos, similar to that shown in our previous study (17). Note that if the regionally synchronized EADs are simply due to heterogeneities, they should occur at the same locations each time; however, they occur dynamically and irregularly in space and time. As shown in our previous study (17), the beat-to-beat chaotic behavior of EADs can facilitate the formation of local PVCs and multiple shifting focal arrhythmias in a homogeneous tissue, so it is not surprising that this can also occur in a heterogeneous tissue. The mechanism of spontaneous termination of arrhythmias is the same as demonstrated in our previous studies (37,38) and those of others (39), which shows that spatiotemporal chaos in an excitable medium of finite size can terminate spontaneously to result in a quiescent tissue.

Fig. 3 D (see Movie S4) shows a case in which multifocal arrhythmias degenerate into reentrant arrhythmias. The multiple shifting foci are due to the same mechanism as in Fig. 3 C. In this case, instead of self-terminating, the multifocal arrhythmias degenerate into reentrant arrhythmias due to local wave breaks caused by heterogeneities and their interactions with the chaotic wave dynamics. Note that during the first few seconds, the action potential repolarizes fully to the resting potential (∼−80 mV). After that the system transitions to a new state in which the action potential fails to full repolarization (the color scale changes from red to green during reentry in the last two panels in Fig. 3 D). Because the sodium current only activates at voltages <−60 mV, the I_Ca,L is the only inward current for depolarization. Therefore, the reentry is mediated by I_Ca,L. One can also see from Movie S4 that the I_Ca,L-mediated spiral waves are stable. Because after the simulation begins, no parameters are changed, this same tissue supports both I_Na-mediated (e.g., wave conduction in the period of multifocal arrhythmias) and I_Ca,L-mediated (e.g., wave conduction in the later period of reentry) propagation. This is a “biexcitable” behavior in tissue, as shown in our previous study (40). Also note that the I_Ca,L-mediated reentry is much faster than was shown in our previous study due to the larger EAD amplitude (or higher I_Ca,L-mediated excitability) in this model (Fig. 2 A).

The probabilities of these behaviors depend on 〈g_Ca〉 as well as other parameters as expected. Fig. 4 shows the probabilities of different behaviors versus 〈g_Ca〉 for different conditions. To facilitate automatic computation of the probabilities, we classified the behaviors into three cases as follows: 1), no PVCs or arrhythmias (activity in tissue stops after the first action potential); 2), a single or a double PVCs (activity occurs after the first action potential but lasts for <2000 ms; Fig. 3, A and B); and 3), arrhythmias (activity persists for at least 2000 ms; Fig. 3, C and D). Interestingly, although each individual cell can only show a single EAD, there are two peaks in which multifocal arrhythmias occur (Fig. 4 A). These multifocal arrhythmias either spontaneously terminate or degenerate into reentry. In the two peaks, in ∼30% of the cases, arrhythmias self-terminate after ∼5000 ms, and ∼70% of the cases develop into one or more stable rotors. The two regions are widened when σ_gCa is increased (Fig. 4 B) or the gap junction conductance is reduced (Fig. 4 C).

Figure 4.

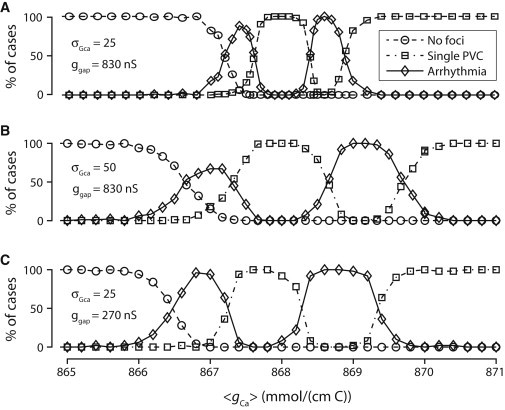
Statistics of PVCs and arrhythmias in two-dimensional tissue. Statistics for simulations of 600 × 600 cell² tissue of phase-3 EAD model cells with random g_Ca drawn from a Gaussian distribution with standard deviation σ_gCa and with gap junction coupling g_gap. Each data point corresponds to 50 simulations of 2000 ms with different realizations of the random distribution. (Dashed lines with open circles) Probability of having no EADs in the tissue. (Dashed-dotted lines with open squares) One or two single propagating PVCs with no further activity. (Solid lines with open diamonds) PVCs that lead to sustained focal activity. (A) Statistics with normal gap junctional coupling and σ_gCa = 25 mmol/(cm C). (B) Statistics with larger fluctuations in g_Ca (σ_gCa = 50 mmol/(cm C)). (C) Statistics with gap junction conductance reduced by 67%.

Discussion

As shown in many experimental studies, EADs tend to occur irregularly from beat to beat in a given cell (8,14–18). Our recent studies (17,18,23) showed that the irregular dynamics is likely dynamical chaos. In these studies, we show how chaos synchronization can result in regional synchronized EADs and thus PVCs and reentrant and focal arrhythmias in homogeneous tissue models. In real cardiac tissue, however, in addition to regional differences in APD (41) and calcium cycling (42), short spatial scale heterogeneities, such as random cell-to-cell variability in ionic current density (21,22) or cell size, also exist. These cell-to-cell heterogeneities cause EADs to vary irregularly from cell to cell. In this study, we used computer simulation to investigate the effects of random cell-to-cell variations in action-potential dynamics on EAD synchronization and EAD-mediated arrhythmogenesis in cardiac tissue.

Our major findings are as follows. In the absence of EADs, electrotonic coupling is effective in smoothing out the APD difference caused by random cell-to-cell variations, agreeing with our previous simulation study that random heterogeneities in small spatial scales have few effects on APD distribution and spiral wave dynamics (43). However, in the presence of EADs, random heterogeneities in small spatial scales can result in large spatial scale changes; i.e., due to the all-or-none nature of EADs, regional synchronization of EADs can occur to result in: 1), large APD gradients or dispersion of refractoriness; 2), PVCs; and 3), multifocal arrhythmias. These properties are modulated by gap junction coupling and cell distributions.

The implications of this study to arrhythmogenesis in cardiac diseases can be drawn as follows:

• 1.Agreeing with other modeling studies (12,33) and experimental observations (34), our study shows that phase-2 EADs cannot propagate in tissue with normal gap junction coupling. Regional synchronization of EADs causes large dispersion of refractoriness, which may serve as a substrate for unidirectional conduction block to result in reentry. On the other hand, due to its lower take-off potential and higher amplitude, phase-3 EADs can propagate in tissue with normal gap junction coupling. Under this condition, arrhythmia-trigger (PVC) and substrate can occur simultaneously to result in focal and reentrant arrhythmias.
• 2.EAD-related arrhythmias have historically been called “triggered arrhythmias” (10,11), however, how triggered arrhythmias are subsequently maintained in tissue for longer periods of time is not clear. In other words, a single cell often exhibits one or several EADs in a stimulated action potential, but in tissue, once an arrhythmia is triggered by EADs, it lasts for seconds to minutes or even becomes sustained. In many cases, the arrhythmias are maintained by multiple shifting foci (5,6). In this study, we show that even though the uncoupled cells can only exhibit a single EAD, in heterogeneous tissue, long-lasting arrhythmias can occur due to the complex spatiotemporal dynamics, a tissue phenomenon that cannot be understood at the single-cell level. More specifically, when multiple PVC sites fire at roughly the same time (as in Fig. 3 A), they run into each other, after which the tissue becomes quiescent. However, when fewer sites fire, or when the PVC sites do not fire at the same time, a PVC in one location propagates to another location and triggers a new beat at that location. This new beat will then propagate as a PVC and trigger a PVC in another location (as in Fig. 3 C), and so on. Although the heterogeneities in cellular parameters are fixed, the foci occur dynamically and irregularly in space and time. This behavior is similar to what we showed in a previous study (17) in which spatiotemporal chaotic EAD dynamics maintains the multiple shifting foci to manifest polymorphic ventricular tachycardia (PVT) and Torsade de Pointes (TdP) in homogeneous tissue. Therefore, this study and the previous one can provide mechanistic insight into the shifting foci that maintain PVT or TdP in long-QT syndrome observed in experimental studies (5,6) and in clinical settings. In addition, spontaneous termination of the shifting foci in our simulation study can also provide mechanistic insights into spontaneous termination of TdP that are widely observed clinically (44–46).
• 3.PVT and TdP in long-QT syndrome are mainly triggered by a single pause in the heartbeat (4,24–26). Although we argue that chaos synchronization can explain the maintenance and spontaneous termination of the multiple shifting foci, it cannot well explain the pause-induced PVT and TdP because it takes several-to-many beats for the instability to develop to cause localized PVCs or foci in homogeneous tissue. In this study, we show that in tissue with random cell-to-cell variations, local PVCs self-organize immediately after a single stimulus. These PVCs may cause reentry or undergo the processes as shown in Fig. 3 to cause focal arrhythmias. The combined effects of preexisting heterogeneities and nonlinear dynamics can better explain the pause-induced PVT and TdP observed clinically and experimentally.
• 4.Our previous study (40) and this study show that when EADs can propagate in tissue, because they occur at a voltage range where I_Na is not available, their propagation is mediated by I_Ca,L. We show that under such conditions, both I_Na-mediated conduction and I_Ca,L-mediated conduction can occur in the same tissue; we call this “biexcitability” (40). Although a direct demonstration of biexcitability in the heart is so far not available, microelectrode recordings during pause-induced TdP show that the voltage only partially repolarizes (4), providing indirect evidence for the I_Ca,L-mediated conduction during PVT and TdP.

Limitations

In this study, we investigated the effects of random cell-to-cell variations on EAD synchronization and arrhythmogenesis in cardiac tissue models. We only varied the maximum conductance of I_Ca,L to obtain different EAD properties and to model random cell-to-cell heterogeneities. In real tissue, EADs and their heterogeneous distributions can result from alterations and heterogeneities of many other ion currents, e.g., the reduction of potassium currents or increase in sodium or calcium currents and heterogeneities in long QT syndrome (1–6). However, altering one or more of these ionic currents randomly from cell to cell might result in similar action-potential properties and EAD behaviors, and thus possibly the same tissue-scale EAD dynamics.

The random cell-to-cell distribution may be a too-idealized setting for real tissue because macroscopic regional heterogeneities and gradients in the ventricles (41,47,48) exist, which may have a critical number of cells to exhibit EADs or triggered activity simultaneously to form PVCs as shown in previous modeling studies (28,49,50). However, preexisting fixed heterogeneities alone cannot explain the dynamical behaviors of PVCs seen clinically (e.g., they vary from beat to beat) (51,52) and shifting foci in multifocal arrhythmias (5,6). In addition to the mechanisms of multiple shifting focal arrhythmias shown in our previous study (17) and this study, it is also possible that multiple shifting foci can arise from synchronization of random-calcium-wave-induced delayed afterdepolarizations in tissue (53,54).

In addition, phase-2 EADs were generated by altering the I_Ca,L kinetics and reducing of I_Ks (17), whereas phase-2 EADs may arise from different mechanisms (55–59), which may affect our conclusions obtained in this study. The phase-3 EADs were generated by adding a Ca-activated nonselective cation current (I_ns(Ca)) to the action potential model (17,28). Although this current has been identified in different species (60–62), its existence is controversial and its physiological or pathophysiological roles remain unclear. However, EADs have been shown to be able to propagate in cardiac tissue (5), and large-magnitude EADs have been observed (34). As long as the EADs propagate, our observations of PVC formation and multifocal arrhythmias may still occur even when the phase-3 EADs are due to other mechanisms. Our changes in parameters to generate phase-2 and phase-3 EADs, especially the changes in I_Ca,L kinetics and conductance, were not validated with experimental data, which raises an issue of how realistic these parameters are.

On the other hand, recent studies from Marder and Goaillard (63) have found that in neural circuits, similar bursting behaviors could result from combinations of very different ion channel conductances. In ventricular myocytes, Banyasz et al. (22) found that the ion channel conductances could differ in many folds while the variation in action potential was much smaller. This is supported by simulations showing that drastically different parameter sets in an action potential model can give rise to almost identical action potentials (64). These observations indicate that multiple choices in a wide range of parameters exist for a biological function, but also raise serious issues on how to select proper parameters and model formulations in mathematical modeling of biological systems.

Nevertheless, the purpose of our study is to understand in general how random cell-to-cell variations affect the manifestation of EADs in the tissue scale and thus the genesis of PVCs and arrhythmias. To study these general behaviors at the tissue scale, it is important for the cell model to exhibit certain characteristic properties though they may result from different combinations of parameters or even different cell models. In fact, the same results as shown in Fig. 1 were obtained (see Fig. S1 in the Supporting Material) using the phase I of the Luo and Rudy model (65) with modifications to generate phase-2 EADs (23). However, whether the theoretical predictions are applicable to real heart needs to be validated in experimental studies.