The Role of Magnesium for Geometry and Charge in GTP Hydrolysis, Revealed by Quantum Mechanics/Molecular Mechanics Simulations

Abstract

The coordination of the magnesium ion in proteins by triphosphates plays an important role in catalytic hydrolysis of GTP or ATP, either in signal transduction or energy conversion. For example, in Ras the magnesium ion contributes to the catalysis of GTP hydrolysis. The cleavage of GTP to GDP and P_i in Ras switches off cellular signaling. We analyzed GTP hydrolysis in water, Ras, and Ras·Ras-GTPase-activating protein using quantum mechanics/molecular mechanics simulations. By comparison of the theoretical IR-difference spectra for magnesium ion coordinated triphosphate to experimental ones, the simulations are validated. We elucidated thereby how the magnesium ion contributes to catalysis. It provides a temporary storage for the electrons taken from the triphosphate and it returns them after bond cleavage and P_i release back to the diphosphate. Furthermore, the Ras·Mg²⁺ complex forces the triphosphate into a stretched conformation in which the β- and γ-phosphates are coordinated in a bidentate manner. In this conformation, the triphosphate elongates the bond, which has to be cleaved during hydrolysis. Furthermore, the γ-phosphate adopts a more planar structure, driving the conformation of the molecule closer to the hydrolysis transition state. GTPase-activating protein enhances these changes in GTP conformation and charge distribution via the intruding arginine finger.

Introduction

Magnesium ions are omnipresent in biochemistry, often appearing in complex with guanosine or adenosine nucleotides. The enzymatic hydrolysis of adenosine triphosphate (ATP) and guanosine triphosphate (GTP) to the corresponding diphosphate is the major reaction involved in energy and in signal transduction (1). An important example in cellular signal transduction is the GTPase Ras. By GTP hydrolysis to diphosphate and P_i, Ras is switched from the active on- to the inactive off-conformation and signal transduction is terminated. The Ras-GTPase-activating protein (GAP) has the role of deactivating the on-complex by accelerating GTP hydrolysis by a factor of 10⁵ relative to intrinsic catalysis by Ras alone. If the downregulation of Ras is disturbed, the nucleus receives an enduring signal for proliferation, resulting in uncontrolled cell growth that may lead to cancer (2). GTP hydrolysis by Ras has been extensively investigated both theoretically (3–14) and by experimental techniques such as x-ray crystallography (15–19), nuclear magnetic resonance spectroscopy (20–22), and Fourier-transformed infrared (FTIR) spectroscopy (23–27). In this study, we investigated the role of the magnesium ion in this hydrolysis by quantum mechanics/molecular mechanics (QM/MM) simulations. Thereby we elucidate the geometry and charge distribution of the Mg²⁺-triphosphate complex in water, Ras, and Ras·GAP.

In many theoretical studies (3,6–11) the hydrolysis reaction in Ras and in the Ras·GAP complex is simulated to investigate the full reaction pathway. Most of the studies compare the calculated energy barriers of mutants with the experimental hydrolysis rates. Some studies (6,10,11) compare the calculated energy barriers and the experimentally determined activation energy of 14 kcal/mol (27). The enzymatic reactions are simulated by a combined QM/MM approach. In this approach the catalytic center is quantum mechanically simulated, and the protein and solvent atoms are treated by classical MM simulation. This combined approach presents a major challenge to computational chemists, especially when transition pathways are simulated (7). Klähn et al. (7) demonstrated the important influence of the Mg²⁺ on the energy barrier. Depending on the position of the magnesium ion, the free energy of activation is 15 kcal/mol or 32 kcal/mol, respectively.

However, the pathway with the 15 kcal/mol energy barrier, being even close to the experimental value, exhibits unreasonable Mg²⁺ coordination. In a later study, this was improved; Klähn et al. (10) presented a pathway with a free energy of activation of 14 kcal/mol and a reasonable Mg²⁺ coordination. Grigorenko et al. (6) first postulated that Gln⁶¹ and one water molecule are crucial for the hydrolysis and calculated an energy barrier of 15 kcal/mol, and later improved their hypothesis by stressing the role of Gln⁶¹ and two nucleophilic attacking water molecules with an energy barrier of 17 kcal/mol (11). Recently, Martin-García et al. (9) also identified two catalytically important waters adjacent to the Gln⁶¹. They validated their results by semiquantitatively comparing the energy barriers of mutants with the experimental hydrolysis rates. Their calculated free energy landscape exhibits a free energy barrier for the transition state (TS) of ∼22 kcal/mol. An alternate proposal for a TS that emphasizes the key role of the magnesium ion was recently reported by Lu et al. (8), but this TS incorporates an unreasonable high energy barrier of ∼70 kcal/mol.

Time-resolved FTIR experiments showed that bond breakage is faster than the intrusion of the arginine finger into the binding niche immediately before hydrolysis (27). Therefore, the experimentally determined value of 14 kcal/mol is only an upper limit. Only a few simulation studies (6,10,11) seem to be reasonably close to this experimental value.

In our study, we used a different approach. We did not simulate the transition pathway. We determined the educt (GTP) and product (GDP) geometry at atomic detail, and the corresponding charge distributions, in water, in Ras, and in Ras·GAP. The advantage of this approach, which was already used for phosphate ions in solution (28,29), is that we can quantitatively compare experimental and theoretical IR spectra, which are very sensitive to geometry and charge distribution. The vibrational spectra of GTP/GDP bound to proteins are experimentally obtained by FTIR difference spectroscopy (30). These spectra are sensitive to structural details below the resolution of x-ray crystallography, and indicate changes in bond length and charge distribution. The hydrolysis from GTP to GDP is followed on the millisecond timescale by time-resolved FTIR (26) in water, in Ras, and in Ras·GAP (25,31,32). The reaction is initiated by a laser flash using caged GTP (33). FTIR investigations thereby provide detailed insights into the molecular reaction mechanism.

However, FTIR spectra do not provide direct detailed three-dimensional structural information. To decode this information from the spectra, QM/MM simulations can be performed. The QM/MM simulation provides the structure and charge shifts in the QM-treated region at atomic detail (12,13). In the case of Ras and Ras·Gap, Klähn et al. (12) and te Heesen et al. (13) have analyzed the charge distributions and GTP geometry in the Ras protein and the Ras·GAP complex at atomic detail. They validated their results by good agreement between experimental and simulated spectra of GTP within an error of ∼2%.

These investigations have shown that structural alterations in GTP at ∼0.1 Å, far below the resolution of x-ray structure analysis, determine the catalysis. Furthermore, they observed the charge shift from γ-phosphate to β-phosphate, which has to take place during hydrolysis, and has been shown to take place in GTP using FTIR spectroscopy (32). This charge shift already in the educt state contributes significantly to catalysis. Here, we extended these former studies by using much longer MM simulation trajectories and a higher level of theory. Particular attention is paid to the role of the Mg²⁺, which, together with its coordinating partners, is now treated quantum mechanically as well. Additionally, our work extends beyond previous studies by also taking GTP and GTP·Mg²⁺ in water into consideration. Furthermore, we analyzed two additional crucial steps in the GTP hydrolysis pathway—the P_i intermediate and the GDP-bound product state.

In summary, we used available crystal structures as starting structures, refined them by MM and QM/MM simulations, and confirmed the accuracy of the GTP and GDP structures and the charge shifts in different environments by comparing calculated and measured GTP and GDP vibrational spectra. By the analysis of the individual conformations of the ligand and its changes during the reaction we identified how the magnesium ion contributes to catalysis.

Material and Methods

Details of the MM and QM/MM simulations, charge and structure calculations, and the validation method for simulated structures are described in the Supporting Material.

Results and Discussion

We deployed a combination of MM and QM/MM simulation (Fig. 1) to acquire charge shifts and structural details of the complex of the triphosphate and the magnesium ion. For evaluation, we analyzed only the last 0.5 ps of the equilibrated QM/MM simulation. We show that our structures are equilibrated and valid by comparing the vibrational modes of the phosphate groups calculated by instantaneous normal mode analysis to experimentally determined values (29). Previous studies of vibrational modes of phosphate groups reached root mean-square deviations (RMSDs) of 22 cm⁻¹ (14), 25 cm⁻¹ (34), and 34 cm⁻¹ (13). In general, an RMSD <30 cm⁻¹ (∼2%) between calculated and measured frequencies indicates good agreement. In accordance with Rudbeck et al. (34), the best results were reached with the B3LYP/6-31++G^∗∗ level of theory. Thus, only these results are reported here. A comparison of the results with different basis sets can be found in the Supporting Material.

Figure 1.

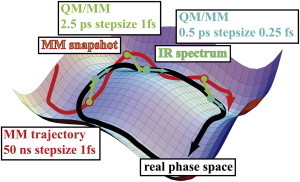
Applied method: Using MM (50 ns) and QM/MM simulations (6 × 2.5-ps equilibration plus 0.5-ps evaluation), we computed different states during hydrolysis. The starting structures of the MM simulations are prepared x-ray structures in a water box with physiological sodium chloride concentration. As starting structures for QM/MM simulations, we took six snapshots, each 5 ns from the last 25 ns of the MM trajectory. After 2.5 ps of QM/MM simulation, vibrational modes were calculated for comparison with the experimental IR spectrum. The last 0.5 ps of the validated QM/MM trajectories were used for a detailed investigation of charge shifts and structural details of the substrate. This procedure is repeated for all six simulations systems (see Table S1 in the Supporting Material).

First, we describe the conformation and coordination of the di-/triphosphate in water, bound to Ras and Ras·GAP. Then the calculated vibrational modes are compared to previous experimental and theoretical studies for such structures. Secondly, we report charge shifts induced by the magnesium ion, and the associated structural changes.

Conformation and spectral features of GTP and GTP·Mg²⁺ in water

As expected, GTP in water is very flexible during the 50-ns MM trajectory. This flexibility is revealed structurally by the standard deviation of the five backbone dihedrals of the triphosphate: O₂₃-P₃-O₃₂-P, P₃-O₃₂-P₂-O₃₁, O₃₂-P₂-O₃₁-P₁, P₂-O₃₁-P₁-O₅, and O₃₁-P₁-O_5′-C_5′. The average of the standard deviation of these dihedrals over all runs is 109°. Spectrally, the flexibility is demonstrated by the high standard deviations of the vibrational modes of ν_a(PO₂)_α (1240 ± 20 cm⁻¹) and ν_a(PO₂)_β (1214 ± 34 cm⁻¹) (see Fig. S2 in the Supporting Material). The overlap between these two bands supports the results of Wang et al. (23) and Takeuchi et al. (35), where only one broad band at 1233/4 cm⁻¹ was observed, precluding the identification of the vibrational modes of ν_a(PO₂)_α and ν_a(PO₂)_β in experimental data. The RMSD between experimentally assigned values (23) and our calculated values for all five vibrational modes was 28 cm⁻¹, further demonstrating the good agreement between theory and experiment. The RMSD between the calculated vibrational modes of Xia et al. (14) and the experimental values was 25 cm⁻¹.

Including Mg²⁺ in the solvent leads to a stable triphosphate with an α-, β-, γ-phosphate-coordinated Mg²⁺. Even if the Mg²⁺ is only coordinated by the γ- and β-phosphates in the starting structure, the MM and QM/MM simulations all converge to α-, β-, γ-phosphate coordination of the Mg²⁺. Three water molecules complete the coordination sphere of Mg²⁺ (see Fig. S1 a). With the coordinated Mg²⁺, the standard deviation of the backbone dihedrals decreases to 32°, compared to 109° for GTP without Mg²⁺. The standard deviations of the ν_a(PO₂)_α and ν_a(PO₂)_β vibrational modes also decrease from 20 cm⁻¹ and 34 cm⁻¹ without coordination, to 13 cm⁻¹ and 19 cm⁻¹ with coordination, respectively (see Fig. S2 and Fig. S3). The stable triphosphate structure also leads to a greater separation of the ν_a(PO₂)_α and ν_a(PO₂)_β vibrational modes.

This explains the two separate bands observed by Takeuchi et al. (35) for the ν_a(PO₂)_α and ν_a(PO₂)_β vibrational modes in the presence of Mg²⁺. The upper ν_a(PO₃)_γ vibrational mode, which was not observed experimentally, changes in the model from 1158 cm⁻¹ to 1188 cm⁻¹ with coordinated Mg²⁺. The other vibrational modes are very similar between the experiments and the models with and without Mg²⁺. Therefore, the vibrational modes of ν_a(PO₂)_α, ν_a(PO₂)_β, and ν_a(PO₃)_γ seem to represent the binding of the Mg²⁺. The RMSD between our calculated vibrational modes of GTP with the α-, β-, γ-phosphate-coordinated Mg²⁺ in water, and the six experimental ones (23,35), is 28 cm⁻¹. The RMSD between the experimental values and the calculated vibrational modes of Xia et al. (14) is 22 cm⁻¹.

Position of Tyr³² in Ras·GTP

In the Ras·GTP·Mg²⁺ complex, the Mg²⁺ is stably coordinated by the β- and γ-phosphates of the triphosphate in a bidentate manner. Ser¹⁷, Thr³⁵, and two water molecules are the other coordination partners of the Mg²⁺ (Fig. 2). The change from an α-, β-, γ-phosphate-coordinated Mg²⁺ in water to a β-, γ-phosphate-coordinated one in Ras is mainly revealed by the ν_a(PO₂)_β vibrational mode, which changes from 1224 cm⁻¹ in water (see Fig. S2) to 1208 cm⁻¹ in Ras (Fig. 3). This is due to the distance between the Mg²⁺ and the oxygen atom O₂₂ of the β-phosphate coordinating the Mg²⁺ (see Fig. S1). In α-, β-, γ-phosphate coordination, this distance is 2.15 Å; in β-, γ-phosphate coordination, the distance is 2.10 Å.

Figure 2.

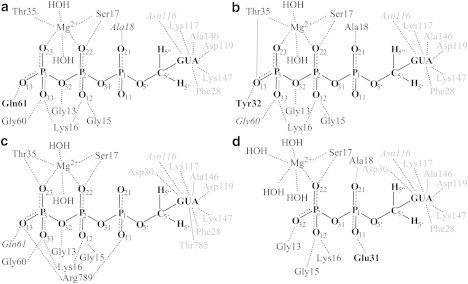
Coordination of GTP/GDP in Ras or Ras·GAP. The coordination partners of the GTP/GDP were estimated by the contact matrix algorithm of MAXIMOBY (41) from the 50-ns MM simulation. The bold-faced amino acids have contacts that occur during MM simulation but are not present in the x-ray structure (PDB:1QRA (18)). The italicized amino acids are contacts that are present in the x-ray structure but are not stable during MM simulation. The other amino acids have contacts in the x-ray structure that are stable during the MM simulation. Shown is the coordination of GTP in the open Ras·GTP·Mg²⁺ structure (a) in the absence of a hydrogen bond between Tyr³² and the γ-phosphate, and (b) with the formed hydrogen bond. (c) Coordination of GTP in Ras·GTP·Mg²⁺·GAP. (d) Coordination of GDP in Ras·GDP·Mg²⁺.

Figure 3.

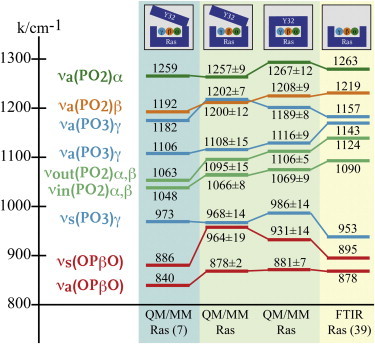
Comparison of calculated and measured vibrational modes for Ras·GTP·Mg²⁺ in water. (Light blue) Calculated vibrational modes from te Heesen et al. (13) based on the open structure. (Far-left side of the light-green shaded area) Our calculated results for the open structure. (Far-right side of the light-green shaded area) Calculated results based on the closed structure. (Light-yellow shaded area) Measured vibrational modes of Allin et al. (39). A detailed list of all calculated vibrational modes for all simulation systems is provided in Table S2.

The Mg²⁺ is not the only component responsible for the stable binding of the substrate. The GTP is also stabilized by amino acids in the active site of the protein. The guanine is coordinated by Phe²⁸, Lys¹¹⁷, Asp¹¹⁹, Ala¹⁴⁶, and Lys¹⁴⁷ (Fig. 2). The important role of Lys¹⁶, Gly¹³, and Gly¹⁵ in stabilizing the nucleotide is indisputable and has been extensively discussed in the literature (15,16,18,36,37). Lys¹⁶ stabilizes the γ- and β-phosphates by hydrogen bonds to O₁₂ and O₃₃, and Gly¹³ and Gly¹⁵ form hydrogen bonds to either the O₃₂ or O₁₂ of the β-phosphate. All these hydrogen bonds are stable during all performed simulations of Ras·GTP. However, there is debate regarding the position of Tyr³². In the only available x-ray structure with bound GTP (PDB:1QRA) (18), the Tyr³² is not hydrogen-bonded to the γ-phosphate and the binding niche is open.

However, an analysis of the crystal contacts reveals that the Tyr³² of the neighboring Ras protein has a hydrogen bond to the O₁₃ oxygen of the γ-phosphate. Therefore, this open structure could also be an artifact of crystallization. We have performed several MM simulations of Ras·GTP·Mg²⁺ starting with the open crystal structure PDB:1QRA (18). In several simulations, the Tyr³² develops a hydrogen bond to the O₁₃ oxygen atom of the γ-phosphate and closes the binding niche of GTP. Because the simulation time is too short, the closing might not be observed in all simulations. However, the closed state is energetically more favorable. Once the structure is closed, it never reopens.

From the different trajectory samples, we were able to calculate vibrational spectra for both the open and the closed structures and compare them to experimental spectra. Nine vibrational modes of the triphosphate have been experimentally assigned for Ras·GTP·Mg²⁺. The RMSDs between previous experimental values (32) and our calculated vibrational modes for the open and closed structures are 33 and 24 cm⁻¹, respectively. A theoretical study by te Heesen et al. (13) yielded an RMSD of 34 cm⁻¹ for the open structure. The RMSD for the closed structure is 9 cm⁻¹ less than that for the open structure (Fig. 3). This is a hint toward the predominance of a closed structure, but due to the error of the calculating method, structures other than the closed structure cannot definitely be excluded. However, the closed structure is also consistent with the spectroscopic investigations of Warscheid et al. (38), who showed that Tyr³² is affected by the release of the caged compound and the effect is reversed after hydrolysis. This clearly indicates the closed structure, because the caged compound is bound to the nucleotide via the O₁₃ atom, which is the same atom that forms a hydrogen bond with Tyr³². Therefore, Tyr³² can only bind to the GTP after the release of the caged compound and before hydrolysis. Also, electron spin resonance studies (21) indicate the presence of the closed conformation. In summary, there is strong evidence for a closed structure, and the open structure appears to be a crystallization artifact. Therefore, we considered only the closed structure for further analysis.

In the closed structure, all amino acids coordinating the GTP in the x-ray structure are stable during MM simulations. In addition to the coordination of Mg²⁺, the Ser¹⁷ has a hydrogen bond to the O₂₂ oxygen of the β-phosphate and Thr³⁵ forms a hydrogen bond to the oxygen atom O₁₃ of the γ-phosphate (Fig. 2 b). In the open structure (Fig. 2 a), the oxygen atoms O₁₃ and O₃₃ of the γ-phosphate form hydrogen bonds to Gly⁶⁰ and Gln⁶¹. The hydrogen bond between Gln⁶¹ and the γ-phosphate is predicted in the MM simulation of the open structure but is not present in the x-ray structure. In the closed structure, there are no hydrogen bonds between the γ-phosphate and Gly⁶⁰ or Gln⁶¹. However, during most of the simulation period, each of these coordinates a water molecule, which has a hydrogen bond to the γ-phosphate. Ala¹⁸ has a hydrogen bond to the α-phosphate via O₂₁ (Fig. 2) in the x-ray structure and is stable in the closed structure, whereas in the open structure the α-phosphate is quite flexible because the oxygen atoms are not fixed by any surrounding amino acids.

Conformations and spectral features of Ras·GTP·GAP

For the Ras·GTP·Mg²⁺·GAP complex (Fig. 2 c), the coordination partners of Mg²⁺ are the same as for Ras·GTP·Mg²⁺ (Fig. 2 b). In addition, Gly¹³, Gly¹⁵, and Lys¹⁶ similarly coordinate the γ- and β-phosphates. Changes in coordination result from the intruding arginine finger (Arg⁷⁸⁹), which displaces the Tyr³² and forms hydrogen bonds to the oxygen atom O₁₃ of the γ-phosphate and to the oxygen atom O₁₁ of the α-phosphate. Thr³⁵ still coordinates the γ-phosphate but via the oxygen atom O₂₃ and not O_13, as in the closed structure of Ras·GTP·Mg²⁺. The γ-phosphate is further stabilized by a hydrogen network between Gln⁶¹, Gly⁶⁰, and two water molecules. The guanine is coordinated by Phe²⁸, Lys¹¹⁷, Asp¹¹⁹, Ala¹⁴⁶, and Lys¹⁴⁷ as in Ras·GTP·Mg²⁺, and additionally by Asp³⁰ and Thr⁷⁸⁵ from the GAP.

It is important to note that the experimental spectrum is measured from the Ras·GTP·Mg²⁺·GAP structure, in which the arginine finger is still outside the binding niche, whereas the vibrational modes are calculated from the structure with the arginine finger already intruding into the binding niche. The lifespan of this structure is too short and cannot yet be resolved by FTIR spectroscopy. This might be an explanation for the differences between the calculated and measured vibrational modes ν_a(PO₃)_γ (1206/1157 cm⁻¹) and ν_a(PO₂)_α (1247/1260 cm⁻¹) (see Fig. S4), because the arginine finger forms hydrogen bonds to the γ- and α-phosphates (Fig. 2 c). The RMSD between the nine calculated vibrational modes and the previously measured values (39) is 26 cm⁻¹. This is an improvement over the RMSD of 37 cm⁻¹ from previous theoretical work (13).

Conformations and spectral features of Ras·GDP

In Ras·GDP·Mg²⁺, the Mg²⁺ is coordinated by four water molecules, Ser¹⁷, and the oxygen atom O₂₂ of the β-phosphate (Fig. 2 d). Ser¹⁷ also forms a hydrogen bond to O₂₂. In addition, the β-phosphate is stabilized by Gly¹³, Gly¹⁵, and Lys¹⁶. The α-phosphate is fixed by Glu³¹ and by a hydrogen bond between Ala¹⁸ and the oxygen atom O₂₁ of the α-phosphate, which is also present in the closed structure of Ras·GTP·Mg²⁺. The hydrogen bond between Glu³¹ and the α-phosphate is formed during MM simulations by a switch of the side chain and is not present in the crystal structure. The guanine is coordinated by Phe²⁸, Lys¹¹⁷, Asp¹¹⁹, Ala¹⁴⁶, and Lys¹⁴⁷ as in Ras·GTP·Mg²⁺, and additionally by Asp³⁰ as in Ras·GTP·Mg²⁺·GAP. For Ras·GDP·Mg²⁺, the RMSD between our calculated vibrational modes (see Fig. S5) and the three available experimental values (39) is 22 cm⁻¹. No other theoretical studies are available for comparison.

Detailed discussion of the conformation and spectral features reveals good accordance between theory and experiment. This shows that GTP and GDP are correctly simulated, and justifies the conclusion drawn for charge shifts and structural details, as described in the next section.

Structural changes and charge shifts

We aim to understand the effect of the magnesium ion on the charges and geometry of the triphosphate in water, Ras, and Ras·GAP, and the extent to which this facilitates hydrolysis. We assume that charge shifts are accompanied by structural changes, which destabilize the educt state, driving the structures closer to the TS, reducing the activation free energy, and thereby catalyzing hydrolysis. As discussed in the Introduction, no reliable data are available regarding a detailed structure of the TS. To compare the precatalytic state with the TS, we have to make the following assumptions about structure and charge distribution in the TS.

Structurally, we assume that the bond between the phosphorus atom P₃ of the γ-phosphate and the oxygen atom O₃₂ of the β-phosphate, which is cleaved, is stretched in the TS. It is known that in the TS, the free oxygen atoms of the γ-phosphate lie almost within the same plane to facilitate the nucleophilic attack of a water molecule. With regard to charge distribution, we assume that the γ-phosphate would be more positively charged as this would further facilitate the nucleophilic attack of a water molecule. A more negative β-phosphate should also facilitate hydrolysis because the β-phosphate is more negative in the Ras·GAP intermediate than in the product state. We assume that the intermediate is quite similar in Ras and Ras·GAP, even if the intermediate in Ras cannot be resolved by spectroscopy due to the rapidity of the P_i release.

We analyzed the overall averaged partial charges (see Table S3 and Table S4) of the phosphate groups (and see Fig. S6) resulting from the charges fitted to the electrostatic potential and averaged structural details (see Fig. 5, later) of six separate, 0.5-ps equilibrium QM/MM simulations for GTP, GTP·Mg²⁺, Ras·GTP·Mg²⁺, Ras·GTP·Mg²⁺·GAP, Ras·GDP·Mg²⁺·P_i·GAP, and Ras·GDP·Mg²⁺.

Figure 5.

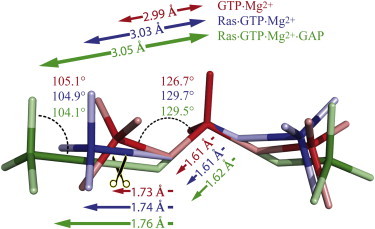
Structural changes of GTP·Mg²⁺ in water bound to Ras and Ras·GAP. Structural changes accompany the charge shifts. These changes lead to a destabilization of the educt state and lower the barrier for hydrolysis; this already occurs in the precatalytic state. Changes are exaggerated for clarity.

Note that the absolute charge value for one atom is dependent on the method, which is used to calculate the charge. Therefore we focus on charge shifts, which are more independent of the method. In analogy to the studies of Klähn et al. (12) and te Heesen et al. (13), we choose electrostatic-potential charges.

Charge shifts from GTP to GTP·Mg²⁺

A precise analysis of the different states demonstrates the correlation of structural changes with charge shifts, revealed by comparison of the charges in two different states (Fig. 4). The tridentate coordination of Mg²⁺ by the α-, β-, and γ-phosphates of GTP in water leads to an electron shift from the γ-phosphate (0.24 e₀), the coordinating waters (0.16 e₀), and the α-phosphate (0.08 e₀) to the magnesium ion (Fig. 4 a). Unequivocal attribution of the flux direction via the magnesium is not possible, but simulations with a classically treated magnesium ion demonstrate the ion's important role in this charge shift (see Table S5). Here, the magnesium ion is treated as a point charge and not as a quantum mechanical wave function; therefore, no charges can be shifted to it. In the simulation without the magnesium ion in the quantum box, there is no effect on the charge of the α-phosphate, and the γ-phosphate receives only 0.06 e₀ more positive charge compared to 0.24 e₀ with the magnesium ion (see Table S3).

Figure 4.

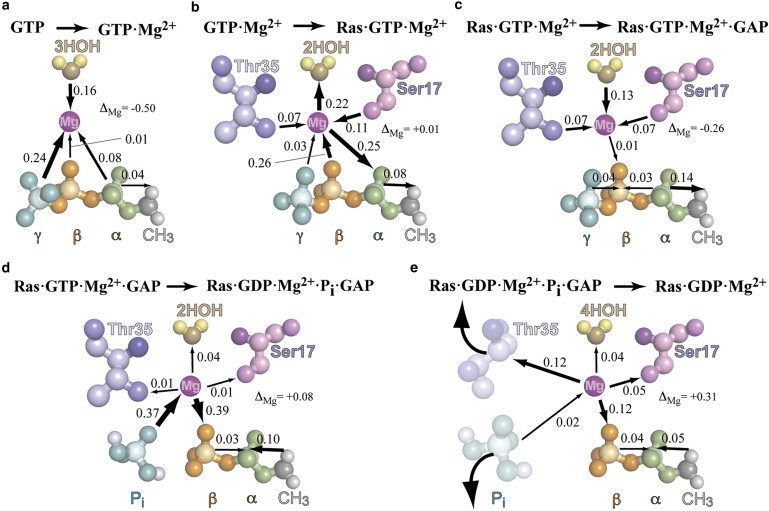
Partial charge shifts during hydrolysis. An electron shift to the magnesium ion occurs before hydrolysis, which is reverted by the bond cleavage and P_i release. The charge shifts result from differences in the charges relative to the previous state starting from GTP in water without a magnesium ion. (a–c) Changes in the precatalytic states, (d) towards the intermediate state and (e) towards the product state. The charges of each state are described in Table S3. All charge shifts are given in the unit of the electron charge e₀. (Arrows) Direction in which electrons are transferred.

GTP·Mg²⁺ to Ras·GTP·Mg²⁺

In Ras·GTP·Mg²⁺ (Fig. 4 b), the magnesium ion is coordinated by the γ- and β-phosphates in a bidentate manner. The coordination change leads to an electron shift of 0.25 e₀ from the magnesium ion to the α-phosphate. To balance this shift, the magnesium ion drags electrons (0.26 e₀) from the β-phosphate. That this shift occurs via the magnesium ion and not directly from the β- to the α-phosphate is indicated by the fact that the charge shift (−0.86 to −0.60 e₀) experienced by the magnesium-coordinating oxygen atom (O₂₂) exactly matches the amount of shifted electrons. Treating the magnesium ion quantum mechanically underlines this hypothesis because it leads to a charge difference between the β-phosphate of GTP·Mg²⁺ and Ras·GTP·Mg²⁺ of 0.27 e₀, which is nearly twice as much as when the magnesium ion is treated classically (0.15 e₀). The effect of the magnesium ion on the β-phosphate is negligible for the α-, β-, γ-phosphate coordination seen in water, but significant for the β-, γ-phosphate coordination seen in Ras. This is demonstrated by the distances between the magnesium ion and the coordinating oxygen atoms (see Fig. S1).

In α-, β-, γ-phosphate coordination, the oxygen atoms O₂₁ and O₂₃ of the α- and γ-phosphates have the shortest distance (2.11 Å) to the magnesium ion and are therefore most affected by the magnesium ion. The distance between the oxygen atom O₂₂ of the β-phosphate and the magnesium ion is 2.15 Å, whereas in β-, γ-phosphate coordination, the distance between O₂₂ and the magnesium ion is significantly shorter by 0.05 Å. Here, O₂₂ and O₂₃ have the shortest distance (2.10 Å). With the coordination change, the charge of the β-phosphate becomes more positive by 0.27 e₀. This is not conducive for approaching the charge distribution of the TS, and at first glance, appears to contradict the experimental observation that Ras shifts negative charges to the β-phosphate; Allin and Gerwert (32) draw this conclusion from the change of 16 cm⁻¹ in the ν_a(PO₂)_β vibrational mode of GTP in water (see Fig. S2) compared to that of GTP in Ras (Fig. 3).

This is in total agreement with the calculated downshift for ν_a(PO₂)_β. Therefore, for comparison with this experiment, we have to take into account only the sum of the charges involved in this vibration, i.e., P₂, O₂₂, and O₁₂ (see Table S3). In accordance with the experiment, the charge of this group becomes more negative (by 0.28 e₀, from −0.43 e₀ in GTP·Mg²⁺ to −0.71 e₀ in Ras·GTP·Mg²⁺). Furthermore, the magnesium ion drags electrons from the coordinating partners of the active side of the Ras protein. The shift of electrons from the Ser¹⁷ (0.07 e₀) and Thr³⁵ (0.11 e₀) to the magnesium ion is balanced by an electron shift to the two waters coordinating the magnesium ion (0.22 e₀). In total, the charge of the magnesium ion remains unchanged between GTP·Mg²⁺ and Ras·GTP·Mg²⁺ but there is a tremendous change in the coordination sphere of the magnesium ion, which leads to significant changes in charge distribution.

Ras·GTP·Mg²⁺ to Ras·GTP·Mg²⁺·GAP

In the Ras·GTP·Mg²⁺·GAP complex, the coordination of the magnesium ion remains unchanged. Thus, the effect of GAP on the magnesium ion/triphosphate charge shift is small. This is in accordance with FTIR measurements, which reveal only small changes between the spectra of Ras·GTP·Mg²⁺ and Ras·GTP·Mg²⁺·GAP. As discussed above, the measured spectra are obtained without the arginine finger in the binding niche. In the calculated spectra, the arginine finger intrudes into the binding niche and affects the ν_a(PO₃)_γ and ν_a(PO₂)_α vibrational modes. This leads us to the hypothesis that the effects on structure and charges are mainly due to the intruding arginine finger. Only a small number of electrons (0.04 e₀) are shifted from the γ-phosphate to the β-phosphate (Fig. 4 c).

The hypothesis that this is not a direct effect of the magnesium ion is underlined by the fact that the charge of the oxygen atom O₂₂ of the β-phosphate that coordinates the magnesium ion remains unchanged. Moreover, the increase in positive charge in the β-phosphate is nearly the same with and without a quantum mechanically treated magnesium ion (∼0.1 e₀). Conversely, the two bridging oxygen atoms O₃₂ and O₃₁ of the β-phosphate become more negative, indicating a direct charge transfer from the γ- and α-phosphates. By this, the β-phosphate becomes 0.09 e₀ more negative. Further, GAP affects the protein environment of the magnesium ion; it becomes 0.26 e₀ more negative by dragging electrons from Ser¹⁷ (0.07 e₀), Thr³⁵ (0.07 e₀), and the two coordinating waters (0.13 e₀). This is in accordance with the shortening of the distances between these groups and the magnesium ion (see Fig. S1 c).

Postcatalytic states

After bond cleavage in the intermediate state, electrons (0.37 e₀) are shifted from the P_i to the magnesium ion, and subsequently to the β-phosphate (0.39 e₀; Fig. 4 d). In total, the magnesium ion receives an increase of 0.08 e₀ in positive charge. In the Ras·GDP·Mg²⁺ state, the P_i is released, and the coordination between the magnesium ion and Thr³⁵ breaks.

For Ras·GDP·Mg²⁺, the coordination partners of the magnesium ion are four water molecules, the β-phosphate, and Ser¹⁷. P_i release has no effect on the partial charge of the magnesium ion, but due to the break in coordination with Thr³⁵, electrons (0.12 e₀) are dragged from the magnesium ion by Thr³⁵. The effects of Ser¹⁷ (0.05 e₀) and the four waters (0.04 e₀) on the charge shift are smaller. The β-phosphate drags electrons (0.12e₀) from the magnesium ion. After P_i release, the magnesium ion returns a total of 0.31 e₀ in charge to its environment (Fig. 4 e).

Summary of the charge shifts

From these results, we conclude for the hydrolysis in Ras and in Ras·GAP that electrons are shifted to the magnesium ion before hydrolysis. This shift is reversed by the bond cleavage and P_i release, shifting electrons back from the magnesium ion to the β-phosphate of the Ras·GDP·Mg²⁺. The magnesium ion temporarily stores electrons, facilitating hydrolysis by shifting the charges closer to the intermediate state and supporting the nucleophilic attack of a water molecule. These results are in accordance with the observation of accelerated hydrolysis after the substitution of the magnesium ion by a manganese ion (40). Manganese has a higher electronegativity than magnesium and therefore has the ability to drag even more electrons.

Structural changes

The charge shifts are accompanied by structural changes (Fig. 5), which destabilize the educt state, driving the structures closer to the transition state, reducing the activation free energy, and catalyzing hydrolysis. The change in Mg²⁺ coordination with the α-, β-, γ-phosphates for GTP·Mg²⁺ in water to a β-, γ-coordination for Ras·GTP·Mg²⁺ induces a rotation of the γ-phosphate into an eclipsed conformation regarding to the β-phosphate compared to a staggered position in water. Along with this goes an elongation of the distance between P₃ and P₂ of 0.04 Å (from 2.99 to 3.03 Å). Further, the bond between the phosphorous atom of the γ-phosphate P₃ and the oxygen atom O₃₂ of the β-phosphate, which is cleaved, is stretched by 0.01 Å to 1.74 Å in Ras·GTP·Mg²⁺ (compared to 1.73 Å for GTP in water). This elongation is accompanied by the stretching of the angle between P₃-O₃₂-P₂ of the β- and γ-phosphates of 3° (from 126.7° to 129.7°). There is only a slight change of 0.2° in the angle O₂₃-P₃-O₃₂, reflecting the planarity of the γ-phosphate.

The changes in bond length and bond angles between GTP bound to Ras·GTP·Mg²⁺·GAP and Ras·GTP·Mg²⁺ (Fig. 5) are mainly induced by the intruding arginine finger forming a hydrogen bond to the γ- and α-phosphate. By this, the α-phosphate is rotated into an eclipsed conformation in relation to the β-phosphate, compared to a staggered one in GTP bound to Ras. The bond between P₃ and O₃₂ is elongated by additional 0.02 to 1.76 Å. Furthermore, the bond between atom O₃₂ and the phosphorous atom P₂ of the β-phosphate is elongated by 0.01 Å (from 1.61 to 1.62 Å). These two bond enlargements lead to a total distance change between P₃ and P₂ of 0.02 Å (from 3.03 to 3.05 Å). Despite the increased distance between P₃ and P₂, the distance between the oxygen atoms O₂₃ and O₂₂ coordinating the Mg²⁺ decreases from 3.04 to 3.02 Å, due to the attractive force of the Mg²⁺. Simultaneously, the γ-phosphate becomes increasingly more planar, bringing the GTP closer to the transition state. This is demonstrated by a decrease of 0.08° (from 104.9° to 104.1°) in the angle O₂₃-P₃-O₃₂.

Though the structural changes are small they contribute to catalysis because, e.g., a change of 0.1 Å in the bond length of a C-C single bond is equal to a raise in energy of 6 kJ/mol. This is already approximately one-quarter of the total difference in the free energy of activation for hydrolysis in Ras (30 min) and in Ras·GAP (50 ms) being equal to a catalysis of 10⁵, which is experimentally determined to be ≤26 kJ/mol.

Acceleration factors of hydrolysis

By combining structural information (Fig. 5) with information regarding charge distribution (Fig. 4) in the different states of hydrolysis, we identified the following steps as important mechanisms for accelerating hydrolysis: The Mg²⁺ drags electrons from the γ-phosphate already in water (Fig. 4 a), and this is enhanced by the guidance of the Mg²⁺ by Ras and further by Ras·GAP. The increased positivity of the γ-phosphate facilitates the nucleophilic attack of the water molecule that is required for hydrolysis. This is accompanied by a loss of 0.5 e₀ from the Mg²⁺. However, the barrier for hydrolysis is still very high, because the Mg²⁺ is coordinated in a tridentate manner by the triphosphate and not guided by the protein to the β-, γ-phosphate coordination. Complexation of GTP with Ras induces a change from a tridentate to a bidentate coordination of the Mg²⁺ (see Fig. S1).

The charge of the Mg²⁺ remains unchanged in this step; however, this step induces a charge transfer from the α- to the β-phosphate via the Mg²⁺, resulting in a more positive β-phosphate (Fig. 4 b). This shift is not conducive for charge distribution. The β-phosphate must become more negative. Ras·GAP overcomes this problem with the help of the intruding arginine finger affecting the structure via hydrogen bonding between the intruding arginine finger and the γ- and α-phosphates (Fig. 2 c). The complexation of Ras and GAP causes a change in the partial charge distribution between the β- and γ-phosphates (Fig. 4 c). The γ-phosphate becomes more positive, whereas the β-phosphate becomes more negative. In addition, the formation of Ras·GAP leads to a decrease in the distance between the magnesium ion and its coordinating partners (Fig. 5). By this, the magnesium ion drags ∼0.3 e₀ of electrons from its surroundings, which are returned to the β-phosphate after bond cleavage.

The change in distance between P₃ and P₂ of 0.06 Å (Fig. 5), from GTP·Mg²⁺ in water (2.99 Å) to Ras·GTP·Mg²⁺ (3.03 Å) and Ras·GTP·Mg²⁺·GAP (3.05 Å) destabilizes the educt state and brings the structure closer to the one of the TS. Simultaneously, the γ-phosphate becomes increasingly more planar, as demonstrated by a decrease in the angle O₂₃-P_3-O₃₂, from GTP·Mg²⁺ in water (105.1°) to Ras·GTP·Mg²⁺ (104.9°) and Ras·GTP·Mg²⁺·GAP (104.1°).

Conclusion

In the only available crystal structure with bound GTP (PDB:1QRA), Y32 is not bound to the γ-phosphate and therefore the binding niche is open. During classical MM simulations of Ras·GTP·Mg²⁺, Y32 changes its position and closed parts of the GTP binding niche in the equilibrated structure. The calculated spectrum for the closed structure fits on average 9 cm⁻¹ better to the experimental one as compared to the open structure. We assume that the open Y32 position in the x-ray structure PDB:1QRA is an artifact of crystallization due to crystal contacts.

QM/MM simulations are able to decode from the experimental IR spectra detailed charge distribution (Fig. 4) and small changes in angles and bond lengths of the protein-bound GTP (Fig. 5) significantly below the x-ray resolution. These observed changes in structure and charge distribution lead to a destabilization of the educt state and facilitation of the nucleophilic attack of the water molecule. Overall, this lowers the barrier for hydrolysis. By the quantum mechanical treatment of the magnesium ion and its coordination partners, we demonstrate that the magnesium ion temporarily stores electrons. The magnesium ion drags electrons from its surroundings before hydrolysis and stores them. The electron shift is reversed by bond cleavage and P_i release. The protein utilizes the tremendous effect of the magnesium ion by guiding it to a catalytically effective position.

The important mechanisms for accelerating hydrolysis are evoked by changes in the coordination of magnesium ion in water, Ras, and Ras·GAP, and the intrusion of the arginine finger. The important effects on charge distribution (Fig. 4) are 1), the γ-phosphate becoming more positive along the reaction coordinate of bond cleavage when bound to Ras, and 2), the β-phosphate becoming more negative due to the influence of GAP. The important structural mechanisms for accelerating hydrolysis (Fig. 5) are 1), stretching of the bond between P3 and O32 that is cleaved during hydrolysis, and 2), the γ-phosphate group becoming more planar. These effects are amplified by complex formation with GAP.