Replication timing and its emergence from stochastic processes

Abstract

The temporal organization of DNA replication has puzzled cell biologists since before the mechanism of replication was understood. The realization that replication timing correlates with important features, such as transcription, chromatin structure and genome evolution, and is misregulated in cancer and aging has only deepened the fascination. Many ideas about replication timing have been proposed, but most have been short on mechanistic detail. However, recent work has begun to elucidate basic principles of replication timing. In particular, mathematical modeling of replication kinetics in several systems has shown that the reproducible replication timing patterns seen in population studies can be explained by stochastic origin firing at the single-cell level. This work suggests that replication timing need not be controlled by a hierarchical mechanism that imposes replication timing from a central regulator, but instead results from simple rules that affect individual origins.

Replication origins: correlated or independent?

The duplication of the genome of a cell by DNA replication is an essential step in the cell cycle. In bacteria, the overall situation is straightforward, in that DNA replication initiates at a single, well-defined location in the genome (e.g. the oriC site in Escherichia coli) and terminates at a second, well-defined region (ter in E. coli) [1]. Eukaryotic organisms, with 10–1000 times more DNA and with 10–100 times slower replication forks, depend on the firing of multiple origins of replication along the DNA. These origins are defined by a two-step process [2]. Licensing, the first step, occurs in G1 phase, when the origin recognition complex (ORC) binds to chromatin and, with the aid of Cdc6 and Cdt1, loads onto the DNA head-to-head pairs of the barrel-shaped heterohexameric MCM complex, the catalytic core of the replicative helicase [3,4]. Each pair of MCM complexes is a potential origin of DNA replication. Initiation (or origin firing), the second step, occurs in S phase, when a pair of MCMs is activated via a complex process involving numerous proteins, including recruitment of Sld2, Sld3, the GINS complex and Cdc45, as well as the phosphorylation of various components by the CDK and DDK replication kinases [5]. The regulation of the spatial binding of the ORC and the temporal activation of MCMs largely determines the kinetics of replication during S phase, which is referred to as the replication program.

The question of how replication programs are regulated is an active, and sometimes controversial, field. Although the specific mechanisms that control timing are still obscure, recent work has revealed basic principles that appear to apply to eukaryotic replication in general. In particular, mathematical modeling of genome-wide replication timing data shows that replication timing can be explained by stochastic mechanisms. The significance of this conclusion is that it explains the regulation of replication timing in terms of simple rules that affect the individual probabilities of origin firing. In such models, replication timing is controlled by changing the firing rate of individual origins, instead of by directly regulating the time at which origins fire. Although this distinction may seem semantic, it is important because it recasts black-box mechanisms of global replication timing in terms of biochemically plausible effects on individual origins.

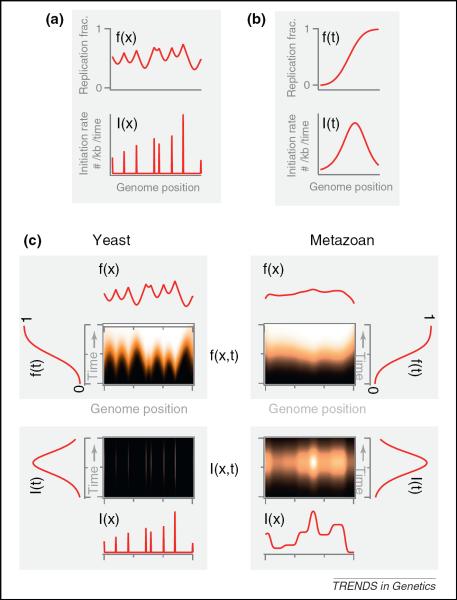
Over the past decade, two views about replication timing mechanisms have been developed. In the first, origin firing is a stochastic event that is (largely) independent of the replication state of neighboring origins. In particular, it has been postulated that there is an initiation function I(x,t) that describes the rate of initiation, per time and per length of unreplicated DNA, of a site x along the genome at time t after the beginning of S phase [6,7] (Figure 1; Box 1). This type of origin firing can manifest in at least three different ways, depending on the experimental model considered. In species such as budding yeast, in which replication initiates at well-defined loci, the function I(x,t) forms a discrete spike at the replication origin [8] (Figure 1a). At the other end of the spectrum, amphibian embryos lack origin specificity, and DNA replication can initiate anywhere along the genome [6]. In an intermediate case, mammalian somatic cells can display clusters of origins or broad initiation zones that are not homogeneously distributed throughout the genome [9–11] (Figure 1b). Each of these three cases is discussed in detail below. We refer to the hypothesis of a locally determined initiation rate as the independent origin hypothesis because it is distinguished by the feature that origins fire independently from the firing of neighboring origins. The attraction of the independent origin hypothesis is its simplicity: one does not need to postulate biological mechanisms that would cause correlated initiations. The potential weakness of the independent origin hypothesis is that, if too simple, it may fail to describe experiments accurately or that implausible coincidences of parameters may be required to fit the data.

Figure 1.

Replication fractions and initiation rates. (a,b) The relation between replication fractions f and initiation rates I, as illustrated for budding yeast. (a) Spatially resolved data, averaged over an asynchronous cell population. (b) Time course data, averaged over the genome. (c) Illustration of typical replication timing data for budding yeast (left) and a metazoan organism (right). Top-left image shows the replication fraction f(x,t), as it might be inferred from a microarray timing experiment with several time points of data from synchronized cell populations. Black represents low-replication levels and white represents high-replication levels. Averaging the replication fraction over the genome gives the curve f(t), depicted to the left of the f(x,t) image, which goes from 0 to 1. Averaging the replication fraction over time, as in an experiment on asynchronous cell populations, gives the curve above the f(x,t) image. The bottom-right group shows the inferred I(x,t) image, as well as the averaged curves I(t) and I(x). Note that, in budding yeast, replication origins are well localized, as indicated by the spikes in the function I(x). [When viewed or printed at low resolution, not all spikes in I(x,t) may be visible.] The right-hand groups illustrate similar concepts for a typical metazoan organism. The main difference is that origins are not well localized, so that the function I(x) has broad features, representing zones where initiations are more or less likely to occur.

In a second scenario, the initiation of an origin, although still stochastic, is linked to the state of the genome in its vicinity. For example, observations of origin clustering [12–14] have led several authors to hypothesize that the presence of a replication fork can increase the firing rate of nearby origins, for instance, the `next-in-line' model [15] and the `domino-cascade' model [16,17]. We refer to this second scenario in general as the correlated origin hypothesis.

Previously, there was considerable debate as to whether replication was stochastic and whether origins are independent. At present, it is generally accepted that all models of replication are stochastic at the level of molecular interactions. It is important to note that stochastic models do not require that origins all fire with the same probability, nor is stochastic firing incompatible with late firing origin [18]. However, there is evidence in some cases for correlation in origin initiation activity. As a result, the current picture is an intermediate one that mixes both stochastic elements and mechanisms for correlations in origin initiation [15,19]. Still, differences remain concerning what is essential and what is incidental in the above picture and what kind of underlying mechanisms are likely to be important in controlling the replication program. In this review, we argue that, for the simpler cases such as unicellular yeast and for the embryonic cells of some multicellular animals, recent experiments and modeling efforts have shown that much of the available replication data may be understood in terms of the simpler independent origin hypothesis and that correlations probably play a minor role in the replication program. Replication in the somatic cells of metazoan organisms is more complex, and we outline recent efforts in this area.

Replication in yeast

The past few years have marked a turning point in the understanding of replication in yeast. First came a series of high-resolution combing and microarray experiments (Box 2). For example, high-resolution timing data of synchronized populations of wild type and clb5Δ Saccharomyces cerevisiae show clear average timing patterns [20]. Their measurements, as mentioned in Box 2, amounted to measurements of f(x,t), with spatial information resolved to a few kilobases and temporal information resolved to 5 min. At around the same time, DNA combing studies in budding and fission yeast showed that initiations at the single-molecule scale are stochastic, with different sets of origins chosen in each cell cycle [21,22]. Indeed, in budding yeast, it is now clear that there are as many as 700 potential origin sites, of which only approximately 200 are used in any given cycle.

In parallel work, the rate of origin firing in budding and fission yeast was shown to be regulated by competition for limiting activators, such as the Cdc45 initiation factor and the DDK initiation kinase [23–26]. Competition for limiting activators provides an explanation for why origin firing is less efficient than might be possible. The stochastic interaction between origins and diffusible activators also provides a mechanism for stochastic firing of origins.

The stochasticity of individual origins turns out to be an important effect. In contrast to earlier models, in which the firing of specific origins was envisaged to be limited to narrow windows of S phase, it is now clear that the width of the firing-time distribution for an individual origin can be a substantial fraction of S phase. Indeed, models that fail to incorporate the width of the timing distribution fail to reproduce many of the experimental details adequately [27]. By contrast, stochastic models that take into account the width of the firing-time distribution can successfully fit the microarray data [8,28,29]. Several notable insights and results come from these analyses: first, it is possible to generate models with independent initiation scenarios [initiation rate I(x,t) and constant fork velocity v] that lead to good fits of the data. This result shows that the independent origin hypothesis suffices to explain microarray data on replication timing in yeast. Second, the intrinsic parameters characterizing each origin have values that are independent of their neighbors, again suggesting that the initiation of each origin is an independent stochastic event [8]. Studies in fission yeast have also led to the conclusion that local initiation models suffice to explain the available experimental data [30,31]. However, several biologically different scenarios can lead to similar overall timing patterns [32], and more complicated mechanisms, such as trans-acting regulators of origin activity and chromosome structure, can affect origin timing [33,34]. Clearly, further iterations of modeling and experiment will be needed to come to a final picture.

Replication in embryos

Embryonic cells in metazoans represent an interesting intermediate case of complexity. On the one hand, they have the full amount of DNA of somatic cells. On the other hand, they undergo a rapid, simplified cell cycle that is largely transcriptionally silent, which removes one major source of complication in the replication of somatic cells. In vitro studies of Xenopus cell-free extracts have been especially detailed and fruitful [13,35–37] and have led to associated modeling efforts [6,7,19,38,39]. The replication program in Xenopus embryos is relatively simple and much faster than in somatic cells. In particular, there are no fixed origin sites, presumably because the lack of transcription and more uniform chromatin structure allows the ORC to load MCM anywhere in the genome [40,41]. Although variation in initiation rates and, hence, replication timing does occur at the megabase scale [37], modeling efforts to date have focused on understanding the temporal variation of the initiation rate, I(t), averaged over the genome. The main conclusion is that the initiation rate increases over most of S phase, before decreasing to zero near the end of it. This variation of initiation rates over S phase is significant because it leads to a relatively narrow distribution of lengths for S phase, which, because of the stochasticity of origin placement and initiation time, varies with each cell cycle [42]. In embryos, it is particularly important that there be little variation in genome duplication time, as the cell cycle lacks checkpoints that can delay the start of mitosis if replication is not complete. In Xenopus embryos, for example, the typical S phase duration is 20 min and that of mitosis is 5 min, all within a 25-min cell cycle [43]. Thus, variations of S phase of more than 5 min can be lethal for a cell. Such variations are proposed to be suppressed by the increasing nature of initiation rate I(t). It has even been postulated that the increasing form of I(t) is a universal characteristic of eukaryotic replication [44]. Preliminary assessment of replication data from S. cerevisiae, Schizosaccharomyces pombe, Drosophila melanogaster and Homo sapiens supports this scenario, although better data and more extensive analysis are required. The initial increase of initiation rate I(t) has been attributed to competition for a limiting factor required for replication fork function [35,38] or origin firing (e.g. the DDK replication kinase [23]), whereas the decrease of I(t) at the end of S phase has been variously attributed to a fork-dependent control mechanism [38] or to increasing diffusion search times for the limiting factor to find its target [39].

Replication in metazoan somatic cells

The replication of DNA in metazoan germline and somatic cells is more complicated than in embryonic cells. Replication in somatic cells can take up to 100 times longer than in embryonic cells [45], and this increase in replication time is not spread equally across the genome. Instead, different regions of the genome replicate at characteristic times during the elongated S phase, and the replication timing of a locus correlates with several other important chromosomal characteristics. The best-established correlation is between late replication and constitutive heterochromatin, the repetitive, transcriptionally inactive regions of the genome that remain condensed throughout the cell cycle [46]. Conversely, gene-rich, transcriptionally active regions of the genome tend to replicate earlier in S phase [47]. The correlation between the transcriptional activity of individual genes and their replication timing is not strong [48]. However, when averaged over large groups of neighboring genes, transcriptional activity correlates well with replication timing [49,50]. An even more remarkable correlation is seen between chromosome interaction maps and replication timing [51,52]. The contiguous regions of the genome that replicate with similar timing are referred to as replication domains. The correlations between the average transcriptional activity, chromatin interactions and the replication timing of replication domains has led to qualitative models in which the chromosome accessibility of a domain affects its replication timing [53].

Although replication domains replicate with reproducible timing, origin firing within domains is heterogeneous because of stochastic origin firing [10,54,55]. As in yeast, origin firing in metazoans appears to be regulated by limiting activators. Mammalian Cdc45 is substoichio-metric, relative to OCR and MCM, and increasing Cdc45 levels increases the rate of origin firing [56]. Moreover, modulating the levels of the CDK replication kinase affects the efficiency of origin firing [57–59]. An additional reason for the heterogeneity of origin firing in metazoans is that metazoan origins are not well-defined loci; at least in some cases, MCM seems to be loaded heterogeneously throughout a region [60–62], which can be thought of as a cluster of many inefficient origins or as a diffuse initiation zone.

Mechanisms for timing

Although replication timing appears to be uniform and well coordinated at the population level, this average behavior hides heterogeneous replication kinetics in individual cells. This apparent conflict between heterogeneity at the single-cell level and organization at the population level is resolved by observing that the average of the heterogeneous single-cell data recapitulates the results from ensemble studies [22]. This observation has led to models in which the average replication time of a locus is a function of the firing probability of individual origins, regardless of whether those probabilities are independent or coordinated (Box 3). Such models predict a correlation between the probability and timing of origin firing, a correlation seen in budding yeast [8,28]. Furthermore, recent budding yeast studies have shown that, in most cases in which the length of S phase is significantly increased, the relative timing program is maintained [63,64]; that is, the overall ordering of replication timing of different regions is preserved, even as the scale of timing is altered. Such a result would be expected if S phase length changes because the initiation rates have been altered globally (Naama Barkai, personal communication). As discussed above, initiation rates are thought to be regulated by competition among origins for limiting activation factors. One recently proposed model makes the case both theoretically and experimentally that the limiting factor is a protein associated with active replication forks [65]. The Cdc45 protein, which is required to activate the MCM helicase complex, is one such candidate [56]. Alternatively, factors such as DDK, which phosphorylates and activates MCM, have been seen to be rate limiting in fission yeast [23].

The competition for limiting activators explains why origins fire stochastically but not why some origins fire with higher probability than others. One obvious explanation for differing probabilities of origin firing is the effect of chromatin structure on the accessibility of origins to initiation factors [53]. In the context of competition between origins for limiting activators, it is natural to imagine that chromatin structure affects that competition, allowing euchromatic origins greater access to activators and so higher firing probabilities. This possibility fits well with the strong correlation observed between heterochromatin and late replication [46]. Another possibility that we have recently proposed is based on the observation that multiple MCMs are loaded at each origin [8,60]. In this model, each MCM loaded has a low probability of firing; however, because multiple MCMs are loaded at each origin, origins that have more MCMs loaded will have a higher aggregate firing probability. Thus, the probability of origin firing is set in part by the number of MCMs loaded at a given origin site. The probability of origin firing can then be subsequently altered by chromatin context. For example, a recent study has shown that Rif1, which affects telomere chromatin structure, also binds to chromosome arms and alters origin initiation rates at these sites, perhaps by altering the loading of the Cdc45 that is required for MCM helicase activation [33].

A scenario comprising stochastically firing origins with different firing probabilities naturally leads to a reproducible replication-timing program [66]. Origins with high firing probabilities will be more likely to fire in early S phase and so will have early average replication times. In general, low-probability origins would be unlikely to fire efficiently even in late S phase. However, if the firing rate, I(t), increases during S phase, as described above, even low-probability origins, if not passively replicated, will have a high probability of firing late in S phase, leading to efficient replication of late-replicating regions [18]. Here, we distinguish between I(t), which describes the timing program, and the underlying biological mechanisms, which try to explain why I(t) has an observed form. This description of origin timing applies not only to the individual origins of simpler genomes, such as budding yeast, but also to the complicated replication domains of metazoan genomes. In the latter case, euchromatic replication domains of high-probability origins reproducibly replicate earlier than do domains of lower-probability origins, but heterochromatic domains, which harbor the lowest-probability origins, nonetheless replicate efficiently in late S phase. Thus, the order in which various domains of metazoan genomes replicate may be a secondary consequence of the effect of their chromatin structure on the firing probabilities of their origins. This possibility is consistent with the strong correlation between chromatin interactions and replication timing [52].

Correlated origin initiations

Although much of observed replication timing can be explained in terms of a picture of independent initiations, there is also evidence for correlations in initiation. For example, DNA fiber studies observe clusters of nearby origins that initiated at approximately the same time [12,13]. One plausible mechanism for origin clustering is that the polymerases and other proteins responsible for replication are localized within the nucleus in small foci known as replication factories [67,68]. As a consequence, if the DNA is tethered to a location in the cell nucleus while replicating, it may loop around and find another set of replication machinery in the same factory. Such looping could increase the likelihood of origin firing of origins located approximately 10 kb from an active fork and decrease origin firing for closer origins [19].

Another line of argument suggesting the possibility of correlated initiation lies in an observation of small biases in the DNA base sequence near certain regions. It has been shown that if a region of the genome is repeatedly replicated by a polymerase on the leading strand, mutations will eventually lead to strand compositional asymmetries (an excess of G over C and T over A) [69]. Indeed, a large proportion of known origins for H. sapiens have been found by looking for signatures of compositional skew [70]. Early replicating regions are then marked by an abrupt jump in the local skew. Because adjacent early replicating regions are separated by approximately 1 Mb and because the average distance between origins is approximately 100 kb, there must be multiple initiations between each early region. To explain the observation that the compositional skew varies linearly between compositional discontinuities associated with origins, it was postulated that a wave of correlated initiations occurs, which leads to a `domino' [16,17,71] or `next-in-line' model [15]. It is not clear whether a looping mechanism [19] can explain such effects, whether some more complicated form of coupling between initiation and fork progression is required, or whether the difference in chromatin structure between early- and late-replicating regions can account for these observations. Such a possibility would avoid the need to invoke coordinated origin firing. In support of this idea, a recent single-molecule replication kinetics analysis of the mouse Igh locus is consistent with a stochastic model that lacks any origin coordination [11] (Paolo Norio, personal communication).

In addition to temporal ordering of origin initiation, some models include spatial correlations in the positioning of origins. Recently, it was proposed that the clustering of initiated origins observed in Xenopus embryos and, to a lesser extent in yeast origins, may speed up the overall completion of S phase [72]. A shorter S phase is particularly helpful in Xenopus embryos, as it prevents the mitotic catastrophe discussed above. Clustering several inefficient origins together can lead to a group that is collectively efficient in that one or the other of the origins is likely to fire early. Although the periodic distribution of such groups of origins would be an efficient way to replicate the genome, mechanisms that could achieve this global order are not clear, at present.

Concluding remarks

The hypothesis that replication is largely controlled by the local rate of initiation has received wide support from recent experiments and analyses. Models based on local replication rates I(x,t) have successfully described the replication process in budding and fission yeast, in Xenopus embryos and in the Igh locus of mouse pro-B cells [6,8,11,28,30,38] (Paolo Norio, personal communication). A limiting factor in this work is that each of the above analyses involved a long-term collaboration between experimental biologists and modeling laboratories (the latter from a variety of fields, including physics, engineering and computer science). To broaden the use of quantitative analyses of replication and to analyze the growing number of data sets, it is important that the software and analysis procedures be usable by non-specialists. The recent derivation of `inversion' formulas (A. Baker, PhD thesis, ENS de Lyon, France, 2011) that give I(x,t) directly from data on the local average replication fraction f(x,t) obtainable from microarray or deep sequencing studies on synchronized cell populations are a first step in that direction.

A second research direction is a more precise understanding of the relation between the replication program, as described above, and the effects of DNA damage, with its concomitant activation of DNA repair mechanisms. For example, one consequence of damage that stalls replication forks is the activation of additional origins, which now have more time to initiate [73,74], an effect that is straightforward to simulate [75] and model analytically [76]. The modeling of fork stalls predicts that there is a critical density of stalled forks (approximately one per replicon), above which there is a global delay in S phase and below which the effects are minor and localized. Interestingly, this threshold density matches the observed stall densities in fragile zones and in cells with activated oncogenes [76]. However, DNA damage can also induce checkpoints that inhibit subsequent origin firing [77], complicating the overall effect of DNA damage on replication timing. A related topic is the interrelation between mutation rates and events in S phase. Although formal models to handle such situations are beginning to be developed [69], more work is needed to understand observations, such as the link between mutation rate and S phase timing [78].

Although the independent origin hypothesis is attractive in its simplicity and so far remarkably successful in its application, there is evidence for correlated initiations in somatic metazoan cells. Some of the correlation is explainable as straightforward consequences of the physical constraints of clustering polymerases. In such a view, the primary method of controlling timing in S phase remains the local modulation of overall initiation rates, and the correlations in the initiation of neighboring origins are produced by the geometrical effects of loops induced by replication factories. Whether such mechanisms suffice or whether a more complicated control mechanism is at play is at present unclear. Time will tell.

Box 1. f and I: mathematical functions that describe replication kinetics.

DNA replication kinetics can be described using two related but distinct mathematical functions: the replication fraction f and the initiation rate I. The first, f, is a complete description of replication kinetics and can be directly determined from experimental data (Box 2). The second, I, only describes the kinetics of origin initiation and cannot be directly measured; it must be inferred from f. However, if fork rates are assumed to be nearly constant, as is frequently done in models of replication kinetics, then I is sufficient to completely determine f. Both f and I can be defined for every spatial point (x) in the genome and every time point (t) in S phase, to give f(x,t) and I(x,t) (Figure 1c, main text).

It is often useful to consider the time-averaged functions, f(x) and I(x) (Figure 1a, main text). f(x) can be thought of as the average replication time of each point in the genome and is generally measured on asynchronous populations of cells. It is closely related to the median replication time t_rep at a site that is inferred from time course data on synchronized cell populations. The peaks in f(x) represent the origins, and taller peaks indicate origins that fire, on average, earlier in S phase. I(x) represents the average initiation rate of each point in the genome. In yeast, where origins are well defined, I(x) = 0 for most of the genome and forms spikes over the origins, with taller spikes reflecting a higher average probability of origin firing (Figure 1a,c). In metazoans, origins appear to be more diffuse, and thus so is I(x) (Figure 1c). It is important to realize that the height of the peaks in I(x) (e.g. the average firing probability of an origin) cannot be directly inferred from the height of the peaks in f(x), because f(x) convolves both passive replication and active firing of each origin; I(x) can only be extracted by mathematical modeling of f(x).

It can also be useful to consider the spatially averaged functions, f(t) and I(t) (Figure 1b, main text). The replication fraction f(t) is generally sigmoidal, as cells go from unreplicated in G1 to replicated in G2. The exact shape of the sigmoid depends on the details of the replication program, such as of the distribution of origins and the shape of I(t). As discussed in the main text, I(t) has been proposed to generally increase for most of S phase and then decline in late S phase.

Box 2. Experimental techniques for analyzing DNA replication timing.

The recent gains in our understanding of replication timing are built on experimental advances that have greatly increased the quality and quantity of data available. Defined patterns of DNA replication were first observed in fiber autoradiography studies of tritiated thymidine incorporation in bacterial and mammalian cells [12,79]. By in vivo pulse-labeling cells with tritiated thymidine and then stretching the labeled DNA on a photosensitive film, it was possible to map replication patterns (which regions have replicated and which have not) at a given time. A significant technical improvement was the substitution of fluorescently labeled thymine analogs, such as BrdU, that could be observed using an optical microscope [80,81]. Molecular combing, which stretches DNA more controllably, improved the latter technique by allowing one to more reliably associate positions on an image of a stretched fiber with genomic positions and by simplifying the identification of individual fibers taken anonymously from the genome [82,83] or with the genome location identified [54,84]. In parallel with fiber-based techniques, live-cell imaging has also yielded much valuable information. Although the size of origins and even their separations are well below the resolution of conventional light microscopy, clever techniques can yield spatial and temporal information. For example, specific sites can be labeled with fusion proteins whose intensity doubles after replication, an event that can readily be observed [85]. In the future, `live' single-molecule studies based on flow and optical or magnetic tweezers [86], nano-engineered capillaries [87,88] and other molecular-scale structures may lead to even greater insights, especially into local mechanisms at the fork and initiation sites.

A second set of techniques provides information about the fraction of cells in a population that has replicated at a particular location x and time t. This fraction of replicated cells can be described by the function f(x,t), if replication kinetics throughout S phase are measured, or simply as f(x), if measurements are performed on asynchronous cell populations (Figure 1, main text). Such measurements originally used microarrays [89,90], with one approach based on local changes in copy number during replication. In a population of unreplicated cells, a baseline intensity is measured at each locus [f(x) = 0]. After all cells have replicated, the measured intensity at each locus should be double [f(x) = 1]. During replication, intermediate levels of replication are detected as intermediate intensity levels [0<f(x)<1]. For example, if half of the cells in the population have replicated at a location x, then f(x) = 0.5. More recently, direct sequencing to determine local DNA copy number has given similar information with fewer artifacts [91,92]. Initial studies used multiple time points in cultures of synchronized cells to directly measure f(x,t) [89,93], and this approach is still the state of the art in yeast [20,64]. However, comparable results can be derived by sorting asynchronous cells of any type into G1 and S populations [90].

Box 3. Theoretical techniques for analyzing DNA replication timing.

Although determining the firing time of an origin would seem straightforward, particularly for the relatively simple yeast genome, the heterogeneous nature of origin firing and the passive replication of origins by forks from neighboring origins mean that the distribution of origin firing times cannot be directly inferred from its average replication time [94]. Therefore, rigorous analysis of replication timing patterns has relied on more sophisticated analytical tools. One of the most straightforward and widespread methods is computer simulation [6,27,28,30,38]. An advantage of simulation is that, with modest computer resources (especially if simulations keep track of only positions of forks and origins rather than use a lattice for each point on the genome [95]), one can recreate in silico not only the ideal experimental scenario envisaged, but also any relevant experimental details. For example, it is straightforward to include the effects of asynchrony in the cell population, finite microscope resolution, labeling artifacts, and the like [96]. Once the artifacts and the replication scenario are chosen correctly, the simulation can reproduce, within statistical error, the data from any given scenario.

The main disadvantage of simulations is that to analyze experimental data, one must first determine both the appropriate type of replication scenario to simulate and ways to incorporate experimental details and then determine the appropriate parameters to use. In situations in which origin firing is not uniformly distributed, each origin will be characterized by several parameters, and so the simulation may depend on hundreds or even thousands of parameters, depending on the type of organism. Curve-fitting techniques, which amount to a search in the space of parameters, require simulating a large number of scenarios. Analytical models, which can be used to directly calculate replication profiles instead of needing to simulate replication step by step, are one way to get around such obstacles. Analytical models may be evaluated faster than simulations. The difficulties are that one must be able to determine an appropriate model and be able to solve it. Thus, beginning with [6], a variety of analytical models have been proposed [8,39,42,94,97]. Because models based on independent origins are simpler than ones that allow correlated initiations, most of the above work has assumed such a scenario. Nonetheless, some analysis of correlated initiations has been done, as discussed in the main text.