What Is the Best Way to Estimate Hospital Quality Outcomes? A Simulation Approach

Abstract

Objective

To test the accuracy of alternative estimators of hospital mortality quality using a Monte Carlo simulation experiment.

Data Sources

Data are simulated to create an admission-level analytic dataset. The simulated data are validated by comparing distributional parameters (e.g., mean and standard deviation of 30-day mortality rate, hospital sample size) with the same parameters observed in Medicare data for acute myocardial infarction (AMI) inpatient admissions.

Study Design

We perform a Monte Carlo simulation experiment in which true quality is known to test the accuracy of the Observed-over-Expected estimator, the Risk Standardized Mortality Rate (RSMR), the Dimick and Staiger (DS) estimator, the Hierarchical Poisson estimator, and the Moving Average estimator using hospital 30-day mortality for AMI as the outcome. Estimator accuracy is evaluated for all hospitals and for small, medium, and large hospitals.

Data Extraction Methods

Data are simulated.

Principal Findings

Significant and substantial variation is observed in the accuracy of the tested outcome estimators. The DS estimator is the most accurate for all hospitals and for small hospitals using both accuracy criteria (root mean squared error and proportion of hospitals correctly classified into quintiles).

Conclusions

The mortality estimator currently in use by Medicare for public quality reporting, the RSMR, has been shown to be less accurate than the DS estimator, although the magnitude of the difference is not large. Pending testing and validation of our findings using current hospital data, CMS should reconsider the decision to publicly report mortality rates using the RSMR.

Pay-for-performance (P4P) and public quality reporting have been proposed as part of the solution to the quality and cost problems plaguing Medicare: through a combination of paying more for better care and steering patients toward higher quality and lower cost care, these programs have the potential to improve value. A central question in the design of these programs is how quality will be assessed and reported.

Quality of health care is frequently defined by process, outcome, and structure measures (Donabedian 1966), along with measures of patient experience. Process measures are often preferred to outcome measures on the grounds that providers have greater control over their performance on these measures and that they provide “actionable” information for quality improvement (Mant 2001; Birkmeyer, Kerr, and Dimick 2006). However, in acute care, given the narrow clinical focus of outcomes and the tenuous association between process performance and patient outcomes (Werner and Bradlow 2006; Ryan et al. 2009), process measures are an inadequate substitute for outcome measures. Krumholz et al. (2007) cite the following as reasons why outcome measures should be included in performance measurement systems: patients care about results (which outcomes assess); process measures might contribute to, but are not surrogates for, outcomes; the updating of process measures is often difficult; and exclusive emphasis on measured processes may divert attention from important unmeasured processes.

The main obstacle to using outcomes as performance measures is the large random variation to which outcomes are subject (Normand et al. 2007). This random variation can obscure the “signal” of true hospital outcome performance, which may result in incorrectly classifying hospitals as above or below their true performance. This problem is exacerbated when hospital outcomes are evaluated based on relatively small patient samples (Normand et al. 2007), a common occurrence for a broad spectrum of diagnoses for which outcome measurement has been advocated (Dimick et al. 2006).

In recent years, a number of methods have been developed to estimate outcome quality in health care in the presence of random variation. However, despite the obvious importance of determining the most accurate estimators of outcome performance, rigorous research on the relative accuracy of alternative estimators of outcome quality has been extremely limited. In this study, we performed a simulation experiment, which eliminates potential risk confounding, that tests the accuracy of five alternative outcome estimators: Observed-over-Expected, the Dimick–Staiger estimator, the Hierarchical Poisson (HP) estimator, the Risk-Standardized Mortality Rate (RSMR), and the Moving Average (MA) estimator. While other outcome estimators could be tested, we focus our analysis on conceptually different estimators that are in common use and whose methods have been published in the literature. The exception to these criteria is the Hierarchical Poisson, which we developed and implemented in this analysis to test its accuracy alongside the Dimick–Staiger estimator, which also exploits the volume and mortality relationship to estimate hospital quality.

Description of Estimators

The standard approach for estimating hospital outcome performance is to condition on a set of observable covariates to account for patient risk. Beginning with the New York coronary artery bypass graft (CABG) mortality public reporting program (Burack et al. 1999), the “Observed over Expected” (OE) estimator of outcome performance has embodied this approach. For admission i in hospital j, the OE estimator is given by:

(1)

and

(2)

where y denotes the observed outcome, e is the expected outcome (with a “hat” denoting its estimated value), and X is a set of risk-adjusters.

The OE has been criticized on the basis that it does not sufficiently account for random variation (Normand et al. 2007). In response, researchers have developed a variety of “shrinkage” estimators to obtain a more valid and reliable measure of hospital quality in the presence of random variation, that can vary substantially across hospitals according to sample size. These estimators have typically been proposed to assess mortality performance but are generalizable to other outcomes. Conceptually, using the logic of Bayesian inference, shrinkage estimators exploit information in addition to a hospital's risk profile and observed performance to estimate a hospital's outcome performance. This information includes outcome performance of other hospitals (Krumholz et al. 2006), hospital volume, or other indicators of quality (McClellan and Staiger 2000; Dimick et al. 2009; Staiger et al. 2009).

The shrinkage estimator currently in use by CMS for public quality reporting for mortality and readmission rates is the RSMR (Krumholz et al. 2006). The RSMR is given by the following:

(3)

and:

(4)

(5)

where f(x) denotes the inverse of the logit link function, w is a hospital-specific random effect, and μ is the conditional grand mean of y, estimated from a hierarchical generalized linear mixed model. (Estimation of the RSMR is described in Krumholz et al., 2006; and software to calculate RSMR and readmission rates can be requested from cmsreadmissionmeasures@yale.edu.) Through hierarchical modeling with random effects, the RSMR “shrinks” individual hospitals' quality scores back to the grand mean of hospitals' scores in proportion to the “noisiness” of a hospital's outcome performance. For instance, a hospital with fewer cases, and thus noisier performance, will be pulled toward the grand mean by a greater extent than a hospital with more cases and the same performance score. The RSMR has been endorsed by the National Quality Forum and is now used by Medicare as the estimator for publicly reported mortality and readmission for acute myocardial infarction (AMI), heart failure, and pneumonia as part of Hospital Compare. Using the RSMR, hospital mortality was initially reported for Hospital Compare using one prior year of data, but it is now reported by pooling three prior years of data. A recent article by Silber et al. (2010) provides an excellent discussion of the logic and implementation of the RSMR for Hospital Compare.

While the RSMR has the advantage of reducing random variation, it may also reduce a hospital's quality signal by shrinking hospital quality scores too much toward the grand mean (Silber et al. 2010). An alternative shrinkage estimator, recently developed by Dimick et al. (2009), uses a composite measure of patient volume and a measure of hospital-specific mortality (either risk-adjusted or unadjusted) observed in the data to estimate hospital quality performance. The approach is based on the well-established empirical finding that higher volume hospitals tend to have better outcomes. For this estimator (referred to as the “DS”), volume-predicted mortality (hospitals' expected mortality rate given their volume) and observed hospital-specific mortality are calculated for each hospital, and these two inputs are weighted based on the reliability of the latter measure. Let O_j denote the observed mortality for hospital j (e.g., either unadjusted or risk-adjusted mortality). Then, the DS is calculated as:

(6)

where O is hospital-specific mortality, β₀ and β₁ are estimated from a regression of mortality on hospital volume, and W is the weight assigned to O_j. In this equation, O_j mortality will receive relatively little weight (relative to volume-predicted mortality) for hospitals with low reliability (resulting from lower volume). Further computational details for this estimator can be found in Appendix 1 of Dimick et al. 2009, where it is shown how (6), as well as estimation of W, is related to the problem of constructing of an Empirical Bayes shrinkage estimator for the mean under a Bayesian normal linear model (Morris 1983). Appendix A of this article also shows a numeric example of calculating the DS and shows how the DS differs from the Hierarchical Poisson estimator. The DS is used by Leapfrog for public reporting of surgical quality and has been shown to have a better predictive accuracy than the OE (Dimick et al. 2009). However, it remains unclear how the DS compares with other estimators in its accuracy.

A related estimator that also incorporates information on volume to estimate hospital mortality is what we have named the Hierarchical Poisson estimator (HP). The HP is an empirical Bayes estimator that is similar to the DS in that it can be defined as a weighted linear combination of two components: volume predicted mortality and observed hospital-specific mortality (either unadjusted or risk-adjusted). However, the HP differs from the DS in that it is derived under a nonlinear model (estimating the hospital death rate using a negative binomial model for the death count that uses a log link and incorporates a known offset term). In addition, the HP uses the principles of maximum likelihood to estimate the weights assigned to volume-predicted mortality and risk-adjusted mortality. The HP is an extension of the Negative Binomial model considered in Lawless (1987), and similar to both the Bayesian HP model described in Burgess et al. (2000) and the extended Gamma model of Meza (2003, section 3). Appendix B provides a detailed description of the HP and demonstrates how the estimator can be easily calculated using Stata software (StataCorp; College Station, TX).

Instead of borrowing signal from other hospitals in the same time period, the MA estimator attempts to address random variation by exploiting the time dimension. Assuming that OE estimates are calculated for each year, in year t, the MA is given by:

(7)

While useful in reducing the effect of random variation and improving statistical power, estimates from the MA, particularly if calculated over a longer period, may be biased toward historical performance, not reflecting quality improvements in recent periods. While commonly used in finance, the MA has been employed sparingly to assess health care quality. While other quality estimators that use hierarchical models to incorporate longitudinal information have been proposed (e.g., Bronskill et al. 2002), these are not considered further in this study.

The OE, RSMR, DS, HP, and MA estimators all have different advantages and disadvantages, which are summarized in Table 1. However, a conceptual comparison of these estimators is insufficient to determine which will be most accurate when applied to the assessment of specific health outcomes.

Table 1.

Summary of Alternative Estimators

Estimator	Pros	Cons
Observed-over-Expected	Incorporates only most recent information on hospital quality	By using only the last year of data, estimator is subject to error from random noise if the underlying data are especially noisy
Risk-Standardized Mortality Rate	Uses quality signal of mean performance from other hospitals and information about noisiness of observed mortality to estimate quality	May shrink hospital performance too much toward the grand mean and ignores volume and outcome relationship
Dimick–Staiger	Uses empirical volume and outcome relationship and reliability of observed mortality to estimate quality	Does not explicitly incorporate time-series information on quality, most appropriate if correlations over time are low. Uses a parametric Empirical Bayes estimator under a normal linear model for the mortality rate
Hierarchical Poisson	Uses nonlinear model to incorporate empirical relationship between volume and mortality to estimate quality	Drawbacks are similar to Dimick-Staiger estimator. Most realistic in settings where events tend to be relatively rare
Simple Moving Average	Uses mortality information for the same hospital in previous periods in a standardized way	If mortality is trending strongly, will be biased toward historical performance. Also, does not use signal from other hospitals or incorporate volume and outcome relationship

Methods

We perform a Monte-Carlo simulation experiment on calibrated data to evaluate the accuracy of the OE (using 1 prior year of data), RSMR (using 1, 2, and 3 prior years of data), DS (using 1, 2, and 3 prior years of data), the HP (using 1, 2, and 3 prior years of data), and the MA (using 2 and 3 prior years of data) estimators. While any outcome could be evaluated for any health care provider, we calibrate our simulation model to correspond to hospital 30-day mortality for AMI. The basic approach is as follows: we create 3,000 simulated hospitals, randomly assign each hospital a sample size, a sample size trajectory, a “true” mortality rate (determined in part by its sample size and our assumed volume and mortality relationship), and a mortality change trajectory. Then, an admission-level dataset is created, and random draws, determining mortality, are taken for each admission. The probability of mortality for a given admission is based on the assigned true mortality for a given hospital in a given year. Using only the “observed” mortality, we then use the previously described estimators to estimate hospitals' “unknown” true quality, and evaluate the performance of these estimators given our knowledge of the assigned true mortality.

The key advantage of our simulation approach is that we are able to assess the accuracy of alternative outcome estimators against a benchmark that we know to be true outcome quality: true outcome quality is known because we assign it to hospitals in the simulation. In real life, true hospital quality is unobserved, and the extent to which an estimator of outcome performance approximates this truth can never be known with complete confidence, particularly because risk adjustment methods always are incomplete in real data. A number of prior studies have applied Monte Carlo simulation methods to the study of provider profiling in health care (Park et al. 1990; Hofer and Hayward 1996; Thomas and Hofer 1999), although we are not aware of studies that have used these methods to explicitly assess the accuracy of alternative estimators of quality.

Parametric Assumptions and Data Generation

To initiate the simulation, sample sizes are randomly generated for each hospital for year 1 of the simulation and, using the change in sample size parameters, sample sizes are assigned to each hospital for years 2–4 of the simulation. Then, using a specified volume and mortality relationship (see Appendix C), each hospital is similarly assigned a true mortality score for years 1–4 of the simulation. Across all simulation specifications, we assume that patient risk is constant across hospitals. This assumption is equivalent to assuming that various risk adjustment techniques would perform identically across hospitals for each estimator examined in the simulation. As a result of this assumption, none of the estimators calculated in the simulation include any measure of patient risk.

Data-generating functions for the simulations were chosen based on their correspondence with mortality and sample size data observed in Medicare inpatient files (see next). For instance, we chose a gamma distribution for sample size to accommodate the highly right skewed distribution (a distribution that is frequently used to model health care costs [e.g., Shang and Goldman 2008]) and chose the truncated normal distribution for mortality rates. Appendix D shows the specific data-generating functions used in the simulation.

Random noise is introduced into observed mortality rates as a result of random draws from the admission-level datasets. Hospitals with fewer admissions will have noisier observed mortality rates because these rates are based on random draws from a smaller number of admissions.

Validation

Analysis showed that estimator accuracy was sensitive to characteristics of the simulated data. For the results of the analysis to be as relevant as possible, we calibrate the simulation parameters (shown in Table 1) so that the mortality rates resulting from the simulation have a close correspondence to risk-adjusted 30-day mortality rates observed in Medicare data for AMI. Using Medicare inpatient data from 2002 to 2006, we calculated the following moment conditions for AMI: mean hospital volume, mean risk adjusted mortality rate (using age, gender, race, 30 dummy variables for the Elixhuaser comorbidities (Elixhauser et al. 1998), type of admission (emergency, urgent, elective), and season of admission as risk adjusters), between-hospital standard deviation in mortality, within-hospital standard deviation in mortality, mean change in mortality, between-hospital standard deviation in the change in mortality, and the within-hospital standard deviation in the change in mortality. The values of these moment conditions in the CMS data are henceforth referred to as the CMS parameters. We then generate 95% confidence intervals for the CMS parameters, using bootstrapped standard errors from 1000 iterations, re-sampling within hospital clusters.

For each simulation iteration, the previously described moment conditions are calculated using the simulated data (henceforth referred to as the simulation parameters). Next, we evaluate whether the parameter value falls within the 95% confidence interval of its corresponding CMS parameter. For each simulation iteration, we then sum the number of parameter failures, that is, the number of parameters falling outside the confidence interval, and include the iteration in the analysis only if there are one or fewer parameter failures (roughly across the range of what would be expected by chance). This process is repeated until 1,000 simulation iterations that meet the inclusion criteria are generated. These methods of sample selection are akin to rejection sampling, where samples that do not meet a specified criteria corresponding to the distribution of interest, are rejected from the simulated sample (Robert and Casella 2004).

We then compare the simulation output from the included iterations with moment conditions observed in the Medicare data. Table 2 shows a comparison of these moment conditions for AMI. It shows that the moment conditions are extremely similar, suggesting that the simulated data closely match the observed data for these moments. Figure 1 shows the distributions of mortality, change in mortality, and sample size in the CMS and simulated data for AMI. It shows that the distributions are very similar, again suggesting that the simulated data well approximate the CMS data. Appendix C shows that the volume and outcome relationship estimates from the CMS data match closely to the relationship that was implemented in the simulation.

Table 2.

Comparison of Acute Myocardial Infarction Moment Conditions between Simulated Data and CMS Data

	CMS Data		Simulated Data
	Mean	95% CI	Mean	Min, max
Mean mortality rate	.209	(.206, .212)	.208	(.206, .211)
Within-hospital standard deviation of mean mortality rate	.091	(.088, .094)	.092	(.088, .097)
Between-hospital standard deviation of mean mortality rate	.078	(.077, .080)	.079	(.076, .083)
Mean annual change in mortality rate	−.007	(−.009, −.006)	−.007	(−.009, −.006)
Within-hospital standard deviation of annual change in mortality rate	.137	(.132, .143)	.135	(.128, .142)
Between-hospital standard deviation of annual change in mortality rate	.031	(.029, .032)	.030	(.027, .032)
Mean sample size	104.8	(100.7, 109.0)	105.1	(101.5, 109.0)

Note. Centers for Medicare and Medicaid Services (CMS) moment conditions are calculated using inpatient data from 2002 to 2006.

Figure 1.

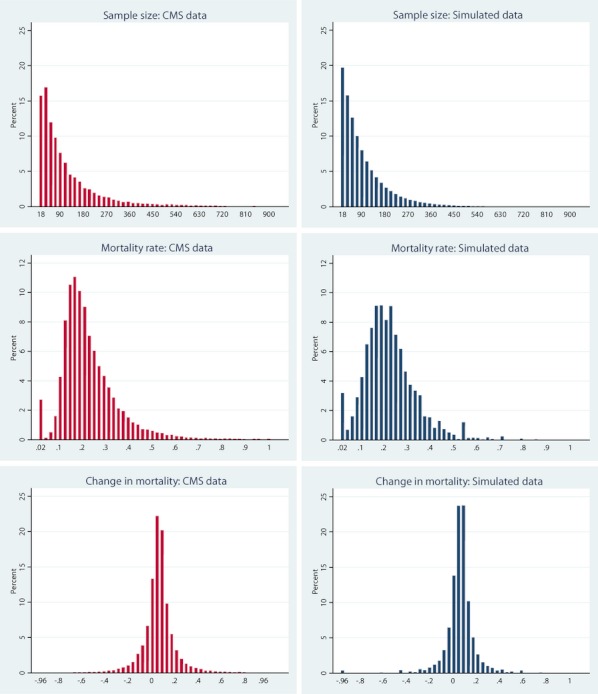
Histograms Comparing Distributions of Moments in Centers for Medicare and Medicaid Services (CMS) Data and Simulated Data

Estimation

Using only information on observed mortality and volume (for the DS and HP estimators), we estimate true mortality using the OE, RSMR, DS, HP, and MA estimators. We assume a 1-year lag between the present time and the year that outcome data are available: Consequently, when estimating a provider's outcome performance for period t, the most recently available data are from period t−1. Each estimator is calculated only for year 4 of the simulation, the year in which all of the estimators can be calculated. The RSMR and DS are calculated using methods described in the literature (Krumholz et al. 2006; Dimick et al. 2009). Appendix E shows a visual depiction of how the estimators are employed in practice.

Evaluation Criteria

To evaluate estimator accuracy, two criteria are used: the root mean squared error (RMSE) and the proportion of hospitals correctly classified (PCC) into quintiles. The RMSE is a common measure of the performance of estimators in the simulation literature (Greene 2004; Plumper and Troeger 2007; Sijbers et al. 2007). A lower RMSE value indicates that the estimator is closer to the true value. The PCC criterion measures the extent to which each estimator correctly classifies the relative quality of hospitals. For each simulation run, hospitals are classified into quintiles based on their true mortality score. We then calculate the proportion of cases in which each estimator correctly classifies hospitals into their respective quintile of true mortality. For a given estimator, the correlation between the RMSE and PCC criteria is moderate, ranging from r = .01 for the OE to r = .32 for the DS estimator (using 2 years of prior data), indicating that the criteria are measuring distinct constructs.

To examine whether the comparison of estimator accuracy varies across hospital volume, in each simulation iteration, we classify hospitals as small (bottom quartile of volume, between 1 and approximately 30 admissions), medium (middle quartiles of volume, between approximately 31 and 143 admissions), and large (top quartile of volume, more than approximately 143 admissions). Both evaluation criteria are calculated for all hospitals and for small, medium, and large hospitals.

Simulation Experiment

The data generation and estimation process described above is iterated over 1,000 repetitions, with 3,000 hospitals included in each iteration. In each iteration, parameter values, RMSE values, and the PCC values are captured. The data generated from the 1,000 repetitions are then combined into an analytic dataset.

Analysis

To evaluate the accuracy of alternative estimators, we calculate the mean RMSE and mean PCC values for each estimator across the 3,000 hospitals in the simulation. For each evaluation criterion, we then estimate a simple regression model in which the evaluation criterion is regressed on a vector of dummy variables for each estimator and test whether the most accurate estimator is significantly more accurate than the other estimators. The standard errors in these models are robust to clustering at the level of the simulation iteration. The analysis is performed using evaluation criteria data from all hospitals, and separately for evaluation criteria from small, medium, and large hospitals.

The simulation experiment and all analyses are performed using Stata version 11.0 (StataCorp 2009).

Results

Table 3 shows the results of the accuracy of each of the estimators on the RMSE and PCC criteria. The left column shows each of the estimators evaluated: the subscript signifies the number of years used in the calculation of each estimator. The columns to the right show the mean RMSE and PCC values overall and for small, medium, and large hospitals.

Table 3.

Evaluation of Estimator Accuracy for Acute Myocardial Infarction

	Accuracy Criterion
	Root Mean Squared Error				Proportion Correctly Classified
Estimator	Overall	Small Hospitals	Medium Hospitals	Large Hospitals	Overall	Small Hospitals	Medium Hospitals	Large Hospitals
OE1	.0968*	.1764*	.0516*	.0259*	.4871*	.3504*	.4728*	.6554*
RSMR3	.0520*	.0794*	.0419*	.0308*	.5712*	.4202*	.5568*	.7543
RSMR2	.0539*	.0847*	.0423*	.0278*	.5535*	.3944*	.5346*	.7540
RSMR1	.0599*	.0947*	.0476*	.0277*	.4926*	.3392*	.4714*	.6917*
MA3	.0611*	.1046*	.0387	.0289*	.5732*	.4369*	.5594*	.7402*
MA2	.0706*	.1260*	.0403*	.0249	.5550*	.4090*	.5383*	.7376*
DS3	.0466*	.0672	.0399*	.0305*	.5821	.4916	.5604	.7184*
DS2	.0462	.0680*	.0396*	.0268*	.5755*	.4772*	.5468*	.7336*
DS1	.0498*	.0715*	.0446*	.0274*	.5356*	.4454*	.4939*	.7115*
Hierarchical Poisson3	.0524*	.0814*	.0404*	.0315*	.5790*	.4905*	.5575*	.7128*
Hierarchical Poisson2	.0529*	.0844*	.0401*	.0280*	.5719*	.4764*	.5426*	.7280*
Hierarchical Poisson1	.0579*	.0918*	.0449*	.0287*	.5322*	.4475*	.4896*	.7042*

Notes. Subscript denotes the number of prior years used in estimator calculation

Bold denotes the most accurate estimator.

^*Difference between estimator and best estimator significant at p < .05.

“Small” hospitals are those in the bottom quartile of volume (between 1 and approximately 30 admissions), “medium” hospitals are those in the middle quartiles of volume (between approximately 31 and 143 admissions), and “large” hospitals are those in the top quartile of volume (more than approximately 143 admissions).

Table 3 shows that, on the RMSE criteria, the DS estimator is the most accurate for all hospitals (using two prior years of data) and for small hospitals (using three prior years of data), while the MA is most accurate for medium-sized hospitals (using three prior years of data) and for large hospitals (using two prior years of data). Table 3 also shows that differences in RMSE among the evaluated estimators are substantial for small hospitals, moderate for medium-sized hospitals, but quite small for large hospitals. As a result of the extremely small standard errors on the estimates (not shown), the difference in the RMSE values between the most accurate estimator and the other estimators is significant at p < .05 for all comparisons.

For the PCC criterion, Table 3 shows that the DS is the most accurate for all hospitals (using three prior years of data), for small hospitals (using three prior years of data), and for medium-sized hospitals (using three prior years of data), while the RSMR (using three prior years of data) is the most accurate for large hospitals. Overall, the DS (using three prior years of data) classifies 58.21% of hospitals into the correct quality quintile, compared to 57.90% for the HP (using three prior years of data), 57.32% for the MA (using three prior years of data), 57.12% for the RSMR (using 3 years of data), and 48.71% for the OE. This difference is more pronounced among small hospitals, for which the DS (using three prior years of data) classifies 49.16% of hospitals into the correct quality quintile, compared to 49.05% for the HP (using three prior years of data), 42.02% for the RSMR (using three prior years of data), and 35.04% for the OE.

For both the RMSE and PCC criteria, using more years of prior data to generate estimates is associated with more accurate estimates for small hospitals across the alternative estimators, while the effect of using more years of prior data on accuracy for larger hospitals varies across the estimators.

Discussion

This is the first study to empirically test the performance of alternative estimators of hospital outcome quality in a simulation study in which true quality is known. We find that, overall, the Dimick–Staiger estimator is significantly more accurate than the Observed-over-expected, RSMR, HP, and MA estimators for both of our evaluation criteria.

We also find interesting variation in the accuracy of estimators across hospital volume. Not surprisingly, each of the estimators is substantially less accurate when estimating mortality for small hospitals (the bottom quartile of volume) relative to medium-sized (the middle two quartiles of volume) and large hospitals (the top quartile of volume). This difference in estimator accuracy is most apparent for small hospitals: the Dimick–Staiger estimator using 3 years of data correctly classifies 49.16% of small hospitals into their mortality quintile compared to 35.04% for the Observed-over-Expected estimator, 33.92% for the RSMR using 1 year of data, and 42.02% for the RSMR using 3 years of data. The HP estimator, which also uses information on hospital volume to derive shrinkage estimates, generates similar, although somewhat less accurate quality estimates than the Dimick–Staiger estimator.

In addition, for the RSMR, Dimick–Staiger, and MA estimators, we found that, for small hospitals, estimators using more years of prior data tended to increase estimator accuracy. However, for large hospitals, which had more precise estimates from large sample sizes, estimates using two years of prior data were similarly accurate to estimates using three prior years of data.

With the exception of the Observed-over-Expected estimator, overall, the magnitude of the differences in estimator accuracy for both criteria is fairly modest: while the Dimick–Staiger estimator is the most accurate, using three years of data, its accuracy on both criteria is close to that of the RSMR and the HP. More substantial differences are observed among small hospitals, where the Dimick–Staiger is substantially more accurate than the RSMR on both criteria, and somewhat more accurate than the HP on the PCC.

Our conclusion that the Dimick–Staiger estimator, which incorporates hospital volume into its shrinkage estimates, is more accurate than the RSMR is the same as that reached by Silber et al. (2010) in a recent study, which contends that estimators that shrink to volume groups are more accurate than those, such as the RSMR, that shrink to the grand mean. However, Silber et al. reach this conclusion by finding that, after classifying hospitals into volume quintiles (for AMI), a volume and outcome relationship is observed using the Observed-over-Expected estimator, but no such relationship is found when using the RSMR. As noted by the authors, this is only an indirect test, and does not evaluate whether the RSMR is an inferior estimator for individual hospitals. Furthermore, Silber et al. only evaluate the RSMR using one prior year of data and do not assess the accuracy of this estimator using three years of prior data. This simulation study has shown the RSMR is substantially more accurate when using three prior years of data to generate estimates, rather than just one prior year of data.

Furthermore, our finding that empirical Bayesian shrinkage estimators, which shrink mortality estimates toward the volume-conditional mean (the Dimick–Staiger and HP estimators) or the unconditional mean (the RSMR), tended to be more accurate than non-Bayesian estimators (the Observed-over-Expected and MA estimators) is not surprising. Empirical Bayes estimators have a long tradition in that statistical literature, going back to the development of the James-Stein estimator, an estimator that was shown to more accurately predict batting averages among major league baseball players (Efron and Morris 1975). It may seem unintuitive for hospitals to be evaluated for pay-for-performance and public reporting programs using shrinkage estimators that are not solely based on their own performance. Nevertheless, if these estimators are a more accurate representation of true hospital quality than estimators not using shrinkage, public reporting programs using shrinkage estimators will more effectively mobilize patient choice, which may also result in greater responsiveness of hospitals to public reporting. Also, through Value-Based Purchasing in Medicare, shrinkage estimators could be used to calibrate hospital payments according to quality, which would have the effect of Medicare paying for higher value services without direct demand-side responsiveness.

Our study has a number of relevant limitations. First, the data used for the analysis of estimator accuracy were simulated. Consequently, as a result of potential differences between the true data-generating process and that which was simulated in this study, the inferences drawn about the performance of outcome estimators may be incorrect. Thus, while suggestive, our findings do not provide a definitive critique of alternative mortality estimators. However, careful attention was paid to calibrate our simulation to match the distributional parameters of risk-adjusted mortality for AMI as observed in Medicare data (see Table 2 and Figure 1). Comparison of the simulated and real data indicates that our simulation models generated output that closely matches the real data-generating process, as observed in Medicare data. As a result, for 30-day AMI mortality, an outcome of great policy interest, we are confident that our results are not merely artifacts of simulation assumptions. Furthermore, a simulation approach, such as ours, is the only way to compare the true accuracy of outcome estimators in the presence of incomplete risk adjustment: in the real world, “true” performance is never known and thus estimator correspondence with true performance cannot be ascertained. In contrast, a predictive validity approach to assessing estimator accuracy using actual data, in which hospital quality is estimated in period t and estimators would be evaluated by how well they predict quality in period t + 1, is interesting and informative, but cannot account for unobserved risk and is potentially compromised by changes in true hospital quality between the two periods. This is why our simulation approach adds something to the literature on outcome estimators that is currently lacking.

Regarding the assumptions of the simulation model, two limitations are worth noting. First, our model assumes that risk adjustment is equally accurate across providers: if unobserved severity is systematic, for instance, if a given hospital has consistently higher unobserved severity over time, this may affect the evaluation of the estimators. However, sensitivity analysis (not shown) modeling systematic differences in unobserved severity yielded similar inferences. Second, we assumed that true mortality followed a smooth time trend: We view this as making intuitive sense as a hospital's labor, capital, and organizational characteristics that determine true outcome performance generally show small year-to-year changes. However, if true mortality is in fact noisy, showing substantial fluctuations over time, the evaluation of the outcome estimators may have yielded different results.

Another potential criticism of our analysis is that the simulation was constructed to yield a favorable result for the Dimick–Staiger and HP estimators. As we specified a volume and mortality relationship in the data-generating process and because these estimators exploit this relationship, it is perhaps not surprising that these estimators were frequently more accurate than the other estimators, including the RSMR. However, the Dimick–Staiger and HP estimators did not use “inside information” from the simulated data-generation process to estimate mortality: instead, the estimators used the volume and outcome relationship as observed in the simulated data, and incorporated this information into their estimates. When comparing accuracy of the Dimick–Staiger and HP estimators, we found that the Dimick–Staiger estimator tended to be more accurate, although the differences were small.

Finally, while we found significant differences in the accuracy of the estimators evaluated, the practical effect of these differences in the context of pay-for-performance and public reporting programs is unknown. Estimating the net effect of an increase in estimator accuracy (e.g., an increase in the proportion of hospitals correctly into quintiles by 10 percentage points) on patient mortality in a public reporting program, by assuming a model of patient behavior based on previous research, would be an excellent topic for further study.

Yet our study has a number of important implications. First, for data calibrated to approximate 30-day mortality for AMI, the RSMR using three years of data has been shown to be less accurate than the Dimick–Staiger estimator on both of the evaluation criteria that we used in our study. While the differences in accuracy are not large, they are significant, and they suggest that the Dimick–Staiger estimator could provide more accurate information to patients and physicians about the quality of hospitals. Second, the study shows that estimators using only one prior year of data are substantially less accurate than estimators using two or three years of prior data, particularly for smaller hospitals. Value-Based Purchasing in Medicare will use an 18-month evaluation period to evaluate hospital outcome performance (Federal Register 2011), which may lead to less accurate assessments of performance than a longer evaluation period would. Third, the methods employed in this study have broad applicability to studying the performance of other quality measures (e.g., process measures, readmission outcomes, complication outcomes) for physicians, hospitals, and other organizational structures in health care. Requiring that similar testing to be performed before endorsing outcome estimators would add needed rigor to the National Quality Forum's measure endorsement process.

Our study also suggests that research to design better estimators should continue. Our results indicate that, overall, even the best estimators examined accurately classify hospitals into their true performance quintile less than 60% of the time, and accurately classify the smallest quartile of hospitals around 50% of the time. More research is required to develop more accurate estimators of hospital outcome performance. Given our finding that the relative accuracy of alternative estimators varies according to hospital volume, a possible approach forward is to develop composite estimators that are weighted combinations of other estimators, with the weights varying across different types of hospitals and derived to optimize a specified objective function (perhaps containing criteria such as RMSE and the proportion of hospitals correctly classified into quintiles). Future research should also test the accuracy of alternative estimators for other outcomes in health care, such as readmission and complication rates.

SUPPORTING INFORMATION

Additional supporting information may be found in the online version of this article:

Appendix SA1: Author Matrix.

Appendix S1: Numeric Example of Dimick Staiger Estimator and Comparison between Dimick-Staiger Estimator and Hierarchical Poisson Estimator

Please note: Wiley-Blackwell is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.