Intrinsically High-Q Dynamic AFM Imaging in Liquid with a Significantly Extended Needle Tip

Abstract

Atomic force microscope (AFM) probe with a long and rigid needle tip was fabricated and studied for high Q factor dynamic (tapping mode) AFM imaging of samples submersed in liquid. The extended needle tip over a regular commercially-available tapping mode AFM cantilever was sufficiently long to keep the AFM cantilever from submersed in liquid, which significantly minimized the hydrodynamic damping involved in dynamic AFM imaging of samples in liquid. Dynamic AFM imaging of samples in liquid at an intrinsic Q factor of over 100 and an operation frequency of over 200 kHz was demonstrated. The method has the potential to be extended to acquire viscoelastic materials properties and provide truly gentle imaging of soft biological samples in physiological environments.

1. Introduction

For microscale or nanoscale mechanical resonant systems operating in a liquid environment, the hydrodynamic interaction between the system and the liquid, and thus the related energy dissipation, is typically significant. Such is the case in typical AFM dynamic imaging in liquid [1–3]. The involved energy dissipation, which is significantly higher than that experienced by the AFM probe operated in vacuum or air environments [4–7], reduces the Q factor down to low single digits, overwhelms the energy dissipations related to the tip-sample interactions for useful studies, and thus significantly limits the sensitivity of the AFM for nanoscale probing of sample properties in liquid, especially on soft samples [8, 9].

One method that has been extensively explored to enhance the Q factor in dynamic AFM operation is active Q-control [10–14], where an external feedback control circuitry dynamically boosts the resonance oscillations and tunes down the non-resonance oscillations of the cantilever by actively modulating the excitation force. Effective Q-factors as high as over one thousand have been demonstrated in practice. However, active Q-control does not fundamentally change the damping intrinsically experienced by the oscillating AFM probe in liquid; adversely, active Q-control amplifies the thermal noise and thus the random thermal fluctuation force experienced by the AFM cantilever, reducing its signal to noise ratio [15, 16]. To compensate for the noise increase in imaging, the oscillation amplitude of the cantilever must be increased, which, however, increases the imaging tapping force, and thus negates the original benefit of having an actively boosted Q. It is thus desirable to have a dynamic AFM resonant system that can achieve an intrinsically high Q factor in liquid to provide sufficiently minimized imaging force and high signal to noise ratio for high force and high spatial resolution imaging. As for many studies in liquid, the involved samples (e.g. membranes, cells, tissues, or even phase boundaries) are usually very soft, it is mostly their dynamic mechanical properties (e.g. the viscoelastic properties) [3, 17] and their spatial difference [18–20] that are most important, which, however, requires a dynamic measurement method that has both a sufficiently high intrinsic Q factor and a high force sensitivity to be able to physically probe and quantitatively study them.

Energy dissipation involved in a dynamic mechanical system originates from the inelastic interactions manifested in internal frictions due to thermoelastic dissipation and defects activation and external frictions due to hydrodynamic damping and sliding, among others [21]. The Q factor, which generally describes the effect of energy dissipation in a dynamic mechanical system, such as a mechanical resonator, is defined as the ratio of the energy stored in the resonator and the energy dissipated per cycle. The Q factor can be related to the damping coefficient c by Q = mω/c, where m is the mass of the oscillating system and ω is the angular resonance frequency. The Q factor and the related damping coefficient is intrinsically related to the ultimate sensitivity of many sensing systems based on mechanical resonance, especially microscale and nanoscale resonators [22]. For example, the thermal fluctuation force 〈F_T〉, or the thermal noise, is related to the damping coefficient c by $\langle F_T\rangle =\sqrt{4k_{B}Tc}$, where k_B is the Boltzmann constant and T is the system temperature. A reduced damping coefficient reduces the thermal noise and thus improves the intrinsic sensitivity limit [21]. The average tapping force (the tip-sample interaction) <F_ts> applied on a sample by an oscillating probe in a dynamic atomic force microscopy (AFM) imaging is related to the Q factor by $<F_{ts}>=\frac{k}{Q}{[{A_0}^2-{A_{sp}}^2]}^{1/2}$, where k is the spring constant of the AFM probe cantilever, and A₀ and A_sp are the drive and set-point amplitudes of the cantilever [16]. An increased Q factor lowers minimal available tapping force for AFM imaging, which is especially beneficial for imaging delicate soft samples and extract useful dynamic information on tip-sample interactions.

The mechanical damping experienced by a micromechanical dynamic system (such as the AFM probe) can be intrinsically minimized by reducing its interaction cross-section with the liquid environment. In the following, we first explore the concept of exploiting a significantly extended needle tip that is shallowly immersed in liquid and operated near the resonance frequency of the AFM cantilever for lowering the mechanical damping associated with the dynamic imaging in liquid as shown in Fig. 1a, and compare its performance with that of an AFM probe fully submersed in liquid. We then demonstrate the intrinsically high Q factor dynamical mode AFM imaging of samples immersed in liquid to show its applicability. This dynamic AFM imaging method was shown to realize an intrinsic Q factor of over 100 without Q feedback control and thus provided the potential for use in imaging and extracting dynamic mechanical properties of very soft sample in liquid.

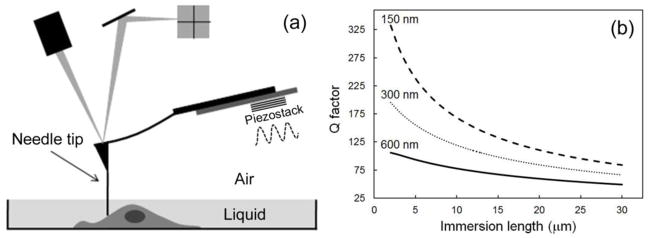
Fig. 1.

(a) Schematic depicting the method of using an AFM needle probe for intrinsically high Q factor AFM dynamic imaging in liquid. The setup keeps the AFM cantilever and the cantilever holder out of the liquid environment, and allows driving the cantilever directly with the piezostack in the cantilever holder to a high Q factor and high frequency resonance. (b) The calculated dependence of the Q factor versus the needle tip immersion length with the use of a needle of 600 nm, 300 nm and 150 nm in diameter.

2. Model Analysis

As shown in Fig. 1a, except the end segment of the needle tip that is immersed in the shallow liquid experiences a hydrodynamic damping due to its interaction with the liquid, the AFM cantilever and the cantilever holder stay in the air ambient environment. In the operation, the AFM cantilever is driven to near its resonant oscillation with the piezostack provided in the cantilever holder in the same way as in typical tapping mode AFM operation in air. The dynamics of this AFM probe with or without the extended needle tip can thus be modeled as a linear oscillator [3] following, m ẍ + cẋ + k x= F_ext, with the quality factor defined as Q = mω/c, in which $\omega =\sqrt{k/m}$, m is the mass of the resonating element, ω is the resonance frequency, k is the force constant, c is the damping coefficient associated with the dynamic system and F_ext is the excitation force. For a cantilever system as shown in Fig. 1a with the needle tip partially immersed in liquid, the contributions to its damping originate mainly from the Stokes drag force [23] on the portion of the needle immersed in the liquid (c_d) and the drag force due to the large velocity gradient across the thin meniscus layer (c_m) formed at the needle/liquid interface [24, 25]. The associated Q-factor of the resonant system, Q_n, can therefore be expressed as: $Q_n=(m_c+m_n^{\prime }){\omega }_n/(c_m+c_d+c_a)$, where m_c is the mass of the cantilever, $m_n^{\prime }$ is the added mass onto the needle during the oscillation (which is negligible when compared to m_c), ω_n is the resonance frequency, which, due to the negligible added mass, hardly reduces from that of the cantilever in air ( ${\omega }_n=\sqrt{k(m_c+m_n^{\prime })}$), and c_a is the hydrodynamic damping of the cantilever in air, which can be practically ignored. The Stokes drag coefficient on a needle vertically moving along its long axis in liquid can be approximated as [23]: c_d ≈ 2 π η L/[ln (L/r) −0.72], where η is the dynamic viscosity of the liquid, L and r are the immersed length and the radius of the needle, respectively. The damping coefficient due to the nanoscale meniscus is described by [24, 25] c_m ≈ 2 π r η ln (δ/a)/θ_d, where θ_d is the dynamic contact angle between the liquid and the nanowire (approximated to be π/4 between water and the nanowire), δ is the evanescent decay length ( $\delta =\sqrt{2\eta /({\omega }_n\rho )}$, where ρ is the density of the liquid), and a is the liquid molecule size (for water, ~0.278 nm).

Fig. 1b shows the dependence of the Q factor of the needle tip attached cantilever on the immersion length of the needle having a diameter of 150 nm, 300 nm and 600 nm in water. Intrinsic Q factor over 100 is possible with the use of a needle of 300 nm in diameter even when the needle is partially immersed by up to 15 μm. In the calculation, the AFM cantilever has the typical dimensions of 125 μm in length, 35 μm in width and 2 μm in thickness, and it has a force constant k of 6 N/m and a Q factor of 450 in air. In comparison, for the same cantilever fully submersed in water, the added mass m_ad due to the dragged water by the oscillating cantilever is ~ 1.7×10⁻¹⁰ g and the hydrodynamic damping coefficient c_L is ~ 8×10⁻⁶ Ns/m. Both are calculated based on $m_{ad}=\rho \frac{\pi }{4}{W}_c^2{L}_c{\mathrm{\Gamma }}^{\prime }$ and $c_L=\rho \frac{\pi }{4}{W}_c^2{L}_c{\omega }_L{\mathrm{\Gamma }}^{″}$, where W_c and L_c are the width and length of the cantilever and γ′ and γ″ are the hydrodynamic functions [4, 5]. The resulted Q factor is merely ~4, which is two orders of magnitude smaller than that in air. Q_L = (m_c + m_ad)ω_L)/(c_c + c_L), where c_c is the damping of the cantilever in vacuum and is ignored, and ω_L is the resonance frequency of the cantilever in liquid. ω_L is significantly downshifted to ~30 kHz from its value in air of ~270 kHz. The use of a needle attached AFM probe that frees the body of the AFM cantilever from being submersed in liquid as shown in Fig. 1a thus acquired significantly lowered mechanical damping and intrinsically high Q factor in dynamic operation. The intrinsically reduced damping coefficient, in the meantime, reduces also the thermal noise 〈F_T〉 by up to an order of magnitude according to the range of parameters analyzed previously, which extends the theoretical sensitivity limit of the dynamic system for force sensing. In addition, due to the small interaction cross-section with the surrounding liquid, the needle probe introduces minimal mechanical disturbance to the liquid and ultimately to the sample when used for AFM imaging.

3. Experimental details

We demonstrate below the fabrication and characterization of such an AFM needle probe. To be useful for the proposed use in AFM, the needle probe must meet several requirements. First, it must be sufficiently long, as practically it is very difficult to prepare and maintain a shallow liquid level only micrometers deep especially with the use of water as solvent for most biological samples. Second, the needle must be of sufficient robustness to avoid being bent or pulled off by the meniscus force or disturbed by the dynamic AFM operation. Third, it needs to be sufficiently uniform in diameter to avoid the variation in drag force simply due to the diameter variation. The final requirement, as generally required for AFM imaging, the needle probe needs to have a sharp tip to provide sufficiently high spatial resolution.

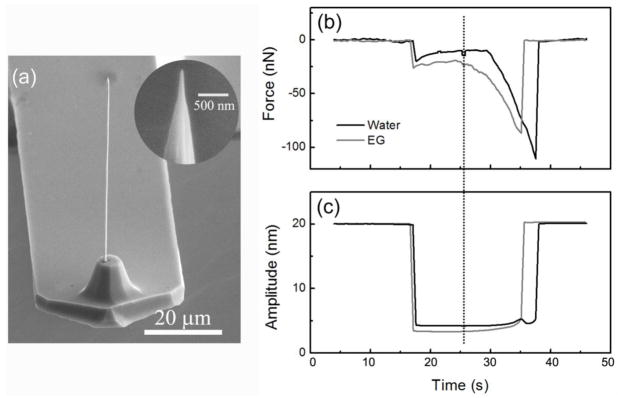
In our following studies, we fabricated, directly on commercial AFM cantilevers, Pt needle probes that are ~60 μm in length, ~600 nm in diameter and have a sharpened tip of 15–25 nm in radius of curvature. The buckling force of such a Pt needle (taking the elastic constant of Pt to be 168 GPa) was estimated to be ~700 nN, significantly above the force needed for AFM imaging, and the natural frequency of the nanoneedle is ~1.4 MHz, much higher than the operating frequency in typical AFM imaging, which is around ~200 kHz in our following operation. There are currently some commercially available AFM probes that have a long needle attachment, but such needle probes are either too short for use in our proposed operation or too flexible to provide stable quality for AFM imaging in liquid. We instead apply a recently developed meniscus-confined electrodeposition fabrication technique [26, 27] to fabricate such a needle probe with uniform diameter and long length. The detailed description of this technique can be found in the referenced articles. In short, the meniscus-confined electrodeposition fabrication technique utilizes an electrolyte-filled glass micropipette as the electrodeposition nozzle. By engaging the nozzle on a substrate surface to initiate an electrolyte meniscus formation between the nozzle and the substrate, electrodeposition is initiated on the conductive substrate (as the cathode) only within the meniscus/substrate interface by applying a deposition potential between an anode immersed in the electrolyte inside the micropipette and the substrate. The micropipette is withdrawn from the substrate surface at a speed coinciding with the growth rate of the metal deposit, maintaining the stable meniscus formation between the micropipette and the growth front of the deposited metal. This allows the continuous fabrication of a freestanding metal wire. The wire diameter is defined by the size of the meniscus (thus the nozzle diameter) and depends also slightly on the withdrawal speed of the micropipette. The length is practically unlimited. We deposited a solid Pt wire with the intended diameter and length onto the distal end of a conductive AFM cantilever (Mikromasch, NSC14 probe) having a nominal force constant of ~6 N/m (Fig. 2a). The Pt wire was deposited with an inclination of ~12° off the vertical direction to the cantilever surface so to compensate for the mounting angle of the cantilever in the instrument and to realize its vertical entrance into the liquid. The wire was uniform in diameter of ~600 nm and had a length of ~60 μm. The tip of the Pt wire was sharpened with focused ion beam milling to attain a tip radius of curvature of 15–25 nm (Fig. 2a, inset).

Fig. 2.

(a) Image showing a ~60 μm long and ~600 nm-diameter Pt nanowire directly deposited onto an AFM cantilever with the meniscus-confined electrodeposition technique. The inset shows the tip end of the needle sharpened down to ~25 nm in tip radius of curvature with focused ion beam milling. (b–c) Static approach and retraction curves of the needle tip into water and ethylene glycol showing the change of the exerted force due to surface tension measured from the cantilever deflection (b) and the change of the cantilever oscillation amplitudes (c). The dashed line marks the starting point of the retraction in the experiment.

Dynamic measurements in liquid were carried out under a stable 100% relative humidity to limit water evaporation and to maintain a stable air/liquid interface. All measurement was performed in a Veeco Dimension 3100 AFM system with a Nanoscope IV controller operated in the amplitude modulation tapping mode. The dynamic oscillation of the AFM cantilever was driven with the piezostack in the standard tapping mode cantilever holder and monitored with the reflected laser off the back of the cantilever onto a typical Quad-position sensing detector in the system. Typical noncontact mode AFM probes (Mikromasch, NSC probe) having a nominal spring constant of ~6 N/m were used for depositing the needle tip and subsequently used for the AFM tapping mode imaging.

4. Results and discussion

The dynamical characteristics of the vertically oscillating needle tip in liquid was studied by gradually dipping the needle into de-ionized water, phosphate buffered saline (PBS), and ethylene glycol (a non-volatile liquid at room temperature). Figures 2b–c show the typical snap-in and snap-back behaviors and the corresponding changes in the deflection (force) and the oscillation amplitude of the cantilever at resonance as the needle tip advances into and retracts out of the air/liquid interface. The forces exerted on the needle tip due to surface tension measured at the points of snap-back in the curves were ~120 nN in water, and ~87 nN in ethylene glycol, which were in good agreement with the force (F_s) estimated according to F_s = πγd with d being 600 nm and the surface energy values γ for water and ethylene glycol being ~ 72 mJ/m² and ~ 47 mJ/m², respectively. The estimated forces due to surface tension in water and ethylene glycol were ~135 nN and ~ 90 nN, respectively. This verified the virtually vertical entrance of the needle into the air/liquid interface, necessary for the optimal operation of the needle tip for AFM imaging.

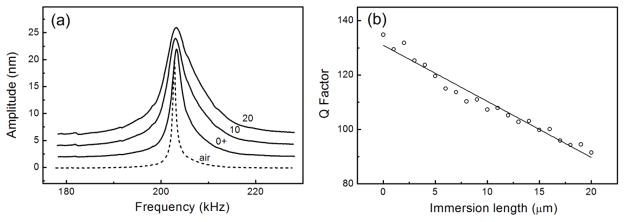
The dynamic response curves of the AFM cantilever were subsequently acquired as the needle was advanced into water in steps of 1 μm. Shown in Fig. 3a is the dynamic response of the cantilever in air along with the corresponding curves acquired for different immersion lengths of the needle. The harmonic behavior of the cantilever in liquid was near perfectly preserved without the appearance of any spurious peaks (an aspect similar to those acquired in AFM Magnetic AC Mode). In addition, there was no obvious shift in the resonance frequency (over 200 kHz) of the cantilever indicating the minimal effect of the added mass onto the needle as expected. Moreover, the Q factor of the resonance remained very high. This is in sharp contrast to the resonance curve acquired in the regular dynamic AFM operation in liquid with acoustic excitation where the existence of spurious peaks in the response curve of the cantilever is very common, which often renders even the identification of the actual resonance peak of the cantilever difficult. It is also significantly different from the resonance curve in the regular dynamic AFM operation with magnetic AC excitation where the Q factor is often much below 10 and the resonance frequency is significantly reduced from the natural resonance frequency of the cantilever in air. The Q factor was evaluated based on each response curve in Fig. 3a by fitting it with a Lorentzian function of a single harmonic oscillator. The immersion length-dependent Q factor is plotted in Fig. 3b. For a cantilever with a Q factor of ~ 450 measured in air, the Q-factor dropped to one third (~135) of that at the moment the needle entered the liquid surface and then almost linearly reduced to 90, one fifth of the Q factor in air, when it was dipped into the liquid by ~20 μm, which, however, is still orders of magnitude higher than that in traditional dynamic AFM operations. The result fits well with our previous analysis represented in Fig. 1b.

Fig. 3.

(a) Acquired resonance curves of the AFM cantilever at different immersion lengths of the needle. Subsequent curves are offset upwards by 2 nm in amplitude to better present the data. Actual resonance curves have the same peak amplitude. (b) Dependence of the measured Q factor as a function of the immersion length. The quality factor of the cantilever system in air is ~450.

We further implemented this AFM needle probe for AFM dynamic mode (tapping mode) imaging of soft samples in liquid. We prepared the biological samples (collagen fibrils and living HeLa cells) in concave glass containers for convenience. A concave liquid container provided sufficient sample areas around the wet perimeter with sufficiently shallow liquid level (<60 μm, the length of the needle) to keep the AFM cantilever out of the liquid surface, while in the meantime provided the necessary liquid environment for preserving living cells and biological samples. For imaging soft samples in liquid, the AFM needle probe installed as a regular AFM probe in the AFM system was advanced towards the liquid surface near the wet perimeter while the amplitude and the deflection of the AFM cantilever were monitored continuously. To engage onto the sample surface immersed underneath a shallow liquid layer, we relied on identifying the transition in the change of the oscillation amplitude versus the distance dependence. The change in oscillation amplitude is more abrupt when the tip of the needle began to sense the presence of the sample surface compared to that due to solely the hydrodynamic drag on the needle. Once the sample surface was engaged on, the drive amplitude and the set-point in the AFM system were adjusted to optimize the imaging quality as in regular dynamic mode AFM practice.

Shown in Fig. 4a is the acquired topography images of individual collagen fibrils [28] (bovine Achilles tendon, Sigma-Aldrich) immersed in ethylene glycol. It was acquired with a drive amplitude at 10 nm and a set point at 80%. Non-disturbed images of the fibrils were clearly resolved. The fibrils in the image had diameters from 50 nm to 200 nm. When the drive amplitude was reduced to 1 nm, no obvious change was noticed in the quality of the acquired image as shown in Fig. 4b, manifesting the sufficient reserve in signal to noise ratio in the AFM needle probe system. The average tapping force <F_ts> estimated based on <F_ts> = k[A₀² − A_sp²]^1/2/Q is less than 60 pN (taking Q ~100 in liquid, k = 6 N/m and A₀ = 1 nm). This tapping force could in principle be further reduced by using an AFM cantilever with a smaller force constant (regular dynamic mode imaging in liquid typically uses an AFM probe having a force constant of ~0.5 N/m). Live HeLa cells cultured in Dulbecco’s modified Eagle’s medium (DMEM) supplemented with 10 % fetal bovine serum (FBS), 100 U/ml penicillin and 100 μg/ml streptomycin at 37 °C under 5% CO₂ were also imaged at a drive amplitude of ~ 20 nm, a set point of 80% and a scan rate of 1 Hz, as shown in Fig. 4c. The acquired topography images of the cells were seen to follow the natural membrane contour and showed no obvious deformation of the cells evidenced by the lack of ostensible protrusions due to the presence of the cell nucleus and cytoskeleton structures. The membrane of a living cell, especially the cancerous type HeLa cell, is recognized to be extremely soft, having an effective elastic modulus in the 1 kPa range. Traditional dynamic imaging method where the AFM cantilever was fully submersed in liquid often severely deforms cells during the imaging scan. Instead of mapping cell membrane surface and the actual cell volume, it profiles the intracellular actin filaments and microtubule networks as well as subcellular organelles including the nucleus.

Fig. 4.

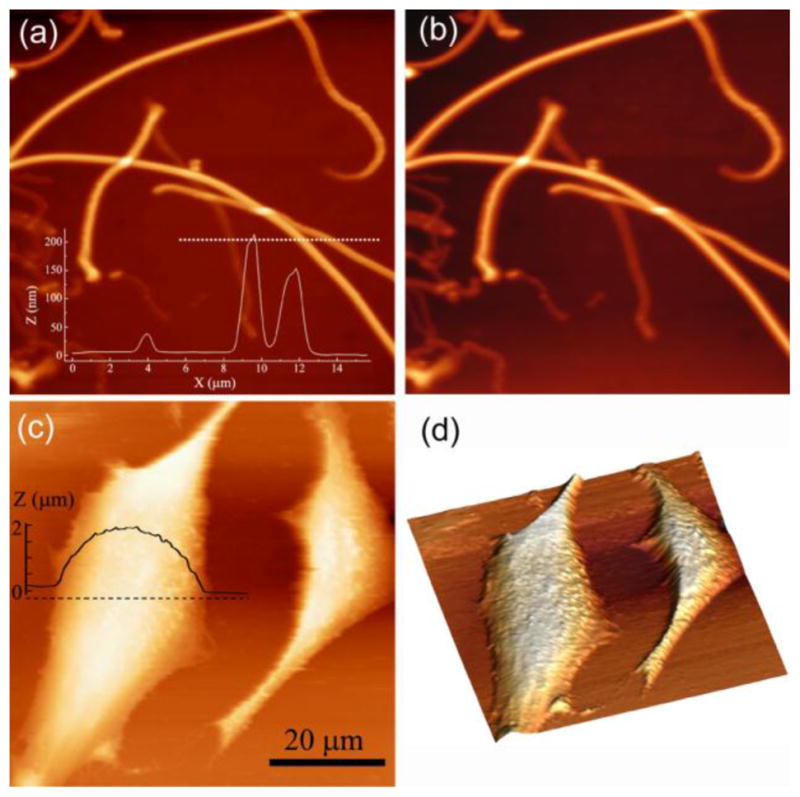
(a–b) AFM images of type I collagen fibrils acquired in ethylene glycol. AFM topographical image acquired at a drive amplitude of 10 nm (a) and 1 nm (b). Overlaid in (a) is the height plotted along the dotted line marked in (a). The scan size is 30 μm × 30 μm. (c) AFM topographical imaging of living HeLa cells in physiological conditions showing minimal cell membrane deformation. Overlaid in (c) is the corresponding height profile acquired along the dashed line marked over the cell. (d) The corresponding 3-D representation of the cell topography in (c). The scan rate for AFM imaging is 1 Hz.

5. Conclusion

In summary, the method of exploiting the dynamic performance of a vertically oscillating needle partially immersed in liquid was studied and evaluated. Intrinsically high Q factor (over 100) resonance with low thermal noise and near perfect harmonic response was realized. Exploiting a new and practical technique for fabricating such special AFM probes integrating the needed needle tip having uniform diameter and extremely high aspect ratio, the method was implemented for imaging soft biological samples, even the extremely delicate membranes of living HeLa cells, with minimal tapping force in physiological conditions. This method for AFM imaging is inherently a dynamic imaging method and can thus be readily adapted for use in any existing AFM instruments especially with the development of better sample holders for liquid samples, such as microfabricated microfluidics chips with open channels.