The placenta in the integrated physiology of fetal volume control

Abstract

Almost all water that enters the conceptus of the sheep enters via the placenta. The forces that drive water are hydrostatic and osmotic. The placental channels that allow water to cross into the fetus have not been identified by microanatomic means. Although an “equivalent pore” system can account for the diffusional entry of small hydrophilic solutes, it can be calculated that the filtration coefficient of this system is too small to account for the demonstrated transplacental water flows. It is possible that a second much less numerous system of large pores permits the flow of water, but that is by no means certain. The placenta does not control the amount of water that enters the conceptus; nor does any other single fetal structure. And water entry is not dependent on the volume of water already present. However, the combined physiological properties of the fetal heart, kidneys, somatic tissues and placenta constitute a consistent explanation of fetal water volume control.

Introduction

The net number of molecules of water that are added to the conceptus per unit of time is far greater than the number of molecules of any other substance, including oxygen (Barcroft, 1946). Perhaps for that reason we were asked to review fetal hydration. But trans-placental flow of water is not controlled by a mechanism that holds the volume of water constant; water is not a master but a servant. The flow of water from mother to fetus is modulated to control the fetal circulation, regardless of the volume of water already present in the conceptus.

No single fetal organ controls fetal fluid volume. True, water flows into the fetus through the placenta since little water is exchanged at any other interface between mother and conceptus (Anderson et al., 1990). But trans-placental water flow is modulated by the fetal kidneys. The kidneys are not masters either, for they take their cue from fetal arterial pressure. Arterial pressure in its turn depends on fetal vascular resistance and that, in turn, depends on the fetal somatic blood flow, generated by the fetal heart. Finally, cardiac stroke volume and, therefore, output depends on the venous filling pressure. Thus, we are back to fluid volume. In this paper, we review how our own work led us to this view of volume control.

To understand how these players make a team we look at each of the players. Most of the experimental data presented here were obtained in sheep; exceptions will be noted. The words water, volume and fluid may be considered to be interchangeable.

First, the placenta

Trans-placental water transfer depends on the pressure that drives it and on the resistance to flow in the barrier. We avoid the term permeability for the reason that it is often used for different, unrelated, physical processes, such as diffusion, fluid flow or even electrical transport. The pressures that drive water transfer are hydrostatic pressures and osmotic pressures. The hydrostatic pressures are the pressures in the maternal and fetal capillaries of the sheep placenta or the pressures in the maternal intervillous space and the fetal capillaries of the human placenta. Those pressures must be lower than the corresponding arterial pressures, an obvious but important consideration in the regulation of trans-placental flow.

The osmotic pressures of interest are only the colloid osmotic (oncotic) pressures generated by the plasma proteins. Proteins cannot cross the placenta and exert their full van’t Hoff osmotic pressures and thus participate in the control of water. This was confirmed by direct experiment in guinea pigs (Anderson et al., 1982). It is true that crystalloid osmotic pressures can generate water flow also (Armentrout et al., 1977; Faber & Anderson, 1995), but crystalloids pass through the placenta (Boyd et al., 1976). Whatever small crystalloid gradients exist may be ignored because the associated water flows are insignificant in comparison to the flows generated by pressure and proteins.

The resistance to trans-placental fluid flow depends on the number, size, shape and length of the channels that let water through. When we provoked an excess water flow through the placenta of the sheep by means of crystalloid osmotic transients (Armentrout et al., 1977; Faber & Anderson, 1995), we found reflection coefficients of 0.85 for Na⁺ and 0.68 for Cl⁻ and a hydraulic conductivity (filtration coefficient) of the whole placenta of 1.02 × 10⁻⁷ cm⁵/(dyne sec), or 2.6 10⁻¹⁰ cm⁵/(dyne sec g) when expressed per gram placenta. From this we calculated that the equivalent pore radius (Curry, 1984) was between 0.35 and 0.44 nm. However, this is the pore radius of a population of small pores only.

It has been demonstrated in sheep that large trans-placental flows of fluid (consisting of water and dissolved crystalloids) can also be provoked by means of intravenous or intra-amniotic infusions of isotonic fluids of as much as 4 liters per day (Brace, 1989; Powell & Brace, 1991; Faber et al., 2005). Since these flows occurred in the absence of large changes in hydrostatic or colloid osmotic pressures, they cannot possibly be explained by a filtration coefficient as small as 1.02 10⁻⁷ cm⁵ /(dyne sec). This indicates the presence of a second set of parallel pores of a radius so much larger than 0.35 to 0.44 nm that crystalloids can freely pass and exert no osmotic pressure.

There already was a suggestion that there were two pore systems after Boyd and co-workers (Boyd et al., 1976) published diffusion permeabilities for a series of tracers of increasing molecular radii. The diffusion permeabilities of the two largest tracers (¹⁴C-mannitol and Cr-EDTA), although small, were still too high to be reconcilable with the diffusion permeabilities of the smaller molecules in a single cylindrical pore system. In the past, we ascribed the discrepancy to some loose label, being reluctant to embrace a complex explanation when a simple one might do and we tried to explain the gestational water needs of the conceptus on the basis of a single small pore system alone (Faber & Anderson, 1990). But after we reproduced the observations of Brace (1989) and Powell & Brace (1991) that large volumes of water and NaCl could flow between mother and conceptus (Faber et al., 2005), we had to concede that these observations couldn’t be reconciled with a single system of small channels across the placenta. There must be a second, parallel, system of passages of much larger size.

There are two quantitative measurements that allow an order of magnitude estimate to be made of the pore radius of the large pore system. First, there are diffusion permeabilities of ¹⁴ C-mannitol and Cr-EDTA measured by Boyd et al. (1976) and, second, there is the observation that 4 liters of isotonic fluid can pass across the barrier without large changes in vascular pressures or plasma protein concentrations. We interpret the second observation to mean that the driving force behind those water flows cannot have been more than 5 mm Hg and this suggests a large pore system with a filtration coefficient (Lp) of the order of1.7 10⁻⁸ cm⁵/(dyne sec g) when expressed per gram placenta. From these two facts one can construct 2 equations with two unknowns, one being the pore radius (r) and the other being (N/l), the ratio of the number of pores per gram placenta (N) and the length (l) of the pores. Thus, we arrived at an estimated radius of the large pore system of the order of 500 nm. The equations that relate the equivalent pore radius to diffusion permeability and filtration coefficient take more space than is available here but can be found in numerous publications (e.g. Curry, 1984). Since a pore radius of 500 nm is much larger than the molecular radii of plasma proteins that are known to not cross the placenta, there must be some sieve or net in series with the large pore system that filters out proteins but does not offer much other resistance. Unfortunately, the number of large pores per gram placental weight (N) cannot be calculated without knowledge of the lengths(l) of the large pores. We only know that the order of magnitude of the ratio N/l is 4.7 10⁷ cm⁻¹ g⁻¹. Powell and Brace (1991) postulated an increase in “permeability” near the venous end of the placental capillaries, which is an explanation similar to ours. But they did not quantify that increase. One caveat: The calculated values are subject to considerable uncertainty. Pore theory (Curry, 1984) is based on a number of geometric assumptions that are only approximately satisfied.

Now, the pressures that drive trans-placental flow: The reflection coefficients of plasma crystalloids in the large pore system are zero so the only osmotic pressures of consequence are the protein osmotic pressures (π); in addition there are the intravascular pressures (P), both maternal, m, and fetal, f, in the microvessels. Trans-membrane flow (Q), therefore, is given by Q=Lp(P_m-P_f -π_m+π_f ).

Adamson et al. (1989; 1992) measured the vascular pressures in various segments of the fetal placental circulation in sheep and found that angiotensin-II preferentially constricted the precotyledonary vessels. From this they drew the conclusion that angiotensin lowered the pressure in the fetal placental exchange vessels and that, therefore, angiotensin promotes transfer of fluid from the maternal into the fetal circulations. This conclusion is shown in graphical form in Fig. 1. There are other changes that could affect the pressures in the exchange vessels, such as fetal arterial and venous pressures. But when we infused angiotensin into sheep fetuses, we saw no increases in these pressures until well after the process identified by Adamson and her coworkers had run its course. Clearly the fetus has some control over its fluid supply and that control is exercised by the fetal kidneys. This is not too surprising since the same holds in the adult. That i.v. angiotensin infusion into the fetus can cause large increases in fetal fluid volume has been convincingly demonstrated (e.g. Faber & Anderson, 1994; Anderson et al., 1995).

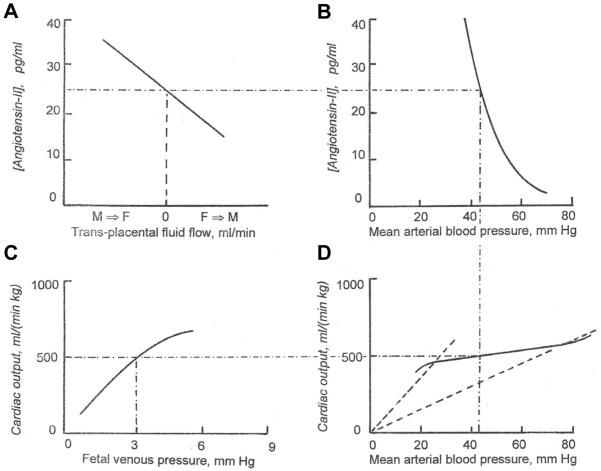
Fig. 1. Dependency of fluid exchange between maternal and fetal placental circulations on the concentration of angiotensin-II in fetal plasma.

The values for fluid exchange on the abscissa are not exactly known, except for the value of zero.

Role of the fetal kidneys

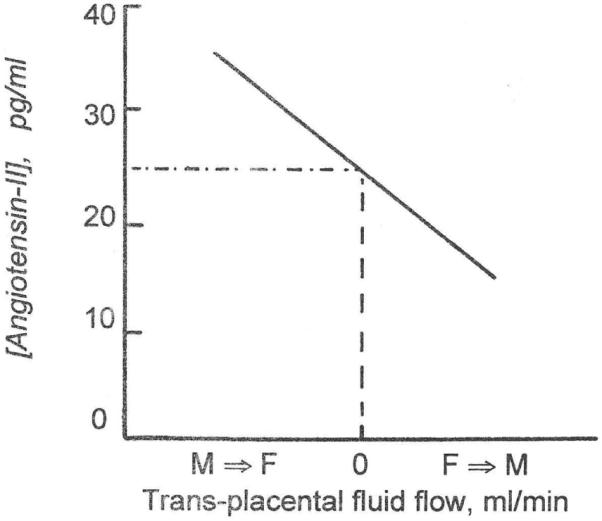
The active circulating autacoid, angiotensin-II, is generated by the familiar sequence of renin acting on angiotensinogen to produce angiotensin-I, which is converted into angiotensin-II in the blood vessels of the peripheral tissues. Binder and Anderson (1992) studied the sensitivity of the fetal kidneys to arterial pressure by placing an inflatable occluder on the fetal aorta immediately upstream of the renal arteries while recording downstream arterial pressure. They then made stepwise reductions of 15 minutes duration in fetal renal arterial pressure and took arterial blood samples to determine the resulting changes in fetal plasma renin activity. The results are shown in Fig. 2.

Fig. 2. Relation between fetal renal artery pressure and fetal plasma renin activity.

From Binder & Anderson, (1992). Note logarithmic ordinate.

Fig. 2 shows that the fetal kidneys are exquisitely sensitive to arterial pressure, so much so that the plasma renin activities were graphed on a logarithmic scale. As arterial pressure goes down, plasma renin activities increase. We have since found that the reverse is true also. When fetal arterial pressures were increased by infusion of sheep plasma into the fetal circulation, the circulating angiotensin-II concentrations showed steep declines (Faber et al., 2006; Giraud et al., 2005). Although plasma renin activity is not the same thing as plasma angiotensin-II concentration, the two are strongly and positively correlated. For this reason, the results of the experiments of Binder and Anderson are replotted as a relation between arterial pressure and angiotensin-II concentration in Fig. 3 for which we used the data of Giraud et al. (2005).

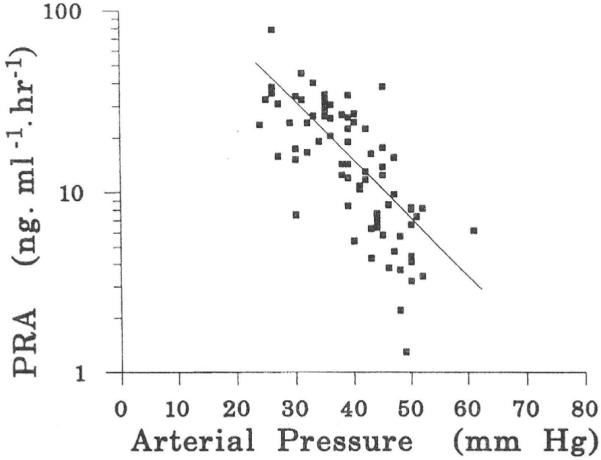
Fig. 3. Relation between fetal arterial blood pressure and fetal plasma angiotensin-II concentrations.

Numerical values are based on data from Giraud et al., 2005).

It should be noted that when Binder and Anderson placed the inflatable occluder on the aorta downstream from the renal arteries, pressure reductions did not result in responses in plasma renin activity.

Hemodynamic properties of the fetal heart

Fig. 1 interprets the hypothesis of Adamson et al.,1992) that when there is sufficient circulating fetal angiotensin-II it causes a net flow of fluid from the maternal plasma into the fetal circulation. The resulting expansion of fetal intravascular volume causes an increase in fetal venous pressure. The increases in venous pressure that result from volume expansion are small (Giraud et al., 2005), except in the extreme cases reported in Faber & Anderson (1994), but not insignificant.

It is known that the stroke volume of the fetal heart is sensitive to venous pressure (Thornburg & Morton, 1986), as it is in the adult heart (Fig. 4). Presumably, in the fetus also, this is an expression of the familiar Frank-Starling mechanism of cardiac striated muscle. In the long run, however, it may not be the Frank Starling mechanism that effects the response to increased diastolic filling for it is known that there is also an increase in fetal cardiac mass that correlates with improved cardiac performance (Pinson et al., 1991). This increase in mass is specially pronounced when there is also an arterial hypertension (Pinson et al., 1991; Jonker et al., 2007). An increase in fetal circulating volume, therefore, augments the output of the fetal heart. Fig. 5 is an adaptation of Fig. 4 showing the resulting relation between biventricular cardiac output and venous pressure.

Fig. 4. Experimentally determined relation between filling pressure and stroke volume in the fetal heart.

From Thornburg & Morton, (1986).

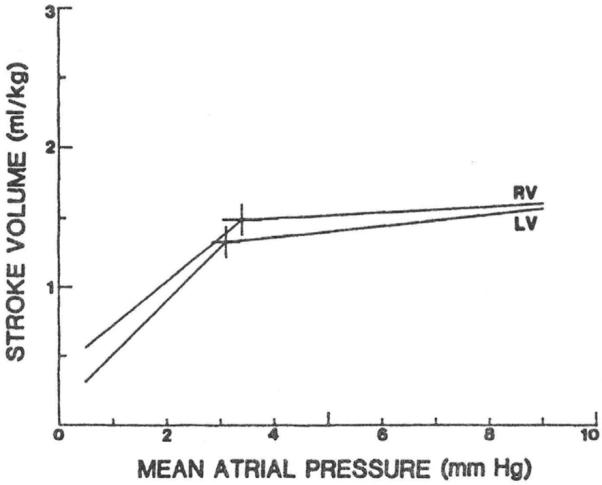
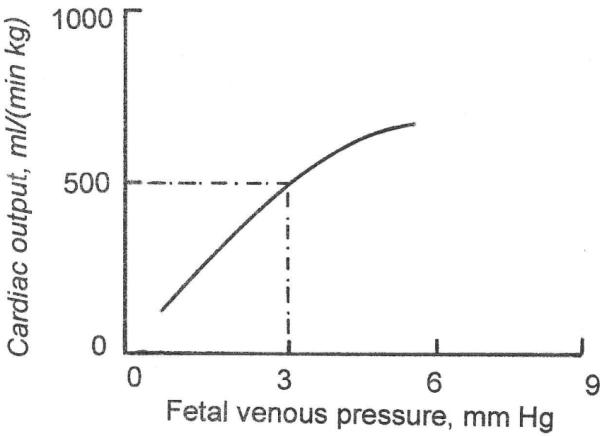
Fig. 5. Relation between fetal venous pressure and biventricular cardiac output, expressed per kg fetal weight.

At constant arterial oxygen content, an increase in cardiac output causes a disproportionate increase in arterial pressure (solid line). This signifies a resistance to flow that is much lower at low flows than at high flows (the sloped dashed lines are lines of constant resistance, low resistance at the left end of the curve and high resistance at the right end). Autoregulation translates minor changes in flow into large changes in pressure.

The somatic circulation of the fetus

The crux of the translation from intravascular volume to cardiac output and then to arterial pressure lies in the response of the peripheral tissues to changes in oxygen delivery, a response often referred to as autoregulation (Guyton et al., 1974). When oxygen delivery is excessive, as in the case of an excessive cardiac output, the resistance vessels constrict, whereas when oxygen delivery is deficient, the resistance vessels dilate. The corresponding changes in arterial pressure are visible only after a long time because short-term changes in pressure are counteracted by the carotid sinus baroreceptor mechanism. For this reason, there are few direct experimental confirmations of autoregulation, except in the coronary circulation where the response is immediate and vigorous.

The excessive flows associated with anemia or hyperthyroidism in the adult are convincing examples of autoregulation and it has been demonstrated that the response to fetal anemia, likewise, is a dramatic decrease in somatic resistance to flow (Davis & Hohimer, 1991). When arterial oxygen content is constant, autoregulation is evidenced by a disproportional relation between arterial pressure and flow, as in Fig. 6.

Fig. 6. Autoregulation of flow.

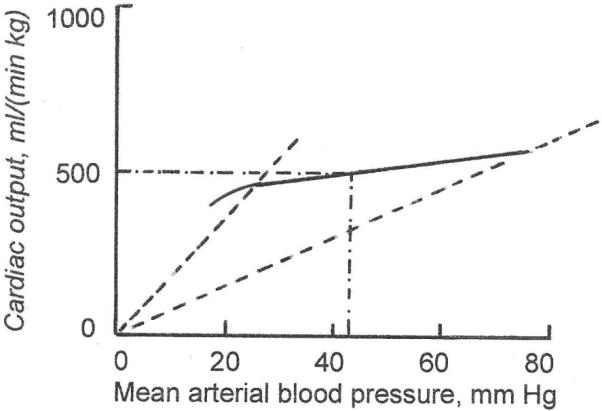
At constant arterial oxygen content, an increase in cardiac output causes a disproportionate increase in arterial pressure (solid line). This signifies a resistance to flow that is much lower at low flows than at high flows (the sloped dashed lines are lines of constant resistance, low resistance at the left end of the curve and high resistance at the right end). Autoregulation translates minor changes in flow into large changes in pressure.

The players as a team

Fig. 7 is a composite of the previous figures. First examine the steady state. A steady state implies that volumes, flows, pressures, resistances and angiotensin concentrations are all constant; all temporary changes have died out. The duration of pregnancy being what it is, a steady state is a reasonable assumption although, in reality, the fetal circulation may oscillate around a steady state because of spontaneous changes.

Fig. 7. Juxtaposition of Figs. 1,3,5,6.

The figure shows that the mechanisms are interdependent.

In a steady state, there must be zero net volume flow between mother and fetus. (The small flow associated with fetal growth will be dealt with below). Panel A of Fig. 7 shows that at zero net transplacental flow, fetal circulating angiotensin-II concentration must have a certain value, typically 25 pg/ml. Panel B shows that a value of 25 pg/ml implies that fetal arterial pressure must have a certain value also, typically 43 mm Hg (Giraud et al., 2005). The arterial pressure that governs angiotensin concentration in panel B is the same arterial pressure that applies to the autoregulation curve in panel C. Panel C then shows that, in order for there to be a steady state, the combined somatic and placental blood flow must have a certain value, typically about 500 ml/(min kg fetal weight). But the blood flow in panel C is the cardiac output of panelD. Panel D shows that for a cardiac output of 500 ml/(min kg), venous filling pressure must have a certain value also, typically 3 mm Hg. But a constant venous pressure implies a certain intravascular fluid volume, which, as demanded by a steady state, is also constant, in agreement with the zero net volume flow across the placental barrier that we stipulated above.

The self-steering nature of fetal circulatory control

It is our contention that water acquisition does not serve to ensure the constancy of water volume but, instead, ensures the proper functioning of the circulation. To illustrate this, assume that the (unknown) mechanism that regulates amniotic fluid volume goes awry and decides to regulate amniotic fluid volume at 1.5 liters instead of at the normal value of about half that. Initially the extra 750 ml must come from the fetal water volume since there is negligible direct exchange of amniotic fluid with the mother. The result is a decrease in fetal somatic fluid volume, intravascular volume, venous pressure, cardiac output, arterial pressure and hence an increase in fetal circulating plasma renin activity and angiotensin-II concentration. The increase in angiotensin-II promotes fluid transfer from the maternal circulation into the fetal circulation. This process reverses the consequences of the initial fluid loss and continues as long as fetal arterial pressure remains below its “prescribed” value (Fig. 7), but stops completely when the fetal circulation has completed the return to its steady state. Two conclusions follow: first the fluid volume of the conceptus is now 750 ml too large, hence placental water transport does not serve total conceptual water control. Second, the fetal circulation is back to its normal steady state, hence placental water transport serves the control of the fetal circulation. This is also an example of why we do not claim that the fetal circulation is always in a steady state but merely assert that it normally oscillates around that steady state, always trying to return to it.

Does the fetus have any leeway?

It may seem that we straight-jacketed the fetal circulation to an unreasonable degree but the fact that the fetal circulation is tethered to a steady state does not imply that it is always the same steady state. A good example is the study of Davis & Hohimer (1991), which demonstrated that when fetuses are made anemic, the resistance of the somatic circulation shows a substantial decrease, whereas somatic flow shows a substantial increase. This means that when we define the autoregulation curve as a relation between flow and pressure (Fig. 6), the anemic fetuses operated on a different (higher) autoregulation curve. For higher flows they had lower arterial pressures. Since in the study of Davis & Hohimer (1991) stroke volumes increased in the absence of demonstrable increases in venous pressure, this suggests that the cardiac function curves (Fig. 5) also no longer were the same. Another striking example of a changing function curve is found in the resetting of the renal sensitivity to arterial pressure that occurs in less than one week after birth, see Fig. 8.

Fig. 8. Relation between arterial pressure and plasma renin activity.

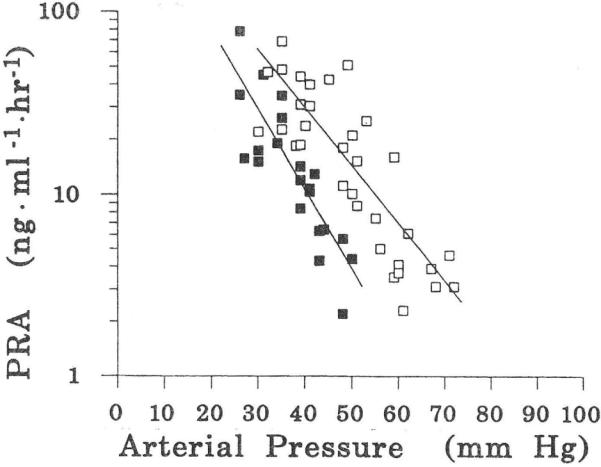
From Binder & Anderson, (1992). Filled symbols from 3 fetuses; open symbols from the same 3 fetuses as lambs in the 1^st week after delivery.

The ultimate steady state, therefore, is determined by the properties of the fetal heart, the fetal circulation, the fetal kidney and the placenta. Those properties are not invariant but, once set, they define a new steady state.

The non-steady state of pregnancy

As Barcroft (1946) emphasized, there is a continuous inflow of water into the conceptus, as needed for sustained growth. Strictly, there cannot be a true steady state. The net water flow in panel A of Fig. 7 is not zero, but slightly to the left of zero. Thus, the angiotensin-II concentration must be slightly higher, the blood pressure (panel B) slightly lower, the cardiac output (panel C) very slightly lower, and the venous pressure, (panel D) slightly lower also. However, it must not be concluded that because of the continuous inflow of fluid and increase in intravascular volume the venous pressure will start to rise. For as the fetus grows, so does its vascular bed, and venous pressure, therefore, remains the same. Nevertheless, as the heart grows, roughly in proportion to somatic growth, the same venous pressure generates a cardiac output that keeps up with the rate of fetal growth. The known small increase in arterial pressure with gestational age must mean, of course, a slowly changing renal function curve in panel B. Fig. 8 shows that such spontaneous changes in renal function curves are an observed phenomenon.

Last, but not least, the human placenta

The diffusion permeabilities of the hemochorial placentas as a group, the human placenta included, are very different from those of the sheep placenta. The pore radii must be much larger than those of the small pore system in the sheep placenta. The tracer inulin (with a molecular weight of 5200 dalton and a molecular radius of about 1.1 nm) passes readily through the barriers of the hemomonochorial placentas of the guinea pig (Thornburg & Faber, 1977) and the human (Thornburg et al., 1988), the hemodichorial placenta of the rabbit (Faber, 1995) and the hemotrichorial placenta of the rat (Faber, 1999). It is unknown, however, if the pore systems that account for the diffusion permeabilities of inulin and smaller molecules present a sufficient filtration coefficient for the required bulk transfer of water and nonprotein solutes. Proteins are known to cross hemochorial placentas in minute quantities only, if at all. Without firm experimental numbers for the filtration coefficients of these placentas we must leave that question to be resolved in the future.

Summary

Almost all water that enters the conceptus of the sheep enters via the placenta. The placental channels that allow water to cross into the fetus have not been visually identified. Although there appears to be an “equivalent pore” system that accounts for the diffusional entry of small hydrophilic solutes, it can be calculated that the filtration coefficient of this system is too small to account for the demonstrated trans-placental volume flows. The forces that drive the transit of water are believed to be hydrostatic and oncotic.

The placenta does not control the amount of water that enters the conceptus; nor does any other single fetal structure. And water entry is not dependent on the total volume of water already present. However, the combined physiologic properties of the fetal heart, kidneys, somatic tissues and placenta constitute a consistent explanation of fetal volume control.