Abstract
The size of dendritic spines and postsynaptic densities (PSDs) is well-known to be correlated with molecular and functional characteristics of the synapse. Thus, the development of microscopy methods that allow high throughput quantification and measurement of PSDs is a contemporary need in the field of neurobiology. While the gold standard for measurement of sub-micrometer structures remains electron microscopy (EM), this method is exceedingly laborious and therefore not always feasible. Immunohistochemistry (IHC) is a much faster technique for identifying biological structures such as PSDs, but the fluorescent images resulting from it have traditionally been harder to interpret and quantify. Here, we report on two new image analysis tools that result in accurate size and density measurements of fluorescent puncta. Anti-PSD-95 staining was used to target synapses. The new technique of vamping, using Volume Assisted Measurement of Puncta in 2 and 3 Dimensions (VAMP2D and VAMP3D) respectively, is based on stereological principles. The fully automated image analysis tool was tested on the same subjects for whom we had previously obtained EM measurements of PSD size and/or density. Based on highly consistent results between data obtained by each of these methods, vamping offers an expedient alternative to EM that can nonetheless deliver a high level of accuracy in measuring sub-cellular structures.
Keywords: Confocal microscopy, electron microscopy, image analysis, stereology, PSD-95, postsynaptic densities
INTRODUCTION
Converging evidence is pointing to a dichotomy in the structure and function of dendritic spines – the main sites of excitatory synaptic transmission in the brain – based on their size. Small spines are highly plastic while big spines are very stable (Kasai et al., 2010,Bourne and Harris., 2007). We have previously shown that a selective loss of small spines in the prefrontal cortex of aging rhesus monkeys is highly correlated with age-related cognitive decline, thus linking synaptic size to cognitive flexibility (Dumitriu et al., 2010). Spine head volume is proportional to the size of the postsynaptic density (PSD) (Harris and Stevens., 1989), which in turn is correlated with the number of AMPA receptors present and ultimately with synaptic strength (Nusser et al., 1998,Matsuzaki et al., 2001,Takumi et al., 1999,Noguchi et al., 2005); therefore, accurate measurement of the size of PSDs can result in a meaningful indicator of synaptic plasticity.
The PSD is the electron-dense aggregation on the postsynaptic side of all excitatory, i.e. asymmetric, synapses. The high density is due to an accumulation of proteins, such as scaffolding molecules, receptors and associated proteins, along with cytoskeletal elements. PSDs are usually disc-like (except in large mushroom spines with perforated or horseshoe-shaped synapses), and their size can vary depending on the species and brain region, but typically ranges from 200–800 nm in diameter and 30–50 nm in thickness (Chen et al., 2008,Kim and Sheng., 2009). By definition, accurate measurements of PSDs can only be accomplished with electron microscopy (EM). While technological advances have led to several new methods for automatic 3D reconstruction of EM, identification of dendritic spines and synapses continues to be manual and is therefore the rate-limiting method. Therefore, the time-consuming nature of unbiased synapse size and density using EM renders it unsuitable for large scale exploratory experiments.
One of the main components of the PSD is the protein PSD-95, a scaffolding molecule that links NMDA receptors to downstream signaling pathways (Sheng and Pak., 2000). PSD-95 is necessary for activity-driven synapse stabilization (Ehrlich et al., 2007). A PSD contains on average 300 PSD-95 molecules (Chen et al., 2005) evenly distributed throughout the entire disc (DeGiorgis et al., 2006). All adult PSDs contain PSD-95 (Petersen et al., 2003) while inhibitory (i.e. symmetric) synapses are not associated with PSD-95 (Aoki et al., 2001), making this molecule a good candidate for an immunohistochemical (IHC) marker of excitatory (i.e. assymentric) synapses.
While the IHC staining of fixed tissue is a well-established technique, the imaging and analysis of puncta is fraught with uncertainty. Brightfield microscopy lacks 3D resolution and standard manual stereological methods (Schmitz and Hof., 2005) are almost as time-consuming as EM. Labeling the puncta with fluorescent antibodies and imaging with laser scanning confocal microscopy (LSM) is a good alternative because of 3D resolution made possible by the pinhole, which rejects out-of-focus light. However, there is a surprising lack of tools for the reliable quantification of the size and density of fluorescent puncta. Most commonly, puncta are analyzed in either single images or 2D projections of confocal stacks. Each of these methods results in a different primary bias, the first toward overrepresentation of small synapses from the puncta that are transected by the optical section at their edges rather than centers, the latter toward overrepresentation of large synapses from superimposition of neighboring puncta.
Although 3D methods of analysis are available through both ImageJ and commercial software such as Metamorph (Molecular Devices), IHC material is not always suitable for them. In order for a 3D method to be employed, one must assume that the tissue is evenly stained throughout the entire depth of the section. However, with standard IHC sections, which are between 40–50 µm thick, antibody penetration is almost invariably uneven. Tissue is commonly over-stained on the surface from antibody stickiness and under-stained in the middle of the section due to limited antibody penetration. In order to avoid antibody penetration problems, tissue can be cut much thinner, at less than or equal to 10 µm, but this type of IHC is more difficult due the fragility of sections. Thus, an “ideal depth” of antibody penetration (usually around 5–10 µm below the surface, varying based on tissue, fixation and use of detergents) restricts the ability to employ true 3D methods. In addition, even in IHC protocols with even staining throughout the depth of the section, a method that can accurately estimate 3D size and density from a narrow z-stack saves the investigator significant time.
We therefore sought to develop tools that can perform accurate analysis of both size and density within a very narrow Z-depth range by mimicking the manual analysis performed in serial section EM for the measurement of true size of all PSDs contained in the reference (middle) section (Hara et al., 2010) and disector method for unbiased synaptic counts (Sterio., 1984). Importantly, the methods presented here differ considerably from conventional 3D methods available through for example ImageJ. Whereas currently available software use algorithms that measure puncta in real 3D, vamping utilizes stereological concepts (Schmitz and Hof., 2005) in order to extract 3D information from 2D data.
MATERIALS AND METHODS
2.1 Animals and tissue processing
Female rhesus monkeys (Macaca mulatta) were used for all experiments in this study. The monkeys were housed in colonies of ~ 40 individuals at the California National Primate Research Center, University of California, Davis. All experiments were conducted in compliance with the National Institutes of Health Guidelines for the Care and Use of Experimental Animals and approved by the Institutional Animal Care and Use Committee at the University of California, Davis. Details of monkey transcardial perfusion and low-temperature embedding of the brain tissue for EM are described elsewhere (Dumitriu et al., 2010,Hara et al., 2010,Hao et al., 2003). Briefly, monkeys were transcardially perfused with 1% paraformaldehyde in 0.1 M phosphate buffer (PB; pH 7.2) for 2 min, followed by 4% paraformaldehyde in 0.1 M PB at 250 ml/min for 10 min, after which the flow rate was reduced to 100 ml/min for 50 min. Tissue was postfixed for 6 hours in 4% paraformaldehyde with 0.125% gluteraldehyde in PB, prior to sectioning. From each animal, tissue was then processed in three different ways. Some sections were embedded for EM (400 µm thick) while others were collected for single cell microinjection with Lucifer Yellow (400 µm thick, stored in 0.12 M phosphate buffer saline [PBS], pH 7.2, until microinjection), or immunohistochemistry (50 µm thick, placed in cryoprotective solution containing 30% glycerol and 30% ethylene glycol in 0.02 M phosphate buffer (PB) and stored at −20°C until needed for experimentation).
2.2 Quantitative analyses of PSD length by EM
Sixteen consecutive ultrathin sections including the dentate gyrus (DG) were cut into 90 nm thick sections using a Diatome diamond knife (EMS, Hatfield, PA) and mounted on formvar-supported slot grids (EMS, Hatfield, PA). Ultrathin sections were examined using a Hitachi H-7000 transmission electron microscope (Hitachi High Technologies America, Inc., Pleasanton, CA) set at 75 kV. A series of electron micrographs were captured at 12,000X magnification in the OML of the DG using an AMT Advantage CCD camera (Advanced Microscopy Techniques, Danvers, MA).
The 4th, 8th, and 12th images were used as references and were identified to contain 102 asymmetric synapses, a sample size deemed to provide sufficient power for adequate estimates of PSD size for this animal. Each PSD was then followed throughout the series to measure its lengths in each section. No synapse spanned beyond the 16 sections. The maximum length for each PSD was recorded. The criteria to define a PSD included the presence of synaptic vesicles in the axon terminal and a distinct asymmetric density in the postsynaptic dendrite or spine. The ruler tool in Photoshop (version 7.0.1 Adobe Systems Inc.) was used to measure all PSD lengths, and the protractor tool was employed for curved PSDs.
2.3 Quantitative analysis of PSD density using the disector method
The disector method has been previously described in detail (Dumitriu et al., 2010,Sterio., 1984,de Groot and Bierman., 1986). Here, density counts were obtained from the CA1 region of the hippocampus of five monkeys. Briefly, twenty pairs of consecutive EM micrograph digital images were used from each of the five subjects (i.e. 100 pairs of serial sections were used in the density study). Only those axo-spinous or axo-dendritic asymmetric synapses contained in one but not both consecutive images were counted. The synapse profiles that appeared in both images were excluded. The included synapses were then divided by the total volume of the two images, which in this case was 20 µm3. No correction for shrinkage was included because it was impossible to measure the surface area of the embedded tissue secondary to microdissections. However, although the absolute amount of shrinkage might be different for EM versus IHC tissue, the objective of this study is to demonstrate a tight correlation between values obtained with each method and not to compare absolute raw values from EM synapses and IHC puncta. The differential shrinkage between the two methods is unlikely to affect the correlation coefficients or p-values.
2.4 Immunohistochemistry
Sections were thoroughly rinsed in 0.01 M PBS, pH 7.2, overnight to completely remove glycerol and ethylene glycol storage solution. The following day, free-floating sections were serially washed (4 × 7 min) in 0.01 M PBS with 0.3% Triton-X 100 (Sigma, St. Louis, MO). Sections were blocked in 0.01 M PBS containing 0.3% Triton-X 100 (Sigma, St. Louis, MO) with 5% bovine serum albumin (Sigma, St. Louis, MO) for 1 hr at room temperature (rt). Free-floating sections were incubated in polyclonal goat anti-PSD-95 primary antibody (ab12093, Abcam, Cambridge,MA) diluted to 5 µg/ml (1:200) in the above described blocking buffer for 24 hrs at rt. Sections incubated without primary antibody were also included as negative controls. All sections were then washed (4 × 7 min) in 0.01 M PBS with 0.3% Triton-X 100, and incubated in secondary Rabbit Anti-Goat IgG (H+L) DyLight 488 AffiniPure antibody (Jackson ImmunoResearch, Suffolk, UK) diluted 1:200 in 0.01 M PBS with 0.3% Triton-X 100 and 2% bovine serum albumin for 1 hr at rt. Sections were then washed (4 × 7min), stained with 4,6-diamino-2-phenylindole (DAPI), a fluorescent nucleic acid stain (Sigma), mounted, and coverslipped with VECTASHIELD mounting medium (Vector Laboratories, Burlingame, MO).
In order to ensure the specificity of the anti-PSD-95 primary antibody, a peptide absorption control was performed by pre-incubation of anti-PSD-95 with 10 µg/ml PSD-95 peptide (ab12419, Abcam, Cambridge,MA). The IHC protocol described above was then run using the pre-absorbed antibody next to a positive control (i.e. no peptide pre-absorption). While regular staining was observed in the positive control, only sparse and very faint puncta appeared in the peptide absorption control (red arrows) when images were taken with the exact same parameters (see Supplemental Figure 1A). The faint puncta in the pre-absorption control are presumably non-specific staining. Based on sequence homology, it is possible that the antiserum also recognizes the two MAGUK proteins DLG4 and SAP-95; however, both of these also localize to the PSD and therefore should not alter the specificity of the staining. Importantly, the faint staining in the pre-absorption control did not reach the fluorescence intensity at which we set the threshold for the puncta in our study (see Supplemental Figure 1B). Additionally, PSDs contain on average about 300 molecules of PSD-95 (Chen et al., 2005), and it is therefore likely that our protocol isolates only synaptic PSD-95, since extrasynaptic (i.e. cytoplasmic) molecules would not be clustered in such a tight space as to reach the threshold for fluorescence intensity.
2.5 Confocal microscopy of fluorescent puncta
Images of PSD-95 immunofluorescence were taken from the outer molecular layer (OML) of the DG for testing VAMP2D and from the CA1 stratum radiatum, defined as 150 µm from the pyramidal cell body layer, for testing VAMP3D. The region of interest was identified under low magnification (10×) using the DAPI stain. Images were captured using an inverted Zeiss 510 Confocal Scanning Laser Microscope (CLSM) (Zeiss, Oberkochen, Germany), using a Zeiss 100× 1.4 numerical aperture (N.A.) oil-immersion objective and a 5.0X digital zoom. Confocal z-stacks of 2 µm thicknesses were taken with a z-step of 0.1 µm at 512 × 512 pixels (final pixel resolution 0.033×0.033×0.1 µm3), and a frame average of 4. All Z-stacks were captured from the depth of 4 to 6 µm below the surface to ensure that sampling was done from the same level of antibody penetration for all animals. In order to further minimize the difference in fixation and antibody penetration, the gain and offset for the images from each animal were chosen by using the “find” function of the LSM software, which uses an algorithm that optimizes the gain and offset such that the entire dynamic range is captured (i.e. gain and offset are chosen so that the brightest one or two pixels are assigned the maximum intensity of 255 on an 8-bit scale, while the dimmest one or two pixels are assigned the minimum intensity of 0). In applications in which an estimate of fluorescence intensity of puncta is of interest, the same gain and offset must be used for all subjects. However, in our application, size and density are the variables of interest, so an equalization of intensity is desired. A total of 16 z-stacks were acquired for each animal. Confocal stacks were deconvolved using AutoDeblur software (version 8.0.2; Autoquant, Troy, NY).
2.6 Single cell microinjections and quantification of spine density
Our lab routinely uses the technique of single cell microinjection and high resolution imaging of dendritic spines. Detailed methods have been described elsewhere (Dumitriu et al., 2011). Briefly, pyramidal cells in fixed sections of the CA1 region of the monkey hippocampus were microinjected with LY using negative current to eject the dye from a glass pipette. Dendrites from cells filled evenly to their tips (2–6 cells per animal and 6–18 dendrites per cell) were imaged in 3 dimensions using an inverted Zeiss LSM 510 confocal microscope equipped with a Plan-Apochromat 100×/1.4NA oil-immersion objective, at a voxel size of 0.033×0.033×0.1 µm3. Confocal z-stacks were deconvolved using AutoDeblur software (version 8.0.2; Autoquant, Troy, NY) and spines were detected and quantified semi-automatically using NeuronStudio (http://research.mssm.edu/cnic/help/ns/index.html).
2.7 Programing
VAMP2D and VAMP3D were originally programmed in MatLab and subsequently translated into JAVA as ImageJ plugins. Plugins are available at http://rsb.info.nih.gov/ij/plugins/vamp/index.html.
2.8 Image analysis
All image analysis was performed in ImageJ. Manual unimodal thresholding was used (Rosin., 2001) (see Supplemental Figure 2). This method is preferable for cases in which the number of pixels constituting the background largely outnumbers the number of pixels that constitute the signal, therefore creating primarily a unimodal distribution of gray values with a right-sided tail. In order to visualize the tail of the distribution better, we used the log of the gray scale histogram. Unimodal thresholding involves drawing a line between the mode of the gray scale distribution (highest peak) and the end of the tail (Supplemental Figure 1B). From this line, a second, perpendicular line is then drawn towards the gray scale histogram; this line is chosen such that it is the longest line possible. The gray level at which the perpendicular line intersects the gray scale is noted and used as the threshold (Supplemental Figure 1C). Following vamping, stacks were collapsed into 2D projections and puncta diameters and counts were evaluated using the “analyze particle” function in ImageJ.
2.9 Statistics
Group data are expressed as mean±standard error of the mean (SEM). A combination of Excel, MatLab and SPSS were used to perform all analysis.
RESULTS
VAMP2D was developed for size measurements, while VAMP3D was developed for density counts. IHC for PSD-95 was performed on tissue from monkeys for which we had previously obtained synaptic indices by EM using serial sections and/or the disector method (Hara et al., 2010,Hao et al., 2006). For VAMP2D, the DG of the hippocampus was processed for IHC and images were taken from the OML. For VAMP3D, the CA1 region of the hippocampus was used and imaging was performed in stratum radiatum, defined as 150 µm from the cell body layer.
3.1 VAMP2D for accurate size measurement
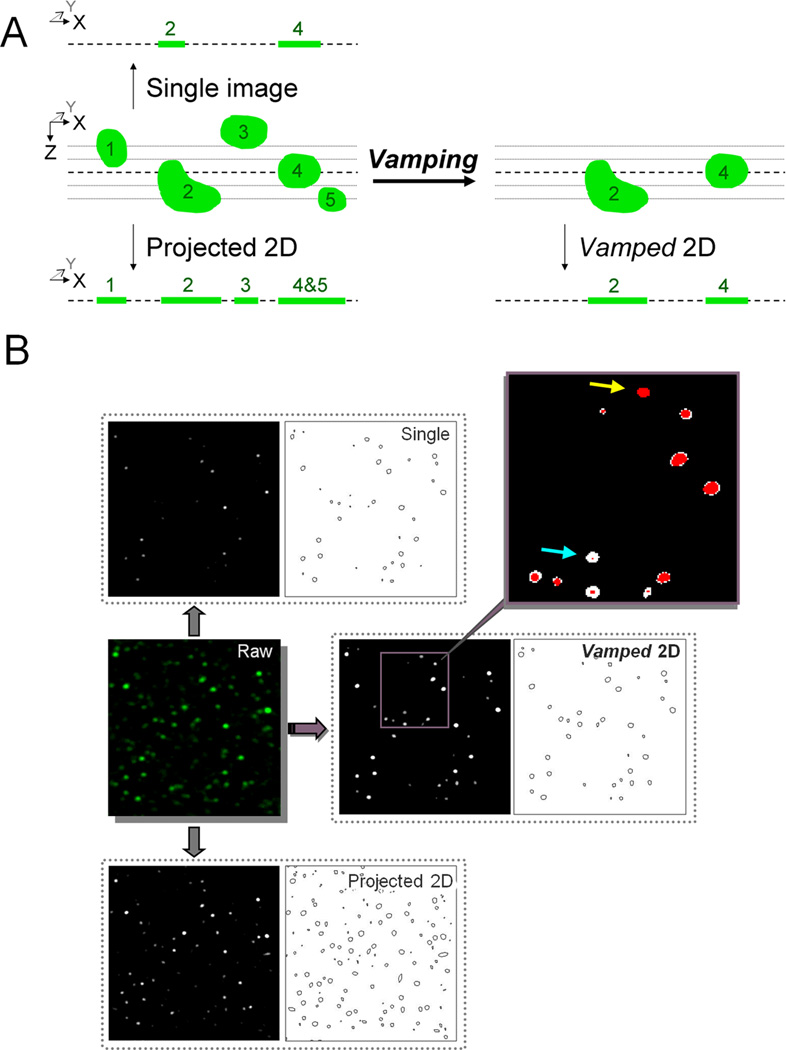
Figure 1A shows a graphical representation of the biases that vamping seeks to circumvent. Punctum 2 appears smaller than punctum 4 in the single image, even though the reverse size relationship can be found in the original 3D stack. Using a traditional 2D projection results in an accurate representation of the size of punctum 2; however, puncta 4 and 5 are now superimposed. In addition, punctum 3 has been included and incorrectly appears smaller than punctum 1. Vamping avoids both the problem of accurate size as well as the problem of superimposition, by removing material that is not transected by the middle layer. The new vamped Z-stack can then be used for 3D measurements or collapsed into a 2D projection for simpler analysis of diameter. Figure 1B shows an example of the data that result from each type of analysis. Note that in the case of both the single image and the projected 2D, there are many tiny specks that are virtually absent in the vamped 2D. Further note that each punctum is treated uniquely; puncta that are at their greatest diameter in the original middle layer remain intact (yellow arrow), while puncta that barely touch the middle layer are enhanced to their true diameter (blue arrow).
Figure 1. Methodological flow diagram for analysis of puncta.
Vamping is compared to evaluation of size in a single image or traditional 2D projection. A. Schematic representation of the biases that vamping seeks to avoid. The analysis of single 2D images results in an overrepresentation of small puncta while projected 2Ds will contain puncta that have superimposed with others. B. Example of a stack treated by the various methods. The vamped image contains less minute puncta compared with other methods. In the inset, red pixels represent voxels from the reference layer of the stack and white pixels represent material pulled in by VAMP2D. Note that there are no white pixels that are not connected to at least one red pixel, indicating that VAMP2D does not pull in material randomly. Further note that each puncta is treated uniquely, with those at their greatest diameter in the reference layer remaining intact (yellow arrow), while those that barely touch the reference layer are enhanced to their greatest diameter (blue arrow).
3.2 The vamping algorithm
Vamping seeks to mimic the process of manually searching for the true size of a PSD that is present in a reference image (fig 2A). Let’s assume that investigator looks at a 2D image of puncta (the reference image) from a small Z-stack and sees 10 puncta of varying sizes. As explained above and shown in figure 1, the 10 puncta might or might not be captured at their maximum size in this reference image. Therefore, an investigator who wishes to know the true size of each punctum will scroll up and down through the z-stack to see where each of the 10 puncta measures the largest. This would have to be done stepwise for each punctum, meaning the investigator will first focus his/her attention on punctum #1, scroll up and down in the Z-stack until the image where this punctum is found to be the largest is found, record the size of punctum #1, then proceed with the same steps for punctum #2 and so on.
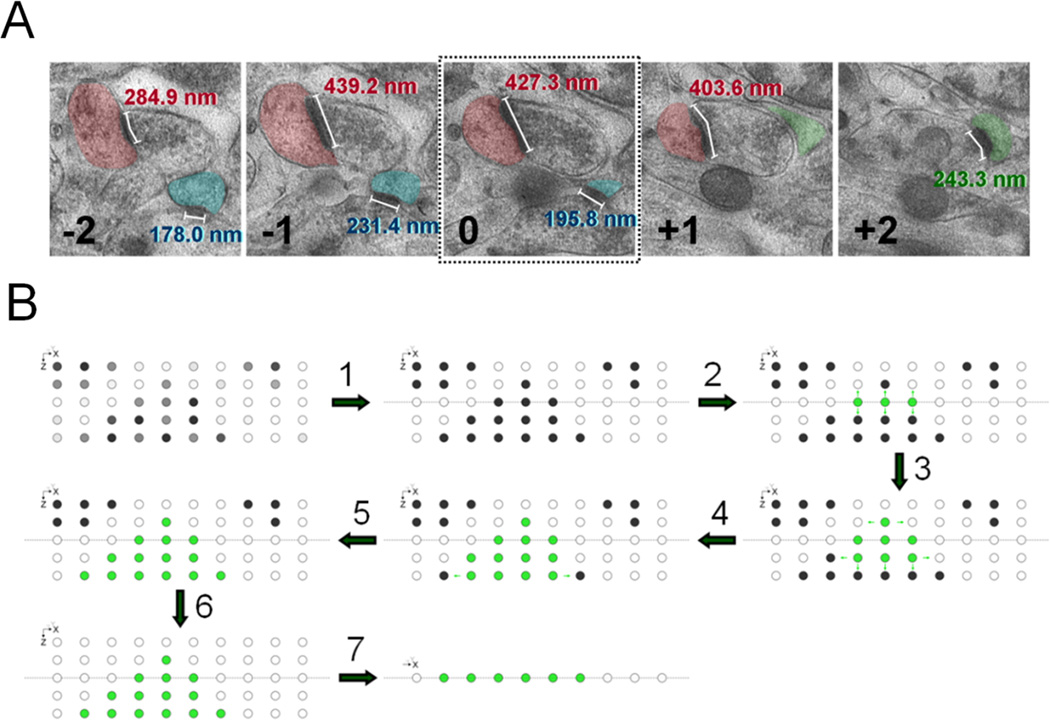
Figure 2. VAMP2D mimics manual serial section EM through the use of a connected threshold algorithm.
A. The most accurate synapse measurements are done by serial section EM. A researcher starts by marking all PSDs that are present in the reference layer (number 0). The length of a marked PSD is measured in each section that it appears in. The final size of the PSD is then recorded as the maximum length found in any of the consecutive images. In the accompanying example, section −1 contains the maximum length for both the red and blue synapses. Synapses not present in the reference layer, such as the green PSD, are excluded. B. VAMP2D starts at a reference layer by marking all pixels above threshold (steps 1 and 2). Both the reference layer and the threshold are user-inputted. The algorithm then travels up and down through the layers searching for pixels that are both connected to the original reference layer pixels as well as above threshold (steps 3–5). When no more connected pixels are available, VAMP2D sets the remaining pixels to zero (step 6). Analysis can then be performed volumetrically in the vamped stack, or in a vamped 2D projection (step 7).
Vamping achieves the above process automatically by using a connected threshold algorithm. The program starts in a reference layer (inputted by user, usually middle image) of a Z-stack and selects all available pixels above an inputted threshold (steps 1 and 2 in fig 2B). These pixels represent all puncta that are present in the reference layer. The algorithm then travels up and down through all layers stepwise, searching for pixels that are both above the threshold and “connected” to the original puncta in the middle layer (steps 3–5 in fig 2B). Here, “connected” means a pixel that has the same x,y coordinates as a pixel in the reference image, at a z coordinate that is either z+1 or z−1 from the reference image. Before moving to the next layers (z+2 and z−2), the algorithm now searches for connected pixels within layers z+1 and z−1 by looking for additional pixels above threshold at x+1, x−1, y+1, and y−1 from newly detected pixels within these two layers (z+1 and z−1). The process then continues by searching for connected pixels at z+2 and z−2. (Note that only pixels from layer z+1 can be connected to pixels from z+2, and only pixels from z−1 can be connected to pixels at z−2.) Once all connected pixels have been extracted, all other voxels are set to zero intensity (step 6 in fig 2B). The result of this final step is that all puncta that exist within the z-stack but do not “touch” the reference layer, are removed. The resulting stack can then be utilized for 3D analysis or collapsed into a vamped 2D (step 7 in fig 2B). It is important to notice that the process of vamping only works for relatively spherical objects. A complex shape cannot be accommodated since the algorithm never “goes back,” meaning once it has found all connected pixels in for example the image z+3, it does not search for additional connected pixels in z+2.
3.3 Testing VAMP2D against known density data obtained by EM
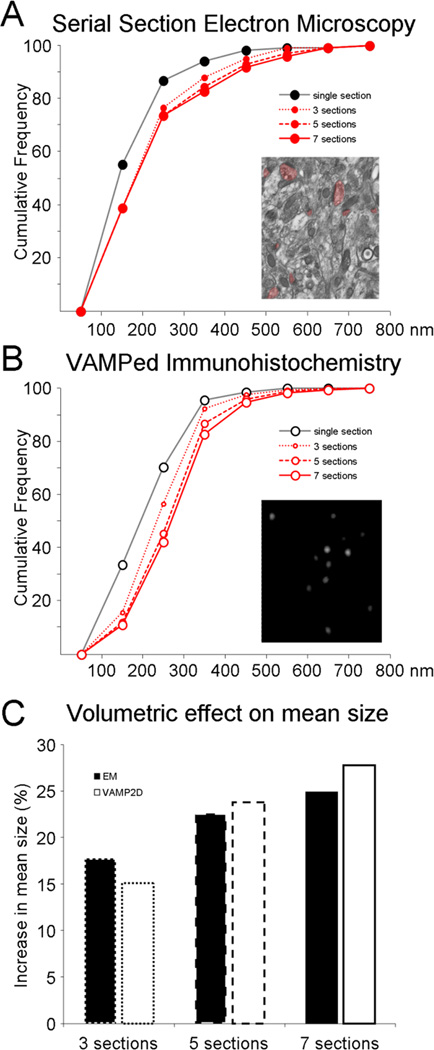
The size of 102 PSDs, including both axo-spinous and axo-dendritic asymmetric synapses, was measured using images of a series of 16 consecutive 90 nm slices from the DG OML. Figure 3A shows the cumulative frequency of the maximum length of PSDs in the reference image and when consecutively more slices in the series were used to get a more precise measurement of the true size of each PSD present in the reference section. Here, as explained above in section 3.2, “true size” is defined as the actual maximum length of a PSD as opposed to its length as it appears in any particular section. Note that true size is 2D as we are not accounting for PSD elongation in the z-direction. For our material, the true PSD size had been reached by the time a max of three images were searched in both directions, meaning that for the monkey DG OML, series of seven sections are needed for the most accurate representation of PSD size. Note that the optimal number of sections will depend on average and maximum size PSDs in the material used, meaning that more sections are needed in brain regions with large synapses, while three sections might suffice for e.g. mouse DG.
Figure 3. Comparison of size data obtained with EM versus vamping respectively.
The length of PSDs (nm) as measured by serial section EM (A) was compared to anti-PSD-95 puncta size using vamping (B) in the DG of the same animal. Cumulative distributions are plotted for size of synapses/puncta in single sections and when evaluated in 3, 5, or 7 consecutive images. C. The resulting increase in mean synapse size for EM (black bars) and punctum size for vamping (white bars) is plotted when using 3 sections (dotted line bars), 5 sections (dashed line bars), and 7 sections (solid line bars).
The same type of analysis was then performed using vamping of 1280 fluorescent puncta representing PSD-95 in the same animal and same region of the DG imaged at 100 nm optical sections on a confocal microscope (fig 3B). The increase puncta size with each additional pair of optical sections around the reference image follows a similar, albeit not identical, trend to the EM data. The EM versus vamping curves primarily differ from each other for really small puncta (less than approximately 250 nm), a consequence of the resolution limit of light microscopy (see Discussion). The average increase in size of PSDs and PSD-95 puncta when evaluated in 3, 5, or 7 consecutive images respectively is plotted in figure 3C. With seven sections, the mean increase in synapse size is 25% (from 214±11 nm to 268±14 nm, n=102 PSDs) when evaluated by serial section EM and 27% (from 212±2 nm to 269±2 nm, n=1280 puncta) when evaluated with vamped IHC.
3.4 VAMP3D for accurate density measurements
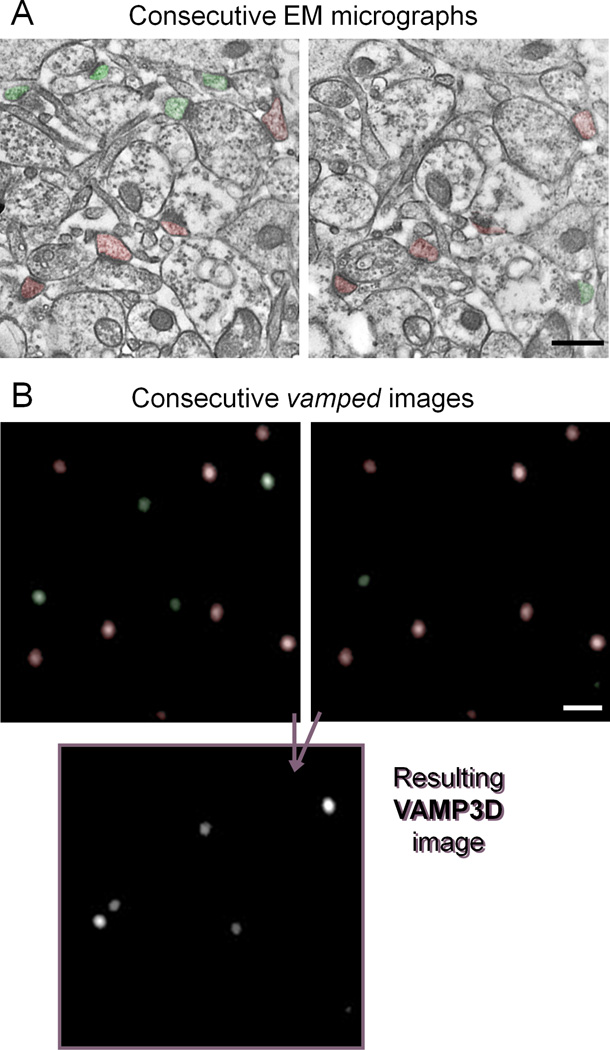
The disector method was developed decades ago for density quantification not biased by the size, shape, or orientation of the objects of interest (Sterio., 1984,de Groot and Bierman., 1986). Since then, it has been used as the gold standard of density measurements in EM. Two consecutive micrographs are used and only asymmetric synapses that are present in one but not the other image are counted (in fig 4A green are counted and red are excluded). The resulting total number of synapses is then divided by the combined volume of the two sections. VAMP3D performs a similar analysis using an “OR-NOT-AND” algorithm (fig 4B). Consecutive images are first vamped using the VAMP2D protocol. The program then removes the puncta that appear in both sections by arithmetic subtraction (red in fig 4B) and adds together the remaining puncta (green in fig 4B), resulting in a final Z-stack that contains only puncta that are present in one but not the other of two consecutive reference images. Notice that there is actually one important difference between the final VAMP3D and the EM disector: the puncta remaining after VAMP3D are actually vamped and therefore represent their true size and shape (though this is of course dependent on using an appropriate size stack). VAMP3D can use any size stack (minimum 2 images), and the reference images are user inputted.
Figure 4. VAMP3D mimics the disector method by an “OR-NOT-AND” function.
A. The gold-standard for evaluation of synaptic density is the disector method which seeks to avoid biases created by differences in size and orientation of PSDs (Sterio., 1984). Two consecutive sections are used and only synapses present in one but not the other image are counted (here, green are counted, red are ignored). The resulting total number of synapses is divided by the combined volume of the two sections. B. VAMP3D mimics the disector method by first vamping two consecutive layers of a stack through the same total volume. The program then removes the puncta that appear in both sections (red) and adds together the remaining ones (green).
3.5 Testing VAMP3D against known size data obtained by EM and single cell microinjection
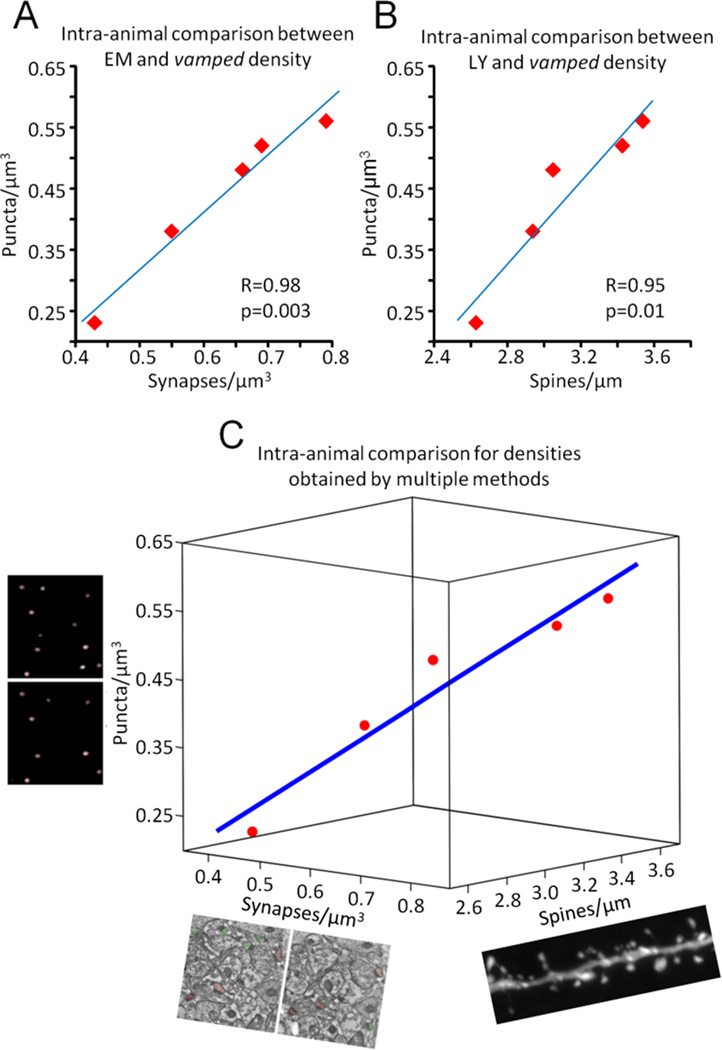
Five monkeys for which we had previously obtained density measurements from the CA1 SR layer with both EM using the disector method and by single cell microinjections followed by NeuronStudio analysis for spine density were chosen for IHC against PSD-95 followed by density vamping. VAMP3D densities correlated remarkably well with both EM (fig 5A, Pearson’s R=0.98, p=0.003) as well as with spine density (fig 5B, Pearson’s R=0.95, p=0.01). Figure 5C shows the 3-way correlation between all three methods using multiple regression analysis. The Kendall’s W, a measure of the concordance between more than two variables, was equal to 1.00 with a p-value of 0.007.
Figure 5. Intra-animal comparison of densities obtained with vamping, disector EM, and NeuronStudio counts of dendritic spines.
Quantitative synapse, puncta and spine densities were obtained from the hippocampal CA1 SR region of five monkeys. A. Correlation between vamping and EM. B. Correlation between vamping and NeuronStudio analysis of spine density along dendrites. C. Three dimensional plot of the concordance between all methods. Blue line in C is the linear fit following multiple regression analysis. Kendall’s W (coefficient of concordance) = 1.0, p=0.007.
Overall, puncta densities were 30% lower than their equivalent synaptic counterparts (mean=0.62 spines/µm3 synapses by EM versus mean=0.43 spines/µm3 puncta with vamping). In order to ascertain whether or not this was a true difference in density, e.g. caused by insufficient labeling by the antibody against PSD-95, we looked at the number of synapses/puncta that were included in the counts from each consecutive set of micrographs. Recall that the disector method involves counting only synapses/puncta contained in one but not both consecutive images; therefore, the greater the proportion of synapses/puncta that appear in both consecutive images, the smaller the proportion of synapses/puncta will be included in the density measure. We found that in EM an average of 48±1% synapses from a series of two micrographs where included (range 26–76% in 93 sets of micrographs), whereas vamping included an average of 38±1% puncta from each stack (range 25–63% in 80 stacks). This significantly lower inclusion by vamping (21% decrease between EM and vamping, p=1×10−7) could indeed account for most of the difference in absolute density found with each method, and likely results from properties of the point spread function in confocal microscopy (see Discussion).
DISCUSSION
We have introduced two new analytic tools for the automated quantification of puncta size and density and tested them by measuring PSD-95 puncta as proxies for asymmetric synapses. When compared to data obtained by EM, vamping produces highly accurate measures for both size and density of PSDs. The striking correlations with EM measures for both VAMP2D and VAMP3D provide strong evidence for the usefulness of vamping as a high-throughput alternative to slower techniques such as serial section EM (Hara et al., 2010) or stereology (Schmitz and Hof., 2005).
One marked difference between EM and vamping is percent included objects by the disector method. A potential explanation is incomplete staining due to inadequate antibody penetration or access to antigen. Alternatively, the lower density in vamping could be a result of the point spread function of confocal microscopy, which yields objects smeared in the Z-direction (Kozubek., 2001). As a consequence, more Z-smeared puncta will be present in two consecutive vamped images, and accordingly, lower densities will be recorded due to more stringent inclusion of puncta by the disector method. Indeed, the high level of concordance between the relative densities found by vamping, EM and NeuronStudio indicates that the latter explanation is the more likely reason for the observed differences in absolute densities.
The Rayleigh limit of resolution, which is on the order of 200 nm (Kozubek., 2001), also contributes to aspects of results presented here. Our average puncta size in a single image of the DG was 212 nm, and in fact, this average is comprised of almost half of the 1280 puncta measuring below 200 nm. Yet the average size of the IHC puncta was highly consistent with average sizes of PSDs, both in single images, as well as in terms of the increase in size with vamping (fig 3). How can we obtain accurate sizes in spite of being below the resolution limit? This is a consequence of global thresholding. Small synapses have less PSD-95 (DeGiorgis et al., 2006,Petersen et al., 2003), which results in a smaller number of antibodies binding to the PSD, and therefore fewer photons emitted from that synapse. The end result is fewer voxels with gray levels above the threshold.
EM remains the gold standard in evaluating synaptic size and density in fixed brain tissue (Mishchenko et al., 2010). However, the enormous time commitment required by serial section EM, in combination with the lack of automated image analysis software [though some semi-automated approaches are becoming available (Chklovskii et al., 2010)], renders this technique too laborious to use except in cases with highly developed and compelling hypotheses. Consequently, exploratory approaches of multiple brain regions (e.g. effects of aging on the whole brain) and subregions (e.g. different layers of the cortex) are not feasible using EM. The alternative of IHC against a postsynaptic marker such as PSD-95 is both simple and rapid. Although 3D image analysis can be performed through ImageJ as well as commercially, to the best of our knowledge no software package can accurately perform 3D size and density analysis on tissue where the staining is optimal only within the first 5–10 µm below the surface. In addition, we have not identified any other software package that can perform stereologic functions such as density measures using the disector method. Thus, vamping opens up the possibility of both accurate and high-throughput pilot studies that can guide follow-up EM analyses in selective regions, subregions or models.
Although not directly tested in the present study, the methods described here can be generalized to other types of material as long as the following requirements are met: the immunolabeling spans the entire structure of interest; the staining is evenly distributed within each structure; the objects are sparse enough not to regularly overlap with one another; a Z-stack spanning the space of the maximum size object of interest is available for imaging; and the immunolabeling throughout the imaged space is constant (i.e. not affected by antibody penetration differences). Examples of other suitable material at different levels of resolution are mitochondria stained with MitoTracker (Shrivastava et al., 2011), nuclei stained with DAPI, and somas of specific cell-types as identified by appropriate markers [microglia using e.g. CR3/43 (Graeber et al., 1994), specific subpopulations of interneurons using e.g. anti-parvalbumin (Liodis et al., 2007), recently activated cells using e.g. anti-c-Fos (Berton et al., 2006)]. Certain pathological markers such as those against beta amyloid (Reilly et al., 2003) could also be punctate enough for quantification using vamping, offering a high throughput approach to screening for increases in plaque size and/or density in various brain regions in Alzheimer’s disease models.
Supplementary Material
Highlights.
We developed stereology-based automated tools for measurement of fluorescent puncta
VAMP2D measures puncta size
VAMP3D quantifies puncta density
Vamping was validated against electron microscopy on same subjects
Acknowledgements
This work was supported by NIA grants AG 006647 (JHM) and AG 010606 to (JHM) and NRSA training grant 1F30MH083402 (DD).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributions:
All authors contributed to the preparation of the manuscript. DD originally conceptualized vamping, performed some immunohistochemical experiments, analyzed data, made the figures and wrote the initial draft of the manuscript. SIB programmed vamping in MatLab and JAVA. CH performed the rest of the immuhistochemical experiements and analysis. YH performed the EM counterpart to VAMP2D. MB performed the EM counterpart to VAMP3D. YG and WGJ provided technical assistance with animal care, protocol development, imaging and analysis throughout the study. JHM provided guidance throughout the experimental phase and improved the manuscript.
Contributor Information
Dani Dumitriu, Email: dani.dumitriu@mssm.edu.
Seth I. Berger, Email: seth.berger@mssm.edu.
Carine Hamo, Email: carine.hamo@gmail.com.
Yuko Hara, Email: yuko.hara@mssm.edu.
Megan Bailey, Email: megan.bailey@mssm.edu.
Yael S. Grossman, Email: whygrossman@gmail.com.
William G. Janssen, Email: bill.janssen@mssm.edu.
John H. Morrison, Email: john.morrison@mssm.edu.
References
- Aoki C, Miko I, Oviedo H, Mikeladze-Dvali T, Alexandre L, Sweeney N, Bredt DS. Electron microscopic immunocytochemical detection of PSD-95, PSD-93, SAP-102, and SAP-97 at postsynaptic, presynaptic, and nonsynaptic sites of adult and neonatal rat visual cortex. Synapse. 2001;40:239–257. doi: 10.1002/syn.1047. [DOI] [PubMed] [Google Scholar]
- Berton O, McClung CA, Dileone RJ, Krishnan V, Renthal W, Russo SJ, Graham D, Tsankova NM, Bolanos CA, Rios M, Monteggia LM, Self DW, Nestler EJ. Essential role of BDNF in the mesolimbic dopamine pathway in social defeat stress. Science. 2006;311:864–868. doi: 10.1126/science.1120972. [DOI] [PubMed] [Google Scholar]
- Bourne J, Harris KM. Do thin spines learn to be mushroom spines that remember? Curr.Opin.Neurobiol. 2007;17:381–386. doi: 10.1016/j.conb.2007.04.009. [DOI] [PubMed] [Google Scholar]
- Chen X, Vinade L, Leapman RD, Petersen JD, Nakagawa T, Phillips TM, Sheng M, Reese TS. Mass of the postsynaptic density and enumeration of three key molecules. Proc.Natl.Acad.Sci.U.S.A. 2005;102:11551–11556. doi: 10.1073/pnas.0505359102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Winters C, Azzam R, Li X, Galbraith JA, Leapman RD, Reese TS. Organization of the core structure of the postsynaptic density. Proc.Natl.Acad.Sci.U.S.A. 2008;105:4453–4458. doi: 10.1073/pnas.0800897105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chklovskii DB, Vitaladevuni S, Scheffer LK. Semi-automated reconstruction of neural circuits using electron microscopy. Curr.Opin.Neurobiol. 2010;20:667–675. doi: 10.1016/j.conb.2010.08.002. [DOI] [PubMed] [Google Scholar]
- de Groot DM, Bierman EP. A critical evaluation of methods for estimating the numerical density of synapses. J.Neurosci.Methods. 1986;18:79–101. doi: 10.1016/0165-0270(86)90113-5. [DOI] [PubMed] [Google Scholar]
- DeGiorgis JA, Galbraith JA, Dosemeci A, Chen X, Reese TS. Distribution of the scaffolding proteins PSD-95, PSD-93, and SAP97 in isolated PSDs. Brain Cell.Biol. 2006;35:239–250. doi: 10.1007/s11068-007-9017-0. [DOI] [PubMed] [Google Scholar]
- Dumitriu D, Hao J, Hara Y, Kaufmann J, Janssen WG, Lou W, Rapp PR, Morrison JH. Selective changes in thin spine density and morphology in monkey prefrontal cortex correlate with aging-related cognitive impairment. J.Neurosci. 2010;30:7507–7515. doi: 10.1523/JNEUROSCI.6410-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumitriu D, Rodriguez A, Morrison JH. High-throughput, detailed, cell-specific neuroanatomy of dendritic spines using microinjection and confocal microscopy. Nat.Protoc. 2011;6:1391–1411. doi: 10.1038/nprot.2011.389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrlich I, Klein M, Rumpel S, Malinow R. PSD-95 is required for activity-driven synapse stabilization. Proc.Natl.Acad.Sci.U.S.A. 2007;104:4176–4181. doi: 10.1073/pnas.0609307104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graeber MB, Bise K, Mehraein P. CR3/43, a marker for activated human microglia: application to diagnostic neuropathology. Neuropathol.Appl.Neurobiol. 1994;20:406–408. doi: 10.1111/j.1365-2990.1994.tb00987.x. [DOI] [PubMed] [Google Scholar]
- Hao J, Janssen WG, Tang Y, Roberts JA, McKay H, Lasley B, Allen PB, Greengard P, Rapp PR, Kordower JH, Hof PR, Morrison JH. Estrogen increases the number of spinophilin-immunoreactive spines in the hippocampus of young and aged female rhesus monkeys. J.Comp.Neurol. 2003;465:540–550. doi: 10.1002/cne.10837. [DOI] [PubMed] [Google Scholar]
- Hao J, Rapp PR, Leffler AE, Leffler SR, Janssen WG, Lou W, McKay H, Roberts JA, Wearne SL, Hof PR, Morrison JH. Estrogen alters spine number and morphology in prefrontal cortex of aged female rhesus monkeys. J.Neurosci. 2006;26:2571–2578. doi: 10.1523/JNEUROSCI.3440-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hara Y, Park CS, Janssen WG, Roberts MT, Morrison JH, Rapp PR. Synaptic correlates of memory and menopause in the hippocampal dentate gyrus in rhesus monkeys. Neurobiol.Aging. 2010 doi: 10.1016/j.neurobiolaging.2010.09.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, Stevens JK. Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: serial electron microscopy with reference to their biophysical characteristics. J.Neurosci. 1989;9:2982–2997. doi: 10.1523/JNEUROSCI.09-08-02982.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasai H, Fukuda M, Watanabe S, Hayashi-Takagi A, Noguchi J. Structural dynamics of dendritic spines in memory and cognition. Trends Neurosci. 2010;33:121–129. doi: 10.1016/j.tins.2010.01.001. [DOI] [PubMed] [Google Scholar]
- Kim E, Sheng M. The postsynaptic density. Curr.Biol. 2009;19:R723–R724. doi: 10.1016/j.cub.2009.07.047. [DOI] [PubMed] [Google Scholar]
- Kozubek M. Theoretical versus experimental resolution in optical microscopy. Microsc.Res.Tech. 2001;53:157–166. doi: 10.1002/jemt.1080. [DOI] [PubMed] [Google Scholar]
- Liodis P, Denaxa M, Grigoriou M, Akufo-Addo C, Yanagawa Y, Pachnis V. Lhx6 activity is required for the normal migration and specification of cortical interneuron subtypes. J.Neurosci. 2007;27:3078–3089. doi: 10.1523/JNEUROSCI.3055-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki M, Ellis-Davies GC, Nemoto T, Miyashita Y, Iino M, Kasai H. Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nat.Neurosci. 2001;4:1086–1092. doi: 10.1038/nn736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mishchenko Y, Hu T, Spacek J, Mendenhall J, Harris KM, Chklovskii DB. Ultrastructural analysis of hippocampal neuropil from the connectomics perspective. Neuron. 2010;67:1009–1020. doi: 10.1016/j.neuron.2010.08.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Noguchi J, Matsuzaki M, Ellis-Davies GC, Kasai H. Spine-neck geometry determines NMDA receptor-dependent Ca2+ signaling in dendrites. Neuron. 2005;46:609–622. doi: 10.1016/j.neuron.2005.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nusser Z, Lujan R, Laube G, Roberts JD, Molnar E, Somogyi P. Cell type and pathway dependence of synaptic AMPA receptor number and variability in the hippocampus. Neuron. 1998;21:545–559. doi: 10.1016/s0896-6273(00)80565-6. [DOI] [PubMed] [Google Scholar]
- Petersen JD, Chen X, Vinade L, Dosemeci A, Lisman JE, Reese TS. Distribution of postsynaptic density (PSD)-95 and Ca2+/calmodulin-dependent protein kinase II at the PSD. J.Neurosci. 2003;23:11270–11278. doi: 10.1523/JNEUROSCI.23-35-11270.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reilly JF, Games D, Rydel RE, Freedman S, Schenk D, Young WG, Morrison JH, Bloom FE. Amyloid deposition in the hippocampus and entorhinal cortex: quantitative analysis of a transgenic mouse model. Proc.Natl.Acad.Sci.U.S.A. 2003;100:4837–4842. doi: 10.1073/pnas.0330745100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosin P. Unimodal thresholding. Pattern Recognition. 2001;34:2083–2096. [Google Scholar]
- Schmitz C, Hof PR. Design-based stereology in neuroscience. Neuroscience. 2005;130:813–831. doi: 10.1016/j.neuroscience.2004.08.050. [DOI] [PubMed] [Google Scholar]
- Sheng M, Pak DT. Ligand-gated ion channel interactions with cytoskeletal and signaling proteins. Annu.Rev.Physiol. 2000;62:755–778. doi: 10.1146/annurev.physiol.62.1.755. [DOI] [PubMed] [Google Scholar]
- Shrivastava M, Vivekanandhan S, Pati U, Behari M, Das TK. Mitochondrial perturbance and execution of apoptosis in platelet mitochondria of patients with amyotrophic lateral sclerosis. Int.J.Neurosci. 2011;121:149–158. doi: 10.3109/00207454.2010.537416. [DOI] [PubMed] [Google Scholar]
- Sterio DC. The unbiased estimation of number and sizes of arbitrary particles using the disector. J.Microsc. 1984;134:127–136. doi: 10.1111/j.1365-2818.1984.tb02501.x. [DOI] [PubMed] [Google Scholar]
- Takumi Y, Ramirez-Leon V, Laake P, Rinvik E, Ottersen OP. Different modes of expression of AMPA and NMDA receptors in hippocampal synapses. Nat.Neurosci. 1999;2:618–624. doi: 10.1038/10172. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.