Abstract
BACKGROUND AND PURPOSE
The operational model provides a key conceptual framework for the analysis of pharmacological data. However, this model does not include constitutive receptor activity, a frequent phenomenon in modern pharmacology, particularly in recombinant systems. Here, we developed extensions of the operational model which include constitutive activity and applied them to effects of agonists at the chemokine receptor CCR4.
EXPERIMENTAL APPROACH
The effects of agonists of CCR4 on [35S]GTPγS binding to recombinant cell membranes and on the filamentous (F-) actin content of human CD4+ CCR4+ T cells were determined. The basal [35S]GTPγS binding was changed by varying the GDP concentration whilst the basal F-actin contents of the higher expressing T cell populations were elevated, suggesting constitutive activity of CCR4. Both sets of data were analysed using the mathematical models.
RESULTS
The affinity of CCL17 (also known as TARC) derived from analysis of the T cell data (pKa= 9.61 ± 0.17) was consistent with radioligand binding experiments (9.50 ± 0.11) while that from the [35S]GTPγS binding experiments was lower (8.27 ± 0.09). Its intrinsic efficacy differed between the two systems (110 in T cells vs. 11).
CONCLUSIONS AND IMPLICATIONS
The presence of constitutive receptor activity allows the absolute intrinsic efficacy of agonists to be determined without a contribution from the signal transduction system. Intrinsic efficacy estimated in this way is consistent with Furchgott's definition of this property. CCL17 may have a higher intrinsic efficacy at CCR4 in human T cells than that expressed recombinantly in CHO cells.
Keywords: operational model, CCR4, agonist efficacy, intrinsic efficacy, CCL17, CCL22, T-lymphocyte, chemokine receptor
Introduction
The development of the operational model (Black and Leff, 1983) was a key milestone in the analysis of functional pharmacological data because its inclusion of a plausible transducer function facilitates the direct fitting of the model to experimental data. This allows estimates of the affinity and efficacy of agonists to be derived from suitable experimental systems without the need to transform the data. This avoids the potential for distortion of the data following linearizing transformations, a particular problem with double reciprocal plots, which are required, for example, in the method of Furchgott (1966) for estimating agonist affinity. Of course, in light of the two-state model (Karlin, 1967; Thron, 1972; Colquhoun, 1973), we must be cautious in our interpretation of the ‘affinity’ derived from such an analysis. While it may well define the midpoint of the binding isotherm of the agonist under the prevailing experimental conditions, it does not represent the affinity of the agonist for any particular conformational state of the receptor and, as such, is not a measure of a thermodynamic constant.
Unfortunately, the more recent observation that receptors may be constitutively active resulting in basal signalling in the absence of agonist (Costa and Herz, 1989) is incompatible with the operational model and prevents its use for the analysis of data from systems which show agonist-independent activity. However, consideration of the limiting cases of the ternary complex model (De Léan et al., 1980) led to the development of a model of receptor interaction with a signal transduction system which does include constitutive receptor activity (Hall, 2006) and the demonstration that this model can also be considered as an operational model of systems with constitutive receptor activity. An interesting consequence of the presence of the constitutive activity in this model is that it results in a natural separation of agonist efficacy (‘efficacy’ and ‘intrinsic efficacy’ in this report are taken to have the definitions specified in Neubig et al., 2003) from the ‘coupling efficiency’ of the associated transduction system, providing a measure of efficacy (‘α’) which quantifies the change in the ability of the receptor to activate the signal transduction system on binding of agonist. To be precise, the ability of the agonist:receptor complex to activate the signal transduction system is equivalent to 1/α times its concentration of free receptor (and note therefore that α < 1 results in agonism whilst α > 1 results in inverse agonism). An advantage of this parameter as a measure of agonist efficacy is that, while it is clearly dependent on the signal transduction system under consideration, it is independent of the amplification of the stimulus associated with the signal transduction pathway and should therefore be independent of the point in the cascade at which the response is measured.
In its original form, this model can only be applied to concentration-response curves with unit Hill coefficients as it was derived with an invariant Hill coefficient of unity. The main objective of this report is to describe generalizations of this model, which allow it to be fitted to concentration-response curves with non-unit Hill coefficients. The mathematical details of this are described in the first section of the Results along with the results of Monte Carlo simulations which explore the precision and accuracy of the parameter estimates when these models are fitted to simulated experimental data. The new models (equations 6, A5 + A6 and 12) are then used to derive estimates of the affinity and efficacy of the chemokine receptor CCR4 agonists, CCL17 (also known as thymus and activation-regulated chemokine; TARC), and CCL22 (also known as macrophage-derived chemokine; MDC), in recombinant cells and for CCL17 in assays of cytoskeletal reorganization in primary human T cells (chemokine and receptor nomenclature follows Alexander et al., 2011). CCR4 is a G-protein-coupled receptor, which is predominantly expressed on leukocytes and mediates chemotaxis of these cells in response to CCL22 and CCL17. The receptor is therefore thought to play a role in the recruitment of immune cells (particularly certain T cell populations) to sites of inflammation (see Hall et al., 2010).
Methods
Monte Carlo simulations
Monte Carlo simulations were performed using equations 6, 7, 8 and 12. Equation 6 was studied most extensively since it is likely to be of most general utility. The level of error in the simulated data was determined empirically to mimic that of the T cell actin polymerization assay (as this had the sparsest data set). Simulated concentration-response curves were generated with 12 points per curve and families of five curves per experimental occasion (an example data set is shown in Supporting Information Figure S1). The simulated within-occasion error was normally distributed with a standard deviation of 3% of the mean response. The between-occasion error was also Gaussian with a standard deviation of 6%. This resulted in individual fit sums of squares of similar magnitude to those of the fits to the T cell filamentous actin (F-actin) data (∼0.13) and similar standard deviations for the replicate determinations at each concentration (∼5% coefficient of variation). Simulations were also performed using equation 6 with within-occasion standard deviations of 6%. The effect of performing duplicate instead of singlet determinations within an assay (and hence 24 point curves) was also determined with this degree of variability.
Fifty experimental occasions were simulated for each condition. The generating equation was then fitted by minimizing the residual sum of squares using the Excel Solver add-in. For each intentional change of a parameter, the other model parameters were adjusted such that the maximal response for the curve with the highest value of χ was approximately equal to Emax (i.e. the agonist was full) and the simulated curves were well described within the agonist concentration range. Tables 1–4 summarize the results of these simulations.
Table 1.
Summary of the input parameters and their estimates derived from 50 simulated data sets using equation 6
| Simulation* | Emax | pKa | logε | logχ1 | logχ2 | logχ3 | logχ4 | logχ5 | logn | basal |
|---|---|---|---|---|---|---|---|---|---|---|
| 1. Input | 1.50 | 9.70 | 3.00 | −2.91 | −2.43 | −1.95 | −1.48 | −1.00 | −0.15 | 0.90 |
| 1. Estimate | 1.50 ± 0.12 | 9.67 ± 0.11 | 3.08 ± 0.25 | −2.99 ± 0.23 | −2.50 ± 0.21 | −2.03 ± 0.19 | −1.54 ± 0.18 | −1.06 ± 0.15 | −0.17 ± 0.05 | 0.89 ± 0.06 |
| 2. Input | 1.50 | 9.70 | 2.00 | −2.29 | −1.89 | −1.49 | −1.10 | −0.70 | 0.00 | 0.90 |
| 2. Estimate | 1.50 ± 0.11 | 9.70 ± 0.12 | 2.01 ± 0.23 | −2.30 ± 0.27 | −1.90 ± 0.22 | −1.50 ± 0.19 | −1.10 ± 0.16 | −0.71 ± 0.11 | 0.00 ± 0.06 | 0.92 ± 0.06 |
| 3. Input | 1.50 | 9.70 | 1.48 | −1.60 | −1.30 | −1.00 | −0.70 | −0.40 | 0.30 | 0.90 |
| 3. Estimate | 1.49 ± 0.09 | 9.75 ± 0.12 | 1.37 ± 0.26 | −1.48 ± 0.28 | −1.21 ± 0.23 | −0.93 ± 0.18 | −0.64 ± 0.14 | −0.37 ± 0.09 | 0.35 ± 0.10 | 0.90 ± 0.05 |
| 4. Input | 1.50 | 9.70 | 1.48 | −1.42 | −1.02 | −0.62 | −0.22 | 0.18 | 0.30 | 0.90 |
| 4. Estimate | 1.47 ± 0.08 | 9.72 ± 0.13 | 1.42 ± 0.26 | −1.35 ± 0.24 | −0.97 ± 0.17 | −0.60 ± 0.12 | −0.21 ± 0.05 | 0.17 ± 0.05 | 0.32 ± 0.10 | 0.90 ± 0.05 |
| 5. Input | 1.50 | 9.70 | 1.48 | −1.60 | −1.30 | −1.00 | −0.70 | −0.40 | 0.30 | 0.90 |
| 5. Estimate | 1.49 ± 0.12 | 9.81 ± 0.33 | 1.25 ± 0.67 | −1.36 ± 0.72 | −1.10 ± 0.57 | −0.85 ± 0.45 | −0.62 ± 0.35 | −0.35 ± 0.21 | 0.52 ± 0.49 | 0.89 ± 0.06 |
| 6. Input | 1.50 | 9.70 | 1.48 | −1.60 | −1.30 | −1.00 | −0.70 | −0.40 | 0.30 | 0.90 |
| 6.Estimate | 1.47 ± 0.11 | 9.70 ± 0.21 | 1.48 ± 0.41 | −1.61 ± 0.44 | −1.32 ± 0.37 | −1.01 ± 0.28 | −0.71 ± 0.22 | −0.42 ± 0.15 | 0.34 ± 0.18 | 0.89 ± 0.05 |
Simulations 1–4 were performed with a within-occasion standard error of 3%, simulations 5 and 6 with a standard error of 6%. Simulation 6 was performed with duplicate determinations.
Parameter estimates are presented as mean ± SD.
Table 4.
Summary of the input parameters and their estimates derived from 50 simulated data sets using equation 8
| Emax | pKa | logε | logχ1 | logχ2 | logχ3 | logχ4 | logχ5 | logm | logn | basal | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Input | 1.50 | 9.30 | 2.30 | −2.29 | −1.89 | −1.49 | −1.00 | −0.70 | 0.00 | 0.00 | 0.90 |
| Output | 1.51 ± 0.11 | 9.47 ± 0.45 | 3.2 ± 5.0 | −3.2 ± 5.2 | −2.7 ± 4.2 | −2.1 ± 3.3 | −1.6 ± 2.6 | −1.0 ± 2.6 | 0.05 ± 0.22 | 0.1 ± 0.6 | 0.90 ± 0.05 |
Parameter estimates are presented as mean ± SD.
To explore the influence of the number of concentration-response curves in an experiment on the curve fits, curves were deleted from a set of 10 simulated five-curve families (generated with equation 6) to generate families of three and two curves.
Finally, the operational model (equation a below) was fitted to pairs of curves taken from 10 five-curve families (parameters as described for simulation 2 in Table 1) simulating two different levels of receptor inactivation (25% or 80% reduction of the control maximal response) to determine the potential inaccuracy in the affinity estimate caused by fitting this model to data with differing basal activity.
| (a) |
Cell culture and membrane preparation
CHO-K1 cells were transfected with cDNA encoding CCR4 (Power et al., 1995). The cells were grown in T175 cm2 flasks or Corning CellSTACKS© (Corning Inc., NY, USA) at 37°C in a 95% O2/5% CO2 atmosphere in Dulbecco's modified Eagle's medium F12 nutrient mix containing 5% heat-inactivated dialyzed fetal bovine serum and 0.5 mg·mL−1 Geneticin.
For use in radioligand binding studies, cells were harvested on the day of experiment from T175 cm2 flasks following treatment with Versene™ and centrifugation at 250×g for 5 min. Cells were washed in PBS before resuspension in radioligand binding assay buffer.
For preparation of cell membranes, frozen (−80°C) cell pellets were prepared by harvesting cells with HBSS containing 0.6 mmol·L−1 EDTA and 10% v/v TrypLE™, and centrifugation at 250×g for 5 min. Cell pellets were defrosted on ice before resuspending in homogenization buffer (HEPES, 50 mmol·L−1; bacitracin 47 µg·mL−1; EDTA, 1 mmol·L−1; leupeptin, 25 µg·mL−1 adjusted to pH 7.4 with KOH) containing 2 µmol·L−1 pepstatin A and 1 mmol·L−1 phenylmethylsulphonyl fluoride. Cells were homogenized in a Waring blender (2 × 15 s, with 5 min incubation on ice between each bout) and left to settle for 30 min. The homogenate was centrifuged at 250×g for 10 min and the resulting supernatant was centrifuged at 48 000×g for 36 min at 4°C. The resulting pellet was resuspended in homogenization buffer. The membrane suspension was then frozen in aliquots at −80°C until required. The protein concentration was determined using the bicinchoninic acid method as described by Smith et al. (1985).
[125I]CCL17 binding studies
[125I]CCL17 binding studies were performed in white, 96-well clear bottomed, scintillation proximity assay (SPA) plates at room temperature (20–22°C) in assay buffer [mmol·L−1: HEPES, 20; NaCl, 100; MgCl2, 10; saponin, 10 µg·mL−1 (membranes only); 0.1% BSA; adjusted to pH 7.4 with KOH]. Wheatgerm agglutinin polyvinyltoluene SPA beads (SPA beads) were pre-coated with CCR4 cells or membranes for 30 min on ice and added to SPA plates containing CCR4 agonist or vehicle (1% DMSO) and [125I]CCL17 (∼0.1 nmol·L−1) to give 0.25 mg·well−1 SPA beads and either 1 × 10−5 cells·well−1 or 2.5 µg·well−1 membrane protein. Non-specific binding was determined in the presence of 10 nmol·L−1 CCL22. Plates were incubated for 4 h before detection of [125I]CCL17 binding, using a Wallac Microbeta Trilux scintillation counter (PerkinElmer LAS UK Ltd, Beaconsfield, UK). The total amount of radioligand added to each well was calculated for data analysis using a Packard Cobra II Gamma Counter (PerkinElmer LAS UK Ltd).
Guanosine 5′-O-(3-[35S]thio)triphosphate binding studies
Guanosine 5′-O-(3-[35S]thio)triphosphate ([35S]GTPγS) binding studies were performed in white, 96-well clear bottomed, SPA plates at ambient room temperature (20–22°C) in assay buffer (mmol·L−1: HEPES, 20; NaCl, 100; MgCl2, 10; EDTA, 1; saponin, 10 µg·mL−1; 0.01% BSA; pH 7.4 with KOH). SPA beads were pre-coated with CHO-CCR4 or CHO-K1 membranes for 30 min on ice before addition of GDP. The SPA bead/membrane/GDP suspension was mixed with CCR4 agonist or vehicle (1% DMSO) and incubated for 30 min. [35S]GTPγS (∼0.4 nmol·L−1) was then added to give a final concentration of 0.25 mg per well SPA beads and 7.5 µg per well membranes and plates incubated for 1 h before centrifugation (250×g for 1 min). [35S]GTPγS binding was detected using a Wallac Microbeta Trilux scintillation counter (PerkinElmer LAS UK Ltd) following a further 2 h incubation.
Measurement of chemokine-stimulated increases in T cell F-actin content
Volunteers gave informed consent for blood donation and denied taking any medication in the 7 days prior to donation. Blood (nine volumes) was taken from healthy human subjects into 3.8% sodium citrate solution (one volume). An equal volume of 1.9% dextran T-500 solution (in PBS) was added to agglutinate and sediment the erythrocytes. After 40 min, the upper layer was collected and centrifuged at 300×g for 8 min. The pellet was resuspended in PBS, applied to a discontinuous Percoll gradient and centrifuged at 1000×g for 15 min. The peripheral blood mononuclear cell (PBMC) fraction was collected, diluted with PBS and centrifuged (400×g for 10 min). The resulting pellet was resuspended at 5 × 107 cells mL−1 in assay buffer (Roswell Park Memorial Institute 1640 medium containing 10 mmol·L−1 HEPES and 1% BSA). The cell suspension was incubated at room temperature with saturating concentrations of fluorescein isothiocyanate (FITC)-conjugated mouse anti-human CD4 and a non-inactivating phycoerythrin (PE)-conjugated mouse anti-human CCR4 (BD Biosciences, Oxford, UK) or appropriate isotype control antibodies for 15 min. The cell suspension was centrifuged at 400×g for 10 min and the pellet resuspended at 107 cells mL−1 in assay buffer.
The PBMC were incubated in the presence of 0.1% DMSO (the standard vehicle for antagonist studies) at 37°C for 40 min. Cells were incubated with agonist (CCL22 from ALMAC Sciences, Craigavon, UK; CCL17 from PeproTech EC, London, UK) for 15 s before addition of three volumes of 10% formalin solution. After 30 min, the cells were centrifuged (1200×g for 5 min) and washed twice with PBS, centrifuging at 1200×g for 5 min to recover them. The cell suspensions were incubated for 20 min with lysophosphatidylcholine (100 µg·mL−1) and Alexa Fluor 647 phalloidin (Life Technologies, Paisley, UK) (0.075 units·mL−1). The cells were centrifuged at 1200×g for 5 min and resuspended in PBS.
The F-actin content of the CD4+ CCR4+ lymphocytes in each sample was determined on a FACSCalibur flow cytometer by measuring the mean Alexa Fluor 647 (FL-4) fluorescence intensity of 1000 cells. This was expressed as a fraction of the Alexa Fluor 647 fluorescence intensity of the CCR4- lymphocytes in the same sample.
Materials
All cell culture media and reagents were purchased from Gibco (Invitrogen Ltd, Paisley, UK). DMSO and T175 cm2 flasks were obtained from Fisher Scientific UK Ltd. (Loughborough, UK). All other chemicals were purchased from Sigma-Aldrich Co. Ltd. (Gillingham, UK) unless otherwise stated. [125I]CCL17 and [35S]GTPγS (specific activity 2200 and 1250 Ci·mmol−1, respectively) were obtained from PerkinElmer LAS UK Ltd.
Data analysis
Experimental concentration-response curves were initially fitted with a Hill function (Hill, 1910; equation 1).
| (1) |
where [A] is the agonist concentration, Emax is the maximal response, EC50 is the concentration of agonist causing 50% of the maximal response, n is the Hill coefficient and basal is the signal in the absence of agonist.
The families of concentration-response curves were fitted with equation 6, A5 + A6 or 12. Least squares regression was performed by minimizing the sum of squared residuals using the Excel solver add-in. To account for their likely log-normal distribution, the parameters of these equations other than Emax and basal were fitted by varying the log of their value and anti-logging, for example, Ka appeared in the equations as 10logKa. For equation 12, t was constrained to 0.25 min.
Results
Derivation of the models
Three potential sources of deviations of the Hill coefficient of a concentration-response curve from unity were considered: the transducer function (generally the default assumption), the equilibrium binding isotherm of the agonist and performing the assay under conditions where the response is measured prior to the agonist achieving steady-state binding. Models of each of these possibilities are derived below.
Hill transducer function
The basic model derived in Hall (2006) can be represented diagrammatically as shown below.
![]()
The agonist (A) binds to the receptor (R) with dissociation constant Ka. Both the free receptor and the agonist:receptor complex interact with the signal transduction system (represented by the dotted lines). The signal transduction cascade was modelled as a rectangular hyperbolic (or linear rational) function of the concentrations of receptor species (which has midpoint Ke for the free receptor and αKe for the agonist:receptor complex). It was assumed that the receptor and agonist:receptor complex compete for binding to the transducer molecules. In this case, the binding of the two receptor species to the transducer (T) is given by 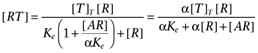 and
and 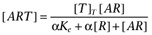 .
.
Hence, 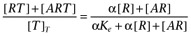 .
.
By identifying [RT]+[ART] with the response (E) and, hence, [T]T with Emax, this approach gives equation 2 as the relationship between the concentrations of receptor species and the response.
| (2) |
Substituting for the concentrations of the receptor species ([R]=Ka[R]T/(Ka+[A]) and [AR]=[A][R]T/(Ka+[A])), this gives
| (3) |
where χ=[R]T/Ke may be taken as a measure of the coupling efficiency of the signal transduction system.
However, we may also derive this model using the classical approach taken in the derivation of the operational model of defining a stimulus, S, and making the response a specified function of this stimulus. Following the example of Leff et al. (1993), let S=[R]+ε[AR] and f(S) =EmaxS/(Ke+S), then
which is of the same form as equation 2 (with ε= 1/α). Substituting for the concentrations of the receptor species this gives
| (4) |
where χ is as previously defined. We may then derive (by inspection; see Hall, 2006) expressions for the activity in the absence of agonist, Emaxχ/(1 +χ), the maximal response to the agonist, Emaxεχ/(1 +εχ), and the midpoint of the concentration-response curve, Ka(1 +χ)/(1 +εχ).
To generalize this model for concentration-response curves with non-unit Hill coefficients, we again follow the approach of Leff et al. Let 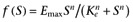 then
then
After substitution for the concentrations of the receptor species, this results in equation 5.
| (5) |
In this case, the response in the absence of agonist is Emaxχn/(1 +χn), the maximal response is Emaxεnχn/(1 +εnχn) and the midpoint is the rather inelegant
To allow equation 5 to be applied to experimental data, it is also necessary to add a term (basal), which accommodates receptor-independent basal activity in the system to give
| (6) |
Hill binding isotherm
In this case, it will be assumed that the binding of the agonist is described by a Hill function (equation 1 with basal= 0) while the transducer function is linear rational. In this case, [R]= (Ka)m[R]T/((Ka)m+[A]m), [AR]=[A]m[R]T/((Ka)m+[A]m), S=[R]+ε[AR] and f(S) =EmaxS/(Ke+S), where m is the Hill coefficient of the binding isotherm, giving
| (7) |
In this model, the response in the absence of agonist is Emaxχ/(1 +χ), the maximal response is Emaxεχ/(1 +εχ) and the midpoint is Ka((1 +χ)/(1 +εχ))1/m.
Analysis of the data from the [35S]GTPγS binding experiments requires a modification of this model (equations A5 and A6), which includes terms for basal activity due to other receptors in the system and the GDP concentration dependence of the basal activity. This is derived in the final section of the Appendix.
Hill binding and transduction
Clearly, it is possible to further generalize the model by allowing both the binding isotherm and the transducer function to have non-unit Hill coefficients, the equation for which is
| (8) |
However, as shown in Table 4, from a statistical perspective, this is a step too far and it is simply not possible to recover accurate estimates of the parameters from this model from simulated data with a realistic degree of variability.
Although of little practical utility, equation 8 could be used to derive the analogues of the formulae for the analysis of equieffective concentrations of two agonists to derive their relative intrinsic efficacy (e.g. Waud, 1969). This is done in the Appendix.
Pre-steady-state binding
Assuming that the agonist binds with pseudo-first-order kinetics, the concentration of the agonist:receptor complex at time t is given by
| (9) |
where, kobs=k-[A]/Ka+k- and k- is the dissociation rate constant of AR. It follows that
| (10) |
Then, defining the stimulus as St=[R]t+ε[AR]t and assuming that f(St) =EmaxSt/(Ke+St)
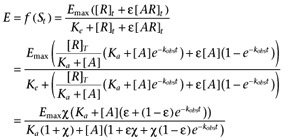 |
(11) |
and allowing for receptor-independent basal activity in the system gives
| (12) |
Note for fitting kobs was replaced by the expression below equation 9 to provide a direct estimate of k-.
Monte Carlo simulations
The results of Monte Carlo simulations on equation 6 are summarized in Table 1. Simulations performed with different values of n showed that the input model parameters were well approximated by the curve fits for all values n tested, although ε is modestly underestimated when n= 2 when singlet determinations are used. The standard deviation of each estimated parameter was similar at each n indicating that the precision of the estimate was not affected by the slope of the transducer function. Increasing the level of constitutive activity from ∼15% of Emax to ∼70% of Emax (with other parameters as for the n= 2 simulations) improved the precision with which the values of χ were estimated but not that of the other parameters.
Doubling the within-occasion error markedly worsened the precision and accuracy of the parameter estimates (except for those of Emax and basal, which were essentially unaffected). Increasing to duplicate determinations with this level of error partially reversed the decreased precision and improved the accuracy of the parameter estimates to such an extent that the mean estimates were generally more accurate than those derived from the singlet determinations with the lower within-occasion error.
The effects of reducing the number of curves within an experiment are summarized in Table 2. Only 10 simulated data sets were used for this exercise. Perhaps surprisingly for a model with six parameters, even reducing the number of curves to two had a relatively small impact on the accuracy of the parameter estimates, however, the precision was adversely affected, standard deviations increasing by up to 80%.
Table 2.
Effect of the number of conditions per experiment on the estimates of the parameters of equation 6
| Simulation | Emax | pKa | logε | logχ1 | logχ2 | logχ3 | logχ4 | logχ5 | logn | basal |
|---|---|---|---|---|---|---|---|---|---|---|
| Input | 1.50 | 9.70 | 1.48 | −1.60 | −1.30 | −1.00 | −0.70 | −0.40 | 0.30 | 0.90 |
| 5 curves | 1.49 ± 0.07 | 9.75 ± 0.12 | 1.36 ± 0.22 | −1.49 ± 0.26 | −1.21 ± 0.18 | −0.94 ± 0.15 | −0.66 ± 0.12 | −0.37 ± 0.08 | 0.34 ± 0.10 | 0.90 ± 0.04 |
| 3 curves | 1.50 ± 0.07 | 9.80 ± 0.18 | 1.27 ± 0.36 | −1.13 ± 0.30 | −0.62 ± 0.19 | −0.35 ± 0.11 | 0.37 ± 0.15 | 0.90 ± 0.05 | ||
| 2 curves | 1.51 ± 0.07 | 9.77 ± 0.19 | 1.33 ± 0.38 | −1.18 ± 0.32 | −0.37 ± 0.12 | 0.35 ± 0.17 | 0.90 ± 0.05 |
Ten simulated experiments with five curves per occasion were analysed. Curves were then deleted from these sets to leave three or two curves per experiment. Parameter estimates are presented as mean ± SD.
The results of simulations using equations 7 and 12 are summarized in Table 3. The parameters of equation 7 were, if anything, estimated more accurately and more precisely than those of equation 6. Simulations of equation 12 were slightly more concerning. Firstly, although most of the parameters of the model were quite well estimated, fits to 2 of the 50 simulated data sets returned values of pKa and log k- which were grossly inaccurate. However, if these very clear outliers were excluded from the data set, then the estimate of pKa was quite accurate. However, the value of log k- was still rather poorly estimated.
Table 3.
Summary of the input parameters and their estimates derived from 50 simulated data sets using equation 7 (simulations 1–4) and equation 12
| Simulation | Emax | pKa | logε | logχ1 | logχ2 | logχ3 | logχ4 | logχ5 | logm | basal |
|---|---|---|---|---|---|---|---|---|---|---|
| 1. Input | 1.50 | 9.30 | 2.70 | −2.42 | −2.02 | −1.62 | −1.22 | −0.82 | −0.15 | 0.90 |
| 1. Estimate | 1.51 ± 0.09 | 9.34 ± 0.20 | 2.75 ± 0.16 | −2.45 ± 0.12 | −2.06 ± 0.11 | −1.65 ± 0.10 | −1.25 ± 0.10 | −0.85 ± 0.08 | −0.16 ± 0.04 | 0.90 ± 0.05 |
| 2. Input | 1.50 | 9.70 | 2.70 | −2.91 | −2.43 | −1.95 | −1.48 | −1.00 | 0.00 | 0.90 |
| 2. Estimate | 1.51 ± 0.10 | 9.72 ± 0.07 | 2.69 ± 0.18 | −2.89 ± 0.17 | −2.43 ± 0.16 | −1.95 ± 0.14 | −1.48 ± 0.13 | −1.00 ± 0.10 | 0.00 ± 0.04 | 0.88 ± 0.06 |
| 3. Input | 1.50 | 9.70 | 2.48 | −2.73 | −2.26 | −1.78 | −1.30 | −0.82 | 0.30 | 0.90 |
| 3. Estimate | 1.52 ± 0.09 | 9.69 ± 0.04 | 2.46 ± 0.13 | −2.72 ± 0.13 | −2.23 ± 0.13 | −1.77 ± 0.11 | −1.30 ± 0.08 | −0.83 ± 0.04 | 0.30 ± 0.04 | 0.89 ± 0.05 |
| 4. Input | 1.50 | 9.70 | 2.30 | −2.01 | −1.41 | −0.81 | −0.20 | 0.40 | 0.30 | 0.90 |
| 4. Estimate | 1.50 ± 0.10 | 9.71 ± 0.07 | 2.30 ± 0.14 | −2.01 ± 0.13 | −1.41 ± 0.12 | −0.81 ± 0.06 | −0.20 ± 0.03 | 0.40 ± 0.06 | 0.31 ± 0.04 | 0.90 ± 0.06 |
| Equation 12 | Emax | pKa | logε | logχ1 | logχ2 | logχ3 | logχ4 | logχ5 | logk− | basal |
|---|---|---|---|---|---|---|---|---|---|---|
| Input | 1.90 | 10.00 | 2.00 | −2.52 | −2.22 | −1.92 | −1.60 | −1.30 | 0.40 | 0.95 |
| Estimate | 1.89 ± 0.15 | 10.2 ± 0.9 | 2.04 ± 0.16 | −2.54 ± 0.15 | −2.27 ± 0.14 | −1.95 ± 0.13 | −1.63 ± 0.11 | −1.31 ± 0.10 | 0.3 ± 1.0 | 0.94 ± 0.05 |
| Trimmed* | 1.89 ± 0.15 | 10.0 ± 0.3 | 2.04 ± 0.15 | −2.54 ± 0.14 | −2.27 ± 0.13 | −1.95 ± 0.12 | −1.63 ± 0.11 | −1.31 ± 0.09 | 0.5 ± 0.5 | 0.93 ± 0.05 |
In the case of equation 12, two of the simulations resulted in extremely aberrant estimates of the ligand binding parameters (pKa= 14.4, 13.7; logk-=−4.05, −3.53). These replicates were excluded from the summary statistics in the ‘Trimmed’ row.
Parameter estimates are presented as mean ± SD.
The simulations of equation 8 (Table 4) gave very poor estimates of ε and of χ for each curve. Thus, it is not possible to achieve good estimates of the pharmacological parameters when two Hill coefficients are included in the model and this equation was not applied to experimental data.
The operational model was fitted to two sets of 10 pairs of curves generated from equation 6 using the parameters listed for simulation 2 in Table 1. These two sets consisted of the curves with the greatest and least values of χ (χ5 and χ1) or those with the greatest and the median values of χ (χ5 and χ3). These sets correspond to pairs of curves where the maximal response has been reduced to 20% or 75% of its control value, respectively. In the case of the simulation using the χ5 and χ3 curves, the affinity of the agonist was quite well estimated (pKa= 9.62 ± 0.15 cf 9.70 as input) while the accuracy of the estimates using the χ5 and χ1 curves was poorer (pKa= 9.41 ± 0.09). Thus, the estimate of affinity appears to be worse when there is a smaller degree of overlap between the two curves. If the simulations are interpreted as irreversible receptor inactivation experiments, the proportion of the receptors remaining after inactivation is given by the ratio of the values of χ for equation 6 and the ratio of the values of τ in the operational model. Again, this was better estimated for the lower levels of inhibition [τ-ratio = 0.11 (0.07, 0.17) cf χ3/χ5= 0.16] than at high [τ-ratio = 0.010 (0.005, 0.017) cf χ1/χ5= 0.026].
Experimental
Recombinant cell studies
[125I]CCL17 bound to CHO-CCR4 cell membranes with a pKD of 9.40 ± 0.06 (n= 3) and to whole CHO-CCR4 cells with a pKD of 9.23 ± 0.13 (n= 3) (data not shown). In the cells, the saturation binding isotherm was consistent with binding to a single class of non-interacting binding sites since the Hill coefficient was 0.87 (95% confidence interval 0.66–1.15). However, that for the membranes did differ significantly from unity 0.85 (0.82, 0.88). In CHO-CCR4 membranes, CCL17 and CCL22 inhibited the binding of [125I]CCL17 (Supporting Information Figure S2A) with pKi values of 9.50 ± 0.11 and 10.34 ± 0.16, respectively (n= 4 in each case). The Hill coefficients of the binding curves were 0.73 (0.67, 0.81) and 0.79 (0.66, 0.95), respectively, both significantly different from unity. In whole cells (Supporting Information Figure S2B), the pKi values were 9.82 ± 0.09 and 10.39 ± 0.18 respectively (n= 4), with Hill coefficients of 0.73 (0.48, 0.98) and 0.79 (0.58, 1.08). The latter was not significantly different from unity, however, a trend towards ‘flatness’ was still apparent since none of the CCL22 competition curves had Hill coefficients greater than unity in these experiments.
CCL17 and CCL22 induced concentration-dependent increases in the amount of [35S]GTPγS which bound to CHO-CCR4 cell membranes (summarized in Table 5 and illustrated in Figure 1). The presence of increasing concentrations of GDP reduced the amount of spontaneous binding to the membranes (an observation which was also true of CHO-K1 cell membranes, Supporting Information Figure S4) and the maximal response to and potency of both agonists. The relative maximal response of CCL17 also decreased with GDP concentration. For CCL22, there was also a decrease in the Hill coefficient with increasing GDP concentration with the Hill coefficient at the higher GDP concentrations being less than unity and those at the lower GDP concentrations being close to unity. This profile suggests that the binding isotherm of CCL22 under these experimental conditions has a Hill coefficient less than unity (consistent with the binding data) and that the transducer function has a Hill coefficient close to unity.
Table 5.
Summary of the parameters (derived from equation 1) of the concentration-response curves to CCL17 and CCL22 in the [35S]GTPγS binding assay at various GDP concentrations
| Agonist | GDP (mmol·L−1) | pEC50 | *Emax (103 ccpm) | basal (103 ccpm) | n |
|---|---|---|---|---|---|
| CCL17 | 0.3 | 8.92 ± 0.14 | 3.6 ± 0.5 | 10.2 ± 1.0 | 1.22 (0.68, 2.18) |
| CCL17 | 0.5 | 8.76 ± 0.10 | 4.4 ± 0.7 | 9.3 ± 0.8 | 0.75 (0.56, 1.01) |
| CCL17 | 1 | 8.86 ± 0.06 | 5.3 ± 0.3 | 7.4 ± 0.7 | 0.91 (0.68, 1.24) |
| CCL17 | 5 | 8.57 ± 0.05 | 5.8 ± 0.4 | 4.9 ± 0.4 | 0.88 (0.73, 1.06) |
| CCL17 | 12.5 | 8.36 ± 0.11 | 4.4 ± 0.6 | 3.3 ± 0.4 | 0.90 (0.78, 1.03) |
| CCL17 | 37.5 | 8.36 ± 0.12 | 2.7 ± 0.3 | 2.0 ± 0.2 | 0.92 (0.69, 1.24) |
| CCL17 | 50 | 8.46 ± 0.13 | 2.2 ± 0.3 | 1.6 ± 0.1 | 1.03 (0.88, 1.22) |
| CCL22 | 0.3 | 9.59 ± 0.05 | 5.5 ± 0.4 | 9.9 ± 1.0 | 0.95 (0.66, 1.36) |
| CCL22 | 0.5 | 9.43 ± 0.06 | 6.2 ± 0.7 | 9.2 ± 1.0 | 0.86 (0.64, 1.14) |
| CCL22 | 1 | 9.38 ± 0.11 | 8.4 ± 1.0 | 7.4 ± 0.8 | 0.82 (0.59, 1.15) |
| CCL22 | 5 | 9.19 ± 0.07 | 9.4 ± 0.7 | 4.6 ± 0.5 | 0.77 (0.66, 0.90) |
| CCL22 | 12.5 | 8.95 ± 0.08 | 9.0 ± 0.8 | 3.0 ± 0.5 | 0.79 (0.73, 0.86) |
| CCL22 | 37.5 | 8.76 ± 0.04 | 6.7 ± 0.3 | 1.8 ± 0.2 | 0.73 (0.65, 0.82) |
| CCL22 | 50 | 8.70 ± 0.04 | 6.0 ± 0.2 | 1.5 ± 0.2 | 0.75 (0.6, 0.95) |
Using equation 1, the upper asymptote of the curves is Emax+basal.
Values are the mean ± SEM of four duplicate determinations except for n, which is presented as geometric mean with 95% confidence interval in parentheses.
Figure 1.
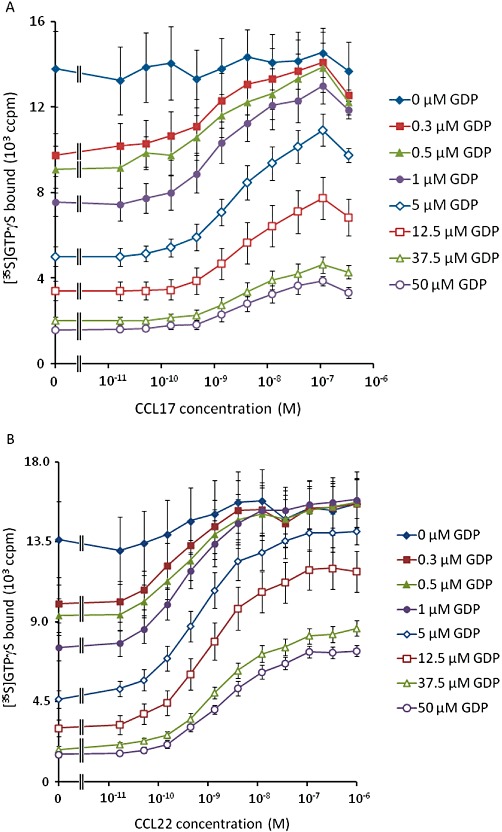
[35S]GTPγS binding induced by CCL17 (A) and CCL22 (B) in the absence or presence of GDP at 0.3, 0.5, 1, 5, 12.5, 37.5 or 50 µM. Data are the mean of four separate determinations and vertical bars show the SEM.
Given these observations, the [35S]GTPγS binding assay data were analysed with equations A5 + A6. Due to the wide span of levels of binding, robust weighting (by 1/Y2) was used when minimizing the sum of squared residuals. The data for CCL22, CCL17 and basal binding to CHO-K1 membranes were analysed simultaneously, sharing all parameters of the model except the affinity and efficacy of the two agonists. The results of this analysis are summarized in Table 6 and Figure 2. From these fits, the dissociation constants of CCL17 and CCL22 were 5.3 nmol·L−1 and 3.3 nmol·L−1, respectively, and their intrinsic efficacies were 10.6 and 33.6 indicating that CCL22 has approximately 1.6-fold higher affinity than CCL17 and approximately threefold higher intrinsic efficacy, in this system.
Table 6.
The parameters derived by fitting equations A5 + A6 to the CCL17 and CCL22 concentration-response curves in the [35S]GTPγS binding experiments at different GDP concentrations
| Parameter | Estimate |
|---|---|
| Emax (103 ccpm) | 16.3 ± 2.1 |
| CCL17 pKa | 8.28 ± 0.09 |
| CCL22 pKa | 8.48 ± 0.07 |
| CCL17 logε | 1.02 ± 0.03 |
| CCL22 logε | 1.53 ± 0.05 |
| Logχ1 | −0.13 ± 0.07 |
| logχ2 | 0.16 ± 0.05 |
| log m | −0.07 ± 0.01 |
| basal (103 ccpm) | 0.68 ± 0.21 |
| log KGDP | −6.26 ± 0.09 |
| log s | −0.11 ± 0.03 |
Data are presented as mean ± SEM.
Figure 2.
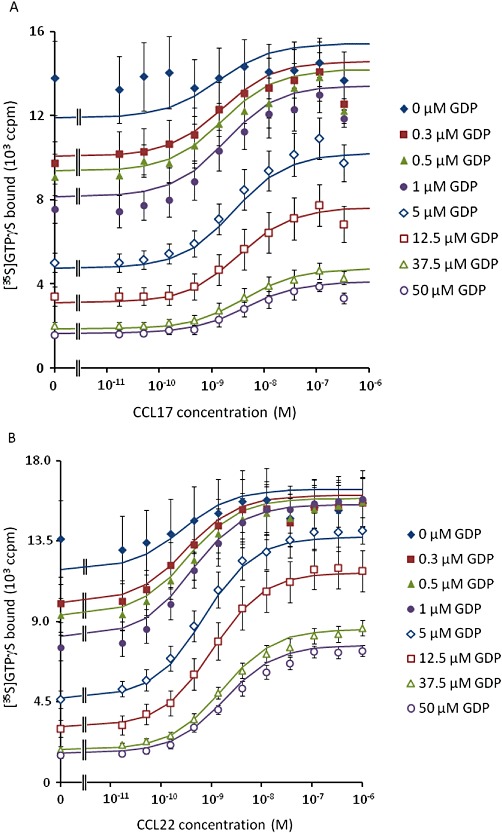
The fit of equations A5 + A6 to the data presented in Figure 1. Solid lines show the curve fit.
T cell studies
As shown in Figure 3, the CD4+ lymphocytes present in a human PBMC preparation show a wide range of expression levels of CCR4. CCL22 and CCL17 induced concentration-dependent increases in the F-actin content of CD4+ CCR4+ lymphocytes (Figure 4). The concentration-response curves to CCL17 were approximately sigmoid while those to CCL22 were not as there is a decrease in F-actin content around 10 nM of this agonist. To allow a Hill function to be fitted to the CCL22 data, the responses at the highest concentrations were excluded from the analysis. However, due to the clear deviation of these data from the assumptions of the mathematical models, the data on CCL22 are not explored further in the main body of this report (the results of fitting equations 6 and 12 to the binned CCL22 data are presented in Supporting Information Table S1, the rationale for the choice of these models is discussed below). The results of fitting a Hill function to these data are presented in Table 7. The potencies of the two chemokines were very similar, however, the maximal response to CCL22 was significantly greater than that of CCL17 (P < 0.005, paired t-test). The maximal response to CCL17 was 89.0 ± 3.4% of that of CCL22.
Figure 3.
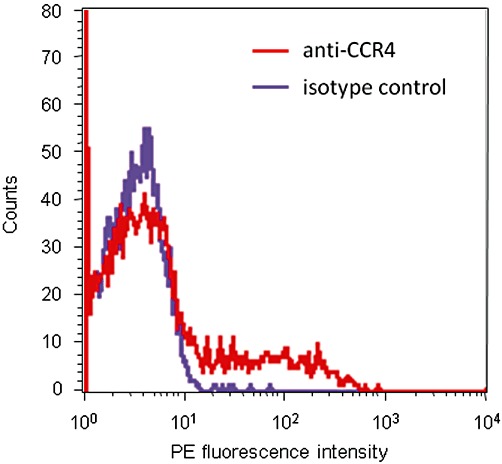
Representative histogram of the PE fluorescence intensity of human CD4+ lymphocytes stained with either PE-conjugated anti-human CCR4 antibody (red) or a PE-conjugated isotype control antibody (purple).
Figure 4.
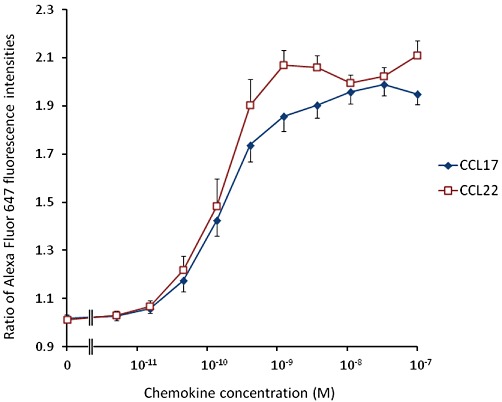
Increases in the F-actin content of human CD4+ CCR4+ cells induced by CCL17 or CCL22. Data are the mean of four determinations in separate donors and vertical bars show the SEM.
Table 7.
Summary of the parameters (derived from equation 1) of the concentration-response curves to CCL17 and CCL22
| Agonist | pEC50 | Emax* | basal | n |
|---|---|---|---|---|
| CCL17 | 9.77 ± 0.09 | 0.94 ± 0.05 | 1.01 ± 0.02 | 1.24 (1.06, 1.44) |
| CCL22 | 9.80 ± 0.12 | 1.06 ± 0.05 | 1.03 ± 0.02 | 1.60 (1.35, 1.90) |
Using equation 1, the upper asymptote of the curves is Emax+basal.
Values are the mean ± SEM of four determinations in separate donors except for n, which is presented as geometric mean with 95% confidence interval in parentheses.
The cell populations were divided into five contiguous ‘bins’ of approximately equal numbers of cells (labelled ‘low’, ‘low-mid’, ‘mid’, ‘high-mid’ and ‘high’). Relative to the ‘low’ population, the mean PE fluorescence intensities of the other populations were (mean ± SEM, n= 4) low-mid: 1.96 ± 0.03; mid: 3.76 ± 0.05; high-mid: 7.21 ± 0.09; high: 16.11 ± 0.73. The CCL17 concentration-response curves were analysed for each bin. These data are shown in Figure 5 and the results of fitting a Hill function to these data are presented in Table 8. The potency and maximal response of the chemokine increased with increasing receptor density. Interestingly, the basal F-actin content also increased in the CD4+ CCR4+ lymphocytes with increasing receptor density (two-factor anova, by CCR4 expression bin and donor, showed a highly significant effect of CCR4 expression level on basal F-actin content, P < 10−6). Two-factor anova also showed a significant effect of CCR4 expression level on all of the curve fit parameters: basal, P∼0.003; pEC50, P∼0.0023; Emax, P∼4 × 10−9; logn, P∼0.015. The maximal response to CCL17 relative to CCL22 in each bin remained essentially constant (low – high: 0.93 ± 0.06; 0.91 ± 0.06; 0.88 ± 0.05; 0.91 ± 0.03; 0.88 ± 0.03).
Figure 5.
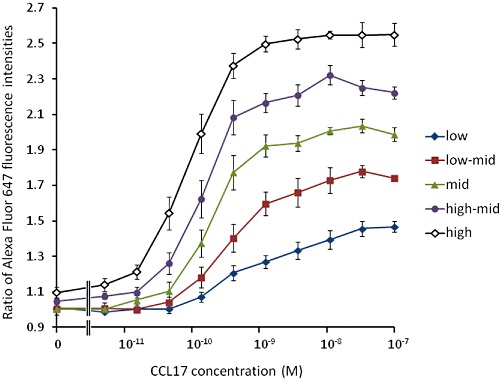
CCL17-induced increases in the F-actin content of human CD4+ CCR4+ cells expressing low, low-mid, mid, high-mid and high levels of CCR4. Data are the mean of four determinations in separate donors and vertical bars show the SEM.
Table 8.
Summary of the parameters of the concentration-response curves to CCL17 at different mean CCR4 expression levels
| CCR4 expression | pEC50 | Emax | basal | n |
|---|---|---|---|---|
| Low | 9.01 ± 0.22 | 0.50 ± 0.03 | 0.98 ± 0.01 | 0.74 (0.52, 1.06) |
| Low-mid | 9.35 ± 0.21 | 0.78 ± 0.03 | 0.99 ± 0.02 | 1.12 (0.71, 1.79) |
| Mid | 9.70 ± 0.11 | 0.99 ± 0.04 | 1.01 ± 0.02 | 1.36 (0.62, 2.97) |
| High-mid | 9.85 ± 0.10 | 1.19 ± 0.05 | 1.06 ± 0.01 | 1.58 (1.38, 1.81) |
| High | 10.04 ± 0.10 | 1.44 ± 0.08 | 1.10 ± 0.03 | 1.38 (1.19, 1.59) |
Values are the mean ± SEM of four determinations in separate donors except for n, which is presented as geometric mean with 95% confidence interval in parentheses.
The data were also analysed using equations 6 and 12 (equation 7 was eliminated as an option since double reciprocal plots of equieffective concentrations of CCL17 and CCL22 were consistent with a binding isotherm Hill coefficient of unity, see Appendix and Discussion, data not shown). The results of the curve fits are shown in Table 9 and representative curve fits are shown in Figure 6. The estimates of Ka and ε from fitting 6 were 0.1 nmol·L−1 and 1.8, respectively, while those from fitting 12 were 0.24 nmol·L−1 and 113.5. In each case, the estimate of χ increased with increasing receptor density (as determined flow cytometrically). Assuming that Ke is the same in each population, the ratios of the values of χ should correspond to their relative receptor densities. The geometric mean ratios χ/χlow for the higher expressing populations were equation 6: 1.1, 1.3, 1.4 and 1.6; and equation 12: 2.2, 4.3, 7.8 and 18.0. The latter are much more consistent with the values obtained flow cytometrically.
Table 9.
Summary of the parameters derived by fitting equations 6 and 12 to the CCL17 concentration-response curves at different CCR4 expression levels
| Parameter | Equation 6 | Equation 12 |
|---|---|---|
| Emax | 1.75 ± 0.07 | 1.90 ± 0.09 |
| pKa | 10.00 ± 0.19 | 9.61 ± 0.17 |
| logε | 0.27 ± 0.21 | 2.05 ± 0.09 |
| logχ (low) | −0.35 ± 0.27 | −2.58 ± 0.11 |
| logχ (low-mid) | −0.29 ± 0.23 | −2.24 ± 0.10 |
| logχ (mid) | −0.25 ± 0.19 | −1.95 ± 0.10 |
| logχ (high-mid) | −0.21 ± 0.17 | −1.69 ± 0.10 |
| logχ (high) | −0.15 ± 0.11 | −1.33 ± 0.09 |
| logn | 1.24 ± 0.29 | n/a |
| log(k-/min−1) | n/a | 0.38 ± 0.12 |
| basal | 0.98 ± 0.02 | 0.97 ± 0.02 |
Data are presented as mean ± SEM.
Figure 6.
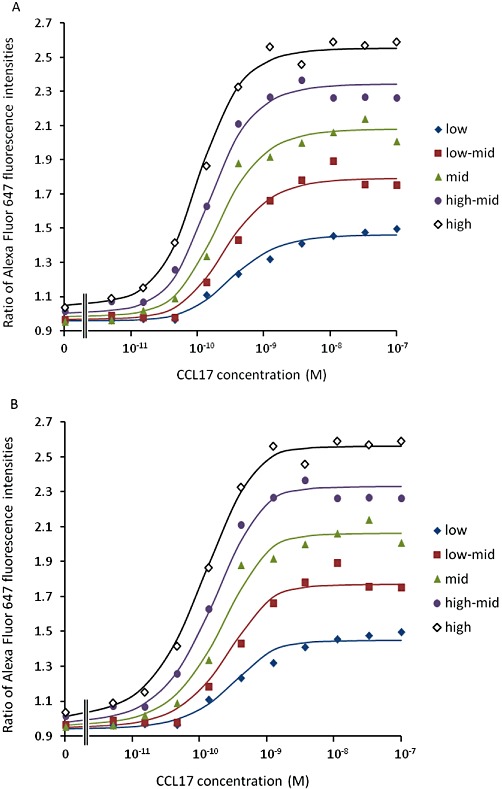
The fit of equations (A) 6 and (B) 12 to the T cell actin polymerization data. Data from the same representative experiment are shown in each case. The solid lines are the curve fits. A single determination of the effect of each concentration of agonist was made.
Discussion
In this report, we have studied two sets of data whose behaviour is consistent with that of an agonist displaying differing levels of efficacy. In the T cell studies, the potency of and maximal response to CCL17 (and indeed CCL22, not shown) increased with increasing receptor density and in the [35S]GTPγS binding experiments, the potency of and maximal response to the agonists decreased with increasing GDP concentration. These data sets thus invite an attempt to determine the affinity and efficacy of the agonists. However, in both cases, the response in the absence of agonist also increased as the coupling efficiency of the assay systems increased, indicating constitutive activity. This alone indicates that the use of the operational model is inappropriate because this model does not include constitutive receptor activity (although the simulations indicate that when the change in maximal response is not large, the estimate of affinity derived from such a fit would not be very inaccurate). Similarly, as demonstrated in the Appendix, Furchgott's method also fails when applied to systems which show constitutive activity. Secondly, the significant deviation of the slope of the concentration-response curve from unity prevents the application of Hall's model (equation 4). This motivated the derivation of equations 6, 7 and 8 (and A5 + A6) to model the potential alternative sources of non-unit Hill coefficients of a concentration-response curve: the transducer function (the approach taken by Black and Leff) and the binding isotherm or indeed both. Also, since the actin polymerization assay has a very short agonist contact time (15 s) due to the rapid decay of the response, another possibility is that low concentrations of the agonist do not reach steady-state with the receptor during the agonist incubation period. To investigate this possibility, a further model was derived (equation 12) in which the binding of the agonist was assumed to be first order, under pre-steady-state conditions and rate limiting for the response.
The viability of fitting these models to experimental data was explored through Monte Carlo simulations. As shown in Tables 1–4, it was generally possible to derive accurate estimates of the parameters of the models described by equations 6 and 7 (and indeed A5 + A6, see Table A2) from simulated data sets, although multiple replicate determinations may be required to achieve a good level of accuracy in some cases. The parameters of equation 6, at least, can be estimated from as few as two concentration-response curves although rather greater precision can be achieved if a larger number of curves are included in the analysis. In contrast, the parameters of equation 8 were very imprecisely estimated in the simulations. Thus, it seems that two Hill coefficients cannot be unambiguously estimated from a family of up to five concentration-response curves. On a further practical note, the derivation of accurate estimates of ε and Ka requires the ligand to be partial for at least one value of χ studied in the experiment. For an inverse agonist, this may require quite high levels of expression. The analysis of an inverse agonist also requires an independent estimate of Emax or simultaneous analysis of a full agonist to estimate this parameter accurately.
The situation with equation 12 was a little more complicated. Most of the parameters were well estimated in the simulations. However, this was not true of k- which was estimated rather imprecisely. This is perhaps not surprising given that estimating k- from these data is an attempt to estimate a rate constant from a measurement at a single time point. Thus, it may be better to treat k- in this model simply as an arbitrary slope parameter (much as a Hill coefficient) rather than as a true estimate of the rate constant. Also, fits to two out of the 50 simulated data sets returned extremely inaccurate estimates of Ka and k- Given the extremely aberrant nature of the estimates from such data sets, it should be possible to identify and disregard them should they occur. Hence, equation 12 may still be of some utility notwithstanding the caveat on the estimation of k- when a single time point is used. Overall, therefore, the Monte Carlo simulations suggest that if the models are an adequate description of the experimental system, the parameter estimates derived from fitting them should be accurate.
In the [35S]GTPγS binding experiments, data were generated in the presence of different concentrations of GDP. As the GDP concentration was increased, the potency of and maximal response to the two agonists decreased and the maximal response to CCL17, relative to that of CCL22, was reduced. This behaviour is consistent with that expected if the efficacy of the two agonists decreases with increasing GDP concentration, presumably due to a decrease in the coupling efficiency of the system. This seems a reasonable interpretation since GDP competes for the binding of [35S]GTPγS to the activated G-protein. The level of spontaneous [35S]GTPγS binding was also reduced, in both CHO-CCR4 and CHO-K1 membranes, by increasing GDP concentrations (as expected; see Bidlack and Parkhill, 2003) again consistent with a decrease in coupling efficiency. Thus, the behaviour of the concentration-response curves at increasing GDP concentrations is consistent with that of a system with decreasing coupling efficiency. Since the receptor density in the membrane preparation is constant, this must be because, in model terms, GDP decreases χ by increasing Ke.
The data from the [35S]GTPγS binding experiments were fitted with equations A5 and A6 (i.e. assuming binding isotherms with non-unit Hill coefficients) since the competition binding studies with CCL22 and CCL17 indicated that the binding isotherms of the two agonists had non-unit Hill coefficients in the SPA assay. Indeed, the estimates of the Hill coefficient from the fits of equations A5 + A6 and those from the binding assays were not significantly different (anovaP > 0.05) supporting the choice of this model. Overall, the fit of this model is adequate. The fits then suggest that CCL22 has 1.6-fold higher affinity than CCL17 at CCR4 under the experimental conditions and approximately threefold higher intrinsic efficacy. However, the estimates of the agonist affinities are rather different from those obtained in the equilibrium binding experiments. This is not unexpected since the binding experiments were performed in the absence of guanine nucleotides with an agonist radioligand and hence measure the affinity of the chemokines for the high-affinity state of the receptor while the [35S]GTPγS binding experiments are performed in their presence and hence measure binding to a different state of the receptor. Interestingly, the affinities of CCL22 and CCL17 derived from the radioligand binding assays were very similar when measured in membranes and whole cells. Given that the binding of [125I]CCL17 to membranes from the CCR4 transfectants was abolished in the presence of GTP (data not shown), this suggests that there are CCR4:G-protein complexes present in the cells which are sequestered from cellular nucleotides and hence exhibit high affinity for the agonist. This putative sequestration appears to have been disrupted in the membranes.
The T cell studies capitalized on the previous observation from several laboratories (e.g. Andrew et al., 2001) that circulating human CD4+ CCR4+ lymphocytes show a wide range of CCR4 expression. When these cells were subdivided into five populations with contiguous ranges of CCR4 expression, the responses to CCL17 also behaved in a manner which is consistent with our expectations from classical receptor theory. That is, both the maximal response to the agonist and its potency increased with increasing receptor density. The increase in basal F-actin content of the T cells with receptor expression suggests either that CCR4 is exhibiting constitutive activity or that an agonist of CCR4 is present in the PBMC preparations. The observation (for an example see Supporting Information Figure S3) that several CCR4 antagonists, which show no inverse agonist activity in the [35S]GTPγS binding assays, had no effect on the basal F-actin content of the T cells suggests that constitutive receptor activity is the more likely explanation. Constitutive activity has been described for other chemokine receptors (Hall et al., 1999; Wan et al., 2002) but we are not aware that this phenomenon has previously been reported for CCR4.
As shown in Figure 6, equations 6 and 12 were both a plausibly good fit to the data. However, there are two aspects of the fitted parameter estimates which suggest that equation 12 is the better model. Firstly, the estimate of the Hill coefficient of the transducer function from the fit of equation 6 is extremely high (17.5), which seems implausible. Secondly, the χ/χlow ratios from the fit of equation 6, which (assuming Ke is constant) should reflect the differences in receptor expression level, were all less than two, much lower than the flow cytometric estimates. The χ/χlow ratios derived from fitting equation 12 are in much better agreement. Also, fitting equation 6 to simulated data generated with equation 12 results in very variable estimates of ε, n and the coupling efficiencies and can result (7/50 families) in estimates similar in structure to those in Table 9 (not shown). Thus, it seems most likely that the steep concentration-response curves to CCL17 in this assay system are due to pre-steady-state binding of the agonist due to the short agonist contact time in the assay rather than due to the properties of the signal transduction system. The fit of 12 then implies that CCL17 is a reasonably efficacious agonist at CCR4 (ε∼110) (although given the lack of published comparators, this is a somewhat subjective judgement). The estimated affinity of CCL17 for CCR4 from the two fits are both consistent with that from the competition binding experiments and with published values (pKi∼9.26; Imai et al., 1998). The value of k- derived from equation 12 is 2.4 min−1, which implies rather rapid binding kinetics (other CC chemokines have been shown to have rather slower dissociation kinetics albeit under rather different conditions, for example Jensen et al., 2008). However, given the results of the simulations, this value should be treated with some caution.
The results of the analysis of the T cell data should perhaps be treated with a degree of caution for two reasons. Firstly, the effects of naturally occurring differences in receptor density were studied rather than the effects of acutely reducing the available receptor number by irreversible modification. The chronic expression of differing levels of CCR4 may result in differing adaptive changes in the expression of the Gi-protein(s) to which it couples affecting Emax, which was assumed to be the same in all cell populations. If Emax did vary systematically with CCR4 expression, this would affect the estimate of ε and χ since it would affect the relationship between receptor density and the basal activity and maximal response. The good agreement between the relative receptor densities estimated from fitting equation 12 and by flow cytometry may therefore indicate that this is not an issue. This, of course, suggests that generation of recombinant cell lines with a variety of receptor densities also provides an experimental strategy for quantifying agonist efficacy if some of these lines display constitutive activity. Modern transient expression technologies such as BacMam transduction or inducible expression systems may be particularly useful in this regard. Secondly, in the derivation of equation 12, it was assumed that the response is dependent on the concentration of the agonist:receptor complex achieved at 15 s after addition of the agonist. This is clearly an approximation at least at low concentrations of agonist (high concentrations will reach steady-state very rapidly due to mass action), which will affect the estimate of Ka (though less so that of ε due to its dependence on the maximal response which is independent of Ka). The fact that the estimate of Ka is in reasonable agreement with the radioligand binding data, however, suggests that this approximation is not unreasonable in this case. A further related complication is the transiency of the increase in F-actin in response to agonist. This may affect the relationship between stimulus and response when measurements are taken at the same time point, particularly if the response kinetics differ at different receptor expression levels. It is not clear whether this was a confounding factor in the current analysis.
Comparing the model fits to the two sets of data, it is particularly noteworthy that the estimates of ε for CCL17 between the two experimental systems are quite different (∼10 vs. ∼110). One trivial explanation for this is simply that one (or both) of the model fits is generating erroneous estimates. However, in general, the theory and assumptions on which they are based are well supported by published data (see below). It is possible that the assumption in the derivation of equations A5 and A6 that Emax can be shared is not correct but this is unlikely to result in such a large difference in the estimate of ε. Also, we should bear in mind that the two experimental systems do differ somewhat. CCR4 is expressed endogenously by T cells and is coupled to human G-proteins in these cells while in the CHO transfectants, the recombinant receptor is coupled to non-human G-proteins, which may well be expressed in different ratios. The assays were also performed at different temperatures. Thus, the difference in the estimate of ε between the two systems may reflect a real difference in the ability of CCL17 to change the interaction of CCR4 with G-proteins in the two systems.
The models themselves follow well-precedented approaches to modelling pharmacological systems. As demonstrated in Hall (2006), equation 3 (and hence 4) can be derived as a special case of the ternary complex model and the ‘Derivation of the Models’ section describes further its close relationship with the operational model. Indeed, Black and Leff's operational model equations are the special cases of equations 4 and 5 when χ < < 1. In this case, 1 +χ ≍ 1 and the χKa term becomes negligible (since there is no measurable basal activity) making, for example, equation 4.
which is the operational model equation. This also reminds us that Black and Leff had to define τ to include both intrinsic efficacy and signal transduction, because it only becomes possible to separate these aspects of agonist action in the presence of measurable constitutive activity. This begs the question of how ε should be interpreted. In a system where receptor expression is sufficiently low and receptor activation poorly coupled, constitutive activity will be undetectable. In that case, the stimulus S=[R]+ε[AR] ≍ ε[AR] and the response is given by E=f(S) =f(ε[AR]), which is identical to Furchgott's assumption. This strongly suggests that we may interpret the ε derived from analysis of a system with constitutive activity as a measure of intrinsic efficacy. In essence, the differences in constitutive activity at different values of χ provide us with sufficient information about the behaviour of the transducer function to separate its contribution from the intrinsic efficacy of the agonist. Ehlert et al. (2011) have recently described a method which exploits constitutive activity to estimate the affinity of ligands for the active and inactive states of a receptor (based on the two-state model) under certain conditions. Our model takes a less mechanistic approach defining agonist intrinsic efficacy as the increase in the ability of an agonist receptor complex to activate signal transduction compared with free receptor, and is hence not dependent on a specific mechanistic model. However, it is possible to map the parameters from either model onto the other and this is shown in the Supporting Information Appendix S1. This analysis shows that Ka/ε derived from equation 6 is equal to the affinity of the ligand for the active state of the receptor (assuming a two-state model is appropriate) and that it becomes impossible to determine the affinity of agonists for the inactive state of the receptor when their binding strongly favours the active state. Also, under certain circumstances, Ka derived from equation 6 is a good approximation for the affinity of the ligand for the inactive state of the receptor and ε is a good approximation for the ratio of the affinities for the active and inactive states (the intrinsic efficacy parameter of the two-state model).
As χ is a ratio of two parameters, it can be varied by changing [R]T or by varying Ke. The most obvious system where the latter may be possible is in the [35S]GTPγS binding assay (or its non-radioactive alternatives) and this is what we have attempted. Part of the standard optimization of this technique is to vary the GDP concentration to identify a concentration (usually low micromolar) at which the agonist-stimulated binding is optimal (Bidlack and Parkhill, 2003). As noted above, the concentration of receptor ([R]T) and G-protein (a contribution to Emax) in the assay is constant, so the effect of GDP must be on the efficiency of coupling to the G-protein, that is, Ke. Also, in many cases, the level of constitutive activity varies markedly over the full concentration-effect curve for GDP providing the opportunity to construct concentration-response curves with a wide range of basal responses, hence providing a large amount of information on the transducer function. Thus, the GTPγS binding assay may provide a simple, routine method for quantifying the intrinsic efficacy of agonists at G-protein-coupled receptors. We note, however, that in our experiments, the estimated affinity and intrinsic efficacy of CCL17 differ somewhat between the two systems studied. This could reflect real differences between the two systems or indicate that varying the GDP concentration is not an appropriate strategy to explore the transducer function. Further experiments comparing receptor inactivation with varying GDP concentrations are required to determine this. Irreversible antagonists are not available for CCR4, preventing us from making this comparison in the present systems.
Another pharmacological phenomenon to which this method of analysis is relevant is that of biased agonism (Urban et al., 2007). The implication of this observation is that to fully characterize an agonist, we would need to define a value of ε for each signal transduction system to which its receptor couples. Of course, these estimates could then be used to measure the degree of functional selectivity exhibited by that agonist. Indeed, the difference between the estimates of ε for CCL17 in this report is essentially a form of biased agonism.
In summary, in this report, we have derived operational models of agonist action which include constitutive receptor activity and allow for non-unit Hill coefficients. These models and the original model presented in Hall (2006) are generalizations of the operational model and are compatible with Furchgott's concept that the response to an agonist is a function of the pharmacological stimulus in the presence of that agonist. Further, we have shown that the parameter which represents efficacy in these models is consistent with Furchgott's concept of intrinsic efficacy and that this can be measured directly when the system under consideration shows constitutive activity. These models have been applied to the effects of CCL22 and CCL17 at the chemokine receptor CCR4.
Acknowledgments
This study was entirely supported by GSK.
Glossary
- F-actin
filamentous actin
- FITC
fluorescein isothiocyanate
- CCL22
macrophage-derived chemokine (MDC)
- PBMC
peripheral blood mononuclear cell
- PE
phycoerythrin
- CCL17
thymus and activation-related chemokine (TARC)
Appendix
Comparison of full and partial agonists to estimate relative intrinsic efficacy
The derivations will be made from equation 8. Let A be the reference (full) agonist and let B be a partial agonist. Equating equieffective concentrations of the two agonists gives:
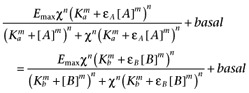 |
where Emax is the maximal response, χ is the coupling efficiency, Ka is the dissociation constant of A, Kb is that of B, εA is the intrinsic efficacy of A, εB is that of B, m is the Hill coefficient of the binding isotherms, n is the Hill coefficient of the transducer function and basal is the activity in the absence of agonists. It has been assumed that the Hill coefficients of both the transducer function and the binding isotherms are common. Cancelling common terms, this becomes
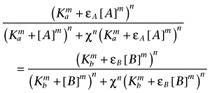 |
Cross multiplying and cancelling the resulting common terms then gives
from which
| (A1) |
In theory then (but see below), a plot of [A]-m versus [B]-m, where [A] and [B] are equieffective concentrations of the two agonists, should yield a straight line and hence allow estimation of m. Of course, when m= 1 a simple double reciprocal plot should yield a straight line. The intercept of these plots can then be used to determine the relative efficacy of the two agonists if the Ka is known: if εB is sufficiently large that εB− 1 ≍ εB then
and if εA is already known this can then be used to estimate εB. Indeed, when both Ka and εA are known the approximations are unnecessary since the expression for the intercept can be rearranged to give,
Alternatively, following the derivation of Waud (1969), if the reference agonist is sufficiently efficacious that we may assume that [A] << Ka, then 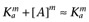 and
and 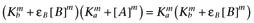 , which leads to the expression
, which leads to the expression
| (A2) |
which again allows a good approximation to the relative efficacy of the two agonists to be determined for all but the least efficacious ligands, assuming Ka is known, and the absolute measurement of εB if both of the pharmacological parameters of A are known. In this case, the affinity of B can also be determined since  This is also true for equation A1 if εA > > εB > 1.
This is also true for equation A1 if εA > > εB > 1.
However, there is a practical issue with the foregoing discussion, at least where we cannot assume that m= 1. The random errors in the data generally result in the concentration-response curves to the two agonists having different Hill coefficients when equation 1 is fitted. Simulations indicate that the resulting double reciprocal plots of equieffective concentrations are curved even when the true value of m is used. They also indicate that the value of m, which results in a straight line for the double reciprocal plot is generally not a good estimate of its true value. Hence, an independent estimate of m, the Hill coefficient of the binding curves, is required for this analysis (if it cannot be assumed to be unity). If the concentration-response curve to A has a Hill coefficient greater than that to B, the double reciprocal plot is convex (the intermediate points lie above the line joining the endpoints) while it is concave if the curve to B is steeper than that to A. Thus, an incorrect estimate for m can be identified if the replots do not obey this rule, though the converse cannot be assumed.
The simulations also suggest that even when the double reciprocal plot is curved, it is still possible to estimate the slope and intercept of the theoretical straight line reasonably well: four sets of conditions were tested, measurable constitutive activity (χ= 0.15 with εA= 300 and εB= 10) and very low constitutive activity (χ= 0.015 with εA= 2000 and εB= 100) with m= 1 and m= 0.7. Other parameters were n= 1, Ka= 1, Kb= 0.2, Emax= 1.5, basal= 0.9. The values of εA and εB gave maximal responses for A of ∼0.97Emax and for B of 0.6Emax. Twelve-point singlet curves (as described in the Methods) were generated for each agonist. Ten simulated pairs of curves were generated under each condition with Gaussian errors with a standard deviation of 3% of the mean response. Ten equieffective concentrations of the agonists were then used to generate the double reciprocal plots which ranged from the EC50 to the EC99 of the partial agonist (this seems to give the best estimates). Linear regression was performed on the resulting curves. The results are summarized in Table A1 and show good agreement between the estimates and the true values.
Table A1.
Summary of the slope and intercept of linear regressions performed on simulated values of 1/[A]m and 1/[B]m for pairs of concentration-response curves generated using equation 8 with the parameters listed in the text. Estimates are mean ± SD
| m | χ | Slope | Estimate | Intercept | Estimate |  |
Estimate |
|---|---|---|---|---|---|---|---|
| 1 | 0.15 | 6.6 | 6.2 ± 1.5 | 32.2 | 29.5 ± 2.6 | −0.69 | −0.69 ± 0.13 |
| 1 | 0.015 | 4.0 | 4.0 ± 0.6 | 19.2 | 18.3 ± 3.5 | −0.68 | −0.65 ± 0.09 |
| 0.7 | 0.15 | 10.8 | 11.6 ± 3.7 | 32.2 | 30.8 ± 5.8 | −0.48 | −0.43 ± 0.20 |
| 0.7 | 0.015 | 6.5 | 6.8 ± 1.1 | 19.2 | 19.4 ± 3.6 | −0.47 | −0.46 ± 0.12 |
The analogous expression to equation A1 derived from equation 12 is
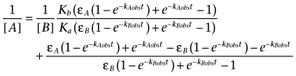 |
which, while rather complicated, shows that the double reciprocal plot should be a straight line if the binding isotherm has a Hill coefficient of unity.
Furchgott's method for analysis of receptor inactivation experiments fails in systems with constitutive activity
In a system without constitutive activity, the assumption that equal responses result from equal stimuli allowed Furchgott (1966) to show that a double reciprocal plot of equieffective concentrations of agonist before and after irreversible inactivation of a proportion of the receptor population should be linear and that the slope and intercept of this line could be used to estimate agonist affinity. However, as shown below, in a system with constitutive activity such a double reciprocal plot does not result in a linearization of the data. Following Furchgott's derivation, let f be the transducer function and the stimulus, again, be given by S=[R]+ε[AR] then, under control conditions we obtain
where, as above, ε is the efficacy of the agonist, Ka is its dissociation constant and [R]T is the receptor density in the preparation. After inactivation of a fraction, q, of the receptor population the response is given by
Assuming that equal responses result from equal stimuli gives
After further manipulation, this yields
| (A3) |
which can be rearranged to give the following double reciprocal relationship
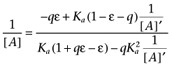 |
(A4) |
which is clearly not linear, indeed the curve it describes is rectangular hyperbolic in 1/[A]'. At first glance, however, there seems no reason not to attempt to fit this relationship to an appropriate set of data. Unfortunately, preliminary investigation of this analysis using simulated data sets suggests that it is very readily confounded by (simulated) experimental error giving extremely poor estimates of ε and Ka. Hence, we have not applied it to the data presented in this report. It is, however, noteworthy that under conditions where terms in ε dominate the numerator and denominator of equation A4, this equation becomes
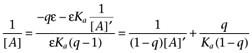 |
which is Furchgott's equation. Thus, equation A4 represents a general relationship from which Furchott's method of analysis may be derived as a special case, when agonist efficacy is high. This provides further support for the proposal that ε defined above is equivalent to Furchgott's intrinsic efficacy.
A model for data derived from [35S]GTPγS binding experiments, which vary basal activity by varying the GDP concentration
To allow the modelling framework to be applied to [35S]GTPγS binding assay data where the basal activity is manipulated by varying the GDP concentration requires the following phenomena to be incorporated into the model. Firstly, there are other receptors present in cell membranes which may contribute to the constitutive activation of the G-proteins (as evidenced by the presence of GDP-sensitive [35S]GTPγS binding in membranes from CHO-K1 cells, see Supporting Information Figure S4). Secondly, the level of constitutive activity is related to the concentration of GDP present in the assay. To allow for the former a second receptor species (R2) will be include in the model. The latter will be included by assuming that the presence of GDP changes Ke by the factor (1 + ([GDP]/KGDP)s) where KGDP is the apparent affinity of GDP and s is a Hill coefficient, to reflect the competition of GDP with the [35S]GTPγS for binding to the G-protein α-subunit.
We may then write
where R is the receptor of interest and R2 represents the contribution of the other receptors in the system. Substituting the binding isotherms (allowing for non-unit slopes) gives
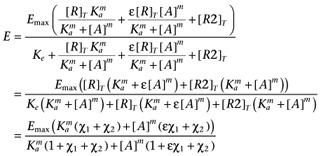 |
where χ1 is the transducer constant of R and χ2 is the transducer constant for R2, Ka is the dissociation constant of A, ε is the intrinsic efficacy of A and m is the Hill coefficient of the binding isotherm for A. The use of the same value for Ke as the midpoint of the transducer function for both R and R2 is a mathematical convenience, however, since the objective of introducing R2 is simply to account for basal activity which is not related to R, this should not present any issues. The GDP dependence can then be incorporated by replacing Ke with the term Ke(1 + ([GDP]/KGDP)s) to give.
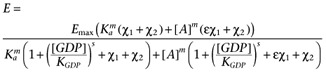 |
In this case, the use of the same value of KGDP for both R and R2 in the model is justified by our observation that the GDP dependence of the basal activity is similar in both CHO-CCR4 and CHO-K1 cells (Supporting Information Figure S4). Again, it is necessary to include the term, basal, to allow for receptor-independent binding of the radioligand to give equation A5.
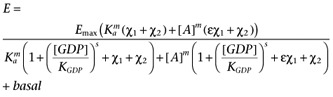 |
(A5) |
Finally, assuming that the process of transfection and selection of a clonal cell line does not alter the overall contribution of the other receptors present in CHO-CCR4 cells, we can estimate χ2 from the GDP dependence of basal [35S]GTPγS binding in CHO-K1 cell membranes by fitting equation A6 (below) to such data simultaneously with fitting A5 to the concentration-response curve data from the recombinant cell membranes and sharing the estimates of the common parameters.
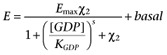 |
(A6) |
Note, A6 is simply A5 with χ1 set to zero. The results of a simulation of fitting equations A5 and A6 to simulated experimental data are summarized in Table A2. As expected for the large number of curves per simulated experiment, the parameters of these equations were found to a high degree of precision and accuracy.
Table A2.
Summary of the input parameters and their estimates derived from 50 simulated data sets using equations A5 and A6. Eight simulated singlet concentration-response curves were generated per data set to partially mimic the replication used in the [35S]GTPγS binding experiments. Simulated variability was as described in the Materials and Methods. Parameter estimates are presented as mean ± SD
| Emax/1000 | pKa | logε | logχ1 | logχ2 | |
|---|---|---|---|---|---|
| Input | 16.3 | 0.48 | 1.48 | −0.12 | 0.18 |
| Output | 16.2 ± 1.1 | 0.48 ± 0.05 | 1.49 ± 0.04 | −0.13 ± 0.05 | 0.18 ± 0.03 |
| logm | basal/1000 | KGDP | logs | ||
|---|---|---|---|---|---|
| Input | −0.07 | 0.70 | −0.30 | −0.11 | |
| Output | −0.07 ± 0.03 | 0.69 ± 0.07 | −0.3 ± 0.04 | −0.10 ± 0.03 |
Conflicts of interest
None.
Supporting information
Additional Supporting Information may be found in the online version of this article:
Figure S1 An example of a simulated family of curves based on Equation 6 with the following parameters: Emax = 1.5, Ka = 0.2, =30, n = 2, basal = 0.9, χhigh =0.4, χhigh-mid = 0.2, χmid = 0.1, χlow-mid =0.05, χlow = 0.0025. The parameters derived from fitting Equation 6 to these data were: Emax = 1.52, Ka = 0.20, = 30.6, n =1.93, basal = 0.92, χhigh = 0.44,χhigh-mid = 0.21, χmid= 0.11, χlow-mid = 0.06, χlow = 0.002. The sum of squared residuals for the fit was 0.1646.
Figure S2 The effect of CCL22 (diamonds) and CCL17 (squares) on the binding of [125I] TARC to CHO-CCR4 membranes (A) or cells (B). Data are the mean of four separate determinations and vertical bars show the SEM.
Figure S3 The effect of the absence (red bars) or presence (blue bars) of the CCR4 inhibitor (300 nmol·L−1) whose structure is inset (from patent WO2004020584A2) on the basal F-actin content of human CD4+ CCR4+ cells expressing different levels of CCR4. The cells were incubated with the antagonist for 30 min prior to the point at which agonist would be added (vehicle was added in this case). In [35S] GTPγS binding experiments in the presence of 1 μM GDP and 1% BSA to match the T cell assays, the basal level of [35S] GTPγS bound was 6.1 × 103 ± 0.2 × 103 ccpm in the absence of the compound and 5.9 × 103 ± 0.1 × 103 ccpm in the presence of the same concentration of the compound (n = 4). These were not significantly different (P > 0.05, paired t-test). The apparent pA2 of the antagonist was 7.61 ± 0.06 (n = 21) in the T cell assays and 8.33 ± 0.10 (n = 4) in the [35S] GTPγS binding experiments. The antagonist was synthesised by Respiratory CEDD Medicinal Chemistry, GlaxoSmithKline, Stevenage.
Figure S4 The effect of GDP on the binding of [35S] GTPγS to membranes from CHO-CCR4 or CHO-K1 cells in the absence of agonist. The level of binding in the absence of GDP was 13 710 ± 1950 ccpm in CHO-CCR4 membranes and 10 130 ± 1440 ccpm in CHO-K1 membranes. Data are the mean of 4 separate determinations and vertical bars show the SEM.
Table S1 Summary of the parameters derived by fitting equations 6 and 12 to the CCL22 concentration-response curves at different CCR4 expression levels generated in the same experiments as the CCL17 curves. Data are presented as mean ± SEM. Two of the replicate determinations for CCL22 were too steep and resulted in highly suspect estimates of the parameters of the model. These replicates have been excluded in the ‘trimmed 12’ column and the two ‘acceptable’ replicates are noted
Appendix S1 The relationship between the models derived in this report and that of Ehlert et al. (2011).
Please note: Wiley-Blackwell are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.
References
- Alexander SPH, Mathie A, Peters JA. Guide to receptors and channels (GRAC), 5th edition (2011) Br J Pharmacol. 2011;164:S1–S324. doi: 10.1111/j.1476-5381.2011.01649_1.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrew DP, Ruffing N, Kim CH, Miao W, Heath H, Li Y, et al. C-C chemokine receptor 4 expression defines a major subset of circulating nonintestinal memory T cells of both Th1 and Th2 potential. J Immunol. 2001;166:103–111. doi: 10.4049/jimmunol.166.1.103. [DOI] [PubMed] [Google Scholar]
- Bidlack JM, Parkhill AL. Assay of G protein-coupled receptor activation of G proteins in native cell membranes using [35S]GTPγS binding. Methods Mol Biol. 2003;237:135–143. doi: 10.1385/1-59259-430-1:135. [DOI] [PubMed] [Google Scholar]
- Black JW, Leff P. Operational models of pharmacological agonism. Proc R Soc Lond B Biol Sci. 1983;220:141–162. doi: 10.1098/rspb.1983.0093. [DOI] [PubMed] [Google Scholar]
- Colquhoun D. The relation between classical and cooperative models for drug action. In: Rang HP, editor. Drug Receptors. London: The Macmillan Company; 1973. pp. 149–182. [Google Scholar]
- Costa T, Herz A. Antagonists with negative intrinsic activity at δ opioid receptors coupled to GTP-binding proteins. Proc Natl Acad Sci U S A. 1989;86:7321–7325. doi: 10.1073/pnas.86.19.7321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Léan A, Stadel JM, Lefkowitz RJ. A ternary complex model explains the agonist-specific binding properties of the adenylate cyclase-coupled beta-adrenergic receptor. J Biol Chem. 1980;255:7108–7117. [PubMed] [Google Scholar]
- Ehlert FJ, Suga H, Griffin MT. Analysis of agonism and inverse agonism in functional assays with constitutive activity: estimation of orthosteric ligand affinity constants for active and inactive receptor states. J Pharmacol Exp Ther. 2011;338:671–686. doi: 10.1124/jpet.111.179309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furchgott RF. The use of β-haloalkylamines in the differentiation of receptors and in the determination of dissociation constants of receptor-agonist complexes. In: Harper NJ, Simmonds AB, editors. Advances in Drug Research. Vol. 3. New York: Academic Press; 1966. pp. 21–25. [Google Scholar]
- Hall DA. Predicting dose-response curve behaviour: mathematical models of allosteric receptor-ligand interactions. In: Bowery NG, editor. Allosteric Receptor Modulation in Drug Targeting. New York: Taylor & Francis; 2006. pp. 39–78. [Google Scholar]
- Hall D, Ford A, Hodgson S. CCR4 antagonists. Prog Respir Res. 2010;39:161–165. [Google Scholar]
- Hall DA, Beresford IJM, Browning C, Giles H. Signalling by CXC chemokine receptors 1 and 2 expressed in CHO cells: a comparison of calcium mobilisation, inhibition of adenylyl cyclase and stimulation of GTPγS binding induced by IL-8 and GROα. Br J Pharmacol. 1999;126:810–818. doi: 10.1038/sj.bjp.0702329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill AV. The possible effects of aggregation of the molecules of haemoglobin on its dissociation curve. J Physiol. 1910;40:IV–VII. [Google Scholar]
- Imai T, Chantry D, Raport CJ, Wood CL, Nashimura M, Godiska R, et al. Macrophage-derived chemokine is a functional ligand for the CC chemokine receptor 4. J Biol Chem. 1998;273:1764–1768. doi: 10.1074/jbc.273.3.1764. [DOI] [PubMed] [Google Scholar]
- Jensen PC, Thiele S, Ulven T, Schwartz T, Rosenkilde M. Positive versus negative modulation of different endogenous chemokines for CC chemokine receptor 1 by small molecule agonists through allosteric vs orthosteric binding. J Biol Chem. 2008;283:23121–23128. doi: 10.1074/jbc.M803458200. [DOI] [PubMed] [Google Scholar]
- Karlin A. On the application of ‘a plausible model’ of allosteric proteins to the receptor for acetylcholine. J Theor Biol. 1967;16:306–320. doi: 10.1016/0022-5193(67)90011-2. [DOI] [PubMed] [Google Scholar]
- Leff P, Dougall IG, Harper D. Estimation of partial agonist affinity by interaction with a full agonist: a direct operational model-fitting approach. Br J Pharmacol. 1993;110:239–244. doi: 10.1111/j.1476-5381.1993.tb13799.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neubig RR, Spedding M, Kenakin T, Christopoulos A. International Union of Pharmacology Committee on receptor nomenclature and drug classification XXXVIII: update on terms and symbols in quantitative pharmacology. Pharmacol Rev. 2003;55:597–606. doi: 10.1124/pr.55.4.4. [DOI] [PubMed] [Google Scholar]
- Power CA, Meyer A, Nemeth K, Bacon KB, Hoogewerf AJ, Proudfoot AEI, et al. Molecular cloning and functional expression of a novel CC chemokine receptor cDNA from a human basophilic cell line. J Biol Chem. 1995;270:19495–19500. doi: 10.1074/jbc.270.33.19495. [DOI] [PubMed] [Google Scholar]
- Smith PK, Krohn RI, Hermanson GT, Mallia AK, Gartner FH, Provenzano MD, et al. Measurement of protein using bicinchoninic acid. Anal Biochem. 1985;150:76–85. doi: 10.1016/0003-2697(85)90442-7. [DOI] [PubMed] [Google Scholar]
- Thron CD. On the analysis of pharmacological experiments in terms of an allosteric model. Mol Pharmacol. 1972;9:1–9. [PubMed] [Google Scholar]
- Urban JD, Clarke WP, von Zastrow M, Nichols DE, Kobilka B, Weinstein H, et al. Functional selectivity and classical concepts of quantitative pharmacology. J Pharmacol Exp Ther. 2007;320:1–13. doi: 10.1124/jpet.106.104463. [DOI] [PubMed] [Google Scholar]
- Wan Y, Jakway JP, Qiu H, Shah H, Garlisi CG, Tian F, et al. Identification of full, partial and inverse CC chemokine receptor 3 agonists using [35S]GTPγS binding. Eur J Pharmacol. 2002;456:1–10. doi: 10.1016/s0014-2999(02)02621-3. [DOI] [PubMed] [Google Scholar]
- Waud DR. On the measurement of the affinity of partial agonists for receptors. J Pharmacol Exp Ther. 1969;170:117–122. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


