A CANDLE for a deeper in vivo insight

Abstract

A new Collaborative Approach for eNhanced Denoising under Low-light Excitation (CANDLE) is introduced for the processing of 3D laser scanning multiphoton microscopy images. CANDLE is designed to be robust for low signal-to-noise ratio (SNR) conditions typically encountered when imaging deep in scattering biological specimens. Based on an optimized non-local means filter involving the comparison of filtered patches, CANDLE locally adapts the amount of smoothing in order to deal with the noise inhomogeneity inherent to laser scanning fluorescence microscopy images. An extensive validation on synthetic data, images acquired on microspheres and in vivo images is presented. These experiments show that the CANDLE filter obtained competitive results compared to a state-of-the-art method and a locally adaptive optimized nonlocal means filter, especially under low SNR conditions (PSNR<8dB). Finally, the deeper imaging capabilities enabled by the proposed filter are demonstrated on deep tissue in vivo images of neurons and fine axonal processes in the Xenopus tadpole brain.

Introduction

In vivo fluorescence microscopy enables the direct observation of living cells within their natural environment. Based on endogenous autofluorescence (Husson et al., 2007; Shibuki et al., 2003) or exogenous fluorochomes such as green fluorescent protein, in vivo fluorescence microscopy can provide 3D information on the structure and the various functions of the cell at sub-cellular resolution. Since its introduction in biology, fluorescence microscopy has enabled the elucidation of numerous biological phenomena. However, despite its many advantages, the utility of fluorescence microscopy for imaging living material is limited by the number of photons exciting the fluorophore of interest and the efficiency in collecting emitted photons. Although the number of fluorescent emitted photons increases linearly in proportion to excitation intensity, excessive fluorophore excitation rapidly leads to cell phototoxicity and photobleaching (Carlton et al., 2010). This problem is compounded for deep tissue imaging in biological specimens, as the scattering of ballistic photons increases exponentially as a function of depth, demanding higher excitation intensities to obtain usable fluorescence signal from deep structures. Although multiphoton microscopy enables deeper imaging and reduced phototoxicity compared to confocal microscopy, these images are still practically limited by scattering to less than 1 mm in depth (Kobat et al., 2009; Theer and Denk, 2006). A low number of photons results in a drastic decrease of the signal-to-noise ratio (SNR) in the obtained image. The low SNR of fluorescence microscopy images of living specimens is the main limitation to reducing exposure time to preserve the health of the specimen, as well as the main factor preventing in vivo imaging at greater depths. Improvement of the SNR under low-light conditions therefore has great potential to alleviate both these constraints. In this study, we propose a new denoising filter dedicated to 3D laser scanning multiphoton microscopy imaging under limited-light excitation and show how this filter can help surpass current limits of in vivo imaging in scattering tissues.

Denoising filters aim to improve the SNR of images by removing the noise component while preserving the structural information. Image restoration is a complex problem that has been intensively investigated. In fact, many methods have been proposed to address this open problem (see (Buades et al., 2005) for a review of restoration methods). Recently, a new family of filters has received attention due to its simplicity and high denoising performance. First introduced by Buades and co-workers in 2005, the non-local means (NLM) filter uses pattern redundancy present in images to achieve efficient image denoising by adaptively averaging different occurrences of similar noisy patches (Buades et al., 2005). Since its introduction, this patch-based filter has been intensively applied leading to significant improvements in computer vision (Dabov et al., 2007; Kervrann and Boulanger, 2008; Mairal et al., 2008), medical imaging (Coupe et al., 2009; Coupe et al., 2008; Manjon et al., 2010) and biological imaging (Boulanger et al., 2010; Wei and Yin, 2010; Yang et al., 2010).

In fluorescence microscopy imaging, noise arises from several sources such as thermal noise, photon shot noise, biological background or read-out noise, and non-uniform fluorophore noise (Boulanger et al., 2010; Luisier et al., 2010a; Santamaria-Pang et al., 2008). In such low-light photon-limited images, the random component of this mixture has been modelled by a Gaussian noise locally stationary (Broser et al., 2005; Chan et al., 1993), by Poisson noise (Fudenberg and Paninski, 2009; Kervrann and Trubuil, 2004; Lefkimmiatis et al., 2009; Nowak and Baraniuk, 1999; Rodrigues and Sanches, 2009; Willett and Nowak, 2007) and more recently as a combination of Poisson and Gaussian noise (Boulanger et al., 2010; Luisier et al., 2010a). In this last model, the Poisson component is used to model the limited number of photons while the additive white Gaussian noise component is incorporated to take into account the electronic noise of the detector. The importance of each source varies according to the SNR of the image (Luisier et al., 2010a). For high SNR images, the electronic noise is preponderant; while for low SNR images, the Poisson noise due to photon-detection becomes the main source. The removal of such noise is thus a challenging task with open questions about not only the noise model to use but also on the denoising strategy that should be adopted. Indeed, in a fashion similar to the denoising of natural images, the denoising approaches used in fluorescence microscopy have followed different paradigms such as Partial Differential Equation (PDE)-based techniques (Broser et al., 2005), wavelet-based methods (Delpretti et al., 2008; Dima et al., 2002; Lefkimmiatis et al., 2009; Luisier et al., 2010a; Nowak and Baraniuk, 1999; Santamaria-Pang et al., 2008; Willett and Nowak, 2007; Zhang et al., 2008) and more recently patch-based approaches (Boulanger et al., 2010; de Deckerk et al., 2009; Deledalle et al., 2009; Kervrann and Trubuil, 2004; Yang et al., 2010).

In this study, we present a new Collaborative Approach for eNhanced Denoising under Low-light Excitation (CANDLE), optimal for deep in vivo 3D multiphoton microscopy. Our method is based on a fast pre-filtering of the image before applying a locally-adaptive optimized NLM filter (Coupe et al., 2008). The proposed collaborative approach takes advantage of the robust and fast filtering behaviour of the median filter and the high denoising performance of the NLM filter. Moreover, this approach has the advantage of dealing with the different sources of noise typically present in fluorescence microscopy over a large range of SNR conditions, being particular efficient for very low SNR typically found in deep tissue multiphoton imaging. We present an extensive validation on synthetic, fluorescent bead images and in vivo images and compare our method to the recently published Puredenoise filter and a locally adaptive nonlocal means filter. Denoising results on in vivo neuron images are used to show the possibility of deeper imaging achieved by our method. Finally, we discuss further improvements and potential impact in biological imaging of this new approach.

Material and Methods

Proposed method: CANDLE

In the photon-limited image denoising literature, the classical solution consists of converting highly signal-dependent Poisson noise into locally-stationary noise considered as pseudo-Gaussian (Makitalo and Foi, 2011; Zhang et al., 2008). To achieve this conversion, several variance-stabilization transforms (VST) have been proposed in the past (Anscombe, 1948; Fryzlewicz and Nason, 2004; Starck et al., 1998; Zhang et al., 2008). Once the problem of Poisson denoising is transformed into a classical Gaussian denoising problem by applying a forward VST, a large variety of standard approaches can be used. In the case of very low SNR images, the two major problems are: VST robustness in low count situations (Starck et al., 1998) and the efficacy of the selected denoising filter under very noisy conditions. In the proposed method, an optimal VST and a NLM-based filter are combined to collaborate in the denoising process.

• VST: The most common and simple VST is the Anscombe transform (AT) for Poisson noise (Anscombe, 1948) and its generalized version (GAT) for Poisson-Gaussian noise (Murtagh et al., 1995; Starck et al., 1998). Despite the many advantages of the AT (e.g, simplicity, parameter-free and low complexity), it has been shown that this kind of transform can be unstable under low-count situations (i.e., usually less than 10 photons on average) (Lefkimmiatis et al., 2009; Luisier et al., 2010b; Starck et al., 1998; Zhang et al., 2008), potentially providing a biased estimation. To overcome this limitation, more complex approaches have been proposed such as a multiscale transform (de Deckerk et al., 2009; Fryzlewicz and Nason, 2004; Zhang et al., 2008) or GAT requiring automatic estimation of parameters (Boulanger et al., 2010; Delpretti et al., 2008). Recently, a study has demonstrated that the limitation to using the AT under photon-limited condition is applicable to the backward (i.e., inverse) transform but not to the forward one (Makitalo and Foi, 2011). Based on this observation, a new optimized inverse AT has been proposed. In our method, we use classical AT and the optimal inverse AT as proposed by (Makitalo and Foi, 2011) to tackle the intensity bias introduced by the inverse AT under very photon-limited conditions (even for less than 1 photon on average). In this way, we avoid any estimation of parameters what is a particularly difficult task in very low SNR conditions.

• Denoising filter: Recently, patch-based denoising filters have been intensively investigated due to their simplicity and their high denoising performance over a large range of SNRs. Numerous types of improvements over the original NLM filter (Buades et al., 2005) have been proposed in the last years and a review of them can be found in (Buades et al., 2010). In our paper, we present an adaptation of the 3D optimized non-local means (ONLM) filter (Coupe et al., 2008) in order to address the noise present in fluorescence microscopy images and to make it more robust to the low SNR conditions often encountered when imaging deep in biological specimens with a laser scanning fluorescence microscope. To achieve these goals, we propose to pre-filter the original image to facilitate the patch comparison required by the NLM filter. Then, noisy samples are aggregated according to the similarity of their filtered neighbourhoods.

Overview

Figure 1 shows the overall workflow of the proposed method. First, a copy of the noisy image is pre-filtered using a median filter. Median filtering was chosen for its robustness (Arce, 2005), its low computational burden and because it works directly on the Poisson noise, before VST. In this fashion, the instability of VST under low SNR conditions can be sidestepped. The original noisy image and the median filtered image are then transformed with the AT (Anscombe, 1948) which is fast, simple and does not require any parameter estimation. Afterwards, local noise levels are estimated within the stabilized noisy image by using the Median Absolute Deviation (MAD) estimator in the wavelet transformed domain (Donoho, 1995). This approach is widely used for Gaussian noise estimation due to its robustness. The core of the proposed approach is then the NLM filtering step. In the proposed method, we adapted our ONLM filter, originally proposed for 3D MRI restoration (Coupe et al., 2008), to multiphoton imaging.

Figure 1.

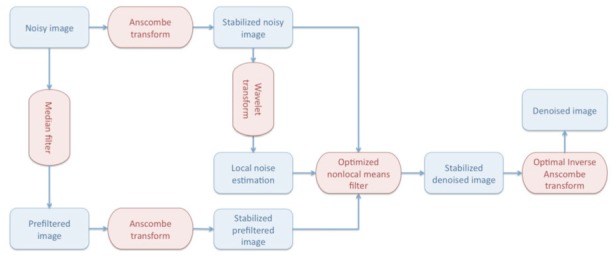
Overall workflow of the proposed method.

The first adaptation of the ONLM is the estimation of patch similarity over the median filtered image, instead of using the noisy input image. By reducing the noise, we provide a more robust patch comparison that enables a better restoration. It is important to note that the weights estimated from the median filtered image are ultimately used to average the noisy input samples. The median filtered image is not used in other steps. The second adaptation of the ONLM is to use the local noise level estimated by using the MAD estimator to deal with inaccuracies of the AT that do not fully handle the non-stationary nature of noise in multiphoton images. The estimated local level of noise is used as the smoothing parameter of the ONLM for each voxel and thus optimally controls the amount of denoising over the image.

Previously, we shown that the ONLM filter yields superior results compared to the classical NLM filter while drastically reducing computational time, which justifies its utilization. Finally, an optimal inverse Anscombe transform (OVST) (Makitalo and Foi, 2011) is used to obtain the final denoised image without intensity bias under very low SNR conditions. The proposed collaborative approach is designed to take advantage of the simplicity and the efficiency of the involved components.

Median pre-filtering

The first step of our collaborative approach is to apply a median filter to the noisy image. Despite the recent proliferation of other denoising methods, the median filter is still the most used filter within the biological community due to its robustness and simplicity. We used a 3×3×3 neighbourhood as is commonly done in the literature (Kobat et al., 2009; Rice et al., 2010). This median filtered image is used exclusively for performing the patch comparison in a more robust manner. The weights estimated from this patch comparison on the median filtered image will by used to average the original noisy samples.

Anscombe and optimal inverse Anscombe transforms

Noise in fluorescence microscopy derives from several sources making the choice of the noise model difficult. At present, the best model to adopt for multiphoton imaging is still an open question. However, in very low SNR situations, the Poisson noise component due to the stochastic nature of photon detection is the most important (Luisier et al., 2010a). Therefore, we consider the VST based on a Poisson noise model.

By considering the observed values z_i as random and independent Poisson variable of underlying intensities y_i, we can write:

$$P(z_i\mid y_i)=\frac{y_i^{z_i}{e}^{-y_i}}{z_i!}.$$ (1)

The main idea of using VST is to transform the signal-dependent noise into quasi-stationary Gaussian noise by applying a square-root-based transform. As widely done in Poisson denoising literature, we used the AT defined as follows (Anscombe, 1948):

$${\text{T}}_a(z)=2\sqrt{z+\frac{3}{8}}.$$ (2)

A denoising filter dedicated to Gaussian noise can be then applied on T_a(z) providing an estimation d̂ of E(T_a(z)| y) (i.e.; the expectation of the desired stabilized value). Due to the nonlinearity of the square-root, the direct inverse transform of the denoised values yields a biased estimation. Therefore, in (Makitalo and Foi, 2011), the authors proposed to build the exact unbiased inverse of the Anscombe transform ${\text{T}}_{ua}^{-1}$ by imposing the mapping of the expectations: ${\text{T}}_{ua}^{-1}:\text{E}({\text{T}}_a(z)\mid y)\mapsto \text{E}(z\mid y)$. Practically, a correspondence table is built using the noise model under consideration. As in (Makitalo and Foi, 2011), we used the following mapping:

$$\text{E}({\text{T}}_a(z)\mid y)=2\underset{0}{\overset{+\infty }{\int }}\left(\sqrt{z+\frac{3}{8}}·\frac{y^z{e}^{-y}}{z!}\right)dz.$$ (5)

This approach can be easily extended to other noise models. In addition, it is parameter-free and fast since it uses a pre-computed correspondence table.

Wavelet-based local noise estimation

The optimal inversion of the AT does not solve the problem of its variance instability within the image. In fact, the AT only asymptotically provides an additive Gaussian noise (Makitalo and Foi, 2011). To address this issue, we propose to locally adapt our denoising of the stabilized image using a robust wavelet-based estimation (Donoho, 1995) of the local noise variance. The wavelet transformation is usually used to obtain a spatial-frequency representation of images. The highest sub-band HHH is essentially composed of coefficients that correspond to the noise, permitting the estimation of noise variance. By using the Median Absolute Deviation (MAD) estimator, the global standard deviation of noise is computed as follows:

$${\widehat{\sigma }}_g=\frac{\mathit{median}(\mid c_i\mid )}{0.6745},$$ (6)

where c_i are the wavelet coefficients of the HHH sub-band. Simultaneously, a local noise estimation is also computed using a restricted area, thus providing an estimation σ̂_i for each voxel. The radius of this restricted area is r_σl = 2r_sv, where r_sv is the radius of the search volume Ω used during the NLM step. Finally, a map of local noise levels is built by assigning σ̂_i = max(σ̂_g, σ̂_l) (see Fig. 2). This approach avoids problems in the background where the stabilized noise can be far from Gaussian noise, resulting in an inaccurate noise estimation.

Figure 2.

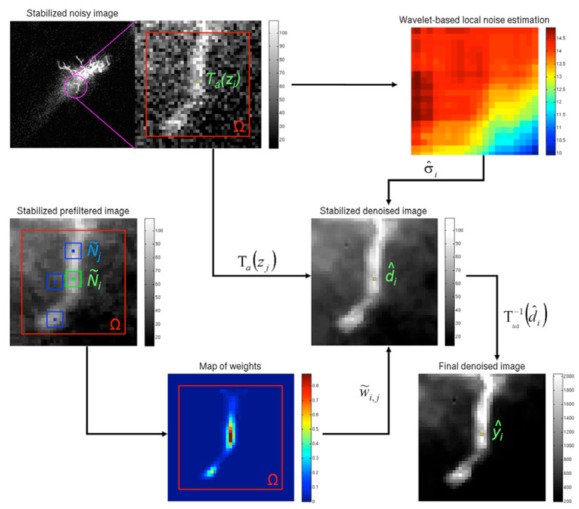
CANDLE illuminated by an example. To obtain the denoised value d̂_i at location x_t, the weights w̃_i,j computed on prefiltered image are used to aggregate the stabilized noisy samples T_a(z_j)by taking into account the local noise level σ̂_i.

The local map of σ̂_i will be used in the weighting function as smoothing parameter. In this way, the amount of denoising is locally adjusted in order to handle the imperfections of the AT transform. In fact, it has been shown that the optimal smoothing parameter of the NLM filter is related to the noise variance (Buades et al., 2005; Coupe et al., 2008). In case of stationary Gaussian noise, a global noise estimation can be used. In our case, we assume that after the AT transform, the noise can be considered as Gaussian and stationary only locally. Therefore, by using the local MAD estimation as local smoothing parameter, we ensure an optimal amount of denoising over all of the image.

Locally adaptive and optimized non-local means filter

Based on the self-similarity properties of the images, the NLM filter is a simple but highly effective method to remove noise while minimally affecting the fine structure of the image. This filter benefits from the high level of pattern redundancy present in the images to average similar realizations of the noisy signal. The NLM filter considers that voxels with similar neighborhoods will tend to have similar original values. Therefore, the NLM performs a weighted average of all the voxels x_j of the image (or in a restricted search volume for practical reasons to reduce the computational burden), assigning a weight to each of them by comparing their surrounding neighborhoods:

$${\widehat{y}}_i=\frac{{\displaystyle \sum _{j\in \mathrm{\Omega }}}{w}_{i,j}{x}_j}{{\displaystyle \sum _{j\in \mathrm{\Omega }}}{w}_{i,j}}\text{with}{w}_{i,j}=e^{-\frac{{\left|\right|N_i-N_j\left|\right|}_2^2}{h^2}},$$ (7)

where Ω represents the search volume of radius r_sv, the weights w_i,j represent the similarity between any two noisy 3D patches N_i and N_j centered around pixels x_i and x_j and h² is a parameter controlling to strength of the filter, usually related to noise variance (such as h² = βσ²). The patch size is defined as |N| = (2 × r_p + 1)³ voxels where r_p is the radius of the patch (i.e. a small cube in 3D). Finally, ǁ.ǁ₂ represents the L2-norm computed between both patches. In the classic formulation, x_i is the observed value considered as corrupted by additive white Gaussian noise and ŷ_i is the estimation of the noise-free intensity.

In our collaborative approach, the weights are based on the comparison of the patches Ñ_i and Ñ_j extracted from the stabilized prefiltered images (see Fig. 2) and the weighted average is performed over the stabilized noisy values T_a(z). Finally, the smoothing parameter is locally adapted by using $h_i^2=\beta {\sigma }_i^2$. Therefore, the proposed approach can be written as follows:

$${\widehat{d}}_i=\frac{{\displaystyle \sum _{j\in \mathrm{\Omega }}}{\stackrel{\sim }{w}}_{i,j}{\text{T}}_a(z_j)}{{\displaystyle \sum _{j\in \mathrm{\Omega }}}{\stackrel{\sim }{w}}_{i,j}}\text{with}{\stackrel{\sim }{w}}_{i,j}=e^{-\frac{{\left|\right|{\stackrel{\sim }{N}}_i-{\stackrel{\sim }{N}}_j\left|\right|}_2^2}{\beta {\sigma }_i^2}}.$$ (8)

The patch size, related to r_p, reflects the scale of the object to denoise. During experiments, r_p was set to 2. This parameter can be adjusted according to the properties of the specimen. The search volume size, related to r_sv, is limited for computational reasons and was set to 3 during all the experiments. Finally, the value of β is used to rescale the L2-norm computed over the filtered image to the noise level estimated on the original image. During our experiments, this value was empirically set to 0.4, providing a good trade-off between visual assessment and denoising performance in terms of peak signal-to-noise ration (PSNR) and correlation. This parameter can be calibrated by the user according to image modality or denoising purpose (e.g., visualization, segmentation,…). The impact of these parameters on denoising performance is studied on in vivo image in the results section below.

As proposed in Coupe et al. (2008), the NLM filter used is optimized by performing a pre-selection of most similar patches in a blockwise implementation. These optimizations accelerate the process and improve the denoising performance (see original paper for details). Finally, the denoised image is obtained by using the optimal inverse transform (Makitalo and Foi, 2011) as described previously:

$${\widehat{y}}_i={\text{T}}_{ua}^{-1}({\widehat{d}}_i)$$ (9)

CANDLE illuminated by an example

In order to provide an intuitive understanding of our method, Fig. 2 presents the main steps on a real multiphoton image of a glial cell in a living Xenopus brain. This figure shows how the use of the median pre-filtering step facilitates the patch comparison between Ñ_i and Ñ_j. In addition, thanks to this proposed pre-filtering, the noise model assumed during patch-pair comparison is less critical since the L2-norm is applied on enhanced structures, slightly corrupted by residual noise. This fact enables our method to be robust to any discrepancy between the chosen noise model and the real one. As shown on the map of weights w̃_i,j in Fig 2, the most similar patches are accurately found within the defined search volume Ω.

Moreover, this figure highlights the importance of averaging the noisy samples T_a(z) instead of averaging the filtered samples, since the median filter tends to slightly remove edge information and may affect the image contrast. In our method, because the aggregation for averaging is performed on unaltered samples, there is no degradation of image quality as would occur if the median filtered sampled were used during weighted average (see Eq. 8). This aspect is further examined in an in vivo experiment where collaborative and traditional sequential approaches are compared (see Fig. 12). Finally, this example shows that even after VST, the noise level over the image is not constant. The local adaptation is thus an important aspect for multiphoton image denoising.

Figure 12.

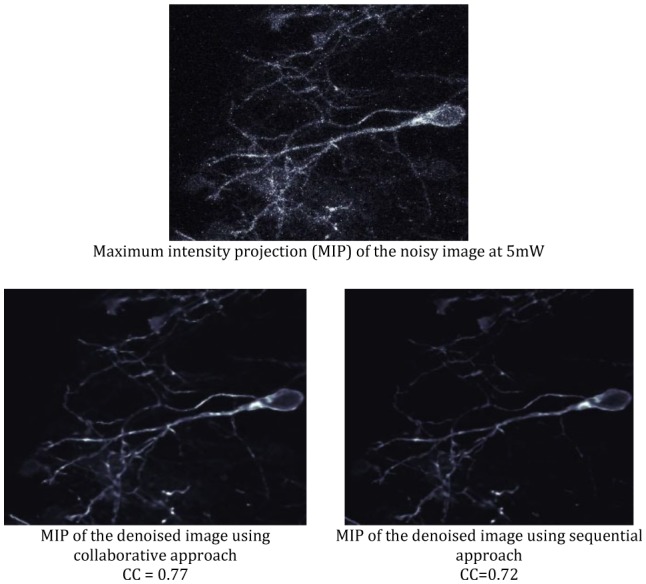
Comparison between collaborative approach used in CANDLE and traditional sequential approach. In the latter, the median filtered image is used as input in the OVST-LAONLM filter. Visually, the contrast of the sequential approach is lower than the result produced by CANDLE. Moreover, the finest dendritic structures are removed during denoising based on sequential approach as assessed by coefficients of correlation (CC). The MIPs of denoised images are displayed with the same intensity range.

Implementation

The proposed method has been implemented by using multithreaded C-MEX and MATLAB code. The 3D wavelet transform used is based on a classical discrete wavelet transform (http://taco.poly.edu/WaveletSoftware/standard3D.html). The optimal inverse Anscombe transform has been re-implemented following the code made freely available by the authors (http://www.cs.tut.fi/~foi/invansc/). Finally, a freely available implementation of CANDLE is provided as a MATLAB application dedicated to 3D tiff stack denoising with a user interface (the url will be communicated after publication acceptance). In order to reduce the computation time, an optional histogram-based background detection has been included in the CANDLE software to fill the background with values obtained by a median filter. In this paper, since the background detection may introduce inaccuracies, the quality metrics reported are based on the full processing of the 3D volumes without this option. The experiments were conducted using an Intel Core 2 Quad Q6600 processor at 2.4 GHz with 4 GB of RAM. The computation time required for a stack of 67 slices of 512×512 pixels (i.e., the full image of glial cell used in Fig. 2) is around 180s (7s for median filter, 15s for local noise estimation and 160s for NLM denoising) with r_p = 2 and r_sv = 3. By using the fast background processing option, this time is reduced to 50s (7s for median filter, 15s for local noise estimation and 30s for NLM denoising of the object). In the CANDLE software, the default values are r_p = 1 and r_sv = 3; these values provide a slightly less optimal denoising result but reduce the computational time to less than 30s.

Validation Framework

Compared filters

In the experiments presented, our method was compared with a version of CANDLE without prefiltering and a recently published state-of-the-art method Puredenoise (Luisier et al., 2010a).

1. OVST-LAONLM: The first method is a locally adapted optimized non-local means denoising (LAONLM) filter with the described optimal variance stabilization (OVST). This OVST-LAONLM filter is similar to CANDLE but does not involve the proposed pre-filtering. In this case, the theoretical optimal value for β is known to be 2 (Buades et al., 2005; Coupe et al., 2008) and was fixed for all the experiments. This type of patch-based method obtained excellent results and outperformed classical approaches in recent reports (Boulanger et al., 2010; Makitalo and Foi, 2011; Wei and Yin, 2010).

2. PureDenoise: The second method is the PureDenoise filter proposed by (Luisier et al., 2010a) based on a mixed Poisson-Gaussian noise model. This optimized PURELET–based filter has demonstrated very high denoising performance compared to a large variety of wavelet-based methods (Luisier et al., 2010a). Moreover, this filter has been proposed for fluorescence images and its ImageJ plug-in for 3D stacks is freely available (http://bigwww.epfl.ch/algorithms/denoise/). During the experiments, the fully-automatic mode of the plug-in was used.

Datasets

Synthetic dataset

First, our method was validated with the synthetic dataset proposed by (Luisier et al., 2010a) (http://bigwww.epfl.ch/algorithms/denoise/dataset.zip). The dataset is composed of 10 slices of 400×400 pixels. In order to perform a fair comparison with PureDenoise which is dedicated to Poisson-Gaussian noise, we first compare the performance of the three filters on synthetic Poisson-Gaussian noise; while CANDLE and OVST-LAONLM are built on a Poisson noise model. This experiment also enabled us to study the robustness of our method in the face of a mixed Poisson-Gaussian noise model. Several levels of noise were simulated by decreasing the intensity range of the downloaded noise-free image. As is usually done in the literature (Lefkimmiatis et al., 2009; Makitalo and Foi, 2011), the intensity range of the original image is first rescaled (i.e., multiplied by a factor < 1) in order to build the noise-free image used as ground truth for a given SNR. Smaller maximum intensity peaks lead to reduced SNR. Then, the ground truth is corrupted by Poisson noise and additive Gaussian noise. The standard deviation of the Gaussian noise was fixed at 5% of the highest intensity value of the ground truth I_max. Finally, the denoised images are compared with the noise-free ground truth (at the same intensity range). This operation is repeated with decreasing multiplication factors, resulting in noisy images with peak signal-to-noise ratios (PSNR) varying from 26dB to 6dB.

Imaging of fluorescent beads

Second, two-photon microscopy was performed using an Olympus FV300 confocal scan head mounted on a BX61WI microscope custom-converted for multiphoton imaging with photomultiplier tubes (PMT) positioned adjacent to the fluorescence filter turret for non-descanned detection. Excitation was produced using a MaiTai-BB Ti:sapphire femtosecond pulsed laser (λ=910 nm). An Olympus LUMFL 60x water-immersion objective (1.1 NA) was used. Images were collected on a PC using Fluoview software (version 5.0). The high-voltage power supply of the PMT detector was set to 750V. Laser power was calibrated at the stage and subsequently measured throughout the experiment using a DET110 - High-Speed Silicon Detector (Thorlabs) in conjunction with Windaq DATAQ Instruments software. FocalCheck^™ Fluorescent Microspheres (Invitrogen) with 15 μm diameter were imaged at varying laser excitation powers (0.3, 0.5, 1, 1.5, 2, 2.5, 3 mW). In this way, images with a range of SNR levels could be collected. To build the reference images, 40 acquisitions were performed at 3 mW intensity for averaging. These acquisitions were then averaged in order to get an effectively noise-free reference image (see Fig. 5).

Figure 5.

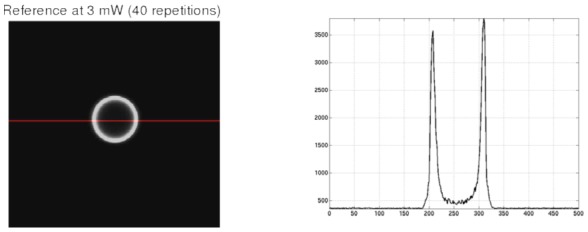
Left: the reference image obtained by averaging 40 acquisitions of the microsphere(15 μm diameter) at 3mW. Right: The intensity profile along the red line in the image on the left.

In vivo datasets with varying power

In vivo two-photon imaging of aspiny Xenopus laevis tectal neurons and olfactory neurons with dendritic spines was performed on the same two-photon microscope and the same settings described above (see dataset acquired from fluorescent beads) but at different laser powers (3, 5, 7, 9 mW), PMT setting (800V) and zoom 1.5). Animals were transfected by electroporation to express farnesylated EGFP (EGFP-F). The aspiny Xenopus leavis tectal neurons data set was composed of 19 optical sections with 512×512 pixels (see Fig. 8). In addition, in order to build the reference image, 20 acquisitions were acquired at 9 mW. These 20 acquisitions were then used to generate a single low-noise image using two different methods: by averaging or by taking the median of all images. During the in vivo imaging, some motion inevitably occurred between image acquisitions. A registration approach based on cross-correlation similarity measure was thus used to estimate the shift between images. A pure translational realignment was then applied without using interpolation in order to not affect the nature of the noise. All images used for the reference image construction as well as the images collected at different powers were corrected in this manner (see Fig 8). For the two-photon imaging of spiny neurons of the olfactory bulb we transfected neurons with EGFP by bulk electroporation in the olfactory bulb. The following two-photon settings were used for acquisition: laser power (3 mW), PMT settings (700 V), λ (910 nm), zoom 8x, 1μm step size in z-direction. Images were acquired using an Olympus LUMFL 60x water-immersion objective (1.1 NA).

Figure 8.

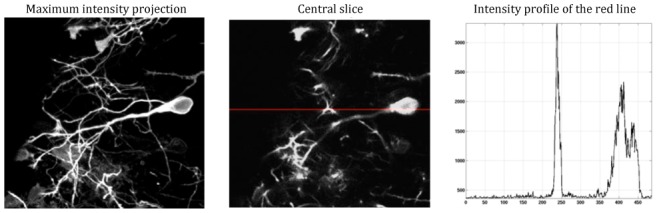
The image stack of xenopus laevis tectal neurons used for the in-vivo experiment. Left: Maximum intensity projection along the z-axis through 19 slices of the reference stack obtained by averaging 20 registered acquisitions at 9mW. Middle: the central slice of the reference stack. Right: The intensity profile of the red line in the reference image.

Deep acquisition in vivo datasets

Using the same two-photon microscope, we imaged through an entire Xenopus laevis brain at the level of the optic tectum. Tectal neurons were labelled with BODIPY^® TR Methyl Ester (Invitrogen) by pressure injection of 5mM solution (in DMSO) into the ventricle. In addition, the retinal ganglion cells were bulk transfected by electroporation in the eye to express EGFP throughout their axonal processes. The following two-photon settings were used for acquisition: laser power (49 mW), PMT settings (channel 1[bodipy]: 560V, channel 2[EGFP]: 760V), λ. 850 nm, zoom (1), 4 μm step size in z-dimension.. Images were acquired using an Olympus UPlanFL 20x air objective (0.5 NA).

Quality metrics

The first quality metric used in this paper is the usual PSNR. This metric is one of the most commonly used quality measures in the denoising literature and is computed as follows:

$$\mathit{PSNR}=10{log}_{10}\left(\frac{I_{max}^2}{\mathit{MSE}}\right),$$ (10)

where MSE is the mean squared error computed between the noise-free and the denoised image. The PSNR can be easily used on synthetic images where the noise-free image is known. However, this measure is sensitive to intensity shift and thus cannot be used during experiments on real images acquired at different powers where the intensity range depends on the power. The comparison between our reference image, used as the gold standard, and the denoised image at another powers was quantified by using the well-known Coefficient of Correlation (CC) as a measure of denoising quality.

Results

Synthetic images

In this experiment, we investigated the denoising performance of filters compared on synthetic images corrupted by different levels of Poisson-Gaussian noise. This experiment provides an initial validation of the proposed CANDLE filter under perfectly controlled conditions. Figures 3 and 4 show the results of application of each of the filters to synthetic data, where Fig. 3 shows the PSNR and the correlation coefficient graphs, and Fig. 4 shows the synthetic images. As shown in Fig. 3, CANDLE yielded better results than OVST-LAONLM and PureDenoise in all cases. For low levels of noise (e.g., PSNR of the noisy image at 26dB), all methods provide high denoising quality. For medium levels of noise (e.g., PSNR of noisy image around 16dB), the NLM-based approaches provided better results. Figure 4 (Middle row) shows that CANDLE and OVST-LAONLM efficiently removed the noise component, although OVST-LAONLM tended to slightly over-smooth the image. At this level of noise, PureDenoise did not fully remove the noise within the object.

Figure 3.

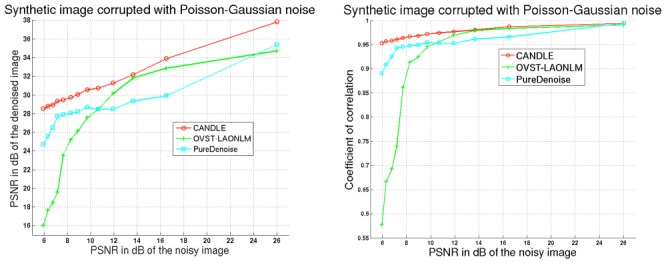
Quantitative comparison of the CANDLE, OVST-LAONLM and PureDenoise filters on synthetic images corrupted by Poisson-Gaussian noise. Left: PSNR in dB of the denoised image according to PSNR of the noisy image. Right: Correlation between noise-free and the denoised image according to PSNR of the noisy image.

Figure 4.

Denoising results obtained by the CANDLE, OVST-LAONLM and PureDenoise filters in experiments on synthetic images. Top: the noise-free synthetic image used during the experiment. Middle: noisy image at 16.5dB and the denoised images obtained by the methods compared. Bottom: noisy image at 6 dB (highest level of noise) and the denoised images obtained by the methods compared.

For very high levels of noise (PSNR of the noisy image < 8dB), CANDLE provided a significantly better denoising result than the two other filters, especially compared to OVST-LAONLM which obtained the worst results. This is evident in the images of the bottom row of Fig. 4. When noise is extremely pronounced, the classical NLM filter considers noise in the background as structure, since the dark, flat area corrupted by shot noise is treated as a repetitive pattern. The amount of residual background noise drastically impacts the quality metrics. At this high level of noise, the advantage of pre-filtering the image as proposed in CANDLE becomes evident. Indeed, pre-filtering enables comparison of quasi-noise-free background patterns that results in efficient background denoising. With the PureDenoise filter, while the background noise was efficiently removed, the structural integrity of the object was not correctly restored and a significant amount of noise remained within the object.

Imaging of fluorescent beads

As noted in the introduction, the nature of noise in multiphoton images is difficult to model due to its various possible sources. Therefore, it is crucial to validate the proposed filter under realistic conditions in order to evaluate the robustness of the filters on real noise. To link the synthetic experiment (above) and the in vivo experiment (below),), we acquired a dataset by imaging microspheres with a very precise size of 15 μm. This experiment has been designed to investigate the denoising performance of the filters on real noise while controlling for other artifacts such as motion. Figures 5, 6 and 7 show the results of application of the filters to the images of the 15 μm diameter microsphere. Figure 5 shows the reference image obtained by averaging 40 acquisitions of the same field of view at the maximum power (3mW). This image was used as a high SNR reference for correlation when comparing the different denoised images. The intensity profile on the right of Fig. 5 demonstrates the very low noise level in the reference image, justifying its use as a correlation target.

Figure 6.

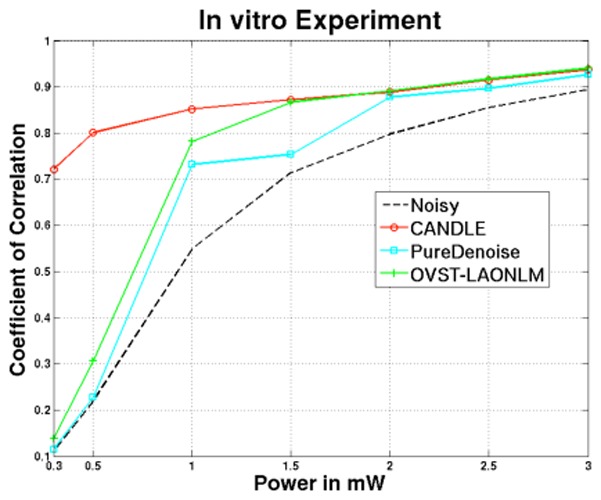
Quantitative comparison of the CANDLE, OVST-LAONLM and PureDenoise filters on images of the microsphere. Correlation between the reference image at 3mW and the denoised image according to excitation power in mW.

Figure 7.

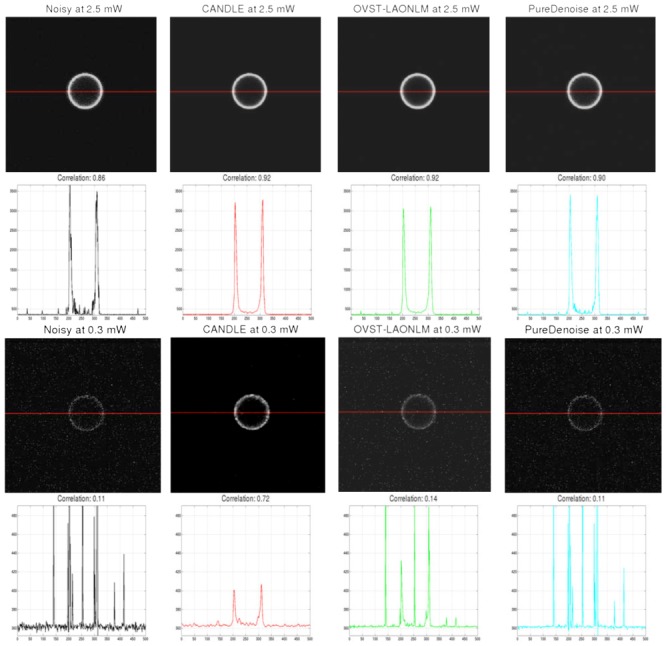
Denoising results obtained by the CANDLE, OVST-LAONLM and PureDenoise filters on images of a microshpere (15 μm diameter).. Top: noisy image at high power (2.5mW) and the denoised images obtained by the methods compared. The values of the red lines are plot for each filter and the corresponding correlation coefficients are given. Bottom: Similar results obtained at very low power (0.3mW). For denoised images, contrast was adjusted manually to minimize the appearance of residual spike noise to avoid saturation in the figure. For intensity profiles, identical axis range is used for all the methods and the noisy image. Saturation of the highest noise peaks was performed to display the signal of interest at an adapted scale.

Figure 6 presents the correlation coefficients obtained on the filtered in vitro microsphere images (see Fig. 7) compared to the reference image. Similar to the experiment with synthetic data, at high excitation power (low level of noise), all the methods provided very good denoising results (see graph Fig. 6 and images top row of Fig. 7). Moreover, for very low power (0.3 mW and 0.5 mW), the residual background noise in the images denoised by the OVST-LAONLM filter reduced its performance as in the synthetic experiment. At low power, the PureDenoise filter only slightly reduced the background noise and resulted in a denoised image that is very similar to the original one (see bottom of Fig. 7). This is in contrast to the results with the synthetic data.

In vivo images

Neuron images

In order to complete the validation of the proposed CANDLE filter, an experiment on in vivo multiphoton images is presented. First, the three filters are compared to laser scanning multiphoton images containing real noise as well as artifacts occurring during in vivo image acquisition. Second, the influence of the filter parameters is studied for acquisition at 9mW in terms of PSNR and correlation coefficient. Finally, collaborative and sequential approaches are compared for acquisition at 5mW. Figure 8 shows the maximum intensity projection of a Xenopus laevis tectal neuron used as reference stack created by averaging 20 acquisitions acquired at 9 mW after motion correction, the central slice of the reference stack, and the right panel shows an intensity profile through the reference image that demonstrates the low level of noise in the background of this reference dataset.

Methods comparison

Figure 9 presents the correlation coefficients obtained on the in vivo images between the denoised images and the reference image. Two strategies have been investigated to construct the reference image. First, the 20 acquisitions are classically averaged and thus the reference image is the mean of the 20 registered images. Second, in order to avoid bias due to the average-based principle of NLM filters, the median image of the 20 registered acquisitions is also used as reference image. As in the data aquired by imaging microspheres and synthetic experiments, for highest SNR images all the methods provided very good denoising results (see top of Fig. 10). For lowest SNR images, the in vivo results are similar to the microsphere data results where, at the lowest power (3mW), the OVST-LAONLM and the PureDenoise filters retained an important amount of residual noise (see bottom of Fig. 10). This in vivo experiment confirms the results obtained with the from imagining microspheres experiment and highlights the competitive performance of the CANDLE filter, even under the lowest studied SNR conditions, this result holds regardless of the strategy used for reference image construction.

Figure 9.

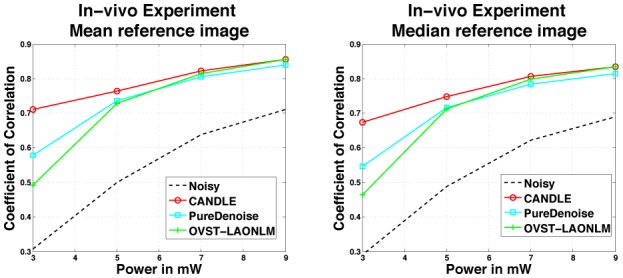
Quantitative comparison of the CANDLE, OVST-LAONLM and PureDenoise filters on in vivo images of xenopus laevis tectal neurons. Correlation between the reference image at 9mW build on 20 acquisitions and the individual denoised images according to acquisition power from 3mW to 9mW. Two different strategies to construct the reference image are compared. Left: The 20 acquisitions are classically averaged; the reference image is the mean of the 20 images. Right: The median of the 20 acquisitions is used as reference image.

Figure 10.

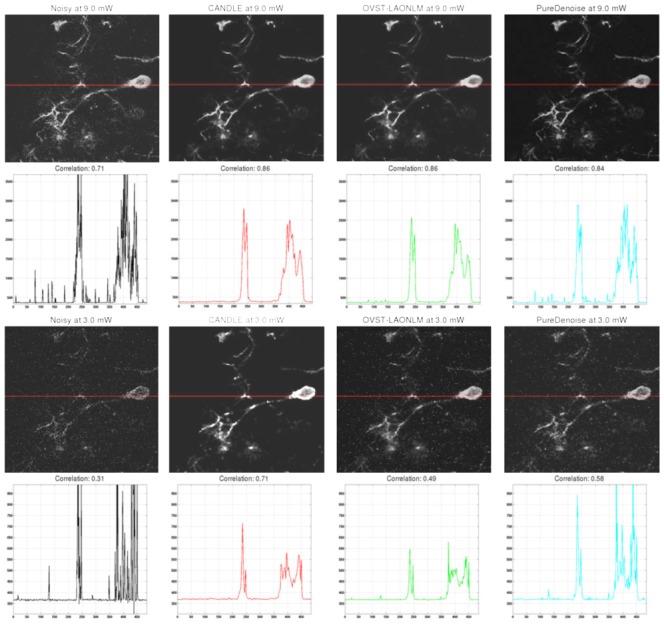
Denoising results obtained by the CANDLE, OVST-LAONLM and PureDenoise filters applied to the in vivo experiments on Xenopus laevis tectal neurons. Top (from left to right): noisy single image at highest power (9mW) and the corresponding denoised images obtained by the three methods compared. The correlation coefficient between each image and the mean reference image is provided just below. Second row: Intensity profiles for the horizontal line for the corresponding image in the first row. Third & fourth row: similar results obtained for images acquired at the lowest power (3mW). For denoised images, contrast was adjusted manually to minimize the appearance of residual spike noise to avoid saturation in the figure. For intensity profiles, identical axis range is used for all the methods and the noisy image. Saturation of the highest noise peaks was performed to display the signal of interest at an adapted scale.

Influence of parameters

Figure 11 shows the influence of filter parameters on denoising quality in term of PSNR and coefficient of correlation. In this experiment, bigger patches (i.e., r_p=2) tended to provide slightly better results while larger search volume marginally decreased the measured quality. The optimal value of β was estimated around 1 in terms of PSNR and CC. However, we used 0.4 during all our experiments since this value provided better tradeoffs between visual assessment and denoising quality measured by PSNR and CC. The optimal amount of denoising remains a difficult question (Wang et al., 2004). In our opinion, the optimal value β is mainly driven by the particular application. For visual inspection, lower values could be preferable while for automatic post-processing such as segmentation or registration higher value could be used.

Figure 11.

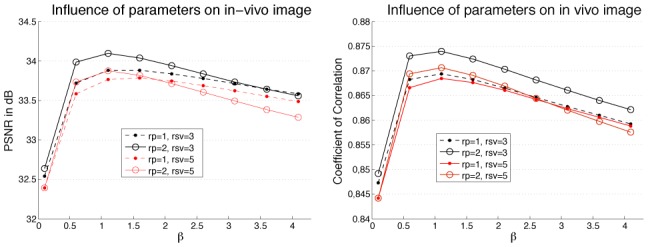
Influence of filter parameters on denoising quality in term of PSNR and coefficient of correlation. The impact of β on denoising quality is studied from 0.1 up to 4.1 with different settings for patch radius (r_p) and search volume radius (r_sv). The test image used is the in vivo acquisition at 9mW and the reference image is the average image of 20 acquisitions at 9mW.

Collaborative vs. sequential approach

Figure 12 presents a comparison of denoising performance provided by the proposed collaborative approach used in CANDLE and the traditional sequential strategy where the median prefiltered image is used as input of OVST-LAONLM filter. First, visual inspection shows that the contrast when using the sequential approach (OVST-LAONLM on median prefiltered image) is lower than the result produced by CANDLE. Moreover, the denoising quality produced by the sequential approach is less efficient than the collaborative approach as assessed by coefficients of correlation (CC). Finally, the finest image features such as dendritic structures are removed during denoising in the sequential approach. This comparison shows the advantage of the collaborative approach and emphasizes that the aggregation of unaltered samples through the NLM filter provides a better result than using prefiltered samples for the weighted average.

Deep acquisition dataset with two channels

One of the most severe limitations in multiphoton in vivo fluorescence imaging is the drop of excitation light intensity as an exponential function of depth due to scattering by tissue. The resultant loss in SNR imposes practical limits on the depth at which useful images may be acquired. Therefore, the final validation step was to demonstrate the improvement in SNR produced by the proposed CANDLE filter on a deep tissue acquisition dataset. For this purpose, a complete z-series though the entire dorsoventral axis of a Xenopus tadpole brain was collected. Tissue structure was captured by staining with BODIPY, a vital dye that labels membranes non-specifically (see Channel 1 of Fig. 13). In addition, GFP-expressing retinal ganglion cells were transfected in the eye using plasmid electroporation to produce bright GFP fluorescence within their axons along the entire retinotectal projection terminating in the optic tectum (see Channel 2 of Fig. 13). As expected, the SNR decreases with the depth of scanning. For clarity, the display intensity range in the example has been linearly adjusted, using the same lookup table for each scanning depth using ImageJ. For a given depth, the intensity ranges between noisy and denoised images are similar. When the acquisition depth crosses 300μm, the low SNR critically limits visual identification of structures, especially for the GFP data in channel 2. After denoising, the tissue contrast between structures in channel 1 is improved, particularly deep within the specimen, where, for example, cell nuclei are only evident on the denoised image, and the structure of the axons coursing through the optic nerve from the eye and along the optic tract become much sharper. Figure 14 shows the maximum intensity projection of channel 2 at the depth of the optical chiasm area. This structure, which is the site where the optic nerves enter the base of the brain, has been chosen since it is the deepest structure in the tadpole brain. Therefore, the optic chiasm is a particularly challenging structure to image for which CANDLE filter can be useful.

Figure 13.

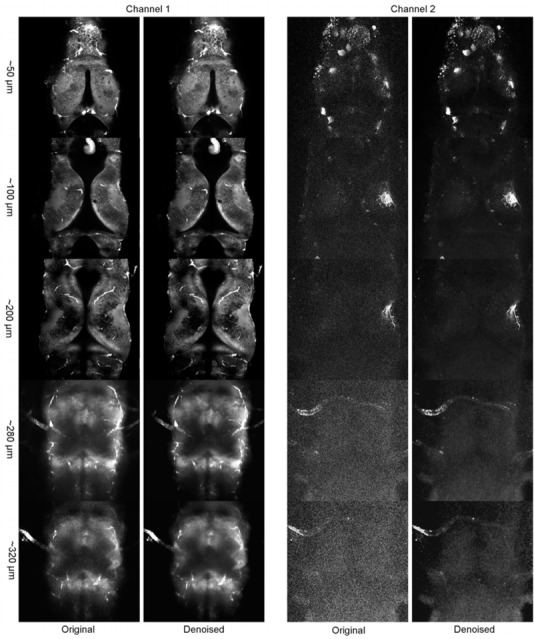
Deep acquisition in a Xenopus laevis brain with two channels: The denoised images were obtained in less than 160 seconds per channel (95 slices each) using the default parameter of CANDLE software for both channels in a fully automatic manner. The display intensity has been set independently for each scanning depth using ImageJ. For a given depth, the lookup tables for the noisy and the denoised images are identical.

Figure 14.

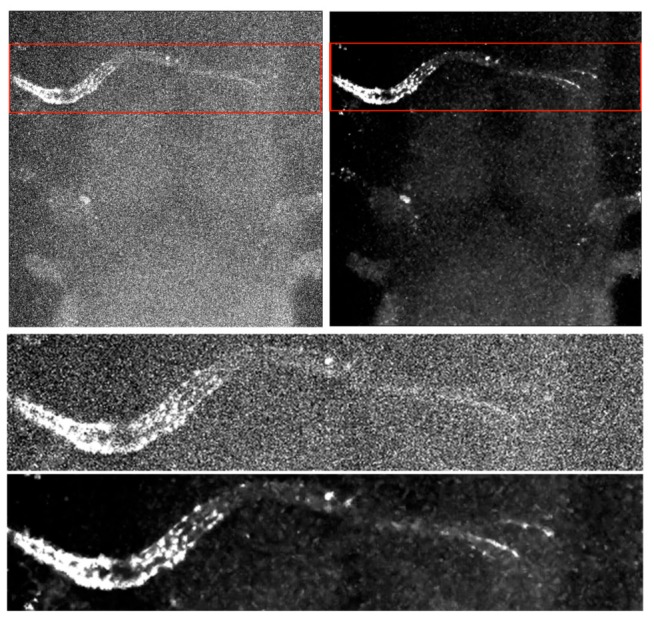
Maximum intensity projection of channel 2 of the deep acquisition image of tadpole brain. The projection was achieved in the optic chiasm area between 275 μm – 320 μm. The lookup tables for displaying the noisy and the denoised images are identical. Top: the full images before and after denoising with red rectangles indicating the area enlarged below. Bottom: Zoomed images of the optic chiasm at the base of the brain before and after denoising.

The bottom of Figure 14 presents a zoomed image of the structure before and after denoising. The improvement in terms of SNR is clearly visible after denoising, demonstrating the deeper imaging capability of the proposed CANDLE filter. Although the impact on biological studies needs further investigation, this first result clearly shows the improvement in image quality for deep imaging and the expected benefit for post-processing tasks such as automatic axon segmentation.

Finally, one important concern regarding the use of denoising algorithms is the potential for loss of critical, fine detail in images near the optical resolution limit of the microscope. Dendritic spines are the structural correlates of excitatory synapses onto certain types of neurons and are therefore of great interest in the neuroscience imaging community. They are found at high density along dendrites and are typically about 1 μm long, only slightly larger than resolving limit of an optical microscope. We therefore sought to determine whether these structures were well preserved in images denoised using CANDLE. Figure 15 presents the result obtained by CANDLE on a spiny neuron in the olfactory bulb of a xenopus tadpole. As can be seen in the zoomed images, CANDLE enables a better visualization of fine structures including broad spine heads and very narrow spine necks.

Figure 15.

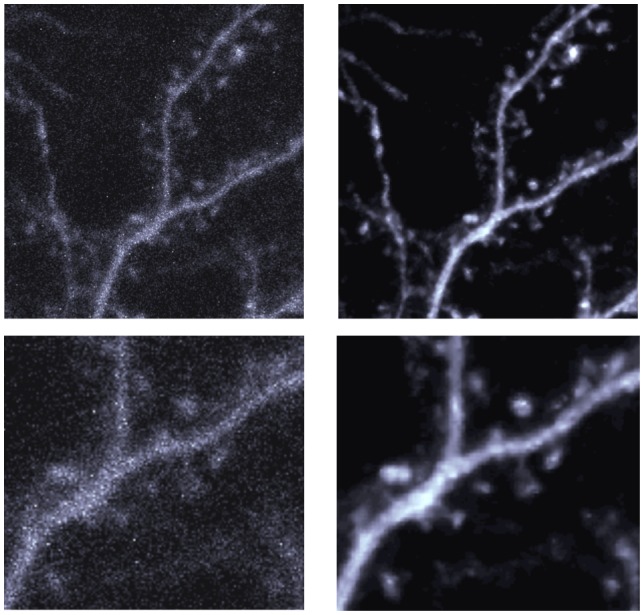
Maximum intensity projection of olfactory neuron of frog. Left: Original acquired image. Right: Denoised image with CANDLE. Top: the full images before and after denoising. Bottom: Zoom on the central part of the image.

Discussion

We have here presented a novel Collaborative Approach for eNhanced Denoising under Low-light Excitation (CANDLE). By combining several existing image processing methods, each selected for their robustness and their simplicity, CANDLE provides high performance denoising compared to Puredenoise and a locally adaptive nonlocal means filter. The improvement is especially evident for the low SNR conditions typically present in deep in vivo imaging where scattering of excitation light results in low density of ballistic photons at the focal point, and impaired acquisition quality. Our experiments have shown that patch-based denoising approaches can reveal deep structures that are hardly distinguishable by the human eye in the original noisy images. Our study on deep imaging is complementary to recent work using NLM denoising for biological fluorescence microscopy to reduce exposure times, resulting in improved sample viability. In fact, the ability to reduce exposure times by applying a patch-based denoising method (Boulanger et al., 2010) has been demonstrated in the recent paper of Carlton et al. (2010). Their paper demonstrated that NLM-based filtering can reduce photobleaching and phototoxicity while permitting higher acquisition rates in fluorescence time-lapse microscopy by allowing lower intensity excitation of fluorescent probes. The great interest in the biological community for this new type of denoising filter has been highlighted in several recent articles (Baker, 2010; Swedlow, 2010).

One of the main drawbacks of many patch-based approaches is the extensive computational time required. Our algorithm has a number of improvements that reduce this constraint to yield a practical tool that is usable in the laboratory. In our software, we allow the user to manually tune the smoothing parameter to achieve an optimal denoising for the given image processing task. For example, image registration and structure segmentation may require more denoising than other tasks like cell counting. It is important to note that automatic estimation of this scaling parameter between filtered patches and the noisy samples should be possible (Deledalle et al., 2010; Van De Ville and Kocher, 2009), but such an estimation is beyond the scope of the work presented here. Investigations on improved prefiltering approaches or adaptation to a more complex noise model estimation could be interesting for future development of the CANDLE algorithm.

The filter presented here has been tailored to increase the SNR while minimizing visible artifacts. We have used typical 3D datasets created in neuroscience by scanning microscopy methods that have distinct properties. These properties include a large array of structural information in combination with a characteristic distribution of the SNR. Because structural information in these images reflects the functional connections of the neuronal circuit, it is therefore most important that very little signal is lost or distorted and that little or no additional artifactual structure as possible be added to the data set due to post-hoc filtering. On the other hand, filtering can help to extract information that otherwise would be buried under the noise that comes naturally during the imaging process. We have shown that CANDLE filter performs particularly well in low light conditions compared to other filtering methods both with regard to image fidelity and information extraction.

The CANDLE NLM denoising algorithm presented here should be widely applicable to many forms of light microscopy in addition to multiphoton fluorescence imaging, wherever detector noise or light scattering lead to degradation of image SNR. Recent improvements in detector technology that offer improved SNR through the use of highly sensitive GaAsp PMTs or of electron multiplying charge coupled devices (EMCCDs) are still ultimately limited for live imaging by the requirement to limit harmful excitation light exposure and by the fundamental scattering nature of biological tissue. Extensive averaging is not the best option due to the damage caused to living tissue by prolonged or repeated light exposure. NLM approaches like CANDLE offer many of the benefits of averaging without any of these detrimental effects and are therefore broadly applicable to in vivo and especially deep tissue imaging. A more recent innovation with great potential for deeper imaging in scattering tissue is the use of adaptive optics, first pioneered in astronomy as a means of correcting for atmospheric distortion (Cui, 2011). By correcting for tissue scattering, image noise caused by non-ballistic photons is further reduced, however instrument noise naturally persists and can be further reduced only by averaging or through computational methods such as CANDLE.

Light sheet microscopy is an alternative 3D optical imaging method that largely by-passes the issue of scattering of excitation light by illuminating the specimen from the side with a sheet of light focused into a single, scanning plane (Voie et al., 1993; Dodt et al., 2007). This method has great potential for improving 3D resolution and reducing out-of-focus fluorescence excitation at greater depths in specimens where illumination from multiple angles is possible, but nonetheless is still limited for live imaging by detector sensitivity and SNR. Furthermore it is obviously limited for in vivo imaging of structures like mammalian brain where epifluorescence excitation from above through the objective is the only practical approach for capturing detail beneath the surface.

Computational methods such as deconvolution can also offer significant improvements in image quality by integrating information from multiple focal planes to reconstruct virtual images. In principle, CANDLE and deconvolution are complementary methods as they each use distinct information to improve image quality, the former incorporating pattern image feature and the latter using prior information about the optical properties of the microscope. Interestingly because deconvolution relies on information contained within the image noise, but is negatively impacted by detector noise, it remains to be determined whether they are indeed mutually beneficial in practice, or, for example, if the order in which the image is processed has a significant impact on the outcome.

Conclusion

In this paper, we present a new collaborative approach for enhanced denoising under low light excitation conditions. Based on the pre-filtering of patches before applying a NLM filter, the proposed method is competitive with the Puredenoise filter, especially in the low SNR conditions typical of deep tissue in vivo imaging. An extensive validation on synthetic, multiphoton in vitro and in vivo images was performed to carefully characterize the performance of the CANDLE method for real images. The results suggest that CANDLE should have great potential for improving fluorescence imaging, especially under conditions where excitation illumination is low, either intentionally as a means to reduce phototoxicity and bleaching or as a consequence of imaging deep within scattering biological tissue.