Heritability at the ecosystem level

In the first article of the first volume of Annual Review of Ecology and Systematics, Lewontin (1) points out that any level of organization that can be grouped into a population of units has the potential to evolve by natural selection. Evolution by natural selection has been seen in experimental studies of individual and group selection, and now Swenson et al. (2) have demonstrated that selection acting at the level of the ecosystem can cause evolutionary change.

Lewontin describes the three properties of a population that are necessary and sufficient for evolution by natural selection to occur. Briefly, these properties are that (i) there must be phenotypic variation, (ii) the different phenotypic variants must be associated with different fitnesses, and (iii) fitness must be heritable. Lewontin goes on to explain that, in principle, any level of biological organization can exhibit these three properties; thus, any level of organization that can be grouped into a population of units has the potential to evolve by natural selection. He then concludes that it is unlikely that natural selection acting above the level of the individual will be an important evolutionary force, in part on the grounds that it is the higher level units that are unlikely to exhibit heritability of fitness.

The conclusion that higher levels of selection would not have heritable variation was, at the time, generally accepted (e.g., ref. 3); however, over the years, this dogma has been challenged by a number of studies that have examined selection acting above the level of the individual (4). Nearly all of these studies have examined group selection, that is, selection among groups of individuals of the same species, although one study examined the selection acting on two species at the community level (5, 6). With one exception (7), these studies have shown that group selection results in a far more rapid response to selection than predicted by theory and that a response much greater than the one suggested by Lewontin's (1) early paper should be expected. The experiment reported by Swenson et al. (2) continues in this tradition and extends it, showing that heritable variation is found not only in single-species groups but also in entire ecosystems consisting of millions of individuals in thousands of species.

Experiments examining higher levels of selection challenge many of the conclusions drawn from traditional theory. An experiment performed by Craig (8) is typical of group selection experiments and illustrates the unexpected results these experiments produce. For his group selection treatments, Craig set up 20 populations of 30 individuals. These populations were raised for a generation and then assayed for emigration rate. Group selection for high emigration rate was performed by selecting the five populations with the highest emigration rate and discarding the remaining 15 populations. Each surviving population then founded 4 populations, bringing the number of populations back up to 20. The group selection for low emigration rate was identical, except that the five populations with the lowest emigration rate were selected to found the next generation. At the end of 14 generations of group selection, the group selection for high emigration rate (with no individual selection) had a mean emigration rate of 74%, whereas the group selection for low emigration rate had a mean emigration rate of 42%, a highly significant difference.

Two important calculations can be made from this experiment. The first is the heritability of the group-level trait. Roughly speaking, heritability is the proportion of the total variance that can contribute to a response to selection (for a more formal definition, see ref. 9). Heritability can be estimated from the standard breeders' equation, R = h²S, where R is the cumulative response to selection over 14 generations, h² is the heritability, and S is the cumulative selection differential. Rearranging this equation gives the realized heritability of h² = R/S (9). Using this equation while making several approximations to estimate the required numbers from the published data gives a rough estimate of the realized heritability for emigration rate on the order of 15%. This value would be considered a moderate heritability for a trait measured at the individual level (9). The second calculation that can be made is the expected inbreeding coefficient, F, at the end of the experiment. The inbreeding coefficient varies between zero and one and is a measure of the homozygosity in a population. An outbred population has an inbreeding coefficient of zero, whereas a completely homozygous population has an inbreeding coefficient of one. The expected inbreeding coefficient can be estimated by using the equation

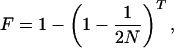where N is the population size and T is the number of generations (10). Based on a population size of 30 individuals at the end of 14 generations, the inbreeding coefficient is expected to be 0.20, and the generation-mean inbreeding coefficient is 0.10. Making the standard assumption of additive gene action, an inbreeding coefficient of 0.10, and a group heritability of 0.15 implies that the underlying individual-level trait had a heritability of at least 8%. In light of this result, it is interesting that in Craig's experiment individual selection was stunningly ineffective. Not only were the individual selection treatments not effective, but in general, they did not rank in the expected order based on the strength of selection.

Craig's experiment is typical not only in its design but also in the observation of a significant response to group selection and no response to individual selection. Thus, the question becomes not whether group selection is effective but why it is so effective. A review of the experimental studies of group selection indicates that group selection can act on components of variance that cannot contribute to a response to selection at a lower level (4). In a sexually reproducing species, individual selection can act only on the average effects of individual genes. At the group level, gene interaction (epistasis) and genetically based interactions among individuals can also contribute to a response to selection. The genetically based interactions among individuals are particularly interesting, because they are a component of group-level variance that does not exist at the individual level.

Selection on whole ecosystems brings in several additional sources of ecosystem-level heritable variance. In addition to those sources available to individual selection (the effects of individual genes) and group selection (epistasis and intraspecies interactions among individuals), we can add genetically based interactions between species and a feature unique to complex ecosystems, changes in species composition (2). These added sources of community-level heritable variance add a richness to the response to community selection that cannot be traced to anything that can be measured on individuals.

Because higher levels of selection can act on a vastly broader range of causes of variation, we have to ask what limits the heritability of group- and community-level traits. There are few data on this topic; however, logically, this limitation must be related to the reliability of the transmission between generations. Thus, heritabilities of individual-level traits are understandable, because sexual reproduction faithfully transmits genetic information (genes) between parent and offspring. Similarly, in the experiment of Swenson et al. (2), in each of the different treatments, samples of the entire community were transmitted between “parent” communities and “offspring” communities. Reliability of transmission of genetic information is the hallmark of individuals. At higher levels of organization, the heritability will depend on the details of transmission. For example, Wade (11) found that migration reduced but did not eliminate the genetic variance among groups of Tribolium flour beetles. Thus, although community selection has the potential to act on a wide range of genetic effects, such action will happen only when the communities are transmitted intact between generations. Clearly, communities that exhibit heritable variation will tend to be small, integrated communities. Indeed, soil communities and pond-water communities similar to those used by Swenson et al. (2) may be good examples of the sort of communities that could respond to community selection.

One of the goals of modern molecular genetics has been to determine the genetic basis of phenotypes and ultimately to be able to use this knowledge to understand how selection works. The community selection study of Swenson et al. (2) points out the limitations of this reductionist program. Although there may be some potential for relating changes in individual-level phenotypes to changes in specific allele frequencies, this hope fades when selection is acting at the group level and becomes unreasonable for ecosystem-level selection. On the other hand, a phenotype-based approach offers no such difficulties. If we can measure the phenotype and apply selection, whether it be at the individual or ecosystem level, and the trait is heritable, we will get a response. This approach does not provide the satisfaction of a mechanistic understanding of the response to selection, but it does provide results. There is, of course, reason to want to understand the mechanisms by which an ecosystem responds to selection, and few would argue with the usefulness of performing such research. However, such study may ultimately prove to be difficult and slow. The community selection study of Swenson et al. (2) clearly shows that we do not need to have a sufficiently detailed understanding of the mechanism of adaptation to apprehend complex phenomena such as community selection.