A “Link-Psi” strategy using crosslinking indicates that the folding transition state of ubiquitin is not very malleable

Abstract

Using a combined crosslinking-ψ analysis strategy, we examine whether the structural content of the transition state of ubiquitin can be altered. A synthetic dichloroacetone crosslink is first introduced across two β strands. Whether the structural content in the transition state ensemble has shifted towards the region containing the crosslink is probed by remeasuring the ψ value at another region (ψ identifies the degree to which an inserted bi-Histidine metal ion binding site is formed in the transition state). For sites around the periphery of the obligate transition state nucleus, we find that the resulting changes in ψ values are near or at our detection limit, thereby indicating that the structural content of the transition state has not measurably changed upon crosslinking. This work demonstrates the utility of the simultaneous application of crosslinking and ψ-analysis for examining potential transition state heterogeneity in globular proteins.

Introduction

The degree of structural heterogeneity in the folding transition state elicits a wide range of opinions.^1–6 This divergence persists in part because it is very difficult to measure this quantity experimentally, especially for proteins that fold in a two-state manner.^7–14 For example, the primary methods for determining transition state structure, ϕ^15–17 and ψ analyses,^18–23 suffer from ambiguities when the measured values are fractional, that is, not 0 or 1. Fractional ϕ and ψ values may arise from the presence of alternative transition state structures. Fractional values, however, may also represent partial structure formation in a homogeneous transition state ensemble (TSE).^{7, 8, 10, 18, 24–27} Thus, fractional ϕ and ψ values are inconclusive on the degree of transition state heterogeneity.

With current single molecule methods, individual pathways are unresolvable during the sub-μsec transit over the major barrier.^{28, 29} Even when there are multiple pathways, single molecule techniques will observe only a single relaxation rate, which is the sum of the individual rates (k_obs = Σk_f).

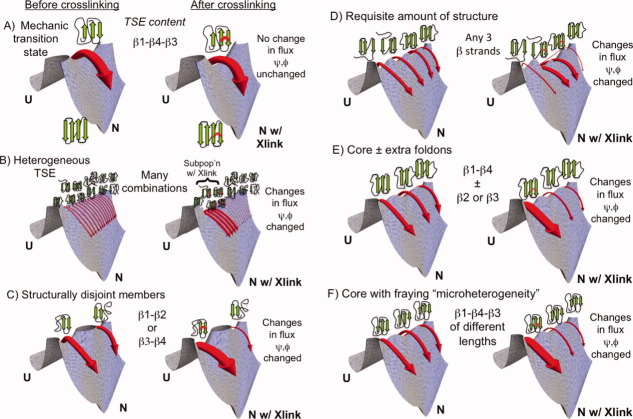
One may consider six scenarios to describe the degrees of transition state heterogeneity, as illustrated with a four stranded β protein in Figure 1. The first scenario considers a “mechanic” nucleus⁸ with minimal heterogeneity [e.g., always the same three strands, e.g., β1, β4, and β3, Fig. 1(A)]. At the other extreme is a highly heterogeneous TSE with no common theme [e.g., having all possible combinations of 1, 2, or 3 strands, Fig. 1(B)]. In between these two extremes are four situations where (i) the members of the TSE are either structurally disjoint [e.g., either Hairpin β1-β2 or Hairpin β3-β4, Fig. 1(C)]; (ii) all members have the same amount of structure [e.g., any three strands, potentially the minimum requisite structure needed to traverse the barrier, e.g., as reflected by the chevron m_f value, Fig. 1(D)]; (iii) all members share a common nucleus but with some structural diversity [e.g., always having β1 and β4 and sometimes either β2 or β3, Fig. 1(E)]; or (iv) all members have the same secondary structure content, albeit to varying extents [e.g., always strands β1, β3, and β4, but with strands of different length, Fig. 1(F)]. We have termed the latter scenario “microscopic heterogeneity.”³⁰

Figure 1.

Different classes of transition state heterogeneity and potential outcomes of the Link-Psi strategy. Depending on the degree and type of heterogeneity, crosslinking may influence the relative flux going through different members of the TSE, as indicated in panels A–F, and alter the ψ values. The width of the arrows reflects the fraction of the molecules folding along this route (and not the rate constant). Figure created using Mathematica 8.0.

We generally envision members of the TSE to be individual states separated by small barriers representing the addition or loss of a secondary structure element or “foldon.” In the case of microscopic heterogeneity, the different conformations, for example, varying length of the β1 strand, may be clustered into a single state “β1 formation” as the interconversion times are likely to be extremely fast with extensive conformational sampling during transit over the macroscopic free energy barrier.

A viable strategy to test for the presence of alternative transition state structures involves perturbing the stability of one region and examining whether the folding flux shifts to other regions (as illustrated by the different depth minima on the saddle point at the top of the free energy barriers in Fig. 1). For example, if the TSE contains either Hairpin β1-β2 or Hairpin β3-β4, stabilizing one hairpin will decrease the relative flux going through the transition state containing the other hairpin. The decrease in flux can be identified by a decreased ϕ or ψ value for a site on the latter hairpin. However, for a homogeneous mechanic TSE, the ϕ or ψ value will remain unchanged. The outcome in the other four scenarios will lie between these two extremes.

The general strategy of introducing destabilizing mutations or loop insertions followed by ϕ or ψ analysis was applied to src⁸ and alpha spectrin SH3,³¹ the B domain of Protein A,²² and the dimeric GCN4 coiled coil.¹⁰ The three globular proteins were found to have a mechanic nucleus. In contrast, the nucleation site in the dimeric coiled coil could be driven from one end of the coil to the other end. Upon crosslinking either end of the coiled coil with a disulfide bond, the TSE became fixed at the crosslinked end, and the ψ values changed in a predictable and quantitative manner that agreed with the mutagenesis studies.¹⁸

Here, we generalize the strategy with the use of a synthetic crosslink followed by ψ analysis to investigate the degree of transition state heterogeneity in a globular protein, ubiquitin (Ub). This 76 residue protein has been extensively characterized using multiple methods.^{15–17, 19, 20, 32–34} The association of two adjacent β strands in the TSE is enforced by the introduction of a short, covalent dichloroacetone (DCA) crosslink between two cysteines³⁴ (Fig. 2). Our previous ψ analysis studies indicated that the TSE is extensive with unity ψ values involving four strands and the α helix.^{19, 20, 32} Given this level of structure, the TSE is unlikely to have structurally disjoint nuclei. However, the TSE may still contain an intermediate level of heterogeneity involving the peripheral regions, which have fractional ψ values, surrounding the obligate core. In the present study, we find that the ψ values in these regions remain largely unchanged after the introduction of crosslinks throughout the protein. Hence, the profile of the saddle point at the top of the free energy barrier remains unchanged upon introduction of a crosslink, indicating that the structural content of Ub's TSE is not very malleable.

Figure 2.

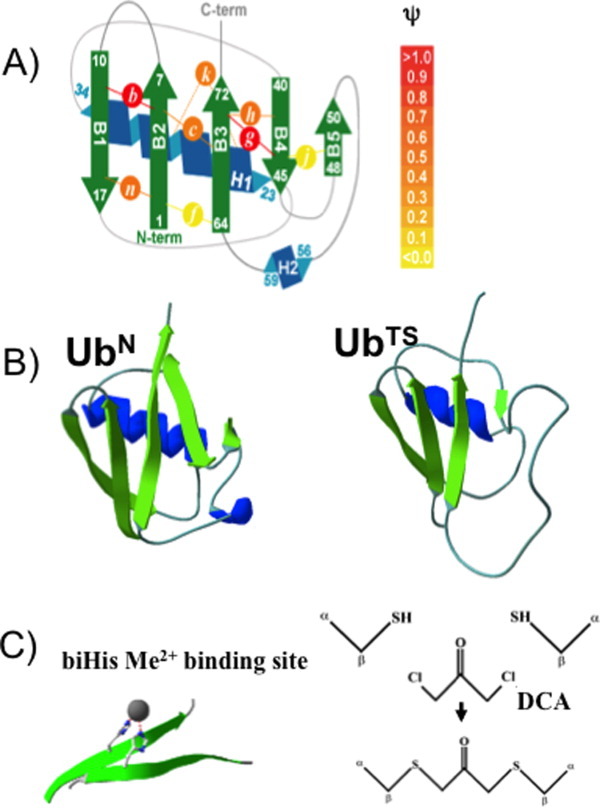
ψ Analysis and crosslinking of ubiquitin. A: Schematic representation of ψ-analysis results for sites investigated in the present study. The biHis sites are shown as circles with italic letters; each site is studied individually. The color intensity represents the value of ψ. DCA crosslinks are inserted at Sites b, h, and n. B: Native Ub structure³⁵ and a model of the TS defined by biHis sites having unitary ψ-values. C: Illustrations of a biHis binding site and the chemical constituents involved in DCA crosslinking at a biCys site. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Results

Background

In ψ analysis, bi-histidine (biHis) metal ion binding sites are introduced at two adjacent residues, for example across two strands or along a helix (Fig. 2). Upon the addition of metal ions, these sites stabilize secondary and tertiary structures because an increase in the metal ion concentration stabilizes the interaction between the two histidine partners. The metal-induced stabilization of the TSE relative to the native state stabilization is represented by the ψ₀ value. This parameter directly reports the proximity of the two partners in the TSE as it depends on the degree to which the biHis site is formed.

ψ values of 0 or 1 indicate that in the TSE, the biHis site is absent or fully native-like, respectively. Fractional values indicate that in the TSE, the biHis site achieves only part of the binding-induced stabilization of the native state; for example, a native-like site formed only in a subpopulation of the TSE, or a site formed in the entire TSE but with non-native ion binding affinity, or a combination thereof. The ψ₀ quantity is the ψ value calculated in the limit of no added metal to remove any potential artifacts related to metal ion binding altering the folding behavior or the structural content of the TSE.

The extent of structure formation in Ub's TSE has been mapped by probing numerous biHis sites introduced throughout the protein.³² The TSE is highly structured with a very native-like topology [Fig. 2(B)]. In particular, sites with unambiguous 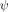values of unity are observed across the four largest strands (β1–β4) and part of the helix. These sites adopt native-like geometries in the entire TSE and define a minimal obligate core consisting of the carboxy-terminus of Ub's α-helix and four aligned β strands. Multiple sites with fractional ψ₀ values are situated along the periphery of this core structure.

Link-Psi strategy using DCA crosslinking

The relationship between two populations in the TSE, for example, containing biHis Sites A or B, can be examined by manipulating the stability of the population containing Site A while observing the resulting changes in the population containing Site B in the TSE (Fig. 1). In the present study, a covalent crosslink is introduced at one site to stabilize the transition state population containing this site and the resulting effect on the ψ value at another site is probed. The crosslink is created by substituting a pair of cysteines (biCys) for the two histidines, followed by the addition of a small molecule, DCA, to create a covalent C_α—S—CH₂— (C=O)—CH₂—S—C_α linkage.^{34, 36} Seven Ub variants are created in this manner where each contains a biHis site at one position and a covalently crosslinked biCys site at another position (Fig. 2).

As this study is the first implementation of the combination of DCA crosslinking and ψ analysis, two control measurements are conducted (Table I). The first control is created with a crosslink across the β1-β2 hairpin (Site b, residues 6–12, ΔΔG_crosslink=1.18 ± 0.04 kcal mol⁻¹).³⁴ Site b is an obligatory biHis site with 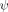= 1.13 ± 0.02. The probed biHis site is across strands β3-β4 (Site h, residues 42–70) and has a fractional value prior to introduction of the crosslink 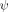= 0.30 ± 0.01 [Fig. 3(A)]. Because Site b is formed in the entire TSE, crosslinking here is not expected to change the composition of the TSE. Hence, it should have no effect on the ψ value at the other site.

Table I.

Link-Psi Results using DCA Crosslinking and ψ Analysis

Site probed with ψ analysis (residues)	Site with crosslink (residues) ΔΔGcrosslink(kcal mol−1)	ψw/o crosslink	ψcrosslink
Site h (42–70)	Site b(6–12) 1.18 ± 0.04	0.30 ± 0.01	0.21 ± 0.01
Site b (6–12)	Site h(42–70) 1.2 ± 0.1	1.13 ± 0.02	0.99 ± 0.02
Site c (6–68)	Site h(42–70) 1.2 ± 0.1	0.23 ± 0.01	0.32 ± 0.01
Site k (24–28)	Site h(42–70) 1.2 ± 0.1	0.17 ± 0.01	0.20 ± 0.01
Site n (2–16)	Site h(42–70) 1.2 ± 0.1	0.50 ± 0.01	0.38 ± 0.01
Site h (42–70)	Site n(2–16) 1.0 ± 0.1	0.29 ± 0.01	0.20 ± 0.01
Site k (24–28)	Site n(2–16) 1.0 ± 0.1	0.20 ± 0.01	0.27 ± 0.01

Figure 3.

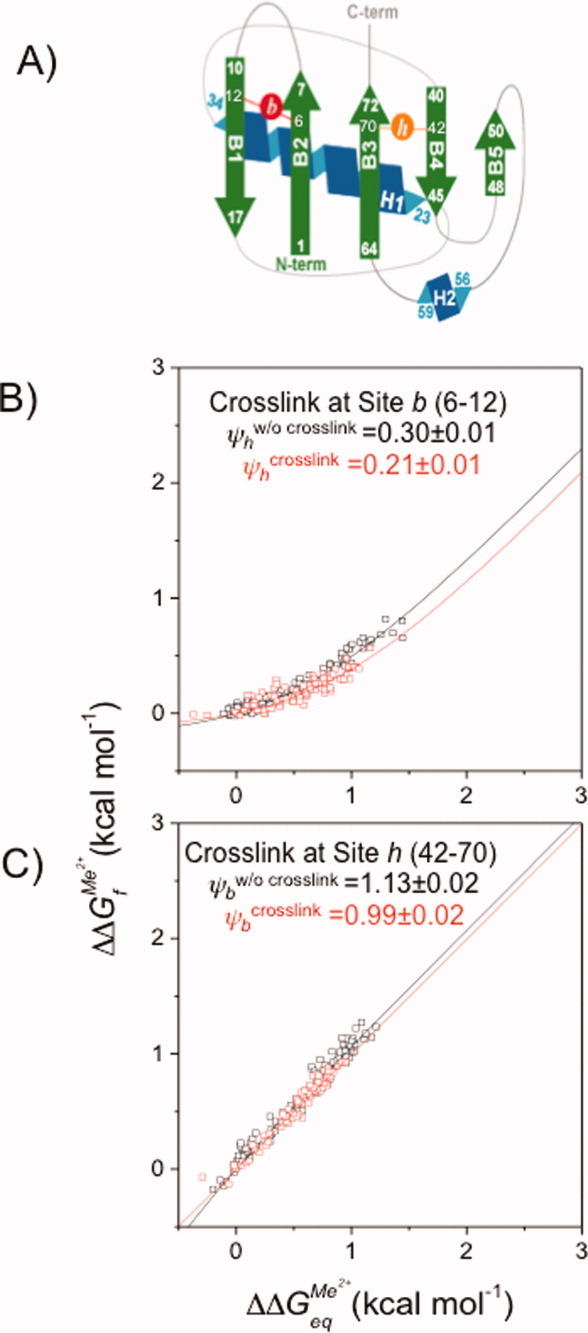
ψ Analysis of fractional and unity ψ₀ value sites in the absence and presence of a crosslink. A: Schematic representation of Sites b and h. B: ψ Analysis of Site h in the presence (□) and absence (□) of a crosslink at Site b. C: ψ Analysis of Site b in the presence (□) and absence (□) of a crosslink at Site h. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The outcome of this control is illustrated with Leffler plots of ΔΔG_f^‡ versus ΔΔG_eq. Relaxation data are recorded under folding and unfolding conditions at dozens of Zn²⁺ concentrations for Site h in the absence and presence of a crosslink at Site b [Fig. 3(B)]. As expected, the data for the two experiments are nearly coincident, with the value being minimally changed, 0.30 ± 0.01 versus 0.21 ± 0.01. Thus, the presence of the crosslink at Site b, which has a unity 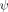value, does not appear to appreciably alter the structural composition of the TSE.

The second control switches the positions of the two types of sites, with the biHis site now at Site b and the crosslink at Site h (ΔΔG_crosslink = 1.2 ± 0.1 kcal mol⁻¹).³⁴ Because Site b already is present in the entire TSE, we expect its ψ value to be unaffected by crosslinking at a site with a fractional ψ₀ value. Again, the data without and with the crosslink are very similar [Fig. 3(C)], with the ψ₀ value for Site b remaining near unity upon crosslinking (ψ₀ = 0.99 ± 0.02 versus 1.13 ± 0.02, respectively). These results indicate that the introduction of a crosslink at a fractional ψ site does not adversely affect structures that already are present in the TSE. These two controls also provide a measure of the reproducibility of the Link-Psi method employing DCA crosslinking and ψ analysis.

Sites with fractional ψ₀

We next examined the relationship between four sites with fractional ψ₀ values. These sites are located across the β1-β2 hairpin (Site n, residues 2–16), strands β2-β3 (Site c, residues 6–68) and β3-β4 (Site h, residues 42–70), and the amino-terminus of the α helix (Site k, residues 24–28). Initially, three variants are created, each containing a crosslink at Site h and a biHis site at each of the three other sites (Sites c, k, and n). For Sites c and n, the data are compared in the form of Leffler plots in the absence and the presence of the crosslink at Site h. For both sites, the results in the absence and presence of the crosslink are nearly coincident [Fig. 4(A,B)]. The ψ₀ values for Site n, which is located on the far side of the transition state structure, are 0.50 ± 0.01 and 0.38 ± 0.01 without and with the crosslink present at Site h, respectively. The values for Site c, which is located next to the crosslink, are 0.23 ± 0.01 and 0.32 ± 0.01, without and with the crosslink present at Site h, respectively. Hence, both Sites c and n are largely indifferent to crosslinking of Site h.

Figure 4.

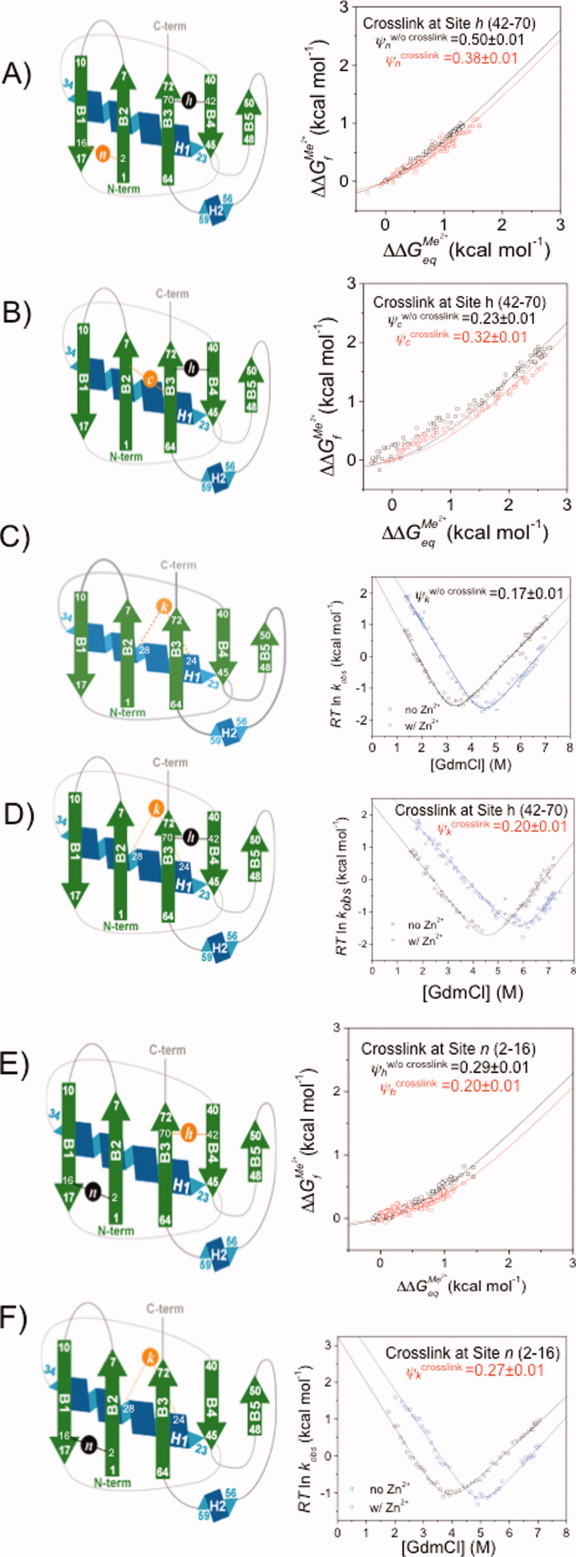
ψ Analysis and crosslinking applied to sites with fractional ψ values. Schematic representation and ψ-analysis for (A) Site n in the presence (□) and absence (□) of a crosslink at Site h (black circle); (B) Site c in the presence (□) and absence (□) of a crosslink at Site h; (C) Site k in the presence (□) and absence (□) of a high [Zn²⁺] in the absence of a acrosslink at Site h; (D) Site k in the presence (□) and absence (□) of high [Zn²⁺] with a crosslink at Site h; (E) Site h in the presence (□) and absence (□) of a crosslink at Site n; (F) Site k in the presence (□) and absence (□) of a high [Zn²⁺] with a crosslink at Site n. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Due to the gain in stability resulting from the combination of crosslinking at Site h and metal ion binding for Site k, it is difficult to obtain the metal ion binding data required for a Leffler plot. Normally Leffler plots are created using changes in k_f and k_u under strongly folding and unfolding conditions, respectively (see Fig. 3 in Ref. 30). For Site k, however, we cannot obtain the data under strongly unfolding conditions. Hence for Site k, both k_f and k_u are measured as a function of denaturant concentration and analyzed using standard “chevron” analysis; the ψ₀ value is calculated from a simultaneous (global) fit of the two chevrons obtained with and without metal ions. In particular, chevron data are obtained at zero and high metal ion concentration in the absence [Fig. 4(C)] and presence of the crosslink at Site h [Fig. 4(D)]. The resulting ψ₀ values for Site k are 0.20 ± 0.01 and 0.17 ± 0.01 when the crosslink at Site h is absent and present, respectively. The similarity of these values indicate that the TSE population fraction having Site k formed is unaffected by crosslinking at Site h.

To further investigate the correlations between the sites, the influence of a crosslink at Site n (ΔΔG_crosslink = 1.0 ± 0.1 kcal mol⁻¹)³⁴ on the populations having biHis Sites h and k formed is examined. The introduction of the crosslink results in a slight decrease of the ψ₀ value for Site h, from 0.29 ± 0.01 to 0.20 ± 0.01 [Fig. 4(E)]. This result is very similar to the reverse situation (crosslink at Site h, probe Site n with ψ) where the ψ₀ decreases from 0.50 ± 0.01 to 0.38 ± 0.01.

To determine the effect of a crosslink at Site n on the ψ value at Site k, denaturant chevron data are obtained at zero and high metal ion concentration in the absence and presence of the crosslink. The presence of the crosslink results in little change in the metal response of Site k [Fig. 4(F)]. The 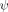values calculated for Site k from the chevron data in the absence and presence of the crosslink at Site n are 0.20 ± 0.01, and 0.27 ± 0.01, respectively.

Discussion

We utilized a Link-Psi strategy to investigate transition state heterogeneity employing a combination of a DCA crosslink at one position and probing using ψ analysis at another position. We investigated seven DCA-biHis combinations in Ub. Two combinations serve as controls while the other five involve sites with fractional ψ values, which are indicative of either transition state heterogeneity or a mildly distorted binding site having a weaker metal ion binding affinity in the TSE than in the native state. For each of the five DCA-BiHis combinations that we investigated involving fractional ψ sites, |Δψ₀| ≤ 0.12. These small changes in ψ₀ indicate that the profile of the saddle point at the top of the free barrier for folding is minimally perturbed upon introduction of a crosslink at another site.

Even though a change of 0.12 exceeds our statistical error, we believe it is insufficient to argue for transition state malleability. Supporting this interpretation are the results of the two controls. When the crosslink is introduced at Site b, which is formed in the entire TSE, no change in ψ is expected at the fractional Site h. Conversely, when this fractional site is crosslinked, the ψ value should not change at Site b, which is expected to be present in the entire TSE. For these two combinations, the observed changes in ψ are small, with Δψ_{before–after} = 0.09 and 0.14, respectively. We consider these values to be estimates of the expected Δψ_{before–after} variability for a negative control using the DCA–biHis combination.

For the five combinations investigated in which both sites have fractional ψ values, the magnitude of the changes (Δψ_{before–after} = −0.09, −0.03, 0.12, 0.09, and +0.07) are typically smaller than the changes observed for the two controls. These results point to a TSE that is only slightly malleable, if at all.

Nevertheless, we consider an alternative interpretation for Sites h and n located at distal regions on the β sheet (Fig. 2), because they have the largest Δψ_{before–after} values. When Site h or Site n are crosslinked, Δ 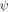= 0.12 and 0.09, respectively, for the other site. Potentially, the small decreases in the ψ values are consistent with a shift in flux away from a member of the TSE having the biHis site formed to another member having the region around the crosslink structured but lacking the biHis site.

However, the magnitudes of these shifts appear to be inconsistent with the degree of stabilization imparted by the crosslink. Upon crosslinking, the TSE is expected to have structure formed near the crosslink, or, at the very least, this region is stabilized by ΔΔG_crosslink ∼1 kcal mol⁻¹ (Table I). In either case, crosslinking should have resulted in larger decreases in ψ values than were observed. For example, when Site h is crosslinked, ψ₀ Site n decreased from 0.50 to 0.38. Had the TSE in fact been heterogeneous, containing distinct populations with structure formed at Site h, Site n or neither site, then the ratio [only Site h formed]:[only Site n formed]:[neither Sites h nor n formed] should have gone from 29:50:21 to 67:23:10. This calculation assumes that the initial population of [structure just at Site n] = 50% and the 1 kcal mol⁻¹ increase for Site h crosslinking produces a 5-fold increase in the ratio of [only Site h formed]:[Site h not formed]. Because this value is less than observed, the data do not support a model where the TSE has structurally disjoint subpopulations that can be influenced by DCA crosslinking.

However, one cannot completely rule out very minor shifts in structure (e.g., microscopic heterogeneity) around the periphery of an otherwise large, relatively homogenous TSE having the four β strands and part of the helix. Our simulations of the origin of fractional ψ values suggests that minor heterogeneous behavior is possible at Sites n and k, but not at Sites c and h due to their adjacency to biHis sites with ψ ∼1, which are present in the entire TSE.²³

Generality

The general strategy of the destabilization of one region followed by the probing of other regions was applied to the src and alpha spectrin SH3 domains, the B domain of Protein A and the GCN4 coiled coil using either mutations,^{8, 10, 18, 22, 37} or loop insertions.^{12, 31} However, heterogeneity was only found for the dimeric version of the coiled coil.¹⁰ An analysis of ϕ values in CI2 likewise failed to find evidence of transition state heterogeneity.⁷

Other work has investigated the interplay between transition state structure and topology using crosslinking or circular permutation. Changes in topology sometimes,^38–41 but not always^{12, 42} result in different transition states. However, these results do not mandate that transition state heterogeneity exists for the single version of the protein.

Evidence for transition state heterogeneity was observed in Titin based in part on the curvature in the chevron plots and denaturant dependent ϕ values.¹⁴ Titan unfolds along two pathways where the larger of the two transition states contains an extra β strand plus some additional structure around a common nucleus. The TSE of acyl phosphatese has a helix with a variable degree of fraying in the TSE according to ψ analysis.³⁰

Previous experimental studies comparing the folding behavior of Protein L and Protein G provided evidence that the amino acid sequence, rather than topology, can control the structure of the transition state.^{24, 43–48} These ϕ analysis data suggest the possibility of two structurally disjoint transition states containing one or the other hairpin. However, a recent ψ analysis study found that Protein L's TSE contains both hairpins, rather than just a single hairpin (Yoo et al., submitted). Therefore, data on these proteins currently should not be used as evidence either for sequence greatly influencing the TS structure or for the possibility of structurally disjoint TSs.

Conclusion

The complexity of the folding reaction along with theoretical modeling suggests that there could be a considerable amount of transition state heterogeneity. However, the experimental evidence for heterogeneity is rather minimal for proteins that fold in a single kinetic step when heterogeneity is defined at the level of having structurally disjoint secondary structural elements. Our Link-Psi strategy employing DCA crosslinking and ψ analysis applied to Ub further supports this view, as does a recent all-atom study on a dozen proteins where most folding routes are best viewed as variations of a single folding pathway.⁴⁹

A lack of transition state heterogeneity can be explained by two factors. The presence of only a few low energy pathways is a consequence of folding occurring through a process of sequential stabilization wherein foldons build on top of existing structures.^{32, 50} Secondly, many TSEs contain a high fraction of the native structure and topology (e.g., the TSE has ∼70% of the native state's relative contact order).^{20–22, 32, 51} This high level eliminates many otherwise possible transition state structures, and further reduces the amount of heterogeneity.

Material and Methods

Expression, purification, and crosslinking of ubiquitin

The biHis/biCys quadruple mutants of Ub F45W were created sequentially using Stratagene's QuikChange mutagenesis kit as previously described.⁵² An additional H68N substitution was introduced into all variants, except the variant containing a metal binding site at Site c, to avoid complications from spurious metal ion interactions. The biCys mutants were crosslinked using the bifunctional thiol-specific reagent DCA.³⁴

Kinetic experiments

Kinetic experiments were performed using a Biologic stopped-flow apparatus⁵² at 20°C, 50 mM hydroxyethyl piperazineethanesulfonic acid (HEPES) (pH 7.6) and a final protein concentration of 1.6 μM. Fluorescence from Trp45 (excitation wavelength 280(± 10) nm; emission wavelength 350 (± 50) nm) was used to monitor the folding and unfolding reactions. Kinetic data were obtained in the presence of a divalent metal ion at a high concentration (1 mM). The kinetic “chevron” data were analyzed assuming that the activation free energies were linearly dependent on denaturant concentration and fit using a non-linear least-squares algorithm (Microcal Origin) accounting for correlated errors.⁵³ For refolding experiments, the final denaturant concentration was fixed for a given variant (between 2 and 3M GdmCl depending on the stability of the variant). Likewise, the unfolding experiments were conducted at a fixed denaturant concentration (between 6.2 and 7.5M GdmCl). Metal ion concentrations were identical in both refolding and unfolding experiments for each variant. The increase in equilibrium stability with [Me²⁺] was calculated according to

1

ψ analysis

ψ analysis uses engineered biHis sites to probe the fraction of native metal ion binding energy realized in the transition state. The kinetic response as a function of metal ion concentration quantifies the degree to which the biHis site is present in the TSE (see Refs. 20 and 30 for detailed treatment). The kinetic response due to metal binding can be obtained from the denaturant dependence of folding rates (“chevron analysis”) at zero and high metal ion concentrations in a manner analogous to ϕ analysis performed using point mutations.

When side chain substitution or metal binding only affects the unfolding rate k_u and not the free energy of the transition state relative to the unfolded state, the structure probed is absent in the TS, and the corresponding ϕ or ψ vanishes. Conversely, when the perturbation only affects the folding rate, k_f, the structure probed is likely to be native-like in the TSE and the associated ϕ or ψ value is unity. When both the folding and unfolding arms shift, the ϕ or ψ value is fractional. The origin of a fractional value can be challenging to discern in both methods. Fractional ϕ may arise either due to partial structure formation in the TS or to the presence of multiple, distinct TS structures.^{7, 8, 10, 19, 24–27} A fractional ψ value indicates that the biHis site is either native-like in a subfraction of the TSE, has non-native binding affinity in the entire TSE (e.g., a distorted site with less favorable binding geometry, or a flexible site that must be restricted prior to ion binding), or some combination thereof.^{19, 32}

ψ analysis has the capability of generating a large quantity of high quality kinetic data to accurately probe the degree to which a particular binding site is formed in the TS. Each biHis variant enables the measurement of dozens of folding rates at increasing concentrations of metal ions. The binding of increasing concentrations of ions to the biHis site produces a nearly continuous increase in the stability of transition state structures that contain the binding site. Hence, the stability is perturbed yet accomplished in an isosteric and isochemical manner. The resulting series of data can be justifiably combined, a process which may be inappropriate in traditional mutation studies where the perturbation can arise from multiple sources, including changes in backbone propensities as well as indeterminate non-local interactions.

The ψ analysis data can be represented as a Leffler plot where the change in activation free energy is plotted relative to the change in the metal-induced stability.⁵⁴ If the biHis site is formed in the TSE, metal binding increases its stability, and folding rates increase. The associated Leffler plot has a positive slope as both ΔΔG^‡_f and ΔΔG_eq increase.

The starting point in the detailed interpretation of the Leffler plot involves fitting the data to a model with a single free parameter ψ_o, which is the slope at the origin in the absence of metal,

2

The interpretation of ψ values is clear in the two cases where the Leffler plot is linear. When ψ₀ is unity, the biHis site is present with native-like affinity in the TSE. When ψ₀ is zero, the site is absent with unfolded-like affinity. Otherwise, the Leffler plot displays curvature as ligand binding continuously increases the stability of the TSE, that is, ψ approaches unity with increasing metal concentration.

When the metal ion-binding equilibrium is established much faster than the folding and unfolding rates, ΔΔG_eq and ΔΔG can be expressed as,

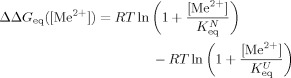3a

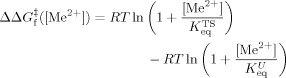3b

Glossary

Abbreviations

biCys

bi-cysteine

biHis

bi-histidine

DCA

dichloroacetone

GdmCl

guanidinium chloride

TSE

transition state ensemble

Ub

mammalian ubiquitin

ψ₀

fraction of the native metal ion binding energy realized in the transition state, extrapolated to zero metal ion concentration