Is there an en route folding intermediate for cold shock proteins?

Abstract

Cold shock proteins (Csps) play an important role in cold shock response of a diverse number of organisms ranging from bacteria to humans. Numerous studies of the Csp from various species showed that a two-state folding mechanism is conserved and the transition state (TS) appears to be very compact. However, the atomic details of the folding mechanism of Csp remain unclear. This study presents the folding mechanism of Csp in atomic detail using an all-atom Go model-based simulations. Our simulations predict that there may exist an en route intermediate, in which β strands 1-2-3 are well ordered and the contacts between β1 and β4 are almost developed. Such an intermediate might be too unstable to be detected in the previous fluorescence energy transfer experiments. The transition state ensemble has been determined from the P_fold analysis and the TS appears even more compact than the intermediate state.

Introduction

When the temperature decreases significantly, Cold shock proteins (Csps) will be expressed at high levels in response to cold shock. Csps can bind to single-stranded nucleic acids and regulate the expression of other proteins.^{1, 2} Owing to their important role in stress response, Csps are generally conserved from bacteria to human and share similar structures and sequences across various species. The structure of Csp from Bacillus subtilis is shown in Figure 1. It is a β-barrel constituted by five β sheets. Meanwhile, Csps have been known as a protein family that can fold fast in a two-state folding mechanism³ as Schmid and coworkers showed that the folding dynamics of CspB from B. subtilis follows a two-state model in 1995.⁴ Folding of Csps from several organisms, for example, B. subtilis,^3–8B. caldolytics,^{3, 9–11}, Escherichia coli,^12–16 and Thermotoga maritima,³ have been studied intensively by ensemble experiments. With the advances in single-molecule techniques, valuable insights have been gained from recent single molecule fluorescence energy transfer (FRET) studies of the Csp from T. maritima.^17–21 The two-state folding dynamics has been demonstrated clearly at the single-molecule level.¹⁷

Figure 1.

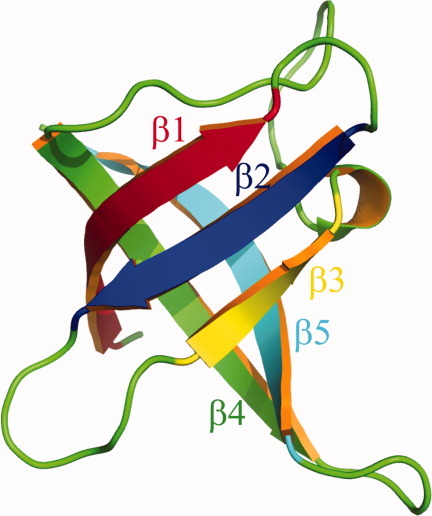
The structure of Csp from B. subtilis (Brookhaven PDB accession code: 1csp) is shown. Five β strands are rendered in different colors. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

In many experimental studies,^{3, 4, 12} the fluorescence of a single tryptophan is used alone to probe the folding dynamics. Vu et al.¹⁵ argued that such measurements might report only on local conformational preferences and their dynamics instead of the global folding dynamics. Other than using W11 in Csp-A from E. coli as the probe, Y42, S52, and T68 have been substituted with tryptophan to study Csp folding.¹⁵ Very similar rate constants of folding were found for tryptophans located in various structural contexts. Furthermore, several different methods, including the use of tryptophan or tyrosine as a probe as well as an ensemble FRET measurement, have been employed to study the folding dynamics of the Csp from B. caldolytics.^{10, 11} Most folding rates in their studies are comparable, which suggests that the folding of Csp indeed follows the kinetic mechanism of a two-state protein.

For the two-state folding dynamics, identifying the transition state ensemble (TSE) is crucial to understand the underlying folding mechanism. As the structures in TSE have relatively high free energies and very short lifetimes,²² it is difficult to study them directly in experiments. The dependence of rate constants of refolding and unfolding on denaturant concentration suggests that the transition state (TS) of Csp should be very compact.^{3–7, 9–13, 15} On the other hand, φ-value analysis, proposed by Fersht et.al.,²³ has served as a powerful method to study the TSE. So far, φ-value analysis has been used to systematically study the TSE of Csp from B. subtilis.⁷ They suggested that in the TS β1 resembles the structure in folded state, the hairpin by β1–β2 is formed, the hairpin by β2–β3 is partially formed, and native contacts between β1–β4 are partially developed. This is partially consistent with the TS suggested by Alm et al.,²⁴ who proposed that β1–β2–β3 form a well-ordered structure and the native contacts in the loop between β3 and β4 are partially developed. Other than experimental studies, Csps have been studied by computer simulations and theories.^24–28 The atomic details of folding pathway, including the TSE, are not easily obtainable from experiments alone. Ab initio computer simulations using an all-atom model might bridge this gap. However, the folding time of Csp is on the order of several milliseconds,³ which is far beyond the time scale that most simulations using all-atom force fields today can reach. Although significant progress has been made in designing specific platforms that can accelerate molecular dynamics by two or three orders of magnitude and run milliseconds simulations with explicit solvents,²⁹ more powerful systems are highly desired as many independent trajectories are needed to gain good statistics on folding pathways. Other than the lack of powerful computational resources, the existing force fields might not be accurate enough for ab initio folding simulations, especially for β-proteins. For example, several commonly used force fields could be too helical.^30–32 In the recent study by Nettels et al.,³³ the Rg of unfolded Csp measured in simulations using AMBER ff03/TIP4P-Ew and OPLS-AA/L force field are around 14 Å, which is significantly smaller than the value inferred from single-molecule FRET experiments, 23 Å.³³ In this case, the unfolded/denatured states of Csp are not correctly modeled by these force fields. Although a knowledge-based force field has been used to fold several helical proteins succesfully,³⁴ it is still very challenging to fold β-proteins. Other than physical and empirical force fields, structure-centric Go-like models have been widely used to study protein folding mechanisms,^35–45 especially when there are no other suitable force fields available. Despite the simplicity and well-known unphysical aspects, Go-like models have been used, with some success, to study folding dynamics^{35, 37–42, 44, 45} and predict folding rates⁴⁶ as it is widely assumed that the folding mechanism is mainly determined by a protein's native structure.^{40, 44, 47} Generally, Go models provide a good description of the energy landscape of the folded state, the TS, and the native-like intermediates.^{40, 44, 47–49} It is possible to extract meaningful results about the folding mechanism and the TS for those small proteins which directly collapse to a native-like TS. Go models are known to have limitation of describing non-native-like collapsed structures, for example, those misfolded structures, and the contributions from non-native interactions.^{48, 49} Experiments show that the unfolded states of Csp behave like a random coil^{17, 20} (instead of a collapsed globule) and they directly collapse into a very compact TS.⁴ Therefore, Go models could be appropriate to study the folding mechanism of Csp.

In this study, we used an all-atom Go potential to study the folding mechanism of the Csp from B. subtilis. It is the first ab initio Csp folding simulations with atomic details. High cooperativity in folding dynamics is observed in our simulations and the detailed folding mechanism is outlined. Our simulations suggest that the unfolded state essentially is a random coil except for the partially formed hairpin by β1–β2 and β2–β3 as well as partially developed native contacts within the loop between β3 and β4. Additionally, our simulations suggest that there is a short-lived (the dwell time is around 1/1000 of the folding time) intermediate although it is so unstable that it might be difficult to detect in existing experiments. Consequently, Csp will exhibit an apparent two-state folding dynamics.

Model and simulations

The all-atom Go model in our study is similar to the models in our previous studies.^{38, 39} All heavy atoms (nonhydrogen atoms) are modeled as beads having same mass. A square well potential with an infinite depth as shown in Eq. (1) is used to model a covalent bond connecting two atoms i and j. r_ij⁰ is the bond length in the native structure and it is assumed as the equilibrium bond length.

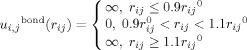1

In our simulations, the X-ray structure of Csp from B. subtilis¹ (Brookhaven PDB accession code: 1csp) is used as the native structure. The missing side-chain atoms in glutamic acid are added using the Swiss-Pdb viewer (http://spdbv.vital-it.ch/) and no collisions are detected in the reconstructed native structure. There are 520 heavy atoms in total. To define the Go potential, distances between two nonlocal atoms (separated by at least two residues along the protein backbone), i and j, in the native structure are calculated (denoted as r_ij) and compared with the cutoff distance of native contact r_{ij_cut} = r_cut(r_i+r_j), where r_i and r_j are the radii of atom i and j (radii data were adapted from Ref.50) and r__cut is a scaling factor. If r_ij < r_{ij_cut}, atoms i and j could form a native contact; otherwise, they will form a nonnative contact for a distance smaller than r_{ij_cut}. The interaction energy is zero for a distance larger than r_{ij_cut}. The depth of the energy well for a native contact pair and for a nonnative contact pair is −ε and 0, respectively. Here, ε is the unit of energy. The hardcore radius for each atom is defined as 0.8r_i, where r_i is the VDW radius for atom i. The distances between any two nonbonded and nonlocal atoms cannot be smaller than 0.80(r_i+r_j). The total energy of any given conformation is calculated as the sum of all pairwise energies for nonlocal atoms. Discrete molecular dynamics with constant temperature^{43, 51} is used in both thermodynamic sampling and the studies of folding kinetics. As shown in Figure 1, residues 2–10, 14–19, 26–29, 44–53, and 58–66 are defined as strands β1–β5, respectively. The loop between β1 and β2 is labeled as loop-1; the loop between β2 and β3 is labeled as loop-2; the loop between β3 and β4 is labeled as loop-3; the loop between β4 and β5 is labeled as loop-4.

The reduced units of energy, length (r), mass, and temperature in our simulations are ε, Å, m, and ε/k_B, respectively. For convenience, reduced units are used for the simulations, that is, E* = E/ε, r* = r/Å, T* = T/(ε/k_B) and t* = t/.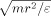

Results and Discussion

The results of the simulations were found to be dependent on the parameters, especially r__cut. Extensive discussion about how parameters (r__cut) and temperature affect the energy landscape of Csp will be reported elsewhere. In the present study, r__cut is set as 1.10. For very small values of r__cut (<1.05), there are not enough native contacts to accurately maintain a stable folded state. Large values of r__cut (>1.20) make side-chain packing more degenerate. Simulations with 1.10 show an apparent two-state folding behavior which is consistent with the experiments. All kinetic simulations are conducted at relatively high temperatures, that is, slightly below the folding temperature.

The intermediate and unfolded state

The replica exchange method⁵² is used in thermodynamic sampling. The temperatures in 64 replicas are set from 0.312 to 0.495. More replicas are allocated in the vicinity of the transition temperature to accurately determine the position of transition temperature. Four independent simulations are conducted to calculate the error bars. The weighted histogram analysis method (WHAM)^53–55 is used for data analysis by combining the data at all temperatures. The Rg, fraction of native contacts (Q), specific heat capacity (C_v/k_B), and potential energy from direct simulations as well as WHAM are shown in Figure 2. We can observe highly cooperative folding and the folding temperature (T_f, the temperature where C_v/k_B reaches its peak value) is found to be around 0.410 with a very narrow transition region. At lower or higher temperature, the protein is either folded or unfolded.

Figure 2.

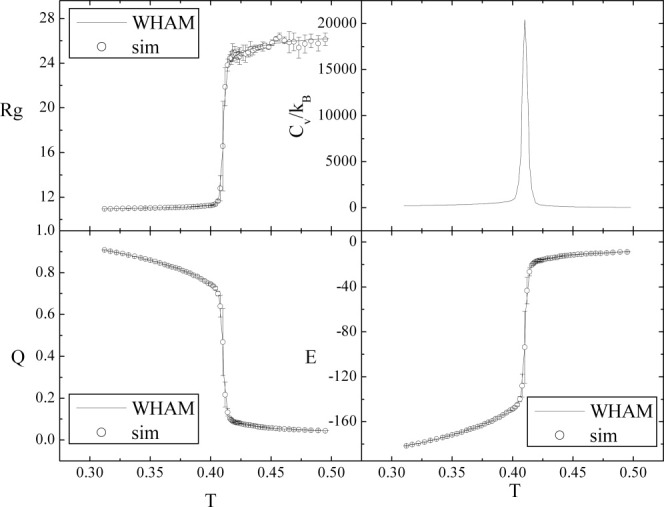
Temperature dependence of Rg, C_v/k_B, Q, and E. Circles represent data from direct simulations and lines represent data obtained by WHAM.

Our kinetic simulations with 1024 trajectories suggest that besides folded and unfolded states there exists an intermediate state. The traces of the time-dependent Q from four typical folding trajectories at T = 0.402 (corresponding to a physical temperature of 44°C considering the experimental unfolding temperature as 50°C⁵⁶) are shown in Figure 3. The intermediate appears obligatory on folding pathway. The intermediate is highly unstable, that is, it can either fold completely or get unfolded. As the time of simulations is not long enough, the intermediate state is never reached in many trajectories, that is, only the unfolded states are observed within simulations. In our 1024 kinetic trajectories, the intermediate has been visited 599 times. Only 124 of them lead to the folded state and the rest unfold quickly. The distribution of dwell times for this intermediate can be fitted well with a single exponential with dwell time as 2.8 ×10⁵ time units. On the other hand, the folding time is estimated to be around 3 × 10⁸ time units by single exponential fitting of time-dependent survival ratio of the unfolded state. Compared with the folding time, the dwell time of the intermediate is 1000 times shorter and would presumably be on the order of a microsecond in experiments, considering that the folding time in experiments is on the order of a millisecond.⁴ Owing to its short lifetime, the intermediate state cannot be detected in current single-molecule FRET experiments, considering the time resolution of FRET is generally around 0.1–1 ms. It would be of great interest to design single-molecule FRET experiments to check the existence of the short-lived intermediate that we observe. A dye system with relative small Förster radius (around 30 Å) should be used to distinguish the intermediate and folded state better as the end-to-end distances in the intermediate and folded state are around 30–40 and 13 Å, respectively. As the intermediate state is not stable (i.e., there are no pronounced barriers to the unfolded and folded states), the solvent with higher viscosity might be helpful to slow down the transitions from the intermediate to unfold and fold structures as demonstrated by Eaton and coworkers.⁵⁷ It should be kept in mind, though, that adjusting solvent viscosity is still tricky as the energy landscape could be changed.

Figure 3.

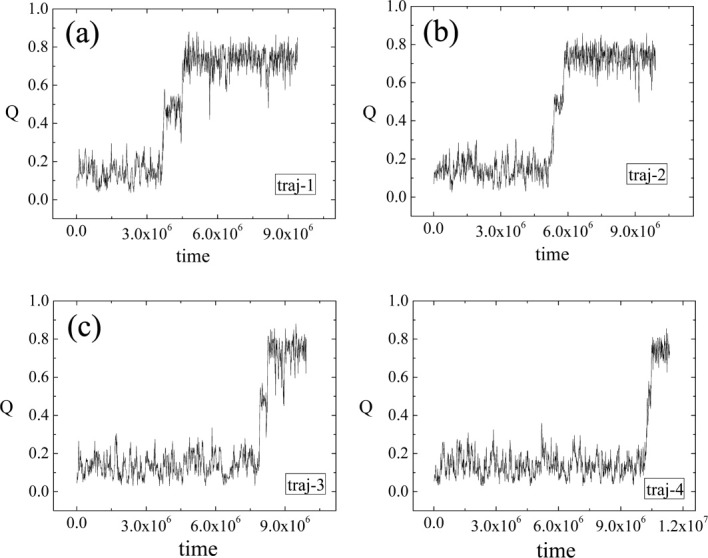
Four typical traces of the time-dependent Q from kinetic simulations.

To relate the folding kinetics and free-energy landscape, one kinetic trajectory is shown in Figure 4 in the 2D free-energy profile for Rg and Q. The intermediate state is highlighted by a circle. As this intermediate is not stable and the simulations time in thermodynamic simulations is relatively shorter than that in kinetic simulations, the intermediate is not observed in the 2D free-energy profile. One typical snapshot of the intermediate is shown in Figure 4. It indicates that β4–β1–β2–β3 forms a well-ordered structure where only β5 is dangling around. Interestingly, the simulation based on a coarse-grained model by O'Brien et al.⁵⁸ also found an intermediate for the Csp from T. maritima. However, their structure of the intermediate is different from ours. They suggested that only β1 is unfolded and the rest is folded. One possible reason for the difference might be that different Csp proteins were used in simulations. The difference of amino acid sequences between Csp from T. maritima and B. subtilis are more than 30%.

Figure 4.

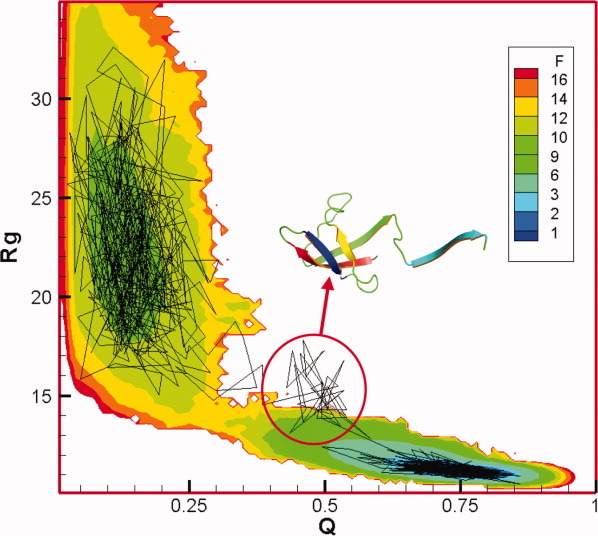
The 2D free-energy profile for Rg and Q at T = 0.402. Different colors represent the corresponding free energy reduced by k_BT. One typical folding trajectory from kinetic simulations is also shown in this plot. The intermediate is highlighted by a circle and one typical snapshot is shown. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

The structures in the unfolded basin (Fig. 4) contain very small number of native contacts. Essentially, it behaves like a random coil and the average Rg is around 23 Å, which agrees very well with single-molecule FRET experiments.³³ The unfolded state has been studied by ensemble FRET experiments^{10, 11} in detail and they suggested that it is similar to a random coil without ordered secondary structures. The reconfiguration time of Csp in the unfolded state in our simulations is on the order of 10⁴ time units (∼100 ns, which is comparable with experimental value,^{20, 59} 50 ns). The work by Schuler and coworkers²¹ suggested that around 20% of the β strands are formed after 1.3 ms dead time. This finding may be owing to the contribution of partially folded β1–β2–β3 strand and may be influenced by a contribution from a small fraction of the folded state. In our simulations, several native contacts within the β-turn area of hairpins, β1–β2 and β2–β3, are partially formed in <10⁵ time units (<1 microsecond). The hairpin by β4–β5 is very unstable compared with the others. Several native contacts within the loop between β3 and β4 are also partially developed. The contacts between β1 and β4 are essentially not formed and the native contacts for β3–β5 are not formed.

As shown in Figure 4, the free energy of the folded state is about 9k_BT lower than the free energy of the unfolded state. On the other hand, we can roughly estimate the free-energy difference between the unfolded state and the intermediate state with Eq. (2).

2

k_unfold->I is the transition rate from the unfolded state to the intermediate state and k_I->unfold is the backward transition rate.is around 1/200 in our simulations. Consequently, the free energy of the intermediate state is about 14 k_BT higher than the free energy of folded state. The potential energy decreases around 50ε (124 k_BT) from the intermediate state to the folded state. Roughly, −TΔS is changed by 110 k_BT, which suggests that there exists a large entropy barrier in the transition from the intermediate state to the folded state.

Characterizing the TSE

As mentioned above, the P_fold of the intermediate is 0.2. Considering that the TS from the intermediate state to folded state has equal transition probability (0.5) to the intermediate state and folded state, its P_fold is around 0.6, which is close to the P_fold of real TS of Csp folding (0.5). Consequently, the TS of Csp folding should be close to the TS from the intermediate to the folded state. All structures in the free-energy landscape shown in Figure 4 around the transition region from the intermediate to the folded state, specifically with Q ∈ (0.35,0.65), Rg ∈ (12,14) Å, and CαRMSD ∈ (5,12)Å, are selected as putative TS conformations. In total, 588 conformations are found satisfying such criteria and the real TS is identified using the P_fold analysis,³⁴ for example, P_fold ∈ [0.4,0.6] in 64 trajectories. The simulation time for the short trajectories used in the P_fold analysis is 8.6 × 10⁵ time units, roughly three times the dwell time in the intermediate. The distribution of P_fold over 588 conformations shows two peaks, that is, one around 0.2 and the other around 1.0, suggesting that 2D projection of free energy landscape Q–Rg plane does not provide an accurate kinetic description, that is that neither Q nor Rg can serve as a good reaction coordinate as was found earlier.^60–62 A similar distribution of P_fold was also observed by Hubner et al.⁶³ Eventually, only 20 out of 588 putative TSE structures have P_fold ∈ [0.4,0.6] and they constitute the real TSE. The average residue–residue contact map for the real TSE is shown in Figure 5. Compared with the contact map of the intermediate state, the major differences are located in the two regions that are highlighted with an ellipse and a circle, respectively, in Figure 5. The representative structures are shown above the contact map. In one representative TS structure, (Fig. 5, left panel) new contacts are developed between β5 and the loop between β3 and β4. Alternatively, new contacts can be developed between β4 and β5 in an alternative representative TS structure (Fig. 5, right panel). The two different pathways are the consequence of the low stability of the β turn between β4 and β5. Following the way we used previously,³⁴ the φ-values are calculated for our TSE and compared with the experimental value⁷ in Figure 6. The residues in β2 and β4 have larger φ-values in our simulations, which suggest β2 and β4 are more ordered in our TSE compared with experimental φ-values. Essentially, the φ-values of the residues located in β1, β3, and β5 are consistent with experiments. Most existing experiments show a very asymmetric chevron plot for the dependence of the apparent refolding rate on the concentration of denaturant. This suggests that the TS is very compact. The average SASA of the unfolded state, TSE and the folded state have been calculated by EDTSurf⁶⁴ as 9000, 6250, and 5210 Å,² respectively. The change of SASA from the unfolded state to TS over the change of SASA from the unfolded state to folded state is around 0.73. If we assume that the change in SASA is roughly proportional to the change in the interactions with the solvent, that is, the m-value in chevron plot, 0.73 is consistent with 0.6–0.9 in the experiments of CspA from E. coli.^{13, 15} However, the m-value for the experiments of Csp from other species³ (from 0.86 to 0.93) is somewhat larger.

Figure 5.

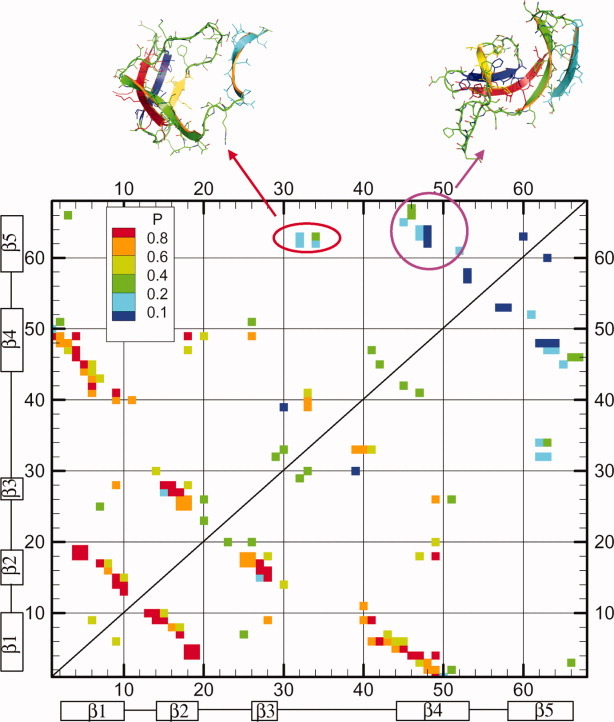
The average residue–residue contact map is shown for 20 transition state structures. Different colors represent the corresponding probability of native contacts. Two representative TS structures are shown in the top. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Figure 6.

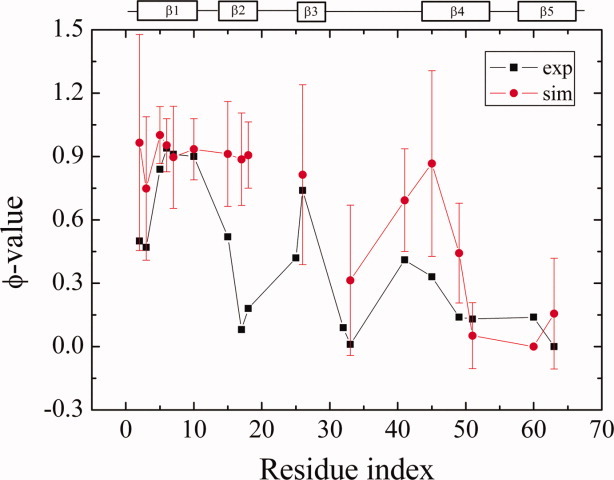
Comparison of φ-values between simulations and experiments. Error bars denote the standard deviation, σ of computed φ-values [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.].

The folding mechanism of Csp

Almost all existing experiments suggest that Csp folds without a stable intermediate except that there may exist a fast collapse phase preceding the folding when Csp is transferred to folding conditions from denaturing conditions.¹¹ Such a fast collapse process was suggested mostly owing to nonspecific interactions¹⁰ and involves a collapsed structure that is essentially unfolded except some structural elements that are similar to the folded state. Furthermore, the single-molecule study by Schuler and coworkers²¹ suggested that around 20% of β sheets are formed in the fast collapse phase occurring in a dead time around 1.3 ms (the folding time under such conditions is around 19 ms). Single-molecule FRET experiments^{21, 65} showed, not surprisingly, that the unfolded states at lower concentration of denaturant are more compact than at higher concentration of denaturant. Intuitively, when Csp is switched from a high concentration of denaturant to a low concentration of denaturant, the former unfolded state will collapse ultrafast and relax to the new unfolded state at this new lower concentration of denaturant. In fact, a similar argument was proposed by one of us in 1997.⁶⁶ Analogously, such a fast relaxation phase is also observed in the temperature jump experiments.¹⁴ The recent single-molecule study by Schuler and colleagues²⁰ suggested that the collapse time of unfolded Csp is comparable with the reconfiguration time at around 50 ns. Such an ultrafast collapse phase is a purely diffusive, “downhill” process. An ultrafast collapse is often associated with the change of environment. In our simulations, the fast collapse phase is not present as the initial configurations were generated by equilibrium simulations (10⁴ time units per trajectory) under the same temperature as in the kinetic simulations. Consequently, there is no such a collapse process in response to the abrupt changes in the environment (temperature, the concentration of denaturant, etc.).

The possible folding pathway for Csp suggested by our thermodynamic and kinetic simulations is shown in Figure 7. In an unfolded state, the hairpins by β1–β2 and β2–β3 are not stable. They interchange quickly between the open and the closed forms. The hairpin by β2–β3 is slightly more stable than the hairpin by β1–β2, which is consistent with the finding from a hydrogen exchange study of the Csp from E. coli.¹⁶ The loop between β3 and β4 is also partially folded. It takes a long time to form a well-ordered β1–β2–β3 structure. When β4 is attached to β1 and the native contacts within the loop between β3 and β4 are fully developed at the same time, an intermediate state is formed. However, this intermediate state is not stable although β1 and β2 resemble the same state in folded structure. P_fold of such intermediate is 0.2, which suggests that the barrier to get folded is larger than the one in breaking the ordered strands, β4–β1–β2–β3. When the native contacts between β4 and β5 as well as β5 and loop 3 are developed, the β-barrel can be closed and the folded state is formed. Our simulations suggest that the TS is very compact and is reached at a very late stage in terms of the magnitude of protein–solvent interactions as proposed by experiments.^{12, 13} A well-ordered structure of β4–β1–β2–β3 is formed in the TS. Either the native contacts between β4 and β5 or between β5 and the loop connecting β3 and β4 are partially formed. Interestingly, the sequence of folding events revealed by our simulations is essentially in the reverse order of unfolding simulations at high temperature.²⁸ The TS is more compact than that suggested by experimental φ-value analysis⁷ and theory.²⁴ The mutation study of F20 and F31 for Csp from E. coli¹³ suggested that these two residues should be present in the TS, that is, β2 and β3 might folded. This argument is also supported by the studies of Reid et al.¹² that the presence of an oligonucleotide can increase the folding rate as such an oligonucleotide can bind the hydrophobic residues located in β2 and β3. Perl et al.⁹ have proposed that the N-terminal region is folded but the C-terminal is not in the TS. Furthermore, Garcia-Mira et al.⁷ suggested that the development of native contacts between β1 and β4 is crucial for reaching the TS. It seems that the TSE identified by this study is consistent with most experiments. However, it is still unknown how β5 interacts with other strands in experiments. It would be very interesting to design experiments to compare the TS in experiments with the TSE we propose here. For example, the change of folding rates of the mutation at residue Gln34 might shed light on the role of the interactions between the loop (residue, 30–43) and β5.

Figure 7.

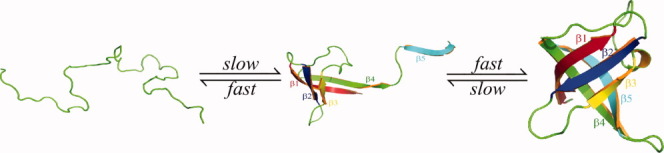
The proposed folding pathway for Csp. The intermediate state is very unstable. In the intermediate state, only β5 is isolated and the remaining parts resemble the native structure. The intermediate state can either unfold (with 80% probability) or fold (with 20% probability). [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]