Theory Testing Using Quantitative Predictions of Effect Size

Abstract

Traditional Null Hypothesis Testing procedures are poorly adapted to theory testing. The methodology can mislead researchers in several ways, including: (a) a lack of power can result in an erroneous rejection of the theory; (b) the focus on directionality (ordinal tests) rather than more precise quantitative predictions limits the information gained; and (c) the misuse of probability values to indicate effect size. An alternative approach is proposed which involves employing the theory to generate explicit effect size predictions that are compared to the effect size estimates and related confidence intervals to test the theoretical predictions. This procedure is illustrated employing the Transtheoretical Model. Data from a sample (N = 3,967) of smokers from a large New England HMO system were used to test the model. There were a total of 15 predictions evaluated, each involving the relation between Stage of Change and one of the other 15 Transtheoretical Model variables. For each variable, omega-squared and the related confidence interval were calculated and compared to the predicted effect sizes. Eleven of the 15 predictions were confirmed, providing support for the theoretical model. Quantitative predictions represent a much more direct, informative, and strong test of a theory than the traditional test of significance.

INTRODUCTION

The development of theories plays a critical role in the advancement of any science. Theory testing serves a critical role in the modification or rejection of a theory. In the behavioral sciences, the testing of theories has typically employed traditional null hypothesis testing procedures. This represents an indirect procedure since the null hypothesis is assumed correct until it is rejected. When the null hypothesis is rejected, the alternative hypothesis (and the theory) is considered to be supported. However, failure to reject the null hypothesis can occur for a number of reasons, including inadequate sample size, poor measures representing the theoretical constructs, and failure to properly operationalise the theory. This traditional practice has been labeled weak use of null hypothesis testing for theory appraisal by Meehl (1967, 1990, p. 116), and as rejection-support by Nickerson (2000, p. 244). By contrast, Meehl’s strong use required that the predictions of the theory—rather than a statement of nil effect or zero relationship—be used as the null hypothesis so that failure to reject would be taken as some degree of support for the theory; this was Nickerson’s acceptance-support.

In this paper, we will consider an alternative procedure that is a development of the strong strategy, and represents a direct test of a theory. Based on the work of Cohen (1962, 1988), standardised effect size estimates have been developed and have become the basis of power analysis and meta-analysis. Effect size estimates—either standardised or expressed in the original measures—can be used as a means of quantifying the predictions from a theoretical model. Observed effect size estimates can then be compared to the predicted effect sizes and confidence intervals can be used to assess how strongly the data support the theory.

This approach requires that the theory have adequate specificity to provide explicit quantitative predictions. The process of deriving such predictions from a theory can force the theorist to make explicit what were previously vague or inadequately articulated aspects of the theory. Broad-bent (1987) gave examples to support his contention that even simple quantitative models represent a great advance over psychology’s traditional “more than” or “less than” predictions, and that developing such models is a salutary discipline for the theory builder. Testing can result in modifications of the theory, guided by the pattern of fit and discrepancies between the predictions and the data, or rejection.

Problems with Null Hypothesis Testing

Null hypothesis procedures are poorly adapted to theory testing. In the commonly used weak strategy, the focus is on the null hypothesis or a prediction of no relationship between two variables. Usually this is not the prediction that is made by the theory. The theory typically predicts that two variables are related. Rejection of the null hypothesis implies support for the theory. However, failure to reject the null hypothesis can occur for many reasons besides an incorrect theory. The most well known is sample size, with small sample sizes resulting in a failure to reject the null hypothesis. Failure to reject can also be the result of employing poor measures of the theoretical constructs and/or poor operationalisation of the theory. The latter is particularly problematic since the theory will have reduced impact on the formulation of the test.

Null hypothesis testing results can only support ordinal claims. Frick (1995, 1996) made an important distinction between ordinal claims and quantitative claims in his discussion about when null hypothesis testing is appropriate in psychological research. Ordinal claims do not specify the size of the effect, only the order or direction of the effect. Unfortunately, knowledge in psychology is mainly based on ordinal claims. Use of effect size measures, however, can increase the extent to which predictions can justifiably be generalised. Based on well-developed measures, an explicit theory, and a representative sample, quantitative predictions are the focus of this paper.

In order to illustrate the use of quantitative predictions to test theory, this paper will employ the Transtheoretical Model and test a series of quantitative predictions based on the model and previous data. The predictions involve a comparison of smokers who were classified at a baseline assessment from a large clinical trial into one of the first three Stages of Change: Precontemplation, Contemplation, or Preparation. Stage was employed as the independent grouping variable. The two Decisional Balance subscales, the three Situational Temptations subscales, and the 10 Processes of Change served as the dependent variables. A series of a priori predictions were made for each analysis. The goal was to employ confidence intervals to evaluate the fit between the observed effect size estimate and predicted effect size for each of the dependent variables.

Alternative Effect Size Estimates

Kirk (1996) described 40 measures of effect size. Many of these estimates can be classified on two broad dimensions (Fidler & Thompson, 2001) as (a) standardised difference versus variance accounted for and (b) uncorrected versus corrected effect sizes. An effect size can be as familiar as a mean or correlation; it can be expressed in original measurement units, or standardised, for example Cohen’s d expressed in SD units. Standardised effect sizes such as Cohen’s d are most appropriate when two groups are being compared. An important class of effect sizes are measures of variance accounted for, including R², η², and ω², for example in an ANOVA (Hays, 1963, p. 414). The latter are the most appropriate when more than two groups are involved. Uncorrected variance-accounted-for indices are positively biased overestimates of the effect in the population. We use ω^2, which is corrected for this bias. The formula for ω² for a one-way between-groups fixed effects ANOVA is

$${\omega }^2=({\text{SS}}_{\text{BETWEEN}}-{(\text{k}-1)}^{\ast }{\text{MS}}_{\text{WITHIN}})/({\text{SS}}_{\text{TOTAL}}+{\text{MS}}_{\text{WITHIN}})$$ [1]

where SS_BETWEEN and SS_TOTAL are the between and total variation (Sum of Squares) terms, k is the number of groups, and MS_WITHIN is the within-group variance (Mean Squared) term.

Calculating Confidence Intervals for Effect Size Estimates

Following decades of advocacy by statistics reformers, the use of confidence intervals is now recommended by the APA Publication Manual: “Because confidence intervals combine information on location and precision … they are, in general, the best reporting strategy. The use of confidence intervals is therefore strongly recommended” (APA, 2001, p. 22). Cumming and Finch (2001, 2005; also see Steiger, 2004) described the advantages of confidence intervals, and discussed how they can be presented and interpreted. In this article, we use confidence intervals illustrated in figures following the advice of the APA Task Force on Statistical Inference: “In all figures, include graphical representations of interval estimates whenever possible” (Wilkinson & TFSI, 1999, p. 601).

Calculating confidence intervals for standardised effect size measures requires use of an iterative computer algorithm, rather than a single formula (Cumming & Finch, 2001). The calculation of confidence intervals for ω² is described by Fidler and Thompson (2001).

Developing Quantitative Predictions

This paper will report the results of 15 tests of predictions based on the Transtheoretical Model. All effect sizes were calculated as Omega Squared (ω²), the population estimate of the accounted for variance. Effect size interpretations were based on Cohen’s (1988) descriptive guidelines. A “small” effect is about 1 per cent of the variance, a “medium” effect is about 6 per cent, and a “large” effect is about 14 per cent or more. Cohen emphasised that his guidelines are arbitrary and that any effect size should be interpreted in its research context. In our judgment the guidelines are appropriate as initial approximations for the behavior change domain, and we will use previous empirical findings to refine the values. Predicting an effect size of 0 per cent also represents a clear prediction.

The prediction of an effect size represents a novel task with little available guidance. Predictions should be based on a combination of theory and previous empirical results. As a theory is developed and tested, the predictions will become more solidly grounded in empirical work. We have followed three different steps to form the effect size predictions, representing an increasing degree of specificity. First, predictions were made based on the hypothesised relationship based on the Transtheoretical Model. These predictions were translated into quantitative statements using the Cohen descriptive guidelines. Second, the effect size predictions were compared to empirical effect size estimates reported in a population-based sample (Fava, Velicer, & Prochaska, 1995) and a smaller sample representing a special population (Johnson, Fava, Velicer, Monroe, & Emmons, 2002). Third, the Cohen guidelines were recalibrated based on the results of the empirical data. The previous studies included effect size estimates but did not include confidence intervals around those estimates.

The process of transforming verbal predictions into quantitative predictions has very limited guidance available. However, the process is an iterative one, with errors at one step correctable as additional information becomes available at a later stage.

Overview of the Transtheoretical Model and Initial Effect Size Predictions

The Transtheoretical Model can be conceptualised as involving three dimensions: the temporal dimension, the independent variable dimension, and the intermediate/outcome variable dimension (Velicer, Rossi, Prochaska, & DiClemente, 1996). The central organising construct of the model is the temporal dimension, represented by five Stages of Change describing different levels of readiness to quit smoking. The independent dimension is composed of the Processes of Change that act as strategies to bring about change. The intermediate/outcome dimension is represented by Decisional Balance, Situational Temptations, and measures of the behavior that act as intermediate outcome variables.

Stages of Change

The Transtheoretical Model uses the Stages of Change (SOC) as an organising framework. People are classified by their readiness to change into one of five stages: Precontemplation (PC), Contemplation (C), and Preparation (PR), Action (A), and Maintenance (M). These stages have predictable relationships with other Transtheoretical Model measures such as Processes of Change, Decisional Balance, and Situational Temptation (Fava et al., 1995). It is those relationships that are the basis of the predictions that will be tested in this paper.

Intermediate/Outcome Variable Dimension

The intermediate/outcome variable dimension (Velicer et al., 1996) includes a series of intermediate outcome measures, including the Decisional Balance Inventory (Velicer, DiClemente, Prochaska, & Brandenberg, 1985), the Situational Temptations Inventory (Velicer, DiClemente, Rossi, & Prochaska, 1990), and measures of the target behavior.

The Decisional Balance Inventory was originally adapted from Janis and Mann’s (1977) work and measures both cognitive and motivational aspects of decision-making. Cross-sectional studies on a variety of behaviors have found predictable relationships between the Pros and Cons subscales of the Decisional Balance Inventory across stages (Prochaska, Velicer, Rossi, Goldstein, Marcus, Rakowski, Fiore, Harlow, Redding, Rosenbloom, & Rossi, 1994). Precontemplators show higher support of the Pros of Smoking than the Cons. People in the Action and Maintenance stages have reversed their support of these scales, with the Cons now outweighing the Pros. The Pros scale is expected to not change across the first three stages. The predicted effect size for the Pros scale is None. The Cons scale is expected to rise sharply from Precontemplation to Contemplation and then remain high into Preparation. The predicted effect size for the Cons scale is Medium.

The Situational Temptations Inventory is based on Bandura’s (1977) concept of self-efficacy. The Temptations construct measures how tempted people are to smoke in different situations rather than how confident they are that they will not smoke in those situations. The measurement model for the inventory involves three first-order factors (Positive/Social, Negative/Affective, and Habit/Addictive) and a single general second-order factor (Velicer et al., 1990). All three scales are expected to remain high in both Precontemplation and Contemplation and then decrease from Contemplation to Preparation. The predicted effect size for the Positive/Social, Negative/Affective, and Habit/Addictive scales is Small. These three measures decrease dramatically in the Action and Maintenance stages, but these stages are not included in the current study.

Processes of Change

The Transtheoretical Model also includes a series of independent variables, the Processes of Change (Prochaska, Velicer, DiClemente, & Fava, 1988). The Processes of Change represent strategies for changing one’s behavior. The 10 Processes of Change for smoking cessation have a correlated higher-order factor structure and measure change processes that represent two broad dimensions, experiential and behavioral. Experiential processes include Consciousness Raising, Dramatic Relief, Environmental Reevaluation, Self-reevaluation, and Social Liberation. Behavioral processes include Stimulus Control, Counter Conditioning, Reinforcement Management, Self-Liberation, and Helping Relationships.

Use of each of the processes increases and then declines across the stages of change, with the peak coming for different stages for each process. The predictions are based on a combination of theoretical considerations and both cross-sectional data and longitudinal data. Consciousness Raising and Dramatic Relief are processes that peak early, rising from Precontemplation to Contemplation and starting to decline in Preparation. The predicted effect size for the Consciousness Raising and Dramatic Relief scales is Medium. Helping Relationship and Social Liberation also peak early but have a much more gradual increase and decrease across all five stages. The predicted effect size for the Helping Relationship and Social Liberation scales is Small. Self-Reevaluation and Self-Liberation are two processes that should increase from Precontemplation to Contemplation and demonstrate a further increase from Contemplation to Preparation. The predicted effect size for the Self-Reevaluation and Self-Liberation scales is Large. Environmental Reevaluation and Stimulus Control peak early in the Action stage. They should show no increase from Precontemplation to Contemplation and demonstrate an initial increase from Contemplation to Preparation. The predicted effect size for the Environmental Reevaluation, and Stimulus Control scales is Medium. Counter Conditioning and Reinforcement Management are two of the last processes to peak and there is little change in these processes over the first three stages. The predicted effect size for the Counter Conditioning and Reinforcement Management scales is Small.

Recalibrating the Effect Size Estimates

The numeric values provided by Cohen were intended only as initial estimates. For each content area, the values should be recalibrated when empirical data become available. For this study, we recalibrated the values based on the two previous studies that report effect size estimates (Fava et al., 1995; Johnson et al., 2002) with a much higher weighting on the former since it involves a much larger and more representative sample. Table 1 reports the effect size predictions and numeric equivalents from Cohen. The numeric results reported by Johnson et al. from the Project KISS study and the numeric results reported by Fava et al. from the Random Digit Dial sample are also reproduced. On the basis of those data, a medium effect size was recalibrated from .06 to .08 and a large effect size was recalibrated from .14 to .18. Small was confirmed as .01. The recalibrated values are also shown in Table 1. Dependent on the results of this study, a further recalibration can be performed.

TABLE 1.

Predicted Effect Size across the First Three Stages of Change: Verbal Descriptions, Numeric Cohen Estimates, Observed Estimates from Two Studies, and Recalibrated Predictions

	Predicted effect size	Cohen ω2	RDD* ω2	KISS** ω2	Recalibrated ω2
Decisional Balance
Pros	None	.00	.000	.000	.00
Cons	Medium	.06	.077	.101	.08
Situational Temptations
Habit Strength	Small	.01	.003	.025	.01
Negative/Affect	Small	.01	.002	.043	.01
Positive/Social	Small	.01	.003	.017	.01
Processes of Change
Cons. Raising	Medium	.06	.112	.158	.08
Dramatic Relief	Medium	.06	.097	.114	.08
Self-Reevaluation	Large	.14+	.177	.221	.18
Social Liberation	Small	.01	.011	***	.01
Envir. Reeval.	Medium	.06	.054	***	.08
Stimulus Control	Medium	.06	.078	.127	.08
Counter Condit.	Small	.01	.048	.099	.01
Self-Liberation	Large	.14+	.207	.133	.18
Helping Rel.	Small	.01	.034	***	.01
Reinf. Man.	Small	.01	.030	***	.01

^*From Random Digit Dial sample, see Fava et al. (1995);

^**From Project KISS, see Johnson et al. (2002);

^***Measure not available in this study.

METHOD

Sample

A total population of 24,178 adults in four offices of a managed care system were screened via mail and telephone surveys. Screening was completed on 19,236 subjects and 4,653 were identified as smokers. Of these, 85.3 per cent (N = 3,967) were recruited at baseline. Eligibility criteria included no serious illness, age between 18 and 75, and competence in English. Of this group 2,882 were randomly assigned to one of the eight treatment groups that compared expert system smoking cessation interventions to tailored manuals over four different dose levels (Velicer, Prochaska, Fava, Laforge, & Rossi, 1999). The remaining 1,085 participated in a separate intervention study designed to study enhancements to the expert system intervention (Prochaska, Velicer, Fava, Ruggiero, Laforge, Rossi, Johnson, & Lee, 2001). The total available sample for each measure was employed in this study.

The average age of subjects in the study was 38.1 (SD = 12.2). The gender composition was 56 per cent female and 44 per cent male. With respect to education, 35 per cent had one year of college or more, 49 per cent had graduated from high school, and 16 per cent had less than a high school education, for a mean education of 12.7 years. The stage distribution of the sample was Precontemplation (PC), 37.9 per cent; Contemplation (C), 44.8 per cent; and Preparation (PR), 17.3 per cent. This is very comparable to the sample characteristics for the random digit sample used in a previous trial of the expert system. The stage distribution is also approximately the same as reported in other large samples (Velicer, Fava, Prochaska, Abrams, Emmons, & Pierce, 1995). Additional information about the sample is provided in the original papers (Velicer, Prochaska et al., 1999; Prochaska et al., 2001).

Measures

Most of the measures were Transtheoretical Model measures used to generate the interactive progress reports. These measures included the 10 subscales of the Processes of Change Inventory, the Pros and Cons subscales of the Decisional Balance Inventory, and the three subscales of the Situational Temptations Inventory.

Stage of Change

The method to be employed to assess the Stages of Change for Smoking Cessation is the algorithm method, which consists of five yes/no questions and a screening question to determine if there is a smoking history. Each response is verified by one or more subsequent questions and subjects can be assigned to the appropriate stage of change. The five stages are: (1) Precontemplation: Subjects report that they are not thinking seriously about quitting in the next 6 months; (2) Contemplation: Subjects report that they are seriously thinking about quitting smoking in the next 6 months; (3) Preparation: Subjects report that they are intending to quit smoking in the next month and have tried to quit in the past year; (4) Action: Subjects report that they are not smoking and that they quit smoking within the past 6 months; (5) Maintenance: Subjects report that they have not smoked for at least 6 months. The order of the stages represents progress.

Decisional Balance

The Decisional Balance Inventory measures cognitive and motivational aspects of decision-making applied to smoking (Velicer et al., 1985). It is composed of two subscales, the Pros and Cons of Smoking. The original long form had 20 items and was shown to be a psychometrically reliable and valid measure (Velicer et al., 1985). The current study used the six-item short form of Decisional Balance (Fava, Rossi, Velicer, & Prochaska, 1991) and measured the Pros and Cons of Smoking with three-item subscales. The short form has also been shown to have good reliability and validity (Fava et al., 1991; Fava et al., 1995).

Temptation to Smoke

The original Situational Temptation Inventory (Velicer et al., 1990) consisted of 20 items and measured temptation to smoke. The Temptation scale is a variation of the self-efficacy construct. This study used a nine-item short form that consists of three subscales measured by three items each: Positive/Social, Negative/Affective, and Habit/Addictive (Fava et al., 1991).

Processes of Change

The original Processes of Change Inventory consists of 40 items measuring 10 subscales of the process of behavior change (Prochaska et al., 1988). Five subscales represent Experiential Processes of Change: Consciousness Raising, Environmental Reevaluation, Self-reevaluation, Social Liberation, and Dramatic Relief. The other five subscales represent Behavioral processes: Helping Relationship, Self-liberation, Counter Conditioning, Reinforcement Management, and Stimulus Control. This study used the 20-item short form (Fava et al., 1991).

Statistical Power

APA (2001) also strongly recommends reporting the statistical power of the research being conducted (Wilkinson & TFSI, 1999). This is especially important for any quantitative testing of effect size predictions because low power would result in wider confidence intervals around our observed effect sizes, which would therefore be more likely to include the predicted effect size and confirm our effect size predictions. Larger sample sizes provide increased precision in estimating population effect sizes and tighter confidence intervals around those estimates, resulting in more stringent tests of our predictions. The sample sizes for the results reported here are large enough that, even for alpha = .01, our power is about .95 for a population effect size (ω²) of .006, and about .99 for a population effect size of .008.

RESULTS

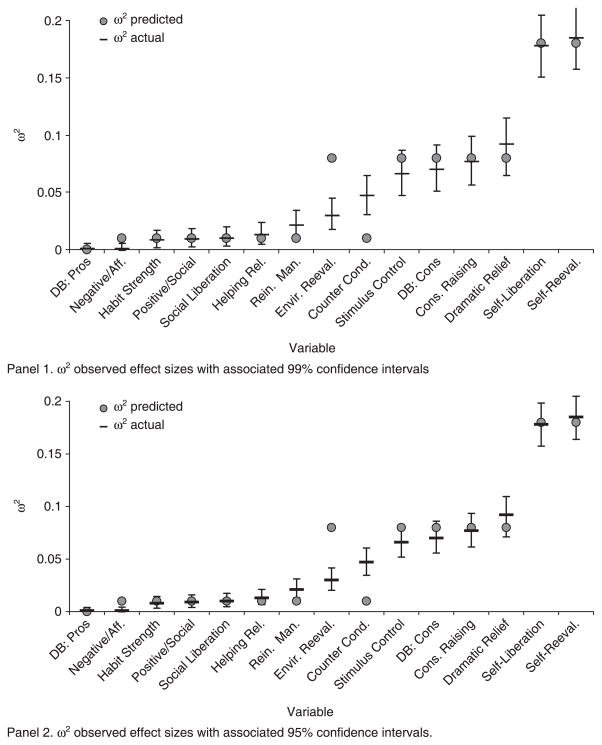
Table 2 presents a summary of the results for the 15 Transtheoretical Model variables. The mean and standard deviation for each stage is presented in standard score form (M = 50; SD = 10). The effect size estimate, ω², was calculated for each of the 15 variables and the confidence interval was calculated around the observed values of ω². The 95 per cent confidence interval was employed because of the relatively large sample size. Figure 1, Panel 1, shows the predicted and observed effects sizes, the latter with 99 per cent confidence intervals. The variables are shown in increasing order of observed effect size.

TABLE 2.

Means, Standard Deviations, Effect Sizes Estimates, and Confidence Intervals for the 15 Transtheoretical Model Variables

Variable		PC*	C**	PR***	ω2	95%	CI
Decisional Balance (N = 3,928)
Pros	M (SD)	50.3 (10.5)	50.0 (9.7)	49.3 (9.7)	.001	−.0005	.0036
Cons	M (SD)	46.7 (9.6)	51.5 (9.7)	53.2 (9.6)	.070	.0555	.0858
Situational Temptations (N = 3,892)
Habit Strength	M (SD)	50.3 (10.5)	50.3 (9.5)	48.0 (10.0)	.008	.0029	.0141
Neg./Affective	M (SD)	49.6 (10.5)	50.4 (9.6)	49.8 (9.8)	.001	−.0005	.0038
Pos./Social	M (SD)	50.4 (10.4)	50.6 (9.4)	48.0 (10.2)	.009	.0036	.0155
Processes of Change (N = 3,811)
Con. Raising	M (SD)	46.4 (9.1)	51.7 (9.7)	53.1 (10.3)	.077	.0612	.0932
Dramatic Relief	M (SD)	46.2 (8.8)	51.6 (9.7)	53.8 (10.5)	.092	.0727	.1091
Self-Reeval.	M (SD)	44.6 (9.1)	52.5 (9.0)	55.2 (9.1)	.185	.1636	.2018
Social Lib.	M (SD)	48.7 (10.4)	50.7 (9.7)	51.0 (9.8)	.010	.0043	.0170
Envir. Reeval.	M (SD)	47.8 (9.3)	50.9 (10.1)	52.2 (10.4)	.030	.0200	.0413
Stimulus Con.	M (SD)	47.2 (8.0)	50.5 (9.8)	54.5 (12.1)	.066	.0516	.0817
Counter Con.	M (SD)	47.6 (9.8)	50.5 (9.4)	53.7 (10.6)	.047	.0342	.0601
Self-Lib.	M (SD)	48.2 (9.6)	50.8 (8.9)	51.8 (8.5)	.178	.1573	.1960
Helping Rel	M (SD)	48.6 (9.8)	50.7 (9.9)	51.6 (10.3)	.013	.0064	.0207
Reinf. Man	M (SD)	48.2 (9.1)	50.8 (10.2)	51.8 (10.8)	.021	.0128	.0309

^*PC = Precontemplation,

^**C = Contemplation,

^***PR = Preparation.

FIGURE 1.

Comparison of the predicted and observed ω² effect size estimates for the 15 variables. The variables are displayed in order of increasing observed effect size.

The confidence intervals and predicted ω² values can then be compared. The first approach is simply to note for each variable whether the predicted value was included in the confidence interval, in which case the prediction was judged to be confirmed. Taking this approach, for the Decisional Balance Inventory, the effect size prediction was confirmed for both the Pros and Cons. For the Situational Temptations Inventory, the effect size predictions were confirmed for the Habit Strength and the Positive/Social scales but not for the Negative/Affect scale. For the five Experiential Processes from the Processes of Change Inventory, the predictions were confirmed for Consciousness Raising, Dramatic Relief, Self-Reevaluation, and Social Liberation and not confirmed for Environmental Reevaluation. For the five Behavioral Processes of the Processes of Change Inventory, the effect size predictions were confirmed for Stimulus Control, Self-Liberation, and Helping Relationship, and not confirmed for Counter Conditioning and Reinforcement Management. Across the 15 variables, there were 11 predictions confirmed and four not confirmed.

DISCUSSION

Our confidence interval presentation permits assessments beyond the simple confirm or not confirm description, which is equivalent to a null hypothesis test for each variable. The vital and challenging question of how the degree of goodness of fit of a theory and some data should be assessed or, more generally, how a theory should be appraised in relation to some data, continues to receive attention in statistics, psychology, and the philosophy of science. Meehl (1990, 1997) is most ambitious by suggesting how a general measure of the discrepancy between a theory’s predictions and the data might be developed. A more generally agreed position is that appraisal of a theory must have a large component of informed subjective judgment (Cohen, 1994).

Technically, a confidence interval is a sufficient statistic, which means that, making the usual assumption of a normally distributed population, it conveys all the information in a set of data that is relevant to estimating the population parameter of interest. We can examine the confidence intervals and how they fall in relation to the predictions to make an informed subjective appraisal of the theory. In doing so, several factors need to be borne in mind. First, if the theory is accurate then about 5 per cent on average of 95 per cent confidence intervals (or 1% of 99% confidence intervals) would be expected not to include the predicted value, simply because of sampling variability, although we would expect almost all of the misses to be near misses. We should therefore not be greatly perturbed by an occasional near miss, especially if many predictions are being made. Second, if, as in our example, the variables are not independent, we cannot assume that the misses and hits of the various predictions would be independent and, further, there is in practice no good way to estimate an overall p value for any particular pattern of misses. Third, in research areas in which there is more than one quantitative theory, our appraisal should include comparisons between theories: The closeness of fit of our theory that we regard as good will depend on how well the competition can do with the same data (Rossi, 1990). Fourth, in appraising any theory we need to consider how many, if any, free parameters of the theory have been estimated from the data we are using to evaluate the fit of the predictions. To the extent that parameters have been estimated in this way, the predictions are bound to fit the data and so a weaker test of the theory is being made.

Evaluation of Predictions

The use of explicit quantitative predictions as a means of theory testing represents an advance over the use of traditional null hypothesis testing procedures. The interpretation of the results can be useful in several different ways. First, the extent to which the predictions are confirmed or rejected can provide an indication of the overall validity of the theory. In this case, 11 predictions were confirmed and four were not confirmed, providing overall support for the theoretical model. We should consider also the third and fourth issues mentioned earlier in relation to assessing the fit of a theory. In our case there is no competing theory that is sufficiently well developed to provide an alternative set of quantitative predictions, so we must consider the fit of our model in absolute terms, rather than in competition with a rival theory. Further, we did not fit any free parameters of the theory to the current data set that we are using to test the fit, so our test is a severe test of the theory, and the close fit we obtained is impressive, and constitutes support for the TTM. Even so, the four predictions that were not confirmed must be evaluated individually.

There are four potential explanations for non-confirmation and each of them has implications for future research. First, the failure to confirm could simply be the result of sampling fluctuations. The higher the confidence level, the less likely we are to observe a non-confirmation if sampling variability is the only cause. If the predicted value is far outside the confidence interval, chance is a highly implausible cause. As the number of predictions increase, the group error rate will increase although, as mentioned earlier, with non-independent variables there is no accurate way to calculate that error rate. The non-confirmation for Reinforcement Management is close and so for this variable chance could be the preferred interpretation.

Second, the failure to confirm may indicate that the theory needs revision. For the example employed here, theory revision is a solution to the failed prediction for Negative Affect from the Situational Temptations Inventory. The predicted value for all three temptation subscales was a small effect size. The assumption was that smokers in preparation would be starting to try to control their level of smoking and a similar decrease would be observed in all three temptation subscales. However, the attempts to control are likely to involve delays and decreases in specific situations under the control of the smoker. In other words, there is experimentation occurring that is under the control of the smoker. Delaying the first cigarette in the morning or smoking five fewer cigarettes is likely to result in a decrease in the Positive/Social and Habit Strength scales. However, Negative/Affect is typically a reaction to a stressful situation and is often the cause of relapse weeks or even months after a successful quit attempt. Therefore, this prediction is now revised from an effect size of Small to an effect size of None.

Third, the failure to confirm may indicate that the theory is incorrect. This assumes that the prediction is central to the theory and that the observed values are so clearly discordant with the theory that all alternative explanations are not feasible; for example, if the observed effect size fell far outside the confidence interval or if the effect was in the opposite direction from what the theory would predict. This did not occur for any of the predictions in this study.

Fourth, the failure to confirm may indicate that further calibration is needed. In this case, recalibration for Environmental Reevaluation and Counter Conditioning is needed. For Environmental Reevaluation, the prediction of a Medium effect size was too high. However, a revision of the prediction to Small would be inadequate since the confidence interval would be too high and would not contain the predicted value of ω² = .01. The correct prediction is somewhere between the Small and Medium effect size predictions. A similar situation exists for Counter Conditioning.

Recalibration as an Intermediate Step

The Cohen classification is still a categorical system. It exists as an intermediate between hypothesis testing, which was a dichotomy, and a full quantitative system. The use of recalibration is an attempt to improve the precision of the system but still relies on four categories. As additional data become available, it will become possible to make true quantitative predictions, assuming that the predictions are consistent with the theoretical model. The process can be seen as an iterative system where the theory makes predictions and the observed data lead to refinement of the theory, resulting in predictions of greater precision.

For the current example, the following predictions can be viewed as a refinement of the values presented in Table 1. The values are an average of the current values and those reported by Fava et al. (1995) rounded to two digits. (The Johnson et al., 2002, study was excluded because of a small sample size, the special population involved, and incomplete data for four of the predictions.) For the Decision Balance Inventory, predicted ω² = .00 for the Pros and ω² = .07 for the Cons. For the Situational Temptations Inventory, ω² = .01 for Habit Strength and Positive/Social and ω² = .00 for Negative Affect. For the Experiential Processes from the Processes of Change, ω² = .09 for the Consciousness Raising and Dramatic Relief scales, ω² = .18 for the Self-Reevaluation scales, ω² = .01 for the Social Liberation scales, and ω² = .04 for the Environmental Reevaluation scale. For the Behavioral Processes from the Processes of Change, ω² = .07 for Stimulus Control, ω² = .05 for Counter Conditioning, ω² = .19 for Self-Liberation, ω² = .02 for Helping Relationship, and ω² = .03 for Reinforcement Management.

An alternative procedure would have been to test the current data against the data reported by the best previous study, the Fava et al. (1995) study. However, there will be error in the Fava et al. data, as in all data sets, and we want to stay close to the theory, with its theoretical rationale for each prediction being None, Small, Medium, or Large. So we used the previous data to recalibrate those benchmarks, rather than directly as numerical predictions. If we had used the previous data directly as predictions, it could be claimed that we are merely doing an empirical match of two data sets, not testing the fit of a well-explicated theory.

Choice of Size of Confidence Interval

Effect of sample size on testing is the opposite of traditional hypothesis testing procedures. It may at first seem strange that choosing a lower level of confidence (95% rather than 99%) gives narrower intervals, and thus what appears to be a more stringent test of the fit between predictions and data. Figure 1, Panel 2 illustrates the application of 95 per cent confidence intervals to the data in this study.

The 95 per cent confidence interval will result in smaller intervals and more rejections of the theory compared to the choice of the 99 per cent confidence interval. However, the choice of the 95 per cent confidence interval will also result in more rejections of the predictions as a function of sampling fluctuations. When a large number of predictions are made, the chance of rejecting a prediction by chance alone becomes a particularly acute problem. In the current case, Figure 1 shows that 11 of the 15 confidence intervals included the predicted value, for both the 95 per cent and 99 per cent intervals.

Strengthening the Specificity of Theories

The use of quantitative theory testing procedures can lead to an improvement in the explicitness of theories in the behavioral sciences. Many theories exist primarily in narrative form. Beyond that, the constructs of a theory are often poorly operationalised. The developers of the theory often do not develop high quality measures for the key constructs. When researchers seek to evaluate the theory and fail, it is not clear if they have failed to develop a good measure of the theoretical constructs. The test could fail because of a poor measure or because the theory was incorrect. The relationships between the constructs are often only vaguely presented and the degree of relationship not specified.

As an example of the specificity of a theory, it should be noted that the quantitative predictions are always made relative to a specific set of measures. In this paper, the short forms of the measures were employed. The effect size estimates would be larger if the long forms of the measures had been employed since those measures are more reliable. The well-known correction for attenuation could be used to adjust the predictions if the reliability information for both scales is available.

As a second example of specificity, the same quantitative relationships would not necessarily be expected if the Transtheoretical Model were applied to a different behavior. Any particular Process of Change might be used earlier or might be less important. As a specific example, the Cons of Smoking are expected to decline after successful quitting occurs and is maintained because the Cons are no longer relevant to a non-smoker. For exercise, the Cons of a Sedentary Lifestyle are expected to stay high even after the person has started and maintained a program of regular exercise since the decision to exercise represents a decision that must continue to be made on a daily basis.

As a third example of specificity, the same quantitative predictions would not be expected if a different set of stages were employed for the comparison. For example, if the study had focused on a comparison between the last three stages (Preparation, Action, and Maintenance), the predicted effect sizes for the subscales from the Situational Temptations Inventory would have been very different. Large effect sizes would have been predicted for all three subscales since a very large decline in the level of the Temptation subscales would be expected over the last three stages. Some predictions may be best made only on more limited parts of the model to tease out the transitions that might be masked by the curvilinear nature of some of the variables like the processes across all five stages. In effect, theory testing using effect size predictions needs to be carefully thought out to decide which aspects of a theory can be tested with a given data set.

Limitations

The type of data presented in this paper cannot provide conclusive validation for any theory. That requires a variety of different types of evidence, starting with verification of the measurement model, testing the proposed relationships with cross-sectional data (as here), testing the proposed relationships with longitudinal data (for examples, see Velicer, Norman, Fava, & Prochaska, 1999; Velicer et al., 1996), and finally testing the efficacy of interventions based on the theory for changing behavior (see Velicer, Prochaska, & Redding, 2006; Noar, Benac, & Harris, 2007). Additional evidence is provided by the demonstration of applicability to other behaviors.

Conclusions

The use of a quantitative testing approach will have the end result of producing theories that are better conceptualised, as well as giving fuller and more accurate accounts of the behavioral phenomena under study. In fact, one of the advantages of the proposed quantitative prediction fitting approach is that it represents the ideal way to use research to develop the theory in ways that have the best chance of giving insight that can improve the theory.