Detecting cognitive impairment by eye movement analysis using automatic classification algorithms

Abstract

The Visual Paired Comparison (VPC) task is a recognition memory test that has shown promise for the detection of memory impairments associated with mild cognitive impairment (MCI). Because patients with MCI often progress to Alzheimer’s Disease (AD), the VPC may be useful in predicting the onset of AD. VPC uses noninvasive eye tracking to identify how subjects view novel and repeated visual stimuli. Healthy control subjects demonstrate memory for the repeated stimuli by spending more time looking at the novel images, i.e., novelty preference. Here, we report an application of machine learning methods from computer science to improve the accuracy of detecting MCI by modeling eye movement characteristics such as fixations, saccades, and re-fixations during the VPC task. These characteristics are represented as features provided to automatic classification algorithms such as Support Vector Machines (SVMs). Using the SVM classification algorithm, in tandem with modeling the patterns of fixations, saccade orientation, and regression patterns, our algorithm was able to automatically distinguish age-matched normal control subjects from MCI subjects with 87% accuracy, 97% sensitivity and 77% specificity, compared to the best available classification performance of 67% accuracy, 60% sensitivity, and 73% specificity when using only the novelty preference information. These results demonstrate the effectiveness of applying machine-learning techniques to the detection of MCI, and suggest a promising approach for detection of cognitive impairments associated with other disorders.

1. Introduction

A critical goal of Alzheimer’s disease (AD) research is to improve the methods of diagnosis so that patients can be identified sooner and, therefore, obtain greater advantage from available therapies. Patients with mild cognitive impairment (MCI) often progress to AD, and accordingly provide an important subject base for this research. A recent study (Crutcher et al., 2009) showed the promise of the Visual Paired Comparison (VPC) task for the detection of memory impairment associated with MCI. There are two phases for each trial of the VPC task. First, during the familiarization phase, subjects are presented with two identical visual stimuli, side by side, on a computer screen. Subjects are allowed to look at the pictures for a specified amount of time. During the test phase, which follows a variable delay, subjects are presented with pictures of the old stimulus and a novel stimulus, side by side. Eye movements are monitored via noninvasive infrared eye tracking, and control subjects typically spend 70% of the time during the test phase looking at the novel stimulus. This indicates that they have a memory for the repeated, and now less interesting, stimulus. In contrast, age-matched MCI patients did not spend more time looking at the novel stimulus than the repeated stimulus (Crutcher et al., 2009), suggesting they did not remember which stimulus was novel and which was familiar.

The VPC task requires no language production, minimal motor output, and has been used successfully across a range of species including rodents (Clark et al., 2000), primates (Zola et al., 2000), human infants (Fagan, 1990) and human adults (Manns et al., 2000; Richmond et al., 2004). Importantly, the VPC task was able to detect impaired memory in MCI patients even in the absence of clinically evident hippocampal neuropathology, as determined by MRI (Crutcher et al., 2009). Further, the VPC task appears to be sensitive to even very minimal damage to medial temporal lobe structures (Zola et al., 2000). Combined, the advantages of VPC are significant for assessing cognitive deficits in individuals with varying educational backgrounds and intellectual capabilities.

However, interpreting the novelty preference data obtained with VPC is not always straightforward. For example, while Crutcher et al. (2009) demonstrated a significant difference between the control and MCI groups, some subjects exhibited novelty preference in the “gray area” between the groups. This finding may reflect inherent variability in task performance. Alternatively, it is possible that other performance measures, when combined with novelty preference, could better distinguish subject groups.

To investigate this possibility, we applied automatic machine learning methods from computer science to analyze and exploit the information contained in the characteristics of eye movement exhibited by healthy and impaired subjects during the viewing of stimuli in the VPC task. Specifically, we hypothesized that additional characteristics of eye movement would help improve classification accuracy of cognitive impairment, thus allowing classification algorithms to more accurately distinguish healthy from impaired subjects. We first trained the classification models on the multidimensional representation of eye movements from a sample of the impaired and control subjects, and then used the model to predict the status of new subjects based on their eye movement characteristics. The results show that eye movement characteristics including fixation duration, saccade length and direction, and re-fixation patterns (defined in next section) can be used to automatically distinguish impaired and normal subjects. Accordingly, this generalized approach may be useful for improving early detection of AD, and may be applied, in combination with other behavioral tasks, to examine cognitive impairments associated with other neurodegenerative diseases.

2. Methods

2.1. Participants

Three subject groups were assessed. (1) The MCI group: 10 subjects diagnosed with mild cognitive impairment (mean age = 72.2 years, SD = 6.9); (2) the AD group: 20 subjects diagnosed with Alzheimer’s Disease (mean age = 72.4 years, SD = 10.0); (3) the NC group: 30 normal age-matched control subjects (mean age = 70.9 years, SD = 7.1). All participants were recruited from the Alzheimer’s Disease Research Center at Emory University. Informed consent was obtained for each participant in accordance with the regulations of the Institutional Review Board at Emory University. A detailed medical, social and family history was obtained from each subject. MCI and AD patients had caregivers or informants who could corroborate their history. Participants completed a neuropsychological battery that included the following subtests: Animal Fluency, Boston Naming Test-15 item (BNT-15), Mini-Mental Status Exam (MMSE), Word List Memory (WLM) and Constructional Praxis (CP). Additional neuropsychological tests included Trail-Making Tests Parts A and B (TMT-A, TMT-B), Digit Span subtest of the Wechsler Adult Intelligence Scale-Revised (WAIS-R), and the Clock Drawing Test (Silverstein, 1996). The Geriatric Depression Scale (GDS) was administered to assess the presence of depressive symptomatology. MCI and AD patients also received a full neurological examination.

The clinical diagnoses of MCI, AD, or NC were established following a standardized assessment and review by three clinicians, expert in evaluation and management of Geriatric Neurology patients. Clinical diagnosis of MCI required evidence of a decline in baseline function in memory and possibly additional cognitive domains, with the severity of symptoms or consequent functional limitations insufficient to meet DSM-III (R) criteria for Dementia. Finally, the NC diagnosis was given if the subjects demonstrated no evidence of cognitive decline from baseline functioning based on their clinical interview and assessment. Exclusion criteria included a history of substance abuse or learning disability, dementia, neurological (e.g. stroke, tumor) or psychiatric illness. Because the VPC task involves visual memory, subjects were also excluded if: (1) the eye tracking equipment could not achieve proper pupil and corneal reflection due to physiological constraints or visual problems (e.g. droopy eyelid, cataracts, detached retinas, glaucoma, pupils too small); and/or (2) they could not complete the eye tracking calibration procedure.

2.1.1. VPC task setup and eye tracking equipment

The VPC task used in our study consisted of 20 trials. The task was administered in blocks of 5 trials. Trials in each block used the same delay interval. Block 1 used a 2 min delay interval, which was followed by two blocks with a 2 s delay interval and the final block used a 2 min delay interval. Each trial consisted of a familiarization phase (5 s), followed by the variable delay and test phase (5 s). An ASL eye tracker (120 Hz sampling rate) was used for data collection. Additional details about the eye tracking equipment, VPC stimuli, and the experimental procedure are reported in Crutcher et al. (2009).

2.2. Eye movement data preprocessing

For each subject, gaze positions were recorded during the VPC test. Each data point had an associated time stamp, and the series of data points were associated with the phase (familiarization, rest, or test) of the VPC task.

Fig. 1 illustrates a trial in the VPC test phase for a normal control subject. Each gaze position is plotted as a blue circle connected with blue lines. The two red rectangle areas (Fig. 1A and B), defined in the eye tracker coordinate system, represent the areas of interest corresponding to the familiar (A) and novel (B) images respectively. The total looking time is computed as the number of sample points with coordinates inside the areas A and B. Gaze positions in the black area between stimuli are excluded from the analysis.

Fig. 1.

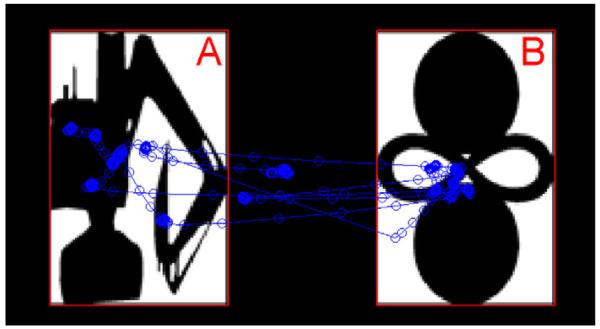
Visual examination behavior in the VPC test phase. In this representative example, the familiar image is on the left (A), and the novel image is on the right (B), for a normal control subject. The detected gaze positions are indicated by blue circles, with the connecting lines indicating the ordering of the gaze positions.

2.2.1. Data filtering

Trials in which the eye tracking system lost pupil recognition (PR) (that is, was unable to detect gaze position due to closed eyes or looking away from the computer screen) were excluded from our analysis. The criterion for excluding a trial was a loss of pupil recognition that resulted in less than 1 s of total looking time for the entire trial. These exclusions were rare, and the vast majority of subjects (48/50, or 96%) had usable data for all 20 trials of the VPC task. In addition, all subjects tested had at least 18 usable trials, providing sufficient data for analysis.

2.2.2. Fixation detection

Instead of focusing on the raw eye movement data, previous research has shown the importance of analyzing the eye fixations (Scinto et al., 1994). Many algorithms have been proposed for fixation detection. In the present study, we used a dispersion-based fixation detection algorithm (Salvucci and Anderson, 2000). This fixation detection algorithm identifies a sequence of eye movement points as a fixation if these points lay within a dispersion threshold δ_th, and the gaze positions are observed within [radicalbig] a duration threshold τ_th. The dispersion is computed as $\sqrt{{\left(\max \right(X_c)-\min (X_c\left)\right)}^2+{\left(\max \right(Y_c)-\min (Y_c\left)\right)}^2}$, where X_c and Y_c – are the x-coordinates and y-coordinates of the points in the candidate set, respectively. The duration is defined as the difference in time between last and first point in the set. The duration threshold τ_th was set to 100 ms, and the dispersion threshold δ_th was set to 5 points in eye tracker units (2° of visual angle). These values were chosen so that the mean duration of detected fixations for the NC subjects, lay in a normal 200–250 ms range as previously reported (Rayner, 1998).

2.3. Eye movement characteristics

2.3.1. Novelty preference (NP)

The novelty preference is computed as the fraction of the total looking time spent gazing at the novel image region. The median novelty preference of the 10 trials with a 2-min delay was used as the NP feature for the classification algorithms. The 2-min delay interval was chosen because that was the delay in which MCI patients demonstrated an impairment relative to control subjects (Crutcher et al., 2009).

2.3.2. Fixation duration (FD)

The duration of fixations during the test phase of the 2 min delay trials was collected, and the median fixation duration across the trials was used as an input feature. The use of this feature is motivated by a previously reported significant difference in fixation durations between NC and AD subjects (Scinto et al., 1994). The change in fixation durations is thought to be related to changes in visual spatial attention, saccade initiation, or inefficiency in planning strategy during visual search observed for AD subjects (Ogrocki et al., 2000).

2.3.3. Re-fixations (RF)

The fixation sequence is used to capture the times when the gaze position re-visits (re-fixates) on previously seen parts of the stimuli. Our algorithm detects re-fixation if there are fixations in the proximity of a previously made fixation and the distance between the centers of the two fixations is less than a specified threshold (5 units in the eye tracker coordinate system, or approximately 2° of visual angle). The “depth” of re-fixation refers to the number of fixations that occurred between the current fixation and the most recent fixation at the same location. Mean re-fixation depth was computed for each trial and the median across the trials was used as an input feature. The use of re-fixations was motivated by the hypothesis that the poor memory in the impaired subjects may be reflected in more frequent or deeper re-fixations.

However, we are not aware of prior work that exploits this information, and we thus explored the value of this feature empirically.

2.3.4. Saccade orientation (SO)

Saccades were defined by the corresponding endpoints of the fixations. To characterize the saccades, we considered the orientation of the saccades – that is, the angles of individual saccades. For this feature, we considered only the absolute value of the saccade angle, ignoring the direction of the movement (i.e., up or down). Specifically, we determined the ratio of vertical saccades (those with the angle of 90 ± 7°) to the overall number of saccades during the test phase. The vertical saccades in the VPC task tend to occur within the same stimulus, whereas others are more likely to move the gaze across stimuli, e.g., switch between the novel and the familiar image. The median value of the vertical saccade fractions over all the test trials for a subject was used as the SO feature in classification.

2.3.5. Pupil diameter (PD)

We constructed a set of features derived from pupil diameter measurements collected during the VPC task. We used the median value from all of the trials for each subject for each PD feature. The specific features explored included:

• Variability of pupil size during the test phase, computed as Std(pd_test)/Mean(pd_test)

• Variability of pupil size during the familiarization phase, computed as Std(pd_fam)/Mean(pd_fam)

• Pupil dilatation in the test phase, computed as (Mean(pd_test) −Mean(pd_fam))/Mean(pd_test)

where pd_fam are the median pupil diameter values during the familiarization phase, and pd_test is the median pupil diameter during the test phase.

2.4. Using eye movement characteristics for automatic classification

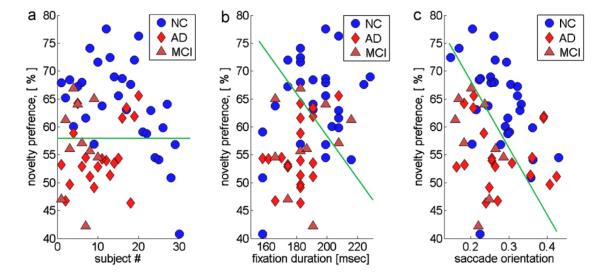
Fig. 2a shows the distribution of the median novelty preference values for the NC, AD, and MCI subjects. While the differences between the medians were significant, there was a region around 55–65% novelty preference that contained a substantial fraction of subjects from each group. Thus, separating NC from AD and MCI subjects with high precision, based on novelty preference alone, was not possible. However, if we consider the data in our feature space (Fig. 2b and c), better separation appears possible. For example, Fig. 2c plots the data in two dimensions, corresponding to the saccade orientation (SO) feature on the X-axis, and the novelty preference (NP) feature on the Y-axis. The vast majority of the NC subjects can now be separated from the AD and MCI subjects by drawing a diagonal line.

Fig. 2.

Separation between groups without using classification algorithms. (a) The novelty preference for NC, AD, and MCI groups; (b) the median fixation duration (X-axis) plotted as a function of novelty preference (Y-axis) for all three groups; (c) median of vertical saccades fraction (X-axis) plotted as a function of novelty preference (Y-axis). The green line indicates a possible linear separation boundary. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

However, multiple separation boundaries can be drawn, and the boundary learning process becomes more complex as the number of features (dimensions) increases, corresponding to the eye movement characteristics described above. Thus, the key question addressed in this manuscript is how to develop an algorithm to automatically learn such a decision boundary to separate the NC from AD and MCI subjects in our high dimensional space of performance measures.

2.5. Machine learning-based classification methodology and algorithms

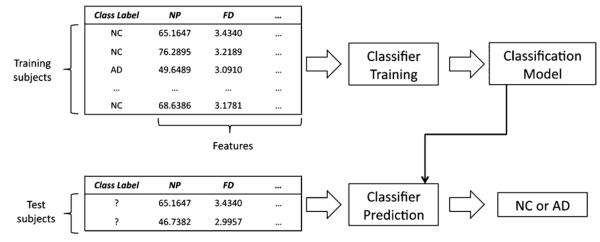
Our approach was to adapt the techniques from machine learning-based classification methodology from Computer Science. Specifically, we used supervised classification methods, which all operate using training and prediction stages, illustrated in Fig. 3. In the training stage (top), a classification algorithm is provided a set of training data values (features), as well as the correct outcome (label). The classifier then tunes the parameters of a classification model, to minimize the error on the predicted vs. actual labels in the training data. At the end of the training process, the parameters of the classification model are fixed. At prediction (testing) stage, the pre-tuned classification model is presented with a new example datapoint (test subject), and the prediction for a most likely class of the test subject is obtained (e.g., NC or MCI). The specifics of thetraining and prediction stages of the classification algorithms are described below.

Fig. 3.

Data flow overview of supervised machine learning-based classification methodology.

We explored a number of popular and state-of-the-art classification algorithms from computer science, ultimately focusing on three representative methods that resulted in the best performances on our preliminary experiments: Naïve Bayes, logistic regression and Support Vector Machines.

More formally, classifiers take an input set of n training examples D = {(x_i, y_i)}, where x_i ∈ R^p and y_i ∈ {−1, +1}, where i =1 … n and p – number of features used in the classification. x_i, y_i in the context of our classification problem, feature vectors are formed from novelty preference, fixation duration and each of the other metrics introduced above. We encoded subject class labels {NC, MCI, AD} using the following mapping:

$$y=\left\{\begin{array}{cc}\hfill -1,\hfill & \mathit{AD}\text{or}\mathit{MCI}\hfill \\ \hfill +1,\hfill & \mathit{NC}\hfill \end{array}\right\}$$

2.5.1. Naïve Bayes (NB)

Naïve Bayes is a simple and perhaps the most well-known probabilistic classifier. It is based on Bayes theorem with strong (naive) assumptions about feature independence (Algorithm 1, below). In the training stage, the prior probabilities as well as feature likelihood are estimated based on the training data. At the testing (prediction) stage, the posterior probability that a given subject belongs to a particular class is computed for every class (e.g., NC or MCI), and the class with the greatest posterior probability is chosen as the prediction. For more details on the algorithm implementation, please refer to John and Langley (1995).

Algorithm 1.

(Training and prediction with a Naïve Bayes classifier)

Training (model generation) stage
1.	For k = {−1, +1} estimate prior probabilities $\mathit{Pr}(Y=K)=\frac{\text{number of examples of class}k}{\text{number of training examples}}$.
2.	Estimate likelihood probabilities Pr(X = x|Y = 1) using technique from John and Langley (1995).
Prediction (testing) stage
1.	For each class calculate posterior probability Pr(Y = k|X = x) = Pr(X = x)|Y = k) × Pr(Y = k)
2.	$\text{Predict}y=\left\{\begin{array}{cc}\hfill -1,\hfill & \text{if}\mathit{Pr}(Y=-1\mid X=x)>\mathit{Pr}(Y=1\mid X=x)\hfill \\ \hfill +1,\hfill & \text{otherwise}\hfill \end{array}\right\}$

2.5.2. Logistic regression (LR)

The logistic regression model is used for prediction by fitting the training data to the parameterized logistic regression function (Algorithm 2, below). The set of parameters w of the logistic function correspond to the feature weights. At test (prediction) stage, the optimal parameters are used to compute the most likely class for each example based on the feature (parameter) values. For moredetails on this classifier’s implementation please refer to Le Cessie and Van Houwelingen (1992).

Algorithm 2.

(Training and prediction with the logistic regression classifier)

Training (model generation) stage
1.	Initialize wm = 0
2.	Estimate log-odds ratio wm using maximum likelihood estimation
	wm = argmax l(w), where log-likelihood
	$l\left(w\right)=\sum _{i=1}^n\left(y_i\log p(x_i,w)+\frac{(1-y_i)}{2}\log (1-p(x,w)\right)$ and
	$p(x,w)=\mathit{Pr}(Y=-1,X=x)=\frac{1}{1+e^{-\left(x^{T}w\right)}}$
Prediction (testing) stage
1.	Calculate posterior probability Pr(Y = −1|X = x) using $p(x,w)\frac{1}{1+e^{-\left(x^T{w}_m\right)}}$
2.	$\text{Predict}y=\left\{\begin{array}{cc}\hfill -1,\hfill & \text{if}\mathit{Pr}(Y=-1\mid X=x)>\mathit{Pr}(Y=1\mid X=x)\hfill \\ \hfill +1,\hfill & \text{otherwise}\hfill \end{array}\right\}$

2.5.3. Support Vector Machines (SVMs)

Recently, the Support Vector Machine (SVM) approach to classification has been shown to be a robust and effective method, with desirable properties of efficiency, scalability, good generalization to unseen data, and particularly well-suited to problems with large numbers of features (Cortes and Vapnik, 1995). More specifically, given a set of training examples the SVM algorithm finds a hyper-plane decision boundary that separates the two classes with minimal error, while maximizing the distance from each class of data points to the decision boundary (Algorithm 3, below). The shape of the decision boundary can be a hyper-plane (for a linear decision boundary), but recent extensions to SVM allow learning almost any convex boundary surface. Based on previous work and our preliminary experiments, we found that using the radial basis kernel to transform the input feature values (Buhmann, 2003), resulted in the highest classification performance. We also used an adjusted loss (error) function that penalized false negative errors twice as much as the false positive errors, thereby optimizing performance on the sensitivity metric. For solving SVM optimization problem we used quadratic programming technique from Coleman and Li (1992).

Algorithm 3.

(Training and prediction with the support vector machine classifier)

Training (model generation) stage
1.	Initialize w = 0
2.	Find w as solution of optimization problem min ∥w∥ subject to $\left(\begin{array}{cc}{y}_i\left(x_i^{T}w\right)\ge 1-\xi \hfill & \hfill \\ {\xi }_i\ge 0,\hfill & \sum {\xi }_i\le C\left(\text{constant}\right)\hfill \end{array}\right)$.
where ξ’s are slack variables of optimization problem (in non-separable case).
Prediction (testing) stage
1.	Compute wTx
2.	Predict y = sign(wTx)

2.6. Training and evaluating classification algorithms

This section describes the evaluation metrics and the experimental procedure used to compare and validate the feature design and classification algorithms.

2.6.1. Evaluation metrics

For evaluation we used the standard classification performance metrics:

• Accuracy: The fraction of correctly classified subjects out of all the subjects in the test set.

• Sensitivity: The ratio of correctly classified impaired subjects tothe total number of impaired subjects in the test set.

• Specificity: The ratio of correctly classified normal control subjects to the total number of the control subjects in the test set.

• Area under the ROC curve (AUC): The area under the Receiver Operating Characteristic (ROC) curve, which is a common way to combine the specificity and sensitivity of a classification algorithm.

2.6.2. Classifier evaluation procedure

Our population consisted of 30 control subjects (NC), 20 subjects diagnosed with Alzheimer’s Disease (AD), and 10 subjects diagnosed with Mild Cognitive Impairment (MCI). Because our goal was to estimate the classification performance in distinguishing the MCI subjects from the NC subjects, our overall experimental procedure consisted of training the algorithms on subsets of the NC subjects and all of the available AD subjects, and then testing the algorithm predictions on the hold-out (unseen data) consisting of the remainder of the NC subjects and all of the MCI subjects. As classifier evaluation in a single train and test cycle is not able to provide a reliable estimate of accuracy, we employed a variant of the bootstrap method (Efron and Tibshirani, 1993) to repeatedly sample different subsets of training and test data for repeated trials of Cross Validation (CV) in order to obtain more robust estimates of the classifier performance.

Specifically, the randomized 3-fold cross validation (CV) scheme was implemented as follows:

1. The NC data were randomly split into 3 folds with 10 subjects in each fold.

2. Two of these folds were combined (comprising the data from the 20 NC subjects), with data from all of the available AD subjects, resulting in the training dataset of 20 NC subjects, and 20 AD subjects. This set of subjects was used for training each of the classification algorithms to distinguish the AD subjects from the NC subjects.

3. The remaining (hold-out) part of the NC data (10 subjects) and all of the MCI data (10 subjects) were used to test the classification algorithm predictions and to compute the evaluation metrics.

This process was repeated 100 times, thus resulting in a good sampling of the different partitions of the NC subjects to be included as part of training vs. hold-out test sets. The evaluation metric values (computed in step 3 of each CV step) were averaged across the 100 repetitions and are reported as the final performance results for the different classification algorithms, and analyzed in Section 3.1.

2.6.3. Choosing the baseline classifier

As part of the algorithm development, we first selected the best available “baseline” classification method to distinguish subjects using the novelty preference (NP) variable alone. This baseline was then used for comparison with our proposed machine learning-based methods that exploit additional eye movement characteristics. Table 1 reports the performance of the three classification algorithms (LR, NB, and SVM), using the evaluation methodology described above. Using only the NP variable, the best accuracy of 0.667, specificity of 0.734 and AUC of 0.667 were exhib-ited by the LR algorithm. Hence we used LR as the baseline method for all subsequent experiments.

Table 1.

Selecting the strongest baseline classification method using novelty preference (NP) as the only input variable. LR: logistic regression, SVM: Support Vector Machines and NB: Naïve Bayes.

Classification Algorithm	Accuracy	Sensitivity	Specificity	AUC
LR	0.667	0.6	0.734	0.667
SVM	0.657	0.604	0.71	0.657
NB	0.637	0.6	0.675	0.637

3. Results

Table 2 reports the classification performance when using the Support Vector Machine (SVM) classification algorithm, with all eye movement features. By exploiting the patterns in the eye movement features, SVM exhibited Accuracy of 0.869, Sensitivity of 0.967, Specificity of 0.772, and AUC of 0.869. For comparison, we also report the “baseline” performance of the best classification method (LR) when only novelty preference is used, as described above. The results demonstrate that SVM, when using the extended eye movement representation features (novelty preference, saccade orientation, re-fixations, and fixation duration), exhibits relative improvements of 30% on Accuracy, 61% on Sensitivity, 5% on Specificity, and 30% on AUC metrics compared to using the novelty preference information alone. The differences of SVM performance on the Accuracy, Sensitivity, and AUC metrics compared to the novelty-preference only baseline were significant at p < 0.001 (see Section 3.1, below). Repeating the procedure with different numbers of cross validation folds (5-fold or 10-fold CV) produced similar results (data not shown).

Table 2.

Classification performance compared to the novelty preference baseline. Asterisks indicate statistical significance over the Baseline method with p-value < 0.001. LR: logistic regression, SVM: Support Vector Machine, NP: novelty preference, SO: saccade orientation, RF: re-fixations, FD: fixation duration.

Method	Features	Accuracy	Sensitivity	Specificity	AUC
Baseline	NP	0.667	0.6	0.734	0.667
LR	NP + SO + RF + FD	0.71	0.712	0.707	0.71
SVM	NP + SO + RF + FD	0.869* (+30%)	0.967* (+61%)	0.772* (+5%)	0.869* (+30%)

3.1. Statistical analysis

The three classification methods, Baseline, LR, and SVM were all trained and tested on exactly the same subsets of the data: that is, at each round of cross validation, the same group of subjects were used as training data for the Baseline, LR, and SVM methods; similarly, the same test group of subjects (disjoint from training group) was used to evaluate the classifier predictions. To establish whether the exhibited Accuracy, Sensitivity, Specificity, and AUC values are in fact different, one-way Analysis of Variance (ANOVA) was performed for each metric:

• Accuracy: The means of Accuracy values for all three methods were significantly different, F(2, 297) = 166.02; p < 0.001, with the effect size = 0.53, interpreted as a medium effect size (Cohen, 1988).

• Sensitivity: The means of the Sensitivity metrics for all three methods were significantly different, F(2, 297) = 1672.86; p < 0.001, =0.92, interpreted as a medium to high effect size (Cohen, 1988).

• Specificity: The three methods were not significantly different on the Specificity metric.

• Area Under the Curve (AUC): The means of the AUC metrics for the three classifiers were significantly different with F(2, 297) = 2119.56; p < 0.001, =0.94, interpreted as a medium to high effect size (Cohen, 1988).

In order to confirm that SVM is in fact the best-performing method with respect to Accuracy, Sensitivity and AUC metrics, post hoc analysis was performed using the Tukey–Kramer test for multiple comparisons (Hochberg and Tamhane, 1987). We find that indeed, SVM significantly outperforms LR and Baseline on these metrics: on mean Accuracy, by 0.16 and 0.18 respectively, p < 0.001; on mean Sensitivity, by 0.28 and 0.37 respectively, p < 0.001; and on mean AUC metric, by 0.16 and 0.19 respectively, p < 0.001 (all at 95% confidence levels).

3.2. ROC analysis

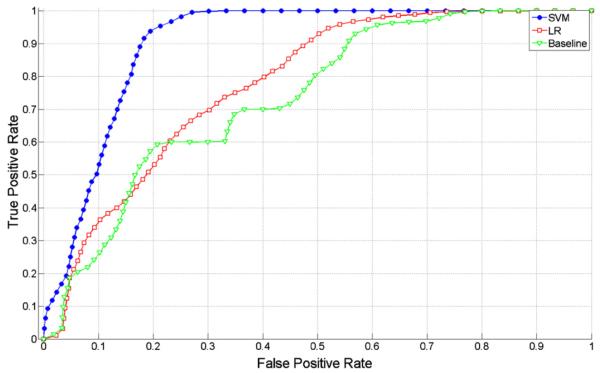
The Receiver Operating Characteristic (ROC) curves are commonly used to compare automatic classification methods to more intuitively understand the tradeoff between sensitivity (true positive rate) and specificity (1-false positive rate). The ROC curves for the Baseline, LR, and SVM methods are reported in Fig. 4. SVM outperforms the other methods at all ranges of specificity. For example, at 20% false positive rate (80% specificity), SVM exhibits over 93% true positive rate, compared to 60% true positive rate of the Baseline method

Fig. 4.

Receiver Operating Characteristic (ROC) curves for three classifiers: Baseline, LR: logistic regression and SVM: Support Vector Machines.

3.3. Feature contribution analysis

Using the SVM classification method, we analyzed feature importance (Table 3). Interestingly, incorporating PD (pupil diameter) features did not improve classification performance. Adding the SO (saccade orientation) feature increased accuracy by 23% over the NP-only baseline; adding the RF (re-fixations depth) feature increased accuracy by additional 6%, to 29% overall improvement over the baseline; finally, adding the FD (mean fixation duration) features further increased accuracy by 1%, to 30% overall improvement over the baseline.

Table 3.

Feature importance analysis (using the SVM classifier). NP: novelty preference, PD: pupil diameter, SO: saccade orientation, RF: re-fixations, FD: fixation duration.

Feature set	Accuracy	Sensitivity	Specificity	AUC
NP (baseline)	0.667	0.6	0.734	0.667
NP + PD	0.626	0.607	0.644	0.626
NP + SO	0.806 (+23%)	0.9 (+34%)	0.713 (−2%)	0.806 (+23%)
NP + SO + RF	0.863 (+29%)	0.989 (+65%)	0.737 (−)	0.863 (+29%)
NP + SO + RF + FD	0.869 (+32%)	0.967 (+61%)	0.772 (+5%)	0.869 (+30%)

4. Discussion

4.1. Significance of results

Our results indicate that machine learning methods can aid the automatic detection of cognitive impairment based on eye tracking data. Our classification results, computed over multiple rounds of cross validation, demonstrate significant and substantial improvement in performance through modeling the eye movement characteristics. Specifically, a Support Vector Machine (SVM) classification algorithm, with the additional eye movement features of saccade orientation, re-fixations and fixation duration, consistently outperformed the baseline (p < 0.001). Our method, when trained with a small number of Normal and AD subjects, achieved the accuracy of 87%, sensitivity of 97%, specificity of 77%, and AUC of 0.869 for separating hold-out normal controls from MCI subjects that were not seen by the algorithm during the training stage.

Our algorithms used a loss (error) function that penalized false negative errors twice as much as the false positive errors, thereby optimizing performance on the sensitivity metric. The sensitivity of 97% exhibited by our method is, as far as we know, higher than the sensitivity values reported for any other test for aMCI (Steenland et al., 2008). The specificity of 77% exhibited by our method is somewhat lower (thus potentially resulting in about 25% of “false alarms”) but is still comparable to existing methods, and can be potentially remedied by following up the positive prediction from the VPC analysis with additional testing.

An additional benefit of our approach is that the tradeoff between sensitivity and specificity can be naturally adjusted by tuning the loss function during classifier training – i.e., to adjust penalties for false positive errors and false negative errors during training, thereby trading off sensitivity for specificity or to maximize the AUC, depending on the clinical requirements.

4.2. Analysis of feature contribution

The combined feature combination (NP + SO + RF + FD) resulted in the best performance overall, on all metrics. Incorporating pupil diameter features (PD), both derived from absolute differences between the novel and familiar image regions, as well as after applying re-scaling and normalization, did not improve classification performance beyond using only the novelty preference values, and actually degraded the classification performance. We conjecture that this effect may be due to characteristics of the elderly population tested, many of whom take medications that may affect pupil dilation and/or retinal reflectance, and many of whom have very small pupils, which are close to, or under, the threshold of discrimination by the eyetracking setup used. We also examined other characteristics of the eye movement trajectory, including the median of saccade lengths, the overall trajectory length, other aspects of the eye movement trajectory, Euclidian distance between familiarization and test phase, and peak angular velocity. None of these additional tested characteristics produced a significant improvement in classification accuracy, beyond the combination of the four features (NP + SO + RF + FD) described above.

4.3. Connection to prior studies of eye movements for cognitive impairment

Previous work on eye movement in AD patients has demonstrated that these patients exhibit saccade dysfunction (Fletcher and Sharpe, 1986) and abnormalities (Crawford et al., 2005). Specifically, Rosler et al. (2000) report longer fixation durations for AD patients than for age-matched controls. In addition, there has been an observed connection between changes in eye movements and attention loss of AD patients (Scinto et al., 1994). More broadly, changes in eye movements have been connected to other neurological conditions including Parkinson Disease (Rottach et al., 1996; Mosimann et al., 2005; Lueck et al., 1990), prefrontal cortex damage (Walker et al., 1998) and autism (Chawarska and Shic, 2009). Some of the eye movement features examined in the present study (fixation duration, and saccade orientation) were inspired by, and extend the previous research. For example, our saccade orienation (SO) feature, was motivated by the study of Rottach et al. (1996) where patients with Parkinson Disease exhibited hypometria type of abnormality for vertical saccades. To our knowledge, the present study represents the first use of SO for detection of MCI and is the first demonstration that distinguishing memory-impaired patients from control subjects can be significantly improved by integrating different eye movement characteristics together as features for automatically trained classification algorithms from computer science.

4.4. Prior work on using machine learning for neurological classification

Classification algorithms have been increasingly adapted for medical research, in particular for neurology and detection of neurodegenerative conditions (Fan et al., 2008; Davatzikos et al., 2008; Tripoliti et al., 2010; Li et al., 2007; Salas-Gonzalez et al., 2009; Duchesne et al., 2008; Kloppel et al., 2008) where classification algorithms were applied to classify functional magnetic resonance imaging (fMRI), single photon emission computed tomography (SPECT), and electroencephalogram (EEG) data. Our work differs in that it involves an analysis of eye movement data acquired during the VPC task, which can potentially detect hippocampal or other structural damage not yet apparent via fMRI imaging.

4.5. Potential limitations of this study

Although we performed our experiments so that the test set had an equal number of control and memory-impaired subjects, this does not match observations in clinical practice, where MCI patients make up 11–17% of the general population (Levey et al., 2006). In future studies with a larger number of subjects, it will be important to explore these classification algorithms using an appropriate loss function during the classifier training, to down-weigh the majority class (NC) examples, while increasing the mis-classification penalty for false negative errors of not detecting impaired subjects.

4.6. Future extensions and potential implications

In summary, the results of this study indicate that machine learning methods can aid the automatic detection of cognitive impairment based on eye tracking data. Our classification results, computed over multiple rounds of cross validation, demonstrate significant and substantial improvement in performance through modeling the eye movement characteristics. A key contribution of this study is a demonstration that with proper feature design, machine learning-based classification methods trained on a relatively small number of Normal and AD subjects, were able to accurately separate new (hold-out) normal controls from MCI subjects that were not seen by the algorithm during the training stage.

The methods demonstrated in this paper are general and require only a set of example subjects for training. In other words, the algorithms automatically learn a decision boundary given examples of visual examination behavior data for normal and impaired subjects. Because of this, the learned decision boundary depends solely on the provided example subjects, their diagnosis, and our general representation of the examination behavior. By changing the examples (i.e., the example subjects and their known diagnosis for a different condition that would affect memory and/or image examination), a new classification algorithm for this condition could be trained automatically. Thus, our methodology could be potentially applied to detect other diseases and conditions, such as ADHD and autism, by training our classifier on the eye movement data acquired for the appropriate patients.