Abstract
Detection of rare events happening in a set of DNA/protein sequences could lead to new biological discoveries. One kind of such rare events is the presence of patterns called motifs in DNA/protein sequences. Finding motifs is a challenging problem since the general version of motif search has been proven to be intractable. Motifs discovery is an important problem in biology. For example, it is useful in the detection of transcription factor binding sites and transcriptional regulatory elements that are very crucial in understanding gene function, human disease, drug design, etc. Many versions of the motif search problem have been proposed in the literature. One such is the  -motif search (or Planted Motif Search (PMS)). A generalized version of the PMS problem, namely, Quorum Planted Motif Search (qPMS), is shown to accurately model motifs in real data. However, solving the qPMS problem is an extremely difficult task because a special case of it, the PMS Problem, is already NP-hard, which means that any algorithm solving it can be expected to take exponential time in the worse case scenario. In this paper, we propose a novel algorithm named qPMS7 that tackles the qPMS problem on real data as well as challenging instances. Experimental results show that our Algorithm qPMS7 is on an average 5 times faster than the state-of-art algorithm. The executable program of Algorithm qPMS7 is freely available on the web at http://pms.engr.uconn.edu/downloads/qPMS7.zip. Our online motif discovery tools that use Algorithm qPMS7 are freely available at http://pms.engr.uconn.edu or http://motifsearch.com.
-motif search (or Planted Motif Search (PMS)). A generalized version of the PMS problem, namely, Quorum Planted Motif Search (qPMS), is shown to accurately model motifs in real data. However, solving the qPMS problem is an extremely difficult task because a special case of it, the PMS Problem, is already NP-hard, which means that any algorithm solving it can be expected to take exponential time in the worse case scenario. In this paper, we propose a novel algorithm named qPMS7 that tackles the qPMS problem on real data as well as challenging instances. Experimental results show that our Algorithm qPMS7 is on an average 5 times faster than the state-of-art algorithm. The executable program of Algorithm qPMS7 is freely available on the web at http://pms.engr.uconn.edu/downloads/qPMS7.zip. Our online motif discovery tools that use Algorithm qPMS7 are freely available at http://pms.engr.uconn.edu or http://motifsearch.com.
Introduction
Detection of rare events happening in a set of DNA/protein sequences often provides the main clue leading to new biological discoveries. One kind of such rare events is the presence of patterns called motifs. For example, regulatory regions in a genome such as promoters, enhancers, locus control regions, etc., contain motifs that control many biological processes such as gene expression (see [1]). Basically, proteins known as transcription factors regulate the expression of a gene by binding to locations of motifs in regulatory regions. For instance, transcription factors such as TFIID, TFIIA and TFIIB usually bind to sequence 5′-TATAAA-3′ in the promoter region of a gene in order to initiate its transcription. Such motifs and their locations in regulatory regions, i.e., binding sites, are important and helpful to decipher the regulatory mechanism of gene expression, which is very sophisticated. As a result, motif identification plays an important role in biological studies.
Motif prediction is usually the first stage in the process of identifying motifs. An extensive amount of research has been done on this topic over the past twenty years. In the literature, many approaches for motif prediction have been proposed. One of them is a combinatorial approach that has proven to be more accurate than the others. Even in this combinatorial approach, many variations can be found such as Planted Motif Search (PMS), Simple Motif Search (SMS), and Edit-distance-based Motif Search (EMS) (see e.g., [2]).
Among the combinatorial variations, the PMS Problem has been the most widely studied perhaps because it offers a higher level of accuracy in modeling the true motifs than the others. Motifs typically occur with mutations at binding sites. The binding sites are referred to as instances of a motif. A motif in this model is referred to as a  -motif where
-motif where  is its length and
is its length and  is the maximum number of mutations allowed for its instances. Given a set of sequences, the objective of the PMS problem is to find all the
is the maximum number of mutations allowed for its instances. Given a set of sequences, the objective of the PMS problem is to find all the  -motifs in them. The formal definition of the PMS Problem is given in Section 0.1. An algorithm that solves the PMS problem is called a PMS Algorithm.
-motifs in them. The formal definition of the PMS Problem is given in Section 0.1. An algorithm that solves the PMS problem is called a PMS Algorithm.
Owing to its importance, the PMS problem has been extensively studied in the past twenty years. Many PMS algorithms have been proposed in the literature. There are two kinds of PMS algorithms, namely, exact and approximate. An exact algorithm always finds all the  -motifs present in the input sequences. An approximate algorithm may not find all the motifs. In this paper we only consider exact algorithms. The (exact variant of the) PMS problem has been shown to be NP-hard which means that there is unlikely to be a PMS algorithm that takes only polynomial time. As a result, all the existing exact PMS Algorithms take time that is exponential time in some of the parameters in the worst case. In practice, all known PMS Algorithms (both exact and approximate) are only able to find
-motifs present in the input sequences. An approximate algorithm may not find all the motifs. In this paper we only consider exact algorithms. The (exact variant of the) PMS problem has been shown to be NP-hard which means that there is unlikely to be a PMS algorithm that takes only polynomial time. As a result, all the existing exact PMS Algorithms take time that is exponential time in some of the parameters in the worst case. In practice, all known PMS Algorithms (both exact and approximate) are only able to find  -motifs for up to certain values of
-motifs for up to certain values of  and
and  . The most recent exact algorithms that have been proposed in the literature are Algorithm PMS6 due to [3], Algorithm PMS5 due to [4], Algorithm Pampa due to [5], Algorithm PMSPrune due to [6], Algorithm PMS3 due to [7], Algorithm Voting due to [8], and Algorithm RISSOTO due to [9]. Some earlier PMS algorithms are due to [10], [11], [12], [13], [14], [15], [16], and [17]. Among these known algorithms, Algorithm PMS6 is considered the fastest one and has been developed closely following the ideas of Algorithm PMS5.
. The most recent exact algorithms that have been proposed in the literature are Algorithm PMS6 due to [3], Algorithm PMS5 due to [4], Algorithm Pampa due to [5], Algorithm PMSPrune due to [6], Algorithm PMS3 due to [7], Algorithm Voting due to [8], and Algorithm RISSOTO due to [9]. Some earlier PMS algorithms are due to [10], [11], [12], [13], [14], [15], [16], and [17]. Among these known algorithms, Algorithm PMS6 is considered the fastest one and has been developed closely following the ideas of Algorithm PMS5.
Approximate PMS algorithms usually tend to be faster than exact PMS algorithms. Typically, approximate PMS algorithms employ heuristics such as local search, Gibbs sampling, expectation optimization, etc. Examples of approximate algorithms are Algorithm MEME due to [18], Algorithm PROJECTION due to [19], Algorithm GibbsDNA due to [20], Algorithm WINNOWER due to [21], and Algorithm RandomProjection due to [22]. Some other approximate PMS algorithms are Algorithm MULTIPROFILER due to [23], Algorithm PatternBranching due to [24], Algorithm ProfileBranching due to [24], and Algorithm CONSENSUS due to [25].
A generalized version of the PMS Problem, namely Quorum Planted Motif Search (qPMS) Problem, was first considered in [6]. The qPMS problem is to find all the motifs that have motif instances present in q out of the n input sequences. The qPMS problem captures the nature of motifs more precisely than the PMS problem does because, in practice, some motifs may not have motif instances in all of the input sequences. The qPMS problem is formally defined in Section 0.1. An algorithm that solves the qPMS problem is called a qPMS algorithm. qPMS algorithms can be used to find DNA motifs and protein motifs as well as transcription factor binding sites. The larger the values of  and d that a qPMS algorithm can handle, the more accurate will be the motifs it finds. So it is important to solve the qPMS problem instances with large values of
and d that a qPMS algorithm can handle, the more accurate will be the motifs it finds. So it is important to solve the qPMS problem instances with large values of  and d. However, solving the qPMS problem is a difficult task since it is even harder than the PMS problem. To the best of our knowledge, the currently best exact qPMS algorithm is Algorithm qPMSPrune due to [6] that can only solve instances up to
and d. However, solving the qPMS problem is a difficult task since it is even harder than the PMS problem. To the best of our knowledge, the currently best exact qPMS algorithm is Algorithm qPMSPrune due to [6] that can only solve instances up to  and
and  for
for  , where n is the number of input sequences. In this paper, we propose a new algorithm named Algorithm qPMS7 that can solve larger instances. Also, qPMS7 is ten times as fast as qPMSPrune. In addition, when applied to the PMS problem, our algorithm is faster than the best PMS algorithm, i.e., Algorithm PMS6 due to [3].
, where n is the number of input sequences. In this paper, we propose a new algorithm named Algorithm qPMS7 that can solve larger instances. Also, qPMS7 is ten times as fast as qPMSPrune. In addition, when applied to the PMS problem, our algorithm is faster than the best PMS algorithm, i.e., Algorithm PMS6 due to [3].
Methods
0.1 Problems Definition and Notations
Definition 0.1
A string  of length
of length  is called an
is called an  -mer.
-mer.
Definition 0.2
Given two  and
and  with
with 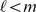 , we use the notation
, we use the notation  if x is a contiguous substring of s. In other words,
if x is a contiguous substring of s. In other words,  if there exists
if there exists  such that
such that  for every
for every  . We also say that x is an
. We also say that x is an  -mer in s.
-mer in s.
Definition 0.3
Given two strings  and
and  of equal length, the Hamming distance between
of equal length, the Hamming distance between  and
and  , denoted by
, denoted by  , is the number of mismatches between them. In other words,
, is the number of mismatches between them. In other words,  , where
, where  is the indicator at position
is the indicator at position  .
.  if
if  , and
, and  otherwise.
otherwise.
Definition 0.4
Given two strings  and
and  with
with  , the Hamming distance between
, the Hamming distance between  and
and  , denoted by
, denoted by  , is
, is  .
.
Definition 0.5
Given a set of  strings
strings  of length
of length  each, a string
each, a string  of length
of length  is called an
is called an  -motif of the strings if there are at least
-motif of the strings if there are at least  out of the
out of the  strings such that the Hamming distance between each one of them and
strings such that the Hamming distance between each one of them and  is no more than
is no more than  .
.  is called an
is called an  -motif for short if the set of strings is clear.
-motif for short if the set of strings is clear.
The definition of Quorum Planted Motif Search (qPMS) Problem is as follows. Given  input strings
input strings  of length
of length  each, three integer parameters
each, three integer parameters  ,
,  and
and  , find all the
, find all the  -motifs of the input strings. The Planted Motif Search (PMS) problem is a special case of the qPMS problem when
-motifs of the input strings. The Planted Motif Search (PMS) problem is a special case of the qPMS problem when  . In this paper, we propose a fast algorithm for the qPMS problem.
. In this paper, we propose a fast algorithm for the qPMS problem.
0.2 The Existing Algorithm qPMSPrune
Algorithm qPMSPrune for the qPMS problem was proposed by [6]. For the sake of completeness, we will describe Algorithm qPMSPrune in this section briefly because our new algorithm is partially based on it. For more details on Algorithm qPMSPrune, the readers are referred to [6].
Algorithm qPMSPrune uses the  -neighborhood concept defined as follows.
-neighborhood concept defined as follows.
Definition 0.6
Given a string  , we define the
, we define the  -neighborhood of
-neighborhood of  ,
,  , to be
, to be  .
.
It is easy to see that  , where
, where  is the alphabet of interest. Notice that
is the alphabet of interest. Notice that  depends only on
depends only on  ,
,  and
and  . For this reason, we define
. For this reason, we define  .
.
Algorithm qPMSPrune is based on the following observation. Any  -motif of the input strings must be in
-motif of the input strings must be in  for some
for some  -mer
-mer  in some input string
in some input string  and also it must be a
and also it must be a  -motif of the input strings excluding
-motif of the input strings excluding  . This observation can be rewritten formally as follows.
. This observation can be rewritten formally as follows.
Observation 0.1
Let  be any
be any  -motif of the input strings
-motif of the input strings  . Then there exists an
. Then there exists an  (with
(with  ) and a
) and a  -mer
-mer  such that
such that  is in
is in  and
and  is a
is a  -motif of the input strings excluding
-motif of the input strings excluding  .
.
The above observation suggests the following algorithm. Compute  for every
for every  -mer
-mer  in each input string
in each input string  for
for  . For each
. For each 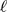 -mer in the neighborhoods thus computed, check if it is a
-mer in the neighborhoods thus computed, check if it is a  -motif of the input strings excluding
-motif of the input strings excluding  . This simple algorithm can be improved further as shown in [6]. The key observation is that it is sufficient to consider each input string
. This simple algorithm can be improved further as shown in [6]. The key observation is that it is sufficient to consider each input string  for
for  :
:
Observation 0.2
Let  be any
be any  -motif of the input strings
-motif of the input strings  . Then there exists an
. Then there exists an  (with
(with  ) and a
) and a  -mer
-mer 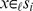 such that
such that  is in
is in 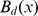 and
and  is a
is a  -motif of the input strings excluding
-motif of the input strings excluding 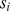 .
.
Algorithm qPMSPrune is based on the above observation. For any  -mer
-mer  , it represents
, it represents 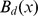 as a tree
as a tree  using the following rules.
using the following rules.
Each node in
 is a pair
is a pair  where
where  is an
is an  -mer and
-mer and  is an integer between
is an integer between  and
and  such that
such that  . A node
. A node  is referred to as a
is referred to as a  -mer
-mer  if
if 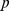 is clear.
is clear.-
Let
 and
and  . A node
. A node  is the parent of a node
is the parent of a node  if and only if
if and only if(a)
 .
.(b)
 (From Rule 1,
(From Rule 1,  ).
).(c)
 for any
for any 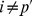 .
.
The root of
 is
is  .
.The depth of
 is
is  .
.
For example, the tree  with alphabet
with alphabet  is illustrated in Figure 1.
is illustrated in Figure 1.
Figure 1. Traverse the tree in qPMSPrune.

 with alphabet
with alphabet  . The value of
. The value of  at each node is the location of its shaded letter. For example,
at each node is the location of its shaded letter. For example,  at node
at node  ,
,  at node
at node  .
.
Clearly, the following properties of  can be inferred directly from the rules.
can be inferred directly from the rules.
Each node in
 is uniquely associated with an
is uniquely associated with an 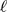 -mer in
-mer in  and vice versa.
and vice versa.If a node
 is a parent of a node
is a parent of a node  , then
, then  . As a result, if a node
. As a result, if a node  is at level
is at level  , then
, then  .
.
The algorithm traverses the tree  in a depth-first manner. At each node
in a depth-first manner. At each node  , it computes
, it computes  incrementally from its parent for
incrementally from its parent for  . This operation can be done in
. This operation can be done in  time by the incremental computation shown in [6]. Let
time by the incremental computation shown in [6]. Let  be the number of input strings
be the number of input strings  such that
such that  . Obviously if
. Obviously if  then
then  is a
is a  -motif of the input strings excluding
-motif of the input strings excluding  . If this condition is satisfied, it outputs
. If this condition is satisfied, it outputs  as a
as a  -motif of the entire input strings.
-motif of the entire input strings.
Algorithm qPMSPrune prunes certain nodes (and their descendants) in  that cannot possibly be
that cannot possibly be  -motifs. Under what conditions can we prune the node
-motifs. Under what conditions can we prune the node  ? Let
? Let  be the number of input strings
be the number of input strings  such that
such that  . Observe that if
. Observe that if  then none of the nodes in the subtree rooted at node
then none of the nodes in the subtree rooted at node  could be a
could be a  -motif. This is because if there is a node
-motif. This is because if there is a node  in the subtree which is a
in the subtree which is a  -motif, then there are at least
-motif, then there are at least  input strings
input strings  such that
such that  . Consider such an input string
. Consider such an input string  . By the triangle inequality,
. By the triangle inequality,  . This inequality will infer that
. This inequality will infer that  . Therefore, if the condition
. Therefore, if the condition  occurs, it can safely prune the subtree rooted at node
occurs, it can safely prune the subtree rooted at node 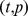 without missing any
without missing any  -motif. The pseudo-code of Algorithm qPMSPrune is described as follows.
-motif. The pseudo-code of Algorithm qPMSPrune is described as follows.
Algorithm qPMSPrune
For each  do:
do:
Traverse the tree  in a depth-first manner. At each node
in a depth-first manner. At each node 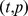 , do the following steps.
, do the following steps.
Incrementally compute
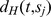 from its parent for
from its parent for  .
.Let
 be the number of input strings
be the number of input strings  such that
such that  . If
. If  , output
, output  .
.Let
 be the number of input strings
be the number of input strings  such that
such that  . If
. If  , then prune the subtree rooted at node
, then prune the subtree rooted at node  . Otherwise, explore its children.
. Otherwise, explore its children.
It is easy to see that the time and space complexities of Algorithm qPMSPrune are  and
and  , respectively.
, respectively.
0.3 A Computational Technique Improving upon Algorithm qPMSPrune
In this section, we propose a speedup technique to improve the runtime of Algorithm qPMSPrune. Specifically, the technique will reduce the time taken for computing Hamming distances  in step (1) of Algorithm qPMSPrune. Recall that the operation takes at least
in step (1) of Algorithm qPMSPrune. Recall that the operation takes at least  time in Algorithm qPMSPrune because it considers every
time in Algorithm qPMSPrune because it considers every  -mer in each input string
-mer in each input string  . We observe that some
. We observe that some  -mers can be ignored without changing the result since we notice that we just need to count
-mers can be ignored without changing the result since we notice that we just need to count  and
and  . Any
. Any  -mer
-mer  in
in  can be ignored, as far as a node
can be ignored, as far as a node  in the tree
in the tree  is concerned, if
is concerned, if 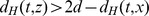 . The reason for this will be given in the next paragraph. Based on this observation, the technique is implemented as follows. At each node
. The reason for this will be given in the next paragraph. Based on this observation, the technique is implemented as follows. At each node  , we store a list of surviving
, we store a list of surviving  -mers for each input string
-mers for each input string  . It is sufficient to store the positions of the
. It is sufficient to store the positions of the  -mers in the input strings. If the list of surviving
-mers in the input strings. If the list of surviving 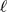 -mers of
-mers of  is empty, then we set
is empty, then we set  . In terms of the incremental distance computation, only the surviving
. In terms of the incremental distance computation, only the surviving  -mers are considered. The runtime of the operation now depends on the sizes of the lists of surviving
-mers are considered. The runtime of the operation now depends on the sizes of the lists of surviving  -mers.
-mers.
The reason for ignoring any  -mer
-mer  in
in  , as far as a node
, as far as a node  in the tree
in the tree  is concerned, if
is concerned, if  is as follows. If this condition occurs, then for any node
is as follows. If this condition occurs, then for any node  in the subtree rooted at node
in the subtree rooted at node  we have:
we have:  . Therefore, ignoring
. Therefore, ignoring  -mer
-mer  at any node
at any node  in the subtree rooted at node
in the subtree rooted at node  will not change its
will not change its  . The value of
. The value of  at node node
at node node  may become smaller as a result of ignoring the
may become smaller as a result of ignoring the  -mer
-mer  . However, the pruning condition based on
. However, the pruning condition based on  in step (3) in the pseudo-code still holds.
in step (3) in the pseudo-code still holds.
Another way to view the ignoring condition is as follows. Consider a node  in the tree
in the tree  and an
and an  -mer
-mer  in the input string
in the input string  . Let us separate each of
. Let us separate each of  and
and  into two parts based on
into two parts based on  , namely,
, namely,  and
and  where
where  and
and  . Notice that
. Notice that  . Then the inequality
. Then the inequality 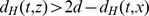 is equivalent to
is equivalent to  . In other words,
. In other words,  and
and  are disjoint. Notice that this condition is independent of
are disjoint. Notice that this condition is independent of  . This view helps us in designing our best algorithm qPMS7 which is described in Section 0.4.
. This view helps us in designing our best algorithm qPMS7 which is described in Section 0.4.
The speedup technique reduces the runtime of Algorithm qPMSPrune drastically because the deeper a node is, the smaller will be the size of its list of surviving  -mers. Note that the number of nodes at a depth of
-mers. Note that the number of nodes at a depth of  from the root will be exponential in
from the root will be exponential in  . In practice, the runtime of Algorithm qPMSPrune is improved by a factor of around 5 when this technique is used (see Table 1 and Table 2). However, it does not change the worst case time complexity of Algorithm qPMSPrune, theoretically.
. In practice, the runtime of Algorithm qPMSPrune is improved by a factor of around 5 when this technique is used (see Table 1 and Table 2). However, it does not change the worst case time complexity of Algorithm qPMSPrune, theoretically.
Table 1. Time comparison of different algorithms on the challenging instances of DNA sequences for the special case - PMS Problem.
| Algorithm | (13,4) | (15,5) | (17,6) | (19,7) | (21,8) | (23,9) |
| qPMS7 | 47 s | 2.6 m | 11 m | 0.9 h | 4.3 h | 24 h |
| PMS6 | 67 s | 3.2 m | 14 m | 1.16 h | 5.8 h | – |
| PMS5 | 117 s | 4.8 m | 21.7 m | 1.7 h | 9.7 h | 54 h |
| qPMSPruneI | 17 s | 2.6 m | 22.6 m | 3.4 h | 29 h | – |
| Pampa | 35 s | 6 m | 40 m | 4.8 h | – | – |
| qPMSPrune | 45 s | 10.2 m | 78.7 m | 15.2 h | – | – |
| Voting | 104 s | 21.6 m | – | – | – | – |
| RISOTTO | 772 s | 106 m | – | – | – | – |
The alphabet  ,
,  ,
,  , and
, and  .
.
Table 2. Time comparison of different algorithms on the challenging instances of DNA sequences for the generalized case - qPMS Problem.
| Algorithm | (13,3) | (15,4) | (17,5) | (19,6) | (21,7) |
| qPMS7 | 34 s | 2.4 m | 16 m | 1.8 h | 11.6 h |
| qPMSPruneI | 14 s | 2 m | 21 m | 3.9 h | – |
| qPMSPrune | 32 s | 9 m | 2.6 h | – | – |
The alphabet  ,
,  ,
,  , and
, and  .
.
0.4 Our Best Algorithm qPMS7
In this section, we propose a fast algorithm called qPMS7 for the qPMS problem. Algorithm qPMS7 is a generalized version of Algorithm qPMSPrune combined with the core idea of Algorithm PMS5 which was introduced in [4].
Recall that Algorithm qPMSPrune considers one  -mer
-mer  in a specific input string
in a specific input string  at a time. Algorithm qPMS7 extends Algorithm qPMSrune by considering two
at a time. Algorithm qPMS7 extends Algorithm qPMSrune by considering two  -mers
-mers  and
and  in two different input strings
in two different input strings  and
and  . An observation similar to that of Algorithm qPMSPrune can be obtained as follows.
. An observation similar to that of Algorithm qPMSPrune can be obtained as follows.
Observation 0.3
Let  be any
be any  -motif of the input strings
-motif of the input strings  . Then there exist
. Then there exist  and
and  -mer
-mer  and
and  -mer
-mer  such that
such that  is in
is in  and
and  is a
is a 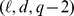 -motif of the input strings excluding
-motif of the input strings excluding  and
and  .
.
Using an argument similar to the one in [6], we infer that it is enough to consider every pair of input strings  and
and  with
with  . As a result, the above observation gets strengthened as follows.
. As a result, the above observation gets strengthened as follows.
Observation 0.4
Let 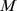 be any
be any 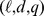 -motif of the input strings
-motif of the input strings  . Then there exist
. Then there exist 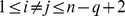 and
and  -mer
-mer  and
and  -mer
-mer  such that
such that  is in
is in  and
and  is a
is a 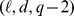 -motif of the input strings excluding
-motif of the input strings excluding  and
and  .
.
Like Algorithm qPMSPrune, Algorithm qPMS7 uses a routine that finds all of the motifs  such that
such that  is in
is in  and is a
and is a 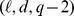 -motif of the input strings excluding
-motif of the input strings excluding  and
and  . Recall that Algorithm qPMSPrune explores
. Recall that Algorithm qPMSPrune explores  by traversing the tree
by traversing the tree  . In Algorithm qPMS7, we also explore
. In Algorithm qPMS7, we also explore  by traversing an acyclic graph, denoted as
by traversing an acyclic graph, denoted as  , with similar construction rules. The rules for constructing
, with similar construction rules. The rules for constructing  are given below.
are given below.
-
Each node in
 is a pair
is a pair 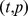 where
where  is an
is an  -mer and
-mer and  is an integer between
is an integer between  and
and 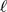 . A node
. A node  is referred to as
is referred to as  -mer
-mer  if
if  is clear. Let
is clear. Let  and
and  where
where  and
and  . Node
. Node  must satisfy the following constraints:
must satisfy the following constraints:(a)
 if
if  , otherwise,
, otherwise,  .
.(b)
 and
and  .
.
-
Let
 and
and  . There is an arc from a node
. There is an arc from a node  to a node
to a node  if and only if
if and only if(a)
 .
.(b)
 .
.(c)
 for any
for any  .
.
It is not hard to see that if we traverse the graph  in a depth-first manner starting from node
in a depth-first manner starting from node  , then all the
, then all the 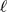 -mers in
-mers in  will be visited. For example, Figure 2 illustrates the visited nodes in the graph
will be visited. For example, Figure 2 illustrates the visited nodes in the graph  in a depth-first manner starting from node
in a depth-first manner starting from node  where the alphabet
where the alphabet  .
.
Figure 2. Traverse the graph in qPMS7.

Visited nodes in  in a depth-first manner when the starting node is
in a depth-first manner when the starting node is  . In this example,
. In this example,  . The value of
. The value of  at each node is the location of its shaded letter. For example,
at each node is the location of its shaded letter. For example,  at node
at node  .
.
Algorithm qPMS7 traverses the graph  in a depth-first manner with the starting node
in a depth-first manner with the starting node  . During the traversal, at each node
. During the traversal, at each node  it computes
it computes  incrementally from its parent for
incrementally from its parent for  . With the same method as the one in Algorithm qPMSPrune, we can achieve this task in
. With the same method as the one in Algorithm qPMSPrune, we can achieve this task in 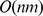 time. Also, it is easy to see that if
time. Also, it is easy to see that if  then
then  is a
is a  -motif of the input strings excluding
-motif of the input strings excluding  and
and  , where
, where  is the number of input strings
is the number of input strings  such that
such that  . If this is the case, it outputs
. If this is the case, it outputs  as a
as a  -motif of the entire input strings.
-motif of the entire input strings.
Algorithm qPMS7 also uses a similar pruning strategy to that of Algorithm qPMSRune and the speedup technique discussed in Section 0.3. In this case, the speedup technique ignores some 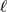 -mers in
-mers in  when computing
when computing  at each node
at each node  during the traversal of the graph
during the traversal of the graph  . The ignoring condition of an
. The ignoring condition of an  -mer
-mer  in
in  for this case resembles that in Section 0.3. Let
for this case resembles that in Section 0.3. Let  and
and  where
where  . It is not hard to see that
. It is not hard to see that  -mer
-mer  can be safely ignored if
can be safely ignored if  is empty. Checking for this condition can be done in
is empty. Checking for this condition can be done in  time using the incremental computation shown in [4]. During the traversal of the graph, at each node
time using the incremental computation shown in [4]. During the traversal of the graph, at each node 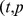 ) we also store a list of surviving
) we also store a list of surviving  -mers for each input string
-mers for each input string  . At node
. At node  , if the list of surviving
, if the list of surviving  -mers of an input string is empty, then the input string will contribute nothing to any descendant node of
-mers of an input string is empty, then the input string will contribute nothing to any descendant node of  in order for that descendant to be a
in order for that descendant to be a  -motif. Therefore, the pruning condition is
-motif. Therefore, the pruning condition is  where
where  is the number of input strings whose lists of surviving
is the number of input strings whose lists of surviving  -mers are not empty. The following pseudo-code describes Algorithm qPMS7.
-mers are not empty. The following pseudo-code describes Algorithm qPMS7.
Algorithm qPMS7
1. For each  do:
do:
(a) Traverse the graph  in a depth-first manner starting from node
in a depth-first manner starting from node  . At each node
. At each node  , do the following steps.
, do the following steps.
Incrementally compute
 from its parent for
from its parent for  .
.Let
 be the number of input strings
be the number of input strings  such that
such that  . If
. If  , output
, output  .
.Let
 be the number of input strings whose lists of surviving
be the number of input strings whose lists of surviving  -mers are not empty. If
-mers are not empty. If  , then backtrack. Otherwise, explore its children.
, then backtrack. Otherwise, explore its children.
Theoretically, the time and space complexities of Algorithm qPMS7 are  and
and  , respectively. In the worst case scenario, the runtime of Algorithm qPMS7 is worse than that of Algorithm qPMSPrune by a factor of
, respectively. In the worst case scenario, the runtime of Algorithm qPMS7 is worse than that of Algorithm qPMSPrune by a factor of  . However, Algorithm qPMS7 is much faster than Algorithm qPMSPrune in practice, as shown in Section 0.5.
. However, Algorithm qPMS7 is much faster than Algorithm qPMSPrune in practice, as shown in Section 0.5.
Algorithm qPMS7 also employs the following observation which has been used in many prior works such as [6] and [26]. Let  be any
be any  motif in inputs strings
motif in inputs strings  . Let
. Let  be an instance of
be an instance of  in
in  (for
(for  ). Then the Hamming distance between
). Then the Hamming distance between 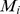 and
and  is
is  for any
for any  and
and  (with
(with  ). In other words, if
). In other words, if  is any
is any  -mer in some
-mer in some  , then it could possibly be an instance of
, then it could possibly be an instance of  only if there are at least
only if there are at least 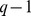 out of
out of  sequences
sequences  ‘s,
‘s,  , that have an
, that have an  -mer
-mer  such that the Hamming distance between
such that the Hamming distance between  and
and  is
is  . This observation can be utilized to preprocess the input strings so that for any input string only those
. This observation can be utilized to preprocess the input strings so that for any input string only those  -mers that satisfy the above condition are kept (and the other
-mers that satisfy the above condition are kept (and the other  -mers are ignored from further processing).
-mers are ignored from further processing).
0.5 Transcription Factor Binding Sites Discovery
In this section we will discuss how to use a qPMS Algorithm, e.g., Algorithm qPMS7, to discover transcription factor-binding sites. Given a set of DNA strings that likely contains transcription factor-binding sites, we propose a general framework to find them. The framework consists of two phases. The first phase will select a set of motifs by repeatedly calling the qPMS Algorithm on different values of  and
and  . The second phase will use a scoring function to eliminate some of the motifs returned in the first phase, and then identify the transcription factor-binding sites based on the surviving motifs.
. The second phase will use a scoring function to eliminate some of the motifs returned in the first phase, and then identify the transcription factor-binding sites based on the surviving motifs.
In the first phase we employ different values, ranging between  and
and  , for the length
, for the length  of motifs, where
of motifs, where  and
and  are user-specified parameters. For each value of
are user-specified parameters. For each value of  , we let
, we let  range from
range from  to
to  , where
, where  is another user-specified parameter, and call the best qPMS algorithm (let it be Algorithm
is another user-specified parameter, and call the best qPMS algorithm (let it be Algorithm  ) to find
) to find  -motifs. In this process, if some
-motifs. In this process, if some  -motif(s) are found, we add them to the set of motifs. The pseudo-code of the first phase follows.
-motif(s) are found, we add them to the set of motifs. The pseudo-code of the first phase follows.
Phase I: selecting candidate motifs
Input: a set of strings
Parameters:
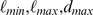 and
and 
Output: a set of  -motifs
-motifs 
1: 
2: for
 to
to 
 to do
to do
3: for
d = 0 to  do
do
4: Run the fastest qPMS Algorithm  to find
to find  -motifs of the input strings
-motifs of the input strings
5: if algorithm  takes too long then
takes too long then
6: Terminate algorithm 
7: break the for loop of 
8: end if
9: Let  be the set of
be the set of  -motifs returned by algorithm
-motifs returned by algorithm 
10: if
 is NOT empty then
is NOT empty then
11: 
12: break the for loop of 
13: end if
14: end for
15: end for
In the second phase, we sort the  -motifs according to their scores and pick the top
-motifs according to their scores and pick the top  motifs, where
motifs, where  is a user-specified parameter. For each picked
is a user-specified parameter. For each picked  -motif
-motif  and each input string
and each input string  , transcription binding sites in
, transcription binding sites in 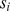 are identified as follows. We consider every
are identified as follows. We consider every  -mer
-mer  in
in 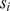 and output the location of
and output the location of  in
in  as a transcription binding site if
as a transcription binding site if  . The following pseudo-code describes the second phase.
. The following pseudo-code describes the second phase.
Phase II: identifying transcription factor binding sites
Input: a set of strings and a set of  -motifs
-motifs 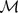
Parameters: a scoring function and 
Output: a set of binding sites on the input strings
1: Sort  -motifs in
-motifs in  according to the scoring function
according to the scoring function
2: Pick the top 
 -motifs in
-motifs in  after sorting
after sorting
3: for each picked 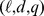 -motif
-motif  do
do
4: for each input string  do
do
5: Identify all the  -mers
-mers  in
in  such that
such that 
6: Output the location of each such  -mer
-mer  in
in  as a transcription factor binding site
as a transcription factor binding site
7: end for
8: end for
The accuracy of the framework in discovering transcription factor-binding sites heavily depends on two factors: the qPMS Algorithm and the scoring function. Of course, the faster the qPMS Algorithm is, the more accurate will be the results it provides. Designing fast qPMS algorithms is our main focus because it is a difficult task. On the other hand, the choice of the scoring function is also critical. In general, the scoring function should measure the biological significance of a candidate motif possibly via a probabilistic model. As a rule of thumb, the smaller the probability that a motif appears (by random chance) is, the more likely will it be to be biologically significant. In addition, the impact of the scoring function on the accuracy also depends on the size of the list of candidate motifs  . The larger the size is, the more will be the scoring function’s impact. For example, the scoring function called “sequence specificity” is usually used. It is defined to be
. The larger the size is, the more will be the scoring function’s impact. For example, the scoring function called “sequence specificity” is usually used. It is defined to be  where
where  is the expected number of times a motif appears in string
is the expected number of times a motif appears in string  with up to
with up to  mismatches [6].
mismatches [6].
Results
In this section we evaluate the performance of Algorithm qPMS7 on simulated as well as real data. With simulated data, we compare its runtime with that of other existing algorithms. With real data, we measure the accuracy of qPMS7 in detecting real motifs. Of course, the larger the values of  and
and  that an algorithm can solve, the more accurate will be the results it yields because it covers a larger search space of motifs.
that an algorithm can solve, the more accurate will be the results it yields because it covers a larger search space of motifs.
0.6 Experiments on Simulated Data
We compared the runtime of Algorithm qPMS7 with other well-known algorithms such as Algorithm qPMSPrune of [6], Algorithm PMS6 of [3], Algorithm PMS5 of [4], Algorithm Pampa of [5], Algorithm Voting of [8], and Algorithm RISSOTO of [9]. Recall that among these algorithms, only Algorithm qPMSPrune deals with the qPMS problem. The rest of the algorithms deal with the simpler version, i.e., the PMS problem. The improved Algorithm qPMSPrune in Section 0.3 is named qPMSPruneI. To evaluate the performance of algorithms, we usually test them on challenging and hard instances of the problem. All of these algorithms have been run on the same machine running Windows XP Operating System with a Dual Core Pentium 2.4GHz CPU and 3GB RAM. The experimental results below show that Algorithm qPMS7 is better than any other algorithm.
0.6.1 DNA sequences
Following [21] and [6], the set of input strings of a challenging instance is typically generated as follows. Each input string is a random DNA string drawn according to the i.i.d model. A random  -mer
-mer  is chosen as a
is chosen as a  -motif and mutations of this
-motif and mutations of this  -mer
-mer  are planted in
are planted in  out of the
out of the  input strings at random positions. The Hamming distance between
input strings at random positions. The Hamming distance between  and any of these mutations is at most
and any of these mutations is at most 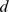 . The number of input strings
. The number of input strings  and the length of each of them
and the length of each of them  are chosen to be 20 and 600, respectively.
are chosen to be 20 and 600, respectively.
In the case of the PMS problem,  . The pairs
. The pairs  corresponding to challenging instances are
corresponding to challenging instances are  ,
,  ,
,  ,
,  ,
, 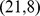 ,
, 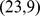 ,
,  , and so on. To the best of our knowledge, there has not been any algorithm that can solve the challenging instance
, and so on. To the best of our knowledge, there has not been any algorithm that can solve the challenging instance  . Therefore, Table 1 reports the runtime of the algorithms on the challenging instances up to
. Therefore, Table 1 reports the runtime of the algorithms on the challenging instances up to  . Algorithms qPMS7, PMS6 and PMS5 can solve any of these challenging instances. In Table 1, the letter ‘–’ indicates that the corresponding algorithm either takes too long or uses too much memory on the corresponding challenging instance.
. Algorithms qPMS7, PMS6 and PMS5 can solve any of these challenging instances. In Table 1, the letter ‘–’ indicates that the corresponding algorithm either takes too long or uses too much memory on the corresponding challenging instance.
Following [6] and [4], we have tested the qPMS algorithms on the most difficult case of  . The challenging instances for this case are identified as
. The challenging instances for this case are identified as  ,
,  ,
,  ,
, 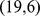 ,
,  ,
,  ,
,  , and so on. Since among the existing algorithms, only Algorithm qPMSPrune deals with the qPMS problem, we compare Algorithm qPMS7 to it. Algorithm qPMS7 can solve any challenging instance up to
, and so on. Since among the existing algorithms, only Algorithm qPMSPrune deals with the qPMS problem, we compare Algorithm qPMS7 to it. Algorithm qPMS7 can solve any challenging instance up to  . Table 2 shows the results for these challenging instances.
. Table 2 shows the results for these challenging instances.
0.6.2 Protein sequences
We have also tested the algorithms on synthetic protein sequences. These sequences have been generated in a manner similar to the generation of DNA strings as explained in Section 0.6.1. The number of the protein strings in each testing dataset  and the length of each protein string
and the length of each protein string  are chosen to be the same:
are chosen to be the same:  and
and  . For the case of
. For the case of  , the
, the  pairs that correspond to challenging instances are
pairs that correspond to challenging instances are  ,
,  ,
,  ,
,  ,
,  , and so on. For the case of
, and so on. For the case of 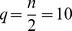 , the challenging instances are
, the challenging instances are  ,
,  ,
,  ,
,  ,
,  , and so on.
, and so on.
Since none of the exact algorithms reported in the literature deals with the qPMS problem for protein sequences, we restrict our comparison to the algorithms qPMSPrune, qPMSPruneI, and qPMS7. Table 3 and Table 4 show the runtimes of these algorithms for the two cases  and
and  , respectively. As the results show, Algorithm qPMS7 outperforms Algorithms qPMSPruneI and qPMSPrune on all the cases.
, respectively. As the results show, Algorithm qPMS7 outperforms Algorithms qPMSPruneI and qPMSPrune on all the cases.
Table 3. Time comparison of different algorithms on the challenging instances of protein sequences for the special case - PMS Problem.
| Algorithm | (11,5) | (13,6) | (15,7) | (17,8) | (19,9) |
| qPMS7 | 1 m | 1.4 m | 1.9 m | 6.8 m | 7.5 m |
| qPMSPruneI | 4.5 m | 21 m | 2.4 m | 17 h | – |
| qPMSPrune | 12 m | 104 m | 16 h | – | – |
The alphabet size  ,
,  ,
,  , and
, and  .
.
Table 4. Time comparison of different algorithms on the challenging instances of protein sequences for the generalized case - qPMS Problem.
| Algorithm | (11,4) | (13,5) | (15,6) | (17,7) | (19,8) |
| qPMS7 | 27 s | 3 m | 18 m | 3.8 h | 11 h |
| qPMSPruneI | 62 s | 16 m | 3.7 h | – | – |
| qPMSPrune | 181 s | 113 m | 29 h | – | – |
The alphabet size  ,
,  ,
,  , and
, and  .
.
0.7 Experiments on Real Data
0.7.1 Finding real DNA motifs
We tested Algorithm qPMS7 on the real datasets discussed in [27] which is commonly used to measure the accuracy of the existing algorithms (see e.g., [27], [19], and [7]). Each of the datasets is a collection of DNA orthologous sequences from many organisms. These real datasets are substantially different from the simulated data because they contain known transcription regulatory elements, i.e, known motifs. Algorithm qPMS7 was able to identify these known motifs for appropriate values of the parameters  and
and  . We report these motifs in Table 5. However, we should mention that our results are similar to those published in [7], [6] as well as other papers.
. We report these motifs in Table 5. However, we should mention that our results are similar to those published in [7], [6] as well as other papers.
Table 5. Results on real datasets.
| Data | Predicted Motifs | Known Motifs |
|
|
| 1 | CCTCAGCCCC | CCTCAGCCCC | (10,2) | |
| 2 | ATTTCGTGGCA | ATTTCnnGCCA | (13,2) | |
| 3 | CCATATTAGGACATCT | CCATATTAGGACATCT | (16,3) | |
| 4 | TTTCCCATTAAGGAAA | TTTCCCnnTnAGGAAA | (16,3) |
Data 1: Preproinsulin; Data 2: DHFR; Data 3: c-fos; Data 4: Yeast ECB. Parameter  is set to
is set to  .
.
0.7.2 Detecting transcription factor-binding sites
We have also tested our algorithms on the biological datasets described in [28]. In this collection there are several datasets. Some strings of each of these datasets contain known transcription factor-binding sites of different lengths and the others do not. Therefore, in order to test these real datasets we rely on the framework for transcription factor-binding sites discovery described in Section 0.5. Recall that this framework needs a qPMS algorithm and a scoring function. Since Algorithm qPMS7 is currently the fastest, we employ it in this framework. Regarding the scoring function, we use the function called “sequence specificity” which is also the one used in [6], which basically is defined to be  where
where  is the expected number of times a motif appears in string
is the expected number of times a motif appears in string  with up to
with up to 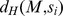 mismatches, assuming the i.i.d model. To complete the tests, we need to choose the parameters of the framework
mismatches, assuming the i.i.d model. To complete the tests, we need to choose the parameters of the framework  ,
,  ,
,  ,
,  , and
, and  . We set
. We set  ,
,  ,
,  ,
,  , and
, and 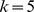 . With this setting, we obtain good results like those in [28], [6], and [4] with many transcription factor-binding sites predicted correctly. Table 6 reports some of these correctly predicted binding sites together with the predicted motifs.
. With this setting, we obtain good results like those in [28], [6], and [4] with many transcription factor-binding sites predicted correctly. Table 6 reports some of these correctly predicted binding sites together with the predicted motifs.
Table 6. Results on real datasets for transcription factor-binding sites discovery.
| Data | Predicted Motifs | Matched Binding Sites |
| mus05r | AGAGGAAAAAAAAAAGGAG | s 1: GGAAAAACAAAGGTAATG |
| mus07r | CTGCCCACCCTCTGCAACCC | s 4: CCCAACACCTGCTGCCTGAGCC |
| mus11r | AGGGCGGGGGGCGGAGCG | s 2: GCCGCCGGGGTGGGGCTGAG |
| s 3: GGGGGGGGGGGCGGGGC | ||
| s 4: GTGGGGGCGGGGCCTT | ||
| s 9: GAACAGGAAGTGAGGCGG | ||
| hm03r | AAAAGAAAAAAAAATAAACAA | s 1: TCAAGCAAAAAAAATAAATAAATACCTATGCAA |
| s 2: ACAAGCAAACAAAATAAATATCTGTGCAATAT | ||
| s 3: TATGAGCAAACAAAATAAATACCTGTGCAA | ||
| hm08r | CGTGCAGTCCCCTTCAT | s 10: TATGGTCATGACGTCTGACAGAGC |
| hm19r | CCCTTCCACCACCCACAG | s 2: CACTTTTAGCTCCTCCCCCCA |
| hm26r | CCCCCCGCCTCCCGCTCCC | s 3: CCCCGCCTCAGGCTCCCGGGG |
| s 7: CTCAGCCTGCCCCTCCCAGGGATTAAG | ||
| s 8: GCGCCGAGGCGTCCCCGAGGCGC |
The datasets are from mouse (resp. human) if their names start with “mus” (resp. “hm”).
Discussion
In this paper we have presented Algorithm qPMS7 for the qPMS problem and tested it on DNA as well as protein sequences. Experimental results indicate that Algorithm qPMS7 is faster than other existing algorithms, especially for large values of  and
and  . Since Algorithm qPMS7 is a search-based algorithm, it uses a small amount of memory. This feature of Algorithm qPMS7 is a major advantage compared to other algorithms such as RISOTTO, Voting, PMS5, and PMS6 which require a large amount of memory when solving instances with large values of
. Since Algorithm qPMS7 is a search-based algorithm, it uses a small amount of memory. This feature of Algorithm qPMS7 is a major advantage compared to other algorithms such as RISOTTO, Voting, PMS5, and PMS6 which require a large amount of memory when solving instances with large values of  and
and  . Another advantage of Algorithm qPMS7 over these algorithms is that they cannot deal with the qPMS problem and in particular they only handle the PMS problem.
. Another advantage of Algorithm qPMS7 over these algorithms is that they cannot deal with the qPMS problem and in particular they only handle the PMS problem.
Algorithm qPMS7 is the result of a combination of an extension of Algorithm qPMSPrune and the core idea of algorithm PMS5. In Algorithm qPMSPrune, a “pivot”  -mer is used. In Algorithm qPMS7, we extended this idea by considering two pivot
-mer is used. In Algorithm qPMS7, we extended this idea by considering two pivot  -mers. This idea can be further generalized by considering more than two pivot
-mers. This idea can be further generalized by considering more than two pivot  -mers,
-mers,
In this paper we have also proposed a framework for transcription factor-binding sites discovery. It should be mentioned that our framework together with Algorithm qPMS7 is currently deployed in our online tools at http://pms.engr.uconn.edu or at http://motifsearch.com. We will be very happy to receive any comments and feedback from users.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: This work has been supported in part by the following grants: NSF 0829916 and NIH R01-LM010101. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No additional external funding was received for this study.
References
- 1.Laurent D, Philipp B. Searching for regulatory elements in human noncoding sequences. Current Opinion in Structural Biology. 1997;7:399–406. doi: 10.1016/s0959-440x(97)80058-9. [DOI] [PubMed] [Google Scholar]
- 2.Rajasekaran S. Computational techniques for motif search. Frontiers in Bioscience. 2009;14:5052–5065. doi: 10.2741/3586. [DOI] [PubMed] [Google Scholar]
- 3.Bandyopadhyay S, Sahni S, Rajasekaran S. Pms6: A faster algorithm for motif discovery. In: Proceedings of the second IEEE International Conference on Computational Advances in Bio and Medical Sciences (ICCABS. 2012;2012):1–6. doi: 10.1109/ICCABS.2012.6182627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Dinh H, Rajasekaran S, Kundeti V. Pms5: an efficient exact algorithm for the (l; d)-motiffinding problem. BMC Bioinformatics 12. 2011. [DOI] [PMC free article] [PubMed]
- 5.Davila J, Balla S, Rajasekaran S. Pampa: An improved branch and bound algorithm for planted (l, d) motif search. Technical report. 2007.
- 6.Davila J, Balla S, Rajasekaran S. Fast and practical algorithms for planted (l; d) motif search. In: IEEE/ACM Transactions on Computational Biology and Bioinformatics. 2007. pp. pp 544–552. [DOI] [PubMed]
- 7.Rajasekaran S, Balla S, Huang CH. Exact algorithms for planted motif challenge problems. Journal of Computational Biology. 2005;12:1117–1128. doi: 10.1089/cmb.2005.12.1117. [DOI] [PubMed] [Google Scholar]
- 8.Chin F, Leung H. Algorithms for discovering long motifs. In: Proceedings of the Third Asia-Pacific Bioinformatics Conference (APBC2005), Singapore. 2005. pp. pp 261–271.
- 9.Pisanti N, Carvalho A, Marsan L, Sagot MF. Risotto: Fast extraction of motifs with mismatches. In: Proceedings of the 7th Latin American Theoretical Informatics Symposium. 2006. pp. pp 757–768.
- 10.Blanchette M, Schwikowski B, Tompa M. An exact algorithm to identify motifs in or-thologous sequences from multiple species. In: Proceedings of Eighth International Conference on Intelligent Systems for Molecular Biology. 2000. pp. pp 37–45. [PubMed]
- 11.Brazma A, Jonassen I, Vilo J, Ukkonen E. Predicting gene regulatory elements in silico on a genomic scale. Genome Research. 1998;15:1202–1215. doi: 10.1101/gr.8.11.1202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Eskin E, Pevzner P. Finding composite regulatory patterns in dna sequences. Bioinformatics. 2002;S1:354–363. doi: 10.1093/bioinformatics/18.suppl_1.s354. [DOI] [PubMed] [Google Scholar]
- 13.Galas DJ, Eggert M, Waterman MS. Rigorous pattern-recognition methods for dna sequences: Analysis of promoter sequences from escherichia coli. Journal of Molecular Biology. 1985;186:117–128. doi: 10.1016/0022-2836(85)90262-1. [DOI] [PubMed] [Google Scholar]
- 14.Sinha S, Tompa M. A statistical method for finding transcription factor binding sites. In: Proceedings of Eighth International Conference on Intelligent Systems for Molecular Biology. 2000. pp. pp 344–354. [PubMed]
- 15.Staden R. Methods for discovering novel motifs in nucleic acid sequences. Computer Applications in the Biosciences. 1989;5:293–298. doi: 10.1093/bioinformatics/5.4.293. [DOI] [PubMed] [Google Scholar]
- 16.Tompa M. An exact method for finding short motifs in sequences, with application to the ribosome binding site problem. In: Proc. Seventh International Conference on Intelligent Systems for Molecular Biology. 1999. pp. pp 262–271. [PubMed]
- 17.Helden J, André B, Collado-Vides J. Extracting regulatory sites from the upstream region of yeast genes by computational analysis of oligonucleotide frequencies. Journal of Molecular Biology. 1998;281:827–842. doi: 10.1006/jmbi.1998.1947. [DOI] [PubMed] [Google Scholar]
- 18.Bailey T, Elkan C. Fitting a mixture model by expectation maximization to discover motifs in biopolymers. In: Proceedings of Second International Conference on Intelligent Systems for Molecular Biology. 1994. pp. pp 28–36. [PubMed]
- 19.Buhler J, Tompa M. Finding motifs using random projections. In: Proceedings of Fifth Annual International Conference on Computational Molecular Biology (RECOMB). 2001. pp. pp 69–76. [DOI] [PubMed]
- 20.Lawrence CE, Altschul SF, Boguski MS, Liu JS, Neuwald AF, et al. Detecting subtle sequence signals: a gibbs sampling strategy for multiple alignment. Science. 1993;262:208–214. doi: 10.1126/science.8211139. [DOI] [PubMed] [Google Scholar]
- 21.Pevzner P, Sze SH. Combinatorial approaches to finding subtle signals in dna sequences. In: Proceedings of Eighth International Conference on Intelligent Systems for Molecular Biology. 2000. pp. pp 269–278. [PubMed]
- 22.Rocke E, Tompa M. An algorithm for finding novel gapped motifs in dna sequences. In: Proceedings of Second International Conference on Computational Molecular Biology (RECOMB). 1998. pp. pp 228–233.
- 23.Keich U, Pevzner P. Finding motifs in the twilight zone. Bioinformatics. 2002;18:1374–1381. doi: 10.1093/bioinformatics/18.10.1374. [DOI] [PubMed] [Google Scholar]
- 24.Price A, Ramabhadran S, Pevzner PA. Finding subtle motifs by branching from sample strings. Bioinformatics. 2003;1:1–7. doi: 10.1093/bioinformatics/btg1072. [DOI] [PubMed] [Google Scholar]
- 25.Hertz G, Stormo G. Identifying dna and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics. 1999;15:563–577. doi: 10.1093/bioinformatics/15.7.563. [DOI] [PubMed] [Google Scholar]
- 26.Kuksa P, Pavlovic V. Efficient motif finding algorithms for large-alphabet inputs. BMC Bioinformatics 11. 2010. [DOI] [PMC free article] [PubMed]
- 27.Blanchette M. Algorithms for phylogenetic footprinting. In: Proceedings of Fifth International Conference Computational Biology (RECOMB. 2001;2001):49–58. [Google Scholar]
- 28.Tompa M, Li N, Bailey T, Church G, Moor BD, et al. Assessing computational tools for the discovery of transcription factor binding sites. Nature Biotechnology. 2005;23:137–144. doi: 10.1038/nbt1053. [DOI] [PubMed] [Google Scholar]


