Solvent-induced infrared frequency shifts in aromatic nitriles are quantitatively described by the vibrational Stark effect

Abstract

The physical properties of solvents strongly affect the spectra of dissolved solutes, and this phenomenon can be exploited to gain insight into the solvent-solute interaction. The large solvatochromic shifts observed for many dye molecules in polar solvents are due to variations in the solvent reaction field, and these shifts are widely used to estimate the change in the dye’s dipole moment upon photoexcitation, which is typically on the order of ~1-10 Debye. In contrast, the change in dipole moment for vibrational transitions is approximately two orders of magnitude smaller. Nonetheless, vibrational chromophores display significant solvatochromism, and the relative contributions of specific chemical interactions and electrostatic interactions are debated, complicating the interpretation of vibrational frequency shifts in complex systems such as proteins. Here we present a series of substituted benzonitriles that display widely varying degrees of vibrational solvatochromism. In most cases, this variation can be quantitatively described by the experimentally determined Stark tuning rate, coupled with a simple Onsager-like model of solvation, reinforcing the view that vibrational frequency shifts are largely caused by electrostatic interactions. In addition, we discuss specific cases where continuum solvation models fail to predict solvatochromic shifts, revealing the necessity for more advanced theoretical models that capture local aspects of solute-solvent interactions.

Introduction

The vibrational frequency of certain chemical groups provides a useful probe of the local environment^1,2. As vibrational probes have gained use in studying local structure and dynamics in biological systems, models for identifying the physical origin of vibrational frequency shifts have become increasingly important. Because many vibrational transitions exhibit a significant sensitivity to electric field, known as the vibrational Stark effect, and are confined to a small number of atoms, vibrational probes have the potential to provide quantitative measurements of local electric fields in complex systems. For a vibrational probe in two different electrostatic environments with a difference in the electric field $\Delta \stackrel{\mathsf{r}}{F}$ (in MV/cm), the shift in vibrational frequency, $\Delta {\overline{\nu }}_{\text{probe}}$ (in cm⁻¹) is given by:

$$hc\Delta {\overline{\nu }}_{\text{probe}}=-\Delta \stackrel{\mathsf{r}}{{\mu }_{\text{probe}}}\cdot \Delta \stackrel{\mathsf{r}}{F}$$ (1)

where h is Planck’s constant, c the speed of light, and $\Delta \stackrel{\mathsf{r}}{{\mu }_{\text{probe}}}$ is the difference in dipole moment between the ground and excited states (in Debye), often expressed as the linear Stark tuning rate [in cm⁻¹/(MV/cm)]. It is important to note that eq 1 specifies the change in frequency due to a difference in field between two states, but does not allow one to equate a particular probe frequency with a particular total field, without a suitable reference where the total field experienced by the probe is known precisely (see below).

Nitrile groups are particularly useful as directional and sensitive probes of electric fields in biological macromolecules, as they absorb in a convenient region of the infrared spectrum where there is little background from other vibrations³, and several methods have been developed to introduce nitriles into biomolecules^2,4. Consequently nitrile frequency shifts have been used to measure changes in local electric fields in proteins^2,5-7, nucleic acids⁸ and membranes⁹ in response to mutations, pH changes, exposure to water, etc. Related to the frequency shifts probes undergo in biomolecules are the effects of solvent polarity on the vibrational frequencies of nitrile-containing solutes. Measurements of these effects can provide an important reference for interpreting the spectra of probes in biomolecular environments; such comparisons are commonly employed for fluorophores and can provide an experimental assessment of the effective dielectric constant in protein interiors^10-12. Given a suitable model for the solvent reaction field, the total field experienced by a probe in the solvent can be determined. The corresponding probe frequencies would then serve as reference states, allowing eq 1 to be used to determine the total field experienced by a probe in other environments.

The contribution of electrostatics to solvent-solute interactions is well established for dye molecules that undergo electronic transitions¹³. The absorbance and fluorescence spectra of many dyes exhibit dramatic solvatochromism, with the frequencies of both absorption and emission varying strongly with solvent polarity¹⁴. Solvation theories, e.g. those due to Lippert and Mataga, can accurately account for these phenomena by considering the solvent reaction fields induced in the polar solvent by the dye molecule’s ground and excited state dipole moments^15,16. The great sensitivity of these dyes to solvent polarity can be attributed to a large change in magnitude and/or direction of the molecule’s dipole moment upon photoexcitation (on the order of 10 Debye). In contrast, the equivalent parameter for vibrational transitions, the linear Stark tuning rate, is at least two orders of magnitude smaller than this, indicating a much lower sensitivity to electric fields^1,17. This fact, combined with the influence of specific solvent effects on the vibrational frequency, has led to a lack of consensus on the contribution of the solvent reaction field to solvatochromic shifts in the case of vibrations^18-21. For nitriles, this situation is exacerbated by the fact that hydrogen bonding produces pronounced blue-shifts of the vibrational frequency that are due to quantum chemical effects that are not accounted for by the vibrational Stark effect^20,22. It remains an open question whether there are regimes where classical electrostatics suffices to describe the environment’s influence on vibrational frequency, and under what conditions solvent effects on vibrations can only be understood from a quantum chemical perspective.

In this study we present data on a series of substituted benzonitriles where the nitrile group’s vibrational frequency exhibits varying degrees of solvatochromism. We show that the different linear Stark tuning rates of these compounds, combined with their molecular dipole moments, fully account for the observed solvatochromic trends, indicating that the solvent reaction field is the primary cause of the observed solvatochromism. We also report data on two compounds whose molecular properties are such that continuum solvation models would predict very small or zero reaction fields. For these compounds, considerable solvatochromism is observed, indicating that for such cases it is necessary to apply more advanced models of the solvent-solute interaction that incorporate local effects.

Experimental Procedures

Synthesis of isotopically labeled compounds

The full synthetic methodology can be found in the Supporting Information. Substituted benzonitriles in which the nitrile group was isotopically labeled with ¹³C and ¹⁵N were prepared using the Rosenmund-von Braun reaction, as described in detail in the supplementary material and in refs ^26,34. Isotopically labeled copper cyanide was prepared from copper sulfate and ¹³C,¹⁵N-labeled potassium cyanide (Cambridge Isotopes) in basic aqueous solution. The product, ¹³C,¹⁵N-labeled copper cyanide, was mixed with the relevant aryl bromide in a 2:1 molar ratio in dimethyl formamide. The reaction was performed at 170 degrees for 2 hours in a microwave (Biotage Initiator). The product was extracted from diethyl ether:water and purified by silica gel chromatography. The compounds were verified by mass spectrometry, NMR and IR spectroscopy.

FTIR spectra

Anhydrous solvents were obtained from commercial sources (Sigma and Acros Organics). Compounds were dissolved in each solvent to 10 mM concentration and loaded into a demountable liquid sample cell with sapphire windows and offset spacers of 75 and 100 mm thickness. Infrared absorbance spectra were recorded on a Vertex FTIR spectrometer (Bruker), at 1 cm⁻¹ resolution and averaged across 64 scans of the interferometer. For the unlabeled aminobenzonitriles, where the nitrile band overlapped with a Fermi resonance, the peak positions were determined by fitting two Voigt lineshape functions to the spectra. For benzonitrile and the isotopically labeled compounds the spectra consisted of single peaks in the nitrile stretch region (with the exception of 3-ABN in three solvents, which was treated as above), and the peak positions were determined using the spectrometer software (Opus).

Vibrational Stark spectroscopy

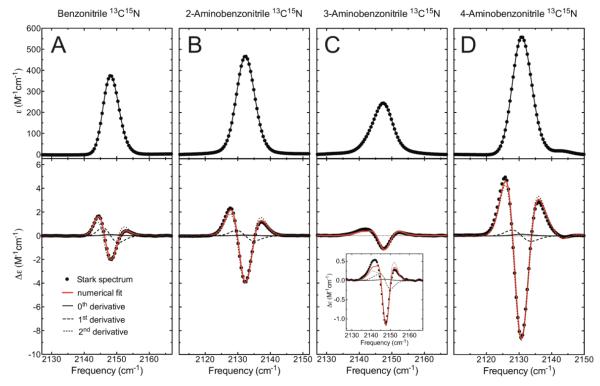
Vibrational Stark spectra were recorded as previously described¹⁷. Briefly, the compounds were dissolved in 2-methyltetrahydrofuran at 100 mM concentration and loaded into a custom-made sample cell consisting of sapphire windows coated with a 4 nm-thick layer of nickel metal. The sample was flash frozen in liquid nitrogen using a custom-built nitrogen immersion cryostat³⁵. A high-voltage power supply was used to apply an external electric field across the sample (typical applied fields were in the range 0.2 - 1.0 × 10⁶ V/cm). Stark spectra were recorded using a conventional FTIR spectrometer (Bruker) with custom electronics to synchronize the interferometer mirror with the high-voltage power supply. Stark spectra were determined by calculating the difference between the field-on and field-off absorbance spectra. 128 scans were averaged for the Stark spectra. The linear Stark tuning rates were determined from a numerical fit of the Stark spectra with derivatives of the experimental absorption spectra. The fitting coefficient of the 2^nd-derivative term gives the linear Stark tuning rate and this dominates the Stark spectra as can be seen in Fig. 2.

Figure 2.

Absorbance and Stark spectra of isotopically labeled (A) BN, (B) 2-ABN, (C) 3-ABN, and (D) 4-ABN. The top and bottom panels show the absorbance and Stark spectra, respectively, measured at a concentration of 100 mM at 77K in 2-methyltetrahydrofuran. All spectra were scaled to M⁻¹ cm⁻¹ (typical absorbance values were ~0.1), and the Stark spectra were additionally scaled to 1.0 MV/cm applied field (typical experimental applied fields were 0.7-1.0 MV/cm), so that the spectra can be directly compared. The red lines in the Stark panels show the numerical fits to the Stark data, consisting of the sum of contributions from the 0^th, 1^st, and 2^nd derivatives of the absorption, and the thin lines show the individual contributions of each derivative. The linear Stark tuning rate is proportional to the square root of the 2^nd-derivative contribution^17,30.

Due to the dielectric properties of the solvent the actual value of the electric field experienced by the solute is larger than the applied field by a factor f, known as the local field correction factor³⁰. For a particular frozen glass solvent the value of f is expected to be a constant, and its value is typically between 1.1 and 1.3 for different solvents (only one solvent, 2Me-THF, was used here). We report the values of the linear Stark tuning rate as $\mid \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}\mid f$ in Table 1.

Table 1.

Molecular parameters and observed solvatochromic slopes for the compounds in this study.

Compound	$\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid$(Debye)	$\mid \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}\mid f$ (cm−1/(MV/cm))	$\stackrel{\mathsf{r}}{{\mu }_0}\cdot \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}∕hc{a}^3$ (normalized to BN)	m (normalized to BN)
BN	4.2 a	0.57	1	1
2-ABN	4.1 b	0.82	1.2	1.4
3-ABN	4.9 b	0.63	1.3	1.4
4-ABN	6.4 a	1.18	3.2	2.9
5-N,2-ABN	7.0	0.65	0	0.8
p-DCB	0	0.55	0	0.7

^aBorst, D. R.; Korter, T. M.; Pratt, D. W. Chem. Phys. Lett. 2001, 350, 485.

^bMiller, D. M.; Morgan, P. J.; Pratt, D. W. J. Phys. Chem. A 2009, 113, 6964.

Results and Discussion

In order to determine whether vibrational solvatochromic shifts can be attributed to electrostatics, i.e. whether these shifts can be described by eq 1, we set out to compare the frequencies of a vibrational probe measured in different solvents to a theoretical model for the electric fields it experiences in these solvents. We used Onsager’s reaction field theory²³ for this purpose, which considers the solute to occupy a spherical cavity inside a continuous dielectric medium representing the solvent. The reaction field is given as a function of the solvent’s static dielectric constant, ε, representing its capacity to be polarized, and the solute’s gas-phase dipole moment in the ground state, ${\overrightarrow{\mu }}_0$, and refractive index, n, representing its capacity to polarize its surroundings:

$$\stackrel{\mathsf{r}}{F_{\text{Onsager}}}=\frac{\stackrel{\mathsf{r}}{{\mu }_0}}{a^3}\cdot \lfloor \frac{2(\epsilon -1)(n^2+2)}{3(2\epsilon +n^2)}\rfloor$$ (2)

The term a in eq 2 is called the Onsager cavity radius and is related to the molecular volume of the solute; while the value of a³ is not known precisely, it is generally taken to be proportional to a molecule’s formula weight and should be similar for molecules of similar size, as is the case for the molecules discussed below.

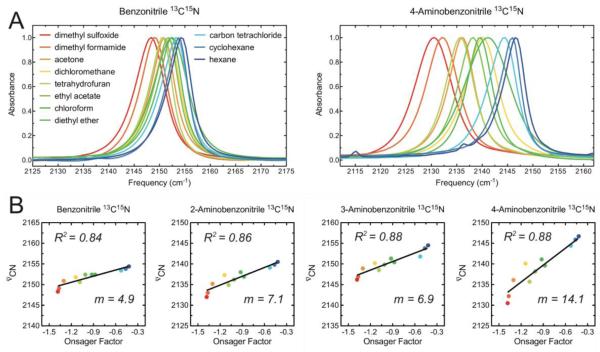
If solvatochromic shifts are primarily due to the solvent reaction field, the shifts should depend linearly on the solute’s dipole moment, as predicted by eq 2 and other solvation models^13,15. To test this dependence we used a series of substituted benzonitriles that exhibit a systematic variation in molecular dipole moment. We used only aprotic solvents because the formation of hydrogen bonds between the nitrile group and solvent molecules is known to perturb the vibrational frequency in a manner that is not described by the vibrational Stark effect^22,24. Aromatic solvents were also avoided as these can form specific electrostatic interactions (complexes) with the solute that are not accounted for with macroscopic descriptions of the solvent polarity²⁵. Control experiments indicated no concentration dependence to the nitrile bands in the IR spectra below 100 mM concentration, indicating the absence of solute-solute interactions in this concentration regime (Figure S1). Infrared absorbance spectra of 10 mM benzonitrile $\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid =4.2\mathrm{D}$, 2-aminobenzonitrile $\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid =4.1\mathrm{D}$, 3-aminobenzonitrile $\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid =4.9\mathrm{D}$ and 4-aminobenzonitrile $\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid =6.4\mathrm{D}$ were measured in eleven different aprotic solvents, varying in static dielectric from 1.9 (hexane) to 47 (dimethyl sulfoxide). In the case of the aminobenzonitriles, the nitrile bands in some solvents overlap with a Fermi resonance that occurs around 2220 cm⁻¹, complicating the assignment of the peak positions. In order to obtain accurate peak positions we synthesized analogs of each compound where the nitrile group was double labeled with ¹³C and ¹⁵N isotopes²⁶; the effect of the heavier isotopes on the reduced mass lowers the vibrational frequency by ~80 cm⁻¹, and the IR spectra of the isotopically labeled compounds displayed single bands in the nitrile stretch region in almost all cases (in the spectra of labeled 3-ABN in hexane, cyclohexane, carbon tetrachloride and chloroform a shoulder to the nitrile band is still observed; for these cases the peak positions were determined by fitting both peak and shoulder with Voigt functions). For simplicity we consider only these isotopically labeled compounds here; the IR spectra of all (amino)benzonitriles studied in this work can be found in the Supporting Information (Figure S2).

For all four compounds the nitrile stretch frequency shifts in concert with the polarity of the solvent, as expected if the solvent reaction field is the primary determinant of the shifts. The magnitudes of the solvatochromic shifts vary greatly between compounds in the series, with the overall spread in the vibrational frequencies across all solvents ranging from 6.1 cm⁻¹ for BN to 16.2 cm⁻¹ for 4-ABN (Figure 1A). There is also a significant increase in line width in the more polar solvents, although this trend is less systematic than the frequency shifts.

Figure 1.

Solvatochromic data of substituted benzonitriles. (A) FTIR spectra of 10 mM isotopically labeled benzonitrile (left) and 4-aminobenzonitrile (right) in 11 different aprotic solvents. The horizontal axes span a 50 cm⁻¹ range in both plots. (B) Plots of the nitrile stretch frequency as a function of the solvent’s Onsager factor, the square bracket in eq 2, for each compound. The colors of the dots correspond to the colors associated with the solvents shown in (A). The vertical axes span a 25 cm⁻¹ range in each plot. The frequencies are for the isotopically labeled compounds.

The reaction field given by eq 2 depends both on properties of the solute and those of the solvent. To focus on making comparisons between solvents, we plotted the observed nitrile vibrational frequencies as a function of the dimensionless term between the square brackets in eq 2. This term, referred to as the Onsager factor, incorporates the effect of solvent polarity, as well as the polarizability of the solute, which is captured by its refractive index, on the reaction field (note that we use the refractive index of benzonitrile, which is a liquid, to approximate the polarizability of all four compounds; for benzonitrile n = 1.528). For all four compounds these plots, which we refer to as Onsager plots, show clear correlations, indicating that an underlying linear relationship exists between the nitrile stretch frequency and the solvent reaction field predicted by eq 1 (Figure 1B).

The slopes of the Onsager plots (the values of m in Figure 1B) increase by a three-fold factor over the series in the order BN, 3-ABN, 2-ABN and 4-ABN, reflecting significant differences in overall sensitivity to solvent among these compounds. Combining equations 1 and 2 produces an expression for the slopes in Figure 1B,

$$m=-\stackrel{\mathsf{r}}{{\mu }_0}\cdot \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}∕hc{a}^3$$ (3)

Assuming that the cavity radius, a, is constant for these compounds, the slopes should depend on the projection of the molecular dipole moment along the nitrile bond axis (which is parallel to $\Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}$)¹⁷, as well as the intrinsic sensitivity of the nitrile stretch to electric field, quantified by the r magnitude of the linear Stark tuning rate, $\mid \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}\mid$. The magnitudes and directions of the molecular dipole moments are known for all four compounds from experimental measurements in the gas phase^27,28, and we determined their linear Stark tuning rates by measuring their vibrational Stark spectra in frozen 2-methyltetrahydrofuran (Figure 2, Figure S3). The tuning rates were determined from numerical fits of the Stark spectra with derivatives of the absorption spectra¹⁷.

Strikingly, 4-ABN displays an unusually large linear Stark tuning rate of 1.2 cm⁻¹/(MV/cm) (typical values for nitriles range from 0.4-0.7 cm⁻¹/(MV/cm)^3,17). 2-ABN has a modestly elevated value of 0.82 cm⁻¹/(MV/cm), whereas the values for BN and 3-ABN are 0.57 and 0.63 cm⁻¹/(MV/cm), respectively. These large differences in the linear Stark tuning rates are readily apparent from the magnitudes of the features in the Stark spectra when the spectra are scaled to the same applied field (Figure 2, lower panels), and are consistent with chemical intuition regarding resonance structures – the electron-donating amino group making the nitrile bond more polar when located in the ortho or para positions. Because the vibrational Stark effect arises in large part from mechanical anharmonicity, more polar chemical bonds are expected to display larger Stark tuning rates²⁹.

When the expression for m is evaluated using the experimentally determined dipole moments and values of $\mid \Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}\mid$ for each compound (eq 3), it becomes apparent that the trends in the solvatochromic data are fully accounted for by the solvent reaction field model (Table 1). Indeed, the much greater sensitivity of 4-ABN to solvent polarity compared to BN, quantified by its three-fold greater value of m, is fully explained by the large Stark tuning rate of 4-ABN, together with its large dipole moment. The larger Stark tuning rate of 2-ABN compensates for its smaller dipole moment, explaining why its solvatochromic shifts are very similar to those of 3-ABN.

The value of the Onsager cavity radius cubed, a³, can be approximated by considering the solute’s molecular volume²⁴. Using the density and molecular weight of benzonitrile, a³ =170 ų. Evaluating eq 2 using this value, as well as the other molecular parameters already described, produces an estimate of the solvent field experienced by the nitrile group. The fields range in magnitude from 2.5 MV/cm for 2-ABN in hexanes to 15 MV/cm for 4-ABN in dimethyl sulfoxide. Plotting the observed vibrational frequencies as a function of these calculated solvent fields gives similar plots to those shown in Figure 1B, but in this case the corresponding slope is the apparent linear Stark tuning rate. The slopes of these plots are 0.7, 1.2, 0.8 and 1.3 cm⁻¹/(MV/cm) for BN, 2-ABN, 3-ABN and 4-ABN respectively, in excellent agreement with the values determined from Stark spectroscopy (Figure S4). This analysis further underscores the good agreement between the experimental solvatochromic data and the Onsager reaction field model, as well as demonstrating that the linear Stark tuning rates measured at experimentally achievable applied electric fields of ≤1MV/cm accurately describe the linear response to fields more than an order of magnitude larger²⁴.

Upon close inspection, the Onsager plots shown in Figure 1B (as well as the plots shown in Figure S4), display systematic deviations from the best-fit lines, in the sense that the same solvents usually deviate in the same direction from the line in each plot. In principle, these non-random deviations could be due either to systematic errors in the model of the reaction field, or to specific interactions with the solvent that perturb the nitrile frequency in ways that are not described by the vibrational Stark effect. However, the magnitudes of the deviations correlate with the slopes of the best-fit line; i.e. BN displays the smallest deviations and 4-ABN the largest. This is reflected in the fact that the R² values are between 0.85 and 0.89 for all four compounds, despite the three-fold variation in slope. The observation that the compound with the greatest intrinsic sensitivity to field also displays the largest deviations, and the least sensitive compound displays the smallest deviations, suggests that these deviations arise primarily from consistent errors in the Onsager model’s prediction of the reaction fields, rather than from specific chemical effects.

Cases where the Onsager model breaks down

By combining Onsager’s theory to model the total field due to the environment (eq 2), and the linear Stark tuning rate to model the sensitivity of vibrational frequency to field (eq 1), we are able to accurately predict solvatochromism data for the four compounds described. In the context of the Onsager model, one would predict a nitrile-containing solute to exhibit zero solvatochromism under one of two circumstances: 1) if its dipole $\stackrel{\mathsf{r}}{{\mu }_0}$ were orthogonal to the nitrile bond (parallel to $\Delta \stackrel{\mathsf{r}}{{\mu }_{\mathit{CN}}}$) such that the solvent reaction field has no projection along the vibration of interest, or 2) if it had zero dipole moment, such that the solvent reaction field is zero. In an effort to further test the Onsager model we directly examined these two limiting cases.

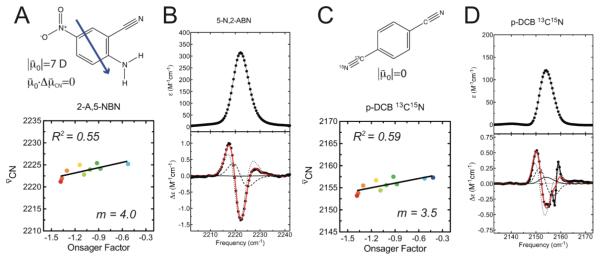
The compound 5-nitro-2-aminobenzonitrile (5-N,2-ABN, Figure 3A and B) has a large calculated dipole moment (7.0 Debye), but the dominant dipole component arising from the NH₂–NO₂ push-pull pair orients the overall dipole at ~90° to the nitrile bond vector as illustrated in Figure 3A (the values of both the dipole moment’s magnitude and direction were obtained from DFT/B3LYP energy calculations at the 6-311G level). To test the case when the molecular dipole moment is zero, we synthesized a symmetric dinitrile compound, [¹³C₁¹⁵N₁]p-dicyanobenzene (p-DCB, Figure 3C and D), in which one nitrile group is isotopically labeled with ¹³C and ¹⁵N isotopes. p-DCB has r zero dipole moment by symmetry ($\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid =0$), but due to its heteroisotopic composition, retains highly local nitrile stretching modes (1.4% potential energy distribution located on the other nitrile for each nitrile stretching mode according to a DFT/B3LYP frequency calculation at the 6-311G++(df,pd) level).

Figure 3.

Solvatochromism of 5-N,2-ABN and p-DCB. A) Chemical structure (top) and Onsager plot (bottom) for 5-N,2-ABN. The blue arrow represents the molecule’s dipole moment. B) Absorbance (top) and Stark (bottom) spectra for 5-N,2-ABN, measured at 77K in 2-methyltetrahydrofuran. C) Chemical structure (top) and Onsager plot (bottom) for p-DCB. D) Absorbance (top) and Stark (bottom) spectra for p-DCB, measured at 77K in 2-methyltetrahydrofuran.

We found that both compounds display diminished but non-zero solvatochromic trends, with a spread in IR frequencies across all solvents of 4.2 cm⁻¹ for 5-N,2-ABN and 4.3 cm⁻¹ for p-DCB (see Supporting Information for the IR spectra). Attempts to quantitatively account for the data using the Onsager model as described above reveals a breakdown in the model. The slope (m) of the Onsager plot (Figure 3A) for 5-N,2-ABN is 4.0, somewhat smaller than seen for BN (note that 5-N,2-ABN was not soluble in hexane or cyclohexane, complicating comparisons of the slope). This data is inconsistent with the reaction field model, as the dependence of m on the angle between the molecular dipole moment and the nitrile bond axis (see eq 3) would predict essentially no sensitivity to solvent polarity for this compound.

In principle, the large magnitude of the dipole moment of 5-N,2-ABN, combined with error in its calculated orientation, could partially rationalize the non-zero solvatochromic behavior for this molecule. A more convincing counterexample is provided by p-DCB, which also exhibits non-zero solvatochromism with a slope similar to that of 5-N,2-ABN (Figure 3C, m = 3.5, R²=0.59, data shown for the ¹³C¹⁵N nitrile; the unlabeled nitrile exhibits identical solvatochromic shifts). This r finding is not consistent with the predicted dependence of m on $\mid \stackrel{\mathsf{r}}{{\mu }_0}\mid$ in the reaction field model (see eq 3), and together these data indicate a failure in the model to describe the solvation environment around these solutes. The R² values for the Onsager plots in Figure 3A and 3C are only 0.55 and 0.59, indicating that the frequency shifts are poorly predicted by a macroscopic description of the solvent polarity. However, the same systematic deviations from the best-fit lines are observed here as noted above for the (amino)benzonitrile series, consistent with electrostatics as the primary mechanism underlying the solvatochromic shifts. Note that, in contrast to the situation in the gas phase, the symmetry of a solute like p-DCB is broken in the liquid if considered at a molecular, as opposed to continuum level. As a result at any instant each nitrile is in a slightly different environment and there is no reason to expect any correleation between these environments. Once the symmetry is broken, each nitrile acts as a local dipole that can organize solvent locally, and local variations, which depend on the dielectric properties of the solvent will enter.

Conclusions

The excellent agreement between experiment and theory for the (amino)benzonitrile series is striking given the crude nature of the solvation model employed here. Like other simple reaction field models of solvation, the Onsager model used in this work treats the solute as a point dipole, located in a cavity inside a continuous dielectric medium, and neglects the fine-grained structural features of both the solute and solvent molecules. The success of this model for these compounds indicates that when the solute’s dipole moment is large and projected along the nitrile, these local details are relatively unimportant. The dipole approximation is generally an adequate simplification for describing the long-range electrostatic interactions between neutral molecules, and so the Onsager model might be accurate at capturing how any solute polarizes distant solvation shells. However, when the solvent reaction field (or its projection along the nitrile) is smaller, the rough nature of the electrostatic potentials of the solute and solvent molecules likely become increasingly important. In particular, nearby solvent molecules, such as the first solvation shell around a solute, will likely polarize in response to local features of the solute’s electrostatic potential. In the limiting case when the solute’s dipole moment is zero, the long-range interactions are zero and only these local effects are present. Thus a likely explanation for the breakdown in the model for 5-N,2-ABN and p-DCB is that the nitrile groups (which have large bond dipoles) themselves polarize nearby solvent molecules to produce a reaction field. In these cases, the nitrile groups sense no effect from distant solvation shells (as expected by the Onsager model), but continue to sense the reaction field from the nearby solvent. This would explain the observation that both 5-N,2-ABN and p-DCB exhibit solvatochromic shifts that are similar to one another’s, albeit smaller than those observed for BN (Table 1). Such effects could probably be captured by a more sophisticated description of the solvent, such as COSMO (Conductor-like Screening Model) ³¹. This approach treats the solute as an arbitrarily shaped cavity enclosing a distribution of QM partial charges, and would be better at capturing how locally polar moieties induce polarization in the environment. Moreover, molecular level fluctuations of the solvent (which cause the electric field experienced by the solute to fluctate) are not captured by the Onsager model, and may also contribute to deviations from the model. A detailed understanding of such phenomena would require QM/MM calculations that represent the solvent explicitly.

Our results underscore that the vibrational Stark effect fully accounts for frequency shifts of aromatic nitriles in the diverse range of physical regimes represented by the aprotic solvents used in this study. However, the nitrile stretch frequency is known to be strongly sensitive to hydrogen bonding, which produces pronounced blue-shifts that are due to quantum chemical effects²². Consequently, the solvatochromism of nitrile-containing compounds in protic solvents cannot be explained by the vibrational Stark effect alone, as noted by others for acetonitrile in water^18,20. Our growing comprehension of nitrile vibrations is nonetheless enabling us to separate this confounding effect, in particular by comparing ¹³C NMR and IR data for the nitrile^24,26. Interestingly, the vibrational frequencies of azides are also strongly dependent on hydrogen bonding, but unlike nitriles, their linear Stark tuning rates and solvatochromic shifts are quite small^3,32. Recent computational work on C-F- and C=O-containing compounds in water suggests that for these probes the vibrational frequency correlates well with calculated field, indicating that the confounding effects of hydrogen bonding observed with nitriles and azides are not a general feature of molecular vibrations¹⁹. Many vibrational groups, including C-F, O-H, and C=O, exhibit larger Stark tuning rates than nitriles^3,25, and so their frequency shifts may be dominated by electrostatics even in cases where hydrogen bonding is present. Unfortunately, these probes are quite difficult to detect in complex systems such as proteins.

The solvatochromic shifts of probes in simple solvents have been used as a qualitative benchmark for interpreting spectroscopic data obtained for the same probe in proteins and other biomolecules^10-12, but conceivably a more quantitative comparison is possible. As explained above, eq 1 allows one to determine the difference in field experienced by the probe in two environments from measurements of the probe frequencies in these environments. If the total field the probe experiences due to one of these environments is known, however, then the total field experienced in the other environment is given by the observed spectroscopic shift. The r theory from which eq 2 is derived casts $\stackrel{\mathsf{r}}{F_{\text{Onsager}}}$ as the total electrostatic field experienced by the solute due to the environment. Thus in principle the data for a probe in simple solvents can serve as a reference to allow the total field the probe experiences in a biomolecular environment to be determined from IR measurements. Because the validity of such an approach would be limited by the accuracy of the calculated solvent fields that serve as the reference, this prospect provides a motivation for more detailed computational studies of the solvation of nitrile-containing compounds, such as explicit solvent QM/MM simulations, which can determine the solvent reaction field with greater accuracy. To date such studies have been focused mostly on water^18-20,33, but in light of our results, it would be interesting to calculate the electric fields in a range of aprotic solvents of different polarity and compare them to experimental IR measurements. In particular, solvents with lower dielectric constants more similar to hydrophobic protein interiors might provide the most suitable benchmarks for probes in proteins. Such calculations will also illuminate the cases in which simple models perform poorly at predicting the solvent field, yielding a deeper appreciation for the role of local solvation.