Real-time tracking of liver motion and deformation using a flexible needle

Abstract

Purpose

A real-time 3D image guidance system is needed to facilitate treatment of liver masses using radiofrequency ablation, for example. This study investigates the feasibility and accuracy of using an electromagnetically tracked flexible needle inserted into the liver to track liver motion and deformation.

Methods

This proof-of-principle study was conducted both ex vivo and in vivo with a CT scanner taking the place of an electromagnetic tracking system as the spatial tracker. Deformations of excised livers were artificially created by altering the shape of the stage on which the excised livers rested. Free breathing or controlled ventilation created deformations of live swine livers. The positions of the needle and test targets were determined through CT scans. The shape of the needle was reconstructed using data simulating multiple embedded electromagnetic sensors. Displacement of liver tissues in the vicinity of the needle was derived from the change in the reconstructed shape of the needle.

Results

The needle shape was successfully reconstructed with tracking information of two on-needle points. Within 30 mm of the needle, the registration error of implanted test targets was 2.4 ± 1.0 mm ex vivo and 2.8 ± 1.5 mm in vivo.

Conclusion

A practical approach was developed to measure the motion and deformation of the liver in real time within a region of interest. The approach relies on redesigning the often-used seeker needle to include embedded electromagnetic tracking sensors. With the nonrigid motion and deformation information of the tracked needle, a single- or multimodality 3D image of the intraprocedural liver, now clinically obtained with some delay, can be updated continuously to monitor intraprocedural changes in hepatic anatomy. This capability may be useful in radiofrequency ablation and other percutaneous ablative procedures.

Introduction

Radiofrequency ablation (RFA) is a percutaneous, minimally invasive, and image-guided alternative to surgical resection for isolated hepatic tumors [1–3]. The most common method for guiding RF applicators to target tumors uses two-dimensional (2D) imaging (ultrasound, fluoroscopy, or axial 2D images from computed tomography [CT]). However, three-dimensional (3D) imaging modalities such as volumetric CT may greatly enhance needle placement by providing a detailed 3D anatomic road map [4,5].

Although CT scanning itself is nearly instantaneous on most recent multislice scanners, delayed and slow reconstruction (2–22 s for 30 slices on a 64-slice scanner [6]) prevents the resulting images from providing immediate feedback on intraprocedural anatomy. An emerging trend of augmenting intraprocedural CT with preprocedural images (e.g., contrast CT, contrast magnetic resonance [MR] imaging, and positron emission tomography [PET]) improves intraprocedural visualization and targeting of the tumor [7–11]; however, the additional computation needed for 3D image registration (often nonrigid) further delays the availability of images for intraprocedural image guidance. Registration of intraprocedural 3D CT with preprocedural contrast-enhanced MR images of the liver has been reported to take 28–52 min [12,13]) because of the computationally intensive task of modeling and recovering complex nonrigid deformation of the liver. Fast 3D nonrigid medical image registration implementations [14–16], including our team’s hardware-accelerated solution [7], which take 1–4 min, depending on image size, similarity metric, deformation model, and optimization algorithm, shorten long computation times, but are not instantaneous. Thus, the latency problem persists.

A consequence of computationally intensive image reconstruction and image registration steps is that the resulting CT, with or without preprocedural image augmentation, depicts the past liver anatomy, which continuously moves and deforms because of respiration and other physiological processes. If the motion and deformation of the liver during this latency period (and beyond) can be followed in real time, the information can be used to warp the latest albeit minutes-old single- or multimodality 3D images such that they match the current intraprocedural anatomy. Because current technology does not allow 3D image reconstruction and 3D image registration to be instantaneous, only a nonimaging solution appears suited to provide the desired real-time liver motion and deformation information now and in the foreseeable future.

In this article, the initial technical feasibility of a novel tissue-tracking solution is presented. The solution builds on the current practice of placing a seeker needle in the vicinity of the target of interest during some tumor ablation procedures [17]. With existing electromagnetic (EM) tracking technology, it is possible to redesign the seeker needle such that its movement and flexion can be tracked in real time. Our solution assumes that the movement and flexion of a single seeker needle can be a proxy for the local tissue motion and deformaton. In other words, the movement and deformation of the tissues surrounding the needle can be estimated from those of the needle. Moreover, the needle tracking data can be used to warp and thus update the latest CT scan, whether presented separately or fused with a preprocedural scan.

Indeed the most commonly used motion compensation strategy during an RFA procedure is respiratory gating using breath holding, in which the RF applicator is advanced into the tissue during the same respiratory phase for which the latest intraprocedural CT was acquired [18]. This stop-and-go approach is inefficient, time consuming, and varies with the level of sedation or anesthesia. Moreover, its accuracy depends heavily on patient compliance and uniformity of respiration from one cycle to the next. An alternative to breath holding is to identify the desired phase automatically during free breathing. Levy et al. [19,20] have reported an EM tracking–based guidance system that uses a tracked internal fiducial (tip of the puncture needle) to identify the end-expiratory pause during resting respiration, the desired phase for the chosen liver intervention. This information was used to advance a puncture needle into the liver percutaneously. An added advantage of having EM tracking is that the puncture needle was tracked continuously in real time and a graphic of it was superimposed on the static CT to provide continuous visual feedback during needle advancement.

Other investigators [21–23] have tested the feasibility of using multiple tracked external skin fiducials to characterize internal organ motion and deformation over a respiratory cycle. Wong et al. [21] specifically tested tracking a fixed location in the liver parenchyma by tracking EM-tracked skin sensors. These methods rely on fixed correlation of internal and external motions during a respiratory cycle, but the accuracy of such correlation can be suspect. In many radiotherapy applications, point fiducials are permanently implanted directly into the tumor [24]. This radiotherapy approach does not extend to liver interventions such as RFA, where the non-rigid motion of the liver tissues between the skin entry point and the targeted tumor is of as much interest as the motion of the target itself. Therefore, permanent implantation of fiducials is not an acceptable solution in RFA [25].

Motion tracking based on multiple internal fiducials may be potentially more accurate than using skin markers alone. One of the earliest methods in this category by Bricault et al. [26] used a 22-gauge needle (called an “anchor needle) to monitor liver motion in real time. Although it was proposed that the anchor needle could be electromagnetically tracked, its internal tip was estimated from its base outside the tissue assuming a rigid needle geometry. The resulting data allowed relatively simple one-point registration. The use of multiple needles for liver motion compensation has been presented by Krücker et al. [27]. In a swine model, the internal tips of the several fiducial needles that were electromagnetically tracked provided the necessary data for multipoint registration. By treating one of the needle tips as the test target, the investigators determined the accuracy of their technique. Maier-Hein et al. [28,29] have reported liver motion compensation based both on inserted fiducial needles and skin markers. Both needles and skin markers were optically tracked. Skin markers and five equally spaced, inside-the-tissue points along each rigid needle constituted control points for registration. The technique was tested on a liver motion simulator as well as in the swine. Orozco et al. [30] considered liver deformation by tracking the motion of an inserted guidewire. Although the investigators identified the shape of the guidewire through imaging and did not discuss real-time implementation, they proved the value of tracking curvature as a surrogate for liver deformation.

In this article, we present a flexible needle-based technique to track liver motion and its complex deformation. Whereas previously reported techniques may employ more than one needle to model nonrigid liver deformation, our technique takes advantage of the information provided by the bending of a single needle to recover nonrigid deformation. We discuss the possible design of a tracked bendable needle using EM tracking (see Appendix A) and a practical way to apply the concept in the clinic. In conjunction with EM tracking, the technique can lead to a real-time image guidance system. Finally, we test and report the accuracy of the technique ex vivo and in vivo and discuss its clinical implications.

Materials and methods

Overview

This proof-of-principle study was conducted both ex vivo and in vivo with a CT scanner taking the place of an EM tracking system as the spatial tracker. A commercially available 18-gauge needle was inserted into excised bovine livers or live swine livers. For excised livers, deformations of the liver and the needle were created by placing the liver on a deformable stage made of saline bags. Deformation of live swine livers were created by free breathing or controlled ventilation. The CT scans visualized the entire length of the needle irrespective of how it was deformed and provided its reference shape for validation purposes.

The first goal was to demonstrate that the needle shape can be reconstructed, with a great degree of accuracy, using the type of data one would obtain if the needle was electromagnetically tracked through several embedded EM sensors. By using a subset of information (i.e., geometric constraints such as locations and slopes) on the known needle shape from CT, we mimicked the data that an electromagnetically tracked needle would generate. We subsequently integrated and reconstructed needle shapes from these data and compared them to the known CT-provided shapes. This strategy helped us determine the optimal configuration of the tracked needle as well as quantify the accuracy of reconstructing needle shape from sparse geometric data.

Having demonstrated the ability to reconstruct needle shapes accurately from simulated EM tracking data, the second goal was to investigate how accurately the displacements of the tissues surrounding the needle can be tracked. For this, the assumption was made that the displacement of the needle and that of the surrounding tissues was correlated. This meant that if the needle point closest to a point target in the tissue moved by x mm when the liver deformed, the point target also moved by x mm in the same direction. A number of CT-visible test targets implanted in the liver served as point targets for this part of the experiments. CT scans taken after each deformation showed the test targets in relation to the needle, which allowed us to: (1) test the fundamental premise that liver tissues in the vicinity of the needle move with the needle; and (2) evaluate the accuracy with which tissues surrounding the needle can be tracked. Overall, these methods led to the recommended design of the electromagnetically tracked needle and the expected accuracy of tissue tracking using this concept.

Experiment setup

Figure 1 shows the ex vivo and in vivo experimental setups. In the ex vivo experiment, an excised bovine liver was placed on a stage created by placing three 1,000-ml saline bags side by side. A 20-cm-long 18-gauge needle was inserted into the liver with approximately two-thirds of its length inside the liver. The needle was straight initially, and deformations of the liver and the inserted needle were created by altering the volumes of the saline bags (i.e., draining the saline) placed under the liver. Different deformations were created by different combinations of saline bag volumes (four deformations in the first liver and nine deformations in the second). After the initial needle placement and after each deformation, a thin-slice helical CT image was acquired with a 64-slice scanner (Brilliance 64, Philips Healthcare). CT slices were reconstructed to a 512×512 matrix with voxel dimensions of 0.72×0.72×0.67 mm. The scan parameters were the following:140 kV tube voltage, 394 mA tube current, and 0.75 pitch.

Fig. 1.

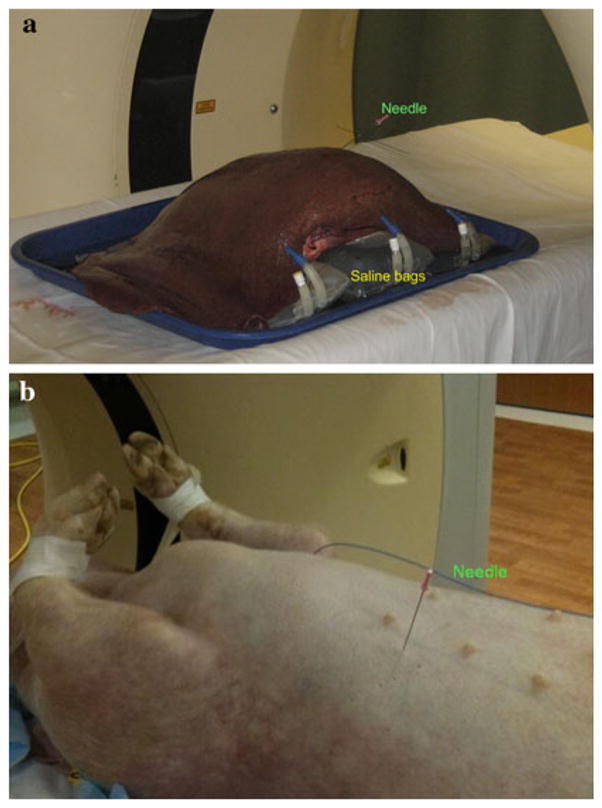
a Ex vivo experimental setup: a bovine liver was placed on three saline bags, with alterations in volumes simulating deformations in the liver and inserted needle. b In vivo experimental setup: a live swine with a needle inserted into its liver

The in vivo experiment was conducted on two live swine. In the first experiment, the swine was allowed to breathe freely and 50 successive CT scans were acquired in the axial mode with no couch movement. Each scan had a scan length of 4 cm and a duration of 36 s. Thirty-two CT slices making up a scan were reconstructed to a 512 × 512 matrix each with voxel dimensions of 0.59 × 0.59 × 1.25 mm. The scan parameters were 120 kV tube voltage and 500 mA tube current. In this experiment, the cranio–caudal excursion of the implanted test targets was used to identify CT scans corresponding to expiratory and inspiratory phases of respiration. One expiration CT scan and four different inspiration CT scans were included for data analysis. In the second experiment, the swine was under volume-controlled mechanical ventilation. Two helical CT scans with roughly 65 cm scan length were acquired with and without ventilation. CT slices were reconstructed to a 512 × 512 matrix with voxel dimensions of 0.72 × 0.72 × 1 mm. The scan parameters were 120 kV tube voltage, 178 mA tube current, and 0.75 pitch.

To evaluate the accuracy of the liver tissue tracking concept, test targets (2- to 4- mm pieces of a 22-gauge nickel titanium alloy guidewire) were implanted into the liver parenchyma. Ten and eight targets were used for ex vivo and in vivo experiments, respectively. Because of the limited CT scan length (4 cm) in the first in vivo experiment, only four targets were common to all CT scans and could be used for data analysis. These test targets were approximately uniformly distributed both longitudinally and transversely with respect to the needle (see Fig. 2). The test targets were identified in each CT scan using a commercial software (Amira 4.0, Visage Imaging) to determine their 3D coordinates.

Fig. 2.

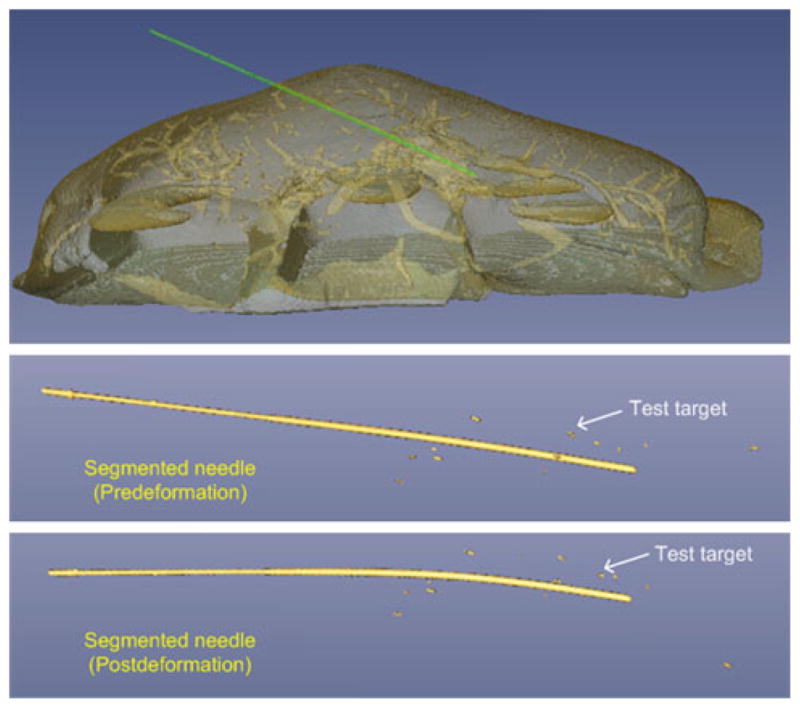
Volume rendering of CT image showing segmented needle and test targets

Reference needle shape

We refer to the shape of the needle as viewed in CT as the “reference needle shape.” This shape served as the ground truth against which we compared and validated reconstructed needle shapes. The first step in constructing the reference needle shape was to segment the needle in the CT scans. The high-intensity contrast between the needle and the liver tissues allowed simple thresholding (threshold CT number of 2000) to accomplish this segmentation task. The segmented needle was then skeletonized in Matlab with the final thickness set to 1 voxel.

The skeletonized needle was continuous but its discrete representation did not permit computing local tangents and normals conveniently and accurately. For this purpose, we converted the skeletonized needle to a parametric curve represented as a piecewise cubic Hermite polynomial [31]. A piecewise cubic Hermite polynomial is fit to four or more points, called control points. In the present case, the control points were the two endpoints—needle tip inside the liver and the skin entry point—and a varying number (2–6) of intermediate points sampled along the skeleton of the needle. The parametric curve, in essence, was a smoothed version of the skeleton, and to ensure that it replicated the skeleton closely, we computed the average separation between the original and the smoothed needle skeleton for the case with maximum deformation of the liver (see Table 1). The average separation reduced with the increasing number of control points initially and then stabilized to 0.7 mm. This suggested that an eight-point smoothing was sufficient in our experiments and was used throughout the rest of the experiments.

Table 1.

Mean separation (mm) between the skeletonized reference needle, before and after smoothing with parametric curve fitting

Number of control points	Mean separation (mm)
4	1.6
5	1.3
6	1.2
7	1.0
8	1.0

Reconstruction of tracked needle

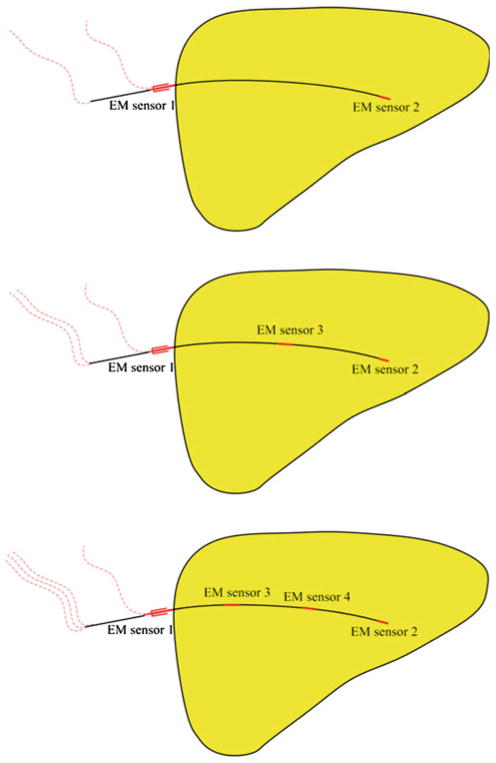
In actual EM tracking, only a handful of needle points where EM sensors would be located (rather than the whole needle) can be directly tracked. In the present work, we considered four practical tracked needle designs: needles with two, three, four, and five EM sensors (see Fig. 3). The EM sensors were assumed to be 5-degrees-of-freedom (5-DOF) sensors capable of reporting their 3D location and 3D orientation (minus rotation about sensor/needle axis). Each needle design assumed one sensor at the needle tip and another at the skin entry point. The three-sensor design assumed a third sensor halfway between the needle tip and the skin entry point. The four-sensor and five-sensor designs likewise assumed equally spaced intermediately positioned sensors. The location and orientation data to be generated by these sensors were mimicked from the parametric form of the reference needle shape. The parametric form, it should be noted, can provide location and slope at any point on the curve it represents. A set of location and orientation data obtained from the parametric curve was termed the “simulated EM sensor data.”

Fig. 3.

Alternative designs of a tracked needle with two, three, and four embedded 5-DOF EM sensors (shown in red) investigated in this study. The five-sensor configuration is not shown

With the simulated EM sensor data, we reconstructed the needle again. The shape of the needle was represented as a cubic Hermite interpolating polynomial that requires the knowledge of the location and tangent at the two endpoints. A two-sensor needle offered exactly the data a cubic Hermite polynomial requires (see Fig. 4). Three-, four-, and five-sensor needle designs offered location and tangent data pairs at more than two endpoints, and therefore, were represented as piecewise cubic Hermite interpolating polynomials.

Fig. 4.

Modeling of a needle as a cubic Hermite polynomial, which is constructed from the location and tangent data at two end-points. The schematic represents the case of a two-sensor needle

Validation of needle reconstruction

The tracked needle was compared with the ground truth, the reference needle. Average separations between the two, for all four needle designs, are presented in Table 2. The numbers demonstrate the feasibility of obtaining the shape of the whole needle by tracking a handful of points on the needle. Only a modest improvement in accuracy with three and more sensors suggested that the two-sensor design was adequate in most practical situations, at least for the needle gauge simulated and tested. All tissue tracking experiments described later were thus conducted assuming a two-sensor tracked needle.

Table 2.

Mean separation (mm) between the “tracked” needle and reference needle for various needle designs

Number of sensors	Mean separation (mm)
2	1.4
3	1.2
4	1.1
5	1.1

For the aforementioned curve fitting, we assumed that any bending of the needle resulting from the user-introduced gross deformations of the liver was confined to a plane. This assumption of coplanarity was verified by computing the Cayley–Menger determinant [32], which represents the volume of a generalized simplex formed from a point list (see Appendix B). In this study, we determined the bounding tetrahedron of the maximally deformed needle. The negligible volume (67 mm³ ex vivo and 97 mm³ in vivo) and largest height (<0.3 mm) of this bounding tetrahedron confirmed the coplanarity of the deformed needle.

Tissue tracking

The displacement of liver tissues in the vicinity of the needle was obtained by assuming that it moved in concert with the needle. This was a reasonable assumption, considering that the liver is locally incompressible because of high water content. Under this assumption, the deformation of liver in the vicinity of the needle could be viewed as a bent cylinder, with the needle describing the axis. To verify the assumption that the needle and tissues move together, the distances between the needle and test targets were compared before and after the case of extreme deformation in the two excised liver experiments.

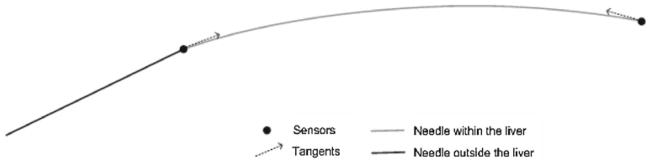
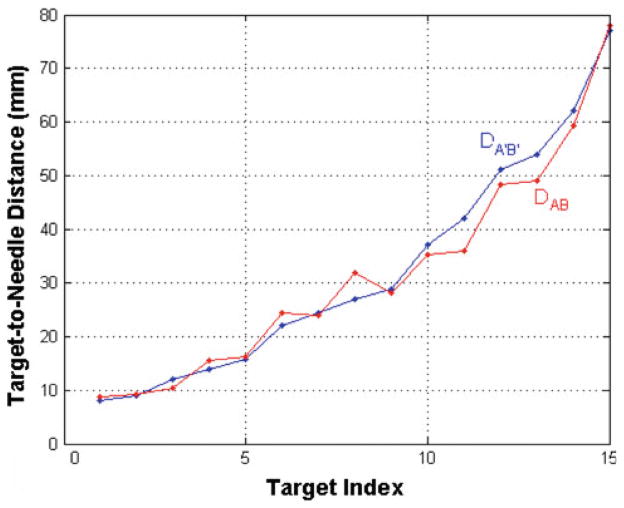
Before any deformation, a specific test target B (location P_B) and the needle point A (location P_A) closest to it were found in the CT image. D _{A B} represented the distance between the locations P _A and P_B. P _A′ and P_B′ denoted the postdeformation locations of points A and B, as seen in CT, respectively, and D _{A′ B′} the new distance between them. D _{A B} and D _{A′ B′} were calculated for every test target and are plotted in Fig. 5. (We refer the reader to the schematic in Fig. 6 for variables introduced in this paragraph and to follow the discussion pictorially.)

Fig. 5.

Distance values between test targets and the needle before (D_AB, red dots) and after (D_A′B′, blue dots) deformation. Any separation between red and blue dots indicates a change in the target–needle distance before and after deformation

Fig. 6.

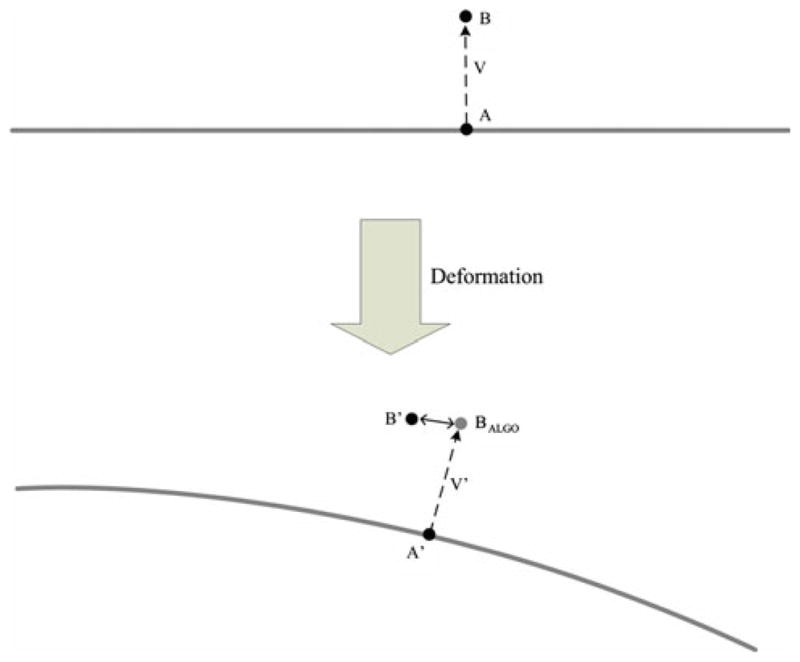
Localization of a tissue point B by tracking its nearest needle point A. The double-headed arrow indicates the localization error

To determine the algorithm-predicted location of test target B, we denoted the vector between points A and B in the predeformation image as V. V′ is the vector V postdeformation, and according to our assumption, vector V′ remains perpendicular to the needle. Therefore, the algorithm-predicted location of test target B is calculated as P_B-ALGO = P_A′ + V′. Ideally, PB-ALGO should overlap with the actual location P_B′; any disagreement is the localization error of the algorithm (Fig. 6).

Validation of tissue tracking

To evaluate the accuracy of needle-based tissue tracking, we compared the true locations of test targets (as seen in CT) with their predicted locations as given by the tracking algorithm. The average error, termed target registration error (TRE), as a function of distance from the needle, allowed us to test the accuracy of our approach as well as establish its limits.

Results

Results from two excised bovine livers and two live swine livers show that the localization of targets was greatly improved by fine needle tracking. The test targets in ex vivo experiments and in vivo experiments were on average displaced by 24.2 ± 7.4 mm and 28.2 ± 2.6 mm, respectively. The TRE following needle tracking were 4.1 ± 3.1 mm and 3.4 ± 1.9 mm, respectively. An improvement in localization was seen for every test target. The in vivo results show that for the eight test targets within the 30-mm neighborhood of the needle, the TRE was 2.8 ± 1.5 mm, and the largest displacement error was 4.5 mm, less than the commonly accepted 10-mm margin added to the tumor boundary in most ablative procedures in current practice [33,34].

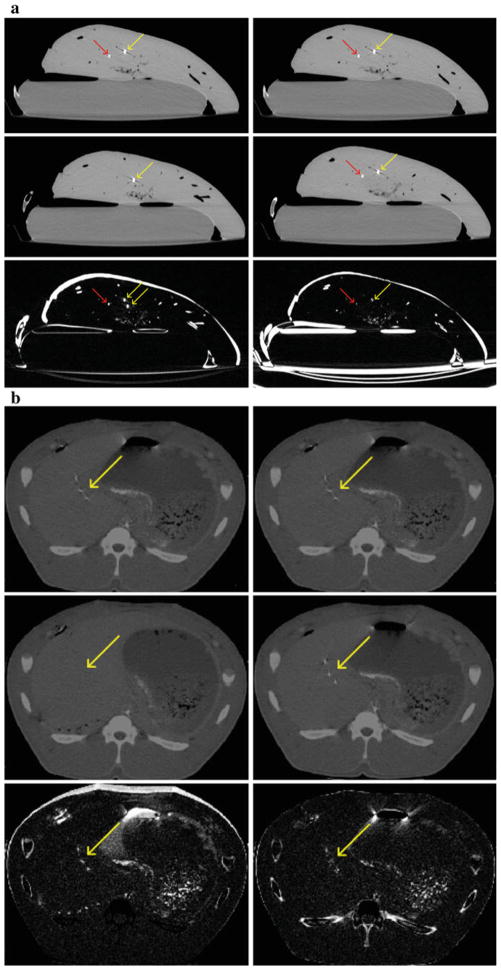
For qualitative evaluation of the results of ex vivo and in vivo experiments, we created difference images, which were subtraction of pre- and postdeformation CT images. When subtracted without any registration, misalignment of the tissues, the needle, and test targets due to the deformation can be seen (see Fig. 7). After correcting for the deformation by needle tracking, misalignment in the difference image was reduced, which confirmed proper functioning of the algorithm.

Fig. 7.

Ex vivo results. a Top row: identical sections of predeformation CT. Middle row: same section of postdeformation CT without (left) and with (right) registration per needle tracking. Bottom row: difference image between the two CT sections in each column. Misregistration near the needle is reduced after recovering the deformation, which means improved spatial alignment. Red arrows: needle positions. Yellow arrows: target positions. In vivo results. b Top row: identical sections of predeformation CT. Middle row: same section of postdeformation CT without (left) and with (right) registration per needle tracking. Bottom row: difference image between the two CT sections in each column. Misregistration is reduced after recovering the deformation, which means improved spatial alignment. Yellow arrows: target positions

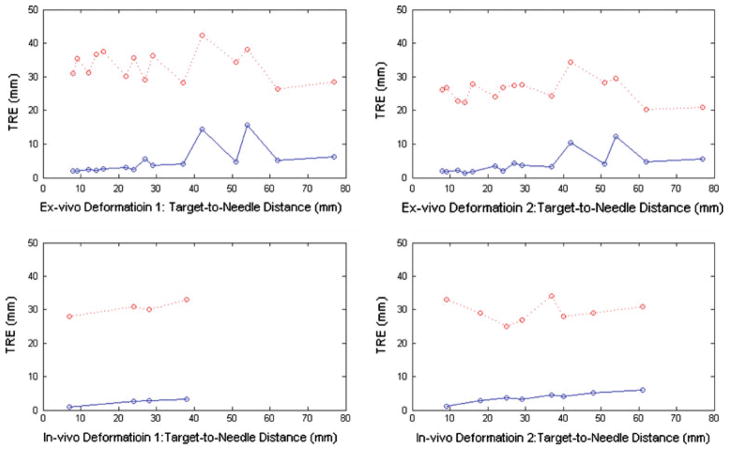
For quantitative comparison, the TRE of test targets is presented in Table 3 (ex vivo data) and Table 4 (in vivo data). For a specific test target, the TRE was calculated as the displacement error averaged over all deformations. The TRE was categorized by the target-to-needle distance (<10, <30, <50 mm, and all). The target-to-needle distance was defined as the shortest distance between a test target and the needle before any deformation. The TRE against target-to-needle distance is also plotted for four deformations (two ex vivo and two in vivo) in Fig. 8. In both ex vivo and in vivo experiments, an improvement in the localization of the test targets can be seen. Although not shown, curves for other deformations followed the same trend.

Table 3.

Target registration error before and after needle-based tissue tracking (ex vivo data)

Test targets	Before correction (mm)	After correction with needle tracking (mm)
Marker-needle distance <10 mm (2 targets)	22.9 ± 7.0	1.5 ± 0.5
Marker-needle distance <30 mm (9 targets)	25.5 ± 7.6	2.4 ± 1.0
Marker-needle distance <50 mm (12 targets)	24.7 ± 7.7	3.6 ± 2.5
Marker-needle distance <80 mm (All 15 targets)	24.2 ± 7.4	4.1 ± 3.1

Table 4.

Target registration error before and after needle-based tissue tracking (in vivo data)

Test targets	Before correction (mm)	After correction with needle tracking (mm)
Marker-needle distance <10 mm (2 targets)	29.4 ± 2.0	1.0 ± 0.2
Marker-needle distance <30 mm (8 targets)	27.1 ± 2.2	2.8 ± 1.5
Marker-needle distance <50 mm (All 12 targets)	28.2 ± 2.6	3.4 ± 1.9

Fig. 8.

Average test target localization errors for four deformations before (red dots) and after (blue dots) needle tracking. Top row has ex vivo deformations, whereas the bottom row has in vivo deformations

Discussion

Real-time 3D imaging that can permit real-time tracking of target anatomy is desirable in many image-guided interventions. Burdened by lengthy reconstruction time, currently available 3D imaging modalities are too slow and thus could only be used intermittently rather than continuously during a procedure. A novel concept is presented here to: (1) track tissue motion and deformation in real time in a local region using a thin, flexible needle; and (2) use the needle tracking data to appropriately warp the latest intraoperative scan (a 3D CT here) to reflect the anatomic changes from the time of the scan. When this warping process is repeated several times per second, it amounts to imaging the anatomy of interest in real time.

The proposed concept is to convert an often-used seeker needle into an electromagnetically tracked needle. The shape of the inserted needle is reconstructed using two EM sensors located on the two ends of the part of the needle into the tissue. The shape data, in turn, are used to predict the non-rigid motion and deformation of liver tissues in the vicinity of the needle. Thus, tracking a pair of EM sensors is sufficient to track the motion and deformation of a volume of tissues. This method does not directly provide images of liver; instead, the real-time tissue motion/deformation information can be used to warp available 3D images without computation latency. Thus, the slow and temporarily discrete 3D images can be extrapolated to permit live 3D visualization.

The need for tissue tracking arises in many situations. In radiotherapy applications, implanted fiducial markers have been used for tumor tracking. In the specific instance of the CyberKnife system [35] for image-guided radiation therapy, three to five radiopaque gold fiducial markers are implanted in or around the tumor to enable their tracking. However, in interventions such as RFA of liver lesions, it is not practical to permanently implant fiducial markers into the tumor. Unlike radiotherapy, the purpose of image guidance in RFA is to help interventional radiologists advance the RF applicator to the targeted tumors. Therefore, not only the information on the location of the tumor but that of its surrounding tissues is needed so that a true 3D anatomical roadmap is available. This may be achieved with a very large number of point fiducials implanted throughout the organ, but such an approach would be impractical. Such information, however, is tremendously valuable, especially during the creation of a composite ablation, when sequential needle placement and repositioning must be performed. Currently, only minimal positional feedback and dynamic tissue deformation are available to an interventional radiologist.

Wong et al. [21] circumvented the problem of internal fiducials by tracking external markers, and working with animal livers showed that correlations exist between internal and external motions. Based on experimental data, the investigators successfully built functions to predict internal liver motion from that of external markers. However, relationships correlating motion of external markers to internal liver motion are expected to be multifactorial and variable with time and subject and, in general, not very reliable. As a result perhaps, the resulting prediction in the cranial–caudal direction achieved an accuracy of 1 mm, but correlations in the other two directions were weak.

Using internal fiducials is arguably a more accurate approach to predict liver motion and deformation, and to make fiducials retrievable, several tracked needle-based approaches wherein the needle tips act as internal markers have been suggested. The Bricault method [26] is an example of using an anchor needle for rigid-body registration. The movement of the tracked internal tip of the percutaneously placed anchor needle was applied to the whole liver, assuming it to be rigid, to recover the liver tissue motion between expiration and inspiration. This rigid registration model achieved an average accuracy (or residual error) of approximately 5.0 mm. As expected, a large nonnegligible residual nonrigid component is not accounted for by the simplistic rigid-body liver motion/deformation model. In a four-patient study, Rohlfing et al. [36] confirmed this observation and showed that the rigid-body model failed to recover up to 10- mm residual misalignment of anatomic landmarks in the liver parenchyma between expiration and inspiration.

Krücker et al. [27] modeled liver motion and deformation using multiple needles and reported a TRE of 6.4 mm. Through a mixed marker (one fiducial needle and four skin markers) approach, Maier-Hein et al. [28,29] reported TRE of 2.0 ± 0.9 mm during free breathing. For the same marker configuration, the maximum TRE, the TRE corresponding to registration of extreme phases, is approximately 4 mm. In our study, we studied registration only between the extreme respiratory phases and thus the TRE we report for the in vivo data compared favorably to the maximum TRE of the Maier-Hein studies.

Because of the nonrigid nature of liver tissue motion and deformation, nonrigid registration model was used in this study. Unlike prior works, we did not ignore needle bending but rather utilized it to obtain the nonrigid motion/deformation of the tissues surrounding the needle. Parametric modeling of the needle shape was used to perform curve matching-based nonrigid registration. To minimize invasiveness and to develop a clinically viable method, we focused on the use of a single needle alone. Using test fiducials, we confirmed the feasibility and accuracy of tracking liver tissues (test target) in the vicinity of an inserted fine needle in excised bovine livers and live swine livers.

A <2.8-mm tracking error in vivo and up to 30 mm from the needle suggests that any target within this range can be tracked with acceptable accuracy. The accuracy of our method is comparable to the accuracy of two most closely related methods reported by Krücker et al. and Maier-Hein et al. Like these methods, our technique can address computational latency issues currently encountered in providing imaging-based feedback during image-guided interventions. If we place a tracked needle in the vicinity of the targeted tumor, a static treatment-room CT can be updated according to the motion and flexion of the tracked needle. Thus, the CT image would be continuous and, most important, real time. If additional image processing such as nonrigid registration to overlay preprocedural images on intraprocedural images is introduced by an image guidance system, the system performance will benefit more from our needle tracking ability.

While TRE within 30 mm was found acceptable, it grew beyond 30 mm. However, the clinicians’ attempt to place the seeker needle as close to the targeted tumor as possible and most probably within 30 mm distance means our approach will maintain an acceptable accuracy when used clinically. Specifically, we expect this technique to help lesion targeting when the RF applicator has been advanced close to the aimed lesion rather than to be used to determine entry site of the applicator. Therefore, we focused on investigating the performance within the vicinity of the needle. As performed by Maier-Hein et al. [29], it is technically feasible to add several external skin markers to our needle-based technique, which may further improve the targeting accuracy of our method.

In this feasibility study, we mimicked EM tracking using CT and, therefore, the often nonuniform tracking error of an EM system did not figure in the TRE measurements. The reported position and orientation accuracies of a commercially available EM tracking system (Aurora, Northern Digital, Inc.) are 0.3 mm and 0.9 degree, respectively (Appendix A). Additional errors from numerous clinical devices may be introduced in an interventional radiology suite. Yaniv et al. have found 0.76 mm and 1.07 degree as mean tracking errors of the Aurora system located in an interventional radiology suite [37]. In light of these tracking errors, our reported TRE numbers may slightly overestimate the accuracy of a fully engineered needle tracking system operating in a clinical environment.

Eighteen-gauge fine needles are commonly used in interventional radiology procedures and are sufficiently flexible for the technique we have proposed. Our attempt of using a thinner 22-gauge needle also achieved a similar accuracy. Thus, our technique shows the compatibility with current clinical procedure setup and the ability of maintaining the minimally invasive nature of these procedures. The 0.55 mm diameter of the commercially available 5-DOF EM sensors currently allows fabrication of needles as thin as 24 gauge. In this study, we also investigated the performance of needle tracking with different numbers of EM sensors. For the deformations created in this study, with magnitudes comparable to those in actual respiration, the two-sensor design was sufficient for tracking the 18-gauge needle shape. The two-sensor design will also minimize the cost and allow simultaneous tracking of a greater number of instruments or targets in the interventional suite.

In summary, the proposed solution shows the feasibility of obtaining nonrigid motion and deformation of liver tissues by tracking the movement and bending of a single inserted fine needle. This technique is clinically viable and potentially applicable to medical interventions that require real-time knowledge of internal anatomy within a localized region of interest.

Appendix

A. EM tracking

EM tracking is performed in real time and is free of the line-of-sight constraints of optical tracking and therefore suitable for the current application. The Aurora Electromagnetic Measurement System (Northern Digital, Inc.) is an example of a commercially available EM tracking system. It can simultaneously track eight 5-DOF sensors (diameter 0.55 mm × length 8 mm). The manufacturer-provided position and orientation accuracies are 0.3 mm and 0.9 degree, respectively.

B. Cayley–Menger determinant

The Cayley–Menger determinant provides the square of the volume enclosed by a point set. The Cayley–Menger determinant for a tetrahedron is as follows,

$$V^2=det\left[\begin{array}{ccccc}0& d{(\text{AB})}^2& d{(\text{AC})}^2& d{(\text{AD})}^2& 1\\ d{(\text{AB})}^2& 0& d{(\text{BC})}^2& d{(\text{BD})}^2& 1\\ d{(\text{AC})}^2& d{(\text{BC})}^2& 0& d{(\text{CD})}^2& 1\\ d{(\text{AD})}^2& d{(\text{BD})}^2& d{(\text{CD})}^2& 0& 1\\ 1& 1& 1& 1& 0\end{array}\right]/288,$$

where V is the volume of the tetrahedron; d(.) is the distance between two vertices; and A, B, C, and D are the four vertices.