Abstract
This Perspective is focused on amide groups of peptides interacting with water. The 2D IR spectroscopy has already enabled structural aspects of the peptide backbone to be determined through its ability to measure the coupling between different amide-I modes. Here we describe why nonlinear IR is emerging as the method of choice to examine the fast components of the water dynamics near peptides and how isotopically edited peptide links can be used to probe the local water at a residue level in proteins. This type of research necessarily involves an intimate mix of theory and experiment. The description of the results is underpinned by relatively well established quantum-statistical theories that describe the important manifestations of peptide vibrational frequency fluctuations.
Introduction
Water makes essential contributions to the equilibrium structures and stability of biomolecules. However the role of the dynamic character of water in association with macromolecules is not so well documented. The structure and motions of water near proteins can be quite different from those of liquid water, and the function of the protein might often require that the water molecules are in rapid motion, interacting with the protein backbone and side chains as well as with one another.
The molecular level descriptions of biological assemblies where mobile water or weak hydrogen bonds participate in their function, are in need of experimental refinement. Because water has an essential role in stabilizing, optimizing the dynamics and functionalizing many living systems, a molecular level description of its structural-dynamics in association with proteins and peptides will signal key aspects of cellular processes [1, 2]. Examples are proton or ion channels or water transport channels like gramicidin or aquaporin where the water structures are determinants of the function of the channels[3, 4]. The water networks at ambient temperatures are intimately related to the disposition of peptide backbone and its potentially hydrogen bonding side chains. Another example concerns the enormously important and hydrophobic amyloid structures where we recently found individual water molecules trapped in the fibrils[5] which suggested water may somehow be involved in fibril formation. The answers to how mobile these water structures are, or how they support protons, other ions or even how these structures are how they are modified by the binding of drugs, remain as significant challenges for physical chemistry and chemical physics.
The dynamic effects of water structures in protein systems have been accessed by many different types of experiments[6]. These include incoherent quasi-elastic neutron scattering[7], dielectric relaxation, magnetic resonance dispersion and other NMR methods, and time resolved fluorescence[8]. Fluorescence Stokes shift dynamics of selected Trp residues [9–11] or other probes[12] have time resolution appropriate to tracking water dynamics. An ongoing theoretical challenge is to relate these time correlations of the fluorescence energy gap fluctuations with specific structures. Molecular dynamics (MD) simulations predict how to decompose dynamical frequency responses into contributions from water, backbone fluctuations, polar groups of biomolecules and so-on. Yet theories have not always agreed[12–15] on the behavior of water at biological interfaces. Although NMR [16–18] provides equilibrium parameters and invaluable structural information, even the nuclear Overhauser effects and dispersion NMR[19] average over the populations that are changing on the sub-50 ps time scale due to dynamic exchange of water H-bond making and breaking. So there is a need for nonperturbative methods having high structural sensitivity but with time resolution more appropriate to ultrafast water motions.
It is natural to turn to vibrational spectroscopy for further knowledge of the dynamics of protein associated water. We now know that the nonlinear method of two dimensional infrared spectroscopy (2D IR) allows visualization of the dynamical responses of water associated with the amide units of proteins and peptides. The situation is illustrated in Figure 1. The optimum experiments involve 2D IR isotopic replacement mapping of the time dependence of amide mode frequencies caused by water distributed along the protein backbone. The main question addressed in this Perspective is how this spectrum, which is associated with rapidly interconverting solvent structures, be accessed and interpreted. It will be seen that the 2D IR approach allows associated identification water with unprecedented spatial precision. The 2D IR isotope mapping of the time dependence of frequency variations of amide modes caused by water distributed along the protein backbone is a powerful residue sensitive approach. The experiments require ultrafast 2D IR methods that can directly access the vibrational modes of the peptide groups and measure the spectral densities related to interacting water structures. It will be seen that these densities show water structures undergoing exchange around single residues of a peptide on the few ps time scale at chemical bond scale spatial resolution. [20–22] and they measure the equilibrium hydrogen-bond exchange kinetics in a non-perturbative manner [5, 22–27]. The uniqueness and power of 2D IR exchange methods in clarifying hydrogen bond dynamics have been highlighted in a recent PNAS Commentary[28].
Figure 1.
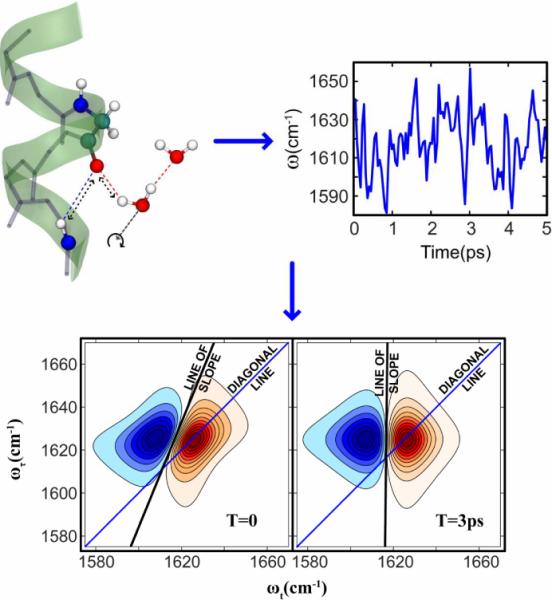
A peptide's perspective of water dynamics: the motions of water nearby to an amide cause the amide vibrational frequency to fluctuate. The time autocorrelation function of these fluctuations (the FFCF) is manifested in the 2D spectra as changes of spectral shape with the waiting time T. The spectral shape change can be quantified by measuring the slope of the 2D contours as a function of T.
The experiments and theories of nonlinear infrared responses are both needed to reveal how water interacts with peptides and proteins. Conventional infrared spectroscopy is very informative on the heterogeneity of water structures but much less clear on the dynamics within the distribution of structures that is exposed by 2D IR spectroscopy. The results of the many experiments on liquid water and its isotopic variants which were recently reviewed[29] have illustrated the advantages of 2D IR in bringing out ultrafast structure changes. However the present perspective is focused on amide groups of peptides interacting with water. Nonlinear spectroscopy has enabled structural aspects of the peptide backbone to be obtained through its ability to measure the coupling between different amide-I modes. The Perspective will describe why nonlinear IR is emerging as the method of choice to examine the fast components of the water dynamics near peptides and how isotopically edited peptide links can be used to probe the local water. This type of research necessarily involves an intimate mix of theory and experiment. It is underpinned by relatively well established quantum-statistical theory that describe the important manifestations of peptide vibrational frequency fluctuations. However experiments are very much needed to test the theories of optical nonlinear responses. Most theoretical approaches that are attempting to provide quantitative explanations of nonlinear experiments, incorporate to one extent or another molecular dynamics simulations and approximate quantum computations that themselves need tested for their applicability in the prediction of spectral properties. The significant effort needed in this field is justified by the essential roles of microscopic properties of the peptide-water structures in many biological dynamic processes. In our view, the relations between theory and experiment concerning this question should not be considered as adequate until accurate predictions become possible: after all, we know approximately what is occurring from elementary chemical principles.
Virtually all the infrared experiments involving the amide-I mode of biological systems use D2O as solvent: does this replacement alter the structures, functional capabilities and time scales of the protein dynamical processes especially since many of them involve modifications the hydrogen bonding? We will first discuss that issue.
Water versus deuterium oxide as a protein solvent
The amide-I mode of peptides and even more so their 13C=18O and 13C=16O isotopomers have infrared spectra that are strongly overlapped with the water bending mode absorption, which prevents their adequate characterization by current methods at the low peptide concentrations needed to avoid aggregation issues. The ultrafast nonlinear signals from water (H2O) and the few picosecond thermal grating evolution significantly complicate attempts to measure the hydrogen bond making and breaking portions of the infrared photon echo decays of amide-I modes. It is for these reasons that 2D IR spectra are generally carried out in D2O where the bending mode is considerably reduced in frequency and shifted from overlapping the amide-I modes. Since most infrared experiments on protein dynamics are done in D2O questions remain as to possible differences in the protein dynamics, the peptide frequency fluctuations and the “hydrogen bond” dynamics in these two solvents. In D2O the peptide group is deuterated and the amide vibrations arise mainly from motions of the -COND- atoms and the mode is usually referred to as amide-I'. The amide-I' mode is still mainly composed of the C=O stretching motion.
There are significant differences between H2O and D2O as solvents. It is known that D2O forms stronger hydrogen bonds than H2O[30] and that protein folding may occur at different rates in the two solvents[31]. The dynamics of the O-H stretching vibrational frequency distributions for HOD in D2O[32] are significantly different from those of the O-D stretch in H2O[33]. These differences are not due to differences between O-H and O-D properties but have been attributed to the different electric fields acting at a point chosen either in neat H2O or D2O. The high frequency dielectric constants of water and heavy water are very similar. The fast dielectric relaxation times, which constitute about 2% of the signals obtained from THz studies are ca. 250 fs for both liquids, with D2O being 7% slower than H2O, which is close to the variation predicted from the masses of H20 in D2O for free translational motion. For a water molecule H-bonded to a carbonyl oxygen (Oc), the rotational motion around the Oc---X bond is 21/2 times slower for X=D. This can give rise to differences in the ultrafast librational part of the vibrational frequency correlation function but does not directly result in hydrogen bond making or breaking. The Oc---X stretch has lower frequency for X=D for which the zero point energy is also smaller. Thus the barrier to hydrogen bond dissociation is larger for X=D so hydrogen bond dynamics is slowed[30, 31].Finally it is textbook knowledge that tunneling rates decrease dramatically as the mass of the displacing particles is increased. Thus exchanging H for D has long been a consistency test the presence of tunneling effects in kinetic processes. Exchanges of H for D also introduces changes in zero point energy and therefore influences heights of barriers in chemical processes. Klinman and coworkers have shown that nuclear tunneling is essential for many enzymatic reactions and that the tunneling processes influence substrate-protein binding interactions and protein dynamics[34].
In addition to kinetic isotope effects of deuterium replacement for hydrogen in water for which there are many examples, the question arises as to how exchanging H2O for D2O influences the structure-function relationship in proteins. One piece of information on this point comes from the M2 channel discussed in the next section. This channel conducts protons from higher pH solvent through the membrane into the aqueous interior of the virus. When the extracellular medium is exchanged to D2O the channel conducts deuterons with about 50% of the efficiency of protons from the H2O medium[35]. A precise cause of this difference is not yet known yet, because of all or some of the aforementioned results of H/D exchange yet it would be surprising if there were no isotope effect. There are many detailed questions regarding nonlinear responses of amides and proteins in light and heavy water that remain as unresolved challenges to chemical physics.
Linear vibrational spectra contain information about vibrational frequencies along with all the dynamical processes undergone by the mode so why is it almost impossible to extract this knowledge from them?
Why is 1D IR not useful for determining vibrational frequency dynamics ?
Certain properties are not readily extracted from linear spectra with confidence. For a single oscillator experiencing frequency fluctuations, δω, due to interactions with its medium, the vibrational frequency-frequency correlation function, C(T) =〈δω(T)δω(0)〉 is one of these properties[36]. To determine C(T) from a linear spectrum it is necessary to measure the curvature of the plot versus t of the logarithm of the real part of the Fourier transform of the observed spectrum! In the presence of noise and water background the fast parts of the response in the tails of the spectral lines are rendered arbitrary so only the very slow parts of C(T) might be estimable by this procedure. The problem is that the electric dipole correlations that determine the infrared spectrum in a dynamic inhomogeneous system are not sufficiently sensitive to the presence of slow fluctuations in the frequency around its mean value of ω10 In the present examples these slow fluctuations would be significantly influenced by the movements of water molecules close to the peptide link: at any instant some of these waters will be H-bonded to the C=O or N-H groups whereas some will only be H-bonded to other water molecules. The infrared band shape is not entirely dependent on these motions but arises from the fast fluctuations caused by rotations and librations of nearby water molecules, inhomogeneous frequency distributions from slowly interchanging water clusters and the population relaxation. Thus the times of experimental interest are often much slower that the characteristic time associated with the bandwidth of the vibrational transition. The difficulty in obtaining the correlation function or frequency correlation time τc from linear spectra is clear from the properties of a simple vibrational oscillator whose transition dipole μ01 is assumed to be constant across the infrared bandwidth. The infrared spectrum is the ensemble averaged version of the real part of the Fourier transform of a dipole correlation function, which we describe as the inhomogeneous linear response RL:
| (1) |
where the third and fourth terms in the exponent are the population relaxation and the rotational diffusion. The dephasing relaxation function g(t) is defined in terms of a real correlation function of the vibrational frequency fluctuations C(t) :
| (2) |
Various applications of the Kubo relaxation function[37], for which the frequency-frequency correlation function decays exponentially, have been discussed by Wiersma and coworkers[38] as well as more recently by Skinner and coworkers[39]. When it is supposed that C(t) = Δ2e−t/τc, which is intended to emulate the homogenization of an inhomogeneous distribution represented by Δ having correlation time τc, the spectrum is found to be sensitive to τc only when Δτc << 1 where the homogeneous dephasing contribution is Δ2τc. This quantity is readily measurable if T1 and D are known from other types of experiments, however the experiment is not capable of distinguishing between and Δ and τc in this limit. Furthermore, in the other limit where τc begins to be comparable or larger than the inverse inhomogeneous bandwidth 1/ Δ, the dephasing contribution to the spectrum becomes insensitive to the correlation time because then as t/τc gets smaller, g(t)≈(Δ2t2/2)(1 − t/3τc+..), approaches a Gaussian shape independent of τc. But this latter case is just the situation of interest here, where the objective is to record the part of the inhomogeneous distribution of frequencies that is relaxing more slowly than the experimental time scale set by the inverse of the whole frequency bandwidth. Similar arguments apply to cases where the correlation function is a combination of Kubo functions in which case even more parameters are need to define the correlation function. Therefore 1D spectroscopy, especially with its associated signal-to-noise and background characteristics present for molecules dissolved in aqueous media, is demonstrably useless for the purpose of measuring τc, a fact that has been demonstrated by experiments[40]. Furthermore, linear IR only involves one coherence evolution and there is no manipulation that allows the separate observation of inhomogeneous and homogeneous dephasing which both occur during the single time interval. Thus even the time analogue of IR absorption displays a functional that is a convolution of these two decay processes. The free decay of the one quantum amide-I mode vibrational coherence occurs on the time scale of ca. 1ps even in the absence of pure dephasing, because of the spontaneous vibrational energy relaxation. Fortunately 2D spectra manifest C(T) in a much more obvious way.
The 2D IR displays the frequency dynamics
The 2D spectroscopy is accomplished in the present work by applying three pulses in sequence and observing the third order generated field at specific time delays. In what follows, the underlying features of 2D IR are discussed with reference to just one of the many quantum mechanical response functions needed to compute the signals. The other terms and our method to incorporate them into a simulation are given in the Appendix or can be found in many other references on nonlinear spectroscopy[41–43] however the main points of our discussion on amide-transitions can be gleaned from the mathematical properties of just one of the responses. Always the sample is subject to three infrared pulses at times 0, τ and τ+T. The signal field is detected by a fourth pulse at time τ+T+t. Neglecting for now any consideration of the population and rotational diffusion and the net shifts of the mean frequency on vibrational excitation, one of the typical 2D photon echo responses of the same simple system that has the linear response of Equation 1, depends on two vibrational coherences that oscillate near to the vibrational frequency, one in the interval τ and the other in t, The two coherence intervals are separated by the waiting time T. The signal, which is normally detected at time t following the third pulse, is assumed to depend on the frequency fluctuations δω(t) about the mean fundamental frequency ω10:
| (3) |
Where the second step of equation 3 can be used if the fluctuations δω(t) have a Gaussian probability density, and the T dependence is contained in the factor δG1 (see Appendix). When δG1= 0 the spectral shapes from pure dephasing are identical along the ωτ and ωt axis and are T independent. For the case there is no incident field bandwidth limitation, the simulated 2D spectra S(ωτ, ωt; T) shown in this paper correspond the real part of a double Fourier transform along the coherence axes t and τ of a sum of responses, some of which are positive in the v=0→v=1 typified by R1, and others negative in the v=1→v=2 spectral regions. The motions of water nearby to an amide cause the amide vibrational frequency to fluctuate. (see Figure 1) The time autocorrelation function of these fluctuations (the FFCF) is manifested in the 2D spectra as changes of spectral shape with the waiting time T. The spectral shape change can be quantified by measuring the slope of the 2D contours as a function of T. The limit of large T where δG1 = 0 the evolution during the two coherence times become statistically independent. In this limit the 2D IR spectrum of Equation 3 can be seen to have circularly symmetric two dimensional contours centered on the diagonal at the vibrational frequency. Equation 3 is written in such a way as to clearly emphasize that the entanglement of the two coherence time intervals t and τ occurs in the δG1 factor. This discussion convinces us that, in contrast to 1D IR spectra, the time evolution of the 2D IR spectral shape is directly caused by the decay of the correlations in the frequency fluctuations, which is the desired experimental property.
In the case of amide modes the population relaxation is comparable with the time evolution of the frequency distribution. The T1 processes occur in each of the time intervals and as a result the 2D IR spectrum also broadens in the antidiagonal direction and 2D IR signals as a function of T are gradually diminished by the relaxation. As a practical guide for amide-I transitions, signals below ca. 1% of the maximum are difficult to detect, so the available time scale is less than ca. 10 ps.
Frequency-frequency correlation functions from 2D spectra
There is already a large amount of information associated with each 2D IR spectrum and the question keeps arising as to whether there are obvious, accurate measures of the shape of the 2D contour diagrams S(ωτ, ωt; T) that we know is extraordinarily sensitive to the correlation function C(T). In the case of amide-I modes there also is a strong effect of the population relaxation that always requires to be considered in choosing a procedure for the estimation of C(T).
The comparison of theory and experiment has often been accomplished by specifying the decay of the inhomogeneous distribution of frequencies through an FFCF which is a sum of Kubo functions representing the frequency or pure dephasing dynamics. Each pair Δ, τc is intended to represent a separately identifiable relaxation within the total inhomogeneous distribution of frequencies. Well separated processes may seldom be realized in real systems, for example disordered media such as liquids, proteins and glasses may manifest a continuous distribution of time scales[38].
In experiments with amide groups it frequently occurs that there is a homogeneous dephasing which can be incorporated as part of Equation 3 by choosing the product Δτ to be very small for one of the terms, so that the relaxation time is . For experiments on amide modes in proteins there is often a need to incorporate processes involving large amplitude changes in backbone or side chain structure that are much too slow to measure with the 2D IR experiment which is curtailed by the complete depletion of the signals in less than ca. 10 ps by population relaxation: the total lack of knowledge about these slow processes can be modeled. Therefore a simplified and commonly used four parameter form for the correlation function is:
| (4) |
The first term contributes a Lorentzian, the second a Gaussian and the third contributes a component that continuously varies between Lorentzian and Gaussian. The relaxation of the coherence involves also the dynamics of the populations. In addition, the correlation function for might include oscillatory terms the amide coupled to solvent modes that are underdamped. For example this is the case for the amide-A mode of formamide[44] and the OH stretch of HOD in D2O[45]. While each of the discussed contributions is given a physical significance here, the signal to noise and dynamic range of 2D IR experiments may not easily distinguish between similar decay functions or functional forms for the relaxation: this remains a significant experimental challenge for future experimental developments.
One way to follow the shape changes is to record the slope of the nodal line between the positive (v=0->v=1) and negative (v=1->v=2) parts of the 2D spectrum[46]. Since the T1 represents a significant influence on the antidiagonal width of the 2D spectrum of amide-1 transitions it is obvious that it must influence the spectral shape and be taken into account in attempts to measure the correlation function C(T) from the slope. The interplay of T1 and in forming the shape of 2D spectra of these short-lived amide modes in water is discussed in the following section which also compares the results with “exact” calculations of the slope. Another measure is the Central Line Slope (CLS)[47]: it is the slope of the locus of the maxima of the positive peak and it is particularly useful when the anharmonicity becomes much larger than the linewidth. These two methods of estimating C(T) measure slopes of lines that are parallel to one another.
Dependence of the “slope” on T1 and T2*
For the FFCF's determined in experiments on amides in biological systems it is essential to know how the slopes depend on the homogeneous width parameters since they vary considerably from system to system. As discussed before, the 2D IR spectrum starts (T=0) by having its inhomogeneous components distributed along the diagonal and it gradually becomes more circular until finally it becomes two overlapping circular components shifted by the anharmonic coupling along ωt, rendering the slope to be zero. At that point the shape of a trace along the ωτ axis at the vibrational frequency is that of the linear spectrum. When the frequency is unrelaxed the 2D spectra are more aligned along the diagonal and the slope is increased toward the maximum possible value of unity. Figure 1 illustrates the evolution of the 2D IR shape with T, and how it is gauged by the change in the slope.
It is only in the so-called `short time approximation' [46] for the response functions[46] that the slope becomes equal to the correlation function C(T) at intermediate values of T. Also it is only in this limit that there is a simple analytic relationship between the diagonal and anti-diagonal widths of the 2D spectral components. The sensitivity of the slope to different decay timescales of the frequency correlation and its failure to reproduce the actual FFCF, is made evident from simulations of 2D spectra with model correlation functions.. The slopes of the 2D spectra S(ωτ, ωt; T) computed from the six response functions in the Appendix yield a number of important issues illustrated by Figure 2. The first is that the parts of the correlation that decay faster than a certain cut-off are not captured by the slope measurement. The time evolution of the slope captures only those frequency relaxations that have longer duration than the inverse bandwidth of the inhomogeneous distribution. This result implies that the theory in which t and τ are considered to be small compared with the correlation time is adequate[46].
Figure 2.
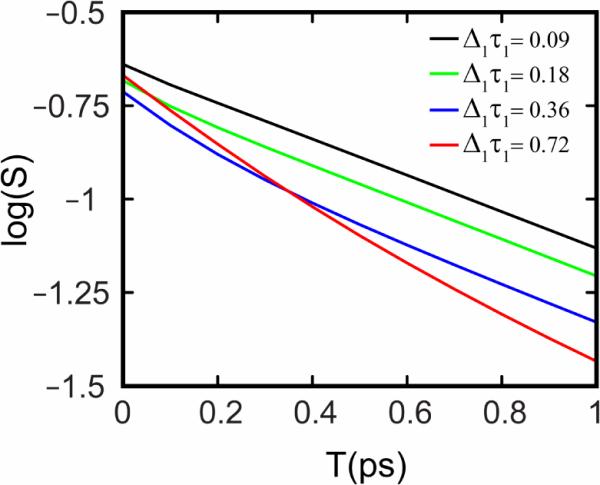
Log(S), the logarithm of the inverse slope, is plotted vs. waiting time T from simulated 2D IR spectra using different correlation functions. For all the simulations a correlation function of the form was used, where values of Δ1 & Δ2 were taken from the work of Skinner and coworkers[50]. The value of τ2 was set to 2ps (Skinner's value was 0.8 ps) and as τ1 is increased the slope begins to show a biexponential decay.
The correlation time-bandwidth product Δτ dictates whether the measured slopes will reflect the fast decay in the frequency correlations. The `initial' values of the slope are influenced by any motionally narrowed components in the FFCF and by the vibrational population lifetime (T1) with the latter being particularly important for amide-I modes. The slopes at T=0, calculated from simulated 2D spectra, are plotted as functions of the correlation time-bandwidth product in Figure 3. The initial correlation, or the slope at T=0, varies significantly with the product Δτ. The amide-I transition widths and correlation timescales typically lie in the intermediate range, and are neither in the motionally narrowed (Δτ << 1) νor the static limit (Δτ >>1). In this regime, the slope at T=0 is always measured to be less than unity. The intercept is sensitive to the vibrational lifetime T1 (see Figure 3) so for an amide mode in solution, the intercept at T=0 is not simply related to the relative magnitudes of the dephasing parameters in Equation 4. However the slope accurately measures the `slow' correlation times, as evidenced by the simulations. If the FFCF of the amide-I mode is known to have the structure of Equation 4, and the vibrational population lifetime is known, then a combination of the 2D IR and the linear infrared spectra will yield Δ and T2*[47, 48]. These points are important to our interpretation of experiments using the amide-I frequency relaxation as a probe of water structural-dynamics in protein channels and other examples.
Figure 3.
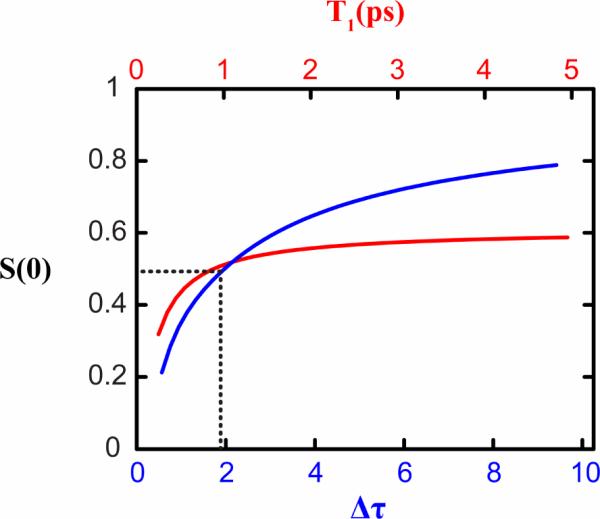
Variation of the inverse slope (S) at T=0 with T1 (red) and the correlation time-bandwidth product Δτ (blue). To estimate the effect of T1 on S(0), the following correlation function was used: C(T) = (10cm−1)2e−T/1ps. To calculate the effect of the product Δτ on S(0), the correlation time was set to 1ps, T1 was set to 800fs and Δ was varied.
Transition dipole fluctuations
It is essential to ask whether the transition dipole moment of the amide-I mode is sufficiently sensitive to the surrounding solvent structure that the fluctuations of its magnitude and direction, and its variation with frequency will contribute to the infrared lineshape and vibrational dynamics. The amide-I mode infrared absorption cross section is known to be dependent on secondary structure and therefore the frequency must depend on various secondary structure based fluctuations. As discussed earlier the fluctuations in amide-I frequency caused by H-bonding to water are also significant. Yet the fluctuations of the dipole moment are usually omitted in the calculation of amide-I spectra[46, 49, 50]: their inclusion is essential for calculations on the OH stretch spectra of water where vibrational frequency and dipole moment both depend significantly on the extent of hydrogen bonding. Since the amide-I vibration bandwidth and anharmonicity are both relatively small at ca 14–16 cm−1 the transition dipole fluctuations across such a small frequency range might be expected to be small, but the dipole fluctuation remains an open question that can only be answered definitively by systematic experiments. Nevertheless to obtain a proper simulation of the 2D IR any fluctuating transition dipoles obtained from theory should be moved into the average displayed in Equation 3.
To estimate the variations of the transition dipole with frequency or displacement, the properties of the transition dipole (dμ / dQ)Q=0Q and the electrical anharmonicity (d2μ/dQ2)Q=0Q2 need to be considered. The characteristic dipole length Q01 = (ℏ / 2ω)1/2 varies with frequency fluctuation δω(t), with δω(t) / 2ω10 being the linear approximation for the corresponding fractional change in transition dipole fluctuation δμ10(t) /μ10. This must introduce small (less than 1%) variations in μ10 across the relatively small spectral bandwidth (〈δω2〉)1/2 ≈ 20cm−1 created by there being a distribution of harmonic frequencies. Such a distribution can arise from the fluctuations in the harmonic force constant. It is interesting that there seems to be no formal, Kubo like, solution for the time dependence of such a distribution [51]. The extent of the transition dipole variation across the inhomogeneous distribution does not only depend on the bond displacement but ultimately depends on what are the specific chemical forces that polarize the molecule, shift the vibrational frequency and create the distribution. A common approach to finding vibrational properties is to employ maps that correlate the vibrational property such as frequency or transition dipole with the electric fields at the vibrator created by the fluctuating charges in the medium[50]. The generation of these maps requires moderately high level computations of the vibrational energy levels in clusters of solvent, so they produce predictions of the variations of the transition dipoles with local structure and their correlation with electric field or frequency. These variations give rise to so-called non-Condon effects [52].
Some of the characteristics of the effect of hydrogen bonding on the amide-I transition can be illustrated by the computation (with DFT B3LYP) of a simple model of NMA in the presence of a water molecule constrained to have a C=O … H-O angle of 135°. As the O----O distance is increased by small amounts δR from the normal H-bonded distance (R0=2.8A), the following approximation is obtained which predicts the vibrational frequency (in cm−1) will increase with increasing R:
| (15) |
A similar approximation for the transition dipole of the amide-I for R≥R0 shows it decreasing with increasing separation of the water. The fractional change in transition dipole is found to be:
| (6) |
These estimates are consistent with the intuitive model whereby the dipole induced in the CO bond by an approaching proton of water has a large component that is parallel to the bond dipole. Therefore the bond dipole increases with decreasing separation of the proton. The frequency shift caused by increasing the separation of the water molecule by 1A along the direction of the H-bond is +12.6 cm-1 according to Equation 7. This change approximately corresponds to the difference between the most probable separation of an H-bonded and a more free but nearby water molecule. These computations support the intuitive notion that the fluctuations of the transition dipole and vibrational frequency of the amide-I mode due to the described effect are anticorrelated and obey the approximate relationship of equation 8 in the linear regime. Equation 8 predicts a very slightly skewed spectrum, but without knowing the dynamical parameters it is difficult to know how this translates into skewness of the absorption or 2D IR spectra. The linear IR spectrum of NMA in D2O (see next section) is asymmetric with skewness parameter approximately 0.27; this asymmetry is not yet reproduced by theoretical models. The simulation of the 2D IR spectra using responses in Equation 3 involve the frequency independent transition dipoles.
The estimates based on Gaussian ab initio computations for a particular water-amide configuration in the gas phase are introduced here only as guides for discussion of the expected behavior of the dipole moment. Nevertheless, the same conclusions are reached by considering that an approaching water molecule changes the balance of the two principal valence bond structures of the planar peptide link, C − N+(H) = C(C) − O− and C − N(H) − C(C) = O. The former is the polarized form with more C-O single bond character and a lower amide-I frequency.
Even when dipole fluctuations are incorporated, theory still predicts that once C(T) has decayed the trace of the 2D spectrum along ωτ will reproduce the linear spectrum [52] as was shown to be the case for Equation 3 where the dipole moment is constant. Unfortunately, in experiments with amide-I transitions the limiting pure dephasing conditions are experimentally challenging because of the short population lifetime.
Do we understand the simplest peptide - N-methylacetamide?
There have been numerous reports of the frequency-frequency correlation functions for amide units in a variety of configurations. For example in alpha helical bundles it is known from infrared spectral transition frequencies and linewidths that the amides exposed to water are significantly more hydrated than those in the interior[53–56]. Water dynamics was also shown to have a significant role in the few ps. conformational exchanges of a tryptophan dipeptide[22] and it dominates the frequency relaxation in some small peptides[57, 58]. Before moving to discuss the 2D IR for some 13C=18O edited protein systems containing amide groups it will be useful to take a closer look at NMA, perhaps the simplest of all amide-I transitions.
The traditional model for the vibrational states of a planar C-NHCO-C peptide link is N-methyl acetamide (NMA)[59]. Early 2D IR experiments on deuterated NMA[57, 60, 61] in D2O showed that C(T) decays on mainly two time scales, one that is sub-hundred femtoseconds and the other that is in the neighborhood of one picosecond. A detailed analysis using MD simulations has supported the notion that the slower time scale is caused by significant translational motion of the H-bonded water molecule at both the carbonyl and N-H group[50]. The fast components of the FFCF are caused by librational motions of waters that need not necessarily be H-bonded to the carbonyl group. The 2D IR spectrum of NMA in D2O is shown in Figure 4 to illustrate how the spectral shape evolves with waiting time T. The decay of the frequency correlations is evidenced by the change of the slope as discussed earlier. The evolution of the slopes, estimated at various values of T, are compared with calculated slopes in Figure 5. When fit to a single exponential the experimental slopes yields a time constant of 1.3ps. This value is similar to those that have reported for the longer time component of the FFCF of NMA in D2O previously[57, 60, 61] and is a result of hydrogen bond making and breaking. The 2D spectra were simulated from spectra computed with the response functions of Equation. 3 (and Appendix) incorporating the correlation function for NMA that was reported by Skinner and coworkers [50] which was:
| (7) |
The slopes obtained from the simulated 2D IR spectra also fit to an exponential decay, with a considerably faster time constant of 0.8ps, which is nevertheless the same as the slow component (0.83ps) of the theoretical FFCF. So it is shown that the slope does indeed measure the input correlation time. There are other key points to note. The experimental slope measurements do not capture a fast component, which from our earlier discussion, implies that component must be motionally narrowed. This is consistent with the time-bandwidth product for the fast component of C(T) in Equation 7 The slope is measured to be only 0.4 at T=0, which is modified from unity by both T1 and the motionally narrowed dephasing. The plots on Figure 2 show clearly that the slope versus T should not evidence the fast relaxing component if Δτ becomes less than about one tenth. At that point the fast part of the dephasing is narrowed and influences the apparent T=0 correlation. While the experiments agree reasonably well among themselves, it is seen that the evolution of the slope is different for the experiments and the spectra simulated using the theoretical FFCF. A more realistic description of the NMA linear and nonlinear spectral shapes may come from first considering the dynamic exchange between the structures involving different numbers of hydrogen bonded water molecules[62]. The amide-water spectrum may not be fully exchange narrowed, in which case the technique of choosing frequency fluctuations from a Gaussian distribution would not give the correct lineshape.
Figure 4.
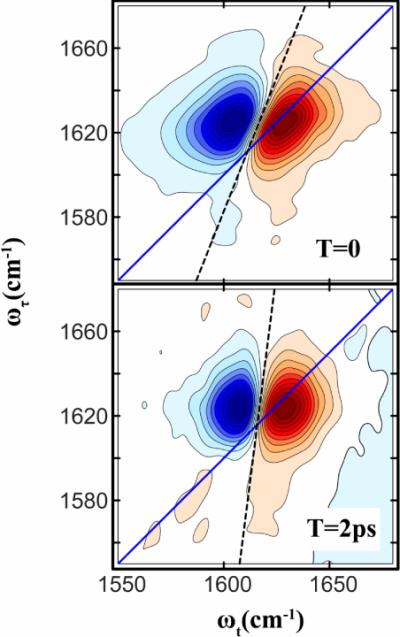
2D IR spectra of NMAD in D2O at two waiting times 0 and 2ps. The slopes are shown as dashed lines.
Figure 5.
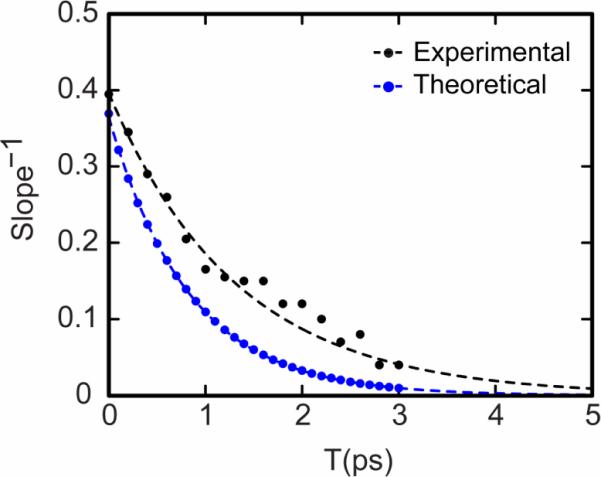
Experiment (black) and simulation (blue) values for the inverse slope for NMAD in D2O. The simulated slopes were obtained from 2D spectra with response functions as given in Equation 3 and the Appendix along with the frequency-frequency correlation function reported by Skinner and coworkers[50]. The inverse slopes were fitted (dashed lines) to single exponential decays: S(T) = 0.4e−T/1.3ps (for the experiment) and S(T) = 0.37e−T/0.81ps (for the simulation).
While there are discrepancies at shorter times the experimental and theoretical data clearly establish a ~1ps decay time of the amide frequency correlations in water, corresponding to displacements of the hydrogen bond between water and the amide unit, thus establishing a benchmark for evaluation of water motions in complex proteins and peptides.
The spectral density
We now ask how the measurement of the C(T) relates to the dynamic-structure of the peptide groups. The Fourier transform of C(T) is a spectral density, which for the approximation of Equation 1.5 is obviously a spectrum with a Lorentz shaped peak, a constant part describing ultrafast motions determined by and a sharp spike associated very slow degrees of freedom characterized by . This spectrum should contain and manifest all the modes that are coupled to the amide-I, but in particular it should be sensitive to the motions of water molecules that are directly coupled to the amide unit. Therefore in the frequency domain there must be a bunch of very low frequency modes (< ca. 1cm−1) giving rise to the spike and a Lorentzian distribution having a full width of 10 cm−1 that describes the hydrogen bond making and breaking dynamics on the C=O and N-H groups of the amide. The C(T) might be considerably more complicated than is implied by this example where the fit is to three Kubo functions, nevertheless for molecular vibrations the spectral density is expected to represent a spectrum of those motions of the medium that modulate the vibrational frequency of the probe. In proteins these motions involve the backbone, side chains and water. This point just makes more evident that C(T) is a highly selective probe of mainly local motions that are effective in fluctuating the frequency. Obtaining an understanding of the amide spectral density. its structural origins and its manifestations of local water is an exciting experimental challenge for nonlinear spectroscopy. For example will 2D IR be able to discriminate the different water structures in exchange around a polar bond? We reported that for isotopically substituted proteins the amide-I band shape is non-uniform and appears to have frequency components that exchange on the 500fs to 1ps time scale. We have speculated that these responses correspond to amide carbonyls with on average zero, one or two water molecules hydrogen bonded! If this interpretation holds up under theoretical and further experimental scrutiny, the dynamics of water near amide carbonyls must be quite different in detail from that of water interacting with other water molecules in the liquid[63]. Treating the amide frequency distribution in water with Gaussian fluctuations in the manner of the summary given above cannot be an entirely correct approach to obtain a valid description of the ultrafast motions manifested in the high frequency tail of the spectral density. We expect that once very clear experimental descriptions of these frequency dynamics are obtained they will also make a significant contribution to testing the gospel of simulations. Furthermore the correlation function involves a trace over the modes of the complete system and so it has a temperature dependence[43] that is not considered here.
The approach presented here depends on the system having Gaussian fluctuations but recent work by Hamm and coworkers[64] on measuring higher order correlation functions of the frequency fluctuations is a move beyond this common assumption. It is evident that a method of obtaining much more accurate spectral density of the states coupled to a vibrator would in turn provide the possibility of significant advances in the structural dynamics of proteins. There are now a number of examples involving quite complex proteins where the dynamics of the frequencies rather than the frequencies themselves are sought in experiments. This experimental approach bears an analogy to the manner in which lifetime imaging[65] adds another dimension to fluorescence microscopy. Before moving to some applications of these ideas we reemphasize that there have been many important advances in both experiment and theory of multidimensional spectroscopy that will be valuable for the questions asked here. For example similar to the advances made by 2D IR compared with linear IR, there is additional knowledge of the spectral density in 3D IR[64], carried out with five IR pulses where three coherences are now measured[40].
As practical illustrations of the foregoing ideas we use two examples for our recent work. In the first the dynamics of the water which known to be essential for the operation of a transmembrane proton channel is discussed. In the second example the spectral densities of some amide modes is discovered to resemble that of mobile water suggesting the unexpected presence of water molecules in amyloid fibrils.
Water confined in proton channels
There are numerous TM channels that transport ions, water or other essential nutrients across cell membranes[3] and water can be present in them in liquid-like form, single file wire-like structures or clusters[4]. Our plan has been to employ specific amide modes located in the interior of channels to `test the water' using the principles summarized above. This is particularly challenging for proton conducting channels which abound in biological systems. They transport solvated protons across a membrane so clearly there must be specialized water structures involved in their function. The operational aspects of these channels are difficult to study using conventional infrared spectroscopy because the signals from the small numbers of water molecules confined in these channels cannot readily be distinguished from bulk water in contact with each side of the channel. In order to overcome this difficulty, isotopically edited amide-I modes located in these channels are used as direct probes of the spectral density of the functional water as described in earlier sections of this Perspective. The amide-I mode frequencies are all near 1600 cm−1 which is in the valley between the D2O bend and stretch frequencies so the bulk water signals in these experiments is small. This manner of investigation of protein dynamics is in its infancy but the expectation is that a map of the dynamic water structures that are confined in narrow channels formed by the association of peptides might ultimately be obtained by the 2D IR methods. The required information regarding dynamics and structure distributions of isotopically labeled amide groups can also be revealed by studies of the spectral line shapes. Such an approach has been used by Zanni and coworkers for isotopomers of transmembrane proteins including channels[55, 56] and fibrils[66]. However, employing 13C=18O probes of the water spectral densities appears at the moment to be a most promising method, even though much remains to be accomplished both in experimental methods and theory and using other vibrational probes. Such methods are essential because the water molecules in biological channels though not necessarily liquid, may still be sufficiently transient that they are not resolved in time averaged x-ray diffraction or NMR experiments. Nevertheless the confined water controls the ability of the channels to conduct protons under the influence of a pH gradient so it is essential to discover its mode of action.
The M2 proton channel
The M2 protein of the Influenza viruses acidifies its interior by transport of protons from bulk solution. As described in more detail in our recent paper[67] the channel protein is a homo-tetramer consisting of N-terminal, TM, and cytoplasmic domains. The twenty five residue TM domain, M2TM, introduced by DeGrado and coworkers is a model peptide that forms the four-helix bundles that bridge the lipid membrane and that conducts protons[68, 69]. Molecular dynamics simulations[70], spectroscopic studies[71] and most recently X-ray diffraction[72, 73] and solution NMR studies[74] have provided very informative structural data for this model system.
Figure 6 shows a cartoon of M2TM with its associated water structure. The thin `water-wire' that extends through the channel pore influences the vibrational dynamics of the pore lining residues, which can therefore be used to report on the mobility of the water confined in the channel. As stated in our recent paper [67], the four histidine residues may act as the gate which activates the conduction of protons [75]. The NMR at high pH and X-ray diffraction at low pH give different tetrameric structures, suggesting that M2 alters its conformation as the pH is reduced, and that this change is correlated with conditions for transporting protons across the channel[72–74]. The channel is more accessible to the aqueous phase than to the viral interior at higher pH whereas the equilibrium shifts towards a conformation more open to the viral interior when the three of the four histidines at location 37 become protonated.
Figure 6.
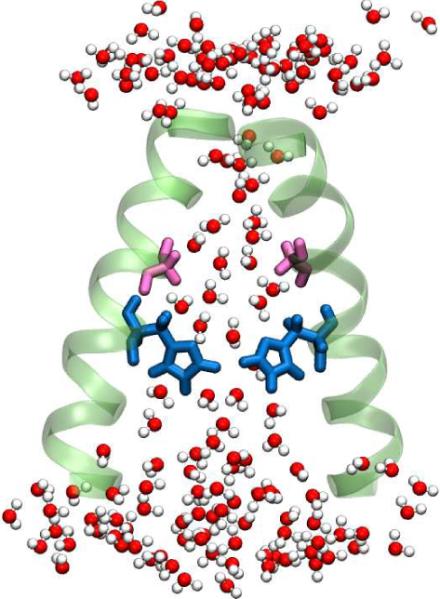
A cartoon of the M2 channel, showing the water structure inside the channel. The number of water molecules accessible to the pore lining residues is significantly less than in bulk solution. The above picture was generated from MD simulation trajectories performed with the 3LBW crystal structure. Only two helices are shown for clarity. The Gly34 residues are shown in pink and the His37 are shown in blue.
Our concept is that the water that flows into and ebbs from the gating region of the channel as protons are brought in and expelled into the viral interior can be probed by finding the changes in the spectral densities of amides in the vicinity of the His37 gate of the channel. The promise of such 2D IR experiments is a direct test of the mechanism whereby hydronium ions first form His+ states, which then direct hydronium ions into the virus. In our recent work[67] we used a particular residue, Gly34, to sense the water structure and dynamics at different pH values using the principles outlined earlier in this article. At first sight there would appear to be many other isotopic or chemically modified residues that could identify the presence of and probe the properties of the channel water at the gate region. However Gly34 is special because of its location and probable sensitivity to `where the action is.'
The dynamics of the glycine-34 amide frequencies
The significant differences [67] in the 2D IR of the Gly34 of the channel at pH's 6.2 and 8 are clear from Figure 7. The 2D IR of the label reveals two bands at pH 6.2, whereas there is only one dominant band at pH 8. representing in total three different conformations or configurations of the channel. The peptide contains only one Gly34 per TM helix so if in each conformation the spread in vibrational frequency of the four edited Gly34 amide-I bands of the TM tetramer is less than the amide-I bandwidth, the observed frequency shift of the single observed band is an indicator of the protein conformation. The time evolution of the spectra are distinctly different at the two pH's. for which the structures are modeled above the spectra in Figure 7. The slope of the nodal line for the Gly34 amide-I 2D IR shows little change from its mean value of ~0.66 with the waiting time at pH 8,. The low frequency peak at pH 6.2, however, shows significant change in slope S(T) that can be fit to the model function of Equation 4 with parameters given by
| (8) |
The frequency relaxes with two characteristic times: 75fs and 1.3ps. when, the M2 channel is in its active, `Open' state. On the contrary at high pH, when the channel is `Closed', the water inside the channel, if any, is `frozen' on the time scale less than 10 ps.
Figure 7.
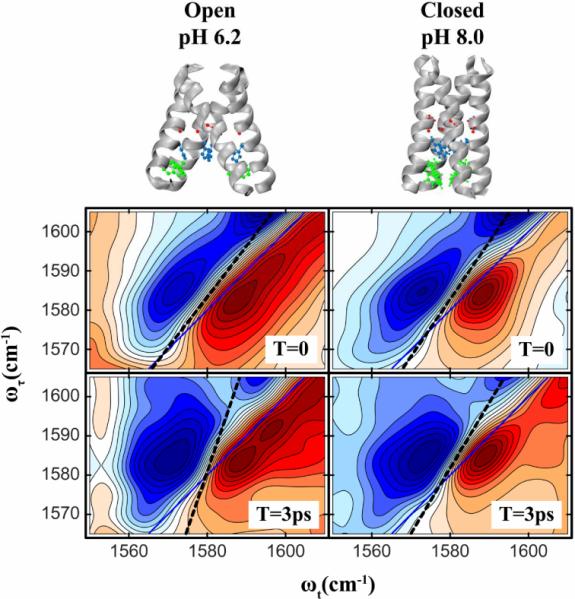
2D IR spectra of isotopically labeled G34 in the M2TM protein at waiting times 0 and 3ps. Spectra are shown for two pH's : 6.2(left) and 8.0(right) at which the channel is known to be in its `Open' and `Closed' states respectively. The `Open' and `Closed' state structures of M2TM are shown above. The PDB structures 2RLF and 3C9J were used to represent the Closed and Open states respectively. The slopes are drawn in dashed lines.
The decay timescales, as revealed by slope measurements from the 2D IR spectra at low pH, are similar to those estimated for NMA in aqueous solutions as discussed above and represented in Figure 5. Therefore, we can expect that the fast ca. 75fs component arises from librational motions of water that remains hydrogen bonded to the Gly34 amide when the three of the histidines are protonated. The 1.3ps component is most likely dominated by a rearrangement of the water-amide hydrogen bond network. The amide frequency fluctuations must be dominated by motions of directly bonded water molecules. For a system like M2, the number of water molecules that are accessible to the Gly34 is much smaller than if the amide were in aqueous solutions; yet the frequency fluctuation timescales are very similar to those measured for amide modes in bulk. This is consistent with the frequency fluctuations being dominated by only one or perhaps two nearby water molecules even in liquid D2O. The spectral density of the amide vibrator needs to be more accurately determined to bring out additional characteristics of the surrounding water structure. The x-ray diffraction suggests there are highly specific water structures involving bridges from Gly34 to the protonated histidines. These structures should lead to spectral shifts and dynamics characteristic of the phase of the water molecules in the channel. Both the amide transitions seen at pH6 and the one at pH8 are typical of modes having nearby water molecules except at high pH the water must be immobilized on the time scale of 10 ps. The outlook for applications of 2D and 3D IR to determine this water structure via spectral densities of vibrational probes is very encouraging based on recent accomplishments in the 2D and 3D IR methodology[64].
Hydration effects on amyloid fibrils
We can also use 2D IR to locate water that is either functionally trapped or kinetically confined in proteins that have otherwise hydrophobic interiors. Although buried water is manifest in a wide variety of transmembrane proteins and may be essential in stabilizing some of them[76]. There had been little evidence for water in extended beta structures. The recent 2D IR experiments on isotopomers of the amyloid fibril Aβ40 [77] and Human Islet Amyloid peptide[66] provide illustrations of how inferred spectral densities of amide groups can reveal hitherto unknown characteristics of structure. The fibrils in our experiments are among those that accumulate as plaques in the brain tissue of persons with Alzheimer's disease and they are composed of the β-amyloid peptide Aβ40 for which structural models have been developed by Tycko and co-workers[78].
The 2D IR experiments involved fibrils made from 13C=18O isotopically labeled strands. which form antiparallel sheets by laying transverse to the fibril axis, with an inter-strand spacing that is typical of a β-sheet. The isotope replacement of one residue of a strand creates, on formation of the fibril, a chain of isotopically replaced amide-I vibrational states that forms a quasi-linear exciton band of 13C=18O edited peptide groups. The nearest neighbor coupling is ca. −5 cm−1 so the exciton bandwidth is ca. 20 cm−1[77]. This is only an approximate picture of the amide-I states which in reality, according to the published structure[78], must be determined from a range of coupling parameters since even the parallel in register β-sheet does not have a sequence of evenly spaced amide-I modes along the fibril axis. These linear chains of amide modes should exhibit infrared absorption bands corresponding to transitions only to the lowest energy portion of the one dimensional exciton band sketched in Figure 8, lying at 10 cm−1 below the uncoupled amide-I transition, and that was exactly what was seen for many of the isotopomers[77]. The multiple peaks seen for a few residues, as illustrated in Figure 8 for the residue 13C=18O Leucine-17 indicate very clearly that the spectra are not from an ideal linear chain. A remarkable result is obtained from the 2D IR spectra of the isotopically replaced residues in these regions. It was found that in most of the spectrally complex regions, and only in those regions, there is a component of the slope having an ultrafast decay. This fast time dependence is absent for the isotopomers that show spectra exhibiting one dimensional exciton characteristics. Figure 9, taken from the work of Kim[5], shows how the slope changes between T=0 and T=300 fs for each of the residues distributed across the strand: a T dependence of the slope is confined to only a few of the residues. The largest effects are associated with the apposed pairs 34,36 and 17,18 which has led us to conclude that water is in the region separating these parts of the strand as illustrated in Figure 9.
Figure 8.
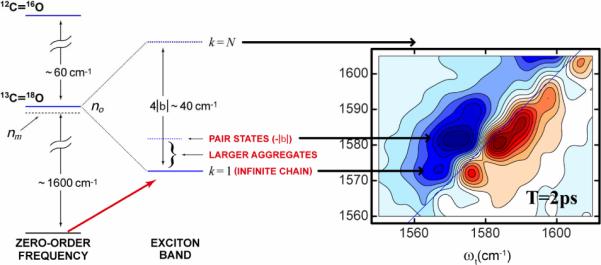
Left: Energy level diagram of a fibril formed from the monomeric Ab40 unit. Right: 2D IR spectra of the isotope label region of 13C=18O L17 residue.
Figure 9.
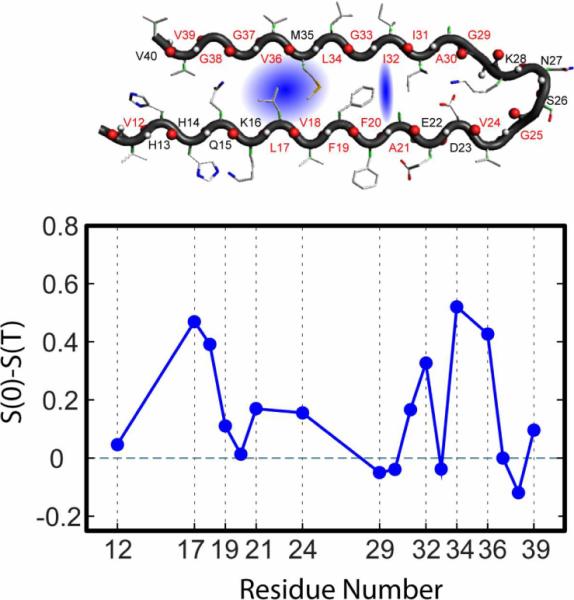
Top: Cartoon of the amyloid Aβ40 protein with isotopically replaced residues marked in red. Water in the blue shaded region would influence the amide-I spectral densities for the apposed residue pairs L17, V18 and L34. V36. The apposed residues A21 and I32 also show a small effect.
Bottom: Plot of the difference in Inverse Slope from T=0 to T=3ps vs. residue number for the amyloid Ab40 protein. For residues L17, V18, L34. V36, A21 and I32 the slope clearly changes with T suggesting nearby water.
The spectrum in Figure 8 is significantly perturbed from the ideal one discussed above. The 13C=18O leucine residue amide-I transition is split into three spectral components. The lowest frequency transition is the sharp line expected for a linear exciton and is likely to represent the leucines in regions of the fibril structure where the isotopomer 2D IR spectra are close to those of excitons that are delocalized along approximately linear chains The higher frequency transitions are strongly T dependent and exhibit relaxation on the picosecond time scale that is typical of amide modes in direct contact with water molecules. The amide-I transitions appear to be localized on specific residues rather than forming linear chains. The spectral density of the amide transition suggests that the water molecules are sufficiently free that they can undergo librational and translational motions on the ca. 1 ps time scale. How the water is bound to the amide units or how the structures might relate to the fibril formation kinetics or stabilization remains as a challenge for future work.
Advances along these lines will enlighten our understanding of the steps in the formation and structure of fibrils. If the hydrophobic cavities were hydrated the sheet association might be optimized [79] and interior hydration may have an important role in the structural stability of fibrils.[80] Simulations show water in hydrophilic loops connecting the two beta-strands, and in the solvent-exposed N-terminal beta-sheets.[81, 82]. This example illustrates the remarkable power of 2D IR spectroscopy in its ability to scan the spectral densities of amide modes and locate secrets of the structural-dynamics that are not seen from other experiments.
Final remarks
The two examples of M2 channels and fibrils illustrate how the time dependence of the frequency of the amide-I mode exposes important properties that are not evident from other experiments, particularly regarding the water confined in biological structures. The conclusions we have made are based on a reasonable quantum theoretical foundation but many questions remain unanswered. For example the effect of all fluctuating charges of the backbone needs careful consideration in trying to define a correlation function. While MD simulations combined with simulated electric field fluctuations and maps have been used with great success to dissect the various contributions to the infrared absorption linewidths references to maps[49], there is as yet no solid connection between the experiment and theory for the detailed composition of the frequency correlation functions of the amide-I group confined in the interiors of proteins. The chemical physics of such elementary interactions is challenging and potentially rewarding for biology. One obvious benefit will be the discovery of new drugs. This promise is exemplified by the story of the Influenza A virus. The drug amantadine was once a significant antiviral medication that saved many lives. Apparently the drug effectively slowed the influx of protons by directly blocking the flow of water containing hydronium ions into M2 channel. However the virus has since mutated its transmembrane region[83, 84] to render this class of drugs totally ineffective so that infection by Influenza A remains as a serious human health issue[85]. Thus, there is a significant medical need to describe the microscopic mechanisms of proton conduction of the M2 proton channel and the role of its confined water. Such knowledge will contribute to the design of new inhibitors that target current forms of M2. The same parable could be repeated for myriads of essential processes in biology and medicine.
Acknowledgements
This work was supported by the National Science Foundation-Chemistry and the National Institutes of Health through grants GM12592 and P41 RR01348. We thank Dr. Daniel Kuroda for helpful discussions and carrying out the DFT calculations on the water-amide configurations.
Appendix
In this article we have considered 2D IR three pulse echo experiments where the signal field is emitted in the phase matched direction . Under the rotating wave approximation, for a single vibrator, we employ only six pathways to compute this signal. The quantum mechanical response functions for these pathways, which are reproduced in many other places[41–43]. are given as :
| (A8) |
| (A9) |
| (A10) |
| (A11) |
| (A12) |
| (A13) |
Where and ωij is the mean transition frequency. In our simulations we have assumed that the vibrational frequencies follow Gaussian statistics, the 1→2 and 0→1 transition frequencies are correlated, and the rotational diffusion and dipole moment fluctuations can be neglected. The above responses are then simplified to become:
| (A14) |
| (A15) |
| (A16) |
| (A17) |
| (A18) |
| (A19) |
where Δ is the anharmonicity of the mode. In the Gaussian approximation the function δG1(t,τ,T)
causes the deformations from circular 2D spectra and we assume the definition:
| (A20) |
which tends to zero as T tends to infinity.
In the limit of δ-function pulses, the 2D IR spectrum is defined as S(ωτ,ωt;T) where:
| (A21) |
where m and n are chosen as +1 or −1 in order that the signals are brought into the first quadrant of the {ωτ,ωt} space. For simulating 2D IR spectra, the above integrals were evaluated numerically using the software package MATLAB.
References
- [1].Levy Y, Onuchic JN. Annual Review of Biophysics and Biomolecular Structure. 2006;35:389–415. doi: 10.1146/annurev.biophys.35.040405.102134. [DOI] [PubMed] [Google Scholar]
- [2].Pal SK, Zewail AH. Chem. Rev. (Washington, DC, U. S.) 2004;104:2099–2123. doi: 10.1021/cr020689l. [DOI] [PubMed] [Google Scholar]
- [3].de Groot BL, Grubmüller H. Current Opinion in Structural Biology. 2005;15:176–183. doi: 10.1016/j.sbi.2005.02.003. [DOI] [PubMed] [Google Scholar]
- [4].Rasaiah JC, Garde S, Hummer G. Annual Review of Physical Chemistry. 2008;59:713–740. doi: 10.1146/annurev.physchem.59.032607.093815. [DOI] [PubMed] [Google Scholar]
- [5].Kim YS, Liu L, Axelsen PH, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:17751–17756. doi: 10.1073/pnas.0909888106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Raschke TM. Current Opinion in Structural Biology. 2006;16:152–159. doi: 10.1016/j.sbi.2006.03.002. [DOI] [PubMed] [Google Scholar]
- [7].Russo D, Murarka RK, Copley JRD, Head-Gordon T. Journal of Physical Chemistry B. 2005;109:12966–12975. doi: 10.1021/jp051137k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Zhong D, Pal SK, Zewail AH. Chemical Physics Letters. 2011;503:1–11. [Google Scholar]
- [9].Qiu W, Kao Y-T, Zhang L, Yang Y, Wang LJ, Stites WE, Zhong D, Zewail AH. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:13979–13984. doi: 10.1073/pnas.0606235103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Li T, Hassanali AA, Kao Y-T, Zhong D, Singer SJ. Journal of the American Chemical Society. 2007;129:3376–3382. doi: 10.1021/ja0685957. [DOI] [PubMed] [Google Scholar]
- [11].Zhang L, Wang L, Kao Y-T, Qiu W, Yang Y, Okobiah O, Zhong D. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:18461–18466. doi: 10.1073/pnas.0707647104. S18461/18461-S18461/18467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Pal SK, Zhao L, Zewail AH. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:8113–8118. doi: 10.1073/pnas.1433066100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Golosov AA, Karplus M. Journal of Physical Chemistry B. 2007;111:1482–1490. doi: 10.1021/jp065493u. [DOI] [PubMed] [Google Scholar]
- [14].Halle B, Nilsson L. Journal of Physical Chemistry B. 2009;113:8210–8213. doi: 10.1021/jp9027589. [DOI] [PubMed] [Google Scholar]
- [15].Furse KE, Corcelli SA. Journal of the American Chemical Society. 2008;130:13103–13109. doi: 10.1021/ja803728g. [DOI] [PubMed] [Google Scholar]
- [16].Harbison GS, Roberts JE, Herzfeld J, Griffin RG. Journal of the American Chemical Society. 1988;110:7221–7223. [Google Scholar]
- [17].Kiihne S, Bryant RG. Biophysical Journal. 2000;78:2163–2169. doi: 10.1016/S0006-3495(00)76763-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Modig K, Liepinsh E, Otting G, Halle B. Journal of the American Chemical Society. 2004;126:102–114. doi: 10.1021/ja038325d. [DOI] [PubMed] [Google Scholar]
- [19].Qvist J, Persson E, Mattea C, Halle B. Faraday Discuss. 2009;141:131–144. doi: 10.1039/b806194g. [DOI] [PubMed] [Google Scholar]
- [20].Kim YS, Hochstrasser RM. Journal of Physical Chemistry B. 2007;111:9697–9701. doi: 10.1021/jp074267x. [DOI] [PubMed] [Google Scholar]
- [21].Kim YS, Hochstrasser RM. Springer Series in Chemical Physics. 2007;88:332–334. [Google Scholar]
- [22].Bagchi S, Charnley AK, Smith AB, III, Hochstrasser RM. Journal of Physical Chemistry B. 2009 in process. [Google Scholar]
- [23].Kim YS, Wang J, Hochstrasser RM. Journal of Physical Chemistry B. 2005;109:7511–7521. doi: 10.1021/jp044989d. [DOI] [PubMed] [Google Scholar]
- [24].Kim Yung S, Hochstrasser Robin M. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:11185–11190. doi: 10.1073/pnas.0504865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Moilanen DE, Wong D, Rosenfeld DE, Fenn EE, Fayer MD. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:375–380. doi: 10.1073/pnas.0811489106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Woutersen S, Mu Y, Stock G, Hamm P. Chemical Physics. 2001;266:137–147. [Google Scholar]
- [27].Zheng J, Kwak K, Asbury J, Chen X, Piletic IR, Fayer MD. Science. 2005;309:1338–1343. doi: 10.1126/science.1116213. [DOI] [PubMed] [Google Scholar]
- [28].Laage D, Hynes JT. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:967–968. doi: 10.1073/pnas.0812306106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Bakker HJ, Skinner JL. Chem. Rev. (Washington, DC, U. S.) 2010;110:1498–1517. doi: 10.1021/cr9001879. [DOI] [PubMed] [Google Scholar]
- [30].Scheiner S, Cuma M. Journal of the American Chemical Society. 1996;118:1511–1521. [Google Scholar]
- [31].Parker MJ, Clarke AR. Biochemistry. 1997;36:5786–5794. doi: 10.1021/bi9629283. [DOI] [PubMed] [Google Scholar]
- [32].Fecko CJ, Loparo JJ, Roberts ST, Tokmakoff A. Journal of Chemical Physics. 2005;122 doi: 10.1063/1.1839179. [DOI] [PubMed] [Google Scholar]
- [33].Asbury JB, Steinel T, Kwak K, Corcelli SA, Lawrence CP, Skinner JL, Fayer MD. Journal of Chemical Physics. 2004;121:12431–12446. doi: 10.1063/1.1818107. [DOI] [PubMed] [Google Scholar]
- [34].Nagel ZD, Klinman JP. Chem. Rev. (Washington, DC, U. S.) 2006;106:3095–3118. doi: 10.1021/cr050301x. [DOI] [PubMed] [Google Scholar]
- [35].Mould JA, Li H-C, Dudlak CS, Lear JD, Pekosz A, Lamb RA, Pinto LH. Journal of Biological Chemistry. 2000;275:8592–8599. doi: 10.1074/jbc.275.12.8592. [DOI] [PubMed] [Google Scholar]
- [36].Kato T. Journal of Chemical Physics. 1983;79:2139–2145. [Google Scholar]
- [37].Kubo R. Advances in Chemical Physics: Stochastic Processes in Chemical Physics. 1969;15:101. [Google Scholar]
- [38].de Boeij WP, Pshenichnikov MS, Wiersma DA. Annual Review of Physical Chemistry. 1998;49:99–123. doi: 10.1146/annurev.physchem.49.1.99. [DOI] [PubMed] [Google Scholar]
- [39].Schmidt JR, Sundlass N, Skinner JL. Chemical Physics Letters. 2003;378:559–566. [Google Scholar]
- [40].Hamm P, Lim M, Hochstrasser RM. Phys. Rev. Lett. 1998;81:5326–5329. [Google Scholar]
- [41].Cho M. CRC Press; 2009. [Google Scholar]
- [42].Hamm P, Zanni M. Cambridge University Press; 2011. [Google Scholar]
- [43].Mukamel S. Principles of Nonlinear Optical Spectroscopy. 1995 [Google Scholar]
- [44].Ha J-H, Kim YS, Hochstrasser RM. Journal of Chemical Physics. 2006;124 doi: 10.1063/1.2162165. 064508/064501–064508/064510. [DOI] [PubMed] [Google Scholar]
- [45].Fecko CJ, Eaves JD, Loparo JJ, Tokmakoff A, Geissler PL. Science (Washington, DC) 2003;301:1698–1702. doi: 10.1126/science.1087251. [DOI] [PubMed] [Google Scholar]
- [46].Kwac K, Cho MH. Journal of Chemical Physics. 2003;119:2256–2263. [Google Scholar]
- [47].Kwak K, Park S, Finkelstein IJ, Fayer MD. Journal of Chemical Physics. 2007;127 doi: 10.1063/1.2772269. [DOI] [PubMed] [Google Scholar]
- [48].Kuroda DG, Vorobyev DY, Hochstrasser RM. Journal of Chemical Physics. 2010;132 doi: 10.1063/1.3285265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Lin YS, Shorb JM, Mukherjee P, Zanni MT, Skinner JL. Journal of Physical Chemistry B. 2009;113:592–602. doi: 10.1021/jp807528q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Schmidt JR, Corcelli SA, Skinner JL. Journal of Chemical Physics. 2004;121:8887–8896. doi: 10.1063/1.1791632. [DOI] [PubMed] [Google Scholar]
- [51].Kampen NGV. North-Holland Publishing Company, Chapter 14. 1981 [Google Scholar]
- [52].Schmidt JR, Corcelli SA, Skinner JL. Journal of Chemical Physics. 2005;123 doi: 10.1063/1.1961472. [DOI] [PubMed] [Google Scholar]
- [53].Manas ES, Getahun Z, Wright WW, DeGrado WF, Vanderkooi JM. Journal of the American Chemical Society. 2000;122:9883–9890. [Google Scholar]
- [54].Walsh STR, Cheng RP, Wright WW, Alonso DOV, Daggett V, Vanderkooi JM, DeGrado WF. Protein Science. 2003;12:520–531. doi: 10.1110/ps.0223003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Manor J, Mukherjee P, Lin YS, Leonov H, Skinner JL, Zanni MT, Arkin IT. Structure. 2009;17:247–254. doi: 10.1016/j.str.2008.12.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Mukherjee P, Kass I, Arkin I, Zanni MT. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:3528–3533. doi: 10.1073/pnas.0508833103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Woutersen S, Pfister R, Hamm P, Mu YG, Kosov DS, Stock G. Journal of Chemical Physics. 2002;117:6833–6840. [Google Scholar]
- [58].Kim YS, Hochstrasser RM. Journal of Physical Chemistry B. 2005;109:6884–6891. doi: 10.1021/jp0449511. [DOI] [PubMed] [Google Scholar]
- [59].Krimm S, Bandekar J. Advances in protein chemistry. 1986;38:181–364. doi: 10.1016/s0065-3233(08)60528-8. [DOI] [PubMed] [Google Scholar]
- [60].Zanni MT, Asplund MC, Hochstrasser RM. Journal of Chemical Physics. 2001;114:4579–4590. [Google Scholar]
- [61].DeCamp MF, DeFlores L, McCracken JM, Tokmakoff A, Kwac K, Cho M. Journal of Physical Chemistry B. 2005;109:11016–11026. doi: 10.1021/jp050257p. [DOI] [PubMed] [Google Scholar]
- [62].Kim YS, Hochstrasser RM. The Journal of Physical Chemistry B. 2007;111:9697–9701. doi: 10.1021/jp074267x. [DOI] [PubMed] [Google Scholar]
- [63].Eaves JD, Tokmakoff A, Geissler PL. J. Phys. Chem. A. 2005;109:9424–9436. doi: 10.1021/jp051364m. [DOI] [PubMed] [Google Scholar]
- [64].Garrett-Roe S, Hamm P. Accounts of Chemical Research. 2009;42:1412–1422. doi: 10.1021/ar900028k. [DOI] [PubMed] [Google Scholar]
- [65].Chang CW, Sud D, Mycek MA. Digital Microscopy, 3rd Edition. 2007;81:495–+. doi: 10.1016/S0091-679X(06)81024-1. [DOI] [PubMed] [Google Scholar]
- [66].Shim SH, Gupta R, Ling YL, Strasfeld DB, Raleigh DP, Zanni MT. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:6614–6619. doi: 10.1073/pnas.0805957106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Ghosh A, Qiu J, DeGrado WF, Hochstrasser R, M. Proceedings of the National Academy of Sciences of the United States of America. 2011 doi: 10.1073/pnas.1103027108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Pinto LH, Lamb RA. Photochemical & Photobiological Sciences. 2006;5:629–632. doi: 10.1039/b517734k. [DOI] [PubMed] [Google Scholar]
- [69].Salom D, Hill BR, Lear JD, DeGrado WF. Biochemistry. 2000;39:14160–14170. doi: 10.1021/bi001799u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Khurana E, Dal Peraro M, DeVane R, Vemparala S, DeGrado WF, Klein ML. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:1069–1074. doi: 10.1073/pnas.0811720106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Takeuchi H, Okada A, Miura T. Febs Letters. 2003;552:35–38. doi: 10.1016/s0014-5793(03)00781-6. [DOI] [PubMed] [Google Scholar]
- [72].Stouffer AL, Acharya R, Salom D, Levine AS, Di Costanzo L, Soto CS, Tereshko V, Nanda V, Stayrook S, DeGrado WF. Nature. 2008;451:596–U513. doi: 10.1038/nature06528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Acharya R, Carnevale V, Fiorin G, Levine BG, Polishchuk AL, Balannik V, Samish I, Lamb RA, Pinto LH, DeGrado WF, Klein ML. Proceedings of the National Academy of Sciences. 2010;107:15075–15080. doi: 10.1073/pnas.1007071107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Schnell JR, Chou JJ. Nature. 2008;451:591–U512. doi: 10.1038/nature06531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Pinto LH, Dieckmann GR, Gandhi CS, Papworth CG, Braman J, Shaughnessy MA, Lear JD, Lamb RA, DeGrado WF. Proceedings of the National Academy of Sciences of the United States of America. 1997;94:11301–11306. doi: 10.1073/pnas.94.21.11301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Renthal R. Protein Science. 2008;17:293–298. doi: 10.1110/ps.073237508. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Kim YS, Liu L, Axelsen PH, Hochstrasser RM. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:7720–7725. doi: 10.1073/pnas.0802993105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Petkova AT, Ishii Y, Balbach JJ, Antzutkin ON, Leapman RD, Delaglio F, Tycko R. Proceedings of the National Academy of Sciences of the United States of America. 2002;99:16742–16747. doi: 10.1073/pnas.262663499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Zheng J, Jang H, Ma B, Tsai CJ, Nussinov R. Biophysical Journal. 2007;93:3046–3057. doi: 10.1529/biophysj.107.110700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [80].Yamazaki T, Blinov N, Wishart D, Kovalenko A. Biophysical Journal. 2008;95:4540–4548. doi: 10.1529/biophysj.107.123000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Buchete NV, Hummer G. Biophysical Journal. 2007;92:3032–3039. doi: 10.1529/biophysj.106.100404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Reddy G, Straub JE, Thirumalai D. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:21459–21464. doi: 10.1073/pnas.1008616107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Grambas S, Bennett MS, Hay AJ. Virology. 1992;191:541–549. doi: 10.1016/0042-6822(92)90229-i. [DOI] [PubMed] [Google Scholar]
- [84].Bright RA, Shay DK, Shu B, Cox NJ, Klimov AI. Journal of the American Medical Association. 2006;295:891–894. [Google Scholar]
- [85].Lamb RA, Krug RM. Virology. In: Knipe DM, Howley PM, editors. Virology. Lippincott, Williams and Watson; Philadelphia: 2001. [Google Scholar]


