FMRI group analysis combining effect estimates and their variances

Abstract

Conventional functional magnetic resonance imaging (FMRI) group analysis makes two key assumptions that are not always justified. First, the data from each subject is condensed into a single number per voxel, under the assumption that within-subject variance for the effect of interest is the same across all subjects or is negligible relative to the cross-subject variance. Second, it is assumed that all data values are drawn from the same Gaussian distribution with no outliers. We propose an approach that does not make such strong assumptions, and present a computationally efficient frequentist approach to FMRI group analysis, which we term mixed-effects multilevel analysis (MEMA), that incorporates both the variability across subjects and the precision estimate of each effect of interest from individual subject analyses. On average, the more accurate tests result in higher statistical power, especially when conventional variance assumptions do not hold, or in the presence of outliers. In addition, various heterogeneity measures are available with MEMA that may assist the investigator in further improving the modeling. Our method allows group effect t-tests and comparisons among conditions and among groups. In addition, it has the capability to incorporate subject-specific covariates such as age, IQ, or behavioral data. Simulations were performed to illustrate power comparisons and the capability of controlling type I errors among various significance testing methods, and the results indicated that the testing statistic we adopted struck a good balance between power gain and type I error control. Our approach is instantiated in an open-source, freely distributed program that may be used on any dataset stored in the universal neuroimaging file transfer (NIfTI) format. To date, the main impediment for more accurate testing that incorporates both within- and cross-subject variability has been the high computational cost. Our efficient implementation makes this approach practical. We recommend its use in lieu of the less accurate approach in the conventional group analysis.

Introduction

Group analysis of fMRI datasets is typically carried out in two levels. In the first level, each individual subject’s dataset is analyzed in a time series regression model to provide a measure of the effect of interest (linear combination of regression coefficients) at each voxel. In the second level, the effect estimates of interest at each voxel in standard space are combined across subjects using Student t-test, ANOVA, ANCOVA, multiple regression, or linear mixed-effects (LME) models. Then, group inferences are made with a general claim about a hypothesized population from which the sampled subjects were recruited. This two-level approach, by far the most common in published neuroimaging studies (Mumford and Nichols, 2009), rests on two assumptions. First, within- or intra-subject variance of the effect estimates is uniform in the group (Penny and Holmes, 2007), or alternatively, the between-subjects variance is much larger than within-subject variance. Second, effect estimates are assumed to follow a Gaussian distribution—i.e., no outliers.

The conventional group analysis strategy works reasonably well if the required assumptions hold to some extent. Given the small effect sizes and high noise levels in FMRI data, it is questionable to assume negligible or equal standard error of the individual subject effect estimates, or to ignore outliers in group analysis. Irregularities from the scanner or outlying BOLD responses can lead to the violation of the assumptions of small or homoscedastic sampling errors in the standard “summary statistics” approach (Penny and Holmes, 2007). Differences in attention to tasks and in habituation effects across subjects may also introduce different precision of effect estimates. Moreover, as sophisticated experiment designs evolve, it is very typical to have unequal numbers of subjects across groups, different numbers of data points (time series lengths), or different numbers of samples of a stimulus/ condition/task type across subjects. For example, due to experiment constraints or subjects missing trials, the data might have unequal number of correct versus incorrect responses, and such a scenario inevitably results in heterogeneous effect estimate precision (within-subject variability), potentially violating the assumptions of conventional group analysis methodologies.

Another potential concern in FMRI group analysis is that the group sample size is often fairly small; thus, one or two outliers can dramatically alter the effect estimate. Even though cross-subject variability is typically considered in practice to account for such inhomogeneity, outliers can inflate its estimate, leading to underpowered statistical testing. Another example is the emergence of aggregated or federated datasets that come from different scanners or laboratories, or with slightly different task/condition variants. The resulting reliability differences in effect estimation from multiple sources necessitate an approach that crucially incorporates the reliability heterogeneity into the model and controls for confounding effects (e.g., personality or phenotypic features) when amalgamating the datasets (Bjork et al., 2012).

Intuitively, a summarizing approach at the group level should consider differentiating each subject’s effect estimate based on its precision; that is, we assign a higher weight to a subject if the effect estimate has a narrower confidence interval (e.g., more reliable), and vice versa. Such weighting strategy can even be found in nature; for example, a high-level behavioral task is performed as an integration of multiple simple operations simultaneously executed by many neurons that weigh each sensory cue proportional to its reliability (Ohshiro et al., 2011). Recent FMRI group analysis approaches have explicitly considered both effect size and its variance at group level. Worsley et al. (2002) combined effect estimates with their standard deviations, and solved the resultant model with an expectation–maximization (EM) algorithm, assisted with spatial regularization. Beckmann et al. (2003) also discussed the incorporation of reliability information from the first level to second level analysis. Woolrich et al. (2004, 2008) adopted a Bayesian approach through Markov chain Monte Carlo (MCMC) sampling and multivariate non-central t-distribution fitting in group inference.

Our contributions here are three-fold. First, we present a computationally efficient frequentist approach that incorporates both within-and cross-subject variabilities at the group level, and model outliers with a Laplace distribution for the cross-subject random effects. We adopt a significance testing statistic that achieves power increase with type I errors still close to the nominal level. Our algorithms involve iterative schemes at the voxel level, and we achieve execution time on the order of minutes for the whole brain with a standard desktop computer. The performance of our approach will be compared with a Bayesian counterpart in activation inference with real data and in power gain and type I error control with simulated data. While the final whole brain statistical inferences may not change significantly from the standard approach in cases with sizeable or homogeneous groups, we make the case for the new approach because it is more accurate, is computationally efficient, and provides a more detailed description of the sources of variance, thereby enabling better insight into the data. Second, a few overall heterogeneity measures across subjects are provided. A statistic is available for significance testing of overall heterogeneity of the group. In addition, outlier testing is suggested at the individual level that may assist the investigator in identifying outlier subjects or in incorporating potential covariates that could account for across-subject variability. Third, we performed simulations in various scenarios to compare different significance testing methods in cross-subject variance estimate, type I error controllability, and power. These simulation results are compared with previous work by Woolrich et al. (2004) and Mumford and Nichols (2009).

Modeling strategy

Mixed-effects multilevel (or meta) analysis (MEMA)

To illustrate the utility of MEMA implemented in the AFNI (Cox, 1996) program suite as 3dMEMA, we consider a test dataset in which 10 subjects viewed audiovisual recordings of natural speech (details in Applications and results). These stimuli evoked robust activity in auditory and visual cortex in each subject, providing a good test bed for group analysis methods.

Using five voxels as examples

Fig. 1 shows effect size and variability estimates in five voxels selected from the 10-subject dataset, and illustrates the inaccuracy of the two assumptions made by traditional group analysis methods (same within-subject variance and no outliers). These five voxels were not randomly selected as representatives – if such voxels exist – of the entire brain; instead they were used to showcase various scenarios of inhomogeneity in effect estimate precision. Voxels 1 and 2 were extracted from right and left visual cortex (middle occipital gyrus) respectively, Voxels 3 and 4 were from a left auditory region, superior temporal gyrus (STS), and Voxel 5 was in left caudate. At least one of two assumptions in the conventional group analysis approach is violated at each of these five voxels. At all five voxels, the within-subject variability is significantly larger than the cross-subject variability, and differs markedly between subjects. At Voxels 1 and 2, only half of the ten subjects had reliable estimates that were significant at 0.05 level (two-sided, uncorrected), while Voxels 3, 4, and 5 had only three or less such subjects. Subject 10 is an outlier at Voxels 2 and 3, but in different ways: Voxel 2 is significantly activated with the same direction of the effect size (outlier with a reliable estimate with the same sign as the mean effect), while the effect at Voxel 3 is not statistically significant and has a different sign (outlier with an unreliable estimate with the opposite sign). The normal probability plots in Fig. 1 further indicate the existence of outliers at all five voxels. More subtly, in Voxel 1, Subjects 5, 6, 7, and 9 have roughly the same effect estimate but with markedly different variabilities.

Fig. 1.

(Upper panel) Individual subject effect estimates and their accuracy at five voxels are shown with amplitudes of FMRI response to an audiovisual speech stimulus in left and right visual cortex (Voxels 1 and 2), left and right auditory cortex (Voxels 3 and 4), and left caudate (Voxel 5). Effect estimates from individual subject analyses are indicated with filled circles (●). The variability of each estimate is shown with an error bar of two standard deviations, and the estimate precision is defined as the reciprocal of variance. The relative size of the filled circle reflects the weight of the estimate from each individual subject, reciprocal of the sum of within- and between-subject variances. The dotted horizontal line indicates the null hypothesis of group effect being 0. The gray horizontal line is the group effect estimated from the conventional approach, equal weighting across subjects with Student t-test. The black horizontal line is the group effect with the MEMA approach described in the manuscript. The gray and black lines overlap for Voxels 3 and 5. (Lower panel) Quantile–Quantile plots of the ten subjects’ effect estimates with circles (°) at the five voxels are shown against standard normal distribution (horizontal axis). The significant deviation of the end points from the solid line y=x at all five voxels indicates the existence of outliers among the subjects.

Presenting the MEMA model

The standard second-level analysis assumes that the within-subject variability for the effect of interest is relatively small or roughly the same across subjects (Penny and Holmes, 2007). The corresponding model with n subjects can be formulated into a regression equation with p+1 fixed effects,

$${\beta }_i=\sum _{j=0}^p{\alpha }_j{x}_{ij}+{\delta }_i=x_i^{T}a+{\delta }_i,i=1,\dots ,n,$$ (1)

where ${\mathbf{x}}_i^T=(x_{i0},\dots ,x_{ip})$ are known independent variables, a=(α₀, …, α_p)^T are parameters to be estimated, β_i is the effect of interest from the ith subject, and in particular, α₀ is associated with the intercept x_i0 =1. (A one-sample Student t-test can be performed using a model that corresponds to p=0). If p≥1, x_ij can be an indicator (dummy) variable showing, for example, the group to which the ith subject belongs, or a continuous variable such as a subject-specific covariate like age, IQ or behavioral data (j=1, …, p), or an interaction between fixed effects. δ_i is the subject-specific error, the amount the ith subject’s data deviates from the fixed effects at the population level, and is initially assumed to follow a normal distribution N(0, τ²).

Of course, we don’t really know the “true” effect β_i from the ith subject. Instead, what we have is its estimate β̂_i in the form of a linear combination of regression coefficients from individual analysis of the ith subject’s time series data. Naturally, such an estimate carries some precision information, where precision is defined as the reciprocal of the estimate variance. Thus, more accurately, we have

$${\widehat{\beta }}_i={\beta }_i+{\epsilon }_i$$ (2)

where ε_i represents the sampling error of β_i in the ith subject, and is assumed to follow $N(0,{\sigma }_i^2)$, where ${\sigma }_i^2$ is the intra-/within-subject variance, which is also unknown but can be estimated with ${\widehat{\sigma }}_i^2$ from the individual subject analysis.

Combining Eqs. (1) and (2), we have a mixed-effects multilevel (hierarchical, or meta) analysis (MEMA) model for data from n subjects ${\widehat{\beta }}_i={\displaystyle \sum _{j=0}^p}{\alpha }_j{x}_{ij}+{\delta }_i+{\epsilon }_i={\mathbf{X}}_i^T\mathbf{a}+{\delta }_i+{\epsilon }_i$, or $\widehat{\beta }i~N({\mathbf{x}}_i^T\mathbf{a},{\widehat{\sigma }}_i^2+{\tau }^2)$, i = 1, …, n or in a concise matrix format,

$$\widehat{\mathbf{b}}=X^T\mathbf{a}+\mathbf{d}+\mathbf{e},or\widehat{b}~N\left(X^T\mathbf{a},{\tau }^2{I}_n+\mathrm{\Phi }\right)$$ (3)

where b̂_n×1 = (β̂₁, …, β̂)^T, X_n×(p+1) =(x₁, …, x_n)^T, d_n×1 = (δ₁, …, δ_n)^T, e_n×1 = (ε₁, … ε_n)^T, ${\mathrm{\Phi }}_{n\times n}=\mathit{diag}\left({\widehat{\sigma }}_1^2,\dots ,{\widehat{\sigma }}_n^2\right)$, and I_n is an n × n identity matrix.

The assumptions underlying model (3) are: (a) ${\epsilon }_i~N(0,{\widehat{\sigma }}_i^2)$; (b) the δ_i’s are independent and identically distributed with N(0, τ²), where τ² is the cross-/inter-/between-subjects variability, sometimes called heterogeneity; (c) Cov(ε_i, ε_j)=0, for i ≠ j, meaning the data from any two subjects are independent; and (d) Cov(ε_i, δ_j)=0 for all i and j, indicating that cross- and within-subject variabilities are independent of each other. The variance of the effect of interest V (b̂) = τ²I_n + Φ reflects the fact that the total variability in the data comes from two sources (or a two-stage sampling process), within-subject variability Φ and cross-subject variability τ². We can also interpret the total variability in a Bayesian sense as two components of the investigator’s uncertainty (Raudenbush, 2009).

Solving MEMA

If we make the (unjustified) assumption that both the cross-subject and within-subject variances, τ² and ${\sigma }_i^2$, are known, the model (3) can be easily solved through weighted least squares (WLS) by minimizing the weighted sum of squared residuals (Kutner et al., 2004), and the solution is â = (X^TWX)⁻¹ X^TWb̂, where the weights in $W=\mathit{diag}\left(\frac{1}{{\tau }^2+{\sigma }_1^2},\dots ,\frac{1}{{\tau }^2+{\sigma }_n^2}\right)$ are the reciprocals of the sum of within-subject and cross-subject variances. The variance for â is a concave function,

$$V(\widehat{\mathbf{a}})={\left(X^{T}WX\right)}^{-1},$$ (4)

and â~N(a, (X^TWX)⁻¹). The derivation in (4) relies on the fact that W^½X is of full rank because W^½ and X are of full column rank and rank(W^½X)=rank(X). In practice both τ² and ${\sigma }_i^2$ are estimated, and so are the WLS solution for â and its variance V(â),

$$\widehat{a}={\left(X^T\widehat{W}X\right)}^{-1}{X}^T\widehat{W}\widehat{b},\widehat{V}(\widehat{a})={\left(X^T\widehat{W}X\right)}^{-1}$$ (5)

where $\widehat{W}=\mathit{diag}\left(\frac{1}{{\widehat{\tau }}^2+{\widehat{\sigma }}_1^2},\dots ,\frac{1}{{\widehat{\tau }}^2+{\widehat{\sigma }}_n^2}\right)$.

Estimating the cross-subject variability τ²

Despite the suggestion that no frequentist solution exists for the model (3) (Woolrich, 2008; Woolrich et al., 2004), there have been important developments in the context of meta-analysis or meta-regression (e.g., combining the results of independent clinical trials) during the past 20 years (Cooper et al., 2009; Hartung et al., 2008). Specifically, several methods of estimating τ² have been proposed (Viechtbauer, 2005), such as the method of moments (MOM) (DerSimonian and Laird, 1986), maximum likelihood (ML), restricted maximum likelihood (REML), empirical Bayesian (EB), among others (Hedges, 1983, 1989; Hunter and Schmidt, 1990; Sidik and Jonkman, 2005a; Sidik and Jonkman, 2005b). Here we will focus on three methods, MOM, REML, and ML using a Laplace distribution assumption of the within-subject variability (to allow for outliers). All the three methods are part of our implementation in 3dMEMA, and the choice of method is made partly depending on the data at voxel level.

Method of moments (MOM)

We start with a fixed-effects model by assuming no cross-subject variability (τ²=0) in Eq. (3),

$$\widehat{\mathbf{b}}=X{\mathbf{a}}_0+\mathbf{e}.$$ (6)

An ordinary least squares (OLS) or WLS solution for Eq. (6) provides a primary or provisional estimate of a₀ in the mixed-effects model (3). While the OLS estimate tends to perform well when τ² is relatively large, the WLS estimate is better when τ² is moderate or small. Here we adopt the WLS estimate,

$${\widehat{\mathbf{a}}}_0={\left(X^T{W}_{0}X\right)}^{-1}{X}^T{W}_0\widehat{\mathbf{b}},$$ (7)

and define the weighted residual sum of squares (WRSS) of the WLS estimate (7) as

$$Q={\left(\widehat{\mathbf{b}}-X{\widehat{\mathbf{a}}}_0\right)}^T{W}_0\left(\widehat{\mathbf{b}}-X{\widehat{\mathbf{a}}}_0\right)={\widehat{\mathbf{b}}}^T{P}_0\widehat{\mathbf{b}}$$ (8)

where $W_0=\mathit{diag}\left(\frac{1}{{\sigma }_1^2},\dots ,\frac{1}{{\sigma }_n^2}\right)$, and P₀ = W₀ −W₀X(X^TW₀X)⁻¹X^TW₀. Q is often called the homogeneity statistic since we pretend that the cross-subject variance τ²=0 in calculating Q, but this pretense allows us to use Q to measure how much cross-subject variability the data contain. In other words, if τ²=0, we expect Q to be small; on the other hand, if τ²>0, Q will most likely be big. The role of Q as an indicator of cross-subject variability is also reflected in its expected value, E(Q) = E(b̂^T P₀b̂ = τ²tr(P₀) + n−p−1. Equating Q to its expected value (Hartung et al., 2008), we obtain the MOM estimate of τ², ${\widehat{\tau }}^2=\frac{Q-(n-p-1)}{tr(P_0)}$. To avoid a negative estimate in computation a truncated version is usually employed,

$${\widehat{\tau }}^2=max\left(0,\frac{Q-(n-p-1)}{tr(P_0)}\right).$$ (9)

The MOM estimate, involving no iterative algorithms and thus computationally economical, is consistent but not necessarily efficient (Raudenbush, 2009; Viechtbauer, 2005), which leads us to a more efficient method, REML, for estimating τ². When the conventional group analysis assumption holds (all subjects have the same within-subject variance, ${\sigma }_1^2=\dots ={\sigma }_n^2={\sigma }^2$), it is instructive to note that the MOM estimate reduces to ${\widehat{\tau }}^2=\frac{1}{n-p-1}{\left(\widehat{\mathbf{b}}-X{\widehat{\mathbf{a}}}_0\right)}^T\left(\widehat{\mathbf{b}}-X{\widehat{\mathbf{a}}}_0\right)-{\sigma }^2$ as in this case tr(P₀)=(n −p−1)/σ². Furthermore, due to the truncation involved in (9), simulations (Viechtbauer, 2005) showed that MOM is slightly positively biased when the within-subject variance is very large or the number of degrees of freedom at individual level is too small, but the bias is negligible when the number of degrees of freedom at the individual level is above 40 and there are 10 or more subjects at group level, conditions typically satisfied in FMRI studies.

REML method

The profile residual log-likelihood for REML is the logarithm of the density of the observed effect treated as a function of the cross-subject variability τ², given the data b̂ (Raudenbush, 2009; Viechtbauer, 2005), $l\left(\mathbf{a},{\tau }^2;\widehat{\mathbf{b}}\right)=-\frac{1}{2}nln(2\pi )+\frac{1}{2}ln[det(W)]-\frac{1}{2}ln\left[det\left(X^{T}WX\right)\right]-\frac{1}{2}{\left(\widehat{\mathbf{b}}-X^T\mathbf{a}\right)}^{T}W\left(\widehat{\mathbf{b}}-X^T\mathbf{a}\right)=\frac{1}{2}nln(2\pi )+\frac{1}{2}ln[det(W)]-\frac{1}{2}ln\left[det\left(X^{T}WX\right)\right]-\frac{1}{2}{\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}$, which leads to a Fisher scoring (FS) algorithm that is robust even for poor starting values and usually converges quickly (Appendix A),

$${\tau }_{k+1}^2={\tau }_k^2+\frac{{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}-tr(P)}{tr(PP)},$$ (10)

where ${\tau }_k^2$ is the kth iterative approximation of τ², and P=W−WX(X^TWX)⁻¹X^TW. It is worth noting that, when all subjects have the same within-subject variance, the REML estimate has a closed and intuitive form (Appendix A), ${\widehat{\tau }}^2=\frac{1}{n-p-1}{\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)-{\sigma }^2$, exactly the same as the respective MOM estimate.

ML method with a Laplace distribution of subject-specific error

It is not rare to see extremely big or small effect estimates b̂ relative to the group effect at a voxel/region level (cf. Fig. 1). Such outliers might come from irregularities from the scanner, outlying BOLD responses, or pure chance. If these outlying effect estimates are unreliable (e.g., have large variances), the impact on the group result is minimal, regardless of the heterogeneity estimate for τ², MOM or REML, thanks to the weighting involved in WLS (5). However, if the outlying effect estimates are reliable (e.g., have small variances), weighting might not be effective enough and we need a more robust strategy to deal with such outliers. For instance, a subject might have been ignoring the stimulus during its presentation, leading to little or no response to the sensory input; this response would be reliable (with small variance), but should obviously not be combined with effect estimates from other subjects who were alert.

The REML estimate of τ² via (10) assumes a Gaussian distribution of individual subject’s sample error, ${\epsilon }_i~N(0,{\sigma }_i^2)$, i=1, …, n, at each voxel. The “default” Gaussian assumption is omnipresent, because of its convenient statistical properties and the central limit theorem. Appealing to this assumption works well if the sample size is reasonably big, which is not always the case in FMRI studies. When the assumption is violated (e.g., outlier voxels/regions/subjects), the cross-subject variability τ² tends to be over-estimated, and one or two outliers could dramatically distort the analysis, leading to inaccurate group effect estimates and/or deflated statistical power. The conventional approach of throwing away outliers is not only impracticable at the voxel level, but also subjective, arbitrary, and controversial in terms of outlier identification. Here we propose a tractable alternative model of cross-subject variability, the Laplace (or double exponential) distribution.

Wager et al. (2005) proposed an iteratively reweighted least squares method to handle outliers by iteratively standardizing the residuals by the median absolute deviation, but their model did not differentiate the residuals between within-subject and cross-subject variability. Woolrich (2008) assumed the mixtures of two Gaussian distributions in the framework of Bayesian approach, one for the normal and the other for the outlier subjects. Baker and Jackson (2008) considered three candidates of long-tailed distributions, Student t, arcsinh, and Subbotin (of which the Laplace distribution is a special case). By extending a method adopted for a case with p=0 by Demidenko (2004) to our model (3) in the frequentist context, we assume, instead of N(0, τ²), the following Laplace distribution for the subject-specific error term in Eq. (3), δ_i ~ L(0, ν), i=1, …, n, where L(m, ν) has density $p(x;m,v)=\frac{1}{2v}exp[-\mid x-m\mid /v]$ with location parameter (mean/mode/median) m and scale parameter ν (with a variance of 2ν²). The Laplace distribution has heavier tails than the normal distribution, allowing us to better handle outliers than REML, when one or two subjects have exceptionally unreliable effect estimates at a voxel or region. This approach reduces the disturbing effects from outliers without requiring arbitrary outlier decisions or thresholds from the investigator.

We adopt the Empirical Fisher Scoring (EFS) algorithm (Demidenko, 2004) in the following format,

$${\left[\begin{array}{c}a\\ \nu \end{array}\right]}_{k+1}={\left[\begin{array}{c}a\\ \nu \end{array}\right]}_k+{\lambda }_k{H}_k^{-1}{g}_k$$ (11)

where k is the iteration index; H_k and g_k are derived in Appendix B.

In description we refer to the Gaussian and Laplace approaches as the intention of adopting REML with Gaussian and ML with Laplace assumption. However, as explained in the Discussion, at voxel level the real implementation of REML with Gaussian and ML with Laplace assumption proceeds with MOM. Only if the MOM result reaches near significance or more would it be followed and materialized by REML or ML.

Statistical inferences with MEMA

Hypothesis testing

For the null hypothesis of a group effect

$$H_0:{\alpha }_j=0,$$ (12)

a testing statistic can be constructed from (5),

$$T_s={\frac{{\widehat{\alpha }}_j}{\sqrt{\left[{\left(X^T\widehat{W}X\right)}^{-1}\right]}}}_{jj}$$ (13)

where A_jj denotes the jth diagonal component of matrix A. When the number of subjects, n, is relatively large, T_S can be taken, with a Gaussian distribution approximation, as a Wald test (Hartung et al., 2008). However, the Wald test tends to be overly liberal when applied to cases with a moderate number of subjects (Hartung et al., 2008; Raudenbush, 2009), such as FMRI group analysis; thereby, it may be better approximated with a Studentized t-distribution.

The Gauss–Markov theorem guarantees that, if the cross- and within-subject variance τ² and ${\sigma }_i^2$ were known, the WLS estimate â in (5) would be unbiased with the lowest variance (X^TWX)⁻₁ among all linear unbiased estimates, the best linear unbiased estimator (BLUE). Furthermore, if the effect estimates b̂ from individual subject analyses follow a Gaussian distribution, the BLUE property can be extended to both linear and nonlinear unbiased estimates, based on the Cramér–Rao inequality. Such property gives the impression that the Studentized t-statistic T_S in (13) would lead to a statistical power from MEMA higher than or at least equal to the conventional approach of ignoring the within-subject variability. In practice, the “true” values of τ² and ${\sigma }_i^2$ are never known; thus, for each specific test, T_S may yield a higher or lower value than its counterpart with the conventional approach with Student t-test.¹ However, the BLUE property indicates that, on average, T_S may provide a more powerful inference to an extent that depends on the combined impact of within- and cross-subject variability (Beckmann et al., 2003) and on the presumed distributions under which the model fits the data.

Another complication about T_S is the determination of its degrees of freedom, due to the uncertainty resulting from estimating the within-subject variance ${\sigma }_i^2$. Various approaches have been proposed for approximating the degrees of freedom, including simply assigning n-p-1 (Viechtbauer, 2010), the Satterthwaite correction (Kiebel et al., 2003), estimation through spatially smoothed ratio of cross-subject variance and average within-subject variance (Worsley et al., 2002), or posterior fitting with a multivariate noncentral t-distribution from MCMC simulations (Woolrich et al., 2004). Mumford and Nichols (2009) showed that the estimate for effective degrees of freedom based on Satterthwaite approximation did not perform well with real and simulated data. Also, as a shortcut for MCMC sampling, the fast posterior approximation approach adopted in FLAME 1 of FSL (Woolrich et al., 2004), although presented under the Bayesian framework, is essentially equivalent to our REML solution (10) because of the non-informative prior with a uniform distribution. In addition, the significance-testing statistic implemented in FLAME 1 of FSL is basically T_S with the same fixed degrees of freedom across the brain, n-p-1.

An approximation method proposed by Kenward and Roger (1997) suggests inflating the estimated variance and then adjusting the degrees of freedom through Satterthwaite (1946) correction. Here we focus on providing a more accurate estimate of variance for the effect estimate â than V̂ (â) in (5). There are three sources of uncertainty that may contribute to biased estimate of V̂ (â) : (a) unknown but estimated within-subject variance ${\sigma }_i^2$, (b) unknown but estimated cross-subject variance τ², and (c) truncation practice in estimating cross-subject variance τ², as shown in MOM (9), REML (10), and outlier modeling with ML (11). The impact of the first two sources is unknown, but the third one would definitely lead to a positive bias. If an estimator is unbiased, the possibility of resulting in a negative estimate when the true τ²=0 is 50% (Viechtbauer, 2005). Thus the truncation practice is expected to cause a positive bias in estimating τ². The amount of bias decreases as the number of subjects, n, increases, or when the cross-subject variance becomes dominant. In other words, the bias is prevalent with small number of subjects or with a high ratio of within-subject relative to total variance. Using a simple case of one-sample test, we obtain V̂ (â) in Eq. (5) as ${\left({\displaystyle \sum _{i=1}^n}\frac{1}{{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2}\right)}^{-1}$, a monotonically increasing function of τ̂², indicating that positive bias in estimating τ² would result in T_S being over-conservative in controlling type I errors and under-powered in identifying activated regions in the brain.

Denote the mean sum of weighted least squares residuals as $S_{\widehat{W}}^2=\frac{1}{n-p-1}{\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}$, where b̂^TPb̂ is the weighted residual sum of squares (WRSS) for the WLS solution (5), and P = Ŵ^1/2P^*W^1/2 = Ŵ −ŴX(X^TWX)⁻¹ X^TŴ. Relative to (5), Knapp and Hartung (2003) suggested an improved estimator, $\widehat{V}(\widehat{\mathbf{a}})=S_{\widehat{W}}^2{\left(X^T\widehat{W}X\right)}^{-1}=\frac{1}{n-p-1}{\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}{\left(X^T\widehat{W}X\right)}^{-1}$, with the intention of using the scale factor $S_{\widehat{W}}^2$ to counteract biased estimate of V̂(â) in (5). Following Viechtbauer (2010), we generalize a t-statistic, proposed by Knapp and Hartung (2003) with the above improved variance estimator V̂(â) instead of the one in (5), to a new testing statistic for the null hypothesis (12),

$$T_{KH}=\frac{{\widehat{\alpha }}_i}{\sqrt{{\left[\frac{1}{n-p-1}\left({\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}\right){\left(X^T\widehat{W}X\right)}^{-1}\right]}_{jj}}}.$$ (14)

Assuming a t-distribution with n-p-1 degrees of freedom, this Studentized statistic T_KH in Eq. (14) has been shown to be more accurate than the Wald test and T_S with n-p-1 degrees of freedom (Knapp and Hartung, 2003; Sidik and Jonkman, 2005a). As b̂^TPb̂ follows a χ²(n-p-1)-distribution with both mean and variance being n-p-1 (Hartung et al., 2008), the scaling factor $S_{\widehat{W}}^2$ in the denominator of TKH can be smaller or greater than 1. As a result T_KH could yield values either larger or smaller than T_S in (13) with n-p-1 degrees of freedom. Hartung et al. (2008) recommended T_KH for the following two reasons: (a) a specific choice of degrees of freedom for T_S is controversial, and may render conservative testing results (see Voxel 5 in Applications and results); and (b) their simulations showed that T_KH was superior to T_S in holding the nominal significance level. We will also explore these two issues later with our own simulations.

Consider the two special cases of within-subject variability underlying the “summary statistics” approach to group analysis, in a one-sample test in the model (3) with only one explanatory variable (p=0 and X=(1, …, 1)^T): assuming negligible within-subject variability ( ${\sigma }_i^2\ll {\tau }^2$, or ${\sigma }_i^2\approx 0$, i=1, …, n), or assuming the same within-subject variability across all subjects, i.e., ${\sigma }_i^2=\dots ={\sigma }_n^2={\sigma }^2$ (Penny and Holmes, 2007). Since the solution (5) reduces to equal weighting among the individual effects, both T_S and T_KH reduce to the conventional one-sample Student t-test (Appendix C).

An extra statistical inference capability with the MEMA model (3) is that we can test the null hypothesis of homogeneity across subjects,

$$H_0:{\tau }^2=0$$ (15)

under which the model (3) reduces to the fixed-effects model (6).

Null hypothesis (15) can be tested by the homogeneity statistic Q defined in (8) with a quadratic χ²(n-p-1)-distribution, often described as Cochran’s χ² test (Viechtbauer, 2010). If null hypothesis (15) holds (the cross-subject variability is negligible), all the variance in the data comes from the within-subject variances, and the WLS solution (5) corresponds to the fixed-effects model in Eq. (6). A region in the brain where τ² is significantly nonzero indicates that there exists some variability or heterogeneity across subjects, and warrants further exploration when τ² is very large (i.e., much of the cross-subject heterogeneity is left improperly identified). Ideally, one would aim to explain as much of the cross-subject variability as possible with subject grouping and/or covariates such as age, IQ, etc., until the cross-subject random-effect component d can be dropped from the model (3) so that the fixed-effects model (6) would be appropriate. However, identifying all the possible explanatory variables for the model (6) is rarely achievable in real practice, especially with the massively univariate approach common in FMRI data analysis. On the other hand, Q-statistic provides a valid approach to defining a region of interest (ROI) that could be used to associate individual subject BOLD response with some behavioral measure (Lindquist et al., 2012), avoiding the problematic practice of ROI definition based on activation significance. One caveat about the Q-statistic is that it may become non-central in χ² distribution when the heterogeneity is noteworthy, i.e., some amount of cross-subject variability is unaccounted for in the model (3). The non-centrality impact on significance testing might be relatively small, but one potential improvement is to use a mixture of χ² distributions as shown in Lindquist et al. (2012).

In addition to the homogeneity Q-test (8), there are alternative statistics for null hypothesis (15) such as likelihood ratio (LR) tests (Lindquist et al., 2012), Wald test and Rao’s score tests. Lindquist et al. (2012) explored LR tests under three numerical solutions of cross-subject variance using a mixture of χ² distributions, and elaborated on the challenge of approximating the asymptotic property of the LR tests. Viechtbauer (2007) showed with simulations that the Q-test (8) has the best overall balance between type I error rate and power compared to the alternatives. For example, all the methods have comparable power in detecting heterogeneity, but the Q-test keeps type I error rate close to the nominal α-value (e.g., 0.05) when the number of within-subject data points is greater than 200, while the LR tests tend to be over-conservative in type I error control.

A side note here is that the fixed-effects model (15) can be applied to group analysis when there are only a few subjects or when summarizing the results from multiple runs or sessions at individual level. In the latter situation, the WLS solution (5) is considered better than the simple unweighted average that is widely used (Lazar et al., 2002) because the WLS method with each weight equal to the reciprocal of each run/session’s or each subject’s variance gives the BLUE for the group effect (Plackett, 1950). For single-subject analysis methods that cannot combine multiple imaging runs, this is the proper way to merge intra-subject results prior to the group level, which is better than simple averaging across runs or sessions that is currently practiced in the FMRI community.

Quantifying cross-subject variability

As a measure of cross-subject heterogeneity, τ² in the MEMA model (3) shows the extent to which the subjects differ from each other, but its value and interpretation are not directly comparable across studies because the effect magnitude is tied up with the factors in each specific experiment design such as task/condition, stimulus duration, brain regions, etc. Similarly, the Cochran’s χ² test, the Q-statistic defined in (8), is another measure of cross-subject heterogeneity, but it depends on the number of subjects, as shown by its expected value E(Q)= τ²tr(P₀)+ n −p−1. Due to these dependences, Higgins and Thompson (2002) proposed two measures of heterogeneity that, in addition to reflecting the amount of variability across subjects, are independent of n and effect magnitude (scale-free). Extending the original definition for simple meta-analysis in Higgins and Thompson (2002), we adopt the first measure of heterogeneity for our MEMA model (3), $H_0=\sqrt{\frac{Q}{n-p-1}}$. Alternatively, we replace Q with its estimated expectation value, τ̂²tr(P₀) + n−p−1, and obtain a slightly different definition,

$$H=\sqrt{\frac{{\widehat{\tau }}^{2}tr(P_0)}{n-p-1}+1}.$$ (16)

The factor (n−p−1)/tr(P₀) in (16) measures the weighted average within-subject variability, which is self-evident when no covariates exist (p=0) in the MEMA model (3). Because H=1 under the null hypothesis (15), H can be interpreted as the ratio of standard deviation at group level and the weighted average standard deviation at individual level; that is, H is an approximate ratio of confidence interval widths between the group and individual subject levels, or between the MEMA model (3) and its corresponding fixed-effects model (6). In other words, the variation across the individual effect estimates is H times what would be expected if cross-subject variability did not exist (Higgins and Thompson, 2002).

The second measure of heterogeneity is defined as,

$$I^2=\frac{H^2-1}{H^2}=\frac{{\widehat{\tau }}^2}{{\widehat{\tau }}^2+\frac{n-p-1}{tr(P_0)}}.$$ (17)

Like the popular concept of intra-class correlation (ICC), I² accounts for the proportion of total variability in the effect estimates that originates from the cross-subject rather than within-subject variability. According to Higgins and Thompson (2002), an H value above 1.5 (I² greater than 0.56) can be considered to show significant heterogeneity across subjects while H<1.2 (I²<0.31) should be of little concern.

Identifying outliers at regional level

With heterogeneous sampling variances incorporated in the MEMA model (3), we not only obtain a more accurate statistical testing, but also are able to estimate the heterogeneity measure τ² and test for the homogeneity of subjects with the Q-statistic (8). Furthermore, if we define

$${\lambda }_i=\frac{{\widehat{\sigma }}_i^2}{{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2},$$ (18)

λ_i can be interpreted as the proportion of total variability that comes from the ith subject, and may be used to identify voxels or regions where a subject has exceptionally low reliability. Conversely, similar to the heterogeneity measures H and I², and like the concept of ICC, $1-{\lambda }_i=\frac{{\widehat{\tau }}^2}{{\widehat{\tau }}^2+{\widehat{\sigma }}_i^2}$ provides a third heterogeneity measure that shows the proportion of total variability that occurs across subjects. In addition, the following Wald statistic

$$O_i=\frac{{\left[W\left(\widehat{\mathbf{b}}-X\widehat{\mathbf{a}}\right)\right]}_i}{\sqrt{{\left\{\mathit{Var}\left[W\left(\widehat{\mathbf{b}}-X\widehat{\mathbf{a}}\right)\right]\right\}}_{ii}}}=\frac{{\left(P\widehat{\mathbf{b}}\right)}_i}{\sqrt{{\left[\mathit{Var}\left(P\widehat{\mathbf{b}}\right)\right]}_{ii}}}=\frac{{\left(P\widehat{\mathbf{b}}\right)}_i}{\sqrt{{(P^T{W}^{-1}P)}_{ii}}}$$ (19)

gives a significance test for the null hypothesis about the residuals of the ith subject (Viechtbauer, 2010), H₀: β̂_i−x_i^Tâ = 0, or, δ̂_i + ε̂_i = 0, serving as another indicator for voxels or regions where a subject has exceptionally high or low effect size. Combining the heterogeneity measure τ̂², the homogeneity Q-test (8), λ_i, and the Wald test O_i (19), one can detect outlier regions or subjects, and further investigate the possibility of including covariates or grouping subjects, potentially fine-tuning the original model and increasing the statistical power.

Applications and results

MEMA: Model performance with real data

Description of the audiovisual experiment and the analyses

Our group analysis modeling strategy was applied to the data from a block-design experiment with 10 subjects, described at length as Experiment 1 in Nath and Beauchamp (2011). A brief account of the data follows. Whole brain BOLD data were acquired on a 3.0 T scanner with voxel size of 2.75×2.75×3 mm³ and repetition time (TR) of 2015 ms. Three 5-min scan runs were acquired for each subject, totaling 450 brain volumes.

Two types of audiovisual speech stimuli were presented to the subjects. In the first type, the video image was degraded, but the auditory content was not degraded, and vice versa for the second type. Each scan series contained five blocks of auditory-reliable and five blocks of visual-reliable congruent words. Each 20-second block contained ten trials, with one different word per trial lasting 1.1 to 1.8 s. Preprocessing steps included slice timing correction, motion registration, voxel-wise mean scaling, and alignment to the Talairach standard space in 2×2×2 mm³ resolution. Spatial smoothing was applied with a kernel size of 4 mm full width at half maximum.

The pre-processed data from each subject were concatenated across the three runs, and were analyzed with an ARMA(1, 1) model for the residual time series using 3dREMLfit. There are three approaches to handling multiple runs of data at individual subject level: a) analyze each run separately; b) concatenate all runs but analyze the data with separate regressors for an event type across runs; or c) concatenate all runs but analyze the data with the same regressor for an event type across runs. Unlike other FMRI data analysis packages that adopts either strategy a) or b), the insertion of a time discontinuity between runs/sessions in 3dREMLfit also allows the investigator to analyze all the data from one subject in a single regression with all runs/sessions included, while still modeling temporal correlations (Appendix D). Option c) could be important when the sample size of an event type is relatively small in a single run. Two regressors of interest, auditory-reliable and visual-reliable stimuli, were created through convolution between stimulus timing with a shape-presumed HDR function (e.g., Cohen, 1997). Six head motion parameters were added in the model as regressors of no interest. In addition, third order Legendre polynomials were included to account for slow drifts in the data. The effect of interest in the analysis was the contrast between auditory-reliable and visual-reliable stimuli. Group analysis was performed on this contrast with four different methods: (a) Student t-test, (b) T_S with the assumption of Gaussian distribution for the cross-subject random effects, (c) T_KH with the assumption of Gaussian distribution for the cross-subject random effects, and (d) T_KH in (14) with the assumption of Laplace distribution of the cross-subject random effects.

Tracking five voxels

Data at five voxels (Fig. 1) were extracted for demonstration purposes. The results of Student t-test and several MEMA analyses are listed in Appendix E. In summary, the cross-subject variability is very small relative to the within-subject variability at all five voxels. The conventional approach might render a lower or higher group effect estimate (lower: Voxels 1, 3; higher: Voxels 2, 4) as well as its statistic value (lower: Voxels 1, 2, 3; higher: Voxel 4) than the MEMA methods, depending on the specific interplay of three factors, varying precision, cross-subject variability and the presence of outliers, as shown in the impacts on the results at all five voxels. The adjustment via the scaling factor in T_KH does not involve the estimate of cross-subject variability τ², which remains the same between the two tests T_S and T_KH, but might increase (Voxels 1, 4) or decrease (Voxels 2, 3) the t-statistic relative to T_S under the Gaussian assumption, and the same holds under the Laplace assumption (increase: Voxel 4; decrease: Voxels 1, 2, 3). The Laplace assumption tends to estimate a smaller cross-subject variability, especially when outliers are present (Voxels 1, 2, 3) than the Gaussian assumption and the conventional method, and might provide higher (Voxels 1, 2) or lower (Voxel 3) statistical values. The Q-statistic, defined in (8) for testing cross-subject variability (null hypothesis τ²=0), depends on within-subject variances only; thus, its value remains the same between the Gaussian and Laplace assumptions and between the two t-tests T_S and T_KH. In addition to the improved accuracy in group effect estimates and significance testing compared to the conventional approach, MEMA also provides statistical inference on the heterogeneity τ² across subjects, compares the two sources of data variability, and assists the investigator in identifying those subjects that have significantly outlying effect estimates.

To reiterate, with outlier modeling combined with adjusted t-test T_KH, MEMA resulted in a higher statistic power for voxels 1, 2, and 3, because effect estimates with large variance were down-weighted and the use of Laplace distribution accommodates better the presence of outliers. However, the conventional method provided a higher group effect estimate and the statistical power in voxel 4 because subjects showing the largest effect also had the largest variance, thereby reducing their contribution to the group effect estimate in MEMA compared to the Student t-test. Voxel 5 yielded similar significance between Student t-test and MEMA when T_KH is applied. This case demonstrates the importance of the adjustment adopted in T_KH: despite the large within-subject variance, the effect is deemed significant because it is consistent across subjects — negligible inter-subject variance (τ²=0); however, if only the precision information is used in T_S, then the statistical power is lost.

Comparisons among various group analysis approaches

As an empirical comparison between our frequentist and a Bayesian implementation, we performed a similar group analysis on the same datasets with FLAME 1 and FLAME 1+2 (Woolrich, 2008) of FSL (version 4.1.4). Significance maps are compared among six group analysis approaches: Student t-test, three MEMA methods, FLAME 1 and FLAME 1+2 (Fig. 2). Results from Student and all MEMA t-tests were converted to z-scores for easy comparison with FLAME in FSL. FLAME 1+2 with and without the outlier assumption generated identical results. All six methods rendered similar one-tailed significance map at the 0.05 level, especially for the two main regions of interest, bilateral superior temporal sulci (STS) for auditory function (upper panel in Fig. 2) and the visual cortex (lower panel). The results from T_S with Gaussian assumption and FLAME 1 (not shown in Fig. 2) were virtually identical in significance map. Runtime comparison is shown in Table 1, and was markedly different, with MEMA being similar to FLAME 1, but 10 to 50 times faster than FLAME 1+2 at comparable settings.

Fig. 2.

Significance maps of five group analysis methods. The upper panel (Z=59) shows the visual cortex activations in axial view with warm colors of z-score while the lower panel (Z=74) indicates the auditory activations in STS with cold colors. One-tailed significance level was set at 0.05 without cluster thresholding. FLAME 1 result (not shown here) is virtually identical to 3dMEMA with TS (13) and Gaussian assumption (column C).

Table 1.

Runtime (in minutes) comparison ^a between MEMA and FLAME in FSL.

Program	3dMEMAb		FLAME 1	FLAME 1+2
Outlier modeling	1 processor	4 processors
Without	8	3	6	385
With	65	20.5	---	847

^aGroup analysis on a Mac OS X 10.6.2 with 2×2.66 GHz dual-core Intel Xeon: 10 subjects, 218,379 voxels in 2×2×2 mm³ resolution inside the brain in Talairach standard space.

^bRuntime difference between MEMA t-tests TS and TKH is negligible.

The subtle difference among the six testing statistics is more revealing in scatterplots and histograms (Fig. 3). There are some small to large differences in z-scores between T_KH and Student t-test (panel (A) in Fig. 3). Among the voxels where these two methods differed by more than 0.5 in z-score, 63.2% had higher statistic value with the MEMA test. The adjustment in T_KH made a big difference relative to its Studentized counterpart T_S, resulting higher statistic values in 85.9% of voxels (panel (B)). The difference between Gaussian and Laplacian assumption is relatively small (panel (C)), indicating few outliers in the group. FLAME 1+2 gave some significantly different results from T_KH. Although the latter had higher statistic values at 60.8% of voxels among those voxels that differed by more than 0.5, FLAME 1+2 had extremely high statistic values at small proportion of voxels, also shown in the significance maps in (E) of Fig. 2. The equivalence between T_S and FLAME 1 is demonstrated in (E) of Fig. 3. The moderate differences between the two methods with those voxels not significant (gray in (E)) at one-sided level of 0.05 were due to the fact that, to save runtime for such voxels, 3dMEMA adopts MOM and avoids the unnecessary REML iterations. Moreover, 3dMEMA has the flexibility to allow a small proportion of subjects to have missing individual subject t-statistics at voxel level, as shown in those voxels on the y-axis in (D) and (E) of Fig. 3, which also gives slightly different results than FLAME 1.

Fig. 3.

Scatterplots (left) and histograms (right) that compare the z-scores of six group analysis methods. The shaded areas in scatterplots indicate that both z-scores are below 1.645 (corresponding to one-tailed significance level of 0.05). The data points on the y-axis in (D) and (E) are due to the fact that 3dMEMA allows missing data while FLAME in FSL does not. The histograms show the corresponding z-score difference to the scatterplots among the voxels not shaded (voxels with missing data were also excluded).

In addition to providing more accurate group effect estimates and significance testing, the MEMA modeling approach can also assess to what extent the subjects within a group differ with each other in terms of effect size. 3dMEMA outputs three measures of such heterogeneity: (a) the Q-statistic (8) measures the overall variability within the group; (b) λ in (18) shows the percentage of total variability that comes from the ith subject; and (c) the Wald test (19) for each subject indicates the significance level of how much the subject deviates from the weighted average effect of the group.

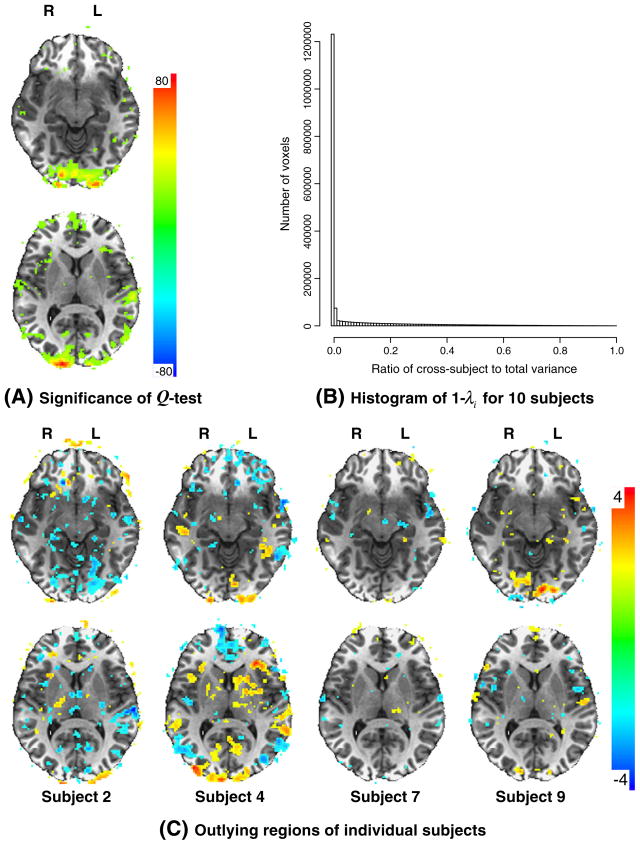
The results of the three measures for the experiment data are shown in Fig. 4. The Q-statistic (Fig. 4A) indicates that there was significant amount of variability in the visual cortex across the ten subjects while moderate amount of heterogeneity existed in the STS area. Such heterogeneity, measured with τ_i, was partly due to the intrinsic differences across subjects and partly due to the imperfect alignment from individual brains to a template in standard space, and it is a daunting job to tease apart these two components. The ICC-type measure 1− λ_i (Fig. 4B) shows that the data variability is dominated by within-subject variance, and that the percent of voxels with the ratio of cross-subject to total variance below 0.01, 0.10, 0.30 and 0.50 was 71.4%, 79.6%, 89.8%, and 95.5%, respectively, among all voxels in the brain. The histogram distribution for those voxels with one-tailed significance level of 0.05 under T_KH is not shown in Fig. 4B but is very similar, and the percentage of voxels with the ratio of cross-subject to total variance below 0.01, 0.10, 0.30, and 0.50 was 75.8%, 81.7%, 88.9%, and 93.6%, respectively. Consistent with the heterogeneity assessment of the Q-statistic at the group level, the Wald test from (19) shows more specific outliers at the individual subject level (Fig. 4C). For example, subject 7 was relatively close to the group average in both visual and auditory response, and so was subject 9 in auditory response. Subject 2 mostly had significantly lower visual response, while the visual response from subjects 4 and 9 was largely higher than average. Similarly, subject 2 had lower response in the auditory region STS, and subject 9 had higher response. These Wald test results can assist the researcher in pinpointing those specific subjects that may need further investigation, including alignment improvement and incorporating auxiliary variables that may account for such outlying effects.

Fig. 4.

Outlier detection with MEMA. (A) Homogeneity of subjects (τ²=0) under Gaussian distribution assumption for cross-subject random effects can be tested with Q-test (8) with a χ²-distribution. (B) Histogram of cross-subject relative to the total variance among 1,829,050 voxels (resolution 2×2×2 mm³) in the brains of 10 subjects. The number of cells at the x-axis is 100 with a resolution of 0.01 for the variance ratio. The cross-subject variance τ² is estimated with REML (14). (C) The Wald test O_i result for four subjects in outlier identification is shown. In both (A) and (C) the upper panel (Z=59) shows the visual cortex region in axial view while the lower panel (Z=74) focuses on the STS. One-tailed significance level was set at 0.05 without cluster thresholding.

MEMA: Model performance with simulated data

Description of the simulations

Simulated data were generated to assess power and controllability for type I errors in a much broader and more controlled spectrum than is possible with the results from real data. We aimed to compare various testing statistics from the following three perspectives: sample size n (number of subjects), heterogeneity among within-subject variances (how different are ${\sigma }_i^2$′s across subjects?), and the relative ratio of within- to cross-subject variance. Six significance testing statistics were considered: Student t(n-p-1), T_S(n-p-1) and T_KH(n-p-1) with the Gaussian assumption for cross-subject random effects, T_KH(n-p-1) with Laplace assumption for cross-subject random effects, and FLAME 1 and FLAME 1+2 in FSL.

The simulated data were in the units of percent signal change. We adopted a similar approach to Mumford and Nichols (2009) with an average within-subject variance σ̄² for the majority (90% or 80%) of subjects and with the rest of the subjects in the sample having a different within-subject variance denoted by ${\overline{\sigma }}_o^2$; 12 different cases were simulated, with ${\overline{\sigma }}_o^2$ ranging over 1/3, 1/2, 1, 2, …, 10 times σ̄² (so the last 9 cases have “outliers”, the first 2 cases have “inliers”, and the third case is the reference situation with all subjects having the same variance). For all subjects, the number of degrees of freedom for individual subject analysis was set as DF=400 (corresponding to over 400 time points in EPI time series), and for the majority (90% or 80%) of subjects, the nominal total variance was fixed at $V_T={\tau }^2+{\overline{\sigma }}_o^2={10}^{-4}$. The nominal cross-subject variance τ² was simulated with 20 cases in the interval [0, V_T), with sampling step of 5.0×10⁻⁶, and the corresponding average within-subject variance was set to σ̄² = V_T −τ² for the majority of subjects. The effect size δ for power simulations with n subjects was chosen to achieve a power of 0.8 for a two-tailed Student t(n−1)-test with a known total variance V_T based on $p_t(q_t(1-a/2,n-1)-\sqrt{n}\delta /\sqrt{V_T},n-1)=b$, where p_t, q_t, a= 0.05, and b= 0.20 are the Student t cumulative distribution, its quantile function, and the types I and II error probabilities, respectively. Group analysis was run with the number of subjects n=10 and 20 respectively for each of the six testing statistics, and with 5000 repetitions sampled with ${\beta }_i~N({\alpha }_0,{\tau }^2+{\widehat{\sigma }}_i^2)$ for the ith subject, where the intercept α₀ in the model (3) is the group mean effect (α₀ =0 for type I error simulations and for power simulations), and ${\widehat{\sigma }}_i^2$ is the estimated within-subject variance drawn from σ̄₂χ²(DF)/DF for the majority of subjects and from ${\overline{\sigma }}_o^2{\chi }^2(DF)/DF$ for the outlying subjects.

In real data the ratio of cross-subject variance to the total variance τ²/ (τ² + σ̄²) varies significantly across different studies. This heterogeneity measure is very small or mostly close to zero for most voxels in our experimental data, as shown in Fig. 4B, with values below 0.01, 0.10, 0.30 and 0.50 being 71.4%, 79.6%, 89.8% and 95.5%, respectively among all voxels in the brain. Among the six group analysis datasets surveyed in Table 2 of Mumford and Nichols (2009), the average values were 0.74, 0.31, 0.54, 0.71, and 0.56. Due to this wide variability, we ran 20 simulation cases with τ²/ (τ² + σ̄²) sampled at 20 equally spaced points within [0, 1), as described above.

To summarize, our simulations were performed for cross-subject variance τ², type I error rate, and power from four dimensions: (a) outlying mean within-subject ${\overline{\sigma }}_o^2$ varied from 1/3, 1/2, 1, 2, …, 10 times of σ̄²; (b) τ² varied at 20 equally spaced points within [0, 1.0×10⁻⁴); (c) sample size n=10 and 20; and (d) proportion of subjects that have outlying mean within-subject ${\overline{\sigma }}_o^2$ was set to 10% or 20%.

Simulation results

The simulation results are summarized from three perspectives: estimated cross-subject variance τ̂² (versus the nominal value τ²), the type I error rate, and the statistical power. These three values are graphed in the three columns of Fig. 5 for the case n=10 with 1 outlying subject, for various values of τ²/ (τ₂ + σ̄²), with the x-axis being the relative amount of outlier variance $\left({\overline{\sigma }}_o^2-{\overline{\sigma }}^2\right)/{\overline{\sigma }}^2$, which ranges from −2 to 9. (Similar figures for n=20 and for two outlying subjects are given in the online Supplemental Material.) Assuming outliers in FLAME 1+2 took much longer time than the analyses without this assumption (total simulation time: 1 week versus 2 days), but it did not lead to any difference in simulation results. The FLAME 1 results (purple) are virtually invisible in Fig. 5 because they are basically the same as and thus hidden underneath T_S with the Gaussian assumption (green). The two plots of type I error and power on the fourth row (with 50% of cross-subject relative to total variance), within the interval [0, 7] of the x-axis, roughly correspond to and are consistent with Fig. 3 in Mumford and Nichols (2009). Note that the x-axis $\left({\overline{\sigma }}_o^2-{\overline{\sigma }}^2\right)/{\overline{\sigma }}^2$ in Fig. 5 here is plotted linearly with respect to the outlying mean within-subject variance ${\overline{\sigma }}_o^2$ while the x-axis $\left({\overline{\sigma }}_o^2-{\overline{\sigma }}^2\right)/\left({\overline{\sigma }}_o^2+{\tau }^2\right)$ in Fig. 3 of Mumford and Nichols (2009) was arranged nonlinearly with respect to ${\overline{\sigma }}_o^2$, leading to the outlying cases being densely populated at the far right end of their x-axis.

Fig. 5.

Simulation results with six testing statistics (color coded as shown in the legend of upper left plot) and n=10 subjects one of which had outlying within-subject variance ${\overline{\sigma }}_o^2$. The 6×3 matrix of plots is arranged as follows. The three columns are estimated cross-subject variance, type I error controllability, and power respectively, and each row corresponds to the proportion of cross-subject variance relative to the total variance, $\frac{{\tau }^2}{{\tau }^2+{\overline{\sigma }}^2}$. The x-axis is $\frac{{\overline{\sigma }}_o^2-{\overline{\sigma }}^2}{{\overline{\sigma }}^2}$, the multiple of outlying within-subject variance more than the average. The dotted black line in the third column shows the nominal cross-subject variance, τ². The curves were fitted through loess smoothing with the second order of local polynomials.

All tests, except FLAME 1+2, converge in type I error rate (second column) and in power (third column) as τ²/ (τ² + σ̄²) approaches 100%, consistent with the fact that all the MEMA methods reduce to the Student t-test when the cross-subject variance σ̄² ≪ τ². Such convergence also holds for cross-subject variance (first column) for all testing methods, except for T_KH with the Laplacian distributional assumption; presumably this mismatch is due to underestimation with the Laplacian assumption since the data is actually sampled from Gaussian distributions. The first row of Fig. 5 corresponds to τ²=0 (i.e., no random effect across all subjects) under which the MEMA model reduces to the fixed-effects model (6) and WLS.

In terms of estimation for the cross-subject variance τ² (first column in Fig. 5), FLAME 1 (purple), T_S (green) and T_KH with the Gaussian assumption (red, overlaying purple and green) have the same estimate. (Student t does not provide such estimation because of the assumption of equal within-subject variance.) When τ²/(τ² + σ̄²) is relatively small (30% or less), the positive bias due to numerical truncation is evident for all three τ² estimates. FLAME 1, T_S and T_KH with Gaussian assumption have the highest bias, while the bias from T_KH with the Laplacian assumption (blue) is the lowest. However, as τ² becomes moderate or large, all methods tend to have unbiased τ² estimates, except that T_KH with the Laplacian assumption gives an exceptionally small estimate.

In regard to type I error controllability (second column in Fig. 5), Student t-test (black) is slightly conservative when the outlying variance ${\overline{\sigma }}_o^2$ becomes relatively large. In contrast, T_S (green) and FLAME 1 (purple, mostly overlaid by green) are overly conservative when τ²/ (τ² + σ̄²) is 50% or below, due to the overestimated cross-subject variance from the numerical truncation involved in the methods. When τ²/ (τ² + σ̄²) is more than 50%, these two methods have type I errors very close to the nominal rate (0.05). T_KH with the Gaussian (red) and Laplacian (blue) assumptions also have type I errors close to the nominal level when τ²/ (τ² + σ̄²) is 10% or below, indicating the effectiveness of modifying the estimated variance adopted in T_KH. When the outlying within-subject variance ${\overline{\sigma }}_o^2$ is relatively big or small, their type I error control becomes a little liberal when τ²/ (τ² + σ̄²) is 30% or above, with T_KH for the Gaussian assumption going up to 0.055 and T_KH for the Laplacian assumption up to 0.06, probably due to the uncertainty in replacing within-subject variances with standard errors. FLAME 1+2 (orange) shows the poorest control in type I errors, that in some cases exceeds 0.1. This assessment of the poor type I error control of FLAME 1+2 is consistent with the simulation results presented in Fig. 6 of Woolrich et al. (2004), which unfortunately seems to have been mistakenly interpreted in the opposite direction in their conclusion.

In power comparisons with 10 subjects, one of which has outlying within-subject variance (Fig. 5), all the MEMA testing statistics are more powerful than Student t, except that T_S and FLAME 1 are slightly underpowered only when ${\overline{\sigma }}_o^2$ is between 1/3 and 3 times of σ̄², probably due to their over-conservative performance in controlling type I errors. The general trend is that more heterogeneous within-subject variance or a higher ratio of within-subject relative to total variance leads to higher power gain of MEMA methods. T_KH with the Gaussian and Laplacian assumptions achieve roughly the same power, with the latter having a slightly higher edge when τ²/ (τ² + σ̄²) is between 50% and 90%. FLAME 1+2 shows the highest power among all methods, but at the significant cost of poorest type I error control.

The above overall assessment is still generally true with a bigger sample size (n=20 subjects, Fig. S1 in Supplementary Material). In addition, the power advantage of MEMA methods with 20 subjects relative to Student t-test is slightly smaller than the case with 10 subjects when τ² is about 50% relative to the total variance, consistent with Mumford and Nichols (2009). However, the power gain for the MEMA methods with 20 subjects becomes bigger than the case with 10 subjects when τ² is 30% or below. With 10 subjects 20% of which have outlying within-subject variance ${\overline{\sigma }}_o^2$ (Fig. S2 in Supplementary Material), the power loss for Student t-test becomes even more significant, and all MEMA methods keep bigger advantage in power than Student t while T_KH with Gaussian and Laplacian assumption also shows slightly increased type I errors.

Also notice that at the origin of the x-axis $\left({\overline{\sigma }}_o^2-{\overline{\sigma }}^2\right)/{\overline{\sigma }}^2=0$, where the assumption for the “summary statistics” lies, presumably all the MEMA methods should converge to Student t-test, as shown in Appendix C, which is mostly true in type I error rate and power for T_KH for both the Gaussian and Laplacian assumptions. However, it is not clear to us why such convergence largely fails to occur in type I error rate and power for FLAME 1+2.

In summary, T_S and FLAME 1 have good control in type I errors and may become too conservative due to numerical truncation when the cross-subject variability is small. They mostly achieve a moderate power advantage over Student t-test, and may become slightly underpowered when the cross-subject variability is small. T_KH for the Gaussian and Laplacian assumption strikes a reasonable balance in type I error control and power achievement, and both are mildly liberal in type I error rate, with the former being slightly less liberal than the latter. The mildly liberal control in type I errors occurs when the outlying subjects have much more or less reliable effect estimates, and likely results from the uncertainty when using the sampled (instead of “true”) within-subject variances. Even with the simulated data sampled from Gaussian distributions, T_KH for the Laplacian assumption performed relatively well in type I errors and power. It is worth noting that the power advantage of all MEMA methods over the conventional Student t-test occurs with the presence of outlying subjects, not only with higher within-subject variance, but also with higher precision for the effect estimate, especially when the heterogeneity measure τ²/ (τ² + σ̄²) is less than 30%. FLAME 1+2 is generally highly powered, but this apparent advantage is associated with its overly liberal type I error control.

Discussion

Overview

Conventional FMRI group analysis hinges on the assumption that the within-subject variance for the effect of interest is the same across all subjects, or alternatively that the within-subject variance is negligible relative to the cross-subject variance. In addition, outliers are commonly not considered in the analysis. These models range from one-, two-sample, or paired Student t-tests, ANOVA, ANCOVA, to multiple regression and, most generically, linear mixed-effects (LME) analysis. We illustrate here that such assumptions about the within-and cross-subject variability are not always accurate, and present a frequentist approach to FMRI group analysis, mixed-effects multilevel analysis (MEMA), that incorporates both the variability across subjects and the precision estimate of each effect of interest from individual subject analyses, and is capable of modeling outliers. That is, we take both the effect estimates (typically referred to as β values or their linear combinations) and their t-statistics from time series analysis at the individual level as inputs for group analysis. If the cross-subject random component is assumed to follow Gaussian statistics, its voxel-wise variance is estimated by maximizing a restricted likelihood (REML) function. Optionally, a Laplace distribution can be used to model outliers for the cross-subject random component, and the corresponding voxel-wise variance is then estimated through maximizing the likelihood (ML). The group effect is estimated through weighted least squares (WLS) based on the estimates of both within- and cross-subject variances, which is more accurate than the equally weighted approach in conventional group analysis. Moreover, we adopt a statistical testing procedure more accurate than the usual alternatives, especially when the sample size is moderate or small.

Our MEMA algorithms involve iterative schemes at voxel level and the computational cost is relatively low. The method allows one-sample tests and comparisons among conditions and among groups. In addition, it has the capability of incorporating covariates such as subject-specific measures (e.g., age, IQ, or behavioral data). It can also include one or more subject grouping (or between-subjects) factors (e.g., sex, genotype, handedness). In addition to group effect estimates and their corresponding t-statistics, our approach provides cross-subject heterogeneity estimates and significance testing with a χ²-test, and for each subject the percentage of within-subject variability relative to the total variance and a Z-score showing the significance of a region in the subject being an outlier.

Theoretically, almost all the methods that incorporate within-subject variability in group analysis (Kiebel et al., 2003; Woolrich et al., 2004; Worsley et al., 2002) share the same estimation philosophy for the effects of interest as our WLS solution (5), but differ in numerical strategy for estimating the cross-subject variance and in significance testing methodology when dealing with the precision issue of estimating the within-subject variances. Worsley et al. (2002) obtained a slightly biased estimate for the cross-subject variance τ² using a few iterations, and then compensated for the increased bias through the effective degrees of freedom for T_S, based on spatial regularization with EM algorithm. Kiebel et al. (2003) proposed that the degrees of freedom be estimated for T_S with the Satterthwaite correction. Woolrich et al. (2004) estimated the effect of interest and the degrees of freedom for T_S through the posterior approximation of MCMC simulations. Here, we present two options for estimating the cross-subject variance τ²: REML approximation with a Gaussian distributional assumption, and ML estimation with a Laplace assumption when outliers might be present. Instead of modifying the degrees of freedom, we make adjustment of the variance estimate for the effect of interest, and achieve a counterbalance between type I error rate and accurate power in significance testing with T_KH. Our simulation results showed that our adoption of T_KH achieved a good balance in type I error control and power. In comparison, FLAME 1 in FSL is equivalent to our T_S with REML estimate of cross-subject variance with the Gaussian assumption. On the other hand, FLAME 1+2, although highly-powered, seems to have unsatisfactory control of type I errors.

Weighted versus unweighted effect estimation

Mumford and Nichols (2009) investigated the specificity and sensitivity of the conventional group analysis in the case of one-sample test, and found that the one-sample Student t-test is valid in the following sense: (a) its type I error was slightly conservative, especially when the number of subjects is small and/or the heterogeneity of within-subject variability is significant; (b) the power loss is little to moderate, depending on the sample size and the precision differences across subjects. Such assessment was consistent with the fact that the sum of within- and cross-subjects variance estimates is unbiased, although not the minimum variance estimate (BLUE) used in MEMA. Our simulations included the scenario explored in Mumford and Nichols (2009) as a special case, and investigated a much wider spectrum of the ratio of within-subject relative to total variance and the proportion of outlying subjects.

Given the fact that our implementation is computationally efficient, we recommend that MEMA be the default approach for testing. We also recommend that users consider the heterogeneity Q-maps, and individual outlier Z-score maps as a guide for potential inclusion of covariates or for subject grouping categories. This approach would also allow users to readily test whether the assumptions of the conventional approach are justified and whether they alter the resultant maps. Moreover, much effort has been invested into modeling the temporal correlation in the residuals of the time series regression model at the individual subject level, leading to relatively more accurate statistical testing (Kiebel and Holmes, 2007; Woolrich et al., 2001; Worsley et al., 2002) and more accurate estimates of effect reliability (i.e., standard error of β̂_i). These results should be used not only at the individual subject level, which is usually not the ultimate goal and interest in FMRI-based research. They can and should further lead to more accurate and fruitful results at the group level by bringing the precision information about the effect estimates as extra inputs for group analyses. With the computationally efficient implementation, the higher accuracy of statistical tests (e.g., T_KH versus T_S), and the potential gain in statistical power, we have no reason not to recommend the MEMA approach instead of the Student t-test. Under most circumstances, the gains are modest but appreciable; in some cases, the MEMA analysis has detected and compensated for outlier results that were otherwise disruptive in a standard group analysis.

Implementation of our modeling strategies in AFNI

Our program 3dMEMA in AFNI is written in the open source statistical language R (R Development Core Team, 2010), taking advantage of parallel computing on multi-core systems. As the FS algorithm for REML (10) is very efficient, convergence is achieved within a few iterations at most voxels, leading to a runtime of a few minutes for a typical analysis on a Mac OS X system with two 2.66 GHz dual-core Intel Xeon processors. The software outputs the estimate (5) for each effect of interest at the population level, and its corresponding significance testing statistic T_KH, plus the cross-subject heterogeneity estimate τ̂² and its Q-statistic. 3dMEMA also provides λ_i, the proportion of total variability that originates from the ith subject based on (18), and Z-value (19) for the significance of residuals of the ith subject. When the outlying within-subject variance is relatively too big or small and when cross-subject variance is moderate or large, the slightly liberal control of type I errors in T_KH especially with the Laplacian assumption may be of some concern; however, the effect of potentially increased false positives would be relatively negligible with regard to cluster thresholding in multiple testing correction.² When comparing two groups, the investigator can presume the same or different within-group variability (homo- or heteroscedasticity) in 3dMEMA, and in the latter case the two within-group variances and their ratios are also provided.

To save runtime, the implementation of MEMA is a combination of all the three methods discussed in this paper: MOM, REML with FS, and ML with EFS. The MOM estimate (9) is tried first, since it does not involve iterations; this method is adequate for most voxels in the brain where the effect size is essentially 0. If outlier modeling is requested by the user, the program implements the iterative Laplace model (11) only when the statistic for MOM is likely significant (e.g., a lenient two-tailed significance level of 0.2 for the effect estimate), or when at least one subject is a potential outlier, evaluated through the significance in (19). If outlier modeling is not requested, the program uses the FS algorithm (10) for REML estimation only when the statistic for MOM is likely significant.

Missing effect estimate data from individual subjects often occurs in FMRI along the edge of the brain, due to imperfect alignment in spatial normalization to standard space, as shown in Fig. 3 with our experiment data. This missing data issue is even more prevalent in electrocorticographical (ECoG) data from neurosurgical patients, because not all patients get the same cortical coverage and the implanted subdural electrodes (SDEs) record from cortex only in the immediate vicinity (Conner et al., 2011). The conventional approach with a Student t-test usually excludes voxels with missing data from analysis or interprets subjects with missing data as having an effect of zero value, leading to distortions in both group effect estimates and significance testing. In our implementation, subjects with missing data are not considered in the analysis at such voxel, and the degrees of freedom are adjusted accordingly as well.

Currently 3dMEMA handles the situation with one effect estimate from each subject, due to the complexity of robustly allowing for within-subject correlations among multiple effects (e.g., deconvolved hemodynamic response function amplitudes). Put differently, it allows generalized t-type tests for individual hypotheses (e.g., no activation difference between two conditions), but not F-type tests for composite hypotheses (e.g., none of the conditions activate a brain region). It is often argued that the conventional ANOVA type analysis is desirable for teasing apart various interactions among categorical variables in FMRI group analysis. Such a popular batch mode approach is appealing from multiple aspects. For instance, all the possible main effects and interactions are obtained in one full model; post hoc tests can be further pursued based on the F-statistic results for main effects and interactions; and ANOVA can gain statistical power if the variances from multiple levels of a between- or within-subject factor (e.g., groups or conditions) are pooled together. Multiple ANOVA programs have long been available in AFNI in the “summary statistics” fashion. However, voxel-wise ANOVA-style analysis either is not widely available in the FMRI software world, or is often misused, leading to distorted and hard-to-replicate statistical inferences. In addition, the convenience and power gains of ANOVA come with constraints on complete data balance and with some rigid underlying assumptions that are not always credible. If the data balance is broken, the decomposition of the data variability into error strata becomes problematic and the estimation of the degrees of freedom for the denominator, sometimes through various adjustments (e.g., Satterthwaite (1946) and Kenward–Roger corrections (Kenward and Roger, 1997)), can be tricky; for instance, the null statistic distribution might not be t or F, as originally assumed. When sphericity is violated, adjustment to the degrees of freedom must be made, but the Greenhouse–Geisser correction tends to be over-conservative while the Huynh–Feldt correction can become too liberal. In addition, the gain in statistical power through error pooling can only materialize when the underlying assumptions, such as compound symmetry (or sphericity/circularity) or homoscedasticity, are satisfied; otherwise, compromised power might actually occur. Such sophisticated assumptions can be tested in small samples, but are impracticable at the voxel level for FMRI data. Because of this practical constraint, the process of modeling building, checking (mostly through visual display), and selection for both random- and fixed-effects is unfortunately impractical in brain imaging. Instead of relying on F-statistics to serve as a guide for further post hoc tests, most of the time individual t-tests are straightforward and can be more robust when these assumptions are violated. In addition to the parsimonious assumptions (e.g., Gaussian or Laplace distribution) involved in the t-type tests, missing data or unbalanced data is no longer an issue. An F-statistic with one numerator degree of freedom is essentially a t-type test. For example, when all the factors in a multi-way ANOVA have two levels (e.g., 2×2 within-subject/repeated-measures or mixed design ANOVA — one within-subject and one between-subject factor), all the tests in such a model can be analyzed with multiple t-type analyses. Currently in MEMA, there is no equivalent test to the omnibus F-test when a within-subject factor has more than two levels. However, an omnibus F-test is of little use in FMRI if it is not followed by pairwise level comparisons to pinpoint the source of significance. If correction for multiple different tests is needed (although not typically practiced in brain imaging community), it should be applied regardless of how the tests are performed, through post hoc t-tests in ANOVA or directly through multiple individual tests via MEMA.

Conclusions

The conventional group analysis using only the subject-level effect estimates is prevalent in the neuroimaging community, but its underlying assumptions are often violated, sometime to large degrees. Heterogeneous effect variance and the presence of outliers particularly affect experiments with small numbers of subjects or unbalanced designs (Mumford and Nichols, 2009). We have implemented a frequentist approach that accounts for outliers and takes into account the reliability of effect estimates, thereby resulting on average in increased statistical power. The approach is comparable to the conventional approach under conditions of normality and homogeneous effect reliability, and is superior otherwise. Under the same t-statistic formulation, results of our frequentist implementation were also comparable with or even better than those from a Bayesian approach (Woolrich, 2008). However, MEMA was at least 10 times faster and readily exploits multiple processors when present. Given MEMA’s more accurate effect estimate and significance testing and its efficient implementation, we recommend its use in lieu of the conventional group analysis approach.

Appendix A. Derivation of FS algorithm for Group REML

The profile residual log-likelihood for REML is the density of the observed effect treated as a function of the cross-subject variability τ² given the data b̂ (Raudenbush, 2009; Viechtbauer, 2005),

$$\begin{array}{l}l\left(\mathbf{a},{\tau }^2;\mathbf{b}\right)=-\frac{1}{2}nln(2\pi )+\frac{1}{2}ln[det(W)]-\frac{1}{2}ln\left[det\left(X^{T}WX\right)\right]-\frac{1}{2}{\left(\widehat{\mathbf{b}}-X^T\mathbf{a}\right)}^{T}W\left(\widehat{\mathbf{b}}-X^T\mathbf{a}\right)\\ =-\frac{1}{2}nln(2\pi )+\frac{1}{2}ln[det(W)]-\frac{1}{2}ln\left[det\left(X^{T}WX\right)\right]-\frac{1}{2}{\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}\end{array}$$

Using the following properties,

$$\begin{array}{l}\frac{\partial In(det(A))}{\partial t}=tr\left(A^{-1}\frac{\partial A}{\partial t}\right),\frac{\partial (AX(t)B)}{\partial t}=A\frac{\partial X(t)}{\partial t}B,\frac{\partial W}{\partial {\tau }^2}-WW\\ \frac{\partial P}{\partial {\tau }^2}=\frac{\partial }{\partial {\tau }^2}\left(W-WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)\\ \frac{\partial W}{\partial {\tau }^2}-\frac{\partial W}{\partial {\tau }^2}X{\left(X^{T}WX\right)}^{-1}{X}^{T}W+WX{\left(X^{T}WX\right)}^{-1}\left(X^T\frac{\partial W}{\partial {\tau }^2}X\right){\left(X^{T}WX\right)}^{-1}{X}^{T}W\\ -WX{\left(X^{T}WX\right)}^{-1}{X}^T\frac{\partial w}{\partial {\tau }^2}\\ =-WW+\mathit{WWX}{\left(X^{T}WX\right)}^{-1}{X}^{T}W-WX{\left(X^{T}WX\right)}^{-1}\left(X^T\mathit{WWX}\right){\left(X^{T}WX\right)}^{-1}{X}^{T}W\\ +WX{\left(X^{T}WX\right)}^{-1}{X}^{T}WW=-PP\end{array}$$

we obtain the first derivative of the log-likelihood function,

$$\begin{array}{l}\frac{\partial l}{\partial {\tau }^2}=\frac{1}{2}tr\left(W^{-1}\frac{\partial W}{\partial {\tau }^2}\right)-\frac{1}{2}tr\left({\left(X^{T}WX\right)}^{-1}\frac{\partial \left(X^{T}WX\right)}{\partial {\tau }^2}\right)-\frac{1}{2}{\widehat{\mathbf{b}}}^T\frac{\partial P}{\partial {\tau }^2}\widehat{\mathbf{b}}\\ =-\frac{1}{2}tr(W)+\frac{1}{2}tr\left({\left(X^{T}WX\right)}^{-1}{X}^T\mathit{WWX}\right)+\frac{1}{2}{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}\\ =-\frac{1}{2}\left[tr(W)-tr\left(WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)\right]+\frac{1}{2}{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}\\ =-\frac{1}{2}tr(P)+\frac{1}{2}{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}\end{array}$$

With $tr(W)={\displaystyle \sum _{i=1}^n}\frac{1}{{\tau }^2+{\sigma }_i^2}={\displaystyle \sum _{i=1}^n}\frac{{\tau }^2}{{\tau }^2+{\sigma }_i^2}{\displaystyle \sum _{i=1}^n}\frac{{\sigma }_i^2}{{\tau }^2+{\sigma }_i^2}={\tau }^{2}tr(WW)+tr\left({\mathit{WWW}}_0^{-1}\right)$, where $W_0=\mathit{diag}\left(\frac{1}{{\sigma }_1^2},\dots ,\frac{1}{{\sigma }_n^2}\right)$, we set $\frac{\partial l}{\partial {\tau }^2}=-\frac{1}{2}\left[tr(W)-tr\left(WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)\right]+\frac{1}{2}{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}$ to 0, and obtain the REML estimate

$$\begin{array}{l}{\widehat{\tau }}^2=\frac{tr\left(WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)+\left[{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}-tr\left({\mathit{WWW}}_0^{-1}\right)\right]}{tr(WW)}\\ =\frac{tr\left(WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)+tr\left\{WW\left[\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right){\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T-W_0^{-1})\right]\right\}}{tr(WW)}.\end{array}$$

When within-subject variance is the same across all subjects $({\sigma }_1^2=\dots ={\sigma }_n^2={\sigma }^2),tr\left(WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right)=\frac{p+1}{{\widehat{\tau }}^2+{\sigma }^2},tr\left\{WW\left[\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right){\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T-W_0^{-1})\right]\right\}=\frac{{\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)-n{\sigma }^2}{{({\widehat{\tau }}^2+{\sigma }^2)}^2},tr(WW)=\frac{n}{{({\widehat{\tau }}^2+{\sigma }^2)}^2}$, and the REML estimate has a closed form ${\widehat{\tau }}^2=\frac{{\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}{n-p-1}-{\sigma }^2$.

With $\frac{\partial PP}{\partial {\tau }^2}=-2\mathit{PPP}$ and $\frac{\partial tr(P)}{\partial {\tau }^2}=tr\left(\frac{\partial P}{\partial {\tau }^2}\right)=-tr(PP)$, we have the second derivative of the log-likelihood function,

$$\frac{{\partial }^{2}l}{\partial {({\tau }^2)}^2}=-\frac{1}{2}\left[\frac{\partial tr(P)}{\partial {\tau }^2}-{\widehat{\mathbf{b}}}^T\frac{\partial PP}{\partial {\tau }^2}\widehat{\mathbf{b}}\right]==\frac{1}{2}tr(PP)-{\widehat{\mathbf{b}}}^T\mathit{PPP}\widehat{\mathbf{b}}$$

As PX=0, E(b̂^TPPPb̂) = tr[PPPE(b̂^Tb̂)] = tr(PPPW⁻¹)E(b̂)^TPPPE(b̂) = tr{PPW⁻¹[W−WX(X^TWX)⁻¹X^TW]} + (Xb)^TPPP(Xb) = tr{PP[I−X(X^TWX)⁻¹X^TW]} = tr(PP), and the information matrix is thus $-E\left[\frac{{\partial }^{2}l1}{\partial {({\tau }^2)}^2}\right]=-E\left[\frac{1}{2}tr(PP)-{\widehat{b}}^T\mathit{PPP}\widehat{b}\right]=\frac{1}{2}tr(PP)$. The general Fisher scoring (FS) algorithm (Demidenko, 2004) is of the following form, ${\tau }_{k+1}^2={\tau }_k^2+{\lambda }_k{\delta }_k$, where ${\delta }_k=\frac{\frac{\partial l}{\partial {\tau }^2}}{-E\left[\frac{{\partial }^{2}l}{\partial {({\tau }^2)}^2}\right]}=\frac{-\frac{1}{2}\left[tr(P)-{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}\right]}{\frac{1}{2}tr(PP)}=\frac{{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}-tr(P)}{tr(PP)}.$. Choosing step length λ_k =1, we have a Fisher scoring algorithm for REML,

$${\tau }_{k+1}^2={\tau }_k^2+\frac{{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}-tr(P)}{tr(PP)}.$$

It is instructive and revealing to compare the REML results with its counterparts of ML. The profile residual log-likelihood for ML has one less term, $-\frac{1}{2}ln\left[det\left(X^{T}WX\right)\right]$, than REML, leading to an ML estimate ${\widehat{\tau }}^2=\frac{tr\left\{WW\left[\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right){\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T-W_0^{-1})\right]\right\}}{tr(WW)}$, which reduces to ${\widehat{\tau }}^2=\frac{{\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)}^T\left(\widehat{\mathbf{b}}-X^T\widehat{\mathbf{a}}\right)-{\sigma }^2}{n}$ when within-subject variance is the same across all subjects ( ${\sigma }_1^2=\dots ={\sigma }_n^2={\sigma }^2$). The denominator in the reduced forms reflects the difference between REML and ML in accounting for the uncertainty of estimating a. A similar Fisher scoring algorithm for ML can be constructed as ${\tau }_{k+1}^2={\tau }_k^2\frac{{\widehat{\mathbf{b}}}^{T}PP\widehat{\mathbf{b}}-tr(W)}{tr(WW)}$.

Appendix B. Derivation of EFS algorithm for Group ML with Laplace assumption of subject-specific terror term

First we start by assuming a Laplace distribution for the cross-subject variability in Eq. (3), δ_i ~ L(0, ν), i=1, …, n, where L(m, ν) has a density $p(x)=\frac{1}{2v}{e}^{-\frac{\mid x-m\mid }{v}}$ with location parameter (mean/mode/median) m and scale parameter ν (variance 2ν²). The Laplace distribution has heavier tails than normal distribution, allowing us to better handle the situation than the convention approach with REML, when one or two subjects have exceptionally unreliable effect estimates at a voxel or region.

Since Cov(ε_i, δ_j)=0 for all i and j, ε_i and δ_j are independent, and the density function of η_i = ε_i + δ_j can be obtained through the following convolution

$$\begin{array}{l}{p}_{\eta i}(x)={\int }_{-\infty }^{\infty }{p}_{\delta i}(u)p_{\epsilon i}(x-u)du={\int }_{-\infty }^{\infty }\frac{1}{2v}{e}^{-\mid \frac{u}{v}\mid }.\frac{1}{\sqrt{2\pi {\sigma }_i^2}}{e}^{-\frac{{(x-u)}^2}{2{\sigma }_i^2}}du\\ =\frac{1}{2v}\left[{\int }_{-\infty }^0{e}^{\frac{u}{v}}.\frac{1}{\sqrt{2\pi {\sigma }_i^2}}{e}^{-\frac{{(x-u)}^2}{2{\sigma }_i^2}}du+{\int }_{-\infty }^{\infty }{e}^{-\frac{u}{v}}.\frac{1}{\sqrt{2\pi {\sigma }_i^2}}{e}^{-\frac{(x-u)}{2{\sigma }_i^2}}du\right]\\ =\frac{1}{2x}{e}^{\frac{{\sigma }_i^2}{2v^2}}\left\{e^{\frac{x}{v}}{\int }_{-\infty }^0\frac{1}{\sqrt{2\pi {\sigma }_i^2}}{e}^{-\frac{{\left[u-\left(x+\frac{{\sigma }_i^2}{v}\right)\right]}^2}{2{\sigma }_i^2}}du+e^{-\frac{x}{v}}{\int }_0^{\infty }\frac{1}{\sqrt{2\pi {\sigma }_i^2}}{e}^{-\frac{{\left[u-\left(x-\frac{{\sigma }_i^2}{v}\right)\right]}^2}{2{\sigma }_i^2}}du\right\}\\ =\frac{1}{2v}{e}^{\frac{{\sigma }_i^2}{2v^2}}\left[e^{\frac{x}{v}}\mathrm{\Phi }\left(-\frac{x+\frac{{\sigma }_i^2}{v}}{{\sigma }_i}\right)+e^{-\frac{x}{v}}\mathrm{\Phi }\left(\frac{x-\frac{{\sigma }_i^2}{v}}{{\sigma }_i}\right)\right]\end{array}$$

where Φ is the cumulative distribution function (cdf) of the standard normal distribution N(0, 1). The joint density function is

$$\prod _{i=1}^n{P}_{{\eta }_i}(x)={\left(\frac{1}{2\nu }\right)}^n{e}^{\frac{{\displaystyle \sum _{i=1}^n}{\sigma }_i^2}{2{\nu }^2}}\prod _{i=1}^n\left[e^{\frac{x}{\nu }}\mathrm{\Phi }\left(-\frac{x+\frac{{\sigma }_i^2}{\nu }}{{\sigma }_i}\right)+e^{-\frac{x}{\nu }}\mathrm{\Phi }\left(\frac{x-\frac{{\sigma }_i^2}{\nu }}{{\sigma }_i}\right)\right]$$

with the corresponding log-likelihood function

$$l_i(a,\nu )=-ln2-ln\nu +\frac{1}{2{\nu }^2}{\sigma }_i^2+ln\left[e^{\frac{{\widehat{\beta }}_i-x_i^{T}a}{\nu }}\mathrm{\Phi }\left(-\frac{{\sigma }_i}{\nu }-\frac{{\widehat{\beta }}_i-x_i^{T}a}{{\sigma }_i}\right)+e^{-\frac{{\widehat{\beta }}_i-x_i^{T}a}{\nu }}\mathrm{\Phi }\left(-\frac{{\sigma }_i}{\nu }+\frac{{\widehat{\beta }}_i-x_i^{T}a}{{\sigma }_i}\right)\right].$$

We adopt the empirical Fisher scoring (EFS) algorithm (Demidenko, 2004) in the following format,

$${\left[\begin{array}{c}a\\ \nu \end{array}\right]}_{k+1}={\left[\begin{array}{c}a\\ \nu \end{array}\right]}_k+{\lambda }_k{H}_k^{-1}{g}_k,$$ (20)

where k is the iteration index, H_k is a positive definite matrix,

$H_s=\sum _{i=1}^n\left[\begin{array}{c}\frac{\partial l_i}{\partial a}\\ \frac{\partial l_i}{\partial \nu }\end{array}\right]{\left[\begin{array}{c}\frac{\partial l_i}{\partial a}\\ \frac{\partial l_i}{\partial \nu }\end{array}\right]}^T=\left[\begin{array}{cc}\sum _{i=1}^n{\left(\frac{\partial l_i}{\partial a}\right)}^2& \sum _{i=1}^n\frac{\partial l_i}{\partial a}\frac{\partial l_i}{\partial \nu }\\ \sum _{i=1}^n\frac{\partial l_i}{\partial a}\frac{\partial l_i}{\partial \nu }& \sum _{i=1}^n{\left(\frac{\partial l_i}{\partial \nu }\right)}^2\end{array}\right],g_k=\sum _{i=1}^n\left[\begin{array}{c}\frac{\partial l_i}{\partial a}\\ \frac{\partial l_i}{\partial \nu }\end{array}\right]$ is the gradient of the likelihood function, and λ_k is the step length with (0, 1], and we usually start with λ_k =1 and then halve it if the objective function value is greater than the value at the previous iteration. Although not as efficient as FS, EFS does not require second derivatives that are often difficult to compute.

Denote

$$\begin{array}{l}{E}_i=e^{\frac{{\widehat{\beta }}_i-X_i^{T}a}{\nu }},{\mathrm{\Phi }}_{i1}=\mathrm{\Phi }\left(-\frac{{\sigma }_i}{\nu }-\frac{{\widehat{\beta }}_i-X_i^{T}a}{{\sigma }_i}\right),{\mathrm{\Phi }}_{i2}=\mathrm{\Phi }\left(-\frac{{\sigma }_i}{\nu }+\frac{{\widehat{\beta }}_i-X_i^{T}a}{{\sigma }_i}\right),G_i\\ =E_i{\mathrm{\Phi }}_{i1}+E_i^{-1}{\mathrm{\Phi }}_{i2}\end{array}$$

we have

$$\begin{array}{l}\frac{\partial E_i}{\partial a}=-\frac{1}{\nu }{E}_i{x}_i^T,\frac{\partial E_i}{\partial \nu }=-\frac{1}{{\nu }^2}{E}_i\left({\widehat{\beta }}_i-x_i^{T}a\right),\\ \frac{\partial E_i^{-1}}{\partial a}=\frac{1}{\nu E_i}{x}_i^T,\frac{\partial E_i^{-1}}{\partial \nu }=-\frac{1}{{\nu }^2{E}_i}\left({\widehat{\beta }}_i-x_i^{T}a\right),\\ \frac{\partial {\mathrm{\Phi }}_{i1}}{\partial a}=-\frac{1}{{\sigma }_i}{\mathrm{\Phi }}_{i1}{x}_i^T,\frac{\partial {\mathrm{\Phi }}_{i1}}{\partial \nu }=\frac{{\sigma }_i}{{\nu }^2}{\mathrm{\Phi }}_{i1},\\ \frac{\partial {\mathrm{\Phi }}_{i2}}{\partial a}=-\frac{1}{{\sigma }_i}{\mathrm{\Phi }}_{i2}{x}_i^T,\frac{\partial {\mathrm{\Phi }}_{i2}}{\partial \nu }=\frac{{\sigma }_i}{{\nu }^2}{\mathrm{\Phi }}_{i2}.\end{array}$$

Now we obtain the first derivatives of the likelihood function

$$\begin{array}{l}\frac{\partial l_i(a,\nu )}{\partial a}=\frac{1}{G_i}\left(-\frac{1}{\nu }{E}_i{\mathrm{\Phi }}_{i1}{x}_i^T+\frac{1}{{\sigma }_i}{E}_i{\mathrm{\Phi }}_{i1}{x}_i^T+\frac{1}{\nu E_i}{\mathrm{\Phi }}_{i2}{x}_i^T-\frac{1}{{\sigma }_i{E}_i}{\mathrm{\Phi }}_{i2}{x}_i^T\right),\\ \frac{\partial l_i(a,\nu )}{\partial \nu }=-\frac{1}{\nu }-\frac{{\sigma }_i^2}{{\nu }^3}+\frac{1}{G_i}\left[-\frac{1}{{\nu }^2}{E}_i{\mathrm{\Phi }}_{i1}\left({\widehat{\beta }}_i-x_i^{T}a\right)+\frac{1}{{\nu }^2}{\sigma }_i{E}_i{\mathrm{\Phi }}_{i1}-\frac{1}{{\nu }^2{E}_i}{\mathrm{\Phi }}_{i2}\left({\widehat{\beta }}_i-x_i^{T}a\right)+\frac{1}{{\nu }^2{E}_i}{\sigma }_i{\mathrm{\Phi }}_{i2}\right].\end{array}$$

Plugging all these results back into the EFS algorithm (20), we have a numerical scheme for outlier modeling.

Appendix C. Equivalence of MEMA t-tests to one-sample Student t-test under the “summary statistics” assumptions

Consider p=0 and X=1_{n × n} in model (3). When within-subject variability is relatively small ( ${\sigma }_i^2\approx 0$), or when it is the same across all subjects ( ${\sigma }_i^2=\dots ={\sigma }_n^2={\sigma }_1^2$), we denote weights W=wI_{n × n}, where $w=\frac{1}{{\widehat{\tau }}^2}$ or $\frac{1}{{\widehat{\tau }}^2+{\widehat{\sigma }}^2}$.As

$$\begin{array}{l}\widehat{V}(\widehat{\mathbf{a}})=\frac{1}{n-p-1}{\widehat{\mathbf{b}}}^{T}P\widehat{\mathbf{b}}{\left(X^{T}WX\right)}^{-1}\\ =\frac{1}{n-1}{\widehat{\mathbf{b}}}^T\left[W-WX{\left(X^{T}WX\right)}^{-1}{X}^{T}W\right]\widehat{\mathbf{b}}{\left(X^{T}WX\right)}^{-1}\\ =\frac{1}{n-1}{\widehat{\mathbf{b}}}^T\left[wI-w1{\left(w{1}^{T}1\right)}^{-1}{1}^{T}w\right]\widehat{\mathbf{b}}{\left(w{1}^{T}1\right)}^{-1}\\ =\frac{1}{n(n-1)}{\widehat{\mathbf{b}}}^T\left(I-\frac{1}{n}{11}^T\right)\widehat{\mathbf{b}}\\ =\frac{1}{n(n-1)}\left[{\left(\sum _{i=1}^n{\widehat{\beta }}_i\right)}^2-\frac{1}{n}\sum _{i=1}^n{\widehat{\beta }}_i^2\right]\end{array}$$

and $\frac{1}{n-1}\left[{\left({\displaystyle \sum _{i=1}^n}\widehat{\beta }\right)}^2-\frac{1}{n}{\displaystyle \sum _{i=1}^n}{\widehat{\beta }}_i^2\right]$ is the variance estimate of the group effect estimate α̂₀, T_KH is simply the conventional one-sample Student t-test statistic. As the variance of α̂₀, $V({\alpha }_0)={\left(X^{T}WX\right)}^{-1}={\left(w{\mathbf{1}}^T\mathbf{1}\right)}^{-1}=\frac{w^{-1}}{n}$, and w⁻¹ = τ̂² or τ̂² + σ̂² is the variance estimate of the group effect estimate α̂₀, we also see the equivalence of T_S to the conventional one-sample Student t-test.

Appendix D. Estimation of Individual Subject β and σ² values

The use of the MEMA methods described in the main body of the paper requires accurate estimation not just of the individual subject effect sizes (the β_i) from each voxel time series, but also accurate estimates of the variances (the ${\sigma }_i^2$) of the β_i in each voxel for each subject i. If just the β_i are needed, then OLS is consistent and accurate, even in the presence of moderate serial correlation in the time series data. However, the OLS estimate of variance can seriously underestimate the variance (negative bias) when positive serial correlation is present.

To allow for serial correlation in the AFNI MEMA processing chain, we implemented generalized least square regression (GLSQ) combined with REML estimation of the serial correlation parameters in each voxel time series. We chose to use an ARMA(1,1) model for the temporal correlation structure, as this is the simplest model that has any plausibility for FMRI data, allowing for the sum of a noise component with exponentially decaying correlation (i.e., an AR(1) model modeling physiological and scanner temporal fluctuations) with a white noise component (modeling the baseline thermal noise level). Our regression model takes the form

$$\begin{array}{l}\mathbf{z}=\mathbf{Y}\beta +\eta \text{with}\eta ~N\left(0,{\sigma }^2\mathbf{R}\right)\\ R_{ij}(p,q)=\left\{\begin{array}{cc}\mathbf{1}& i=j\\ r_1{p}^{\mid \kappa (i)-\kappa (j)\mid }& i\ne j\end{array}\right\}\text{where}{r}_1\equiv \frac{(p+q)(1+pq)}{1+2pq+q^2}.\end{array}$$

Here, R_ij denotes the correlation coefficient between the noise at time indexes i and j; z = voxel data time series vector (∈ℝⁿ); Y = FMRI regression design matrix (∈ℝ^n×n); and β = unknown parameters of the model (∈ℝ^m). The two unknown ARMA parameters (p,q) are best understood as p as being the decay rate of the correlation, and via the combination r₁, which is the noise correlation coefficient at lag=1 TR. An AR(1) noise model with decay parameter p and variance ${\sigma }_A^2$ summed with a white noise model with variance ${\sigma }_W^2$ has the temporal correlation structure of an ARMA(1,1) model with the same value of p and with $r_1=p{\sigma }_A^2/({\sigma }_A^2+{\sigma }_W^2)$. The natural range of both p and q is (−1,1). The term κ(i) denotes the “original” time index of data point number i, which allows for censoring of time points and for temporal discontinuities resulting from the catenation of multiple imaging runs (we add 10,000 to κ between runs); in the plainest case of one imaging run with no censoring, κ(i)=i. The simple device of κ(i) allows us to analyze multiple imaging time series, with their time discontinuities, from one subject in a single regression model, thereby eliding the problem of how to combine data from multiple runs. (The use of κ(i), however, means the R matrix is not necessarily Toeplitz, except for the case of a single imaging run with no time points censored out.)

The REML log-likelihood function to be minimized over (p,q) in each voxel is (after removing constant terms)

$$l_{\text{GLM}}(p,q)=(n-m)log\left({\mathbf{z}}^T\mathbf{Pz}\right)+logdet[\mathbf{R}(p,q)]+logdet\left[{\mathbf{Y}}^T\mathbf{R}{(p,q)}^{-1}\mathbf{Y}\right]$$

where P(p, q) = R⁻¹−R⁻¹Y[Y^TR⁻¹Y]⁻¹Y^TR⁻¹ (∈ℝ^n×n).

Note that the last two terms in the log-likelihood function do not depend on the data vector z; these terms act as a “penalty” favoring some values of (p,q) over others. In the case of the ARMA(1,1) noise correlation model, the values p=q=0 are the most penalized, meaning that these terms favor nonzero correlations.

Once (p̂, q̂) are estimated, then the noise variance estimate is σ̂² = z^TP(p̂, q̂)z/(n−m) and the regression parameter estimate is given by GLSQ as β̂ = [Y^TR(p̂, q̂)Y]⁻¹Y^TR(p̂, q̂)z.

For computational efficiency, the calculations are organized somewhat differently than the bare matrix formulas above indicate. The matrix R(p,q) is truncated to a limited bandwidth by setting correlations |R_ij| ≤0.001 to zero, and then it is stored in a sparse structure. Define its upper triangular Choleski factor C∈ℝ^n×n by R=C^TC; C shares the same sparsity pattern as R, since there are no zero entries inside the sparsity profile. (C^−T is a pre-whitening matrix for R.) Also define the (dense) upper triangular matrix D∈ℝ^m×m as the Choleski factor of Y^TR⁻¹Y=D^TD; there is no need to form the matrix Y^TR⁻¹Y explicitly at any point, since D is easily seen to be the upper triangular factor in the QR decomposition of the matrix C^−TY. Since the matrices C and D are triangular, their determinants are easily calculated, and the “penalty” terms in the log-likelihood function l_GLM become

$$logdet[\mathbf{R}(p,q)]+logdet\left[{\mathbf{Y}}^T\mathbf{R}{(p,q)}^{-1}\mathbf{Y}\right]=2\sum _{i=1}^{n}log{C}_{ii}+2\sum _{j=1}^{m}log{D}_{jj}.$$

Noting that z^TPz = z^TP^TC^TCPz = |CPz|², the following 8 step algorithm is used to compute the vectors needed for estimation:

1. Solve triangular system C^Tb₁ = z for b₁∈ℝⁿ

2. Solve triangular system Cb₂ = b₁ for b₂∈ℝⁿ

3. Multiply b₃ = Y^Tb₂ to get b₃∈ℝ^m

4. Solve triangular system D^Tb₄ = b₃ for b₄∈ℝ^m

5. Solve triangular system Db₅ = b₄ for b₅∈ℝ^m (= β̂)

6. Multiply b₆ = Yb₅ to get b₆∈ℝⁿ (= fitted model time series)

7. Solve triangular system C^Tb₇ = b₆ for b₇∈ℝⁿ

8. Subtract to get CPz = b₁−b₇(∈ℝⁿ) (pre-whitened residuals; sum of squares of CPz is used in l_GLM).

In this progression of matrix–vector operations, “solve” operations are always forward or back solutions with triangular matrices; explicit matrix inverses are never needed. Matrix Y is also stored sparsely, since in FMRI it is common that less than 20% of Y’s entries are nonzero. Using the sparse structure of various matrices speeds the computations up significantly. For further speed, the program is carefully written for efficiency (in C) and utilizes the OpenMP parallelization API to take advantage of multi-core processors. This code is named 3dREMLfit in the AFNI software suite, and is invoked by the AFNI single-subject processing script afni_proc.py and graphical user interface uber_subject.py.

Voxel-wise optimization over (p,q) is done by restricting their potential values to a 2D grid 2^G+1 on each side; the default value of G is 4 over the domain (−0.8,+0.8)×(−0.8,+0.8), resulting in a grid spacing of 0.1. The matrices C and D are pre-computed for each (p, q) grid point before the voxel-wise calculations begin. Binary search in this grid is used to find the values (p̂, q̂) that minimize l_GLM in each voxel. This low resolution in (p,q) might seem crude, but in our trials we found that higher precision in estimating these parameters made very little difference in the final results. In fact, it seems that any reasonable attempt at pre-whitening to allow for serial correlation produces adequately accurate results for most FMRI purposes (Marchini and Smith, 2003).

Finally, the variance estimate for any particular linear combination g^Tβ of the regression parameters is given by ${\widehat{\sigma }}_{{\mathbf{g}}^T\beta }^2={\widehat{\sigma }}^2{\mid {\mathbf{D}}^{-T}\mathbf{g}\mid }^2$. This estimate is used to form t-statistics of interest at the individual subject level, and is also carried to the group level in MEMA.

Appendix E. Group effect estimates and their statistical significances at five voxels

Test			Student t-test	MEMA
				Gaussian		Laplacian
Results				TS	TKH	TS	TKH
Voxel 1	Group effect	Estimate	0.643	0.667		0.682
		t	4.542	5.006	5.153	5.942	5.443
		pa	0.0014	7.33e – 4	6.01e – 4	2.17e – 4	4.09e – 4
	Cross-subjects heterogeneity	t̂2b	0.200	0.0633		0.0296
		Qc	–	15.11 (0.0880)
		H, I2d	–	1.296, 0.406		1.149, 0.242
Voxel 2	Group effect	Estimate	0.508	0.381		0.364
		t	3.89	5.536	4.705	7.334	5.156
		pa	3.67e – 3	3.63e – 4	1.11e – 3	4.40e – 5	5.98e – 4
	Cross-subjects heterogeneity	t̂2b	0.171	0.0177		0.0004
		Qc	–	18.49 (0.0299)
		H, I2d	–	1.30, 0.409		1.009, 0.018
Voxel 3	Group effect	Estimate	− 0.319	−0.319		−0.323
		t	− 3.168	− 5.020	− 4.501	− 4.564	− 4.308
		pa	0.011	7.20e – 4	1.49e – 3	1.36e – 3	1.97e – 3
	Cross-subjects heterogeneity	t̂2b	0.101	0		0.007
		Qc	–	11.20(0.2622)
		H, I2d	–	1.0, 0.0001		1.081, 0.145
Voxel 4	Group effect	Estimate	− 0.193	− 0.138		− 0.138
		t	− 5.449	− 2.971	− 3.915	− 2.971	− 3.915
		pa	4.1e – 4	1.57e – 2	3.54e – 3	1.57e – 2	3.54e – 3
	Cross-subjects heterogeneity	t̂2b	0.0013	0		0
		Qc	–	5.18 (0.8183)
		H, I2d	–	1.0, 0.0		1.0, 0.0
Voxel 5	Group effect	Estimate	0.0496	0.0493		0.0493
		t	4.7152	0.8937	4.6376	0.8937	4.6376
		pa	0.0011	0.3947	0.0012	0.3947	0.0012
	Cross-subjects heterogeneity	t̂2b	1.1e-4	0		0
		Qc	–	0.3342 (1.0)
		H, I2d	–	1.0, 0.0		1.0, 0.0

Talairach coordinates (x, y, z) of the five voxels: (31, −91, −2) (Voxel 1), (−23, −89, 0) (Voxel 2), (−53, −17, 10) (Voxel 3), (−51, −11, 6) (Voxel 4), and (−5, 11, 0) (Voxel 5), where + x, y, z=RAS (neurological coordinates)

^ap-values for the t-statistics with 9 degrees of freedom are two-sided.

^bThe variance for the conventional approach (paired Student t-test) is the estimated τ²+σ² in the effect estimates, including both within- and inter-subject variances, assuming the within-subject variability being homogeneous in the group. The adjustment in T_KH relative to T_S does not involve the estimate of inter-subject variability τ², which remains the same between the two tests.

^cThe conventional approach assumes equal or no within-subject variance; thus, all the variability in the data is assumed to come between subjects. There is no way to test the significance of the inter-subject variability in the case of paired Student t-test under this assumption. The Q-statistic, defined in (8) for testing inter-subject variability (null hypothesis τ²=0), follows a χ²(9) distribution with the data at the five voxels (p-value shown within parentheses).

^dApproximate criteria for heterogeneity: H>1.5 (or I²>0.56), significant; 1.2<H<1.5 (or 0.31<I²<0.56), moderate; H<1.2 (or I²<0.31), negligible.

Appendix F. Supplementary data

Supplementary data to this article can be found online at doi:10.1016/j.neuroimage.2011.12.060.