A method for analyzing temporal patterns of variability of a time series from Poincaré plots

Abstract

The Poincaré plot is a popular two-dimensional, time series analysis tool because of its intuitive display of dynamic system behavior. Poincaré plots have been used to visualize heart rate and respiratory pattern variabilities. However, conventional quantitative analysis relies primarily on statistical measurements of the cumulative distribution of points, making it difficult to interpret irregular or complex plots. Moreover, the plots are constructed to reflect highly correlated regions of the time series, reducing the amount of nonlinear information that is presented and thereby hiding potentially relevant features. We propose temporal Poincaré variability (TPV), a novel analysis methodology that uses standard techniques to quantify the temporal distribution of points and to detect nonlinear sources responsible for physiological variability. In addition, the analysis is applied across multiple time delays, yielding a richer insight into system dynamics than the traditional circle return plot. The method is applied to data sets of R-R intervals and to synthetic point process data extracted from the Lorenz time series. The results demonstrate that TPV complements the traditional analysis and can be applied more generally, including Poincaré plots with multiple clusters, and more consistently than the conventional measures and can address questions regarding potential structure underlying the variability of a data set.

the study of biologic variability provides insight into the nature of physiological system dynamics and can be used to detect the presence and progression of disease. A change in the variability or regularity and complexity of heart rate has been associated with health status following cardiac arrest (4), aging, and clinical outcomes related to heart failure (17, 24), sepsis (9), asthma (6), and traumatic brain injury (13). In this regard, we present a novel method for quantifying Poincaré plots, commonly used to visually assess heart rate variability.

The Poincaré plot is used to quantify recurrence, self-similarity, or periodicity in a time series. It is based on the concept of a return map, and in its simplest form provides a means for displaying sequential pairs of points as an x-y plot. Traditional analysis methods were pioneered to visualize and investigate heart rate variability (HRV). The discovery that Poincaré plots of heartbeat intervals successfully characterize abnormal cardiac function has been integrated in clinical assessment (1, 2, 7, 8, 11, 26).

Techniques to quantify Poincaré plots are continually developing and improving but have limitations that our method overcomes (12, 18). The primary method for quantifying the Poincaré plot is an ellipse-fitting technique (23), although the ellipse serves only as a visual guide with no actual mathematical fit of the data to the equation of an ellipse (18). This technique assumes a clustered distribution of points and defines short- and long-term variability, which correspond to the length of the minor (SD1) and major (SD2) axes in Fig. 1A. Because SD1 and SD2 are statistics based on the distributions of variance (1), the method does not directly quantify the temporal dynamics of the time series contained in the Poincaré plot, a limitation that we and others address (11). Furthermore, with data sets that form multiple clusters in a Poincaré plot due to complex dynamic behaviors, the SD1/SD2 statistic yields mixed results. This is because the technique relies on the existence of a single cluster or defined patterns (5, 19). The limitations of the SD1/SD2 analysis are important to understand when attempting to investigate the physiological underpinnings of the time series or when analyzing data where the occurrence of nonlinear behavior may be a distinguishing feature between health and disease.

Fig. 1.

Illustrative example of a Poincaré plot, units are arbitrary. A: example of an ellipse fit along the line of identity (dotted line). SD1 is the short-term variability and SD2 is the long-term variability. B: a plot with a slow linear trend from lower to higher values. Highlighted points represent the general short-term behavior of the trend, with intermediary steps removed. C: nonlinear behavior can produce loops, and SD1 is not a meaningful measurement of temporal behavior.

We propose a novel analytical method for Poincaré plot analysis that can be applied to data sets more generally than the traditional approach because it can quantify distributions that are not represented well by an ellipse. Termed TPV for temporal Poincaré variability, it is derived from geometric principles and emulates the short- and long-term variability described by the SD1 and SD2 statistics. Furthermore, because the technique retains information about individual points, it ensures that temporal correlations are preserved in the analysis, a necessary step for analyzing complex Poincaré plots. We demonstrate how this analysis can incorporate a series of Poincaré plots with successive time delays, yielding a richer insight into system dynamics than the traditional circle return (n vs. n+1) plot by analyzing a synthetic Lorenz system that has high levels of nonlinear behavior. We conclude with a comparison to traditional methods on a standard congestive heart failure data set obtained from the PhysioNet Databank (http://www.physionet.org/physiobank/database/html/mitdbdir/mitdbdir.htm) and from a patient being monitored in a neurological intensive care unit.

METHODS

Traditional Poincaré Analysis

Plot creation and SD1/SD2 calculation.

Given a time series {x₀,x₁,…,x_n,…} the standard Poincaré plot is a scattergram constructed by locating points from the time series on the coordinate plane according to the pairing (x_n, x_n+τ). In our analysis,τ is the time delay, which is a multiple of the cycle length or of the sampling time of the signal (21). In most conventional analyses, the time delay is chosen as one for a single period, yielding a plot in which each point contains information about x_n (x-coordinate) and its successor x_n+1 (y-coordinate). The choice of τ affects the dependency between the variables, therefore, τ = 1 generally ensures a high (linear) correlation between points for most time series. To more fully investigate the dynamics of a system, τ should vary in the analysis so that the successive values used in the plot have different levels of dependence.

Due to the construction of the plot, successive points with equal values (e.g., equivalent R-R intervals in a heart rate signal) will fall along the 45° diagonal, the line of identity. To quantify the variability using the SD1 and SD2 statistics, the equations in Brennan et al. (1, 2) are used and an ellipse is visually fit to the data as shown in Fig. 1A. Outliers were not considered in the analysis to avoid distortion.

The width (minor axis) of the ellipse (SD1) is defined as the dispersion of points perpendicular to the line of identity, whereas the length (major axis) of the ellipse (SD2) is measured along the line of identity. Short-term variability in heart rate is associated with SD1 and long-term variability, with SD2 (1, 2). The ellipse-fitting method is prevalent in the HRV literature because of its intuitive and geometrically based interpretation.

Assumptions and limitations of SD1/SD2.

The SD1/SD2 technique can only be applied to Poincaré plots that consist of one geometrically symmetric cluster. For analysis of HRV from a subject with normal cardiac function, this is a minor restriction because heart rate is sufficiently regular so as to satisfy this constraint. This limitation becomes problematic when analyzing abnormal cardiac (heart rate) activity. As mentioned by Brennan et al. (1, 2), premature ventricular contractions create clusters of ectopic beats that are discrete from the sinus rhythm cluster and cannot be included in the variability measurements. These beats are treated as outliers so as to not affect the final analysis. However, with strong respiratory sinus arrhythmia, the majority of the cluster is highly irregular, which reduces the applicability of the SD1/SD2 analysis. Nevertheless, Poincaré plots are widely used because they provide a useful qualitative assessment even in this instance.

Correlating SD1 with short-term variability and SD2 with long-term variability is valid for HRV, but is misleading and easily misinterpreted. The common usage incorrectly assumes that these measures have temporal meaning, although they were not defined that way by Tulppo et al. (23). Short term is inferred to mean a short duration, just long enough to include a few R-R intervals. Similarly, long term implies that SD2 develops over time and multiple beats. These interpretations are only correct when the data have slow linear trends (Fig. 1B), but are incorrect otherwise (Fig. 1C). This subtle point emphasizes that SD1 and SD2 do not represent the expected variability at a given point in time or location in the Poincaré plot. The traditional method refers to SD1 as beat-to-beat variability. However, a more accurate definition is that SD1 is the total amount of beat-to-beat variance across the entire plot. Likewise, SD2 is the variance of the entire plot minus the beat-to-beat variance. This is the basis for the mathematical representation derived by Brennan et al. (1, 2) that defines SD1 as the standard deviation of successive differences (SDSD) and SD2 as the standard deviation of R-R intervals (SDRR).

Limitations of traditional Poincaré construction.

Time is an implicit parameter in a Poincaré plot, so time-sequence information is lost and only distributional information is represented. Thus the same plot can be generated by data sets with different underlying dynamics. Although methods to visualize plot density have proven useful in detecting point distribution not apparent from the raw Poincaré plot (10), methods that capture time-based information have not been developed yet.

Temporal information is important for the detection of nonstationary behavior, although in some instances the complex behavior of a system can be inferred by its distribution on the attractor. A simple but effective technique to include temporal features is to animate the construction of the Poincaré plot. A qualitative analysis of the animation guides the interpretation of the quantitative methods and gives insight into the type and degree of variability. For instance, the animation will determine whether the data are interpreted as a slow linear trend (Fig. 1B) or containing complex dynamics (Fig. 1C).

Novel Poincaré Analysis

Definition.

TPV analysis emulates the ellipse-fitting technique by calculating both interval-to-interval and long-term variabilities. Unlike the SD1/SD2 method, TPV is calculated point-by-point, capturing time-dependent information in a sequence of values.

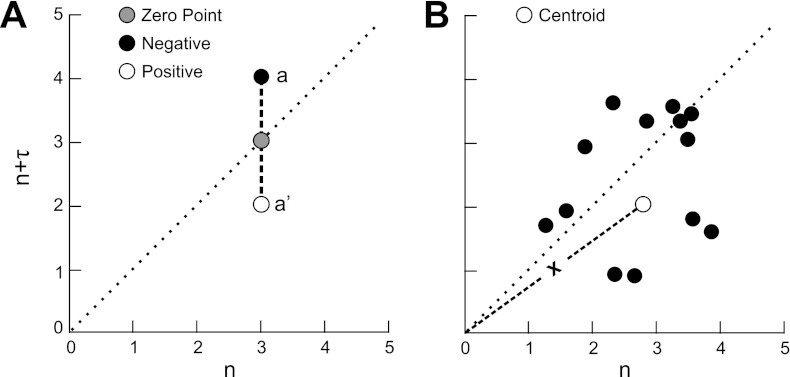
Time-delayed TPV (TPVtd) measures the similarity of an interval to a successor, such that period-1 motion is represented by a single point (with x-coordinate, x; and a y-coordinate, y) on the 45° line of identity. Identical intervals will thus cause the points to fall on the diagonal. Consequently, we define the variability of an interval in terms of the distance from the line of identity, as demonstrated in Fig. 2A. Then the time series of intervals is summarized through the standard deviation and is equivalent to SDSD. To scale TPVtd to SD1, we divide by √2 (Eq. 1) per the Brennan equation (1, 2). This means that TPVtd at a time delay of 1 is equivalent to SD1, while at larger time-delays it highlights dynamics at reduced levels of correlation.

$$\begin{array}{c}\overline{\text{XY}}=\frac{1}{\text{N}}{\displaystyle {\sum }_{\text{i}-1}^{\text{N}}{\text{x}}_{\text{i}}-{\text{y}}_{\text{i}}}\\ \text{VAR}\left(\text{XY}\right)={\displaystyle {\sum }_{\text{i}-1}^{\text{N}}\left[{\left({\text{x}}_{\text{i}}-{\text{y}}_{\text{i}}\right)}^2-\overline{{\text{XY}}^2}\right]/\text{N}}\\ {\text{TPV}}_{TD}=\sqrt{\text{VAR}\left(\text{XY}\right)}/\sqrt{2}\end{array}$$ (1)

Fig. 2.

Definition and difference between time-delayed temporal Poincaré variability (TPVtd) (A) and long-term temporal Poincaré variability (TPVa) (b). A: geometric definition of TPVtd. Shaded circle on the line of identity represents zero variability. Black and white points have the same magnitude of TPVtd but different signs. B: geometric definition of TPVa, with a w of 13. White centroid is the average of w (in this case w = 13). Centroid can be off the line of identity especially if w is small number. Distance from the origin (X) for every centroid is calculated, and TPVa is the standard deviation of those distances (see Fig. 3).

To calculate long-term TPV (TPVa), a moving average or sliding window (w) of p points is computed (Eq. 2). In contrast to TPVtd where the distance is computed from the line of identity, TPVa is calculated using the distance from the center of mass to the origin. Thus TPVtd characterizes interval-to-interval variability whereas TPVa measures longer-term basins of attraction. The dynamics of this position time series are also used to check for discrete changes in behavior that could signify nonstationary behavior.

$$\text{C}=\left(\frac{{\displaystyle {\sum }_{i=1}^{\text{p}}{\text{x}}_i}}{\text{p}},\frac{{\displaystyle {\sum }_{i=1}^{\text{p}}{\text{x}}_j}}{\text{p}}\right)$$ (2)

TPVa is defined as the variance of the centroid position over time. Generally, the coefficient of variation for the TPVa timeline should be reported. This will ensure that the reported long-term variability is normalized by the average centroid position and allows for direct comparison of plots that have differing ranges. Varying the size of the window (w) by varying the number of points used to create the centroid will provide a more complete picture of the average dynamics over multiple timescales and thus provide more insight into the data being analyzed.

Unlike TPVtd, SD1, and SD2, TPVa is able to discriminate between Poincaré plots that have identical point distributions but differing dynamics. For example, Fig. 1, B and C, have the same SD1, SD2, and TPVtd, but different TPVa. In essence, the dynamics of TPVa over time are a quantitative description of the animated Poincaré plot and may provide greater discriminatory power than SD2 alone.

Common statistical limitations that TPVtd shares with SD1 and SD2 are sensitivity to outliers and to the presence of multiple clusters. The preprocessing required depends on the nature of the analysis and dynamics of the data set. By contrast, TPVa is robust to outliers and the presence of multiple clusters; if the dynamics contain transient outliers then averaging with a sufficient w will result in a TPVa with little change from a filtered data set. By contrast, if the dynamics contain a cluster of outliers then TPVa will be greatly affected. Animating the Poincaré plot (or using the TPVa timeline) reveals whether multiple clusters are the result of complex dynamics, nonstationary behavior, or both. (Fig. 3).

Fig. 3.

Illustrations of a time series of heart beats (R-R intervals) from a normal individual (A) and of animating TPVa in Poincaré plots for heart beats (R-R intervals) from a section (circled in A) of that time series (B). A: periods in seconds of sequential heart beats (solid line) and the data underlying TPVa (dashed line) are plotted as the distance from the origin. Circled area shows the portion (151–195) of the time series from which the analysis in B is taken. B: screen shots of the animated TPVa Poincaré plots for the heart beats between 151 and 295. Every 20th Poincaré plot is shown, all the points for n+1 vs. n (n = 1,142, light gray circles), the 25 points (w = 25, dark-gray solid circles) being averaged (NOTE 4-point overlap in the selected screen shots), and a TPVa data point (black solid circle). TPVa data points form the black dashed line in A. With this number of points being averaged, TPVa moves along the line of identity. The coefficient of variation for TPVa correlates with SD2.

Comparison across successive time delays.

Traditionally a time delay of one (τ = 1) is used to create the Poincaré plot, maximizing the amount of (linear) correlation in the data. Low levels of nonlinearity may be obscured at this time-delay selection, yielding little advantage over traditional linear analysis methods. Similarly, a large time delay will significantly reduce the correlations and the plot will not capture the system dynamics. Creating a set of Poincaré plots with different time delays yields more insight into the dynamics of the data set than any single selection. TPVtd is constructed to be identical to SD1, with the exception that it should always be calculated across a series of time delays and compared with the autocorrelation function for interpretation.

Comparison across epoch sizes.

Due to fractal scaling and nonstationary behavior inherent in biological signals, SD2 and TPVa vary with epoch size. Subdividing the time series data into epochs and comparing the dynamics of each of the partitions to the average behavior of the entire time series provides insight into the nature of the variability. If the behavior is uniform across the recorded data set then the variability measurement of the partitions should not be statistically different from that of the entire time series. By contrast, a data set that alternates between regions of high and low variability may produce partitions that show statistically significant differences.

Moreover, SD2 and TPVa should both be used to determine the source of changes across partition size. SD2 captures the total variance in the plot and will be affected primarily by the distribution of variability. TPVa is affected by both distributional variance and temporal correlations and may show significant changes when SD2 does not. These complementary properties are used to highlight structural differences that are not otherwise apparent. In the analysis sections, we refer to the properties captured by SD1/SD2 as variance, whereas variability is used more generally to describe both variance and temporal structure.

Availability of executable analytical program.

The analysis program is available at the web address: http://engineering.case.edu/eecs/research for your unrestricted use.

RESULTS

Exploration Using Synthetic Data

Construction of synthetic data.

We chose the Lorenz attractor with parameters σ = 10, β = 8/3, ρ = 27 to investigate the application of TPV on a stationary system that contains complex but fully deterministic long-term behavior (Fig. 4). In this study, the intervals between successive peaks (maxima) of the x-system Lorenz dynamics define the point process. This idea is similar to extracting R-R intervals from a continuous ECG signal.

Fig. 4.

Comparison of TPV analysis on 2 Lorenz systems (A: Process 1; B: Process 2), differing only by constraints (see text for details). A and B: 1) Poincaré plots show similar distributions for 4 equal partitions (n = 2,500) from each data set (n = 10,000). 2) Autocorrelation functions are highly similar for Processes 1 and 2, with Process 1 having slightly more correlation within each partition. 3) TPVtd curves are highly similar for each data set (n = 10,000) and have little temporal variability in short-term dynamics. 4) SD2 is identical for both systems and all subepochs whereas TPVa trends differently in the nonstationary Process 2. Note the subepochs consist of 1 epoch, n = 10,000 points; 2 epochs, n = 5,000; 4 epochs, n = 2,500; and 8 epochs, n = 1,250.

To evaluate the effect of nonstationary behavior on TPVtd and TPVa, two different point processes, each consisting of 10,000 points, were created. The Process 1 time series was derived from the chaotic Lorenz system with fixed initial conditions, whereas a constraint on the dynamics of the system was used to introduce nonstationary behavior in the Process 2 time series. The construction of Process 2 includes the following steps: 1) define a sphere B in R³ with center c and radius r; 2) select a point at random on the Lorenz system attractor, set c equal to this initial point and simulate the Lorenz dynamics from this point; 3) continue the simulation until the trajectory hits the boundary of B, at this point reinitialize the Lorenz dynamics using a point chosen at random from inside B and return to step 2 using this point as the initial condition; 4) repeat steps 2 and 3 until the required number of point process samples have been obtained for each subepoch. The fixed neighborhood was chosen so that r = 5. This algorithm ensures that the dynamics of Process 2 will be very similar to Process 1 over the short term, but will have long-term regions of resetting that cannot be determined a priori.

SD1/SD2 for Process 1 was 0.92 compared with 0.87 for Process 2. The high ratios for both systems are reflective of the square shape of the Poincaré plots (Fig. 4, A1 and B1).

TPVtd.

When comparing TPVtd of different systems, it is necessary to investigate the contribution of linear correlation to TPVtd by calculating the autocorrelation functions. The autocorrelation functions were similar for both Process 1 and Process 2, with Process 2 having a correlation consistently lower than Process 1 (Fig. 4, A2 and B2) due to the introduced nonstationary behavior.

The TPVtd curves were extremely similar as well (Fig. 4, A3 and B3). After a minor increase over the first few delays, the curves reached an asymptote and TPVtd was consistently larger for Process 1 than Process 2. The leveling of the curves implied that the structure of the interval-to-interval variability was dominated by linear correlations. This property is interesting, as both point processes were generated from highly nonlinear systems. The autocorrelation functions, as well as the similarity in shape of the TPVtd curve, suggest that differences in TPVtd values were due to decreased linear correlations introduced by the resetting of Process 2.

Comparison of SD2 and TPVa.

The synthetic data sets were constructed to highlight the differences in SD2 and TPVa sensitivity across partition sizes. The epoch consisting of 10,000-point process samples was iteratively divided in half to create groups of partitions. The original epoch was divided into two subepochs of 5,000 samples, four of 2,500, and eight of 1,250. SD2 and TPVa were calculated over each partition and then grouped (Fig. 4, A4 and B4).

For both data sets, SD2 was nearly identical regardless of partition size. This suggests that the amount of variance in the systems was relatively independent of sample size, a hypothesis supported by the very similar subepoch Poincaré plots. By contrast, both systems displayed large changes in TPVa as the sample size decreased. Process 1 exhibited an increase in TPVa and reflected a system where the long-term structure was highly ordered, whereas smaller segments contained more variability. By contrast, Process 2 had diminished variability as the subepochs diminished in size. This was due to the constraints on the system that forced the nonstationary behavior.

The effect of w on TPVa differed. For Process 1, relative TPVa values were consistent across subepochs for w of 500, 750, and 1,000; however, in Process 2, the smallest subepochs were not significantly different than the entire epoch at w of 500, but did become different at w of 750 and 1,000 (Fig. 4, A5 and B5). Again, this reflects nonstationary behavior in the system. Smaller compared with larger values of w will be more sensitive to rapid changes in behavior and report a higher level of variability as they capture the switching dynamics more accurately. However, the longer-term dynamics of the system are fully ordered and relatively repetitive, so increasing w will average the nonstationary behaviors and reflect deterministic properties of the system. Process 1, with its fully ordered dynamics, requires only a small w to capture the nature of the system. The SD2 and TPVtd results demonstrate that both systems have variability that is primarily long term, as differences in short-term variability would lead to a change in the TPVtd curve and changes in SD2 across subepochs.

In summary, SD2 cannot distinguish differences between the unfolding dynamics of the full epoch and subepochs that have the same, or similar, distributions. By contrast, TPVa, which preserves the temporal pattern, identifies trends in the systems that have identical SD2 values. This property of TPVa is especially useful in systems that are highly nonlinear or contain inherent nonstationary behavior.

Comparison of Traditional Analysis and TPV on R-R Intervals

Data.

Normal (n = 7) and heart failure (HF) (n = 7) subjects were selected from the PhysioNet Databank to compare traditional with TPV analyses of their Poincaré plots. Epochs of 2,000 beats were selected for the analysis. In this analysis, epochs with interbeat intervals longer than 3 s or shorter than 0.2 s were not used. The data in Fig. 7 were obtained from a single individual enrolled in a study in which we are assisting in the analysis (data collected and de-identified under approval of the Institutional Review Board of the University of Pennsylvania, and processed at Case Western Reserve University). All sequential heart beats were accepted.

Fig. 7.

Utility of TPV analysis: comparison of traditional (SD1 and SD2) and proposed (TPVTD and TPVA) measures of elliptical (A) and nonelliptical (B) Poincaré plots. In A and B: 1) sequential R-R intervals for 2 epochs acquired 24 h apart from the same ICU patient, the inverse of R-R interval is instantaneous heart 2ate; 2) Poincaré plot in which the next R-R interval (s, n+1) was plotted against the current R-R interval (s, n); 3. TPVtd, which was equivalent to SD1 at a time delay of 1 (τ=1), whereas <120>>1, TPVtd reflected the changes in correlation between points with increasing τ (inset: autocorrelation function); 4) SD1, SD2, and TPVta, at progressively increasing number of partitions; TPVa, which is a moving average or sliding window of w points. TPVa with w = 1 was similar to SD2. A: with a single cluster of points forming an elliptical distribution, minimal differences existed between SD1 and TPVtd except TPVtd increases with increasing τ as the correlation between points decreases as well as between SD2 and TPVa except with partitions ≥4 and w ≥ 10 indicating nonstationarity even in this data set. B: with multiple clusters of points forming a nonelliptical distribution, differences between these analytical approaches were accentuated. B1 and B2: short, long inter-digitating R-R intervals were apparent in the plot of sequential R-R intervals and resulted in a Poincaré plot with multiple clusters. Plot of TPVtd (B3) showed repetitive oscillations as τ increased from 1. This oscillatory behavior reflected alternating high and low correlation between points at varying τ (see B3 inset). Although this pattern could not be reflected in values of SD1 with a single partition of the data set (black bar B4), the values of SD1 did not decrease (as in A) but remained similar with increasing number of partitions. B4: SD2 was similar to that in A and decreased slightly as the number of partitions increased as in A. In contrast, TPVa with w=1 was greater than SD2 at the various partitions of the data. With w≥10 and number of partitions ≥4, TPVa decreased reflecting sensitivity to the changing distributions.

Traditional analysis.

Heart rate in HF subjects was significantly higher (P < 0.05) than normal subjects. The normal subjects had a heart rate of 81 ± 11 beats/min, whereas HF subjects had a rate of 94 ± 7 beats/min. The significant difference (P < 0.01) in the coefficient of variation between normal (0.14 ± 0.033) and HF (0.075 ± 0.038) indicated a decrease in variability in HF. These results are consistent with the literature (3).

Poincaré plots were constructed at τ = 1 and compared (representative plots in Fig. 5, A1 and B1). The Poincaré plots of the normal subjects were symmetrical and long. By contrast, the HF subjects had Poincaré plots that were shorter, wider, and more irregular in shape. The HF plots fell into both the “fan” and “complex” categories as defined by Woo et al. (26). The SD1 and SD2 statistics were calculated to characterize the plots and SD1/SD2 for normal subjects was 0.18 ± 0.09; for HF subjects, 0.66 ± 0.32. The larger SD1/SD2 ratio for the HF subjects (P < 0.01) reflected that a greater percentage of its overall variance was beat-to-beat variance; thus the shorter/wider characteristics of these plots compared with those of normal subjects.

Fig. 5.

R-R interval analysis for normal and heart failure (HF) subjects. 1) Representative Poincaré plot for normal subject shows subepochs having some separation of variability. HF subject has less variability both in absolute terms and between subepochs. 2) Similar autocorrelation functions show the 2 subjects have comparable linear correlation structure. 3) Group data for TPVtd highlights increasing beat-to-beat variance in normal subjects as the τ increases. In HF, beat-to-beat variability appears consistent across the range of τ. 4) Group Data from normal (n = 7) and HF (n = 7) subjects. SD2 decreases with subepochs in normal but not in HF whereas TPVa measurements decrease in subepochs for both subject groups.

TPV analysis.

The autocorrelation functions were calculated to a time delay of 100 to assess linear correlations (Fig. 5, A2 and B2). The autocorrelation functions for the subjects were nearly identical across all τ, suggesting similar linear dynamics independent of disease state.

TPVtd was computed from τ = 1 through 100 (Fig. 5, A3 and B3). As shown, at τ = 1 (which is the same as SD1) the normal group had a lower but not significantly different value than the HF group (0.026 ± 0.015 vs. 0.030 ± 0.013). However, as τ increased, TPVtd for the normal group increased significantly, whereas the HF group remained unchanged, with significance (P < 0.05) attained at τ = 48. This result provides insight into the underlying dynamics indicating that normal HRV has structure that is complex and occurs across varying time scales. By contrast, HF subjects not only have reduced variance in traditional measures, but their variability does not have much structure across time. Because the autocorrelation functions were very similar for both groups, the difference was not due to linear correlation and must be a function of nonlinear or nonstationary dynamics. These results are consistent with the literature, particularly detrended fluctuation analysis (25). The TPVtd result highlights the need to investigate Poincaré plots across multiple time delays to uncover differences that are not apparent at τ = 1. Future investigations will determine whether TPVtd is capable of detecting mild-moderate cases of HF in which the Poincaré shapes do not fit into Woo's categories (26) but the underlying dynamics are altered.

SD2 and TPVa (w = 100) were calculated on epochs partitioned as described (Fig. 5, A4 and B4). SD2 diminished as partition size decreased for the normal subjects (partitioning 1 time compared with partitioning 8 times yielded a P < 0.05) but was consistent across partition sizes in HF subjects (P = 0.42). We interpreted this difference as being due to similarity across segments from HF subjects, whereas in segments from normal subjects there was a steady, long-term drift in rates across the epoch. As shown in the representative Poincaré plots, each partition in the normal individual had a portion that was not covered by another partition. In contrast, all the partitions in the HF individual were highly overlapped.

The HF subjects demonstrated reduced TPVa when the time series data were divided into eight partitions (P < 0.1), suggesting the presence of localized correlations not detected by SD2. As previously mentioned, SD2 is only able to capture distributional changes, so the TPVa result implies that in HF the order of the variability changes in small partitions although the distributions are similar to the epoch as a whole. Possibly the HF exhibits nonstationary transitions after brief periods of time, similar to the dynamics of the Lorenz system Process 2 that was introduced in the prior section. Normal subjects also had reduced TPVa when divided into eight partitions (P < 0.05). However, the accompanying decrease in SD2 suggests that the reduced TPVa is primarily a reflection of reduced variance, in addition to minor temporal changes.

An important difference between TPVtd and TPVa is that TPVtd measures variability at a specific time scale by comparing intervals directly (i.e., τ = 100 compares each interval to the interval 100 beats later), whereas TPVa measures the variability of the averaged dynamics (i.e., a w of 100 averages the dynamics over a sliding window 100 beats long and TPVa reports the variance of the averaged values). Thus averaging gives TPVa a temporal component and therefore a true measure of “long-term” variability. This allows it to detect and quantify complex behavior that TPVtd is incapable of capturing.

Comparing TPVa with varying w.

The TPVa analysis was repeated with a w of 10 (Fig. 6, A1 and B1). At this selection of w, normal subjects continued to have a TPVa between partitions that was highly similar to SD2 (TPVa P < 0.05). However, the TPVa between partitioning 1 and 8 times was not significant (P = 0.27). Again, this result is very similar to the synthetic Process 2 data described in the previous section in which a smaller w did not show significance whereas a larger w did.

Fig. 6.

TPVa analysis with varying w. 1) Group analysis shows similar behavior across w for both normal and HF subjects. 2) Partition analysis completed on representative subjects with increasing w. The normal subject has consistent relationships between subepochs across w, whereas HF patient differences are magnified as w increases.

The result demonstrates that it cannot be known a priori how to select w, and a complete analysis should include an investigation across a wide range of reasonable selections of w to form a more complete picture.

Utility of TPV analysis.

The TPV analyses were developed to derive the temporal dependence to the distribution of values displayed within the Poincaré plot. The utility of TPV analysis is revealed by comparing the results of traditional (SD1 and SD2) and proposed (TPVtd and TPVa) measures of Poincaré plots with either a single or multiple clusters (Fig. 7). The ECG data for these plots were gathered from a single, spontaneously breathing, neurological intensive care unit patient during the 4th day of an 11-day stay. At the start of the day (shortly after midnight), the heart rate was stable and the sequential R-R intervals (Fig. 7A1) formed a Poincare plot with an elliptical distribution (Fig. 7A2). Both traditional and TPV analyses concur; TPVtd is equivalent to SD1 at a time delay of 1 (τ = 1), increases progressively with increasing τ (Fig. 7A3), which is consistent with the progressively decreasing autocorrelation function (Fig. 7A3, inset); and SD2 and TPVa have similar values with a small w but increasing w to 50 or 100 points decreased TPVa at the higher number of partitions (Fig. 7A4). In contrast, ∼24 h later the heart beat had long and short R-R intervals that were alternating for a prolonged period of time (Fig. 7B1). This pattern formed a Poincaré plot that had multiple clusters (Fig. 7B2). Again, TPVtd was equivalent to SD1 at τ = 1; but for <120>>1, TPVtd reflected time dependent dynamics (Fig. 7B3) that were consistent with the autocorrelation function (Fig. 7B3, inset). The SD2 was similar to that of the single cluster of the elliptical distribution in Fig. 7A. However, TPVa was greater than SD2 at w = 1 with a single partition. Furthermore, TPVa decreased with partitions ≥4, especially with w ≥ 10 points. This difference results from the sliding window averaging of points from various clusters, thereby minimizing the variance along the line of identity.

DISCUSSION

The genesis of this paper was grounded in the need for more quantitative assessments of irregular Poincaré plots and the incorporation of time series analysis methods into the study of variability. The traditional SD1/SD2 measurements provide the foundation for analysis, but are augmented by looking across time delays with TPVtd and at different time scales with TPVa. In addition, calculating the measures across different sized partitions gives clearer insight into how shorter time scale behaviors combine to form long-term patterns, which is critical when the data are highly complex. In summary, TPV analytical tools provide measures of time-dependent variability in the distribution of points in Poincaré plots, thus complementing other time-dependent methods for analyzing temporal patterns associated with nonlinear dynamics.

TPVa, like detrended fluctuation analysis (DFA) (16), uses averaging to investigate the variability in complex signals. However, the purpose of averaging is very different between DFA and TPVa. DFA averages data to remove long term/nonstationary trends for the computation of a fractal-scaling exponent, whereas TPVa averages data as a low pass filter to highlight longer term/nonstationary trends. In this sense, TPVa is a more direct measure of the long-term behavior of a Poincaré plot than DFA.

The concept of “variability” itself is in need of greater standardization. There are many facets of variability: linear vs. nonlinear, relative vs. absolute, and short term vs. long term to name a few. The analysis of biological systems is fascinating yet frustrating because they often contain multiple types and degrees of variability. The importance of each to physiological and clinical understanding is not yet understood and is hampered by the lack of standardized approachs for more unified analysis. Previous methods (11, 20–23) have proven successful for investigating specific conditions, but are not directly generalizable across diseases or system types. However, statistical tools for each individual aspect of variability have matured to the point that complete analyses are possible and the TPV tools are an example of a carefully defined, multipurpose approach.

The complex correlation measure (CCM) has been developed recently to quantify nonlinear temporal properties contained within the Poincaré plot (12). In this index the point-to-point rather than the population variation is calculated, by determining the area of a triangle formed from three consecutive points from the Poincaré plot. The CCM proved to be a sensitive index compared with SD1 and SD2 in identifying patient populations. However, the temporal information of the time series is limited to a short-time scale defined by the three points of the triangle, whereas TPVa can be used to examine longer time scales. In addition, our partitioning method combined with TPVa identifies whether long-term variability is due to nonstationary behavior, whereas their technique is not able to distinguish between the two types of synthetic data presented.

Although generally a time lag equal to a single cycle is chosen for Poincaré analysis, multiple-lag rather than single-lag Poincaré plots can provide more information (14). With the single time lag, the previous R-R interval is assumed to affect the subsequent R-R interval, whereas multiple lag plots assume the previous interval can affect multiple successive intervals (14, 15). Effects on subsequent cycles not apparent in the pattern can exist for seven cardiac or respiratory cycles (14, 15). Thus the Poincaré plot at multiple lags should be assessed and this can be addressed by including multiple lag times in the TPVtd and TPVa analyses.

The human data acquired from the neurological ICU clarifies the physiological utility of the TPV measures. All measures (SD1, SD2, TPVtd, and TPVa) can assess an elliptical distribution of points. But even in an elliptical distribution, partitioning the data set identifies a subtle difference between the analytical approaches and can provide insight into the stationarity of the data. In Fig. 7A4, SD1 and SD2 decrease progressively, indicating that the large ellipse is composed of smaller ellipses showing decreases in short- and long-term variability with smaller data sets. However, TPVa decreases sharply when averaging a sliding window of 50 points at 4 partitions (n = 589 R-R intervals/partition; Fig. 7A), indicating nonstationary data because subsets with ∼600 R-R intervals have smaller TPVa. These are apparent in the plot of sequential R-R values with abrupt changes in patterning with 500 and 1,100 R-R intervals. TPV analysis also is a robust tool for the analysis of Poincaré plots that contain multiple clusters of points that result in nonelliptical distributions of points (Fig. 7B). Although we used SD1 and SD2 to measure the distribution of points, SD1 cannot quantify the time-dependent oscillations in the autocorrelation function and SD2 is similar between Fig. 7, A and B. On the other hand, TPVtd reflects the characteristics of the autocorrelation function, and TPVa with a single partition is greater for the multi- than single-cluster data set (compare Fig. 7B4 to 7A4). Furthermore, TPVa decreases with as few as 4 partitions at (n = 770 R-R intervals/partition) and the nonstationary behavior of the bigeminy that occurred between intervals 1,600 and 2,025. Finally, it is beyond the scope of this methods paper to associate changes in heart rate variability as measured by TPV to clinical outcomes; but during the period in which the patient data was acquired cardiovascular support was initiated. The TPV analysis of the synthetic data, normal and HF data from PhysioNet, and clinical data from the neurological ICU analyzed in the paper clearly suggest the applicability of this technique to longitudinal studies in patients where temporal patterning in physiological leads to Poincaré plots with nonelliptical distributions.

The Poincaré plot is a powerful tool because it captures many types of variability, especially when investigated over multiple time delays. The visual and intuitive nature provides a foundation for the analysis and explains its prevalence. TPV analysis provides flexibility in plot quantification by relating to accepted measures while enabling the use of emerging techniques.

GRANTS

We gratefully acknowledge that this work was supported by National Institutes of Health (NIH) HL-080318, NIH HL-087377 (to T. E. Dick), and Award No. I01BX000873 from the Biomedical Laboratory Research & Development Service of the VA Office of Research and Development (to F. J. Jacono).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: M.F., F.J.J., K.A.L., and T.E.D. conception and design of research; M.F., S.P., and R.J. performed experiments; M.F., S.P., R.J., A.T., and T.E.D. analyzed data; M.F., F.J.J., S.P., R.J., A.T., K.A.L., and T.E.D. interpreted results of experiments; M.F., R.J., A.T., and T.E.D. prepared figures; M.F. and T.E.D. drafted manuscript; M.F., F.J.J., S.P., K.A.L., and T.E.D. edited and revised manuscript; M.F., F.J.J., S.P., R.J., A.T., K.A.L., and T.E.D. approved final version of manuscript.