Behavioral and neural correlates of visuomotor adaptation observed through a brain-computer interface in primary motor cortex

Abstract

Brain-computer interfaces (BCIs) provide a defined link between neural activity and devices, allowing a detailed study of the neural adaptive responses generating behavioral output. We trained monkeys to perform two-dimensional center-out movements of a computer cursor using a BCI. We then applied a perturbation by randomly selecting a subset of the recorded units and rotating their directional contributions to cursor movement by a consistent angle. Globally, this perturbation mimics a visuomotor transformation, and in the first part of this article we characterize the psychophysical indications of motor adaptation and compare them with known results from adaptation of natural reaching movements. Locally, however, only a subset of the neurons in the population actually contributes to error, allowing us to probe for signatures of neural adaptation that might be specific to the subset of neurons we perturbed. One compensation strategy would be to selectively adapt the subset of cells responsible for the error. An alternate strategy would be to globally adapt the entire population to correct the error. Using a recently developed mathematical technique that allows us to differentiate these two mechanisms, we found evidence of both strategies in the neural responses. The dominant strategy we observed was global, accounting for ∼86% of the total error reduction. The remaining 14% came from local changes in the tuning functions of the perturbed units. Interestingly, these local changes were specific to the details of the applied rotation: in particular, changes in the depth of tuning were only observed when the percentage of perturbed cells was small. These results imply that there may be constraints on the network's adaptive capabilities, at least for perturbations lasting only a few hundreds of trials.

cortical neurons have the ability to adapt their tuning properties in the face of a variety of environmental perturbations. In sensory deprivation experiments, it has been shown that the tuning curves of neurons in somatosensory (Merzenich et al. 1983; Rasmusson 1982), visual (Keck et al. 2008), and auditory cortical areas (Robertson and Irvine 1989; Schwaber et al. 1993) can reorganize to represent remaining functional sensory inputs (for review, see Kaas 2002). In auditory discrimination tasks, neurons in primary auditory cortex can change their tuning on a timescale of minutes to adapt to changes in the behavioral task (Fritz et al. 2003, 2005). This type of context-dependent encoding has also been demonstrated in the motor system, where neurons in primary motor cortex exhibit changes in tuning when switching between tasks (Davidson et al. 2007; Hepp-Reymond et al. 1999). Similarly, directional tuning curves in primary motor cortex have been found to change in complex ways during sensorimotor learning (e.g., Ganguly and Carmena 2009; Li et al., 2001; Mandelblat-Cerf et al. 2011; Paz et al. 2003; Wise et al. 1998). The bulk of the literature would seem to indicate that there are few limits on the kinds of adaptive responses cortical networks can demonstrate.

This work is of particular interest in the context of motor learning. When faced with a novel perturbation, how does the motor system discover a set of neural activations that effectively counters it? Furthermore, given a potentially redundant manifold of neural activations that could counter the perturbation (as described in Rokni et al. 2007), how does the motor system arrive at one particular solution? Brain-computer interfaces (BCIs) can help us address this problem. In a BCI, the activity of dozens of recorded neurons can be used to control the movement of a computer cursor (Hochberg et al. 2006; Mulliken et al. 2008; Taylor et al. 2002), movement of a robotic arm (Chapin et al. 1999; Velliste et al. 2008), or selection in a categorical choice task (Musallam et al. 2004; Santhanam et al. 2006). During operation of these devices, there is a defined link between the activity of individual neurons and behavior, making it possible to understand the behavioral relevance of particular neural changes.

We trained monkeys to perform two-dimensional (2-D) center-out movements of a computer cursor using a BCI. To assess the selectivity of adaptive responses within the motor cortex, we then applied a perturbation by randomly selecting a subset of the recorded units and rotating their directional contributions to cursor movement by a consistent angle. In essence, we separated the recorded units into two populations and applied a visuomotor rotation to the decoded output of one of those populations. The cursor movement was then computed as the sum of the output from the perturbed and nonperturbed populations. Perceptually, this manipulation induced a combined visuomotor rotation and gain reduction in the decoded cursor movement, and we found that monkeys adapted to these visuomotor rotations with a time course similar to humans using natural arm movements. However, our subjects showed only a limited adaptation to the gain reductions in these experiments.

In previous work (Jarosiewicz et al. 2008), we used a similar version of this task in 3-D to demonstrate that the tuning curves of perturbed units changed more than the tuning curves of units that were not perturbed. The present work extends that previous work in two ways. First, we examined the adaptation to several different perturbations, ranging in the percentage of randomly chosen units that were perturbed as well as the amount of the rotation we applied. Second, we applied a recently developed analysis (Chase et al. 2010) that allows us to mathematically decompose the observed firing rate changes into global changes that are common to the entire population of units and local changes that are specific to individual units. The method allows us to separate the subject's intended aiming direction from the actual target direction and to infer the neural tuning as a function of this intent. As a consequence, we can compute how much of the error reduction stems from global vs. local mechanisms and compute how this relationship changes as a function of the perturbation parameters.

Although the perturbation was applied to only a subset of units, we found the dominant adaptation strategy employed by the subjects was global, accounting for ∼86% of the total error reduction. The remaining 14% of the error reduction could be attributed to local changes in tuning curves. As we argue below, the global adaptation strategy is a suboptimal response to these perturbations, implying that there are constraints on the network's ability to rapidly identify the optimal solution to a given perturbation. We discuss implications of this work for theories of motor control.

METHODS

Data recording.

Two male Rhesus monkeys (Macaca mulatta) were each implanted with one 96-channel Utah array (Blackrock Microsystems, Salt Lake City, UT). All implantations were visually placed in the proximal arm area of primary motor cortex. Recordings were amplified, filtered, and sorted online with a 96-channel Plexon MAP system (Plexon, Dallas, TX). Some of the units recorded were well-isolated single cells, and some contained two or more cells that could not easily be isolated from one another but were nevertheless tuned to intended movement direction as a group. All procedures were performed with the approval of the Institutional Animal Care and Use Committee of the University of Pittsburgh.

Establishing the BCI.

Establishing the BCI involves three steps: choosing an encoding model that describes how movement is represented in the firing rates, choosing a decoding algorithm for mapping those firing rates back into cursor movement, and performing a calibration to fit the parameters required by the decoding algorithm. We assumed a linear encoding model for the BCI where the tuning curves were functions of direction only, and we used the population vector algorithm (Georgopoulos et al. 1986) to translate firing rates into cursor velocities. [A full analysis of the effects of linearity assumptions on decoding accuracy can be found in Koyama et al. (2009).] Thus, if the intended direction of movement is described by the vector [d_x, d_y], then the firing rate of the cell, λ, is assumed to take the form

$$\begin{array}{c}\lambda =b_0+b_x{d}_x+b_y{d}_y\\ =b_0+m\cos \left(\theta \right),\end{array}$$ (1)

where b₀ represents the baseline firing rate of the cell and b_x and b_y represent the tuning coefficients. The modulation depth of the cell, m, is defined as the length of the vector b = [b_x, b_y], and the preferred direction (PD) p is defined as b/m. The angle between the intended direction of movement and the cell's PD is represented by θ. For notational convenience, we will denote the estimate of any quantity with a hat, e.g., the estimate of b₀ derived from ordinary linear regression is denoted b̂₀.

Spikes from each of the N recorded units (indexed by i) were binned into Δt = 33.3-ms intervals and converted to rate estimates f̂_i[t] by dividing by the sampling interval. Smoothed, normalized rates r_i[t] were computed through the equation

$$r_i\left[t\right]=\frac{1}{5}{\displaystyle \sum _{j=0}^4\frac{f_i\left[t-j\Delta t\right]-b_{0,i}^{\text{D}}}{m_i^{\text{D}}}}$$ (2)

where the superscript D indicates that these are decoding parameters that must be estimated from a calibration procedure, described below. These smoothed, normalized rates were then translated into cursor velocity C_v[t] through the equation

$$C_v\left[t\right]=\frac{k_s\delta }{N}{\displaystyle \sum _{i=1}^N{r}_i\left[t\right]p_i^D.}$$ (3)

where δ is the number of control dimensions (in this case, 2) and k_s represents the speed factor, a parameter set by the experimenter to convert the magnitude of the population vector from a normalized range to a physical speed; in these experiments, chosen values ranged from 65 to 80 mm/s. Finally, p_i^D represents the decoding preferred direction (dPD) of unit i. All of the perturbations discussed in Experimental task below were implemented by manipulating these p_i^D parameters. The cursor position C_p[t] was derived by integrating the cursor velocity

$$C_{\text{P}}\left[t\right]=C_{\text{P}}\left[t-\Delta t\right]+\Delta t{C}_{\text{v}}\left[t\right].$$ (4)

Trajectories always started at the origin.

Note that the filtering step of Eq. 2 will impose a lag between the neural signal and the resultant cursor movement. We estimate the lag in our system to be one-half the filter length plus a system processing time of about one monitor frame (16.7 ms), for a total lag of ∼100 ms. This lag is actually slightly less than the typical lag between neural activity in primary motor cortex and the corresponding arm movement (cf. Fig. 7 of Georgopoulos et al. 1982).

Fig. 7.

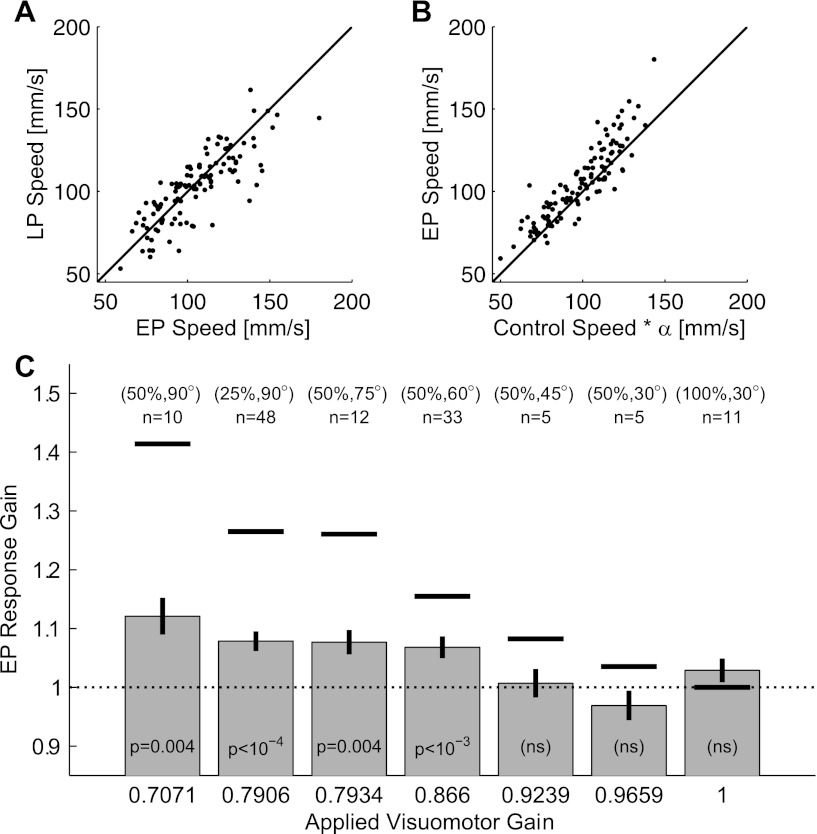
Adaptive speed increases are rapid but show limited dynamic range. A: cursor speed during the LP session plotted as a function of the cursor speed in the EP session. Roughly equal numbers of experiments show increases as show decreases between the 2 sessions. Data are from the 113 experiments that had a visuomotor gain reduction. Black line indicates the identity line. B: speed during the EP session plotted as a function of expected speed (calculated as the corresponding speed in the control session times the visuomotor gain reduction factor α). Speeds in the EP session are typically higher than expected. Format is the same as for A. C: response gain during the EP session for each applied visuomotor gain reduction. A value of 1 would indicate no adaptive response. The response gain required to fully compensate for the speed reduction is the inverse of the applied gain and is denoted by the horizontal black lines. Although the response gains for all experiments with applied gain reductions of <0.9 are statistically significant, the gains are much less than required to fully compensate for the speed reduction.

As expressed above, to perform decoding with these algorithms, the decoding parameters must be known. We calibrated the system in the following way. To initialize the system, the dPDs were chosen randomly from values on the unit circle, and m^D and b₀^D were set to 40 Hz for every cell. Targets for the center-out task were then presented, one at a time in random order, and left on the screen until a movement time-out period elapsed (typically, 1 s). Firing rates modulate in response to this target presentation. However, during this first cycle of target presentation, the cursor does not move much due to the randomized dPDs and large initial values of m^D. Once an entire cycle set consisting of one presentation of each target was completed, the average observed spike rates for each trial were regressed against target direction to compute estimates of the linear tuning function parameters b̂_0,j, m̂_i, and p̂_i. The decoding parameters were set equal to these estimated values. Another cycle set of targets was then presented, and the process was repeated until the monkey was able to complete the center-out task reliably. Typically, only four to six cycle sets of data (about 2 min of data collection) were needed to achieve good control. Cells with modulation depths of <4 Hz were not used for control. The median number of cells used to control the cursor in a given experiment was 26; the interquartile range was 23 to 30, and the full range was 15 to 66.

Experimental task.

Monkeys were trained to perform a center-out reaching task in 2-D under brain control. Monkeys sat in a primate chair facing a mirror that reflected an image from a stereoscopic computer monitor above in a periscope-like design. Both of the monkey's arms were restrained; movement of the cursor was achieved by modulating the spiking activity of recorded neurons, as described above. Center-out movements were made to 16 targets equally spaced around a circle 85 mm in radius, centered on the origin. The cursor and the target were always the same size (typically, 8 mm in radius). To successfully complete a trial, the subject had to move the cursor from the center of the workspace to a randomly presented target within a movement time-out period typically lasting 2 s. After either successful or failed trials, we moved the cursor back to the center of the workspace and initiated another trial after an intertrial period typically lasting about 1 s. The variable parameters of this task (the cursor and target radii, movement time-out period, and intertrial interval) were always fixed within an experiment but were slowly changed across experiments to keep the task difficulty roughly equivalent as the subjects improved due to practice. The ranges and median values of these parameters are given in Table 1.

Table 1.

Center-out movement parameters

Parameter	Median	Minimum	Maximum
Intertrial interval, s	1.25	0.75	2.00
Movement time out, s	2.00	1.2	3.00
Cursor/target radii, mm	8	7	15
No. of control movements	161	80	257
No. of perturbation movements	240	176	416
No. of washout movements	160	0	1,008

Values are median, minimum, and maximum values for parameters of the center-out task.

For our analysis of the neural mechanisms underlying this adaptation, we wanted to ensure that the results could be explained purely on the basis of a forward estimation process, and not be influenced by perceived visual error. To tease apart these effects, in some experiments we added a circular “invisible zone” extending 45 mm from the center of the workspace. The trial started with the cursor inside this invisible zone, and the monkey received no visual feedback about the location of the cursor until it had crossed the invisible zone barrier (trial start was indicated by the appearance of the target). Once the cursor crossed the barrier, full visual feedback was restored, regardless of where the cursor moved, i.e., even if the cursor moved back within 45 mm of the center of the workspace, it would still be visible. Targets were visible throughout the entire trial.

Each perturbation experiment consisted of four sessions: a calibration session (∼64 target presentations), in which the decoding parameters were estimated and fixed; a control session, in which the monkey performed center-out movements using the decoding parameters estimated from the calibration session (typically, around 160 successful movements); a perturbation session, in which the monkey performed center-out movements using a perturbed set of decoding parameters, described below (typically, around 240 successful movements); and a washout session, in which the subject performed center-out movements with the original set of decoding parameters (typically, around 160 successful movements or until the subject stopped working). Table 1 provides the ranges of the number of successful movements performed in each session.

Perturbations were applied by taking the dPDs (p_i^D in Eq. 3) of a randomly chosen subset of cells and rotating them clockwise (CW) or counterclockwise (CCW) by a certain number of degrees. For a given experiment, the dPDs of all of the chosen subset were rotated in a consistent fashion, e.g., all might be rotated CW by 60°. A number of different perturbations were tested, varying in the percentage of units that were perturbed, the extent of the rotation, and whether or not there was an invisible zone present throughout the experiment. Nine different experimental conditions were tested in total. Table 2 gives a list of these conditions, the expected rotations and gains for each condition, the number of experiments run in each condition, and the total number of units studied under each condition. For notational convenience, we refer to each experimental condition in the following shorthand notation: (%, °, V/I), giving the percentage of cells rotated, the extent of the perturbation in degrees, and whether there was an invisible zone (I) or no invisible zone (V) used in the experiment. Thus an experiment in which 50% of the cells were rotated by 60° with an invisible zone is denoted (50%, 60°, I); the same perturbation with no invisible zone is denoted (50%, 60°, V). With the exception of the (50%, 90°, I) perturbations, CW and CCW perturbations were randomly intermixed to help alleviate carryover effects from day to day. In the (50%, 90°, I) case, all perturbations were CW. We include this data set because all of the trends observed in the other perturbation conditions were also observed in this data set. The majority of the data reported here come from one monkey: of the 124 total experiments included in the analysis, 107 were from one monkey and 17 were from the other. We did not observe any differences in the data trends between the two monkeys. A breakdown describing which experiments were performed by each monkey is included in Table 2.

Table 2.

Perturbation conditions

Perturbation	No. of Experiments	θ, °	α	No. of Cells	Subject
(100%, 30°, V)	11	30	1	278	A
(50%, 30°, I)	5	15	0.97	279	A
(50%, 45°, I)	5	22.5	0.92	107	W
(50%, 60°, I)	13	30	0.87	363	W (2), A (11)
(50%, 60°, V)	20	30	0.87	544	A
(50%, 75°, I)	12	37.5	0.79	313	A
(50%, 90°, I)	10	45	0.71	460	W
(25%, 90°, I)	43	18.4	0.79	1109	A
(25%, 90°, V)	5	18.4	0.79	115	A

Values for each of the different perturbation conditions tested include the number of experiments run in each perturbation condition, the expected rotational error (θ) and speed gain (α) in each experimental condition, the total number of units (cells) studied under each perturbation condition, and the subject that performed the experiments. Notation for perturbation conditions is in the form (%, °, V/I), giving the percentage of cells rotated, the extent of the perturbation in degrees, and whether there was an invisible zone (I) or no invisible zone (V) used in the experiment.

Calculation of the expected cursor perturbation.

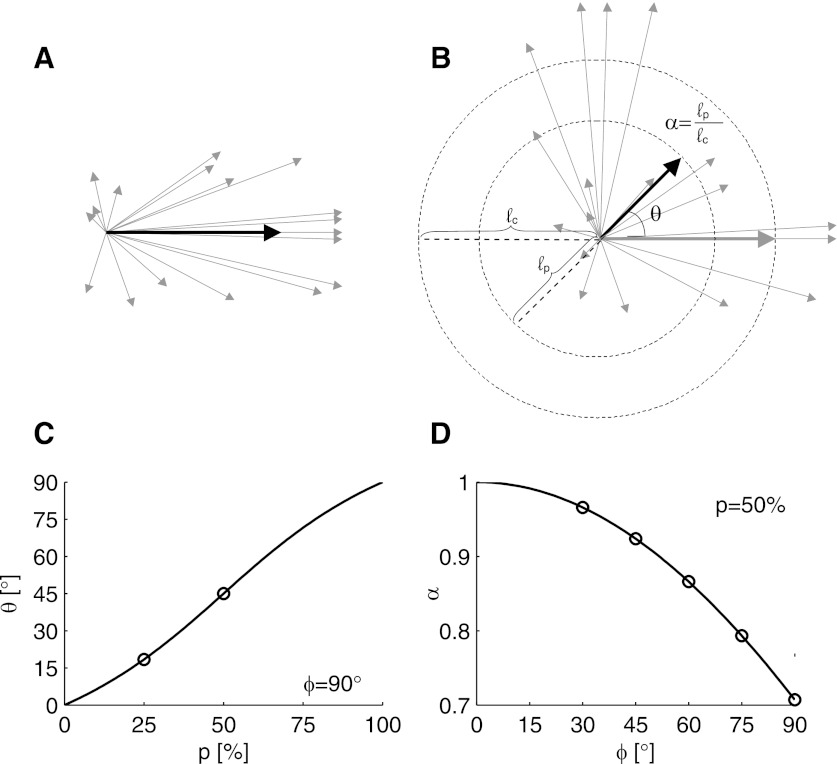
Globally, the perturbations applied in these experiments create both a visuomotor rotation and a visuomotor gain reduction, as shown schematically in Fig. 1, A and B. Both of these effects can be estimated from first principles, under the assumption that the PDs of each subpopulation of cells (rotated and nonrotated) are uniformly distributed.

Fig. 1.

Schematic of the applied perturbation, highlighting both the angular deviation and the speed reduction. A: schematic of activity during a movement in the control session. Thin gray lines represent the contributions of each neuron to the population vector, where each arrow points in the neuron's preferred direction (PD) and is scaled by its normalized firing rate. Thick black arrow represents the population vector. B: the same neural activity as represented in A, but decoded as if it occurred in the perturbation session. Half of the neurons are being decoded at a 90° angle to their original PDs. Thick black line shows the new population vector, with the thick gray line showing the control population vector, for reference. The perturbation shows both an angular deviation (θ) and a speed reduction (α). C: plot of the expected global rotation (θ) as a function of the percentage of cells rotated (p) when the decoding preferred directions (dPDs) are rotated by 90°. Circles denote experimental conditions we tested. D: speed gain (α) plotted as a function of the extent of the perturbation (ϕ) when 50% of the cells are rotated. Again, circles denote experimental conditions we tested (see Table 2 for a list of these experiments).

Mathematically, we can decompose the estimated cursor velocity into a component that comes from the rotated subpopulation and a component that comes from the nonrotated subpopulation:

$$C_{\text{v}}\left(t\right)=p{C}_{\text{v;r}}\left(t\right)+\left(1-p\right)C_{\text{v},\text{nr}}\left(t\right)$$ (5)

where the subscripts r and nr refer to the rotated and nonrotated subsets of cells, respectively, and p represents the proportion of the total number of recorded cells that are in the rotated subset. A full derivation of Eq. 5 is provided in the supplemental material of Jarosiewicz et al. (2008).

When the PDs of the recorded population of cells are uniformly distributed (and correctly estimated), the population vector algorithm returns an unbiased estimate of the intended velocity. Thus, in the control session, if the intended velocity was [1,0]^T, then C_v = [1,0]^T (where the superscript T denotes vector transpose). In the perturbation session, the same intended velocity would be decoded as

$$C_{\text{v}}=p\text{R}\left(\phi \right)\left[\begin{array}{c}1\\ 0\end{array}\right]+\left(1-p\right)\left[\begin{array}{c}1\\ 0\end{array}\right]=\left[\begin{array}{c}p\cos \phi +1-p\\ p\sin \phi \end{array}\right],$$

where R(ϕ) is a 2 × 2 rotation matrix and ϕ is the extent of the perturbation. By comparing the angle and magnitude of this perturbed vector with the angle and magnitude of the intended vector, we can calculate the expected gain, α, and rotation, θ, of the perturbation:

$$\alpha =1-2p\left(1-p\right)\left[1-\cos \left(\phi \right)\right];\theta =\arctan \left[\frac{p\sin \left(\phi \right)}{p\cos \left(\phi \right)+\left(1-p\right)}\right].$$ (6)

The results are plotted for certain ranges of p and ϕ in Fig. 1, C and D.

Trajectory averaging.

Average trajectories are displayed in Fig. 2. To combine trajectories of different durations, the time axis of each trajectory was uniformly scaled to the mean movement duration, τ_avg. That is, the time samples for an individual trajectory of duration τ were scaled by a gain factor, τ_avg/τ, to create a new set of time samples. Each x and y component of the trajectory was then independently resampled using linear interpolation to a common time axis consisting of 300 evenly sampled points ranging from 0 to τ_avg. The mean and SD of the position components were then computed at every time point. For experiments that included an invisible zone, the time rescaling could potentially have produced mixing of visible and nonvisible portions of the trajectory at the invisible zone border. To avoid this problem, the averaging was performed separately for trajectory fragments inside and outside of the invisible zone.

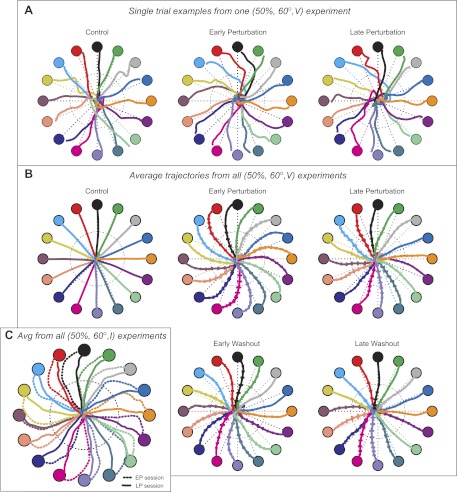
Fig. 2.

Trajectories show evidence of adaptation and predictive compensation. A: examples of single trials taken from the control, early perturbation (EP), and late perturbation (LP) sessions of 1 of the (50%, 60°, V) experiments (notation indicates 50% of the cells were rotated by 60° with no invisible zone). Each color denotes a different target. Dotted circles indicate the halfway point where the angular error is assessed. Dashed lines indicate the straight line between the origin and target, for reference. B: average trajectories from all 19 experiments of the (50%, 60°, V) condition. Format is the same as in A. C: average trajectories from the (50%, 60°, I) experimental condition (where 50% of the cells were rotated by 60° with an invisible zone), demonstrating the reduction in error between the EP and LP session trajectories. Dotted circle shows the location of the invisible zone. Dashed lines indicate trajectories from the EP session, and solid lines indicate trajectories from the LP session.

The adaptation to CW and CCW perturbations was qualitatively similar but of opposite sign, so to combine them for averaging, we “flipped” trajectories from CW perturbations in the following way. Each point in trajectories to targets located at angle Ψ were first rotated by an angle −Ψ, so that the target lay along the positive x-axis. CW perturbations would then tend to push the trajectory in the negative y-direction, whereas CCW perturbations would tend to push the trajectory in the positive y-direction. We therefore multiplied the y-components of points in trajectories from CW perturbations by −1. Finally, all points in the trajectory were rotated back by an angle Ψ. This transformation can be written as

$$p_F=F_p,$$ (7)

where p is a 2 × 1 point in a CW trajectory, p_F is the corresponding flip-transformed 2 × 1 point, and F is the 2 × 2 flipping transform matrix:

$$F=\left[\begin{array}{cc}\cos \left(\psi \right)& -\sin \left(\psi \right)\\ \sin \left(\psi \right)& \cos \left(\psi \right)\end{array}\right]\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right]\left[\begin{array}{cc}\cos \left(-\psi \right)& -\sin \left(-\psi \right)\\ \sin \left(-\psi \right)& \cos \left(-\psi \right)\end{array}\right]=\left[\begin{array}{cc}\cos \left(2\psi \right)& \sin \left(2\psi \right)\\ \sin \left(2\psi \right)& -\cos \left(2\psi \right)\end{array}\right].$$ (8)

Behavioral data analysis.

Angular errors were calculated as the signed angular deviation between the line connecting the origin to the cursor and the line pointing from the origin to the target, assessed when the cursor had moved one-half the distance to the target (i.e., 42.5 mm out from the center). Errors were assigned a positive value when they were in the direction of the perturbation or a negative value if they were counter to the perturbation.

To assess learning, we compared the errors immediately after application of the perturbation with errors after lengthy exposure to the perturbation. Specifically, we divided both the perturbation and washout sessions into early and late parts. The early perturbation (EP) session was defined as the first 16 successful trials after the perturbation was applied (1 successful trial to each of the 16 targets). The late perturbation (LP) session was defined as the last 16 successful movements before the perturbation was removed. The early and late washout sessions (EW and LW, respectively) were defined similarly: EW was the first 16 successful trials after the perturbation was removed, and LW was the last 16 successful trials performed in the washout session, provided the washout session consisted of at least 112 successful movements.

With natural arm movements, gain adaptation is typically assessed as a change in the peak movement speed. However, single-trial movements in these BCI experiments tended to lack a clear peak in the speed profile. Instead, we computed the speed command as the magnitude of the decoded population vector computed from firing rates averaged over a fixed window of time: 300 to 500 ms after target presentation. This window was chosen because it allows the subject time to react to the target but is early enough to prevent most corrective movements. For experiments with an invisible zone, this time window was entirely contained within the invisible zone during the perturbation session on 99.5% of trials.

Neural data analysis.

One of the goals of this study was to differentiate “global” adaptive responses that influence the entire population of units (re-aiming) from selective “local” adaptive responses that differentially influence specific neurons (re-tuning). We did this using a recently developed iterative method that associates an unobserved latent input with every target that represents the subject's presumed re-aiming point or intended direction when presented with that target. This method, fully described in Chase et al. (2010), ensures that even if the amount of re-aiming varies from target to target, firing rate changes that are common to the population are factored out when tuning curve changes are computed. The method proceeds as follows. Assume that the firing rate of unit i to a direction of intended movement d→ can be described as a Poisson process whose rate parameter λ_i is a log-linear function of direction:

$$\log \left({\lambda }_i\right)=b_{0,i}+m_i{\overrightarrow{p}}_i·\overrightarrow{d}.$$ (9)

We used general linear model (GLM) regression to fit these log-linear tuning curves and derive estimates of the baseline firing rate of the unit, b_0,i, the modulation depth, m_i, and the preferred direction, p→_i. Log-linear tuning curves were used instead of standard linear (cosine) tuning curves because it has been demonstrated that most neurons in primary motor cortex exhibit narrower-than-cosine tuning (Amirikian and Georgopoulos 2000), and it is well known that neural firing is typically described better by Poisson than by Gaussian statistics. Furthermore, these log-linear tuning curves fit our data better than standard cosine tuning curves (data not shown, but Fig. 8 is an example).

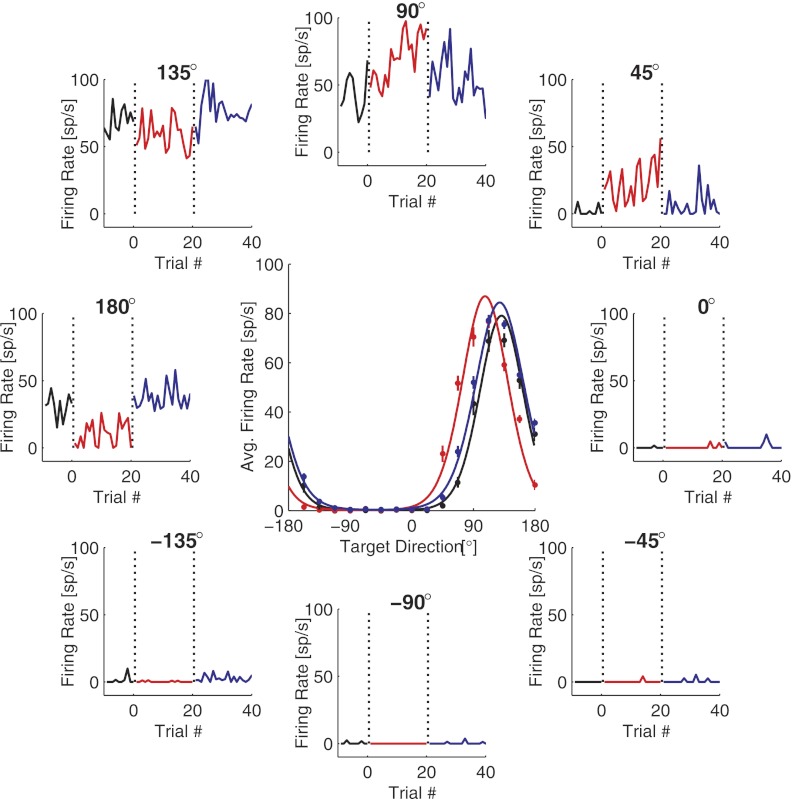
Fig. 8.

Firing rates of single neurons change in response to the perturbation. Data shown are from 1 example nonrotated neuron during a (50%, 60°, V) experiment. Center: average firing rate of the neuron plotted as a function of the target direction during the control (black), perturbation (red), and washout sessions(blue). Solid lines show the log-linear tuning curve fits, whereas data points and vertical lines show the means ± SE of the firing rates at each target direction. Surrounding plots show firing rate of the neuron to 8 of the 16 targets as a function of the number of sequential trials to that target. Target directions are indicated above each plot (as well as by the polar position of the plot). The zero value on each abscissa and the first vertical dotted line indicate when the perturbation was applied; the second vertical line indicates when the perturbation was removed.

Note that the tuning curve variables b_0i, m_i, and p→_i are different from the decoding parameters b_0,i^D, m_i^D, and p→_i^D. The tuning curve variables describe how the neuron maps intended direction into firing rate; as experimenters, we have no direct access to these quantities, we can only infer them through measurement. The decoding parameters, on the other hand, describe how these firing rates contribute to cursor movement. They must be set by the experimenter.

We computed the re-aiming points as follows. Let y_i,k represent the observed spike count of unit i to target k measured over the time interval Δt. The re-aiming point d→_k for target k was computed as the direction that maximized the quasi log-likelihood function,

$$l\left({\overrightarrow{d}}_k\right)\equiv {\displaystyle \sum _{i=1}^N\frac{y_{i,k}\log \left[\Delta t{\lambda }_i\left({\overrightarrow{d}}_k\right)\right]-\Delta t{\lambda }_i\left({\overrightarrow{d}}_k\right)}{{\tau }_i},}$$ (10)

Essentially, the computed re-aiming point is the direction that maximizes the probability of having observed the given spike counts with the given tuning curves, under the assumption that units are conditionally independent given direction. The overdispersion parameter, τ_i, is a correction for cases in which the variance/mean relationship is not perfectly Poisson, but rather is better described by the more general equation Var[F_i] = τ_iE[F_i]. For details on GLM regression and the quasi log-likelihood derivation, see McCullagh and Nelder (1989).

The algorithm proceeds by alternating between the regression step used to estimate the tuning curves (Eq. 9) and the maximum likelihood step used to compute the re-aiming points (Eq. 10), continuing until a particular convergence criterion is reached. We considered convergence to be reached when the average tuning curve error decreased by <1% on subsequent iterations. As noted by Chase et al. (2010), there is a nonidentifiability in the solution that emerges: it is not possible to distinguish between one set of preferred directions and re-aiming points and another set in which all of the re-aiming points are rotated CW by a certain amount and all of the preferred directions are rotated CCW by an equivalent amount; the two cases produce equivalent log-likelihoods. To break this nonidentifiability in the control session, we initialized the algorithm by setting the first-iteration re-aiming points equal to the target directions. This results in a set of final re-aiming points (and corresponding tuning curves) that are in some sense “closest” to the target directions. In the perturbation session, we anchored the solution by fixing the PDs of the nonrotated cells to have zero average rotation. That is, we computed the average rotation of the PDs of the nonrotated units between the perturbation and control sessions, and rotated all of the PDs so that these nonrotated units had zero average rotation across sessions. We then rotated the re-aiming points in the opposite direction by an equivalent amount. Therefore, rotations of both the re-aiming points and the PDs of the rotated population are computed relative to the nonrotated population.

To compute the re-aiming points and tuning curves, we analyzed spikes from a 200-ms window ending when the cursor moved one-half the distance to the targets. This is the same window used by Jarosiewicz et al. (2008) and was chosen in an attempt to isolate a time period after the subject had reacted to the target presentation but before he had a chance to visually correct for perceived movement errors. This time window was entirely within the invisible zone, when it was used. To make accurate estimates of tuning curves and aiming points, we combined data across trials, i.e., we fit one set of tuning curves and aiming points in each of the control, perturbation, and washout sessions. When computing re-aiming points and tuning curves from either the perturbation or washout sessions, we discarded the first seven repetitions of each target (112 trials in total) to avoid the period of most rapid adaptation (see Fig. 4C).

Fig. 4.

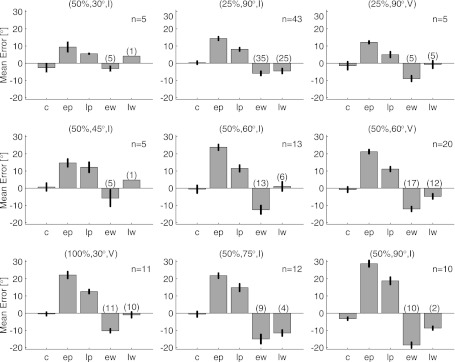
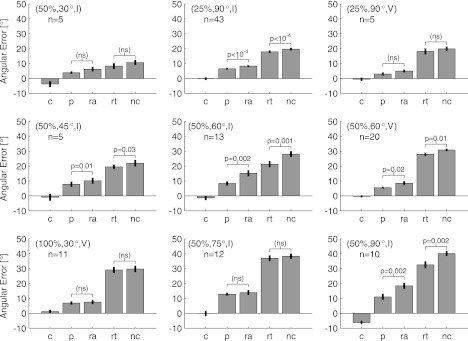
The overall pattern of angular errors is consistent across experimental conditions. Each plot gives the mean signed angular error as a function of the session within the experiment. Positive numbers denote errors in the direction of the applied rotation, negative numbers denote errors in the opposing direction, and vertical bars denote ±SE. The perturbation condition of each experiment is shown above its plot, and the number of experiments (n) performed in each condition is given at top right of each plot. Occasionally, the subjects would stop working before an adequate number of trials had been collected to compute the average error in the EW or LW session. Numbers in parentheses above the EW and LW bars state the number of experiments used to compute these values. Note the lack of error bars for the (50%, 30°, I) and (50%, 45°, I) LW cases, which only included data from 1 experiment each. Plots are arranged according to the extent of the rotational perturbation (Table 2).

For cosine tuning curves, the modulation depth represents half of the total dynamic range of the firing rate. To maintain this intuitive measure, the modulation depths (MDs) we report here for these log-linear tuning curves are computed as

$${\text{MD}}_i=\exp \left(b_{0,i}\right)\sinh \left(m_i\right).$$ (11)

With this definition, the MDs again represent half the total dynamic range of the tuning curve.

RESULTS

We analyzed 124 experiments in total, spanning 9 different perturbation conditions. Success rates in the control session were uniformly good, with an average across all experiments of 91%. The perturbation session was slightly more difficult, with an average success rate of 69%. In the washout session, the average success rate climbed to 75%. It should be noted that the success rates given here are biased downward, because the trials were not self-initiated; they proceeded at a set pace regardless of success or failure. We made no attempt to remove runs of failed trials (which were rare but occurred when the monkey was not paying attention) from the success rate calculation.

Evidence for predictive compensation.

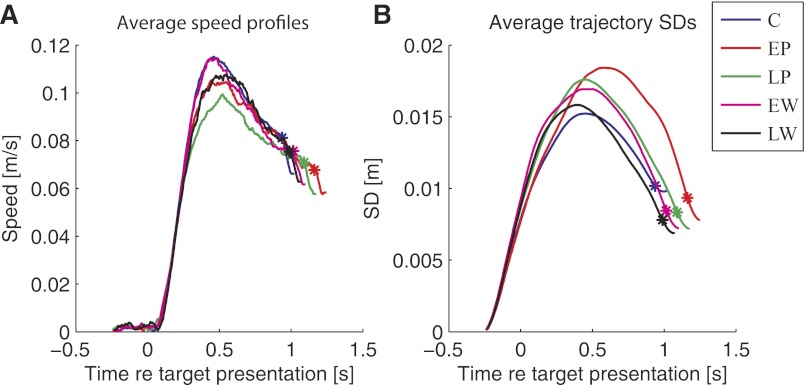
Single trajectories for the control, EP, and LP sessions are shown in Fig. 2A for one of the (50%, 60°, V) experiments. Although there is a fair amount of variation in individual trials, the “pinwheel” effects of the perturbation are clearly visible in the trajectories of the perturbation session. These effects are much clearer in trajectories that are averaged across all of the (50%, 60°, V) experiments (Fig. 2B). During the control session, trajectories were, on average, quite straight to the target. They were also quite fast, for a BCI: the average movement time (time between target presentation and target acquisition) for these experiments was 0.94 ± 0.02 s. (All reported results are means ± SE unless otherwise stated.) In comparison, the average time for hand movements performed under the same conditions would be ∼550 ms (Georgopoulos et al. 1982; Moran and Schwartz 1999; Schwartz et al. 1988).

In the EP session, trajectories showed clear curvature, with average angular errors at the halfway point (indicated by the dashed black circle) of 21.3 ± 1.2°. Average movement times were also slower in this session, taking 1.15 ± 0.03 s. Errors were clearly reduced in the LP session, averaging 11.1 ± 1.3° (P < 10⁻¹⁰, paired t-test). The movement times in this session showed a slight but significant decrease from the EP session, averaging 1.10 ± 0.02 s (P < 0.01, paired t-test). Immediately after removal of the perturbation, the trajectories showed a tendency toward residual curvature in the opposite direction of the applied rotation (−12.1 ± 1.4°). These aftereffects indicate that the adaptation to these perturbations involved predictive compensation and were not solely due to an increased responsiveness to visual error, for example. Movement times in this session were 1.01 ± 0.02 s, faster than in the LP session (P < 10⁻³, paired t-test) but still slower than in the control session (P < 10⁻³, paired t-test). The aftereffects diminished over time.

Speed profiles and SDs of the average movement trajectories made during the (50%, 60°, V) experiments tell a similar story (Fig. 3). In all sessions, the average trajectory exhibited a truncated bell-shaped profile with a reaction time of roughly 100 to 150 ms. If anything, this reaction time is fast for monkey movements, indicating that the spike rate filtering we applied in Eq. 2 did not appreciably delay the monkey's response time. The truncation occurs because subjects were not required to hold the cursor in the target for more than 100 ms, and so did not come to a complete stop before the reward was issued. For comparison, a similar plot for unperturbed arm movements is given in Fig. 2 of Moran and Schwartz (1999). Peak speeds decreased with the application of the perturbation and increased again when the perturbation was removed. The maximum trajectory SD decreased between the EP and LP sessions (Fig. 3B), indicating that trajectories became slightly more stereotyped during adaptation, but this result was not statistically significant.

Fig. 3.

Speed (A) and standard deviation (SD; B) of the average trajectory in each session, plotted as a function of time elapsed since target presentation. Asterisks denote target acquisition time; trials end with the administration of reward. In B, SD = $\sqrt{\left({\text{SD}}_X^2+{\text{SD}}_Y^2\right)}$, where SD_X and SD_Y denote SDs in the X and Y components of position, respectively. C, control session; EW and LW, early and late washout sessions, respectively.

More evidence that the adaptation involved a prediction of the upcoming perturbation and was not reliant on immediate visual feedback comes from experiments that included an invisible zone. Figure 2C shows averaged trajectories from the EP and LP sessions from the (50%, 60°, I) experiments, with the invisible zone boundary indicated by a dotted black circle. These trajectories show that angular errors decreased over time, even though the subject had no feedback, visual or otherwise, about cursor position when these errors were assessed. Using just the history of perceived errors, subjects were able to adapt their motor commands to decrease future errors.

In the two following sections, we analyze the behavioral correlates of adaptation to the visuomotor rotation and gain components separately. It should be noted, however, that because gain decreases were always presented with rotations, we cannot say with certainty that adaptation to a gain decrease in isolation would have proceeded in the same manner. These implications are considered in discussion, Differences between these results and adaptation with natural movements.

Behavioral correlates of adaptation to visuomotor rotation.

The patterns of angular errors observed during the (50%, 60°, V) experiments were consistent across all of the experimental paradigms we tested. Figure 4 shows the mean signed angular error in the cursor trajectories for all of the perturbation conditions tested. With the exception of the (50%, 90°, I) session, errors in the control session were uniformly small, indicating no preference, on average, for deviations toward one side of the trajectory or another. As mentioned earlier, the (50%, 90°, I) perturbations were all applied in the CW direction, and the fact that the control session errors for these perturbations are biased in the opposing direction suggests that the subject exhibited carryover effects from day to day for this experimental condition. Adaptation in all experimental conditions followed the same general profile: angular errors were initially large in the EP session and were reduced to a greater or lesser extent when assessed in the LP session. These trends tended to reverse in the washout session, when the perturbation was removed: there was a clear aftereffect in that errors in the EW session were in the opposite direction of the applied perturbation, and these errors were diminished in the LW session.

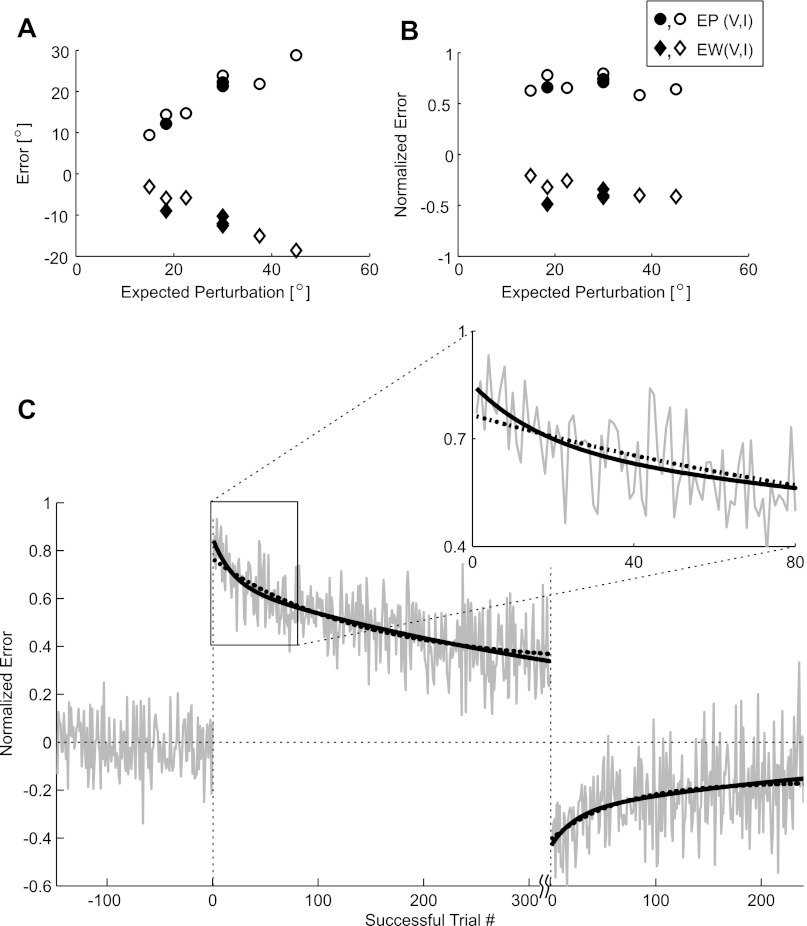
We investigated the time course of adaptation for the rotation portion of this perturbation by fitting a learning curve to the angular error as a function of the sequential trial number. Because individual movements (and their corresponding measured angular errors) could be fairly noisy, we increased the power of the analysis by combining data across the various perturbation conditions. To do this, we accounted for the differing amounts of applied visuomotor rotation by normalizing all of the errors by the expected rotation error computed from first principles (see methods, Calculation of the expected cursor perturbation; also see Table 2). Figure 5A shows the average angular errors in the EP, LP, EW, and LW sessions plotted as a function of the expected angular error. Figure 5B shows the same data, except that the angular errors have been normalized by the expected angular error (Eq. 6). Note that the linear trends observed in Fig. 5A are removed by the normalization.

Fig. 5.

Learning curves suggest multiple timescales of adaptation. A and B: to combine data across multiple experimental conditions, it is necessary to normalize by the effective perturbation. A: angular errors during the EP (circles) and EW sessions (diamonds), plotted as a function of the expected angular error (computed as described in methods). Open and filled symbols denote experiments with and without an invisible zone, respectively. B: same as A, but now the measured EP and EW errors have been normalized by the corresponding expected errors (as computed using Eq. 6). These data indicate that normalized errors may be compared across different experimental conditions. C: adaptation as a function of the number of successful trials. Left section shows data from the control session, middle section shows data from the perturbation session, and right section is from the washout session (section breaks are denoted with vertical dashed lines). Jagged gray line shows the normalized error as a function of the number of successful trials, averaged over all of the experiments. Black lines show the best biexponential (solid) and single-exponential (dotted) fits to this data, respectively. Inset shows a close up of the first 80 trials after the perturbation was applied. Note that not all experimental sessions contained the same number of successful trials. We show data only for trial numbers reached in at least 25 experiments.

Figure 5C shows the normalized angular errors in the control, perturbation, and washout sessions plotted as a function of sequential (successful) trial number. The jagged gray line indicates the average normalized angular error at each successful trial number, where the average is taken across all 124 experiments. Because there is evidence from human reaching and saccade movements that adaptation occurs on two timescales (Chen-Harris et al. 2008; Smith et al. 2006), we fit biexponential learning curves to the errors from the perturbation and washout sessions (thick black lines). Single exponential fits are also shown, for reference (dotted black lines). Qualitatively, it appears the biexponential fits do a better job of capturing the rapid reduction in errors observed in the first 10–20 trials (see inset). However, we cannot definitively state that there are two—and only two—timescales of adaptation from this data. It seems likely that there are several timescales involved in visuomotor transform adaptation, but these data cannot adequately resolve them. The process might be better described as a power law (Drew and Abbott 2006).

Behavioral correlates of adaptation to visuomotor gain reduction.

In addition to the visuomotor rotation, this perturbation also induced a visuomotor gain reduction. Across all experimental sessions, movement times increased immediately after the perturbation was applied, usually showed a slight decrease between the EP and LP sessions, and often reduced again after the perturbation was removed (Fig. 6). Occasionally, but not always, the movement times would decrease between the EW and LW sessions, although they rarely came back to their preperturbation values.

Fig. 6.

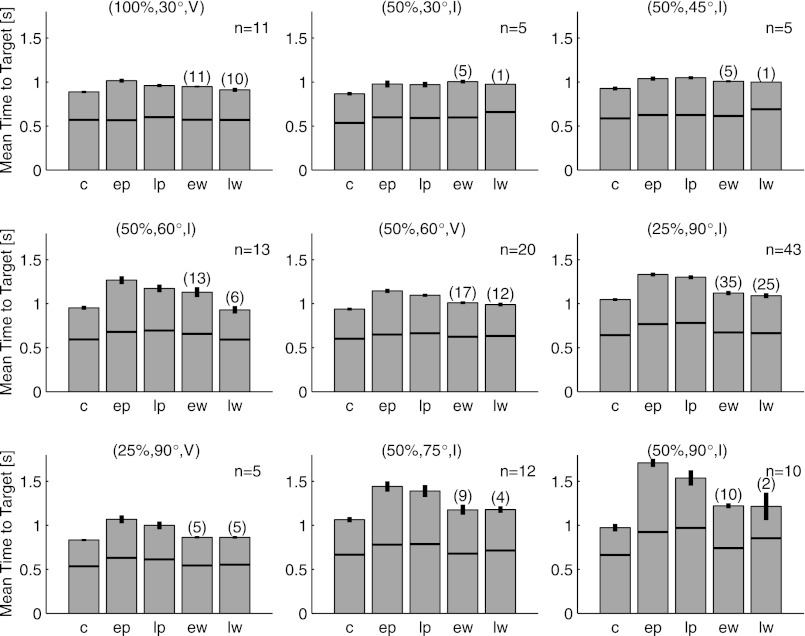
The overall pattern of movement time changes is consistent across experimental conditions. Each plot shows the average time it took to move the cursor from the center of the workspace to the presented target as a function of the session within each experiment. Overall format is the same as for Fig. 4. Horizontal black lines denote the average time at which the cursor had moved one-half the distance to the targets, i.e., the average time at which the angular errors were assessed. These times were not significantly different between experiments with and without an invisible zone.

The movement time decrease between the EP and LP sessions was statistically significant (EP movement time − LP movement time = 53 ± 10 ms; P < 10⁻⁶, paired t-test). Two factors could account for this decrease: a true adaptive increase in cursor speed or a decrease in path length as trajectories straightened during adaptation to the visuomotor rotation. When we compare the cursor speed between these two sessions, if anything we see evidence for a speed decrease (Fig. 7A): EP speed − LP speed = 2.5 ± 1.2 mm/s (P = 0.04, paired t-test). This effect can also be seen in the speed profiles of Fig. 3A. Thus the movement time decrease between the early and late parts of the perturbation session are driven entirely by straightening of the cursor trajectories.

However, recall that the EP session includes 16 trials of data: the first movement to each of the 16 targets. Data from visuomotor gain adaptation studies in humans (Krakauer et al. 2000) and nonhuman primates (Paz et al. 2005) indicate that the time course of visuomotor gain adaptation is very fast and can be complete within 10 trials. Furthermore, unlike rotations, adaptive gains can generalize across different directions of movement, at least for arm reaches (Krakauer et al. 2000). Thus it is possible that the reason we do not see evidence for adaptive changes between the EP and LP sessions is that the adaptation is already complete within the EP session. This appears to be the case in our data. In Fig. 7B, we compare the average speed in the EP session with the expected speed, computed as the average speed in the control session multiplied by the visuomotor gain reduction, α, shown in Table 2. In 88 of 113 experiments that included a visuomotor gain reduction, the speed during the EP session was larger than we would expect if the subject had not adapted at all to the speed decrease (P < 10⁻⁸, sign test). This adaptive response was so fast that it precluded a trial-by-trial analysis such as that performed for the rotation adaptation in Fig. 5. In fact, speeds in the second trial after the perturbation was applied were already larger than expected (74 of 113 experiments, P < 10⁻³, sign test). The same computation for the first trial after the perturbation was applied yields no significant difference, as expected (59 of 113 experiments, P = 0.64).

To investigate the extent of this gain adaptation, we computed the “response gain” during the EP session as the ratio of the average cursor speed to its expected speed. This quantity is 1 if the subject does not adapt at all the to the speed reduction and would be 1/α if the subject compensated fully for the speed reduction and returned the cursor speed to its control session value. These response gains are plotted in Fig. 7C separately for each applied gain condition. Although the response gains are statistically different from 1 for all experimental conditions where α was <0.9, the gains are far from the values required to fully compensate for the speed reduction. We discuss potential reasons for this in the Differences between these results and adaptation with natural movements section of the discussion.

Neural mechanisms of adaptation.

Because these perturbations are implemented through a BCI, the adaptive compensation must be due to changes in the firing rates of our recorded cells. Figure 8 shows an example of firing rate changes observed in one nonrotated unit recorded during one of the (50%, 60°, V) experiments. After the perturbation was applied, this unit showed an abrupt firing rate decrease to the target at 180°. Meanwhile, firing rates to the targets at 45° and 90° exhibited gradual increases as a function of trial number. After the perturbation was removed, these changes reverted to roughly the control session values. What do these firing rate changes indicate about the underlying mechanisms of adaptation?

The firing rate changes of individual units to particular directions are not very informative. Consider the case of a 50%, 90° rotation, as shown schematically in Fig. 9A, right. When the subject aims at a target located at 0°, cells with PDs near 0° will increase their firing rates. Whereas activity of the nonrotated neurons (gray arrows) will push the cursor toward the target, activity of the rotated neurons (black arrows) will push the cursor upwards. The result is cursor movement at a 45° angle. Figure 9A, left, shows the response of one example rotated neuron with a PD at 0° to this hypothetical situation.

Fig. 9.

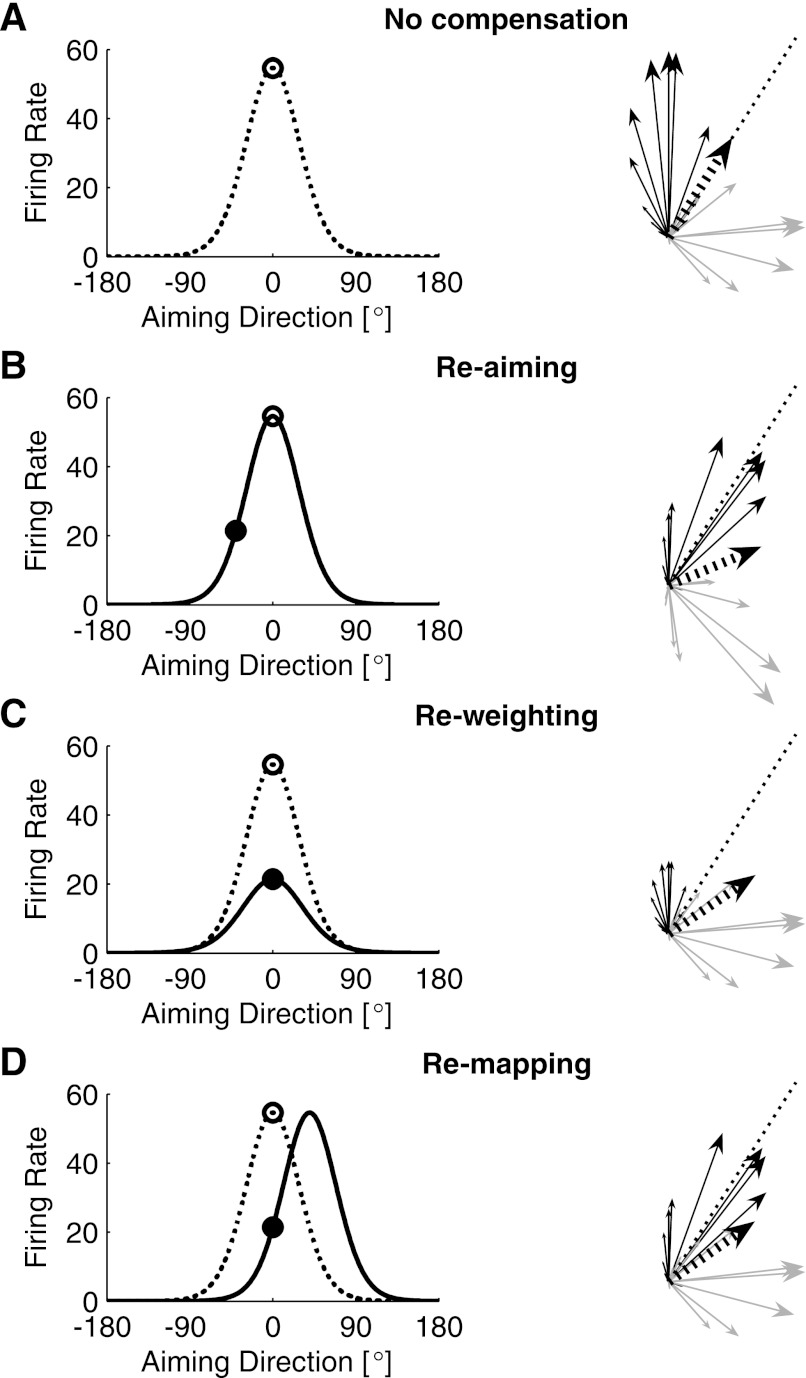
Simulation showing 3 different compensation mechanisms that could all be responsible for an observed firing rate change in a rotated neuron. At right of each plot is an arrow schematic that shows the population response. Each thin arrow points in the decoding direction of 1 neuron (the direction in which it pushes the cursor) with its length proportional to the neuron's firing rate. Black arrows denote rotated neurons, gray arrows denote nonrotated neurons, and thick black dashed arrow indicates the population vector average (the direction of cursor movement). At left of each plot is a tuning curve of 1 of the rotated neurons showing the firing rate as a function of aiming direction. The dashed line shows this cell's tuning curve during the control session, where it had a PD of 0°, and the open circle indicates its firing rate when a target at 0° was presented in the control session. In each panel, the subject is trying to hit a target placed at 0° under the perturbation. Solid black lines and filled circles show the tuning curve and firing rate of the cell for the various compensation cases. A: no-compensation case. The subject is aiming at a target located at 0° (directly to the right), but the perturbation causes the cursor to move at 45°. B: re-aiming compensation. The subject aims toward −40° to create a movement nearer the target. C: re-weighting compensation. The subject aims directly at the target, and the rotated population contributes less to the overall cursor movement. D: re-mapping compensation. The subject aims at 0°, and the tuning curves of the rotated cells are altered to map this aiming direction to a decoded direction that is closer to the aiming direction.

One possible way for a subject to adapt to this perturbation is to aim at a point in the opposite direction of the rotation. For example, if the subject aimed at a virtual target located at −40°, neurons with PDs around −40° would increase their firing rates (Fig. 9B, right). The nonrotated subset of these cells would be pushing the cursor toward −40°, whereas the rotated subset would be pushing the cursor toward 50°. The net result is a cursor movement that is much closer to the actual target at 0°. Under this situation, our example neuron will show a decrease in firing rate, because its PD is at 0° and the subject is aiming at −40° (Fig. 9B, left). Note that the tuning function of this cell has not changed: the transfer function between the subject's aiming direction and the firing rate is the same as it was in the “no-compensation” case. The observed decrease in firing rate is entirely due to re-aiming.

Another possible way to adapt to this perturbation is to stop using the rotated cells. If the subject could identify the rotated cells and somehow stop modulating their firing rates with aiming direction, their contribution to the population vector average would decrease, allowing the movement to rotate back toward the target direction (Fig. 9C, right). We call this re-weighting. For the example shown in Fig. 9C, the re-weighting strategy produces the exact same firing rate decrease to this target as did the re-aiming strategy. In this case, however, the firing rate decrease indicates a true change in the tuning curve of the cell, where the modulation depth of the transfer function between aiming and firing rate is severely reduced (Fig. 9C, left).

A third way to adapt to this perturbation is to change the way in which the rotated neurons are recruited (Fig. 9D, right). As a case in point, if the subject were to increase the firing rate of our example neuron when he wanted the cursor to move upwards, it would push the cursor in the correct direction (Fig. 9D, left). This is equivalent to changing the tuning curve of the cell so that its PD aligns with the rotated decoding PD that was assigned to it. We refer to this strategy as re-mapping.

Re-aiming is a global strategy: by changing the inputs to the tuning curves, it affects all of the cells in the population equally. On the other hand, re-weighting and re-mapping (or more generally, re-tuning) are local strategies: they both require that the subject solve the credit-assignment problem and selectively change only the transfer functions of the cells that were randomly assigned to the rotated subgroup. Although all of these strategies can be equally effective at compensating for the angular error, the re-aiming strategy maintains the dispersion in the population that contributes to the PVA (spread in the arrows in Fig. 9A, right), which results in shorter population vectors and slower, less efficient movements. To counter this, the subject would also have to increase the dynamic range of modulation of all cells in the population. The re-weighting strategy reduces the contributions of perturbed cells, resulting in a smaller population used to control the cursor. This strategy may be ineffective if the total number of cells is already small. It also would result in shorter population vectors, because the vector average is still being taken across all of the neurons. Therefore, to counter both effects, the subject would have to simultaneously increase the dynamic range of the unperturbed population. Only the re-mapping strategy is capable of completely countering all of the effects of the perturbation without changes in dynamic range. If we consider the noise in the neural output to be signal dependent (which is true for Poisson processes), the optimal strategy is re-mapping. Figure 9 emphasizes the point that to understand which underlying compensation strategy is being employed, it is necessary to consider the firing rates changes of the entire population simultaneously.

Evidence for each compensation mechanism.

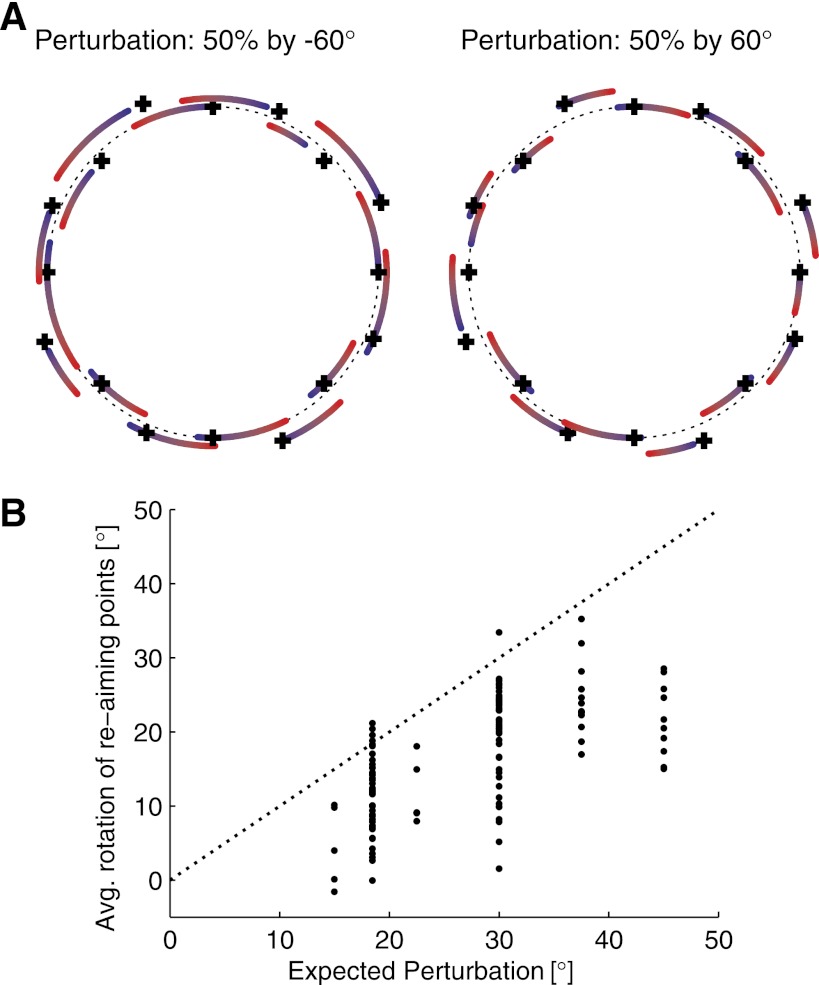
To investigate these various compensation strategies, we used the latent-target algorithm (Chase et al. 2010) to compute both the re-aiming directions and the tuning curves that describe the firing rates as a function of aiming direction. Two examples of the adaptive re-aiming point shifts are shown in Fig. 10 for the (50%, 60°, V) perturbation condition. In Fig. 10A, the crosses denote the target directions, and the blue ends of each arc show the re-aiming points for each target during the control session. These examples are typical in that the re-aiming points in the control session are usually quite close to the target directions. The red end of each arc shows the re-aiming points used during the perturbation session. Notice that the re-aiming points show a tendency to rotate counter to the direction in which the PDs were rotated. Figure 10B shows the average rotation of the re-aiming points plotted as a function of the expected perturbation. There is a tendency for the re-aiming to increase with the perturbation, although re-aiming alone almost never fully compensates for the applied visuomotor rotation.

Fig. 10.

Re-aiming points move to counter the applied perturbation. A: 2 examples of re-aiming point changes measured during the (50%, 60°, V) experimental condition (left, −60°; right, +60°). The blue end of each arc shows the location of 1 target's re-aiming point measured in the control session, whereas the red end shows its location measured in the perturbation session. The corresponding black crosses denote the 16 target locations. The arcs and crosses have been offset from the circle by random amounts to aid visibility. B: average rotation of the re-aiming points plotted as a function of the expected perturbation. The average rotation is computed as the mean angular shift of the re-aiming point (averaged across all 16 targets), where positive values are opposite to the applied perturbation (and therefore represent compensatory changes). Data from experiments with and without invisible zones are combined in the plot, since there were no visible differences between the 2 conditions.

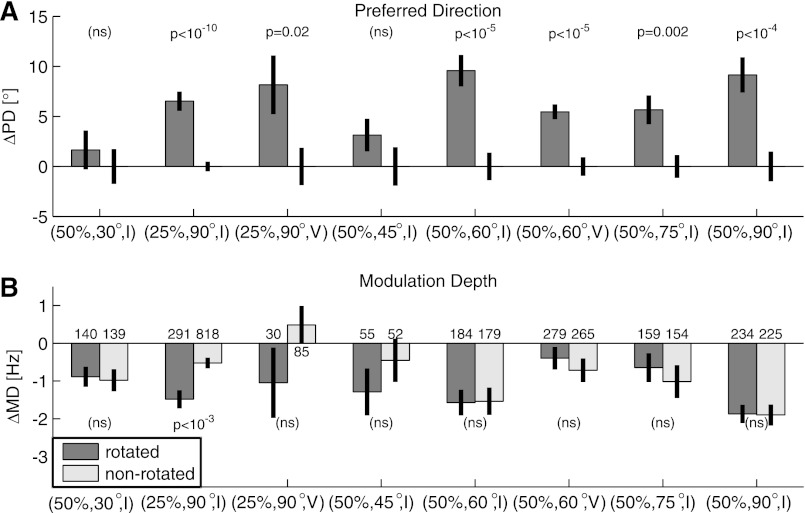
Figure 11 examines the change in tuning parameters that occurs during adaptation. In Fig. 11A, we show the change in PD from the control to the perturbation sessions, broken down both by experimental condition and according to whether the unit belonged to the rotated or nonrotated population. With the exception of only the two smallest perturbation conditions tested, there is a statistically significant difference in the amount of the PD shift between the rotated and nonrotated populations for every experimental condition. In all cases, the PDs of the rotated units shifted farther in the direction of the perturbation than the nonrotated units did. This is consistent with the re-mapping strategy discussed above. [Note that we do not present results from the (100%, 30°, V) condition. When 100% of the cells are rotated, it is impossible to tell if the adaptive response is entirely global, entirely local, or a combination of the two.]

Fig. 11.

Adaptation-related changes in tuning curve parameters, broken down by experimental condition and arranged from left to right according to the extent of the applied rotation. All changes are measured as the difference between the value in the perturbation session and the control session. Values above each plot are P values of a t-test comparison between parameter changes of the rotated and nonrotated neurons (ns indicates P > 0.05). No attempt was made to correct for multiple comparisons. A: changes in preferred direction (ΔPD). Positive values are in the direction of the applied perturbation. B: changes in modulation depth (ΔMD).

Figure 11B shows a similar plot for changes in the modulation depths (MDs) of the units. In this case, however, the only statistically significant difference between the rotated and nonrotated populations occurred for the (25%, 90°, I) condition. Interestingly, there is also a general trend for all units to show a decrease in MD between the perturbation and control sessions. This persists into the washout session and is most likely related to fatigue or a decrease in desire as the monkey gets satiated. However, another possibility is that slow drift in the waveforms causes a reduction in the discrimination of the unit over time, which would cause MDs to decrease. We also investigated whether the differential tuning changes persisted into the washout session. However, we found no significant difference between the rotated and nonrotated values for either PD or MD in any of the experimental conditions tested (data not shown).

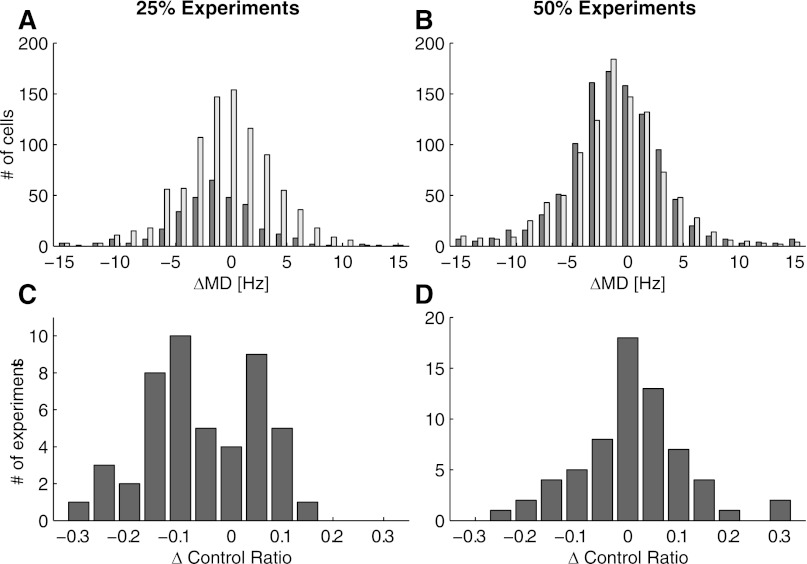
We investigate the differential change in MD more closely in Fig. 12. First, we computed a histogram showing the changes in MD for all units, broken down separately for the rotated and nonrotated units. We combined all of the 25% experiments in Fig. 12A, even though the (25%, 90°, V) experiments did not show statistically significant differences between the rotated and nonrotated populations in Fig. 11B. This could be because we only performed 5 experiments under this condition, for a total of 30 and 85 rotated and nonrotated units, respectively. The relatively small sample power could have made the MD shifts difficult to detect, although their trend was in the right direction. Figure 12B shows the same results for all units recorded during the 50% experiments. In Fig. 12A, there is a clear separation in the average shifts of the two populations: the mean for the rotated population is −1.4 ± 0.2 Hz, whereas the mean for the nonrotated population is −0.4 ± 0.1 Hz (P < 10⁻³, unpaired t-test). The difference between these populations under conditions where 50% of the units were rotated is not statistically significant (mean, rotated: −1.1 ± 0.1 Hz; mean, nonrotated: −1.2 ± 0.1 Hz; P = 0.58, unpaired t-test).

Fig. 12.

Re-weighting occurs only when the percentage of perturbed cells is small. A and B: histograms of the ΔMD (perturbation MD − control MD) for all units, shown separately for the 25% (A) and 50% experiments (B). C and D: histograms of the change in control ratio (perturbation − control) for the 25% (C) and 50% experiments (D).

To further investigate these MD changes, we define the control ratio to be the ratio between the average MD of the rotated subgroup and the average MD of the nonrotated subgroup:

$$\text{Control}\text{ratio}\equiv \frac{\text{avg}\left({\text{MD}}_{\text{rotated}}\right)}{\text{avg}\left({\text{MD}}_{\text{nonrotated}}\right)}$$ (12)

Changes in the control ratio can indicate a shift in the control from one subgroup for another: increases in the control ratio indicate that the influence of the rotated subgroup of units on cursor movement has increased, whereas decreases indicate that the influence of the nonrotated subgroup of units on cursor movement has increased. In Fig. 12C, we show a histogram of the changes in the control ratio between the perturbation and control sessions in every experiment in which 25% of the units were rotated. The control ratio decreased 32 of 48 times (P = 0.02, sign test), indicating that control tended to pass to the nonrotated subgroup during the perturbation session. However, in experiments where 50% of the units were rotated (Fig. 12D), the control ratio was just as likely to increase as to decrease (decreased 28 of 65 times, P = 0.27, sign test). Together, these results indicate that the re-weighting compensation strategy is only applied when the number of rotated units is small relative to the population.

Given that this re-weighting result is so subtle, we re-analyzed data from the 3-D cursor control sessions published in Jarosiewicz et al. (2008), to see if the result that re-weighting only occurs when the proportion of rotated units is small could be independently verified in another data set. Of the 36 experiments performed in that work, 24 of them involved cases in which 25% of the cells were rotated, and the remaining 12 involved cases in which 50% of the cells were rotated. For the 25% experiments, the control ratio decreased 19 of 24 times (P = 0.004, sign test); for the 50% experiments, the control ratio decreased 6 of 12 times (P = 1, sign test). Thus the finding that re-weighting occurs only when the proportion of rotated cells is small holds up independently across the two data sets.

Computing the effectiveness of each compensation mechanism.

We have found evidence for both re-aiming and re-tuning compensation strategies in the neural responses. How much of the total error reduction is due to each mechanism? We address this question in the following way. Because we can calculate both the re-aiming points and the tuning curves in each session, we can simulate the firing rates of the units when we allow the aiming points to change, but not the tuning curves, and we can also simulate the firing rates when we allow the tuning curves to change, but not the aiming points. We can then decode these firing rates to simulate the cursor error that would have occurred under each manipulation and compare it with the actual cursor error measured in the late part of the perturbation session.

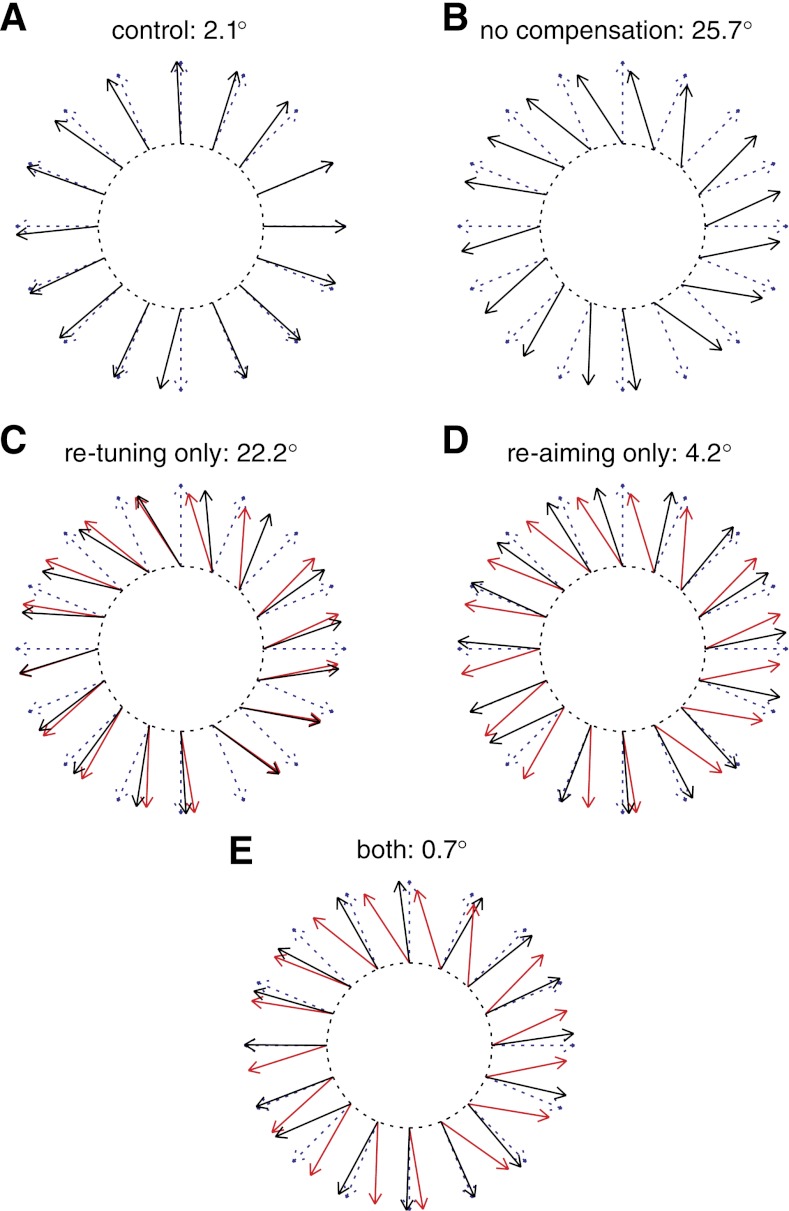
An example of this calculation is shown in Fig. 13 for one of the (25%, 90°, V) experiments. First, we took the re-aiming points and the tuning curves computed during the control session and used them to predict the firing rates of the units to each target. If we decode these firing rates off-line with the same decoder used in the control session, the decoded cursor movements should point toward the targets. This turns out to be the case. The dashed arrows in Fig. 13A point toward the 16 targets, whereas the solid arrows are the directions we predict the cursor would go, given these re-aiming points and tuning curves. On average, the signed angular difference between the decoded cursor directions and the target directions is small (2.1°). We could also decode these firing rates with the decoder in use during the perturbation session. The angular deviation between the decoded cursor direction and the target direction would then indicate how much error there would be without any compensation at all. Figure 13B shows these results for the same experiment. Without any compensation, the perturbation induces 25.7° of angular error, on average. In Fig. 13C, we show the cursor directions that would result if the neural tuning curves changed, but not the aiming points. That is, we simulated firing rates using the tuning curves from the perturbation session but the aiming points from the control session. When decoding with the perturbation session decoder, we get cursor movements that are slightly closer to the target directions than the no-compensation case: the average signed angular error remaining after re-tuning compensation is 22.2°. We can also simulate the amount of error correction that would occur with just re-aiming (Fig. 13D). In this case, we use the re-aiming points from the perturbation session and the tuning curves from the control session to generate the firing rates to each target. Re-aiming accounts for the majority of the error, leaving a remainder of only 4.2°, on average. Finally, we can simulate the firing rates using both compensation mechanisms, by using both the re-aiming points and tuning curves computed during the perturbation session. When both mechanisms are included, the remaining signed angular error averages to only 0.7° (Fig. 13E).

Fig. 13.

Computing the error reduction that can be attributed to global and local mechanisms. Cursor movement direction can be estimated by decoding firing rates simulated with different re-aiming point and tuning curve combinations. Each solid black arrow indicates the direction of cursor movement that results from decoding these simulated firing rates. Data are from one of the (25%, 90°, V) experiments. A: firing rates are simulated with the tuning curves and re-aiming points measured in the control session and decoded with the control session decoder. The dashed arrows indicate the target directions, for reference. The average angular error between the cursor movement directions and the target directions is indicated. B: same calculation as in A, but now the firing rates are decoded with the perturbation session decoder. This indicates the error that would result if the subject did not adapt at all. C: firing rates are simulated with re-aiming points from the control session but with tuning curves from the perturbation session, decoded with the perturbation session decoder. This indicates the movements that would result from re-tuning compensation only. Red arrows indicate the “no-compensation” cursor movement directions, for reference. D: same as in C, but using re-aiming points from the perturbation session and tuning curves from the control session. E: firing rates are simulated using re-aiming points and tuning curves from the perturbation session.

Figure 14 presents the results of this analysis for all of the experimental conditions we tested. Clearly, the largest reduction in cursor error comes from re-aiming, rather than re-tuning. However, re-tuning accounted for a significant reduction in cursor error for the majority of cases tested. Exceptions include the experiments where 100% of the units were rotated (and so re-aiming and re-mapping compensations are equivalent) as well as the mildest perturbation condition tested, the (50%, 30°, I) experiment. The largest re-tuning effect was observed in the (50%, 90°, I) experiments. As mentioned in methods, this was the only set of experiments in which CW and CCW perturbations were not intermixed; rather, CW perturbations were always performed. Although it appears that this difference resulted in carryover effects across multiple sessions (there is a small but consistent bias in the control session that is opposite to the upcoming perturbation), this cannot explain the relatively large contribution of re-tuning in these experiments; the subset of units that were perturbed was randomly chosen anew each day.

Fig. 14.

Histograms showing the residual angular error predicted from different combinations of re-aiming points and tuning curves, as described in Fig. 13. nc, Error with no compensation; rt, remaining error after re-tuning only; ra, remaining error after re-aiming only; p, error in perturbation session with full compensation; c, error in control session. Each histogram shows data from a different perturbation condition, denoted at top left with the number of experiments (n) run in that perturbation condition.

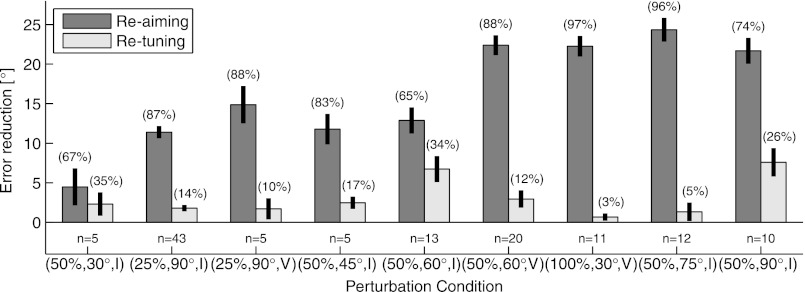
Global vs. local compensation mechanisms are further summarized in Fig. 15, where we present the total error reduction that can be attributed to either re-aiming or re-tuning mechanisms. This error reduction was calculated as the difference between the average signed angular error with no compensation (“nc” in Fig. 14) and the average angular error remaining after only re-aiming or re-tuning compensation (“ra” and “rt” from Fig. 14, respectively). Across all experimental conditions, the error remaining after only re-tuning is substantially larger than the error remaining after only re-aiming. The percentage of the total error accounted for by re-aiming and re-tuning is listed above each bar of the histogram in Fig. 15. Note that these percentages are not constrained to sum to 100%, because the error reductions are computed under independent modeling assumptions, but in practice the percentages do sum to nearly 100%. On average, the relative proportion of error reduction due to re-aiming and re-tuning is 84% and 16%, respectively.

Fig. 15.

Error reduction that can be attributed to global (re-aiming) or local (re-tuning) adaptation mechanisms. The error reduction is calculated as the difference between the error in the no-compensation case and the error with only re-aiming (ra) or only re-tuning (rt) allowed. The percentage of the total error accounted for by each method is given above each bar. Experiments are arranged according to the extent of the rotational perturbation (Table 2).

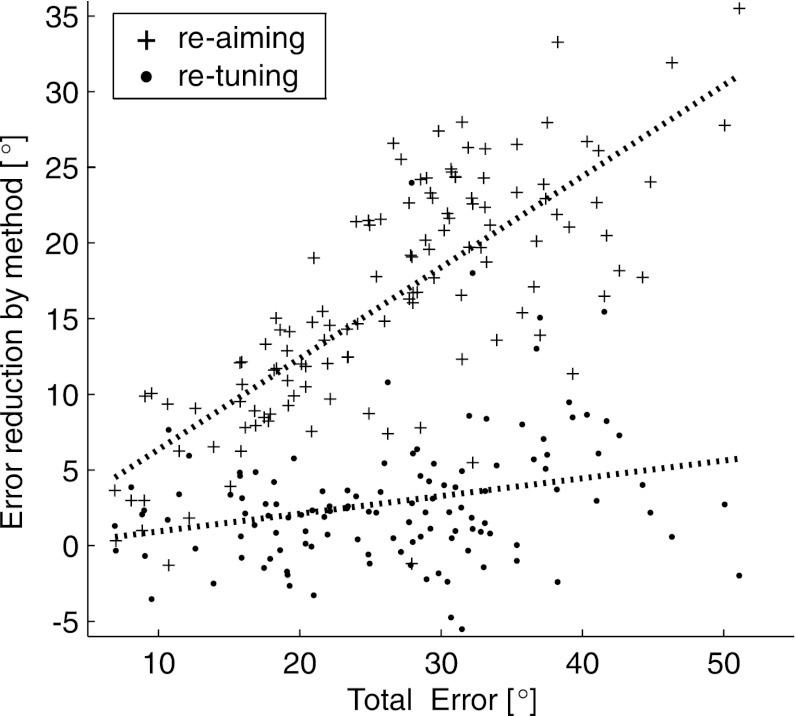
Both the re-aiming and re-tuning compensation mechanisms exhibit a statistically significant dose-response effect in which the amount of error corrected by each mechanism increases as the total error caused by the perturbation increases. In Fig. 16, we plot the error reduction that can be attributed to each mechanism as a function of the total error (the no-compensation error from Fig. 13B). The dotted lines in Fig. 16 indicate the best-fit linear regression model of the relationship between the error reduction from each mechanism and the total error induced by the perturbation. Both the global and local adaptation mechanisms have a significant positive relationship to the total error (see Fig. 16 legend for details). However, the ratio of the amount of total error accounted for by global and local mechanisms remained relatively constant.

Fig. 16.

Dose-response effects. The error reduction that can be attributed to re-tuning and re-aiming is plotted as a function of the total error induced by the perturbation. Dotted lines show the linear regression fits of each relationship (re-aiming: y = 0.33 + 0.60x, P < 10⁻¹⁰, F-test; re-tuning: y = −0.24 + 0.12x, P = 0.003).

DISCUSSION

We performed a series of motor adaptation experiments on subjects controlling cursors through a BCI. In particular, we rotated the pushing direction of a randomly chosen subset of units. Perceptually, this perturbation consists of a combination of visuomotor rotation and gain reduction, and there are a number of qualitative similarities between adaptations observed to visuomotor perturbations applied under hand control and the adaptations observed in this study under brain control. In particular, subjects readily reduced the angular error in the cursor trajectory (Fig. 4), with learning curves that appear to have more than one time constant of adaptation (Fig. 5).

Even though only a portion of the recorded units actually contributed error to the decoded cursor movement, the predominant adaptive response globally affected all of the recorded units (Figs. 10 and 15). This re-aiming accounted for 84% of the total error reduction. The remaining 16% of the error reduction was due to individual changes in tuning curves that describe how motor intent is mapped into firing rate. The preferred directions of perturbed units tended to rotate in the direction of the applied perturbation (Fig. 11). Modulation depths of perturbed units tended to decrease relative to unperturbed units, but only in experiments in which the percentage of rotated units was small (Fig. 12). Both of these re-aiming and re-tuning processes were dose dependent, increasing as the perturbation error increased (Fig. 16).

Error signals and visuomotor rotation adaptation.

There has been a bit of debate in the literature about the types of error information that are necessary for visuomotor adaptation. Although some researchers have argued that simultaneous proprioceptive and visual feedback is necessary for visuomotor adaptation (Shabbott and Sainburg 2010), there is evidence that deafferented human patients, without intact proprioceptive feedback pathways, are still capable of learning visuomotor transformations (Bernier et al. 2006). Our data provide further insight into this problem. In the experiments described in this article, subjects controlled the cursor by modulating the neural activity of a small population of neurons. Furthermore, they performed these experiments with arms restrained and produced no obvious fidgeting movements that correlated with cursor movement. Previous studies that have recorded electromyograms (EMGs) while subjects performed cursor movements through a BCI have shown that EMGs gradually decrease with training, eventually disappearing entirely (Carmena et al. 2003; Taylor et al. 2002). It is therefore unlikely that our subjects had access to any kind of meaningful proprioceptive or tactile error signal to compare with the visual error signal they received. Despite this absence, our subjects show rapid decreases in angular error when exposed to visuomotor rotations. Therefore, our data suggest that proprioceptive error signals are not necessary for visuomotor rotation adaptation. We cannot discount the possibility, however, that proprioception is necessary for a full adaptive gain response. This point is discussed in more detail below.

Differences between these results and adaptation with natural movements.

There are some definite differences in the adaptations we observe compared with adaptations observed in hand control. One of the biggest differences between our results and others relates to the visuomotor gain adaptation. When visuomotor gain changes are applied to the visual feedback of real hand movements, both humans (Krakauer et al. 2000; Ojakangas and Ebner 1991; Pine et al. 1996) and monkeys (Paz et al. 2005) rapidly learn to adjust the peak velocity of their movement profiles to compensate. We also see evidence for rapid compensation. However, the response is much less than the amount necessary to compensate fully for the perturbation, and the subjects stop adapting very quickly: if anything, we see only a speed reduction between the early and late portions of the perturbation session (Fig. 7).

There are a few potential explanations for this limited gain response. First, it should be emphasized that all of our experiments that included a gain reduction also included a rotation: we never studied the visuomotor gain response in isolation. In fact, it is probably best to interpret these results in terms of adaptation to a visuomotor transform composed of combined rotation and gain components, and our analysis of the neural data does not attempt to separate these two effects. There is evidence from psychophysical studies of arm reaching that indicates direction and scale learning proceed independently (Krakauer et al. 2000; Vindras et al. 2005), a finding that also appears to hold for other, less well-practiced movements (Liu et al. 2011). However, in a study of novel finger movements, Liu et al. (2011) demonstrated that learning to scale recently acquired finger coordination patterns is fundamentally different from learning to scale arm reaching movements: scale learning of finger patterns does not generalize across the workspace as readily as scale learning of arm movements. Whether the BCI movements we studied are more like natural reaching movements or novel coordination patterns remains to be tested.

It is also possible that the experimental setup was not conducive to enforcing visuomotor gain adaptation. The task was set up such that subjects had to hit the target anytime within a particular time-out period (usually 2 s); they did not have to complete the reach at a certain average speed or hit the target at a particular time. Furthermore, these movement timeout constraints were usually quite generous (well above the average time to complete a movement, even in the perturbation session), and so it could be argued that there was little behavioral drive to increase the cursor speed. It could also be that the effort required to increase cursor speed was greater than the effort required to maintain the lower speed for longer.

Another possibility is that our subjects simply could not adapt their neural activity to appropriately compensate for this type of perturbation. Our decoder assumes that velocity is linearly encoded in the neural population. Although trajectory speed has been accurately reconstructed off-line with large neural populations (Moran and Schwartz 1999), there appears to be a large amount of variability in the speed representation of single neurons (Churchland and Shenoy 2007). With our moderate-sized populations (we recorded from a median of 26 units in any given experimental session), it is possible that the linear estimation of speed was not sufficiently accurate to allow full adaptive speed control over the cursor. It is also possible that our subjects were operating at the upper range of their speed abilities. If the subjects were “pushing” the cursor as fast as possible during the calibration session, the dynamic range of these cells would have already been maximized, leaving little room to compensate for reductions in gain.

Finally, it is also possible that proprioceptive feedback is necessary for accurate gain control. Unfortunately, we cannot speculate further on this point until more sensitive experiments are performed that carefully examine our assumptions about the linearity of speed encoding. Accurate control of movement speed remains an elusive goal for neuroprosthetic devices; further studies are necessary before closed-loop speed control is understood.

Along with the differences in visuomotor gain adaptation, there are also some slight quantitative differences between our visuomotor rotation results and results from similar hand-control experiments. In particular, our adaptation proceeded more slowly and was never as complete: even after about 300 successful trials, the residual normalized angular error was still about 0.4 (Fig. 5). Although adaptation to visuomotor rotations is never quite complete, even with natural hand movements, we still seem to have less complete adaptation than with natural arm movements. A good comparison is the visuomotor rotation study of Krakauer et al. (2000). In their work, they compared the learning rates of subjects exposed to visuomotor rotations presented in 1, 4, and 8 directions. Although they found an interaction between the learning rate and the number of directions (subjects adapted more slowly when there were more targets), their 8-target subjects still showed normalized angular errors of <0.3 after fewer than 60 movements (cf. Fig. 3 in Krakauer et al. 2000). One of the reasons for the slower learning might be that we used 16 targets instead of 8. However, it is unlikely that this is the main factor: learning rates should stabilize as the target spacing gets within the rotation generalization limits, which have been estimated to have a width of ∼45° (Krakauer et al. 2000; Thoroughman and Shadmehr 2000). Another explanation could be that the brain-control experiments are noisier than hand-control experiments, and therefore the subjects have a harder time adapting. A third possibility is that monkeys, for whatever reason, adapt more slowly to these types of visuomotor transforms than humans do. In a series of visuomotor adaptation tasks including visuomotor rotations, Wise et al. (1998) also found that their monkeys adapted more slowly than humans, and the results of Paz and Vaadia (2005) indicate that their monkeys asymptote with roughly one-third residual angular error (cf. Fig. 5 in Paz and Vaadia 2005). Finally, a fourth factor to consider is that movement may have begun before the cognitive processing was complete. Studies involving mental rotation have shown that reaction time increases as a function of rotation angle (Georgopoulos and Massey 1987), suggesting that natural arm movements are somehow gated such that movement initiation does not occur until the cognitive processing is complete. It is currently unknown how this gating of movement is achieved. The BCI decoder that we used, however, does not take into account the possibility of an independent gating signal that could trigger the onset of movement. If such a gating signal exists and we ignore it, the angular errors we measure might not be an accurate reflection of the current adaptive state. The interplay between cognitive load and movement initiation deserves further study.

Finally, it is worth mentioning that although these perturbations globally mimic standard visuomotor rotations and gain transformations, there are some differences. It is well known that the population vector algorithm can suffer from estimation error when the distribution of preferred directions of the units is not uniform (Chase et al. 2009; Scott et al. 2001). In the case where either of the rotated or nonrotated subpopulations of units does not constitute a uniform distribution of preferred directions, the exact amount of visuomotor rotation or gain will depend on the direction of movement. This effect can be modeled by simulating a population of cosine tuned cells with PDs drawn randomly from a uniform distribution, perturbing half of them, and characterizing the deviation from a uniform rotation. For the median number of cells used in these experiments (26), the SD of the visuomotor rotation ranges from 7.1° for the (50%, 30°) perturbations to 10.3° for the (50%, 90°) perturbations. This variation may also have contributed to the slower learning rates for our subjects.

Timescales of adaptation.

The adaptation we have investigated in this report is very rapid, occurring within a single experiment over ∼200–300 movements. On this timescale, the majority of the response can be explained by global mechanisms related to re-aiming. What would have happened if we had allowed the perturbation to persist for several days, or even weeks? Ganguly and Carmena (2009) performed an experiment in which they randomly permuted the decoding parameters of a number of chronically recorded neurons used to control a BCI device and forced the subject to work with this single perturbation for days. Their subjects were able to adapt to these perturbations, showing a gradual improvement in success rate with complete recovery occurring in about a week. This behavioral improvement was accompanied by a gradual change in the firing patterns of the neurons. When they computed tuning curves by regressing firing rates against target directions, they noted a complete rearrangement in the tuning curves that gradually stabilized as performance improved. Although they did not factor global, intention-related changes out of their tuning curve calculations, it seems likely given the nature of their perturbation that the tuning curve changes they observed are indicative of re-tuning adaptation mechanisms, and not re-aiming adaptation. It could be the case, then, that re-aiming adaptation happens very quickly, over the course of several tens of trials, whereas re-tuning adaptation takes thousands of trials or more to complete. However, given the short perturbation sessions, the small effect size of the re-tuning response, and the speed of adaptation, we are not yet able to resolve the temporal evolution of these re-aiming and re-tuning responses during adaptation. This will be an interesting topic of future study.

Potential mechanisms of adaptation.

According to our iterative fitting algorithm, the majority of the adaptive response was global, consistent with a change in the intended direction of movement. As we indicated in methods, Neural data analysis, the algorithm cannot differentiate between a global response and an equivalent local response applied to every cell in the population. Therefore, it is possible that what we have called a global response was actually a result of local, synaptic level rearrangements on the cells we are recording. However, we favor the interpretation that the change is happening to the inputs of this neural population. This would be consistent with studies showing that transcranial magnetic stimulation of motor cortex interrupts the retention, but not the acquisition, of adaptive motor processes (Hadipour-Niktarash et al. 2007; Lin et al. 2010; Richardson et al. 2006). This interpretation also agrees with the results of Tanaka et al. (2009), whose modeling of generalization patterns suggests an upstream source for visuomotor rotation learning.

In addition to these global responses, there was a small but significant local adaptation response. What does this change represent? It is possible that these local changes actually represent changes in unidentified global signals. Evidence suggests that neurons in motor cortex can be tuned to a multitude of signals in addition to direction, including speed (Churchland and Shenoy 2007; Moran and Schwartz 1999), posture (Scott and Kalaska 1997), and load force (Kalaska et al. 1989; Sergio and Kalaska 1998), among others. If these other sources of tuning represent additional independently controllable inputs to this population of neurons, the subjects might be able to take advantage of the extra redundancy to reduce errors in the lower dimensional task space. That is, learning could occur in a higher dimensional space than that which defines the task(as in Liu and Scheidt 2008; Liu et al. 2011). As an example, suppose (for illustration purposes only) that there are a few neurons tuned to grip force as well as direction and which have PDs that point upwards. Further suppose that by random chance, the majority of these cells were selected into the rotated population. By learning to correlate differing amounts of imagined grip force with each direction, the subject could somewhat compensate for the perturbation. The latent-target algorithm we used to recover the tuning curves as a function of direction implicitly assumes that the neurons are tuned to direction only. Modulation of grip force, or any other signal that affects only a subset of cells, would appear as a change in the tuning curves of those cells. The structure of the space in which motor learning occurs is an open question and needs further exploration.

The alternate possibility is that the tuning curve changes we observe represent actual changes in the input/output transfer functions of individual neurons that serve to reduce global error. The identification of specific neuronal contributions to a global error signal is called the credit-assignment problem in the artificial intelligence literature (Minsky 1961). In collaboration with Legenstein and Maass, we have recently shown that a certain class of Hebbian learning rule (Hebb 1949) can solve this credit-assignment problem, leading to global error-reducing changes in individual synapses (Legenstein et al. 2010). This learning rule updates synaptic weights based on the correlation between short timescale changes in the global reward and noise-driven short timescale changes in the firing rate. Interestingly, when the model neurons are driven with the same noise levels found in the 3-D rotation perturbation experiments of Jarosiewicz et al. (2008), the model reproduces several aspects of the measured data. Carmena and colleagues have also developed a model that describes how individual neurons may update their tuning to reduce environmental perturbations (Heliot et al. 2010), based on an error descent learning algorithm proposed by Cauwenberghs (1993). When they apply their model to perturbations of the type we applied, they note two phases of compensation. At short times, the main effect is a global shift in parameters across all cells. At longer times, this global shift resolves itself into differential changes between the rotated and nonrotated populations. Ultimately, the model converges to a 100% re-mapping compensation, which as we noted in results is the most efficient solution to this perturbation.

Implications for theories of motor control.

We suggest that two processes are involved in adapting to the perturbations applied in these experiments. The first involves the association between stimulus (target presentation) and response (intended or imagined movement). When the perturbation is applied, the subject needs to associate a different response with the given stimulus, i.e., produce a different correlation between the target direction and the motor command. We call this re-aiming. The second process involves a change in how the response is actually encoded. When the perturbation is applied, the subject does not change his stimulus/response association, but rather changes the way in which the response is encoded or represented such that it re-achieves the desired outcome. We call this re-tuning. Redding and Wallace have described two mechanisms of adaptation in their prism adaptation studies: a fast process related to “strategic motor control responses (including skill learning and calibration)” and a “slower spatial realignment among the several unique sensorimotor coordinate systems” (Redding and Wallace 2001, 2002). Although it is tempting to speculate that the two mechanisms we observe might somehow be neural correlates of those processes, more work is required to fully understand the psychophysical interpretation of our data.

We favor a two-stage interpretation of the results: first the system undergoes a stimulus/response reassociation, because this leads to the largest reduction in error in the shortest amount of time. At the end of this process, however, the neural configuration is suboptimal. The next stage is a slower re-tuning process that changes how the responses are encoded, eventually leading to the optimal neural configuration for this perturbation. However, it is an open question as to whether re-aiming and re-tuning actually represent two different mechanisms of adaptation. Models based entirely on synaptic plasticity can reproduce both effects (Heliot et al. 2010; Legenstein et al. 2010). Meanwhile, models based entirely on cognitive reassociation could conceivably reproduce both of these effects in our data, if the response space is larger than the task space.

Reassociation alone could never arrive at the optimal, fully re-mapped response. If arbitrary perturbations are learnable, they must rely on some kind of synaptic level change in neural representation. Whereas the results of Ganguly and Carmena (2009) suggest that arbitrary perturbations are learnable, they did not investigate whether the stabilized tuning curves they measured after days of adaptation were optimal or not. Our results indicate that if this optimum is achievable, it takes longer than a single experiment to achieve. The extent to which a neural population can settle into the optimal configuration in response to an arbitrary perturbation is unknown and deserves further exploration.

GRANTS

This project was supported by National Institutes of Health Grant R01EB005847 from the Collaborative Research in Computational Neuroscience (CRCNS) program.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: S.M.C., R.E.K., and A.B.S. conception and design of research; S.M.C. performed experiments; S.M.C., R.E.K., and A.B.S. analyzed data; S.M.C., R.E.K., and A.B.S. interpreted results of experiments; S.M.C. prepared figures; S.M.C. drafted manuscript; S.M.C. edited and revised manuscript; S.M.C., R.E.K., and A.B.S. approved final version of manuscript.