Visuomotor feedback gains upregulate during the learning of novel dynamics

Abstract

At an early stage of learning novel dynamics, changes in muscle activity are mainly due to corrective feedback responses. These feedback contributions to the overall motor command are gradually reduced as feedforward control is learned. The temporary increased use of feedback could arise simply from the large errors in early learning with either unaltered gains or even slightly downregulated gains, or from an upregulation of the feedback gains when feedforward prediction is insufficient. We therefore investigated whether the sensorimotor control system alters feedback gains during adaptation to a novel force field generated by a robotic manipulandum. To probe the feedback gains throughout learning, we measured the magnitude of involuntary rapid visuomotor responses to rapid shifts in the visual location of the hand during reaching movements. We found large increases in the magnitude of the rapid visuomotor response whenever the dynamics changed: both when the force field was first presented, and when it was removed. We confirmed that these changes in feedback gain are not simply a byproduct of the change in background load, by demonstrating that this rapid visuomotor response is not load sensitive. Our results suggest that when the sensorimotor control system experiences errors, it increases the gain of the visuomotor feedback pathways to deal with the unexpected disturbances until the feedforward controller learns the appropriate dynamics. We suggest that these feedback gains are upregulated with increased uncertainty in the knowledge of the dynamics to counteract any errors or disturbances and ensure accurate and skillful movements.

as many motor tasks involve interactions with the environment, from writing with a pen to eating with utensils, our sensorimotor control system must learn to control the forces necessary for skillful interactions. This learning process involves the gradual formation of an internal representation of the external world, termed an internal model (Kawato 1999; Wolpert and Kawato 1998). When presented with novel stable dynamics during repeated movements, subjects gradually straighten their movements until they return close to their original preperturbation path (Izawa et al. 2008; Lackner and Dizio 1994; Shadmehr and Mussa-Ivaldi 1994). However, during early stages of learning, when this internal model of the dynamics has not yet been learned, subjects can limit their error through both corrective feedback responses (Thoroughman and Shadmehr 1999) and coactivation of their muscles (Franklin et al. 2003b), both of which gradually reduce as the internal model is learned (Emken et al. 2007; Franklin et al. 2008; Franklin et al. 2003b) to decrease the metabolic cost (Huang et al. 2012).

The increased corrections seen during early learning of dynamics could arise through different possible mechanisms. It could simply depend on large errors with the same feedback gains as before the perturbation. Alternatively, the feedback gains could be modified during learning. The gains could be reduced to minimize the risk of instability that might arise with large errors. Provided the product of the (larger) error and the (reduced) gain exceeds the magnitude of the preperturbation product of error and gain, the net amount of feedback would still increase. However, the gain could instead increase, leading to a multiplicative effect of increased error and gain and to a substantially increased feedback response. Here, we investigated whether the sensorimotor control system modulates the feedback gains during the learning of novel dynamics.

Previous studies have found that the optimal response to increased uncertainty is a decrease in feedback gains (Izawa and Shadmehr 2008; Kording and Wolpert 2004). However, in these studies, the uncertainty was simply observation noise, that is, uncertainty on sensory feedback. In contrast, when novel dynamics are learned, there is uncertainty about the structure and parameters of the dynamics (Orban and Wolpert 2011), that is, uncertainty in the input-output relation that has to be learned by an internal model. Therefore, when there is uncertainty in the dynamics, it may be prudent to rely more on cocontraction and feedback mechanisms while the internal model is being learned. The optimal change in feedback gains to increased uncertainty may, therefore, depend on whether the uncertainty is in the sensory observation or in the knowledge of dynamics.

The rapid corrective responses to errors during reaching result both from muscle stretch-dependent motor responses (stretch reflexes) (Kimura and Gomi 2009; Kurtzer et al. 2009) and rapid visuomotor responses that respond to shifts in the visual location of the hand (Bagesteiro et al. 2006; Sarlegna et al. 2003; Saunders and Knill 2005, 2003; Saunders and Knill 2004). Here, we examined whether the gain in one of these two components, the visuomotor response, is modulated during motor adaptation. It has been previously shown that the rapid component of the visuomotor response is involuntary in nature (Franklin and Wolpert 2008), similar to other visuomotor responses to target or background motion (Day and Lyon 2000; Gomi et al. 2006). Understanding such rapid involuntary responses is important in its own right but also informative with regard to voluntary control (Franklin and Wolpert 2011a, 2011b). This is because the same neural circuitry underlying rapid motor responses is also involved in voluntary control (Pruszynski et al. 2011), as proposed by the optimal feedback control framework (Scott 2004; Todorov 2004).

Previous studies have shown that stretch reflex responses (rapid motor responses) are adapted to the dynamics of the environment after extensive learning (Franklin et al. 2007a; Wagner and Smith 2008). However, it is not known whether rapid motor responses are modified during learning. Here, we examined whether the sensorimotor control system modifies visuomotor feedback gains during the learning of novel dynamics. Specifically, we probed the feedback sensitivity throughout the adaptation and deadaptation to a curl force field by measuring the magnitude of rapid visuomotor responses to temporary shifts in the visual location of the hand (Franklin and Wolpert 2008). Importantly, we also examined the sensitivity of this involuntary rapid visuomotor response to changes in the level of background force to disassociate two possible contributing factors: namely, whether changes in feedback sensitivity occur only as a byproduct of the changes in background load and therefore muscle activity [such as occurs with stretch responses (Matthews 1986; Pruszynski et al. 2009)] or whether these changes occur through directly controlled upregulation of the feedback pathways.

MATERIALS AND METHODS

Fourteen subjects were recruited to take part in the main learning experiment (5 men and 3 women; age: 27.8 ± 6.7 yr, mean ± SD) and the force dependence experiment (lateral force: 8 men and 2 women, age: 26.5 ± 7.5 yr). Two subjects participated in both of the experiments. All subjects were right handed according to the Edinburgh handedness inventory (Oldfield 1971) and had no reported neurological disorders. Subjects gave informed consent, and the institutional ethics committee approved the experiments.

Experimental Setup

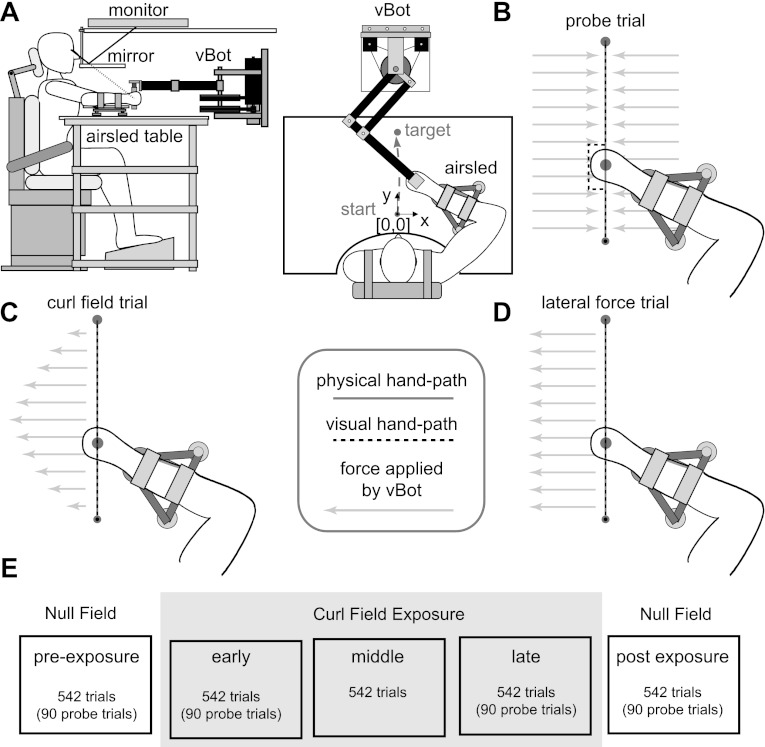
Subjects performed reaching movements with their right arm while grasping a robotic manipulandum. The reaching movements were confined to the horizontal plane ∼10 cm below the subjects' shoulder level. The forearm was supported against gravity with an air sled. The physical environment was generated using the vBOT robotic manipulandum (Howard et al. 2009) that the subjects grasped (Fig. 1A). Position and force data were sampled at 1 kHz. End point forces at the handle were measured using an ATI Nano 25 6-axis force-torque transducer (ATI Industrial Automation). The position of the vBOT handle was calculated from joint position sensors (58SA, IED) on the motor axes. Visual feedback was provided using a computer monitor mounted above the vBOT and projected veridically to the subject via a mirror. This virtual reality system covers the manipulandum and arm and hand of the subject, preventing direct visual feedback of the hand location. Full details of the experimental setup can be found in Howard et al. 2009. The exact onset time of the visual stimuli presented to the subjects was determined using the video card refresh signal and confirmed using an optical sensor.

Fig. 1.

Experimental setup and protocol. A: the subject grasped the handle of the robotic manipulandum (vBOT) while seated. Visual feedback of movements was presented veridically using a top-mounted computer screen viewed through a mirror. The subject's forearm was fixed to the handle and supported by an airsled. B: visual perturbations (probe trials) were used to examine the magnitude of the visually induced motor response. On random movements throughout the experiments, the physical location of the hand (solid gray line) was constrained to a straight-line trajectory to the target using a mechanical channel (grey arrows). During these trials, at a location 6.25 cm from the start of the movement, the visual cursor representing the subject's hand (dotted black line) was displaced by 2.0 cm for 250 ms of the movement before being returned back to the actual hand position. C: learning was examined by introducing a velocity-dependent curl force field (CF). On a straight movement to the target, the force applied by this field to the subject's hand (gray arrows) varied with the forward movement velocity. For hand movements (black line) with a normal bell-shaped velocity profile, the forces are shown. D: to test the dependence of the rapid visuomotor response on background load, experiments were introduced in which a constant background load orthogonal to the direction of motion of various magnitudes was introduced. The load was applied before the movement onset and removed after subjects completed the movement. The forces applied to the hand (gray arrows) were constant in Cartesian coordinates regardless of the movement kinematics. E: experimental protocol in the learning experiment. Each of 5 different stages in the experiment consisted of 542 trials that alternated between forward and backward movements. Subjects proceeded through the experiment by first making movements in the null force field (NF; preexposure). The CF was then introduced over three stages of the experiment (CF exposure, 1,626 trials total). Finally, subjects again made movements in the NF (postexposure) to assess the degree of learning achieved in the force field. Probe trials to assess feedback gain were applied in four of the five stages.

Subjects were seated with their shoulders restrained against the back of a chair by a shoulder harness. Movements were made from a 1-cm-diameter start circle centered 28 cm in front of the subject to a 2-cm-diameter target circle centered 25 cm in front of the start circle. During the main experiment, the start and target positions alternated from trial to trial, so that subjects were required to make alternating forward- and backward-reaching movements. The subjects' arm was hidden from view by the virtual reality visual system, on which the start and target circles as well as a 0.6-cm-diameter cursor used to track instantaneous hand position were projected. Subjects were instructed that they were required to perform successful movements to complete the experiment. A successful movement required the hand cursor to enter the target (without overshooting) within 700 ± 75 ms of movement initiation. Overshoot was defined as movements that exceeded the target in the direction of movement. When subjects performed a successful movement they were provided with feedback as how close they were to the ideal movement time of 700 ms (“great” or “good”) and a counter increased. When subjects performed an unsuccessful movement they were provided with feedback indicating why the movement was not successful (“too fast,” “too slow,” “overshot target”). Trials were self-paced; subjects initiated a trial by moving the hand cursor into the start circle and holding it within the target for 450 ms. A beep indicated that the subjects could begin the movement to the target. The duration of the movement was determined from the time that the subjects exited the start target to the time that subjects entered the final target.

Electromyography

A surface electromyograph (EMG) was recorded from two monoarticular shoulder muscles (pectoralis major and posterior deltoid), two biarticular muscles (biceps brachii and long head of the triceps), and two monoarticular elbow muscles (brachioradialis and lateral head of the triceps). The EMG was recorded using the Delsys Bagnoli (DE-2.1 single differential electrodes) electromyography system (Boston, MA). The electrode locations were chosen to maximize the signal from a particular muscle while avoiding cross-talk from other muscles. The skin was cleaned with alcohol and prepared by rubbing an abrasive gel into the skin. After the abrasive gel was removed with a dry cloth, conductive gel was applied to the electrodes, and they were secured to the skin using double-sided tape. EMG signals were analog band-pass filtered between 20 and 450 Hz (in the Delsys Bagnoli EMG system) and then sampled at 2.0 kHz.

Probe Trials

Throughout the experiments, visually induced motor responses were examined using perturbations of the visual system similar to those previously described (Franklin and Wolpert 2008) to assess the feedback gain. On random trials, at a location 25% of the distance to the target (6.25 cm from the start), the cursor representing the hand position was jumped laterally away from the current hand position, held at 2 cm away from the actual hand trajectory for 250 ms, and then returned to the actual hand position of the movement (Fig. 1B, dashed line). The entire visual perturbation lasted 250 ms. During these trials, the hand was physically constrained by the vBOT to the straight path between the start and final targets, so that any force produced in response to the visual perturbation could be measured against the channel wall using the force sensor. The mechanical channel was implemented as a stiffness of 5,000 N/m and damping of 2 N·m·s⁻¹ for any movement lateral to the straight line joining the starting location and the middle of the target. As this visual perturbation returns to the actual hand trajectory, subjects are not required to respond to the visual perturbation to produce a successful movement to the target. These visual perturbations were applied perpendicular to the direction of the movement (either to the left or right). For comparison, a zero perturbation trial was also included in which the hand was held to a straight-line trajectory with the mechanical channel but the visual cursor remained at the hand position throughout the trial. The mechanical wall of the channel also limits the production of stretch reflex responses or other physically induced motor responses that could contribute to the change in force or muscle activity. Specifically, the channel is simulated throughout the movement guiding the hand from its initial stationary position to the target. Any mechanical effects of the channel on the arm are the same across our three trial conditions, that is, the rightward, leftward, and zero visual probes. As we always compared the responses between these conditions (through subtraction of the responses), any effects of the mechanical channel were removed. Therefore, our paradigm allowed us to measure the response of the hand that was purely related to the visual perturbation. Perturbation trials were randomly applied during movements in a blocked fashion so that one of each perturbation was applied within a block of trials. Specifically, a block of trials consisted of a consecutive number of trials (18 trials in the main learning experiment and 9 trials in the constant lateral force experiment) wherein one of each of the three probe trials was applied.

Novel Dynamics and Visuomotor Response Modulation

Subjects were required to make forward and backwards point-to-point movements with their right arm while we investigated the feedback sensitivity of their visuomotor system. In particular, we examined whether the visuomotor response magnitude changed throughout adaptation to novel dynamics. Subjects initially performed movements in the null force field to get an estimate of the baseline visuomotor feedback sensitivity in the normal environment (paradigm shown in Fig. 1E). In this stage, subjects were required to make 542 trials (271 forward movements and 271 backward movements). We then introduced a velocity-dependent clockwise curl force field for the subsequent 1,626 trials (3 sets of 542 trials). The curl force field was implemented on the vBOT as follows:

$$\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=\left[\begin{array}{cc}0& -0.2\\ 0.2& 0\end{array}\right]\left[\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right]$$

where the force exerted by the vBOT [F_x,F_y (in N)] depends on the subjects' hand velocity [ẋ,ẏ (in m/s); Fig. 1C]. Finally, the dynamics were returned to the null force field for 542 trials. Probe trials were applied to measure feedback sensitivity on random trials in the first null force field (preexposure phase), first curl force field (early exposure phase), last curl force field (late exposure phase), and final null force field (postexposure phase) pseudorandomly within the set of movements. No probe trials were applied during the middle phase of curl force field learning. Specifically, one of each of the types of probe trials (left, zero, right) was applied randomly within a block of 18 movements in a particular direction. Within each set of 542 trials, 90 probe trials were applied on random trials throughout the set of movements. These 90 probe trials were comprised 45 trials in the forward-reaching movements (15 to the left, 15 to the right, and 15 at zero) and 45 trials in the backward-reaching movements (15 to the left, 15 to the right, and 15 at zero).

We ensured that the first movement in any new environment was not a probe trial. While lateral movement in the random probe trials was constrained by the mechanical channel, the subjects were free to move in any manner during all of the other trials. Subjects were required to take short breaks every 300 movements throughout the experiment. They were also allowed to rest at any point they wished during the experiment. The main learning experiment took on average 177 ± 9 min/subject (including breaks). This time does not include any of the setup time (for example, electrode placement and testing), which was ∼30 min/subject.

Force Dependence of the Visuomotor Response

A second experiment was performed to determine the relation between background force applied by the subjects and the rapid visuomotor response. In each of these experiments, subjects made reaching movements in the forward direction (+y) while a constant force was applied laterally to the arm by the vBOT robotic manipulandum. The constant force was applied in the same direction as experienced in forward movements in the curl force field (lateral force experiment; Fig. 1D). The constant force was applied on all trials. Three visual perturbation or probe trials (rightward, zero, or leftward) were presented pseudorandomly within a single block of nine trials (3 probe trials and 6 unperturbed trials) to assess the visuomotor response. Each probe trial was repeated 50 times for each background force level. Unless specifically mentioned, all features of the movements were identical to those in the main learning experiment.

In the experiment, a constant force was applied in the direction perpendicular (−x) to the direction of movement (Fig. 1D). The constant force was experienced at three levels (2, 4, and 6 N) where all the trials at a particular force level were blocked together. The order of the blocks of constant forces was randomized across subjects. For each force level, 541 trials (of which 150 were probe trials) were performed. Subjects were required to take short breaks every 100 movements throughout the experiment. They were also allowed to rest at any point they wished. To initiate a trial, subjects moved into the start target, and the background load was then ramped up over 300 ms. Once the desired background load was achieved and subjects had stabilized their hand within the start target for 1,000 ms, a tone indicated that the subject should perform the reaching movement to the target. Once subjects had maintained the hand within the target position for 400 ms, the background force was ramped back down over 300 ms. Throughout the movement, the background force level and direction were constant in Cartesian space. The control experiment took on average 95 ± 8 min/subject (including breaks but not including the setup time, which was ∼30 min/subject).

Analysis

Analysis of the experimental data was performed using Matlab R2009a. Statistical analysis was performed using the general linear model in SPSS 16.0 (SPSS, Chicago, IL) to perform ANOVAs. If a significant main effect was found, Tukey's honest significant difference post hoc test was used to examine differences. Statistical significance was considered at the P < 0.05 level for all statistical tests.

Hand path error.

The maximum perpendicular error (MPE) was used as a measure of the straightness of the hand trajectory. On each trial, the MPE is the maximum distance on the actual trajectory that the hand reaches perpendicular to the straight-line path joining the start and end targets (errors to the left are defined as negative and errors to the right are defined as positive). The MPE was calculated for each nonprobe trial throughout the learning experiment and averaged across the trials within a block.

End point force.

The end point force experienced by the subjects during the force field learning experiment was calculated for comparison against the constant force experiments. The mean force in the x-axis direction was calculated over a 230-ms period overlapping the middle of the movement on every trial. Individual trial data were averaged across trials and subjects to examine differences in conditions.

Muscle activation.

EMG data were high-pass filtered at 30 Hz using a fifth-order Butterworth using the filtfilt function in Matlab to remove any movement artifacts. The integral of the rectified EMG data was taken over 500 ms from 50 ms before movement start until 450 ms after movement start. Subject data were scaled by the mean across all conditions and averaged across subjects on a block-by-block basis for display purposes.

Rapid visuomotor responses.

The lateral force on individual trials was aligned on visual perturbation onset and averaged across repetitions. The response to the right visual perturbation was subtracted from the response to the left perturbation to provide a single estimate of the motor response to the visual perturbation. To examine the magnitude of the visuomotor responses at a involuntary feedback latency, we calculated the force integral between 180 and 230 ms from the onset of the visual perturbation, as previously determined (Franklin and Wolpert 2008). In this previous work, it was determined that the earliest detectable voluntary change in force produced by a single subject occurred at 230 ms after the onset the visual perturbations (probes) used in this experiment. This means that any estimate before 230 ms can be thought to be involuntary in nature. This does not suggest, however, that later components must be due only to voluntary responses. Due to the transitory nature of the probe trials, responses to the shift in hand position are not required; therefore, it is likely that most of the measured visuomotor feedback responses are involuntary. However, constraining the force analysis to this early interval (180–230 ms) ensures that the estimated responses are involuntary in nature.

The time course of the force response during the learning experiment was examined by determining the difference in the force response between the left and right visual perturbations for each block of trials where one of each type of visual perturbation was applied. Within a block of 36 trials, each of the 3 types of visual perturbations or probe trials was introduced for both the forward and backward directions. Therefore, an estimate of the force magnitude response can be made for each block of 36 trials. The speed at which this force magnitude changes between the conditions and stages during the learning experiment can then be examined. To examine whether the magnitude of the response was affected by learning within a condition, and to see whether the response was immediately changed as subjects went from the null field to the curl field or vice versa, force responses on the last three blocks in the preexposure, the first block in early exposure, the last three blocks in late exposure, the first block in aftereffects, and the last three blocks in postexposure were examined with ANOVA. If a significant main effect of block (5 levels) was found, a Tukey's honest signficant differnence post hoc test was used to examine whether significant differences existed between different blocks.

RESULTS

Adaptation to Novel Force Field

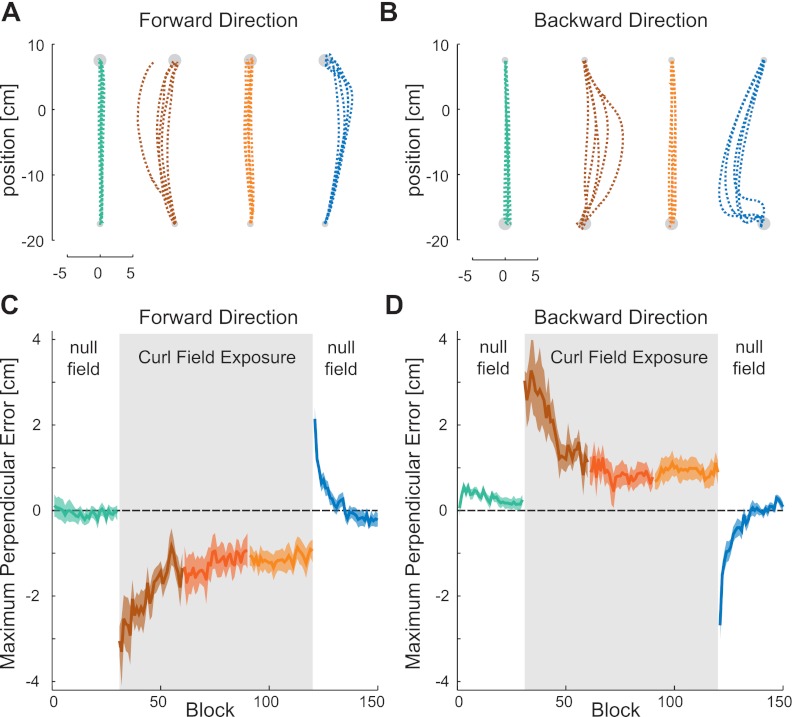
Subjects initially made movements (alternating between the forward and backward directions) in the null force field. In this “preexposure” condition, all subjects were able to make relatively straight, smooth movements of the appropriate duration to the target (Fig. 2, A and B, green traces). After the subjects had completed 542 movements, the novel curl force field was introduced (exposure phase). Subjects reaching trajectories, which had been roughly straight, were perturbed by the change in experienced forces, causing the initial movements in the force field to be curved (Fig. 2, A and B, brown traces). Subjects continued to alternate forward- and backward-reaching movements in the curl force field over the following 1,626 movements. Gradually, subjects were able to reduce the disturbance created by the novel dynamics by learning to compensate for it. By the end of learning, subjects were able to consistently perform straight movements under this force field (Fig. 2, A and B, orange traces). When the force field was removed, strong deviations were seen in the opposite direction to initial perturbed trajectories (called “aftereffects”; Fig. 2, A and B, blue traces), indicating that subjects had learned to compensate for the field by changing the applied forces rather than through a cocontraction strategy. To examine the changes in the trajectories over the experiment, the signed hand path error was calculated on a block-by-block basis (Fig. 2, C and D). As expected, the trajectories were disturbed by the force field and only gradually returned toward the hand path error values in the null force field. Once the curl force field was removed, large hand path errors were again produced, which gradually returned to the original values in the preexposure phase.

Fig. 2.

Trajectory correlates of adaptation. A: data from one subject showing the forward movement paths in four stages during the learning experiment. The movement paths are shown for the last five movements in the preexposure NF (green), first five movements in the force field (early exposure stage, brown), last five movements in the force field (late exposure stage, orange), and first five movements in the postexposure stage (blue). B: data from one subject showing the backward movement paths in four stages during the learning experiment. C: maximum perpendicular error in the forward direction movements during the five stages of learning: preexposure (green), early exposure (brown), middle exposure (red), late exposure (orange), and postexposure (blue). The sold line represents the maximum perpendicular error across all subjects (mean value across all nonprobe trials within each block of the experiment). The colored shaded region shows the SE. The gray shaded bar indicates the period in which the CF was applied. D: mean values of maximum perpendicular error across all subjects in each block throughout the experiment during movements in the backward direction.

During movements in a curl force field, the end point forces that are experienced depend on the velocity of the movement. As subjects were required to make movements within a 700 ± 75-ms duration, the range of velocities, and therefore forces, was fairly consistent throughout the learning experiments. During the curl field trials, the mean ± SD of the magnitude of force in the x-axis was 6.91 ± 1.23 N in the forward direction and 7.03 ± 1.01 N in the backward direction. No significant changes throughout the three different phases of the curl field were found (F_2,18 = 2.669, P = 0.097), nor were the magnitude of forces in the forward and backward movement directions significantly different (F_1,9 = 0.157, P = 0.701).

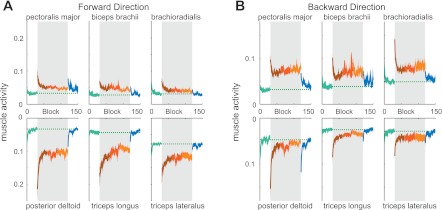
Muscle activity was measured throughout the learning experiment. The changes in activity of six muscles of the arm are shown arranged in antagonist pairings in Fig. 3. In the first trials after the curl field was introduced, increased activity in all muscles, including antagonist pairs, was found. Gradually, muscle activity reduced, returning close to the null force field level for the flexor muscles in the forward direction movements and for the extensor muscles in the backward direction movements. When the force field was removed, a small increase in cocontraction was found, prominent in the single joint shoulder muscles (pectoralis major and posterior deltoid). The increase in coactivation was quickly reduced in the subsequent trials.

Fig. 3.

Electromyographic correlates of adaptation. A: integrated electromyographic activity of six arm muscles [mean (solid line) and SE (shaded region) across all eight subjects] during nonprobe trial movements in the forward direction during the five stages of the learning experiment: preexposure (green), early exposure (brown), middle exposure (red), late exposure (orange), and postexposure (blue). The gray shaded bar indicates the period in which the CF was applied. The green dotted line shows the mean muscle activity level in the last half of the preexposure NF trials for comparison. Muscles are arranged as antagonistic pairs (left to right: single joint shoulder muscles, biarticular muscles, and single joint elbow muscles) with flexor muscles on the top and extensor muscles on the bottom. B: integrated electromyographic activity of six arm muscles (mean across all eight subjects) during nonprobe trial movements in the backward direction during the five stages of the learning experiment.

Visuomotor Rapid Responses Adapt to Changes in Dynamics

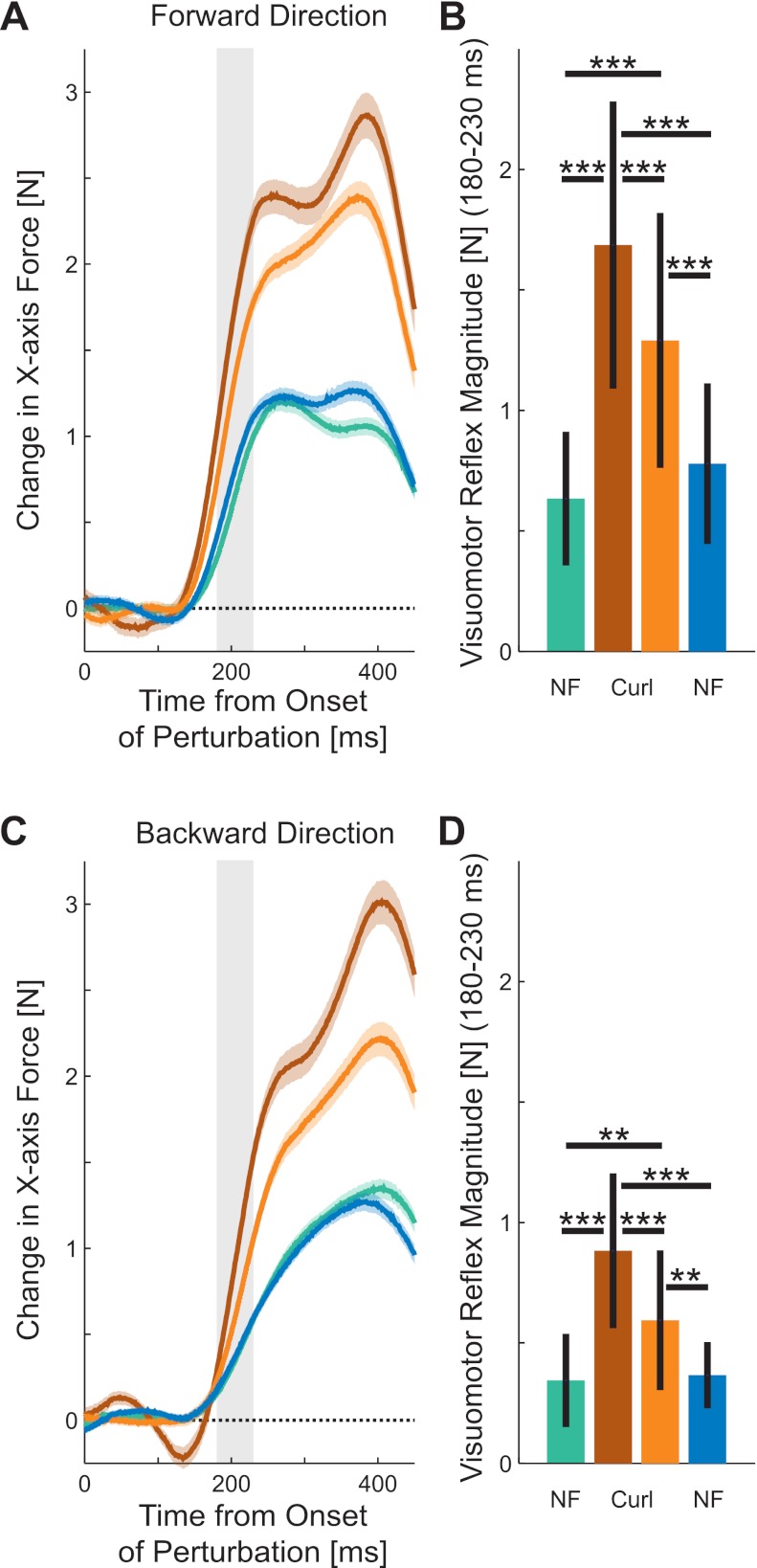
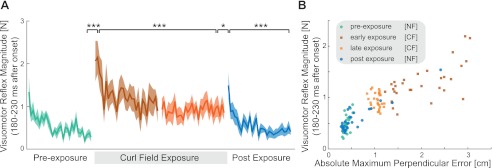
Throughout four of the five stages of the reaching movements in the learning experiment, probe trials (in which a short visual perturbation of the visual location of the hand representation occurred) were applied randomly to measure the feedback sensitivity during adaptation. Specifically, these probe trials were introduced in the null force field before learning (preexposure), in both early and late exposure stages in the curl force field, and in the return to the null force field (postexposure). The force response produced by the subjects against the mechanical channel shortly after the visual perturbation was used to quantify the magnitude of this rapid response. A rightward visual perturbation of the hand representation led to subjects generating a force into the leftward wall of the channel: the direction appropriate to compensate for the movement of the hand had it been physically moved. Similarly, a leftward visual perturbation produced the opposite response into the rightward channel wall. There were no differences in the force responses to the left and right perturbations throughout any of the experiments. Therefore, to summarize the response, the difference in the force response between the left and right visual perturbations was calculated across all trials for each subject. The force responses to the visual perturbation varied depending on the experimental stage (Fig. 4, A and C).

Fig. 4.

Magnitude of rapid visuomotor responses during adaptation. A: force produced in response to a shift in the visual representation of hand position (probe) during forward movements in four stages of learning: preexposure (green), early exposure (brown), late exposure (orange), and postexposure (blue). Magnitude of force represents the difference between visual perturbations to the right and visual perturbation to the left. The solid line indicates the mean responses across subjects, and the shaded colored region represents the SE. The shaded bar shows the time interval (180–230 ms) over which the response was examined in B. B: mean force magnitude across all subjects in response to visual perturbation (left-right visual perturbation) during the 180- to 230-ms interval after the onset of the perturbation during movements in the forward direction. The black line indicates the SD of response magnitudes across all subjects. Significant differences, as assessed with Tukey's honest significant difference (HSD) post hoc test, are indicated (*P < 0.05; **P < 0.01; ***P < 0.001). C: force produced in response to a shift in the visual representation of hand position (probe) during backward movements in four stages of learning. D: mean force magnitude across all subjects in response to visual perturbation (left-right visual perturbation) during the 180- to 230-ms interval after the onset of the perturbation during movements in the backward direction.

To quantify the changes due to involuntary responses, the force traces were integrated between 180 and 230 ms after the onset of the perturbation (Fig. 4, B and D). This is before the fastest time of voluntary response that was measured to this type of stimuli (Franklin and Wolpert 2008). We found a significant main effect of visuomotor feedback magnitude as a function of experimental stage for forward movements (F_3,27 = 22.517, P < 0.001). A post hoc test was used to examine specific differences across the stages. In the forward movements (Fig. 4B), the involuntary visuomotor response was larger in the early exposure stage compared with either the preexposure (P < 0.001) or postexposure (P < 0.001) as well compared with the late exposure stage (P < 0.001). The involuntary visuomotor response was larger in the late exposure stage compared with either the preexposure (P < 0.001) or postexposure stages (P < 0.001). However, no significant difference was found between the responses in either of the null force field stages (preexposure and postexposure, P = 0.331).

Similar differences were found also for the backward movement trials (Fig. 4D). We found a significant main effect of experimental stage for backward movements (F_3,27 = 19.164, P < 0.001). A post hoc test was then used to examine specific differences across the stages. In the backward movements, the involuntary visuomotor response was larger in the early exposure stage compared with either the preexposure (P < 0.001) or postexposure stages (P < 0.001) as well as the late exposure stage (P < 0.001). The involuntary visuomotor response was larger in the late exposure stage compared with either the preexposure (P = 0.005) or postexposure stages (P = 0.007). However, no significant difference was found between the responses in either of the null force field stages (preexposure and postexposure, P = 0.994).

To examine the time course of the changes in the involuntary visuomotor response, we calculated the mean response across all subjects block by block throughout the experiment. The magnitude of the mean response was calculated for each block of 36 movements (containing one of each probe trial type for both the forward and backward movements; Fig. 5). As in our previous study (Franklin and Wolpert 2008), the visuomotor response magnitude was raised at the beginning of the experiment (initial preexposure phase) as subjects adapted to the passive dynamics of the robotic manipulandum. To compare the changes in the rapid visuomotor response, we compared the size of the force response in the first block and last three blocks when the dynamics changed. Specifically, we examined the last three blocks in the preexposure, the first block in the early exposure, the last three blocks in late exposure, the first block in the postexposure, and the last three blocks in the postexposure stages with ANOVA. We found a significant main effect of block (5 levels, F_4,321 = 29.226, P < 0.001). A post hoc test was then used to examine these differences. Compared with the response at the end of the preexposure stage, the visuomotor response was increased within the first block of trials in the curl force field (P < 0.001). This decreased over the trials in the early exposure stage and was significantly smaller at the end of the late exposure stage (P < 0.001). Once the force field was removed, the response in the first block of postexposure trials was increased relative to the previous magnitude in the curl force field (P = 0.04) and significantly larger than the magnitude at the end of null force field trials both for preexposure (P < 0.001) and postexposure (P < 0.001). Over the rest of the postexposure trials, the response gradually reduced until the magnitude at the end of the postexposure stage was not significantly different from that in the preexposure stage (P = 0.840). Even at the end of late exposure in the curl force field, the force magnitude was still larger than the responses found in the null force field at the end of the preexposure (P < 0.001) or postexposure stages (P < 0.001).

Fig. 5.

Feedback correlates of adaptation. A: changes in the visuomotor feedback magnitude during blocks of probe trials throughout four stages of learning: preexposure (green), early exposure (brown), late exposure (orange), and postexposure (blue). The mean response over an early interval (180–230 ms after the visual perturbation onset) before voluntary action was calculated. The data shown are means (±SE) of eight subjects. Statistically significant differences between certain blocks across the stages were tested using Tukey's HSD post hoc test (*P < 0.05; **P < 0.01; ***P < 0.001). B: visuomotor feedback magnitude as a function of the mean maximum perpendicular error in each block. The first five blocks in the initial preexposure phase are not shown.

The results suggest that the magnitude of the rapid visuomotor response increased primarily in response to changes in the dynamics, specifically resulting in large responses during the periods in which there were large errors in the hand paths. We therefore examined whether there was a relation between the rapid visuomotor responses and hand path errors (Fig. 5B). The results suggested that the magnitude of this rapid visuomotor response increases with larger errors in the movement trajectories. However, there is another possibility: that is, the visuomotor response could scale with the variability of the movements (which also increases early in learning) rather than with the size of the errors themselves. Therefore, this was examined using analysis of covariance (ANCOVA). The first five blocks in the preexposure phase were not included in this analysis as these were familiarization trials that allowed subjects to become familiar with the passive dynamics of the manipulandum. ANCOVA with a fixed effect of movement direction (2 levels), a fixed effect of force field (2 levels), a random effect of subjects, and covariates of MPE and variability of movements was performed. For each block of trials, both the mean MPE and SE of the MPE were calculated. There was a significant effect of MPE on the magnitude of the visuomotor response (F_1,2254 = 36.437, P < 0.001) but no significant effect of movement variability (F_1,2254 = 1.258, P = 0.262). This suggests a relation only between the size of the kinematic error and the visuomotor feedback magnitude, which is independent from the effect of force field (null or curl force field), which was also significant (F_1,10.2 = 16.894, P = 0.002).

Force Dependence of the Visuomotor Response

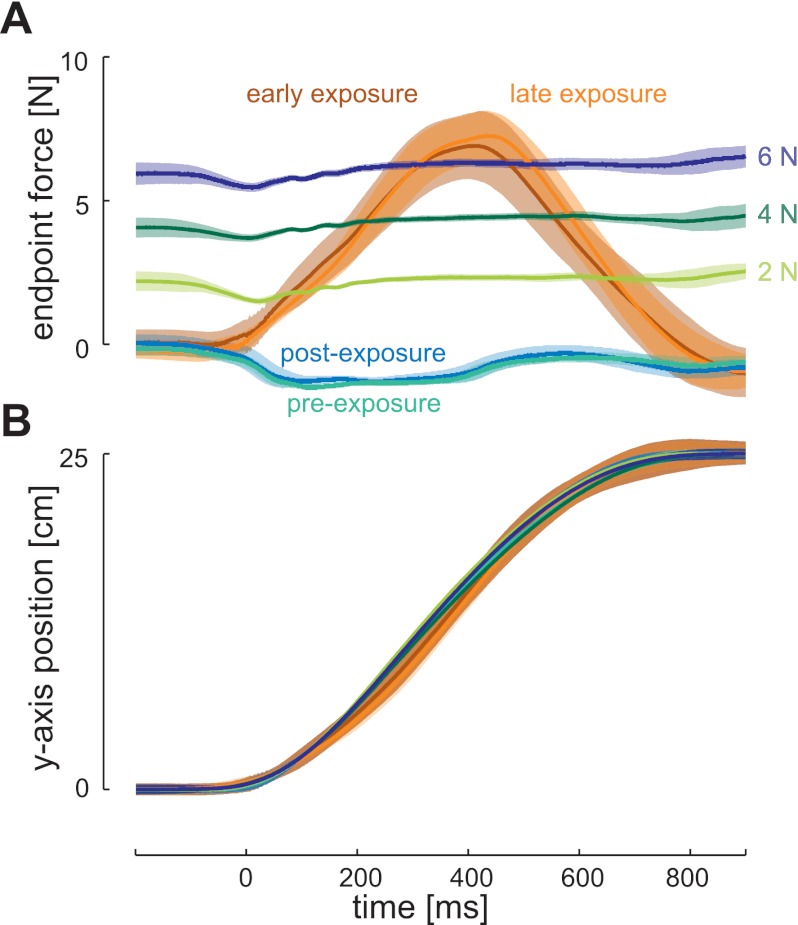
The results of the learning experiment demonstrated changes in the involuntary visuomotor response magnitude when the dynamics changed and throughout the stages of the experiment. This could be due either to controlled changes in the feedback sensitivity of the sensorimotor control system or could occur as a side effect of other changes associated with dynamic learning (e.g., changes in applied force or muscle activity). For example, the short latency stretch reflex response scales with the background force level (and therefore muscle activity) (Matthews 1986; Pruszynski et al. 2009). To determine which explanation best explains the change in rapid visuomotor magnitude during adaptation, a second experiment was performed using constant background force levels. In these experiments, the constant background load (2, 4, and 6 N) was applied orthogonal to the direction of movement and in the same direction as the curl force field (Fig. 6). Although both the learning and constant background force experiments required similar reaching motions (Fig. 6B), the forces experienced were different (Fig. 6A). The levels of the constant background loads were chosen to cover the range of forces experienced in the curl force field. This ensured that the effect of visuomotor feedback responses were examined over a comparable range of muscle activation levels to the curl force field.

Fig. 6.

Comparison of end point force in the learning and constant background load experiments. A: end point force in the x-axis as a function of time in the NF (preexposure, green; postexposure, blue), CF (early exposure, brown; late exposure, orange), and constant background loads (2 N, light green; 4 N, dark green; 6 N, navy). The solid line indicates the mean, and the shaded region represents the SD of all nonprobe trials within a condition. B: position in the y-axis as a function of time for all of the conditions. Data are shown for a single subject who participated in both experiments.

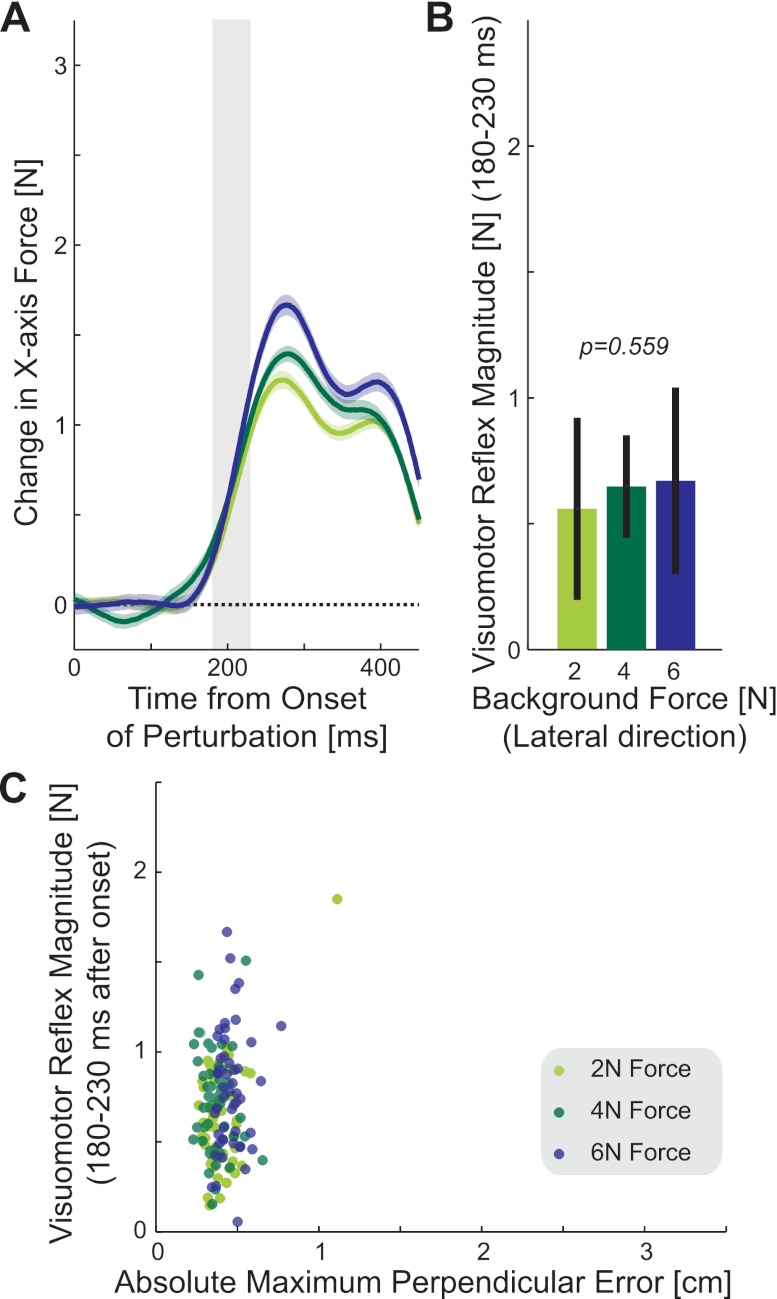
In the lateral force experiment, the magnitude of the visuomotor response was examined under the three constant background loads (Fig. 7A). The response in the early feedback interval (180–230 ms) after the perturbation onset (Fig. 7B) was examined using ANOVA. No significant main effect of background load was found (F_2,18 = 0.601, P = 0.559). Instead, the magnitudes of the visuomotor responses in both of the background load experiments across all levels of background load were similar to those found for the same forward-reaching movements in the null force field of the main experiment (compare all bars in Fig. 7B with the green and blue bars in Fig. 4B). The size of the visuomotor response could also be plotted as a function of MPE (Fig. 7C). The results show that the constant background forces do not cause large deviations in the trajectories as the force is present (and compensated for) before the start of the movement. Overall, this experiment shows that increases of a constant background load do not alter the rapid visuomotor response magnitude.

Fig. 7.

Magnitude of rapid visuomotor responses during movement with constant background loads. In all elements shown, the scale is identical to the results in Fig. 4 for ease of comparison. A: force produced in response to a shift in the visual representation of hand position (probe) during movements with three different constant background loads applied in the direction lateral to motion (2 N, light green; 4 N, dark green; 6 N, navy). The magnitude of force represents the difference between visual perturbations to the right and visual perturbation to the left. The solid line indicates the mean responses across subjects, and the shaded colored region represents the SE. The shaded bar shows the time interval (180–230 ms) over which the response was examined in B. B: mean force magnitude across all subjects in response to visual perturbation (left-right visual perturbation) during the 180- to 230-ms interval after the onset of the perturbation during movements with constant lateral load. The black line indicates the SD of response magnitudes across all subjects. The P value indicates the result of ANOVA. C: visuomotor feedback magnitude as a function of the mean maximum perpendicular error in each block. The scale is identical to that of Fig. 5C.

DISCUSSION

We examined the rapid visuomotor response magnitude during adaptation of reaching movements in the presence of a velocity-dependent curl force field. We found large increases in the rapid visuomotor response both at the beginning of the force field adaptation and when the force field was subsequently removed (aftereffects). A second experiment demonstrated that the visuomotor rapid responses are not sensitive to changes in background loads. Therefore, we confirmed that these increases in rapid visuomotor response were independent of any background force level. Overall, our results suggest that when the sensorimotor control system experiences errors, it increases the gain of the feedback pathways to deal with the unexpected disturbances until the feedforward controller is able to appropriately learn the dynamics.

Stretch-induced short latency reflex responses are known to be highly dependent on the background muscle activity (Matthews 1986; Pruszynski et al. 2009). However, we found no significant changes in the magnitude of the visuomotor responses with changes in the background load when the load was constant throughout the movement. In fact, the magnitude of the visuomotor responses in the constant load experiments were of similar size to those measured in the null force fields, despite the background loads being of similar level to the peak forces experienced in the curl force field. This suggests that the rapid visuomotor responses do not exhibit the “automatic gain scaling” (reflex size depending on preperturbation background activity) that exists in stretch responses (Matthews 1986; Pruszynski et al. 2009). Interestingly, we did find that the size of the visuomotor responses were larger after adaptation to the curl force field compared with those measured in the null force field. This could indicate that the visuomotor feedback gain itself was tuned to the environment as part of the learning process, but this possibility is not clear from the present study.

Previous work has shown that early responses to changes in dynamics involve both corrective feedback responses and increased coactivation (Franklin et al. 2003a; Franklin et al. 2003b; Thoroughman and Shadmehr 1999) to limit the disturbing effects on the movement from the unlearned dynamics. Similar to this previous work, we also demonstrated increases in coactivation in response to the kinematic errors produced by force field adaptation and deadaptation. The increases in coactivation on subsequent trials in response to errors during movement (Milner and Franklin 2005; Osu et al. 2002) have been suggested to be an element of the computational algorithm that underlies dynamic motor adaptation (Franklin et al. 2008). Through increased muscle coactivation, the limb impedance (stiffness and damping) can be increased to both limit the trajectory disturbance produced by the novel dynamics (Hogan 1984, 1985) and also to limit the effects of self-generated motor noise (Gribble et al. 2003; Lametti et al. 2007; Selen et al. 2005; Selen et al. 2009), which can cause further disturbance when interacting with the environment (Burdet et al. 2006).

Here, we extend this previous work to show that not only are corrective responses more prominent early in learning but that these feedback pathways, specifically those of the visuomotor responses of the hand (Brenner and Smeets 2003; Franklin and Wolpert 2008; Sarlegna et al. 2004; Saunders and Knill 2003; Saunders and Knill 2004), are upregulated when errors induced by changes in the dynamics are produced. These visuomotor responses have been shown to be modulated depending on the task performed by the subjects. For example, they can be excited or inhibited depending on the task relevance of visual stimuli (Franklin and Wolpert 2008) or the shape of targets to which subjects are reaching (Knill et al. 2011). However, to our knowledge, this is the first time that they have been shown to be controlled to assist adaptation to novel dynamics. Although visual feedback is not required for force field adaptation (DiZio and Lackner 2000; Franklin et al. 2007b; Scheidt et al. 2005; Tong et al. 2002), these results suggest that the visuomotor response may significantly contribute to corrective feedback of errors.

The visuomotor responses to perturbations to the left or right produced similar-sized responses (symmetric responses) throughout all dynamic environments. This is expected, as the lateral force required to return the hand back to the unperturbed trajectory (had it been physically moved) is the same for left and right perturbations, independent of the field type (null force field, curl force field, or constant background loads). To be precise, small differences due to the limb geometry will likely exist, but they will be unrelated to the force fields. Similarly, the overall response may be different in different force fields, but the symmetry of the response in these particular force fields is expected. There is, however, one major difference with respect to the curl force field, which is potentially interesting but cannot be measured in our paradigm. That is, perturbations in the visual hand position to the left in a forward movement could also be expected to produce a force in the forward direction if the visuomotor response was also tuned to the curl force, similar to the results of Wagner and Smith 2008. The visuomotor response to a perturbation to the right could therefore be expected to also include a force in the backward direction after learning. However, these types of effects cannot be examined in the present setup as the mechanical channel can only measure forces in the lateral direction.

Early in the learning of the novel dynamics, both cocontraction and increased visuomotor feedback responses were found. One possibility is that the cocontraction causes this increase in the visuomotor feedback gain. Although we cannot demonstrate that our results are independent from cocontraction per se, we have shown that increased muscle activation, such as always occurs in cocontraction, does not itself cause an increase in the visuomotor response. Therefore, if our results are due to some cocontraction-based response, this would be independent of changes in muscle activation, suggesting some higher level-based control process.

Based on studies using transcranial magnetic stimulation over the sensorimotor cortexes (Kimura et al. 2006; Shemmell et al. 2009) and neural recordings (Evarts and Tanji 1976; Pruszynski et al. 2011), task-dependent feedback modulation has been shown to depend on cortical processing. On trials in which the transcranial magnetic stimulation was applied, task-dependent changes in rapid motor response magnitude were depressed, whereas changes relating to instruction were enhanced (Shemmell et al. 2009). A study that examined event-related potentials using electroencephalography during the learning of visuomotor rotations found much larger error trial waveforms early in learning compared with late in learning, independent of the sizes of the errors experienced (Anguera et al. 2009). Although explained by theories involved in the feedforward learning processes, these responses also mirror the relative changes in visuomotor feedback sensitivity that we found during learning. Although it is not yet clear what brain structures are involved in these rapid visuomotor responses, similar motor responses elicited by target jumps (Day and Lyon 2000; Diedrichsen et al. 2004; Prablanc and Martin 1992) are related to activity in the parietal cortex (Diedrichsen et al. 2005).

We suggest that our findings can be explained by the idea that these feedback gains are modulated by the uncertainty in the state of the body. This uncertainty in the state of the limb can arise from multiple factors (Orban and Wolpert 2011): sensory noise, feedback delays, and the interaction between the motor and planning noise (Churchland et al. 2006; Jones et al. 2002) and the environment. Although environmental instability can be hand tailored to amplify noise (Burdet et al. 2001), even marginally stable force fields such as the curl force field can also have a significant impact on uncertainty. This is due to the interaction between the variations in the trajectory from trial to trial and the forces produced by the force field. Specifically, noise in the cortical planning processes (Churchland et al. 2006; van Beers 2009) has a large effect on the trial-by-trial variability, which, in turn, means that the force experienced by the limb on each trial varies (compare the variance of the forces on the curl force field with that of the null or constant force loads in Fig. 6A). This variation affects the experienced force, thereby amplifying the initial variability. Thus, we expect higher uncertainty and therefore predict higher rapid visuomotor feedback gains during the movements in the curl force field compared with the null force field even after learning is completed. However, this does not suggest that the feedback gain simply increases due to any increased variability in the trajectories. For example, it has been shown that the visuomotor feedback response can be either increased or decreased with increased trajectory variability depending on the task relevance of such variability (Franklin and Wolpert 2008). In contrast, although movements in the constant background load conditions are subject to the same planning and motor noise variability as in the force field, the trajectory variability is not enhanced by the environment simply because the force generated by the robot does not depend on the trajectory (Fig. 6A). In this environment, therefore, the only possible increase in uncertainty relative to the null force field is produced by the motor noise purely due to its signal-dependent nature (Hamilton et al. 2004; Jones et al. 2002). Thus, we expect little change in feedback gain in the constant background load experiment (small increases with background load), as we found experimentally. Finally, maximum uncertainty in the state of the limb and environment occurs when the dynamics change (either initial trials in the force field or initial aftereffect trials). This is also reflected in increased uncertainty in the internal model, both in terms of the parameters of the present internal model and whether or not a different internal model would produce better predictions. This is paralleled with our finding of large increases in the visuomotor feedback gain during early trials in both the curl force field and null force field. Therefore, we suggest that the upregulation of these fast feedback gains are driven by the sensorimotor control system's need to counteract the increased uncertainty in the world.

It is important to note that the optimal response to increased uncertainty is not always upregulation of feedback gains. Specifically, it will depend on where the uncertainty exists within the coupling between the environment and the sensorimotor control system (Orban and Wolpert 2011). If, as in the present study, the uncertainty exists in the external environment or in the internal model, then the optimal response will rely on increased cocontraction (Franklin et al. 2008; Franklin et al. 2003b) and increased feedback gains while decreasing the contribution due to predictive responses (Crevecoeur et al. 2010). On the other hand, if the increased uncertainty occurs within the sensory system, then the optimal response will be to decrease the feedback responses (Izawa and Shadmehr 2008; Kording and Wolpert 2004). For example, in a sensory-based estimation task, as the sensory uncertainty of the hand was increased, subjects relied more on the prior (Kording and Wolpert 2004). Similarly, when the certainty of target location varies during the movement, the feedback gains are reduced (Izawa and Shadmehr 2008). Under these types of increased sensory uncertainty, the optimal response is reduced feedback gains; when you do not know where the target is, there is little point setting up strong reflexes.

Although the present work examined visuomotor feedback modulation during adaptation, we expect that the stretch-dependent rapid motor response sensitivity (at least for longer latency responses) might show similar changes to the introduction of new dynamics, as long latency rapid motor responses have been shown to exhibit extensive task dependency. For example, the gain of the long latency rapid motor responses varies with environmental dynamics (Franklin et al. 2007a; Kimura and Gomi 2009; Krutky et al. 2010; Perreault et al. 2008; Wagner and Smith 2008), with the limb dynamics (Kurtzer et al. 2009; Kurtzer et al. 2008), and with task (Dimitriou et al. 2012; Pruszynski et al. 2008). An interesting, but experimentally challenging, question is whether our finding of the upregulation of the rapid visuomotor response gain during adaptation extends to stretch-dependent motor responses.

In conclusion, we have shown that the visuomotor feedback gain can be modulated by the sensorimotor control system depending on the changes in the dynamics of the environment. This demonstrates that the sensorimotor control system exhibits flexible control of feedback pathways and feedforward processes such as coactivation to limit the disturbances produced by the introduction of novel dynamics. Such intervention allows for the quick reduction of kinematics errors while the internal model of the new dynamics is learned, which, with its properties of generalization, can form the basis for skillful control.

GRANTS

This work was supported by the Wellcome Trust.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.F., D.M.W., and D.W.F. conception and design of research; S.F. performed experiments; S.F. and D.W.F. analyzed data; S.F. and D.W.F. drafted manuscript; S.F., D.M.W., and D.W.F. approved final version of manuscript; D.M.W. and D.W.F. edited and revised manuscript; D.W.F. interpreted results of experiments; D.W.F. prepared figures.