Assessing potential errors of MRI-based measurements of pulmonary blood flow using a detailed network flow model

Abstract

MRI images of pulmonary blood flow using arterial spin labeling (ASL) measure the delivery of magnetically tagged blood to an image plane during one systolic ejection period. However, the method potentially suffers from two problems, each of which may depend on the imaging plane location: 1) the inversion plane is thicker than the imaging plane, resulting in a gap that blood must cross to be detected in the image; and 2) ASL includes signal contributions from tagged blood in conduit vessels (arterial and venous). By using an in silico model of the pulmonary circulation we found the gap reduced the ASL signal to 64–74% of that in the absence of a gap in the sagittal plane and 53–84% in the coronal. The contribution of the conduit vessels varied markedly as a function of image plane ranging from ∼90% of the overall signal in image planes that encompass the central hilar vessels to <20% in peripheral image planes. A threshold cutoff removing voxels with intensities >35% of maximum reduced the conduit vessel contribution to the total ASL signal to ∼20% on average; however, planes with large contributions from conduit vessels underestimate acinar flow due to a high proportion of in-plane flow, making ASL measurements of perfusion impractical. In other image planes, perfusion dominated the resulting ASL images with good agreement between ASL and acinar flow. Similarly, heterogeneity of the ASL signal as measured by relative dispersion is a reliable measure of heterogeneity of the acinar flow distribution in the same image planes.

arterial spin labeling (ASL) is a noninvasive MRI technique applied to produce blood flow maps. A series of MRI pulse sequences tags the blood, permitting it to be used as an endogenous tracer. This technique has predominantly been used to measure perfusion in the brain (9), but more recently, the techniques have been adapted and applied to the lungs to investigate blood flow distribution and heterogeneity under various conditions (2–4, 19, 23, 26, 32).

In the lung, the ASL FAIRER (arterial spin labeling flow-sensitive alternating inversion recovery with an extra radiofrequency pulse) technique works by taking two cardiac-gated images that are the same in terms of acquisition, but that differ in terms of a preceding tagging pulse, so that in one image, blood that enters the image plane is bright whereas in the second image it is dark. The tagging is done by applying a 180-degree radiofrequency pulse that inverts the longitudinal magnetization of the protons in the water of blood. The magnetization relaxes back toward equilibrium with a time constant T1, passing through zero (the null point) before becoming positive. The blood signal in the subsequent image is proportional to the longitudinal magnetization at the time the image is acquired. In lung ASL the time delay between tagging and image acquisition is such that the signal of blood is near the null point, which is why we refer to these images as “dark blood” images. In contrast, if the magnetization of blood is not inverted before imaging, the longitudinal magnetization is large and blood produces a bright signal. This effect is exploited in ASL by measuring two images. For the first image a spatially selective inversion pulse is applied that inverts the magnetization of the tissue within a volume encompassing, but slightly thicker than, the image plane. After a wait that includes one systolic ejection period, the image is obtained. During this time, blood that flows from outside the inversion plane into the image plane appears bright at the time of imaging, as it was not subjected to the inversion by virtue of its spatial location at the time the inversion was applied. In the second, nonselective image, the inversion is applied to the entire chest volume, effectively reducing signal in all blood at the time of image acquisition, and so any blood that flows into the imaging plane during the subsequent systolic ejection period that precedes imaging appears dark in the image. Signal resulting from stationary structures is the same in both images and so when the images are subtracted, what is left is an image of blood that has traveled from outside the spatially selective inversion band into the imaging plane in one systolic period; anatomical features such as the diaphragm subtract out and are not visible. We will refer to the difference between bright blood and dark blood images as the ASL image, and blood that was not inverted by the spatially selective inversion pulse as labeled or tagged blood. The tagging region is the volume outside of the spatially selective inversion pulse.

From a theoretical standpoint, several aspects of ASL as implemented in the lung raise questions as to the exact nature and specificity of the measurement. First, to ensure a uniform inversion of the magnetization across the image plane, the thickness of the inversion plane must be greater than that of the image plane (a function of the inability of the MRI scanner to produce a perfectly rectangular spatially-selective inversion pulse). This creates a “gap” between the edge of the inversion region and the edge of the imaging plane, commonly referred to as the inversion gap (3). To be recorded in the ASL image, labeled blood must cross this gap and enter the image plane. Put another way, the blood that is within the gap, and which will enter the plane during the next systolic period, was not labeled and does not contribute to the ASL signal because it was inverted prior to both of the images. This results in a degree of uncertainty in the measurement of pulmonary blood flow, with a likely underestimation. Second, given the complicated anatomy of the pulmonary circulation the ASL measurement of pulmonary blood flow is expected to be different depending on the orientation and location of the imaging plane in the lung. As recent studies have used multiple planes in an attempt to cover most of the lung (e.g., 2, 23) it is important to consider the effect of different plane locations on the ASL signal. Third, in any selected image plane there are blood vessels that supply or drain regions of the lung outside the image plane and yet pass through the image plane. These “conduit vessels” contribute to the overall ASL image if they contain labeled blood, but the signal from them is not a contribution to perfusion (the delivery of blood to the capillary bed) within the image plane. In this sense ASL is different to an experiment in which signal unequivocally comes from capillary perfusion, such as microspheres (e.g., 15, 33) or single pass tracers (e.g., 31). Fourth, unlike ASL in the brain, ASL-FAIRER in the lung cannot apply the inversion in an anatomical location that is “upstream” of the image plane. Because in the brain the arterial and venous flows into the plane come from opposite directions, the inversion scheme can be manipulated to only label blood on the arterial side. For the lung, however, with the FAIRER approach, blood on both sides of the image plane is labeled. Consequently the venous circulation may also contribute to the ASL image. Therefore in this study we set out to answer the following questions using an anatomically structured in silico model of the pulmonary circulation:

1. What is the effect of the gap on the measured ASL signal?

2. How does image plane location affect the ASL signal?

3. What is the signal contribution from the arterial and venous conduit vessels?

4. Can the effect of the signal from the conduit vessels be reduced?

METHODS

Model basis.

The geometry of the lung surface, central airways, and the largest pulmonary arteries and veins were derived from MDCT data acquired at the University of Iowa Comprehensive Lung Imaging Center (I-Clic) within the framework of the Human Lung Atlas database and extensively described previously (20, 21). The model is based on data from a healthy man (age: 25 years, weight: 90.9 kg, height: 1.90 m) acquired in the supine posture with inflation level held at 95% vital capacity (assumed here to be representative of total lung capacity, TLC) and at functional residual capacity (FRC) and has formed the basis of previous studies (8, 11, 34). Lung volumes for this subject measured in the seated position were 4.47 and 8.47 liters at FRC and TLC, respectively.

Model components.

In this study we applied a model of the pulmonary circulation developed in previous studies (6–8, 10, 11). From the flow solution in the full lung model, the ASL signal calculations were performed in both lungs separately; however, the results were largely similar and for clarity we report results from the right lung only, matching the predominant use of the right lung for imaging studies (2, 4, 16, 19, 23, 26, 32). This model includes the following features:

Anatomically based geometry of the lung surface and central blood vessels (7) derived from high resolution CT data from the Lung Atlas database (20) for a single male subject [this is the same subject used in previous computational studies and more details can be obtained from (11, 34)];

Computationally generated morphometrically consistent models of the arterial and venous vessels to the level of an acinus (accompanying vessels only, excluding supernumerary vessels). There are ∼30,000 each arterial and venous branches in a single lung model (left or right) and each terminal vascular branch in this model is associated with a single acinus (of which there are ∼15,900 in the right lung model applied here) (7, 35). Each vessel is represented with a one-dimensional (1D) line and radius information derived from morphometric studies (28);

A simplified intra-acinar flow model (10) consisting of 9 symmetric branches of intra-acinar arteries and veins coupled through a sheet flow representation of the pulmonary capillaries (12) was used to connect each terminal (extra-acinar) artery and vein;

A model of parenchymal tissue deformation (34), to which the vascular networks are tethered. Tissue deformation influences perfusion via: 3D vascular locations as a function of tissue [the Slinky effect (26)], elastic recoil pressures acting to distend the extra-capillary vessels, and the effect of alveolar inflation levels on capillary sheet distensibility (8, 11).

Blood flow simulation.

On application of two boundary conditions, a prediction of blood flow through the full pulmonary circuit—arteries, capillaries, veins—can be obtained. In this study a steady inlet flow of 5,000 ml/min (83 ml/s) was applied as the first boundary condition at the pulmonary trunk [solution of the full lung model resulted in a delivery of 2,523 ml/min (42 ml/s) to the right lung], and a left atrial pressure of 5 mmHg was applied as the outlet boundary condition. Solutions were obtained in the supine posture at FRC, the lung volume at which the majority of the published ASL studies have been performed (2, 4, 16, 24, 26, 29, 32), with the direction of gravity acting on both the fluid and on the tissue in the model to mimic that in the supine posture. 1D blood flow predictions were obtained within the lung model via solution of Poiseuille resistance, conservation of mass equations, and a microcirculatory model [further details of the model methodology and validation can be found in (11)]. Blood within the larger vessels was assumed to be Newtonian; however, in the microcirculatory vessels the shear-thinning properties of blood are accounted for. Solutions provide a prediction of steady-state blood flow, pressure, and vessel radius throughout the network. Predictions within the full pulmonary circuit model have been validated against measurements of blood flow distribution and pulmonary vascular resistance across the pulmonary circuit; details can be found in (11).

ASL signal calculation.

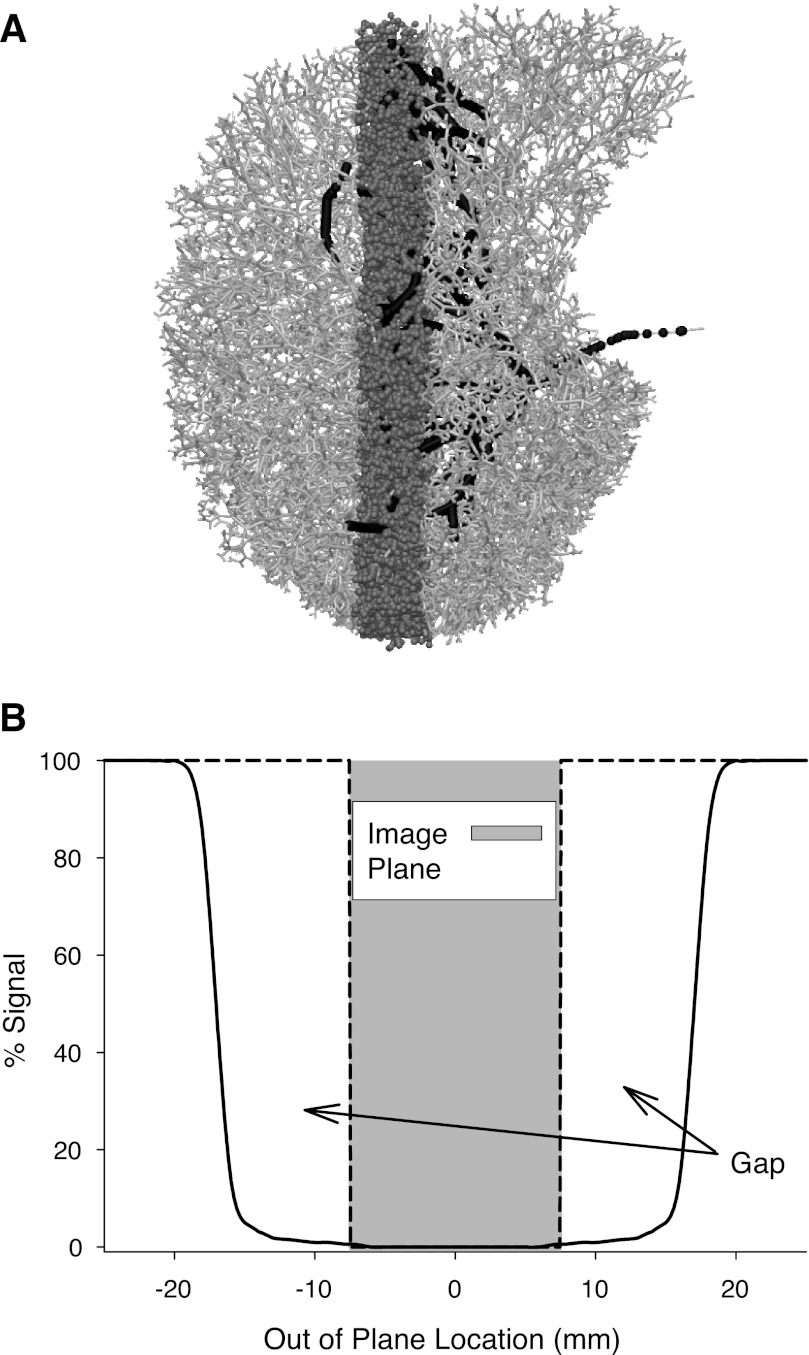
After obtaining the blood flow solution, a series of postprocessing steps was applied to predict the ASL signal using a time reverse approach. Given the vascular model (Fig. 1A), with branches distributed in 3D space and the predictions of blood velocity within each vessel, the following steps were applied.

Fig. 1.

Illustration of the time reverse calculation method used to predict arterial spin labeling (ASL) signal. A: right lung model, arterial vessels illustrated in light gray in an axial projection of a sagittal image plane shown in darker gray. Black points illustrate the arterial blood within the imaging plane 1 s prior to image acquisition. B: characterization of the labeling profile based on a typical inversion band taken from a Bloch equation simulation of the inversion plane used in an ASL experiment (26). Image plane extends to ±7.5 mm (a total thickness of 15 mm) whereas the inversion plane is wider (∼30 mm). An ideal inversion plane is illustrated with the black dashed line and would exactly match the boundaries of the image plane.

1) The location and thickness of the image plane was defined and all arterial, venous, and capillary blood within this plane at the time of imaging was identified (displayed in mid-gray in Fig. 1A);

2) For a given time delay (representative of the time between tagging and image acquisition), the blood velocity solution (calculated at model nodes—a node corresponds to either a bifurcation point or a point along a given vessel's 1D centerline) for each element of blood¹ was used to determine the location of the blood at the time of tagging (shown as the black vessels in Fig. 1A). Note that the simulation provides a steady time-averaged flow solution. Thus changing the time delay in this step is the equivalent of changing the volume of blood delivered by one systolic ejection, the cardiac stroke volume. In practice the ASL experiment is performed to capture the effects of one systolic ejection.

3) Depending on the location of the blood at the time of tagging, the percent labeling of each blood element was determined from the shape of the inversion pulse used in the ASL experiment (Fig. 1B). Blood fully outside the inversion band contributes 100% signal in the ASL image, whereas blood within the inversion band contributes signal that is defined by its out-of-plane position and the shape of the inversion band shown in Fig. 1B (i.e., if the blood is located near the edge of the inversion profile it will be only partially inverted, and in the ASL difference image this blood will contribute a signal less than 100%, and blood that is entirely within the inversion plane at the time of tagging contributes 0%).

4) The ASL signal within the image plane was calculated as the absolute signal (i.e., ml of fully tagged blood).

5) For the purposes of comparison, acinar blood delivered was defined as all blood exiting the terminal arterioles that lie within the image plane (i.e., blood delivered to the capillary bed within the image plane).

In these simulations we explicitly excluded the effect of T1 decay on the MRI signal. Doing so permitted us to examine effects that correspond to ASL simulations covering the equivalent of multiple systolic ejections to permit a full examination of the venous contribution to the signal. However, in reality T1 decay limits ASL in the lung to 1 (or at most 2) systolic ejection periods and the derived estimates of perfusion must correct for this decay.

Assessing the effect of the gap.

The effect of the gap was determined by comparing the signal resulting from the simulation described above with a simulation in which the shape of the inversion band matched that of the imaging plane (the dashed line in Fig. 1B). In that ideal case, any blood outside the image plane at the time of tagging receives a perfect 100% labeling and any blood within the plane receives 0% labeling.

Conduit vessels and perfusion.

The contributions to the total ASL signal from conduit vessels and true perfusion were calculated using a combination time-forward and time-reverse approach. Each labeled element of blood within the imaging plane at the time of imaging, and with the ASL signal as defined in ASL signal calculation, was assigned to one of three categories based on the following criteria.

For a blood element within the arterial network at the time of imaging: 1) if the downstream capillary network for which this blood element was destined lies within the imaging plane, this element was considered perfusion; 2) if the downstream capillary network for which this blood element was destined lies outside the imaging plane, this element was considered arterial conduit signal.

For a blood element within the capillaries at the time of imaging: all labeled capillary blood was counted as perfusion. Blood in a capillary must have come from the arterial network, and so the signal is that determined from ASL signal calculation.

For a blood element within the venous network at the time of imaging: 1) if the blood was in the arterial network at the time of tagging then this element was considered perfusion (because it must have passed through a capillary bed). 2) All other venous blood was considered venous conduit signal.

Image plane location.

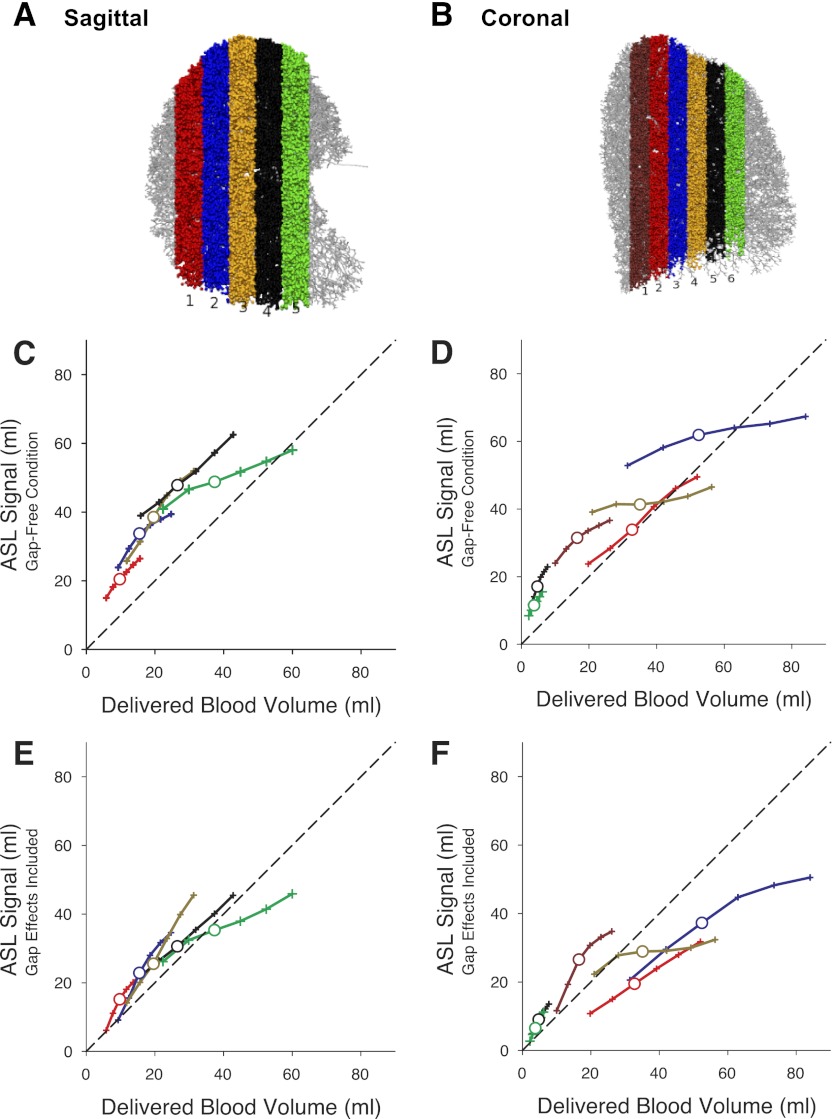
A typical ASL implementation [as in references (2–4, 19, 23, 26, 32)] uses 15-mm-thick image planes and has a gap that is up to 15 mm thick on both sides of the image plane. Analysis was performed in both the sagittal (5 planes) and coronal (6 planes) planes within adjacent, nonoverlapping 15-mm-thick planes (illustrated in Fig. 2, A and B, respectively). These planes covered >80% of the total right lung volume. Each plane was considered as an independent simulation, matching the imaging of single planes seen in the experimental situation [e.g., (3, 19, 26, 32)]. A typical time delay between tagging and imaging is one systolic ejection period (∼1 s).

Fig. 2.

Location of the image planes (A and B). Observed ASL signal from a given image plane plotted as a function of arterial blood delivered to that plane in the absence of a gap is plotted in C and D. ASL signal observed in the presence of a gap as a function of arterial blood delivered to the plane is plotted in E and F. Larger symbols in C–F show the results for a typical total arterial blood delivery of 83 ml (corresponding to a cardiac output of 5 l/min at 60 beats/min). Small symbols on each line show the simulation when the cardiac output was increased (to 8 l/min maximum) or decreased (to 3 l/min minimum) from the reference condition of 5 l/min in steps of 1 l/min. In the sagittal plane, the ASL signal when the effect of the gap is included was 64–74% of the possible signal and there was little effect of the position of the image plane location. In the coronal plane the observed ASL signal when including the effect of the gap is more variable ranging from 53 to 84% of the gap-free condition with the most posterior plane (coronal-1) having the least signal loss.

Reducing the conduit vessel contribution to the ASL signal.

Using the known spatial distribution of the blood elements in the image plane and their known ASL signal intensity, we constructed model maps by assigning all nodes within the image plane to a voxel based on their x-y position and based on a voxel size of 1.5 × 3 mm (image plane thickness 15 mm, therefore voxel volume = 67.5 mm³) (3). In cases in which more than one node was inside a specific voxel, we added their contributions to the ASL signal. In cases where the node contributed more ASL signal than the voxel volume (meaning that in reality this vessel would span multiple voxels), we assigned multiple voxels at the same spatial location to that node such that the total ASL volume delivered matched the simulations, thus a large conduit vessel might comprise several completely filled voxels and one partially filled voxel. We then eliminated the highest intensity voxels in the model map in 5% steps starting from the uppermost value of the intensity histogram. At each step the corresponding apportioning of the ASL signal between the three vascular compartments was recalculated based on the nodes remaining after the application of the threshold.

To further assess the effects of eliminating the signal contributions from the conduit vessels, we constructed maps of the distribution of blood flow in 20-mm-thick strips of the right lung of the model running either from medial to lateral in coronal planes or from posterior to anterior in sagittal planes. In this manner every strip runs from apex to base of the lung, and mimics prior studies [e.g., (27, 32, 36)]. For the purposes of brevity we present graphical data for sagittal planes, as these directly compare to prior published studies and encompass a gravitational gradient in blood flow distribution [e.g., (22, 27, 32)] and simply refer to the corresponding data from coronal planes. These distributions of blood flow, with and without the effect of the conduit vessels, were compared with the distribution of delivered blood from the arteriole outflow in the model. In the same fashion the effect of the gap on the distribution of ASL signal was assessed from simulations with and without the gap effect (see Assessing the effect of the gap).

Heterogeneity of pulmonary blood flow.

Because the nodes that comprise the model do not have a spatial extent (vessels are represented as 1D lines rather than 3D cylinders), the structure of the blood vessels in this model map is not realistic in a geometrical sense, and this precludes accurate calculation of measures of heterogeneity at the scale of the imaging parameters typically used in prior studies (1.5 × 3 × 15 mm) (1, 5, 17, 18, 25, 30). To assess heterogeneity in the face of this limitation we took the now filtered data set (described above in Reducing the conduit vessel contribution to the ASL signal) and, to appropriately simulate the actual ASL experiment, removed all voxels with a value <5% of the theoretical maximum ASL signal. This mimics the elimination of negative voxels in actual ASL images that result from the noise-dominated region with very low signal (18). We then smoothed the remaining data to a voxel size of 10 × 10 × 15 mm. This averaging approach largely eliminates cases in which ASL signal exceeds voxel volume, the basis of the nonrealistic problem described above. We then calculated relative dispersion (RD; standard deviation of the distribution divided by the mean) as our index of heterogeneity, because this has been used extensively in previous studies (1, 5, 17, 18, 25). RD was calculated from both the blood delivered from the terminal arterioles in the model (considered the ground truth) and from the calculated ASL signal. It should be noted that because RD varies with voxel size (14) our use of large voxels results in values for RD that are smaller than those in the prior publications. To assess the validity of these values we introduced an arbitrary modification to the model by randomly occluding ∼50% of arterial vessels with a radius of 5 mm. This modification was chosen as a simple perturbation to the model that would be expected to increase RD and thus permit us to assess changes in RD in both blood delivery from terminal arterioles and in the ASL signal.

RESULTS

Figure 2 shows the ASL signal resulting from different acinar blood delivery volumes for different values of cardiac output ranging from 3 to 8 l/min, which might be alternatively thought of as stroke volumes ranging from 50 to 133 ml at a heart rate of 60 beats/min. Results are shown for both the ideal (gap free) condition in the sagittal and coronal planes (Fig. 2, C and D, respectively) and for the realistic (gap included) condition (Fig. 2, E and F).

Effect of the gap.

The overall effect of the gap was to delay the arrival of tagged blood to the imaging plane. As a consequence, a lesser amount of tagged blood is delivered to the imaging plane than would otherwise be the case (in essence the first blood to be delivered to the image plane during the RR interval is untagged or partially tagged because it was within the gap outside the image plane). Fig. 2, C and D, presents the ASL signal in a gap-free condition plotted as a function of delivered blood volume to the image plane for cardiac outputs from 3 to 8 l/min. Fig. 2, E and F, shows the ASL signal resulting when a gap is included in the simulation. It can readily be appreciated that the gap reduces the ASL signal in all image planes, although with some variability in the magnitude of the reduction depending on image plane location.

Effect of image plane position on the ASL signal.

To assess the effect of image plane position on the ASL signal and how the gap affects that, we calculated the ASL signal as the percentage of the gap-free condition across multiple image planes. The effect of the gap is larger at low values of delivered blood volume as expected. At a typical total delivered blood volume of 83 ml (a cardiac output of 5 l/min at 60 beats/min) the effect of the gap is to reduce ASL signal in the sagittal plane to between 64 and 74% of the gap-free condition. In the coronal plane the effect was more variable, ranging from 53 to 84%, with the smallest effect being seen in the most posterior image plane (signal in the presence of gap 84% of gap free).

Contribution of the conduit vessels and the venous circulation.

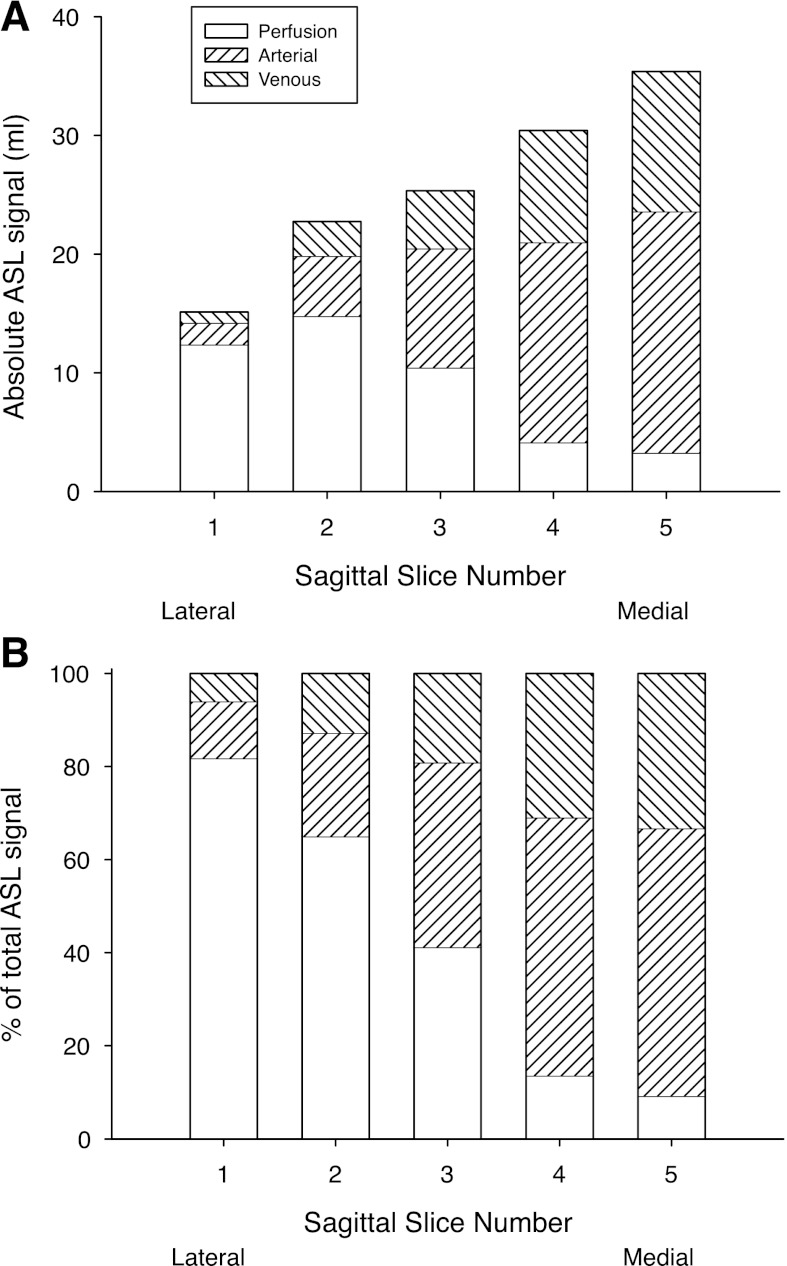
The partitioning of the ASL signal is shown in Fig. 3 for the sagittal plane and in Fig. 4 for the coronal plane. In both cases the results are presented as absolute ASL signal, which permits the effects of different image plane locations on the amount of blood delivered to the image plane to be readily observed, and how that delivered blood is apportioned in the ASL signal as recorded. For clarity, the data presented are for a time delay between tagging and imaging of 1 s, corresponding to a cardiac stroke volume of ∼83 ml (of which 42 ml enters the right lung). We chose this particular time delay because it is most representative of how the ASL experiment is conducted in practice in which one systolic ejection is captured.

Fig. 3.

A: absolute ASL signal in each of the 5 sagittal image planes studied. Location of the image planes are shown in Fig. 2A. B: fraction of the observed ASL signal (which necessarily adds to 100%) in each image plane resulting from the 3 blood compartments, arterial, venous, and true perfusion (blood delivered to or destined for capillary beds contained within the image plane).

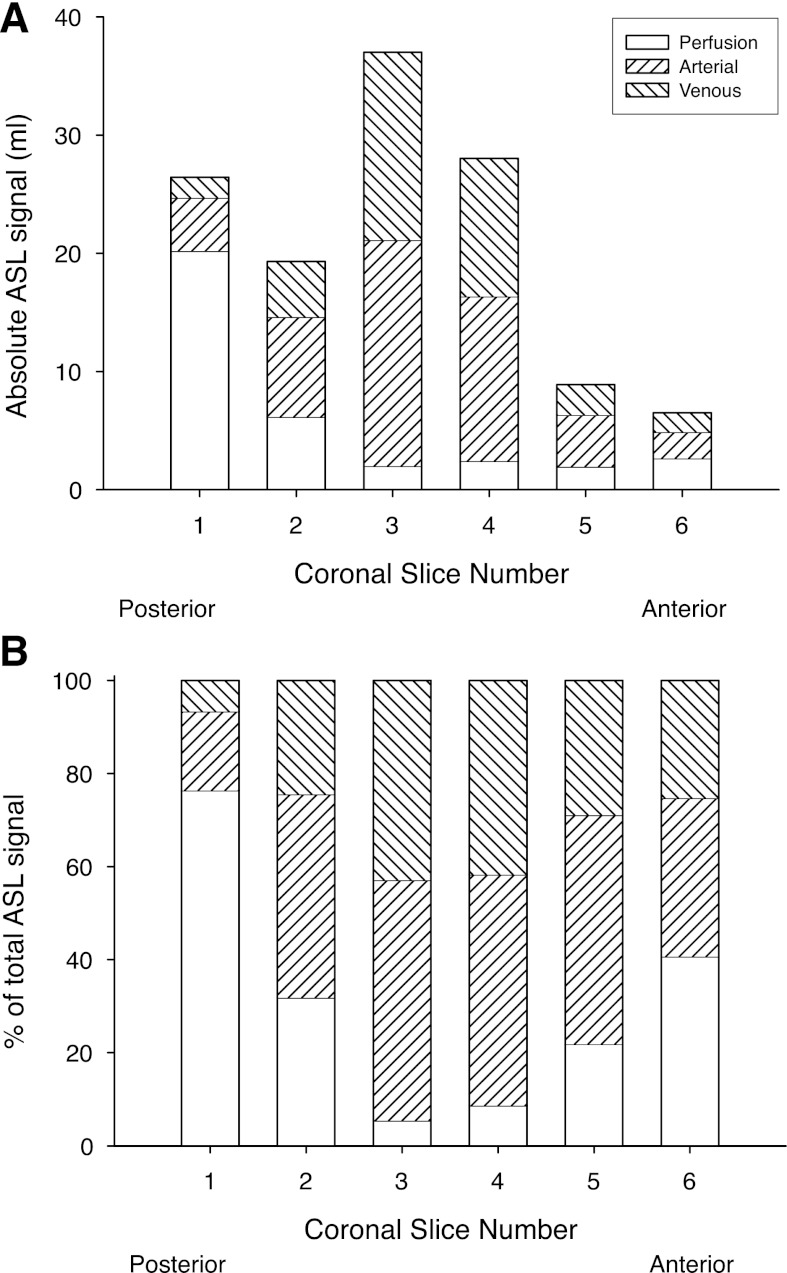
Fig. 4.

A: absolute ASL signal in each of the 6 coronal image planes studied. Location of the image planes are shown in Fig. 2B. B: fraction of the observed ASL signal (which necessarily adds to 100%) in each image plane resulting from the 3 blood compartments, arterial, venous, and true perfusion (blood delivered to or destined for capillary beds contained within the image plane).

The results in Fig. 3A show a clear progression in overall ASL signal which is low in the most lateral image plane (sagittal-1) and steadily increases moving to more medial image plane locations [sagittal-5 being the nearest to the midline (see Fig. 2A)]. There is a similar progression in the amount of ASL signal that comes from conduit vessels (arterial and venous) that is maximal in the most medial image plane. Perfusion, in contrast, increases as the image plane moves from medial to lateral, with the exception of a slight fall in the most lateral image plane studied. When expressed as the percentage to the total ASL signal (and where the sum of the perfusion, arterial, and venous contributions is by definition 100%) in cases in which the image plane is medial, signal from the conduit vessels dominates the overall ASL signal, whereas in the lateral image planes, perfusion is the dominant source of signal.

Figure 4 presents comparable results to those in Fig. 3, but for image planes in the coronal orientation. In the coronal orientation the image plane with the largest overall ASL signal is coronal-3 (see Fig. 2B), which is that containing the majority of the vessels emanating from the pulmonary trunk in the hilum (Fig. 4A). As was the situation in the sagittal orientation, the image planes that contain the majority of the large conduit vessels also have the greatest conduit signal portion of the ASL signal (Fig. 4B), with the proportion of the signal that is perfusion rising as the image plane is moved away in either the anterior or posterior direction. With the exception of the image planes that include the pulmonary trunk (coronal-3 and -4), there is a systematic reduction in ASL signal moving from the most posterior (gravitationally dependent) image plane (coronal-1) to the most anterior (gravitationally nondependent), consistent with the expected gravitational gradient in blood flow in the supine posture (26).

The venous contribution to the signal from overall conduit vessels (arterial + venous) is remarkably constant across image planes in the sagittal orientation, with the percentage of the conduit vessel signal arising from the venous circulation being 35 ± 2% (range 33–37%). In the coronal orientation the venous contribution was slightly higher 39 ± 7% (range 28–46%) and varied more between image planes with coronal-3 and coronal-4 (those image planes encompassing the pulmonary trunk and main pulmonary veins) being the highest.

Reducing the conduit vessel contribution to the ASL signal.

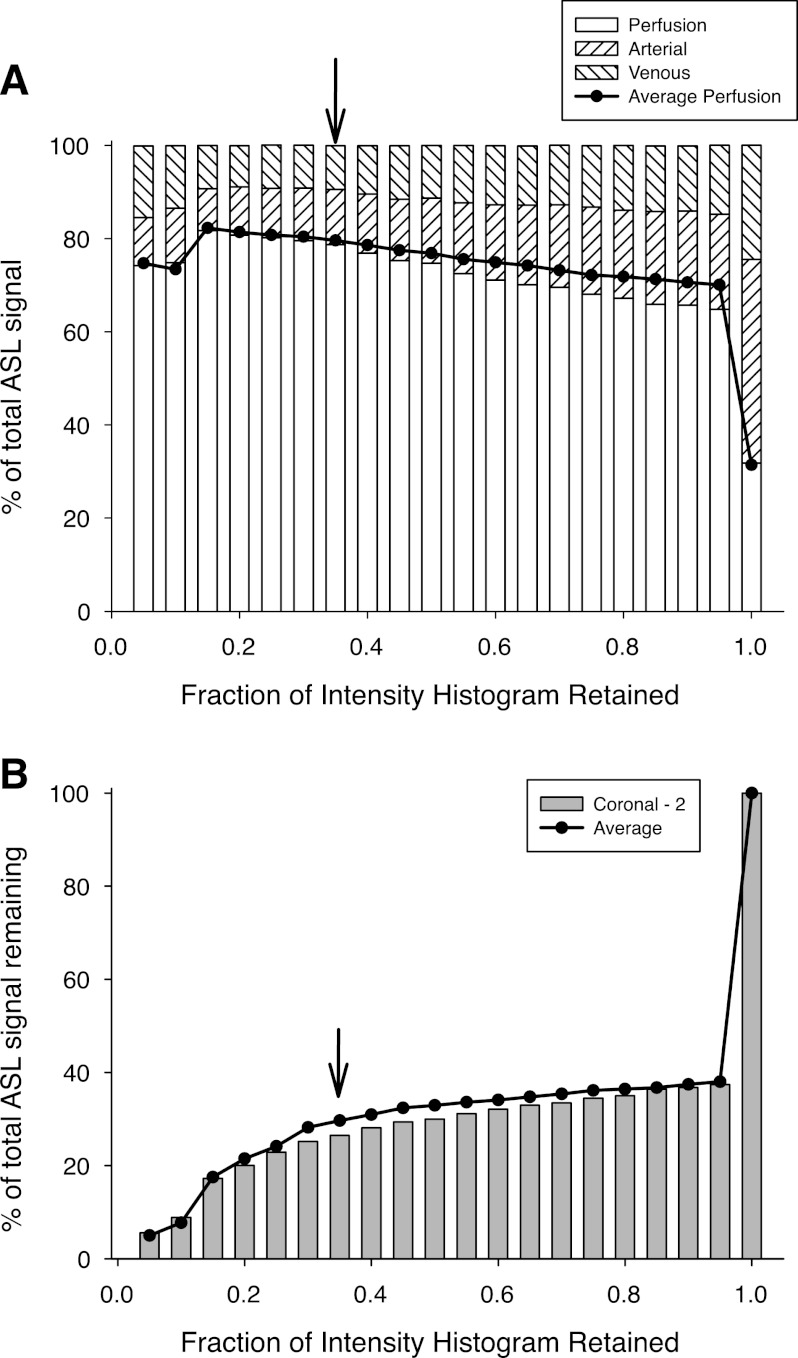
Figure 5A shows that as the highest intensity voxels (those that encompass the conduit vessels) are removed from the model map, there is an initial abrupt increase in the perfusion fraction that remains, followed by a more gradual rise in perfusion fraction as the cutoff intensity is further reduced. This is accompanied by an overall reduction in the total ASL signal that remains (Fig. 5B). Below an intensity cutoff of ∼0.3, there is a more rapid reduction in the loss of ASL signal accompanied by an increasing degree of variability in the perfusion fraction, likely reflecting the elimination of signal from the main peak in the intensity histogram, which includes elements of ASL signal attributable to perfusion. The arrow shows the 35% cutoff used in subsequent calculations.

Fig. 5.

A: bars show the partitioning of the ASL signal between the 3 vascular compartments (see Reducing the conduit vessel contribution to the ASL signal for details) for coronal plane 2, plotted as a function of the amount of the intensity histogram remaining. Bar on the extreme right in which all of the histogram remains is the same as that for coronal image plane 2 in Fig. 5A. As higher intensity voxels are removed from the histogram the proportion of the remaining signal that results from perfusion is progressively increased until most of the signal has been removed. Line is the average perfusion fraction across all 6 coronal image planes. B: percentage of the ASL signal that remains as the highest intensity voxels are eliminated with the bars showing data from coronal image plane 2. Line is the average value across all 6 coronal image planes. Following an initial abrupt drop there is a slow reduction, which subsequently accelerates when the intensity cutoff is reduced below 0.35. On the basis of the balance between maximizing the fraction of the ASL signal that results from perfusion, while retaining an adequate amount of signal, a cutoff at 0.35 of the maximum intensity is suggested as indicated by the arrows in the figures.

Blood flow distribution and heterogeneity with intensity cutoff.

Figure 6 shows the vertical distribution blood flow in 20-mm-thick iso-gravitational strips in the lung for sagittal planes 1–5 (Fig. 6, A–E, respectively; see Fig. 2A for plane locations). In each panel the vertical distribution of blood delivered from the terminal arterioles (perfusion) is shown by the solid black line, the dashed black line shows the total ASL signal, and the gray line the ASL signal following removal of voxels with an intensity >35% of maximum. Note that Fig. 6, A–C, shares the same scale but that this differs from Fig. 6, D and E. As in previous publications [e.g., (27, 32)] the vertical axis is used to show height above the most dependent lung region. It can be readily appreciated that conduit vessel signal varies greatly both between image planes and within a given image plane. Furthermore, although the 35% intensity cutoff serves to bring the ASL signal closer to blood delivered in planes 1–3, it results in a substantial overcorrection in planes 4 and 5.

Fig. 6.

Vertical distributions of blood delivered from terminal arterioles (acinar flow, solid black lines), total ASL signal (black dashed lines), and ASL signal following the removal of all voxels with an intensity >35% of maximum (solid gray lines). A–E: correspond to sagittal image planes 1–5 respectively. Scale for A–C is the same, as is the scale for D and E, but these are different from each other. Data were collected into 20-mm-high strips (each strip is iso-gravitational in orientation). Note that in A–C, the intensity filter results in a reasonable agreement between acinar flow and ASL signal. However, in the more medial image planes (D and E) the result is a substantial overcorrection as a result of a very high proportion of in-plane flow in these locations (see Blood flow distribution and heterogeneity with intensity cutoff for details).

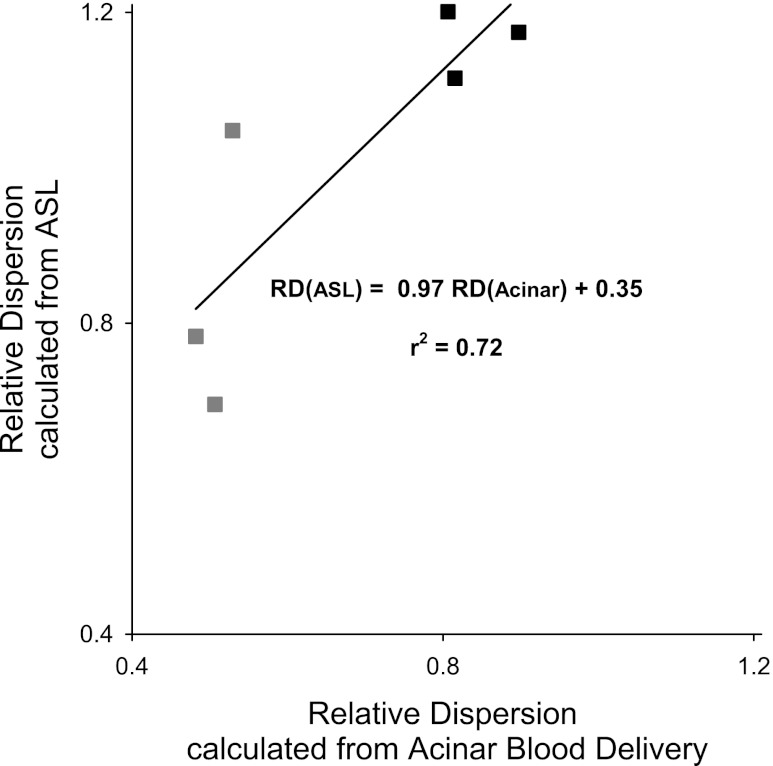
Figure 7 shows the RD calculated from the distributions of terminal arteriole blood delivery and from the ASL calculation plotted as a function of each other. In the latter case, the data were intensity filtered to remove all voxels with a value >35% of maximum (conduit vessels) and all voxels with an intensity < 5% (noise). The RD data are for a voxel size of 10 × 10 × 15 mm. The results are shown from sagittal planes 1–3 for both the case of an unperturbed blood flow distribution (gray symbols) and following the artificial perturbation of the flow distribution (black symbols, described in Heterogeneity of pulmonary blood flow in methods). It can be seen that the RD of delivered blood was largely independent of plane location (as evidenced by the tight clustering of the points at the lower end of the x-axis), and was increased by the perturbation. RD calculated from the filtered ASL distributions is different in magnitude from that of acinar flow, but well-correlated with it with a r² of 0.72.

Fig. 7.

Relative dispersion (RD) of the filtered ASL blood flow distribution plotted as a function of RD of the acinar flow distribution for sagittal image-planes 1–3 both with (black symbols) and without a perturbation (gray symbols) to the underlying pulmonary blood flow distribution (see Blood flow distribution and heterogeneity with intensity cutoff for details). Although the values of RD are different in the 2 methods they are well-correlated with each other.

DISCUSSION

ASL in the lung.

ASL was originally developed for measurement of blood flow and its distribution in the brain (9) and has been extensively used in that setting. It has subsequently been utilized in other organs, and in the lung one particular implementation (3) has been used extensively in numerous physiological studies (2, 4, 16, 23, 24, 26, 29, 32). ASL depends on the ability of MRI to produce a short-lived tag of the blood flowing into the organ, with the imaging of the distribution of the tagged blood at some short time interval later. In essence, ASL can be thought of as a microsphere experiment in which the microspheres subsequently disappear, permitting repeated studies as required (9). However, ASL, as implemented in the lung, has characteristics that are distinct from microsphere experiments that must be considered.

First, in the cerebral circulation in which the tagging region is spatially distinct from that of the image plane, tagging can be performed upstream of the imaging plane, ensuring that the signal subsequently recorded is indeed arterial blood delivery. ASL as typically implemented in the lung does not have this characteristic. As implemented by Bolar et al. (3), ASL in the lung uses a tag plane that overlays the imaging plane. Thus ASL reflects the delivery of blood that is outside the tagging plane at the time the tag is applied and that is subsequently located in the image plane at the time of imaging. Given the interwoven and similar nature of the pulmonary arterial and pulmonary venous circulations it is therefore expected that there is a contribution of the pulmonary venous flow to the measured ASL signal; however, to date there has been no quantification of this contribution. Second, to ensure a complete tag of the blood across the imaging plane, the tagging plane is made somewhat thicker than the imaging plane, which in essence introduces a gap that blood must cross to reach the imaging plane (see methods and Fig. 1 for a description of this). Although considering the effect of a gap in a single vessel is relatively straightforward—it simply produces a small delay before signal is observed (3)—the effect of a gap in a geometry as complicated as the pulmonary circulation is less intuitively obvious. Finally, when considering the treelike structure of the pulmonary vasculature, the position of the imaging plane within the thoracic cavity might reasonably be expected to produce different “efficiencies” of the ASL experiment, where a variable percentage of the potential ASL signal might be expected to be seen depending on whether the image plane encompasses the large pulmonary vessels originating in the hilum or whether the plane is solely within the lung periphery. As the physiological studies have moved from single plane studies (26, 32) to multiple plane studies (23), consideration of this latter effect becomes germane.

Addressing the key questions using a detailed network flow model.

Addressing the four key questions that arise from the nature of ASL in the lung (the effect of the gap, the effect of image plane location, the contribution from the conduit vessels, and how much of that comes from the venous circulation) is difficult if not impossible in an experimental setting. Although some studies might be possible in animal models, the vascular geometry differs greatly between species, and this has the potential to confound the results. Instead we chose to use the model of the pulmonary circulation developed by Burrowes and colleagues (6–8, 10, 11), permitting us to interrogate the arterial, capillary, and venous compartments as required and to consider the effects of image plane location and orientation as desired.

Effect of the gap.

Bolar (3) showed that the effect of the gap formed by the inversion band being thicker than the imaging plane on a single vessel was a small delay introduced by the need for blood to cross the gap before being registered in the image. Figure 2 addresses the effect of the gap on the total ASL signal by considering a case in which the gap is zero (the image plane has zero signal following the tag, and all regions outside the image plane have 100% signal, a condition the electronics of the MRI scanner cannot create). It can be seen by comparing Fig. 2, C and E, and Fig. 2, D and F, that, as expected, the effect of the gap is to reduce the observed ASL signal for a given blood delivery. This reduction varies in magnitude depending on the image plane selected. At low blood delivery volumes (corresponding to either low cardiac output or short delay times) the gap prevents much of the ASL signal from reaching the image plane. As delivered blood volume increases the effect of the gap becomes smaller.

In the sagittal orientation there is a remarkable consistency of the effect of the gap across image planes. For a typical stroke volume of 83 ml (corresponding to a cardiac output of 5 l/min at 60 beats/min), ASL signal was reduced to between 64 and 74% of the gap-free value across all image plane locations (Fig. 2, A, C, E). There is, however, more variability in the effect of the gap in the coronal orientation (Fig. 2, B, D, F) where the ASL signal is reduced to between ∼53% and ∼84% depending on image plane location. It is notable that the effect of the gap is smallest in image plane coronal-1, the most posterior image plane (where only ∼16% of the signal is lost), and largest in image planes coronal-5 and coronal-6 (up to a 47% signal loss). Thus, in image plane coronal-1, which has the highest absolute ASL signal of image planes without a predominance of large conduit vessels, the total ASL signal is well captured even in the presence of a gap, likely a reflection of the higher blood flow in this gravitationally dependent location.

Contribution of the conduit vessels.

Although the effect of the gap is relatively invariant across imaging planes, the same is not true of the contribution of the conduit vessels to the total ASL signal. Figures 3 and 4 present the results for the ASL signal broken down into the contributions arising from arterial and venous conduit vessels and that resulting from perfusion for the sagittal and coronal orientations, respectively. In this context, perfusion, which we define as tagged blood delivered to, or destined for, capillary beds within the image plane, can be considered the equivalent of a perfusion measurement by microspheres in which the microspheres lodge only in the capillary bed [e.g., (13, 15)] or by use of a single pass tracer such as a very low solubility dissolved gas that evolves into the alveolar air space [e.g., (31)]. The means by which we assigned blood to each of these three compartments are defined in the section, Conduit vessels and perfusion in methods.

In the sagittal orientation (Fig. 3A) there is a clear and steady progression in total ASL signal moving from a maximum in the most medial image plane (sagittal-5) to a minimum in the most lateral (sagittal-1). Given that such a transition between image planes moves the vessels with each plane further from the pulmonary trunk, which combined with a decreasing number of large conduit vessels as the image plane becomes more peripheral and with no expected effect of gravity moving between image planes, this is largely what would be expected. In the coronal orientation (Fig. 4A) the picture is more complicated. In this orientation the pulmonary trunk and the associated major branch vessels lie near the middle of the collection of image planes, coronal 3–4. These image planes show the largest absolute ASL signal, consistent with the presence of these vessels. The surrounding image planes show a steady progression in absolute ASL signal from plane coronal-6, the most anterior, which has the lowest ASL signal, to coronal-1 (the most posterior), which has the highest ASL signal of the noncentral image planes. This progression is consistent with the expected gravitational gradient in blood flow that has long been observed (37) and the zone model of perfusion (38).

The apportioning of the ASL signal between the vascular compartments (Figs. 3B and 4B) largely depends on the presence or absence of the conduit vessels. In the image planes in which the large conduit vessels are present (sagittal 4–5, coronal 3–4) the ASL signal is dominated by the arterial and venous vascular signals such that the ASL signal from perfusion is less than 20% in all these planes. This is likely both a reflection of the fact that a considerable proportion of the lung volume in these regions is composed of conduit vessels and that the ASL signal derived from a vessel completely filled with tagged blood is high compared with that in a largely air-filled region of the lung involved in gas exchange.

The more peripheral the image plane becomes, the more the contribution of perfusion to the ASL signal increases (see Fig. 3). In the sagittal plane the two most lateral image planes simulated (sagittal 1–2; Fig. 3B) the ASL signal is dominated by perfusion. Similarly in the most posterior coronal image plane (coronal-1, Fig. 4B), perfusion dominates. However, in the coronal orientation in planes that might reasonably have been thought to be largely beyond a large influence of the conduit vessels (coronal-2, -5, -6) although perfusion is a substantial fraction of the total ASL signal, more than 50% of the signal is still derived from conduit vessels.

The relatively low perfusion fraction in many image planes is an important finding in the context of studies of pulmonary blood flow and in particular perfusion using ASL. It suggests that although the total ASL signal is reasonably well characterized given a relatively constant effect of the gap across image planes (Fig. 2), the same cannot be said for perfusion (blood that is delivered to, or destined for, the capillary bed in the image plane). If ASL is to be used for perfusion measurements, then the effect of the conduit vessels must be accounted for.

Contribution of the venous circulation.

Despite the name of arterial spin labeling as implemented in the lung there is a contribution from the pulmonary venous circulation to the ASL signal. The results in Figs. 4 and 5 permit the calculation of the proportion of the conduit vessel signal that results from the venous circulation. For most image planes, except those coronal planes that encompass the pulmonary trunk, the venous signal is 30–35% of the total conduit vessel signal, which is consistent with the blood volume distribution that exists within the model, and the relative similarity of the arterial and venous conduit vessel vascular trees. Thus it seems likely that the ASL method includes signal from both arterial and venous vascular compartments and that for the most part this is apportioned in the same ratio as the actual volumes of these compartments.

Correcting the ASL images to address the effects of conduit vessels.

The substantial, and at times dominant, contribution of the conduit vessels to the ASL signal raises the question of how to adequately deal with them. Although the approach of using more peripheral image planes is helpful in this context, even the most peripheral planes we simulated showed an appreciable signal from conduit vessels (often >20%). Given the single 2D image plane implementation of the ASL acquisition and given the limited ability to spatially resolve structures within the lung, it is impractical to eliminate the conduit vessels through some form of vascular-tree growth and subsequent elimination approach. Henderson et al. (19), reasoning that the conduit vessels would for the most part be the highest intensity voxels in the ASL image, proposed an approach in which a cutoff threshold above the peak of the intensity histogram provided an approach that minimized the effect of the “large vessels” and yet which preserved the characteristics of the log-normal distribution of the intensity histogram.

Figure 5 examines the effect of a systematic elimination of the highest intensity voxels in model maps, a process matching that suggested in Ref. 19. As the very highest intensity voxels are eliminated there is an abrupt rise in perfusion fraction (Fig. 5A) and corresponding fall in signal (Fig. 5B). The abruptness of this transition is to some degree an artifact of the process used to generate the model maps on which this calculation is based. In that process, all nodes were assigned to voxels based on their in-plane location in the model and total signal from each voxel calculated. However, for nodes that exceeded the actual voxel volume, we divided these into as many fully filled voxels as were required to ensure mass balance was maintained. This results in a population of voxels that are fully filled, whereas in a real image, the adjacent voxels are not truly independent of each other. The effect is that cutting off only the upper 5% of the intensity histogram produces an abrupt change, whereas in reality we would expect a more gradual rise in perfusion fraction as the upper part of the histogram is removed.

Previous examination of the removal of the upper part of the intensity histogram by Henderson et al. (19) showed that provided the main peak was preserved, there was virtually no effect on parameters of the log-normal distribution and only modest effects of other dispersion indices such as relative dispersion. That study suggested an intensity cutoff well below 50% of maximum was appropriate. These simulations place that suggestion on firmer ground, suggesting that a cutoff at ∼35% results in a high perfusion fraction (Fig. 5A) while preserving most of the ASL signal (Fig. 5B). Cutoff values below ∼30% result in a steep reduction in ASL signal consistent with removal of voxels dominated by true perfusion. A cutoff of 35% results in the elimination of on average 4.2% of the total voxels in the sagittal plane and 4.6% in the coronal plane, and so this retains the vast majority (>95%) of the total number of voxels in the remaining image. This result emphasizes that although a significant fraction of the total ASL signal in an image is due to conduit vessel signal, this signal tends to be in a relatively few bright voxels that can be identified and removed.

Although data for other image planes are not shown, the 35% cutoff point was largely independent of image plane position and orientation, suggesting it is a reliable point that can be applied across different experiments with confidence. The effect of this intensity filtering is to increase perfusion fraction in all image planes such that it dominates the image, with the average perfusion fraction across all coronal planes rising to 80% (range 70–94%) and across all sagittal planes to 78% (range 60–91%).

Blood flow distribution changes with intensity cutoff.

Figure 6 summarizes the key findings pertaining to the distribution of ASL signal for the sagittal plane simulations. These results divide themselves clearly into two groups based on the degree to which conduit vessels contribute to the overall ASL signal. In planes 1–3 (Fig. 6, A–C) the reduction in ASL signal following filtering is modest and comparable to what would be expected based on the observed partitioning of ASL signal between perfusion and conduit vessels (Fig. 3). Removing voxels with high intensity results in a reduction in ASL signal so that it more closely approximates perfusion. In the most lateral image planes, ASL signal remains above perfusion, most notably in dependent regions of the lung with a higher blood flow. In these regions, residual conduit vessel signal from blood vessels smaller than the voxel size serves to raise voxel intensity, but not to a level exceeding the 35% cutoff threshold, and so results in an elevated ASL signal.

The situation is clearly different in medial image planes (sagittal planes 4 and 5, Fig. 6, D and E). In these locations the ASL signal is dominated by signal from the large conduit vessels (Fig. 3). In these planes an intensity cutoff of 35% results in a substantial overcorrection of the ASL signal such that the filtered ASL signal is considerably less than arteriolar delivery. When we varied the intensity cutoff from our chosen 35%, there were only very minor effects on the level of agreement with ASL signal remaining below perfusion, a result consistent with the flat nature of the perfusion contribution to the ASL signal over a wide range of intensity cutoff values (Fig. 5A). Furthermore, examination of the model shows that because of the geometry of the blood vessels in the medial image planes there is a dominant component of terminal arteriole blood delivery that results from in-plane flow at the time of the ASL tag. While in image planes 1 and 2 ∼60% of the blood exiting the arterioles was outside the tagging band at the time of the tag (and so delivers full ASL signal), this number falls to <10% for planes 4 and 5. Thus most of the blood exiting the arterioles in these image planes fails to receive a full tag. Image plane 3 is intermediate. Although not shown, a similar situation exists for coronal planes 3 and 4, the most central of these planes.

This result, especially when taken in conjunction with the very low fractional perfusion signal present in the most medial sagittal image planes (Fig. 3) leads to an important outcome of this study. ASL as currently implemented in the lung is an inappropriate technique to measure perfusion in image planes that are dominated by conduit vessels. There are two principal reasons for this. 1) The fraction of the overall ASL signal that comes from perfusion in these image planes is small, and so attempting to subtract out the confounding (and dominant) signal from conduit vessels is fraught with difficulty. 2) The degree to which perfusion results from in-plane flow in these image planes is high, and so the majority of that blood is not appropriately tagged in the ASL technique.

Gap effects on blood flow distribution.

In a manner analogous to determining the regional effects of the filtering algorithm on the ASL signal we calculated the effects of the gap by considering the filtered signal (as described above) both with and without the gap (see Assessing the effects of the gap in methods). As was the case with global effect of the gap (Fig. 2) the effect was a largely uniform reduction in ASL signal, which was independent of both image plane location and position within a plane. Given the uniform nature of this effect we have not included a figure on this topic.

Heterogeneity measured from ASL.

We set the ground truth for measuring RD as that resulting from blood exiting all terminal arterioles within the image plane. In the context of the model, all arterioles feed acini and as such this is a direct measure of acinar blood flow. RD was calculated on a scale of 10 × 10 × 15 mm for both the perfusion and the filtered ASL signal. To perform a realistic simulation of the actual ASL experiment, we also had to filter the low end of the intensity distribution. In this region the ASL signal is dominated by noise and this leads to the presence of negative values for some voxels (an unrealistic outcome), which are removed from the distribution (18). To mimic this we removed all voxels with intensity <5% of the maximum value with this cutoff chosen to be somewhat lower (and thus more conservative) than a cutoff that would be suggested by the typical signal-to-noise threshold seen in actual ASL images that is ∼13–14 (2).

The calculated values of RD in the sagittal plane from both the acinar flow distributions and the filtered ASL distributions both before and after the application of an arbitrary perturbation to the blood flow distribution are plotted as a function of each other in Fig. 7 for sagittal image planes 1–3 (excluding those planes dominated by in-plane and conduit vessel flow). Although the absolute values do not match (a consequence of residual conduit vessel signal following filtering from both the arterial and venous compartments, whereas acinar RD is exclusively from perfusion) in most cases experiments that use RD as a descriptor focus on the change in RD in response to an intervention (1, 5, 17, 25). As such, the fact that acinar flow RD and ASL RD are tightly correlated is important.

Limitations.

The model as implemented uses a steady flow solution, whereas blood flow in the lung is pulsatile. However, as implemented, the ASL experiment is carefully cardiac gated so that the tag occurs during diastole (when flow is minimum) and image acquisition occurs during the subsequent diastole (one cardiac cycle later) when flow is again minimum and when one cardiac stroke volume of blood has been delivered to the lung. Thus, by choosing a time delay in these simulations of 1 s, we simulated the same situation of a delivered blood volume of one stroke volume.

In using a model such as this we were careful not to draw conclusions that fall outside the capabilities of the model itself. As implemented, the vessels in the model are not a series of connected pipes but rather a spatially distributed series of 1D nodes connected with 1D lines. This results in nodes with blood volumes that are greater than the voxel volume in our imaging that we treated as a stack of voxels at a single node location, whereas in fact that node is spatially distributed along the actual vessel. Although our approach satisfies mass balance constraints, it does not adequately simulate the distribution of blood that would be seen in an actual ASL image, and for that reason we calculated RD using a smoothed data set. This, however, serves to reduce the values of RD, which is scale dependent. Furthermore, in testing the validity of RD we chose a relatively simple means of perturbing pulmonary blood flow in the model. This was not intended as a physiologically relevant simulation of some condition, but rather as a test case. As such, the actual changes in RD should not be attributed to those that might be expected in an actual physiological study.

Implications of these results on prior studies.

Some prior studies have focused on how pulmonary blood flow is distributed in the pulmonary vasculature (especially vertically), and it is appropriate to consider the implications of these results on those prior studies. In particular, Hopkins et al. (26) and Prisk et al. (32) examined the distribution of pulmonary blood flow in sagittal image planes covering the entire lung and in doing so included image planes with large contributions from conduit vessels. This raises the question of whether the results of these studies are invalid. Hopkins et al. (26) focused on the deformation of the lung caused by regional lung weight and how that deformation alters the interpretation of regional blood flow, the so-called Slinky effect. The arguments put forward in that paper remain valid as do similar arguments in the examination of the effects of lung volume on vertical blood flow distribution found in Ref. 23, because they focus on the effects of distortion of the lung due to the mass of blood in a region.

Other studies that focused on the effects of some intervention on pulmonary blood flow distribution such as the effects of hypoxic pulmonary vasoconstriction (2) and of the lingering effects of heavy exercise (4) remain valid. There may be some potential for slight alterations in the volume of blood within conduit vessels (either through constriction or dilation) that might serve to slightly skew the results, but these studies employed image planes that do not encompass great numbers of large vessels and in which examination of the frequency distribution of voxel intensities shows only a modest contribution from conduit vessels (19).

Other studies, or parts of studies, have focused on heterogeneity of blood flow [e.g, (2, 4, 24, 29)]. The results of this study suggest that provided the image planes used do not encompass large numbers of conduit vessels the conclusions remain valid. On the basis of the results of Henderson et al. (19), elimination of the highest intensity voxels (from actual ASL data in an image plane equivalent to the coronal-2 plane used in this study) to a cutoff of 50% reduced RD by 35%, and a cutoff to 25% reduced RD by 45%. Thus, although there is a reduction in the actual value of RD, this applies to all values of RD in the study, minimizing the consequences on the conclusions drawn in those studies. The results in Fig. 7 suggest that in prior studies, although the exact value of RD from ASL is not a reflection of the RD of acinar flow, the changes in both are well correlated.

Summary.

In summary, we used the previously developed in silico model of the pulmonary circulation to address some of the fundamental questions that surround the use of the ASL technique in the human lung. This modeling approach is likely the only means of addressing some of these questions, as experimental studies in humans to address such questions are impractical and animal studies bring with them the difficulties and uncertainties associated with different vascular geometries from those in humans. The results show that ASL as typically implemented in the lung, encompassing one systolic ejection, provides an estimate of arterial blood delivery that is 60–70% of the actual value, with this loss of signal due to gap effects (in which the inversion band is thicker than the imaging plane) being largely constant across different imaging planes. In contrast however, there is marked and important variation in the contribution of the conduit vessels (arterial and venous) that exist within an image plane to the overall ASL signal. Depending on the choice of image plane location and orientation, the fraction of the total ASL signal that is attributable to perfusion (tagged blood delivered to, or destined for, capillaries within the image plane) can vary from >80% to less than 10%. Those image planes that encompass the large vessels of the pulmonary trunk show the greatest contribution from conduit vessels, whereas those image planes in the lung periphery show the least. The contribution to the conduit vessel signal from the venous circulation is approximately in proportion to the relative blood volumes of the pulmonary arterial and venous vascular trees. To minimize the effects of the large vessels on the measurement of perfusion to an image plane, the simulations suggest that a threshold cutoff approach, where image voxels with an intensity >35% of the image maximum are masked out, can reduce the contribution of the conduit vessels to ∼20% of the total ASL signal so that the signal is then dominated by perfusion. However, in those planes in which conduit vessels dominate (medial for sagittal planes, central for coronal) the combined effects of a very low perfusion fraction and a significant amount of in-plane flow make such a correction impractical. As a result, studies that need to assess perfusion likely cannot be conducted in these planes using ASL as currently implemented in the lung. Finally, measurements of heterogeneity appear to be consistent in the presence of perturbations to the actual flow distribution, suggesting that (within the caveat that we used large voxels to calculate RD) following removal of the majority of the effects of the conduit vessels, RD provides a useful reflection of the heterogeneity of pulmonary perfusion.

GRANTS

This research was supported by National Heart, Lung, and Blood Institute Grants HL080203 and HL104118 and an EPSRC post-doctoral Fellowship.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: K.S.B., R.B.B., and G.K.P. conception and design of research; K.S.B. and G.K.P. analyzed data; K.S.B., R.B.B., and G.K.P. interpreted results of experiments; K.S.B. and G.K.P. prepared figures; K.S.B., R.B.B., and G.K.P. drafted manuscript; K.S.B., R.B.B., and G.K.P. edited and revised manuscript; K.S.B., R.B.B., and G.K.P. approved final version of manuscript.