Abstract
Amino acids committed to a particular function correlate tightly along evolution and tend to form clusters in the 3D structure of the protein. Consequently, a protein can be seen as a network of co-evolving clusters of residues. The goal of this work is two-fold: first, we have combined mutual information and structural data to describe the amino acid networks within a protein and their interactions. Second, we have investigated how this information can be used to improve methods of prediction of functional residues by reducing the search space. As a main result, we found that clusters of co-evolving residues related to the catalytic site of an enzyme have distinguishable topological properties in the network. We also observed that these clusters usually evolve independently, which could be related to a fail-safe mechanism. Finally, we discovered a significant enrichment of functional residues (e.g. metal binding, susceptibility to detrimental mutations) in the clusters, which could be the foundation of new prediction tools.
Introduction
Some protein functions are maintained by concerted changes of a group of residues forced to co-evolve (i.e. when a residue is mutated, other residues must change to preserve or restore the structure or function of the protein). Such is the case of enzymes, where the environment of the active site must conserve certain characteristics so that the protein maintains its function during the course of evolution [1]. It is also known that protein folds have evolved under constraints imposed by function, so their structure is robust against random mutational events, yet extremely sensitive to perturbations at key positions [2].
Likewise, functionally important residues undergo sequence variations as they evolve and form spatial clusters in the protein structure. Such clusters may be part of binding sites, catalytic sites or allosteric pathways [3]. Previous works have suggested a link between functionally important sites (for specificity or allosteric regulation) and neighbouring co-evolving residues [1], [4], [5]–[9]. Halabi et al., using sequence-based analysis, introduced the concept of groups of correlated amino acids that evolved quasi-independently, called sectors. Strikingly, those sectors were observed to be physically in contact in the 3D structure [10].
In addition, the information within a protein must be transmitted, at least partly, between residues in physical contact, some being important to maintain a short path in the distance network [2], [11]. Thus, it is reasonable to consider a protein as an undirected network of contacting residues. Decomposing protein structures into modules of densely-interconnected residues using this kind of network representations has been useful to explain allosteric communication [12].
In this work we analyse the mutual information networks between residues (MIN) in 187 families of enzymes and describe the relationship between co-evolution and the 3D structure of the protein. We introduce a new concept, the analysis of MI3D clusters which combine both evolutionary and three-dimensional information. In accordance with Halabi et al., we observed that networks of co-evolving residues tend to be close, forming a sector (which we called MI3D cluster) when mapped onto the 3D structure [10]. Furthermore, we found that, amongst the many MI3D clusters usually present in a protein domain, those containing catalytic residues have distinguishable network properties. This finding could be used to predict such catalytic residues. Finally, we measured the enrichment of the clusters in residues with different functionalities, e. g: catalytic activity, metal binding, and susceptibility to detrimental mutations.
Results and Discussion
Are Mutual Information Networks and Distance Networks Topologically Different?
We created the Mutual Information Networks (MINs) by connecting residues with a mutual information value > = 6 since such value was determined to be indicative of a significant evolutionary relationship [13] (see Methods). The Distance Networks (DNs) were created by connecting any two residues if any heavy atom of each was closer than 5 Å. As an example, figure S1 shows the MIN and DN for the Pfam family PF00884.
We observed that the topological properties of MINs and DNs cannot be inferred from one another. The degree distribution of the DN of any protein structure follows a bell-like Poisson distribution as would be expected for a statistically homogeneous random model (Figure 1). This has been observed by other authors, and has been attributed to a restriction in the number of residues occupying a volume in the protein space [14]–[16]. The distribution degree of the MINs displays a mixture of distributions ranging from fast-decaying power-law to Poissonian (Figure 1). Since co-evolution demands some degree of physical proximity [17], [18], deviations from a purely scale-free architecture may be due to a limit in the possible number of neighbours that a node can have. Also, there are a number of biological factors influencing the ability of two residues to co-evolve (e.g. their functional roles, their biochemical nature, their structural surroundings, etc.), which can possibly hinder the existence of a large number of simultaneously co-evolving residues. This would prevent the existence of nodes with distinctly large numbers of neighbours in the MINs, thus truncating the characteristic long tails in power-law degree distributions.
Figure 1. Degree distribution of the MIN and DN.
Fraction of amino acids versus the normalized degree in the MINs (blue dots) and DNs (orange dots). Degrees were normalized with respect to the average degree. All DNs followed a Poisson distribution (α = 0.01, KS test). 43.8% of MINs followed a power-law distribution and 29.9% followed a Poisson distribution (α = 0.01). Red dots: normalized degree distribution in the MIN for Pfam family PF01432, showing a truncated power-law distribution. Green dots: normalized degree distribution in the MIN for Pfam family PF00118. Logarithmic scale.
The clustering coefficient distribution of the MINs and DNs is shown in Figure 2. The mean values for the distributions are 0.365 for MINs, and 0.514 for DNs. This implies networks with very dense regions, which is in line with the observations of some other biological networks [19]. However, the dispersion of the clustering coefficient in MINs is significantly larger than in DNs (p-value <2.2*10−16, KS test; Figure 2, inset). This large dispersion is characteristic of modular architectures [20]. This means that residues in the MINs tend to form small clusters where all residues evolutionarily influence one another, while there is very little evolutionary dependence between clusters. Finally, analysis of clustering coefficient and characteristic path length shows that MINs and DNs show a small-world structure as described by Watts and Strogatz in their seminal work [21]: characteristic path length L > = Lrandom and clustering coefficient C >> Crandom, where Crandom and Lrandom are parameters for random networks (details in text S1). We also compared MINs and DNs to regular networks (see text S1). Our results for DNs agree with the observations of Vendruscolo et al. for protein structures [22]. Results for MINs are similar to those observed by Chakrabarti and Panchenko [23]. The only difference is that, in our case, C < Cregular in most MINs (95.6%), while in theirs C > Cregular on average. Two possible explanations for this discrepancy are: (1) Chakrabarti and Panchenko used a lower number of aligned sequences in order to calculate MI values (which can be source of bias [24]), and (2) a different method for mutual information threshold calculation was used, which in our case produced sparser networks.
Figure 2. Distribution of the mean clustering coefficient for MINs, DNs, MI clusters.
Thick blue line: MINs. Thick orange line: DNs. Thin blue line: MI clusters. The average clustering coefficient is 0.365 for MINs and 0.514 for DNs. Both values are statistically larger than random expectation with p-value <2.2*10−16. Inset: dispersion of the data measured as Inter-Quantile Range (IQR). Only the giant components of the MINs and DNs are considered.
Are Groups of Co-evolving Amino Acids Close in the 3D Structure?
The MCL algorithm was used to identify clusters of co-evolving residues in the MINs (see Methods), hereinafter called MI clusters. These MI clusters contain groups of co-evolving residues, regardless their distance in the 3D structure of the protein. Figure S2 shows the modularity of the MINs (see Methods).
It has been demonstrated that co-evolving residues are distributed in a particular fashion in the 3D structure [1]. For instance, two distant residues can actually belong to the same MI cluster (this is, they co-evolve) while two neighbouring residues may evolve separately despite their physical proximity. We investigated the spatial arrangement of MI clusters by mapping them onto the DN (i.e. onto the 3D structure of the reference protein, see Methods). The resulting clusters were called MI3D clusters (see Methods). These MI3D clusters contain groups of co-evolving residues which are close (<5 Å) in the 3D structure of the protein.
About 80% of the MI clusters generate MI3D clusters once mapped onto the DN (clusters with less than four residues were not considered in our analysis). The number of MI3D clusters per Pfam and their size distribution are shown in figures S3 and S4. About 75% of MI clusters are preserved as a single cluster and only about 6% of the MI clusters are split into two or more isolated MI3D clusters when mapped onto the structure of the protein. These results confirm that groups of co-evolving amino acids tend to be spatially close [25], [26] Although previous studies have shown that co-evolution does also occur between non-contacting residues [27], [28], our findings show that there is a link between co-evolution and physical contact. However, the fact that about 6% of MI clusters are broken into several isolated MI3D clusters means that a pair of residues can actually co-evolve even though they are neither in physical contact nor “connected” by single-linkage of co-evolving residues. A common selective pressure in two separated areas of the protein could explain this observation (e.g. two interaction patches, allosterism, etc.).
Catalytic MI3D Clusters
We next identified those MI3D clusters which either contain a catalytic residue or are close to one (<5 Å). We called those clusters catalytic MI3D clusters. Figures S5 and S6 show that, on average, non-catalytic MI3D clusters are more than twice as frequent as catalytic MI3D clusters. This can be explained given the singularity of the catalytic site. Other noticeably feature is that, within a Pfam domain, the catalytic MI3D clusters are, on average, 4-fold larger than the non-catalytic ones (see figure S7).
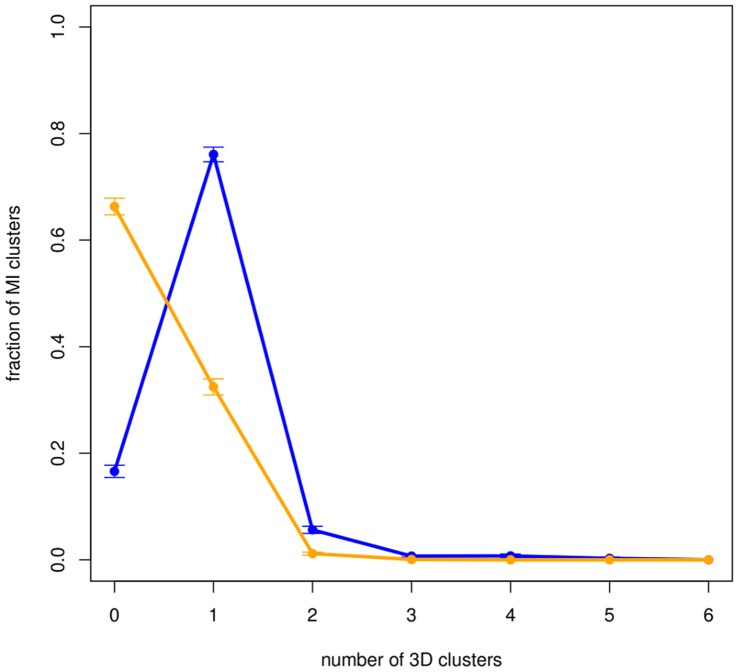
Although the majority of MI clusters (72.9%) do not produce catalytic MI3D clusters (but produce non-catalytic MI3D clusters), it is worth noting that, when they do, they mostly produce only one (Figure 3). As expected, considering that they originate from different MI clusters, catalytic MI3D clusters within the same Pfam are less likely to co-evolve than random expectation (figure S8).
Figure 3. Distribution of the number of 3D clusters generated by mapping the MI cluster onto the 3D structure.
Blue line: all MI3D clusters. Orange line: only catalytic MI3D clusters. 74.1% of MI clusters are preserved as a single MI3D cluster after mapping (93.1% according to random expectation). 25.9% of MI clusters produce one catalytic MI3D cluster after mapping (92.0% according to random expectation).
Taking into account that there are, on average, more than 3 catalytic MI3D clusters per Pfam, this implies that catalytic MI3D clusters usually evolve independently despite their physical proximity. This is suggestive of either an integrative process (which “connects” different parts of the protein to the catalytic site) or a fail-safe mechanism where mutual information connects functional residues, for instance, in the event of losing a catalytic MI3D cluster (e.g. due to a mutation).
Furthermore, we observed that a catalytic and a non-catalytic MI3D cluster can actually co-evolve, as 23% of the Pfams with catalytic and non-catalytic MI3D clusters, at least one catalytic and one non-catalytic MI3D cluster are derived from the same MI cluster (figure S9).This suggests the presence of catalytic subsites, e.g. positions that determine specificity or other necessary residues for the accomplishment of the catalysis (e. g. allosteric sites).
Prediction of Functional Sites Using MI Information
It is reasonable to expect important residues to be subject to co-evolutionary pressures. In agreement with the idea of using communities of correlated amino acids to uncover sets of residues defining functional characteristics in a protein family [29], we investigated whether MI clusters were enriched in residues relevant for the enzymatic activity, such as metal-binding residues and residues forming the active site. Our results indicate that the UniProt features ACT_SITE, BINDING, MUTAGEN and METAL are significantly over-represented in MI clusters (Table 1). We also investigated if each residue’s degree in MI clusters (i.e. the number of residues to which it is linked by co-evolution) has any influence on its functional relevance. We grouped the residues of each Pfam’s MI clusters into three ranges according to their degree (see Methods). As shown in Table 2, ACT_SITE, BINDING and METAL features are significantly more frequent in residues with large degrees than in those with medium and low degree. Similarly, we calculated that METAL and ACT_SITE features are significantly more frequent in residues with a large clustering coefficient.
Table 1. Enrichment of functional features in MI clusters and MI3D clusters.
| MI clusters | MI3D clusters | catalytic MI3D clusters | non-catalytic MI3D clusters | |
| Odds ratio | Odds ratio | Odds ratio | Odds ratio | |
| ACT_SITE | 1.345* | 1.341* | 2.457* | 0.141* |
| BINDING | 1.312* | 1.428* | 2.431* | 0.446 |
| METAL | 1.333* | 2.210* | 3.292* | 0.166 |
| SITE | 1.237 | 1.264 | 3.011 | 0.403 |
| MUTAGEN | 1.652* | 1.931* | 2.754* | – |
| MOD_RES | 1.200 | 0.982 | 1.527 | 0.032 |
Enrichment (average odds-ratio) of functional features in MI clusters, MI3D clusters, catalytic MI3D clusters and non-catalytic MI3D clusters. Stars indicate statistical significance at α = 0.01 (Fisher’s exact test).
Table 2. Enrichment of functional features in MI clusters associated to degree and clustering coefficient.
| Small k | Medium k | Large k | Signif. | Small C | Medium C | Large C | Signif. | |
| MOD_RES | 0.521 | 0.700 | 1.383 | – | 0.629 | 0.911 | 1.085 | – |
| MUTAGEN | 0.136 | 1.397 | 1.582 | – | 1.201 | 0.189 | 1.116 | – |
| METAL | 0.600 | 0.904 | 1.605 | * | 0.574 | 0.920 | 1.236 | * |
| ACT_SITE | 0.330 | 0.735 | 1.574 | * | 0.762 | 0.884 | 1.055 | * |
| BINDING | 0.311 | 0.513 | 1.843 | * | 0.666 | 1.303 | 0.949 | – |
| SITE | 0.433 | 1.196 | 1.424 | – | 0.664 | 0.929 | 0.980 | – |
Enrichment (average odds-ratio) of functional features in MI clusters associated to degree (k) and clustering coefficient (C). Stars indicate statistical significance at α = 0.01 (Kruskal-Wallis test).
Prediction of Functional Sites Using MI and 3D Information
We next investigated whether MI3D clusters are also enriched in residues important for the enzymatic activity. As shown in Table 1, MI3D clusters were significantly enriched in residues with UniProt features ACT_SITE, BINDING, METAL and MUTAGEN as compared to MI clusters. For instance, the enrichment in metal-binding residues increases more than 2-fold as compared to random expectation. This shows the advantage of combining mutual information with structural information.
We also found that features such as ACT_SITE and BINDING are associated with residues with larger degrees (Table 3). Also, the ACT_SITE feature was slightly (but significantly) more frequent in residues of MI3D clusters with a low clustering coefficient. It is probable that they act by functionally influencing many other residues, which are not close to one another. Consequently, an alteration of these low-clustering-coefficient residues might greatly disrupt their surroundings.
Table 3. Enrichment of functional features in MI3D clusters associated to degree and clustering coefficient.
| Small k | Medium k | Large k | Signif. | Small C | Medium C | Large C | Signif. | |
| MOD_RES | 0.665 | 1.172 | 1.617 | – | 0.940 | 1.101 | 0.708 | – |
| MUTAGEN | 0.248 | 1.317 | 0.307 | – | 0.371 | 0.932 | 1.182 | – |
| METAL | 0.956 | 0.949 | 1.054 | – | 1.498 | 1.264 | 0.796 | – |
| ACT_SITE | 0.441 | 0.948 | 1.202 | * | 1.349 | 1.091 | 0.508 | * |
| BINDING | 0.714 | 0.930 | 1.381 | * | 1.304 | 1.198 | 0.651 | – |
| SITE | 0.112 | 0.723 | 1.428 | – | 1.349 | 0.969 | 0.294 | – |
Enrichment (average odds-ratio) of functional features in MI3D clusters associated to degree (k) and clustering coefficient (C). Stars indicate statistical significance at α = 0.01 (Kruskal-Wallis test).
Next, we focused on the functional enrichment in catalytic MI3D clusters, finding that UniProt features ACT_SITE, BINDING, METAL and MUTAGEN are significantly enhanced in such clusters (Table 1). This result is expected for the ACT_SITE feature, but it might be potentially predictive for the other features. ACT_SITE and BINDING are also associated to lower clustering coefficients (Table 4). The ACT_SITE feature is significantly under-represented in non-catalytic MI3D clusters (ten times less likely to occur than random chance on average). No statistical association was found between functional residues and topological parameters for non-catalytic MI3D clusters (Table 5).
Table 4. Enrichment of functional features in catalytic MI3D clusters associated to degree and clustering coefficient.
| Small k | Medium k | Large k | Signif. | Small C | Medium C | Large C | Signif. | |
| MOD_RES | 0.580 | 1.223 | 1.322 | – | 0.894 | 1.218 | 0.828 | – |
| MUTAGEN | 0.677 | 1.437 | 0.229 | – | 0.461 | 0.767 | 1.368 | – |
| METAL | 0.997 | 0.961 | 1.021 | – | 1.205 | 1.164 | 1.023 | – |
| ACT_SITE | 0.721 | 0.856 | 1.137 | – | 1.229 | 0.862 | 0.620 | * |
| BINDING | 0.930 | 1.024 | 1.253 | – | 1.343 | 1.016 | 0.636 | * |
| SITE | 0.487 | 1.249 | 0.773 | – | 1.137 | 0.980 | 0.405 | – |
Enrichment (average odds-ratio) of functional features in MI3D clusters associated to degree (k) and clustering coefficient (C). Stars indicate statistical significance at α = 0.01 (Kruskal-Wallis test).
Table 5. Enrichment of functional features in non-catalytic MI3D clusters associated to degree and clustering coefficient.
| Small k | Medium k | Large k | Signif. | Small C | Medium C | Large C | Signif. | |
| MOD_RES | 1.308 | 2.492 | 0.744 | – | 1.417 | 0.000 | 1.288 | – |
| MUTAGEN | – | – | – | – | – | – | – | – |
| METAL | 1.972 | 0.279 | 0.190 | – | 1.545 | 0.413 | 0.928 | – |
| ACT_SITE | 0.000 | 2.084 | 1.500 | – | 0.667 | 4.212 | 0.000 | – |
| BINDING | 1.032 | 1.047 | 0.523 | – | 0.659 | 1.130 | 1.156 | – |
| SITE | 0.000 | 0.000 | 2.116 | 1.961 | 0.801 | 0.000 | – |
Enrichment (average odds-ratio) of functional features in MI3D clusters associated to degree (k) and clustering coefficient (C). Stars indicate statistical significance at α = 0.01 (Kruskal-Wallis test).
Prediction of Catalytic MI3D Clusters
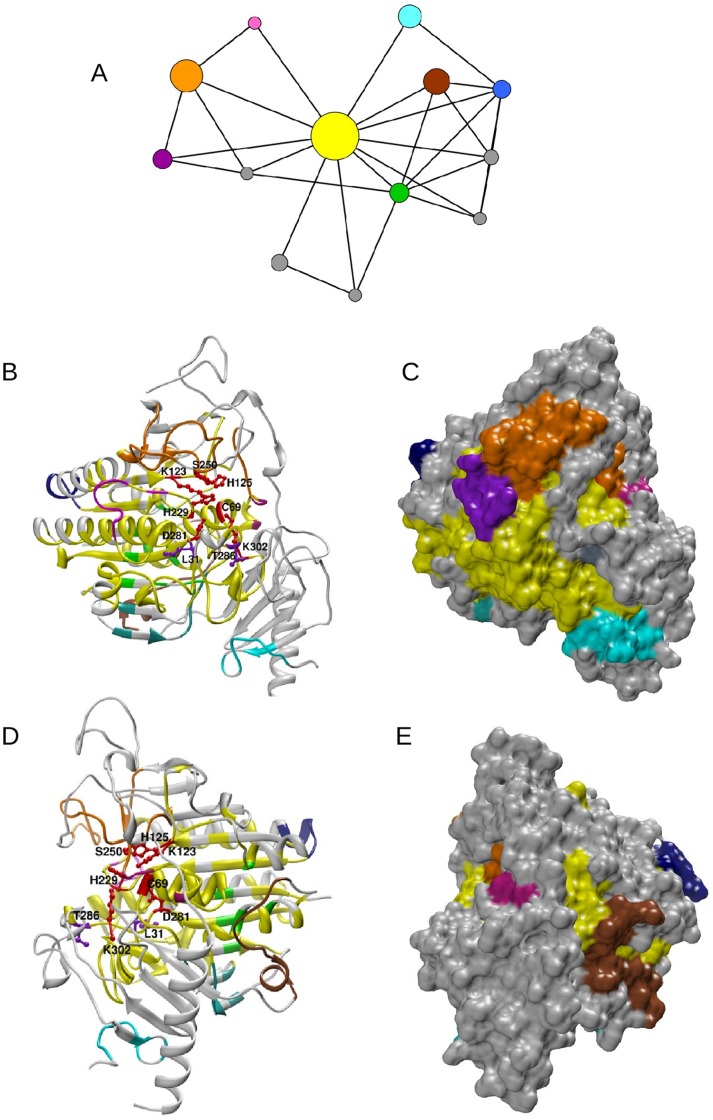
For each Pfam, a network of MI3D clusters was defined as follows: each MI3D cluster is a node, and edges between pairs of nodes exist if at least two residues (each from a different node) are closer than 5 Å. This network was named MI3D cluster Network (3DCN; see Methods). A graphical representation of the 3DCN and structural mapping for Pfam domain PF00884 is shown in Figure 4. Other examples are shown in figures S10 (PF01979) and S11 (PF00118).
Figure 4. Network of MI3D clusters and mapping onto the protein structure.
(A) 3DCN of the arilsulfatase A (pdb code: 1AUK chain A, PF00884). Catalytic MI3D clusters: yellow, orange and green. Non-catalytic MI3D clusters: magenta, brown, blue, cyan and pink. The size of a node in the 3DCN is proportional to the number of residues in the MI3D cluster. Clusters with less than 10 residues were coloured grey. (B) Ribbon representation of the MI3D clusters of a representative structure of PF00884. Colours are as in panel A. Catalytic residues are highlighted as red balls and sticks in the ribbon plot. Disease-related mutations are represented as violet balls and sticks. (C) Surface representation of the view in panel B. (D) Same as panel B rotated 180 degrees. (E) Surface representation of the view in panel D.
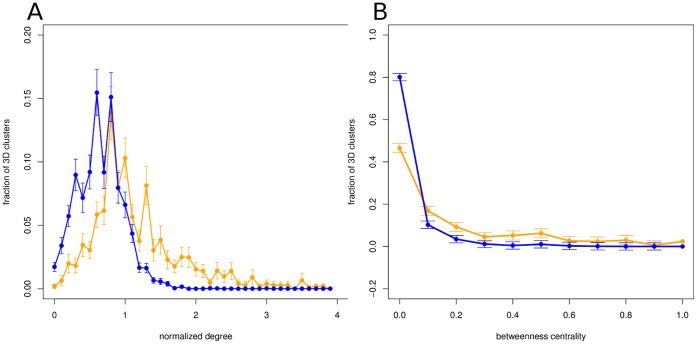
We then sought distinctive topological characteristics in the 3DCNs which could be used to identify catalytic clusters in the protein. Figure 5a shows the distribution of the normalized degrees of catalytic and non-catalytic MI3D clusters in the 3DCN. Non-catalytic MI3D clusters have significantly smaller degrees than catalytic ones, without a noticeable correlation between the degree and the size of the 3DCN (r = 0.187). Furthermore, non-catalytic MI3D clusters have, on average, significantly lower values of betweenness centrality in the 3DCN than catalytic MI3D clusters (Figure 5b). Those values are largely independent from the size of the 3DCN (r = 0.159). Also, the ratio of the betweenness centrality values of a Pfam’s catalytic and non-catalytic MI3D clusters is around 12 on average (figure S12). This suggests a central role of catalytic MI3D clusters in the distribution of information from the catalytic site to the rest of MI3D clusters.
Figure 5. Topological parameters in the MI3D cluster network.
(A) Frequency of MI3D clusters vs the normalized degree in the 3DCN. We define the normalized degree of a node as the degree divided by the average degree in the 3DCN. Orange line: catalytic MI3D clusters. Blue line: non-catalytic MI3D clusters. Mean for catalytic MI3D clusters = 1.315 (median = 1.2). Mean for non-catalytic MI3D clusters = 0.847 (median = 0.8). Both distributions are significantly different (KS test, p-value<2.2*10−16). (B) Frequency of MI3D clusters vs betweenness centrality in the 3DCN. Orange line: catalytic MI3D clusters. Blue line: non-catalytic MI3D clusters. Mean betweenness centrality for catalytic MI3D clusters = 0.159 (median = 0.059). Mean betweenness centrality for non-catalytic MI3D clusters = 0.034 (median = 0.0064). Both distributions are significantly different (KS test, p-value<2.2*10−16).
The size, betweenness centrality and degree of MI3D clusters in the 3DCN could be used to predict catalytic MI3D clusters. We measured the performance of our method by means of an F-measure (see Methods). With optimal thresholds for the three predictors (relative size = 0.67, betweenness = 0.06, relative degree = 0.85), we achieved a 73.2 F-measure. A comparison of our results with the results if we used only spatial clusters (i.e. clusters of residues close in space) highlights the benefits of using co-evolutionary information (text S2).
Mining OMIM Mutations in 3DCNs
We mined OMIM database searching for enzymes with specific functional words, such as increasing and decreasing, related with action or activity. For all Pfams under study, we identified 11 mutations falling within a MI3D cluster, 10 located in catalytic clusters and one in a non-catalytic MI3D cluster (table S1). We chose to analyse the mutations of the Pfam families PF00884 and PF02779, since their reference sequence is human and their 3D structure is known. The reference sequence of PF00884 is ARSA_HUMAN (UniProt accession: P15289). This Pfam family contains a N-acetylgalactosamine-4-sulfatase (Arylsulfatase B; ARSB_HUMAN; UniProt accession: P15848) and a N-acetylgalactosamine-6-sulfatase (GALNS_HUMAN; UniProt accession: P34059). The catalytic residues of ARSA_HUMAN are 69C, 123 K, 125 H, 150 S, 229 H, 281 D and 302 K. The mutation LEU72GLN in ARSB_HUMAN (OMIM code 611542) is known to cause type VI mucopolysaccharidosis, as is the mutation THR312SER in GALNS_HUMAN (OMIM code 612222). These mutations are located at 31 L and 286 T in the reference protein, respectively, both in the same catalytic MI3D cluster. Figure 4 shows the positions of both mutations, relatively close to two catalytic residues (31 L is close to 281 D and 286 T is close to 302 K).
We also found the mutation ARG183PRO of human piruvate dehydrogenase (ODPB_HUMAN; UniProt accession: P11177; OMIM code 248611) in the Pfam family PF02779. Arginine 183 corresponds to 115 R in the Pfam reference protein with known structure (PDB code 1NI4). This position was found in a catalytic MI3D cluster, therefore co-evolving with other residues close to the catalytic residues. According to OMIM, this mutation induces a structural change in the protein and impairs proper folding. According to our result, even if the protein could fold, the mutation would impair the catalytic cluster, thus impairing the activity of the enzyme. In both cases, its result would be the loss of or a deficiency in dehydrogenation of piruvate.
Concluding Remarks
In conclusion, we have presented a study on the topology of the mutual information network and how it can be exploited to predict the location of different functional residues of enzymatic protein families. We observed that combination co-evolutionary with spatial information unveils a dense network of physically close co-evolving residues within the protein structure, which can be identified by clustering methods. The topological properties of these clustered structures suggest a role in increasing the tolerance to functional disruption and to enhance the adaptativeness of the protein. Also, these properties can be used to functionally characterize the clusters. In addition, we measured the enrichment of the clusters in functional residues, a feature that can be exploited as a prediction tool by reducing the search space when looking for functional sites. We applied the analysis in two relevant biological examples.
Materials and Methods
Dataset
The dataset was constructed based on the CSA database (version 2.2.11, released August 2009) [30]. CSA provides catalytic site annotation for enzymes in the PDB. Catalytic residues were defined as those residues thought to be directly involved in some aspect of the reaction catalysed by an enzyme (for a detailed description of the classification see [31]. CSA contains 968 original literature entries, which belong to 455 PFAM families [32]. We selected those families containing more than 400 unique sequences/clusters (sequences with less than 62% identity). This condition was necessary to provide a reliable estimation of MI as shown by Buslje et al. 2009 [13], so that we ended up with a dataset of 172 protein families, each one containing at least one PDB entry. When more than one PDB entry with catalytic site annotation was available for a given family, one reference PDB entry was selected according to the following criteria: highest sequence coverage of the Pfam MSA, the year of structure determination (preferably later than 2000) and resolution. In all cases, MSAs were gap trimmed to remove positions with gaps in the reference sequence. In addition, all positions with >50% gaps, as well as sequences covering <50% of the reference sequence length were removed, as described in [13].
MI Calculation
Mutual Information (MI) was calculated between pairs of columns in the MSA as described in [13]. Briefly, the frequency for each amino acid pair was calculated using sequence weighting techniques and low count corrections and was compared to the expected frequency assuming that mutations between amino acids were uncorrelated. Next, the MI was calculated as a weighted sum of the log-ratios between the observed and expected amino acid pair frequencies. The APC method of Dunn et al. 2008 [17] was applied to reduce the background mutual information signal for each pair of residues and the MI scores were finally translated into MI z-scores by comparing the MI values for each pair of position with a distribution of prediction scores obtained from a large set of randomized MSAs. The z-score is then calculated as the number of standard deviations that the observed MI value falls above the mean value obtained from the randomized MSAs. Although the concept of z-score normalization was introduced by [17], [33]–[35], we use our particular score that gave better performance in both biological and in silico-generated benchmarks by applying APC, sequence weighting, low-count corrections and sequence permutations to calculate a sequence based z-score for MI distribution [13]. This combination gave the best performance, significantly improved the prediction accuracy and allows for direct comparison of information values across protein families. We found that an average sequence-based z-score threshold of 6.5±2.5 for a Pfam-tested benchmark (and of 6.1±1.1 for another set of biologically meaningful proteins) defined a sensitivity of 0.4 and a specificity of 0.95 [13]. Based on these results, in this work we chose a MI score threshold of 6.0.
MI and DN Network Creation
MI networks were defined for each Pfam family as graphs G(N,E), where nodes (set N) were defined as positions in the MSA of a family (i.e. the columns of the MSA) and edges (set E) were defined between any pair of nodes with MI>6 (figure S13a). These networks were called MI Networks (MINs). MINs might be made of several components (disconnected subnetworks) of varying size. We focused our topological analysis on the largest component (also called giant component).
Distance networks (DN) were defined for the reference protein of every Pfam family of the dataset as graphs G′(N′,E′), where nodes (set N′) are the residues (i.e. residue numbering) of the reference protein, and edges (set E′) were defined between pairs of residues at a distance shorter than 5 Å (figure S13a). The distance between pairs of residues was defined as the smallest distance between any two heavy atoms of each residue. The value of 5 Å approximates the upper limit for attractive London-van der Waals forces [16]. Although interactions of charged atoms can occur at distances of about 8 Å (being the electrostatic energy linearly proportional to the inverse of the distance) they are not considered here. All DNs but one were composed of a single component, the exception being the result of loss of structural data in the PDB database.
Network Clustering
Several graph-clustering methods have been devised to partition a network into clusters based on connectivity parameters. We used the MCL algorithm [36], which has been extensively used for biological network clustering and has been proved to outperform other methods [37]. Briefly, the MCL algorithm simulates random flows through a network by calculating successive powers of the associated adjacency matrix. Upon each iteration, high-flow and low-flow regions are enhanced until the process converges, partitioning the network into a set of high-flow regions surrounded by regions without any flow. The value of the inflation parameter strongly influences the number of resulting clusters. In order to calculate the optimal inflation for our networks, we used the cml info utility provided by the MCL software, which computes performance measures for different clusterings. For each one of our 187 MINs, we calculated the inflation value which yielded a better partition and we used it to cluster the MIN (figure S13b). The resulting clusters were termed MI clusters. All MI clusters with less than 4 residues were discarded.
The quality of the division was tested by calculating the modularity of the partition [38], a global parameter which can be used to test such a clustering process. Ranging between −1 and +1, positive modularity values mean that the partition of the network yielded denser subnetworks than random expectation, while negative values mean that the resulting subnetworks are not as dense as random expectation. Modularity was calculated with the community.modularity function of the networkx package in Python programming language [39].
Network Mapping
Each MI cluster was mapped onto the DN of the reference protein. An edge between two residues was defined if they were also connected in the DN (less than 5 Å apart). The resulting subnetworks within the DNs are hereinafter defined as MI3D clusters. This sometimes brakes up the MI clusters into separate subnetworks (figure S13c). The MI3D clusters containing catalytic residues (or residues in close contact with any of the catalytic residues) were labelled as catalytic MI3D clusters. The rest of the MI3D clusters were named non-catalytic MI3D clusters.
Network of MI3D Clusters
A network of MI3D clusters of a reference protein (and the corresponding Pfam) was defined as a graph G(N”,E”), where nodes were the MI3D clusters (set N”) and edges (set E”) were defined between MI3D clusters if at least one pair of residues of each cluster was in contact (distance <5 Å; figure S13d). These networks were named MI3D cluster Networks (3DCN).
Topological Parameters
In order to characterize the topology of the different kinds of networks that we generated, we calculated a number of parameters (defined in table S2). Local parameters: degree, clustering coefficient. Global parameters: modularity and characteristic path length. Betweenness centrality was also used for the characterization of the MI3D cluster networks. Power-law and Poisson degree distributions were fitted to the MINs and DNs by means of the fitdistr function in R using a maximum likelihood estimation [40], and then compared by means of a Kolmogorov-Smirnov test. All topological parameters were calculated using the networkx package. Spearman’s rank correlation coefficient was used to calculate correlations between parameters since their relationship was monotonical but not necessarily linear [41]. Also, Spearman’s rank correlation coefficient is less affected by the presence of outliers than Pearson’s correlation coefficient. To assess the statistical significance of the topological parameters, for each type of network in our study (MINs, DNs, MI clusters and MI3D clusters), a rewired model consisting of 1000 networks was built, where edges were randomly exchanged and the degree of each node was unchanged. All statistical calculations were performed using the R statistical programming language [40].
Prediction of Functional Sites
We extracted the information on relevant single-residue positions of the sequence from UniProt, as it appears in the feature (FT) section [42]. Since the positions of UniProt entries are relative to unique protein sequences (and not to Pfam domains), we associated those functional features identified in >10% of the sequences used to build the MSA to a Pfam. The UniProt sequence features are defined as: MUTAGEN (site which has been experimentally altered, usually affecting protein activity); MOD_RES (site undergoing post-translational modification); METAL (binding site for a metal ion); BINDING (binding site for any chemical group, such as co-enzymes, prosthetic groups, etc.); ACT_SITE (site involved in the catalytic activity of the enzyme); SITE (any interesting single amino acid site on the sequence that is not defined by another feature key). We obtained features for 168 Pfams, averaging 1.7 features per Pfam.
We defined the baseline probability (PPfam) of picking one residue of interest (e.g. a catalytic residue) in a Pfam domain by chance as the number of catalytic residues divided by the total number of residues of the domain. The probability of picking one catalytic residue within any of the MI clusters (PMI) was defined as the number of catalytic residues divided by the total number of residues in the MI clusters of the Pfam domain. Thus, the odds ratio (odds ratio = PMI/PPfam) shows the increase in the likelihood of finding a catalytic residue in a MI cluster as compared to random chance. Likewise, the probability of picking one residue of interest (e.g. a catalytic residue) within any of the MI3D clusters of a Pfam (P3D) was defined as the number of catalytic residues divided by the total number residues on the MI3D clusters of that Pfam. Thus, the odds ratio (odds ratio = P3D/PPfam; PPfam defined as above) shows the increase in the likelihood of finding a catalytic residue in a MI3D cluster as compared to random chance. The statistical association between a feature and a cluster of residues was quantified by means of a Fisher’s exact test, using 1000 sequences where the features had been randomly placed as a random model.
In order to associate features to topological parameters of the residues (namely, degree and clustering coefficient), we binned the values into three groups: SMALL, MEDIUM and LARGE, using the 33th and 66th percentile of the distribution of the degree and clustering coefficient values for each Pfam as thresholds. For MI clusters, we obtained the odd-ratio of the ranges by calculating the frequency of each feature over the all residues in the MI clusters as baseline (PMI) and the frequency of featured residues amongst those within a particular degree range (PMI K). The odds ratio was PMI K/PMI. A similar procedure was applied for the binned clustering coefficient (odds-ratio = PMI c/PMI). For MI3D clusters, the odds ratio was calculated as P3D K/P3D and P3D C/P3D.
Performance Analysis
We evaluated the performance of all different combinations of betweenness, relative degree and relative cluster size values as predictors of catalytic MI3D clusters in the 3DCN. For each 3DCN, we calculated relative degree of each cluster as the degree divided by the average degree of the 3DCN. Relative cluster size was calculated as the size of the cluster (number of residues) divided by the average cluster size of the 3DCN. We did so in order to make the parameters comparable across all Pfams. We used the F-measure as a measure of performance. It was defined as the harmonic mean of sensitivity and specificity: (2×sensitivity×specificity)/(sensitivity + specificity), where sensitivity is the ratio of correctly predicted catalytic MI3D clusters vs all predicted catalytic MI3D clusters and specificity is the ratio of correctly predicted non-catalytic MI3D clusters vs all predicted non-catalytic MI3D clusters.
Supporting Information
MIN and DN for the Pfam family PF00884. (A) Representation of the MI network of the PF00884 family. Colours other than grey indicate the eight largest MI clusters. (B) Representation of the distance network calculated from the PDB structure 1AUK chain A, representative of the PF00884 family. Residues are coloured as in A.
(PNG)
Distribution of modularity of MI clusters and MI3D clusters. Fraction of Pfam families versus the modularity of the partition. Blue: partition of MI clusters (mean = 0.461). Orange: partition of MI3D clusters (mean = 0.359). Modularity values larger than 0 indicate a partition of the network resulting in denser clusters than random expectation.
(TIFF)
Distribution of the number of MI clusters and MI3D clusters. Thick line: distribution of the number of MI clusters (mean = 11.97). Thin line: distribution of the number of MI3D clusters (mean = 10.47).
(TIFF)
Size distribution of MI and MI3D clusters. Blue dots: size distribution of MI clusters (mean = 13.53; median = 6). Orange dots: size distribution of MI3D clusters (mean = 13.25; median = 6).
(TIFF)
Distribution of the number of MI3D clusters. Orange line: distribution of the number of catalytic MI3D clusters (mean = 3.40, median = 3). Blue line: distribution of the number of non-catalytic MI3D clusters (mean = 7.28, median = 7.28).
(TIFF)
Ratio of the number of non-catalytic MI3D clusters vs catalytic MI3D clusters. Ratio of the number of non-catalytic MI3D clusters vs catalytic MI3D clusters per Pfam (mean = 2.65, median = 2).
(TIFF)
Size ratio of catalytic MI3D clusters vs non-catalytic MI3D clusters. Size ratio of catalytic MI3D clusters vs non-catalytic MI3D clusters of the same Pfam (mean ratio = 4.12, median = 2.97).
(TIFF)
Fraction of co-evolving residues between catalytic MI3D clusters. The fraction of co-evolving residues between catalytic MI3D clusters is compared to random expectation by means of a z-score. The higher frequency of negative z-scores means that, for most Pfams, co-evolution between catalytic MI3D clusters is smaller than expected by chance.
(TIFF)
Origin of catalytic and non-catalytic MI3D clusters. Blue line: fraction of all MI clusters in a Pfam which produce non-catalytic MI3D clusters when mapped onto space (only Pfams with at least one non-catalytic MI3D cluster considered). Orange line: fraction of all MI clusters in a Pfam which produce catalytic MI3D clusters (only Pfams with at least one catalytic MI3D cluster considered). Black line: fraction of all MI clusters in a Pfam which produce both catalytic and non-catalytic MI3D clusters (only Pfams with catalytic and non-catalytic MI3D clusters considered). For 76.8% of the Pfams with catalytic and non-catalytic MI3D clusters, no MI clusters produce both catalytic and non-catalytic MI3D clusters when mapped onto space, with significantly less than random expectation (97.6%), KS test p-value = 9.67*10−11 (consequently, for 23.2% of Pfams there is at least one MI cluster which produces both catalytic and non-catalytic MI3D clusters). 10% of MI clusters out of 17.6% of Pfams produce catalytic and non-catalytic MI3D clusters.
(TIFF)
Network of MI3D clusters and mapping onto the protein structure of PF01979. (A) 3DCN of the Pfam family PF01979 (pdb code: 1KRA). Catalytic MI3D clusters were coloured yellow, orange and cyan. Clusters with less than 10 residues were coloured grey. The size of a node is proportional to the number of residues in the MI3D cluster. (B) Ribbon representation of the MI3D clusters of the representative structure of PF1979. Catalytic residues represented as red balls and sticks. (C) Surface representation of the view in B. (D) Same as A rotated 180 degrees. (E) Surface representation of the view in D.
(PDF)
Network of MI3D clusters and mapping onto the protein structure of PF00118. A) 3DCN of the Pfam family PF00118 (pdb code: 1A6D). Catalytic MI3D clusters were coloured yellow, orange, green and blue. Clusters with less than 10 residues were coloured grey. The size of a node is proportional to the number of residues in the MI3D cluster. (B) Ribbon representation of the MI3D clusters of the representative structure of PF00118. Catalytic residues represented as red balls and sticks. (C) Surface representation of the view in B. (D) Same as A rotated 180 degrees. (E) Surface representation of the view in D.
(PDF)
Ratio of betweenness centrality in the MI3D cluster network. Ratio of the betweenness centrality of catalytic MI3D clusters vs non-catalytic MI3D clusters within the same Pfam (mean = 12.89; median = 6.5).
(TIFF)
Flowchart of the clustering process. (A) In the MIN, residues are connected if they share a MI value >6 (black lines); in the DN, residues are connected if they are closer than 5 Å (red lines). (B) The MCL clustering algorithm identified MI clusters according to their density of connections. (C) MI clusters are mapped onto the 3D space of the protein, forming MI3D clusters (note that their connectivity pattern is no longer based on their MI values but on their physical distance). (D) MI3D clusters are connected if any of their residues are close in space, forming a MI3D cluster network.
(PDF)
OMIM mutations within MI3D clusters. Mutations described by OMIM database in human proteins and their corresponding mutated position in the reference sequence. All mutations but one fall within a catalytic MI3D cluster.
(XLS)
Definition of topological parameters. A local parameter characterizes a single node. A global parameter characterizes the whole network.
(PDF)
Small-world characteristics in MINs and DNs. Calculation of clustering coefficient (C) and characteristic path length (L) for random networks and regular networks. Comparison of MINs and DNs to random and regular networks highlights their small-world structure.
(PDF)
Spatial clustering of Distance Networks. Description of the clustering process of DNs to obtain spatial clusters. Evaluation of the performance of the prediction of functional residues using spatial clusters.
(PDF)
Footnotes
Competing Interests: GRIB-UPF/IMIM is not the name of a commercial company but a research center in a university (GRIB:Grup de Recerca en Informatica Biomedica; UPF: Universitat Pompeu Fabra; IMIM: Institut Municipal d’Investigacio Medica). The authors have now clarified this in the Affiliation section. Because all three authors of the manuscript are working in publicly-funded academic research, no competing interests exist. The authors have declared that no competing interests exist.
Funding: This work was supported by grants from the Spanish Ministry of Science and Innovation and the Argentine Ministry of Science AR2009-0015. BO and DA acknowledge support from the European Regional Development Fund BIO2008-0205. CMB acknowledges support from Consejo Nacional de Investigaciones Científicas y Técnicas. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Marino Buslje C, Teppa E, Di Doménico T, Delfino JM, Nielsen M. Networks of High Mutual Information Define the Structural Proximity of Catalytic Sites: Implications for Catalytic Residue Identification. PLoS Comput Biol. 2010;6:e1000978. doi: 10.1371/journal.pcbi.1000978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.del Sol A, Fujihashi H, Amoros D, Nussinov R. Residues crucial for maintaining short paths in network communication mediate signaling in proteins. Mol Syst Biol 2. 2006. [DOI] [PMC free article] [PubMed]
- 3.Venner E, Lisewski AM, Erdin S, Ward RM, Amin SR, et al. Accurate Protein Structure Annotation through Competitive Diffusion of Enzymatic Functions over a Network of Local Evolutionary Similarities. PLoS ONE. 2010;5:e14286. doi: 10.1371/journal.pone.0014286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Byung-Chul L, Keunwan P, Dongsup K. Analysis of the residue-residue coevolution network and the functionally important residues in proteins. Proteins: Structure, Function, and Bioinformatics. 2008;72:863–872. doi: 10.1002/prot.21972. [DOI] [PubMed] [Google Scholar]
- 5.Chakrabarti S, Panchenko AR. Coevolution in defining the functional specificity. Proteins: Structure, Function, and Bioinformatics. 2009;75:231–240. doi: 10.1002/prot.22239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Kuipers RKP, Joosten H-J, Verwiel E, Paans S, Akerboom J, et al. Correlated mutation analyses on super-family alignments reveal functionally important residues. Proteins: Structure, Function, and Bioinformatics. 2009;76:608–616. doi: 10.1002/prot.22374. [DOI] [PubMed] [Google Scholar]
- 7.Gloor GB, Martin LC, Wahl LM, Dunn SD. Mutual information in protein multiple sequence alignments reveals two classes of coevolving positions. Biochemistry. 2005;44:7156–7165. doi: 10.1021/bi050293e. [DOI] [PubMed] [Google Scholar]
- 8.Lockless SW, Ranganathan R. Evolutionarily Conserved Pathways of Energetic Connectivity in Protein Families. Science. 1999;286:295–299. doi: 10.1126/science.286.5438.295. [DOI] [PubMed] [Google Scholar]
- 9.Shi Z, Resing KA, Ahn NG. Networks for the allosteric control of protein kinases. Current Opinion in Structural Biology. 2006;16:686–692. doi: 10.1016/j.sbi.2006.10.011. [DOI] [PubMed] [Google Scholar]
- 10.Halabi N, Rivoire O, Leibler S, Ranganathan R. Protein Sectors: Evolutionary Units of Three-Dimensional Structure. Cell. 2009;138:774–786. doi: 10.1016/j.cell.2009.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Amitai G, Shemesh A, Sitbon E, Shklar M, Netanely D, et al. Network Analysis of Protein Structures Identifies Functional Residues. Journal of Molecular Biology. 2004;344:1135–1146. doi: 10.1016/j.jmb.2004.10.055. [DOI] [PubMed] [Google Scholar]
- 12.del Sol A, Arauzo-Bravo M, Amoros D, Nussinov R. Modular architecture of protein structures and allosteric communications: potential implications for signaling proteins and regulatory linkages. Genome Biology. 2007;8:R92. doi: 10.1186/gb-2007-8-5-r92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Buslje CM, Santos J, Delfino JM, Nielsen M. Correction for phylogeny, small number of observations and data redundancy improves the identification of coevolving amino acid pairs using mutual information. Bioinformatics. 2009;25:1125–1131. doi: 10.1093/bioinformatics/btp135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Amaral LAN, Scala A, Barthélémy M, Stanley HE. Classes of small-world networks. Proceedings of the National Academy of Sciences. 2000;97:11149–11152. doi: 10.1073/pnas.200327197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Atilgan AR, Akan P, Baysal C. Small-World Communication of Residues and Significance for Protein Dynamics. Biophysical Journal. 2004;86:85–91. doi: 10.1016/S0006-3495(04)74086-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Greene LH, Higman VA. Uncovering Network Systems Within Protein Structures. Journal of Molecular Biology. 2003;334:781–791. doi: 10.1016/j.jmb.2003.08.061. [DOI] [PubMed] [Google Scholar]
- 17.Dunn SD, Wahl LM, Gloor GB. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics. 2008;24:333–340. doi: 10.1093/bioinformatics/btm604. [DOI] [PubMed] [Google Scholar]
- 18.Shackelford G, Karplus K. Contact prediction using mutual information and neural nets. Proteins: Structure, Function, and Bioinformatics. 2007;69:159–164. doi: 10.1002/prot.21791. [DOI] [PubMed] [Google Scholar]
- 19.Wagner A, Fell DA. The small world inside large metabolic networks. Proceedings of the Royal Society of London Series B: Biological Sciences. 2001;268:1803–1810. doi: 10.1098/rspb.2001.1711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jeong H, Tombor B, Albert R, Oltvai ZN, Barabasi AL. The large-scale organization of metabolic networks. Nature. 2000;407:651–654. doi: 10.1038/35036627. [DOI] [PubMed] [Google Scholar]
- 21.Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’ networks. Nature. 1998;393:409–10. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- 22.Vendruscolo M, Dokholyan NV, Paci E, Karplus M. Small-world view of the amino acids that play a key role in protein folding. Phys Rev E Stat Nonlin Soft Matter Phys. 2002;65:061910. doi: 10.1103/PhysRevE.65.061910. [DOI] [PubMed] [Google Scholar]
- 23.Chakrabarti S, Panchenko AR. Structural and functional roles of coevolved sites in proteins. PloS one. 2010;5:e8591. doi: 10.1371/journal.pone.0008591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dunn SD, Wahl LM, Gloor GB. Mutual information without the influence of phylogeny or entropy dramatically improves residue contact prediction. Bioinformatics. 2007;24:333–340. doi: 10.1093/bioinformatics/btm604. [DOI] [PubMed] [Google Scholar]
- 25.Socolich M, Lockless SW, Russ WP, Lee H, Gardner KH, et al. Evolutionary information for specifying a protein fold. Nature. 2005;437:512–518. doi: 10.1038/nature03991. [DOI] [PubMed] [Google Scholar]
- 26.Yeang CH, Haussler D. Detecting coevolution in and among protein domains. PLoS Comput Biol. 2007;3:e211. doi: 10.1371/journal.pcbi.0030211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Kowarsch A, Fuchs A, Frishman D, Pagel P. Correlated Mutations: A Hallmark of Phenotypic Amino Acid Substitutions. PLoS Comput Biol. 2010;6:e1000923. doi: 10.1371/journal.pcbi.1000923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Knaggs MH, Salsbury Jr FR, Edgell MH, Fetrow JS. Insights into Correlated Motions and Long-Range Interactions in CheY Derived from Molecular Dynamics Simulations. Biophysical Journal. 2007;92:2062–2079. doi: 10.1529/biophysj.106.081950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Bleicher L, Lemke N, Garratt RC. Using Amino Acid Correlation and Community Detection Algorithms to Identify Functional Determinants in Protein Families. PLoS ONE. 2011;6:e27786. doi: 10.1371/journal.pone.0027786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Porter CT, Bartlett GJ, Thornton JM. The Catalytic Site Atlas: a resource of catalytic sites and residues identified in enzymes using structural data. Nucl Acids Res. 2004;32:D129–133. doi: 10.1093/nar/gkh028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Bartlett GJ, Porter CT, Borkakoti N, Thornton JM. Analysis of Catalytic Residues in Enzyme Active Sites. Journal of Molecular Biology. 2002;324:105–121. doi: 10.1016/s0022-2836(02)01036-7. [DOI] [PubMed] [Google Scholar]
- 32.Finn RD, Tate J, Mistry J, Coggill PC, Sammut SJ, et al. The Pfam protein families database. Nucl Acids Res. 2008;36:D281–288. doi: 10.1093/nar/gkm960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.White RA, Szurmant H, Hoch JA, Hwa T. Melvin I. Simon BRC, Alexandrine C, editors. Features of Protein–Protein Interactions in Two-Component Signaling Deduced from Genomic Libraries. 2007. pp. 75–101. Methods in Enzymology: Academic Press. [DOI] [PubMed]
- 34.Weil P, Hoffgaard F, Hamacher K. Estimating sufficient statistics in co-evolutionary analysis by mutual information. Computational Biology and Chemistry. 2009;33:440–444. doi: 10.1016/j.compbiolchem.2009.10.003. [DOI] [PubMed] [Google Scholar]
- 35.Hamacher K. Relating sequence evolution of HIV1-protease to its underlying molecular mechanics. Gene. 2008;422:30–36. doi: 10.1016/j.gene.2008.06.007. [DOI] [PubMed] [Google Scholar]
- 36.Van Dongen S. Graph clustering by flow simulation. PhD thesis. 2000.
- 37.Brohee S, Faust K, Lima-Mendez G, Vanderstocken G, van Helden J. Network Analysis Tools: from biological networks to clusters and pathways. Nat Protocols. 2008;3:1616–1629. doi: 10.1038/nprot.2008.100. [DOI] [PubMed] [Google Scholar]
- 38.Reichardt J, Bornholdt S. Statistical mechanics of community detection. Physical Review E. 2006;74:016110. doi: 10.1103/PhysRevE.74.016110. [DOI] [PubMed] [Google Scholar]
- 39.Hagberg A, Schult D, Swart P. Exploring network structure, dynamics, and function using NetworkX. Proceedings of the 7th Python in Science Conference (SciPy2008) Edited by Gäel Varoquaux, Travis Vaught, Jarrod Millman. 2008. 6
- 40.R Development Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. 2010.
- 41.Maritz J. Distribution-Free Statistical Methods. London: Chapman & Hall. 1981.
- 42.The Uniprot Consortium. The Universal Protein Resource (UniProt) in 2010. Nucl Acids Res. 2010;38:D142–D148. doi: 10.1093/nar/gkp846. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
MIN and DN for the Pfam family PF00884. (A) Representation of the MI network of the PF00884 family. Colours other than grey indicate the eight largest MI clusters. (B) Representation of the distance network calculated from the PDB structure 1AUK chain A, representative of the PF00884 family. Residues are coloured as in A.
(PNG)
Distribution of modularity of MI clusters and MI3D clusters. Fraction of Pfam families versus the modularity of the partition. Blue: partition of MI clusters (mean = 0.461). Orange: partition of MI3D clusters (mean = 0.359). Modularity values larger than 0 indicate a partition of the network resulting in denser clusters than random expectation.
(TIFF)
Distribution of the number of MI clusters and MI3D clusters. Thick line: distribution of the number of MI clusters (mean = 11.97). Thin line: distribution of the number of MI3D clusters (mean = 10.47).
(TIFF)
Size distribution of MI and MI3D clusters. Blue dots: size distribution of MI clusters (mean = 13.53; median = 6). Orange dots: size distribution of MI3D clusters (mean = 13.25; median = 6).
(TIFF)
Distribution of the number of MI3D clusters. Orange line: distribution of the number of catalytic MI3D clusters (mean = 3.40, median = 3). Blue line: distribution of the number of non-catalytic MI3D clusters (mean = 7.28, median = 7.28).
(TIFF)
Ratio of the number of non-catalytic MI3D clusters vs catalytic MI3D clusters. Ratio of the number of non-catalytic MI3D clusters vs catalytic MI3D clusters per Pfam (mean = 2.65, median = 2).
(TIFF)
Size ratio of catalytic MI3D clusters vs non-catalytic MI3D clusters. Size ratio of catalytic MI3D clusters vs non-catalytic MI3D clusters of the same Pfam (mean ratio = 4.12, median = 2.97).
(TIFF)
Fraction of co-evolving residues between catalytic MI3D clusters. The fraction of co-evolving residues between catalytic MI3D clusters is compared to random expectation by means of a z-score. The higher frequency of negative z-scores means that, for most Pfams, co-evolution between catalytic MI3D clusters is smaller than expected by chance.
(TIFF)
Origin of catalytic and non-catalytic MI3D clusters. Blue line: fraction of all MI clusters in a Pfam which produce non-catalytic MI3D clusters when mapped onto space (only Pfams with at least one non-catalytic MI3D cluster considered). Orange line: fraction of all MI clusters in a Pfam which produce catalytic MI3D clusters (only Pfams with at least one catalytic MI3D cluster considered). Black line: fraction of all MI clusters in a Pfam which produce both catalytic and non-catalytic MI3D clusters (only Pfams with catalytic and non-catalytic MI3D clusters considered). For 76.8% of the Pfams with catalytic and non-catalytic MI3D clusters, no MI clusters produce both catalytic and non-catalytic MI3D clusters when mapped onto space, with significantly less than random expectation (97.6%), KS test p-value = 9.67*10−11 (consequently, for 23.2% of Pfams there is at least one MI cluster which produces both catalytic and non-catalytic MI3D clusters). 10% of MI clusters out of 17.6% of Pfams produce catalytic and non-catalytic MI3D clusters.
(TIFF)
Network of MI3D clusters and mapping onto the protein structure of PF01979. (A) 3DCN of the Pfam family PF01979 (pdb code: 1KRA). Catalytic MI3D clusters were coloured yellow, orange and cyan. Clusters with less than 10 residues were coloured grey. The size of a node is proportional to the number of residues in the MI3D cluster. (B) Ribbon representation of the MI3D clusters of the representative structure of PF1979. Catalytic residues represented as red balls and sticks. (C) Surface representation of the view in B. (D) Same as A rotated 180 degrees. (E) Surface representation of the view in D.
(PDF)
Network of MI3D clusters and mapping onto the protein structure of PF00118. A) 3DCN of the Pfam family PF00118 (pdb code: 1A6D). Catalytic MI3D clusters were coloured yellow, orange, green and blue. Clusters with less than 10 residues were coloured grey. The size of a node is proportional to the number of residues in the MI3D cluster. (B) Ribbon representation of the MI3D clusters of the representative structure of PF00118. Catalytic residues represented as red balls and sticks. (C) Surface representation of the view in B. (D) Same as A rotated 180 degrees. (E) Surface representation of the view in D.
(PDF)
Ratio of betweenness centrality in the MI3D cluster network. Ratio of the betweenness centrality of catalytic MI3D clusters vs non-catalytic MI3D clusters within the same Pfam (mean = 12.89; median = 6.5).
(TIFF)
Flowchart of the clustering process. (A) In the MIN, residues are connected if they share a MI value >6 (black lines); in the DN, residues are connected if they are closer than 5 Å (red lines). (B) The MCL clustering algorithm identified MI clusters according to their density of connections. (C) MI clusters are mapped onto the 3D space of the protein, forming MI3D clusters (note that their connectivity pattern is no longer based on their MI values but on their physical distance). (D) MI3D clusters are connected if any of their residues are close in space, forming a MI3D cluster network.
(PDF)
OMIM mutations within MI3D clusters. Mutations described by OMIM database in human proteins and their corresponding mutated position in the reference sequence. All mutations but one fall within a catalytic MI3D cluster.
(XLS)
Definition of topological parameters. A local parameter characterizes a single node. A global parameter characterizes the whole network.
(PDF)
Small-world characteristics in MINs and DNs. Calculation of clustering coefficient (C) and characteristic path length (L) for random networks and regular networks. Comparison of MINs and DNs to random and regular networks highlights their small-world structure.
(PDF)
Spatial clustering of Distance Networks. Description of the clustering process of DNs to obtain spatial clusters. Evaluation of the performance of the prediction of functional residues using spatial clusters.
(PDF)