A 250 GHz Gyrotron with a 3 GHz Tuning Bandwidth for Dynamic Nuclear Polarization

Abstract

We describe the design and implementation of a novel tunable 250 GHz gyrotron oscillator with >10 W output power over most of a 3 GHz band and >35 W peak power. The tuning bandwidth and power are sufficient to generate a >1 MHz nutation frequency across the entire nitroxide EPR lineshape for cross effect DNP, as well as to excite solid effect transitions utilizing other radicals, without the need for sweeping the NMR magnetic field. Substantially improved tunability is achieved by implementing a long (23 mm) interaction cavity that can excite higher order axial modes by changing either the magnetic field of the gyrotron or the cathode potential. This interaction cavity excites the rotating TE_5,2,q mode, and an internal mode converter outputs a high-quality microwave beam with >94% Gaussian content. The gyrotron was integrated into a DNP spectrometer, resulting in a measured DNP enhancement of 54 on the membrane protein bacteriorhodopsin.

1. Introduction

Dynamic nuclear polarization (DNP) increases the sensitivity of NMR experiments by transferring the relatively large polarization of electron spins to nuclear spins [1; 2]. The theoretical limit of increased polarization enhancement is a factor of 657 in the case of DNP of ¹H nuclear spins and experimentally achieved DNP enhancements of up to 400[3] have resulted in reductions of signal averaging times by factors of 160,000. Pioneering demonstrations of the improvement in sensitivity available with DNP in a wide range of biological and material science applications,[4–10] in conjunction with advances in high-resolution solid-state NMR methodology,[11; 12; 13; 14] offer the promise of major advances in the understanding of biological molecular architecture at the atomic level. As relatively lower (15–40) enhancements are achieved on biologically relevant samples [6; 11; 12] there is considerable room for improvement in DNP as it applies to investigating problems of biomedical importance. In particular, the efficiency of the DNP process depends on many parameters but one of the most straightforward ways to improve DNP performance is to deliver additional millimeter radiation to the sample by increasing the power output of the microwave source.[13]

Gyrotron oscillators (cyclotron resonance masers) are an excellent microwave power source for DNP[14] due to their relatively high power levels compared to solid-state devices (roughly three orders of magnitude more power), long lifetimes, and efficient scaling to higher frequency. In applications with an NMR experiment in a magnet without a sweep coil, the gyrotron should have a wide tuning bandwidth. Furthermore, in order to gain significant improvement in NMR sensitivity it is of paramount importance, that a substantial power level be maintained over the entire band to be utilized for DNP. Obtaining stronger microwave fields across the sample can improve DNP enhancements from the cross effect mechanism, which is effective at high frequencies.[15; 16] The enhancement ε is defined as the ratio of the signal intensities with and without microwave power. For example, the cross effect (CE) performs much better with 10 W of 250 GHz gyrotron power (ε=120 on a standard sample of urea dissolved with TOTAPOL[17] in frozen in a glassy matrix) compared to 5 W (ε=80).[18] DNP enhancements from the solid effect (SE) have an even stronger, nearly linear dependence, on the microwave field strength. For example, Smith et al.[19] recently demonstrated a solid effect enhancement of ε=94 at 80 Kelvin (with an electron nutation frequency of 3.5 MHz), which is a drastic improvement from the previously reported highest enhancement using the SE at 140 GHz of ε=15.[20] We note that such substantial B_1S field strengths were achieved with ~140 mW of power from a solid-state source and a high quality factor resonator at 140 GHz.

For magic angle spinning (MAS) experiments, geometrical restrictions on the sample holder such as the large volume (~60 μl) of a lossy sample and the sample coil constrain the design of a high-Q resonator. Thus, the most straightforward strategy to increase the strength of the B_1S field at the sample (and thus the DNP enhancement) is to increase the output power of the microwave source, in this case a gyrotron oscillator. In addition to higher continuous wave output powers, expanding the bandwidth of DNP gyrotrons[21] is advantageous while developing polarizing agents and polarization transfer mechanisms that rely on different microwave frequency matching conditions[22].

2. Design

A schematic of a high-power and widely tunable gyrotron is shown in Fig. 1 and its operating parameters are listed in Table 1. The source of microwave power is an electron beam generated from a magnetron injection gun labeled at the bottom of Fig 1.[23] The emission cathode of the gun is an annular ring of a barium impregnated tungsten matrix (Semicon Associates, KY). The gyrotron is a vacuum electron device, in which the chamber inside the tube must be kept at very low pressure, typically ≤ ~10⁻⁸ torr. Careful attention must be paid to the vacuum seals (welds, brazes, compression flanges) and tube components to ensure a clean and tight inner vacuum space. Substantial gas in the tube can react with the inorganic substrate surface of the heated cathode, thus poisoning the cathode and terminating the emission.

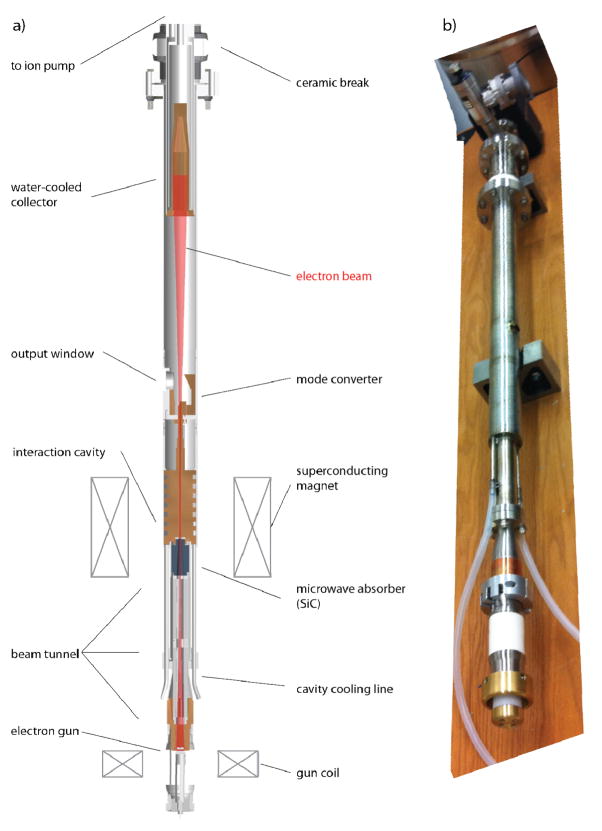
Fig. 1.

Schematic (a) and photograph (b) of the 250 GHz tunable gyrotron oscillator. The electron beam is launched from the electron gun and is focused by the magnetic field gradient, which can be finely adjusted with the gun coil magnet. After depositing energy in the form of microwave power in the interaction cavity, the electron beam is safely collected in the water-cooled collector at the top of the vacuum tube.

Tab. 1.

Gyrotron operating parameters

Operating mode TEm,n,q	TE5,2,q
Frequency	248.2 GHz
Tuning range	2.9 GHz
Cavity magnetic field B	9.03–9.29 T
Cyclotron harmonic	First
Beam Voltage Vb	8–13.5 kV
Beam current Ib	50–180 mA
Output power	>10 W over band, >35 W peak
Compression	28

A high voltage power supply (Spellman, NY) maintains a ≤15 kV potential between the cathode and anode while drawing up to 200 mA, thus generating a maximum of 3 kW of beam power. Roughly 2.5 A of alternating current rides on top of the high-voltage to heat the cathode for electron beam emission. Thus, even if the device operates at a modest efficiency of 2.5%, the microwave power output is 150 W of ~250 GHz radiation. This is one of the appealing features of using gyrotrons for DNP microwave sources.

The electron beam power to microwave power conversion efficiency of gyrotron oscillators varies widely, ranging from ~10 % in a recently published commercially available gyrotron for DNP,[24] to 55% in gyrotrons designed for fusion heating experiments.[25]

Gyrotrons operating in the higher efficiency regime can output >1 MW of power continuously for >1000 seconds.[25] DNP gyrotrons therefore can be designed for output power levels well above the levels required for saturation of DNP enhancements.

The annular electron beam is emitted from the cathode with a radius of r_c = 5.38 mm and is adiabatically compressed by the magnetic field gradient to a radius of r_g = 1.02 mm in the interaction cavity, where the beam interacts with the TE_5,2,q mode supported by the cylindrical copper cavity. The transverse electric (TE) eigenmodes of the cavity are denoted TE_m,n,q, where m is the azimuthal index; n the radial index and q the axial index. For long cavities, the modes with different q values are closely spaced and can form a continuum when the electron beam is present. This family of axial modes, when m=5 and n=2 is denoted as the TE_5,2,q mode or, in some cases for convenience, simply the TE_5,2 mode. Adiabatic beam compression, $B_c{r}_c^2=B_0{r}_g^2$ where B_c and B₀ are the axial magnetic fields at the cathode and cavity, allows for fine tuning using a resistive gun coil magnet (Fig. 1) to optimize the overlap of the beam with the first radial maximum of the interaction cavity mode (Fig. 2).[26] This interaction leads to bunching of the electrons in phase space allowing them to coherently deposit energy into the operating mode as microwave power near the cyclotron resonance frequency,

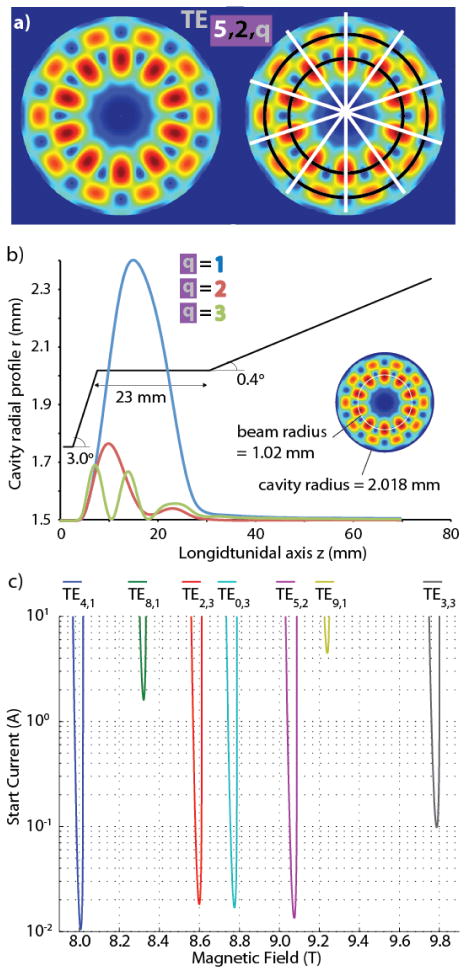
Fig. 2.

The interaction cavity a) the transverse electric field distribution of the TE_m,n,q = TE_5,2,q mode (left), with the m=5 radial lines of symmetry shown in white, and the n=2 azimuthal lines showing the radial maxima in black (right). b) The cavity geometry profile and intensity of the electric field along the long axis of the cavity of the first 3 axial modes are shown in blue, red, and green, respectively. The beam (white circle) overlaps with the 1^st radial maximum in the interaction mode to promote optimal interaction (right). c) Mode map showing accessible modes within 1 Tesla of the target TE_5,2 mode.

$${\mathrm{\Omega }}_C={eB}_O/\gamma m_e$$ (2)

where e is the charge of the electron, B₀ is the static magnetic field, γ is the Lorentz factor, and m is the mass of the electron.[27] For gyrotron oscillators operating in the fundamental cyclotron resonance condition such as this device, eq. 2 leads to an operating magnetic field roughly ~2% higher than the NMR magnet required for the gyrotron. We emphasize that tuning of gyrotron oscillators is not merely a case of leveraging the linear relationship of the cyclotron resonance frequency and gyrotron magnetic field described in eq. 2; all gyrotrons cannot be effectively tuned by changing the magnetic field due to the quantized nature of the electromagnetic radiation in the interaction cavity. Careful attention must be paid to making the beam interaction with the cavity mode continuous with frequency, as we discuss in the following section.

Following the interaction cavity, a mode converter and window allow for coupling of the ~250 GHz radiation out of the tube. The electron beam expands as it leaves the interaction cavity and is safely collected in a water-cooled collector indicated at the top of Fig 1.

Interaction Cavity

The rotating TE_5,2,q mode was selected because of its efficient interaction with the 1 mm radius electron beam and isolation from competing modes. For example, the nearest mode is the TE_9,1 at 253 GHz as is illustrated in Fig 2c. Even with the full 4 GHz of separation (see Fig 2c) between the two modes, mode competition with the TE_9,1 ultimately limited the bandwidth of this tunable oscillator, emphasizing the importance of selecting well-separated modes while designing highly tunable gyrotrons. Microwave power spanning 15 GHz (but not continuous tuning) was generated from operating the device in the TE_2,3, TE_0,3, and TE_9,1 along with the targeted TE_5,2 mode. However, each mode has a different electric field distribution and thus a single optimal electron beam radius to promote optimal interaction between the cavity mode and electron beam. This makes it challenging to run the device efficiently in modes other than the target mode, as both the cavity geometry and beam radius were designed specifically for the TE_5,2,q mode. Additionally, the mode converter discussed in the next section is specific for mode conversion of the TE_5,2,q mode, and cannot generally convert another mode efficiently to a Gaussian distribution. These constraints prohibit continuous, extremely wideband (>5 GHz) operation of the device between transverse modes.

To increase continuous tuning performance in the TE_5,2,q mode, the cavity profile was optimized to support hybridized axial modes by extending the length of the cavity to 23 mm (19λ, where λ is the free-space wavelength).[23] Calculations performed with the gyrotron simulation code MAGY[28] of the electric field intensity of the first three axial modes (q = 1,2,3) are shown in Fig. 2b. The first axial mode (q = 1, blue) interacts much more strongly with the electron beam, but there is still considerable intensity in the second and third (q=2, 3) modes as well. This manifests as a higher beam power requirement (190 mA beam current) while operating the device in the higher order axial modes in order to achieve the same output power as the fundamental (q=1) axial mode (50 mA beam current). Operation in each axial mode tunes the frequency output by a few hundred MHz and can yield continuous tuning of the device.[29]

As is usual for gyrotron cavities, the up-taper was designed to minimize wave reflections and mode conversion of the microwave radiation as it exits the cylindrical resonator. However, whereas previous designs have employed several steps in the radius after the interaction cavity to vary the taper angle, this design incorporates a single straight up-taper that allows the cavity and up-taper to be directly machined in oxygen free high conductivity copper (Midwest Precision Tool and Die, SD) rather than electroforming.

Internal Mode Converter

The microwave power is transmitted with low loss from the interaction cavity to the sample which is located ~3.5 meters away in an NMR magnet using corrugated overmoded waveguide, quasioptics, and an NMR/DNP probe described previously.[18; 30; 31] To couple into the Gaussian-like HE₁₁ mode supported inside the corrugated waveguide with low insertion loss, and to transmit efficiently through the waveguide and quasioptics, the power distribution of the millimeter waves should have a Gaussian field distribution. However, the microwave radiation generated in the TE_5,2,q mode leaves the cavity as a traveling TE_5,2 mode having the transverse field distribution shown in Fig. 2a. Such a higher order mode is then converted to a Gaussian-like mode by an internal mode converter A helically cut Vlasov launcher shown in Fig. 3 radiates the rotating TE_5,2 mode onto an off-axis parabolic mirror. The radiation then reflects off two concave mirrors that focus the beam, directing it out of the tube through a sapphire window. The launcher and mirrors are designed to convert the TE_5,2 to a beam with >94% Gaussian content (Fig. 4), resulting in low insertion loss while coupling into the corrugated waveguide external to the gyrotron tube. The beam pattern shown in Fig. 4., as well as the power measurements discussed in the results section were recorded 1.5 m from the output window, directly out of the aperture of the 22 mm corrugated waveguide. The power was measured with a calorimeter calibrated to the absorption of 250 GHz microwaves.

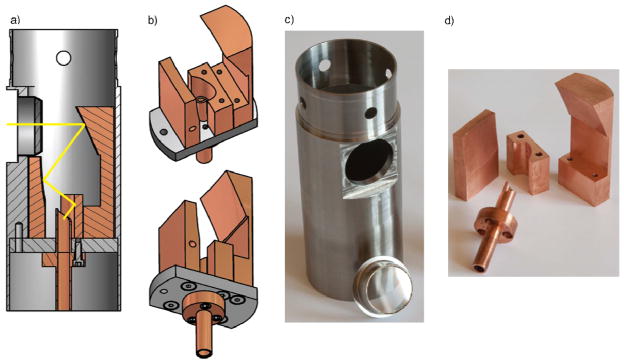
Fig. 3.

Internal mode converter and window a) schematic of the cross section showing the path of the microwaves in yellow b) solid rendition schematic showing how the mirrors and launcher are bolted to the stainless steel mount c) photograph of the viewport and stainless steel housing prior to assembly d) photograph of the copper helical cut Vlasov launcher and three mirrors of the mode converter

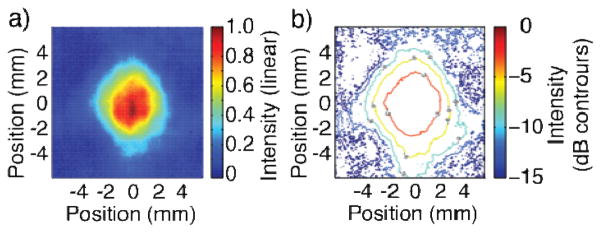
Fig. 4.

Output millimeter beam intensity recorded with a pyroelectric camera showing a high-quality beam with >94 % Gaussian content demonstrating successful mode conversion from the TE_5,2. a) linear intensity b) logarithmic contour plot

Fabrication

The majority of the stainless steel and copper components of the gyrotron tube were fabricated in machine shops with conventional capabilities. However, certain components required custom machining services for example, for hard materials or tight tolerances. Thus, the SiC used in the beam absorber (Fig. 1) was fabricated by a company specializing in ceramics machining (International Ceramic Engineering, Worcester, MA). Furthermore, the radius of the cavity, which primarily defines the gyrotron output frequency, was machined to the highest available tolerances (Midwest Precision Tool and Die, Sioux Falls, SD). The output frequency varies roughly 120 MHz per μm of cavity radius, which was fabricated 5 μm wider than we specified, resulting in a bandwidth centered 600 MHz lower than targeted. However, the bandwidth of the gyrotron was sufficient to compensate for this 600 MHz frequency shift, as described in the next section.

The gyrotron is a vacuum electron device in which the pressure inside the tube is typically maintained at ≤10⁻⁸ torr. Accordingly, careful attention to the vacuum seals (welds, brazes, compression flanges) and tube components is required to ensure a clean and tight inner vacuum space. The copper sections in the electron gun and collector were nickel-brazed at ~1050 °C (Tecomet, Wilmington, MA) and checked to be vacuum tight before installation into the remainder of the tube assembly. The ceramic breaks (see Fig. 1) were purchased (Insulator Seal Inc, Sarasota, FL), and then welded to the tube body at the MIT central machine shop. Similarly, the sapphire window was fabricated (Insaco, Quakertown, PA), and brazed into a standard Kovar/stainless steel composite viewport (Insulator Seal, Inc., Sarasota, FL). The viewport was electron-beam welded into the stainless supporting structure shown in Fig. 3 (PTR-Precision Technologies, Inc., Enfield, CT). All stainless steel sections were assembled by conventional tungsten inert gas (TIG) welding, and subsequently leak-checked.

3. Results

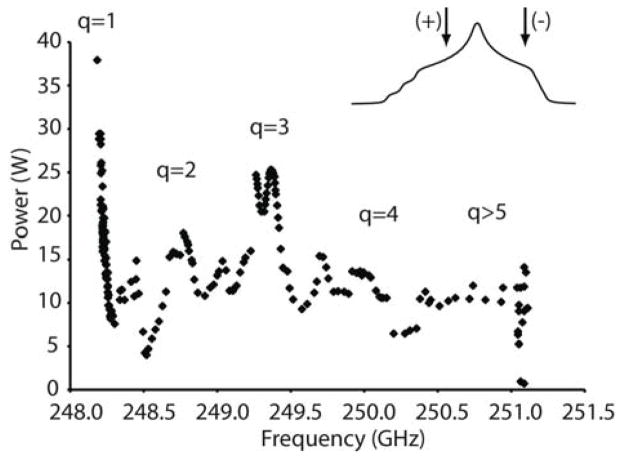
Fig. 5 shows the output power as a function of frequency in continuous operation of the gyrotron. The gyrotron magnetic field was varied between 9.01 to 9.26 T, the cathode potential from 8.5 to 10.5 kV, and the beam current from 40 to 190 mA. The power frequency profile in Fig. 5 illustrates high-power tuning across the first 5 axial modes. Pure, or hybridized mixtures of the q=1–5 axial modes results in the power output being continuous, maintaining >5 W over the entire 3 GHz band, with only two small dips below the 10 W power level at 248.5 and 250.3 GHz. Greater than 35 W of output power (average γB_1S/2π ~ 2 MHz across the NMR sample) is available in the fundamental q=1 axial mode with a modest beam current of 60 mA, and access to the q=3 axial mode generates greater than 25 W at 249.4 GHz.

Fig. 5.

Power and bandwidth of the 250 GHz gyrotron. 10 W is available over most of the 3 GHz band The nitroxide EPR lineshape at the given NMR field strength along with the optimal cross effect conditions leading to positive and negative enhancement (spectra in Fig. 6) are shown in the upper right.

The frequency stability of the output is ≤±30 MHz over a > 36 hour period. The spectral purity, although not specifically measured from this gyrotron is expected to be <1 MHz, similar to that demonstrated previously, [32; 33] [34] and is governed by the voltage stability of the power supply. Maintenance of stable electron beam power through control of the beam current minimizes microwave power fluctuations and results in < ±1% short-term and long-term power deviation. [23; 24; 35]

The high frequency edge of the 3 GHz band has 10 W of output power available over most of the nitroxide EPR lineshape, with the NMR/DNP magnet set at 8.93 T (see Fig. 5). Even using this lower power edge of the bandwidth, a positive enhancement of 54 (Fig. 6) was achieved on a membrane protein sample with 10 W of 250.572 GHz power output. This value is ~25% higher than previous enhancements of 42 achieved on the same sample[36]. Remarkably, the gyrotron frequency can be shifted by 460 MHz to the high-frequency side of the nitroxide lineshape by altering only the cathode potential by 1.2 kV, resulting in a negative enhancement of −42.

Fig. 6.

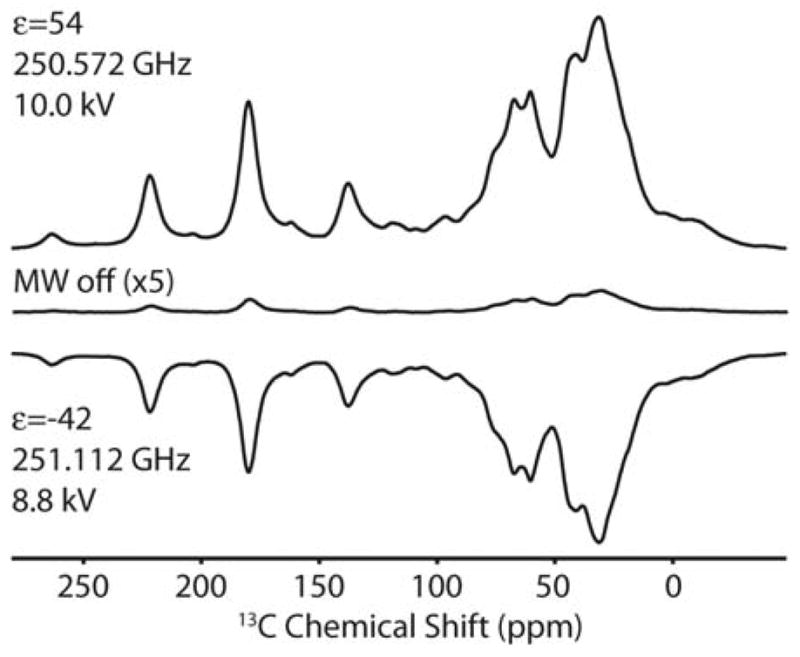
Enhancements on the membrane protein, bacteriorhodopsin, with the tunable gyrotron. Changing the cathode potential by 1.2 kV shifts the output frequency 460 MHz, which is sufficient to lead to a positive enhancement of +54 (top) and negative enhancement of −42 (bottom). The gyrotron and NMR magnets were held constant at 9.12 T, 8.93 T (¹H resonant frequency of 380.378 MHz), respectively. The spinning frequency was 4 kHz and the sample temperature 81 K.

4. Conclusions and Outlook

Significant improvements of the continuous power output (~10 W) over a substantial 3 GHz tuning bandwidth have been demonstrated and explained employing a long interaction cavity that allows access to higher order axial modes. Even while operating this device at the lower-power edge of the band, DNP enhancements 25% higher than previously reported are achievable on membrane protein samples. Changing the magnetic field of the NMR magnet to shift the nitroxide EPR lineshape into the higher-power region of the bandwidth, or changing the radius of the interaction cavity to shift the frequency band of the gyrotron, should result in further improvements in enhancement.