Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2012 Jul 26;2:521. doi: 10.1038/srep00521

Measuring the Evolution of Contemporary Western Popular Music

Joan Serrà 1,a, Álvaro Corral 2, Marián Boguñá 3, Martín Haro 4, Josep Ll Arcos 1
PMCID: PMC3405292  PMID: 22837813

Abstract

Popular music is a key cultural expression that has captured listeners' attention for ages. Many of the structural regularities underlying musical discourse are yet to be discovered and, accordingly, their historical evolution remains formally unknown. Here we unveil a number of patterns and metrics characterizing the generic usage of primary musical facets such as pitch, timbre, and loudness in contemporary western popular music. Many of these patterns and metrics have been consistently stable for a period of more than fifty years. However, we prove important changes or trends related to the restriction of pitch transitions, the homogenization of the timbral palette, and the growing loudness levels. This suggests that our perception of the new would be rooted on these changing characteristics. Hence, an old tune could perfectly sound novel and fashionable, provided that it consisted of common harmonic progressions, changed the instrumentation, and increased the average loudness.

Isn't it always the same? This question could be easily posed while listening to the music of any mainstream radio station in a western country. Like language, music is a human universal involving perceptually discrete elements displaying organization1. Therefore, contemporary popular music may have a well-established set of underlying patterns and regularities1,2,3,4, some of them potentially inherited from the classical tradition5,6,7. Yet, as an incomparable artistic product for conveying emotions8, music must incorporate variation over such patterns in order to play upon people's memories and expectations, making it attractive to listeners3,4,5. For the very same reasons, long-term variations of the underlying patterns may also occur across years9. Many of these aspects remain formally unknown or lack scientific evidence, specially the latter, which is very often neglected in music-related studies, from musicological analyses to technological applications. The study of patterns and long-term variations in popular music could shed new light on relevant issues concerning its organization, structure, and dynamics10. More importantly, it addresses valuable questions for the basic understanding of music as one of the main expressions of contemporary culture: Can we identify some of the patterns behind music creation? Do musicians change them over the years? Can we spot differences between new and old music? Is there an ‘evolution' of musical discourse?

Current technologies for music information processing11,12 provide a unique opportunity to answer the above questions under objective, empirical, and quantitative premises. Moreover, akin to recent advances in other cultural assets13, they allow for unprecedented large-scale analyses. One of the first publicly-available large-scale collections that has been analyzed by standard music processing technologies is the million song dataset14. Among others, the dataset includes the year annotations and audio descriptions of 464,411 distinct music recordings (from 1955 to 2010), which roughly corresponds to more than 1,200 days of continuous listening. Such recordings span a variety of popular genres, including rock, pop, hip hop, metal, or electronic. Explicit descriptions available in the dataset15 cover three primary and complementary musical facets2: loudness, pitch, and timbre. Loudness basically correlates with our perception of sound amplitude or volume (notice that we refer to the intrinsic loudness of a recording, not the loudness a listener could manipulate). Pitch roughly corresponds to the harmonic content of the piece, including its chords, melody, and tonal arrangements. Timbre accounts for the sound color, texture, or tone quality, and can be essentially associated with instrument types, recording techniques, and some expressive performance resources. These three music descriptions can be obtained at the temporal resolution of the beat, which is perhaps the most relevant temporal unit in music, specially in western popular music2,4.

Here we study the music evolution under the aforementioned premises and large-scale resources. By exploiting tools and concepts from statistical physics and complex networks16,17,18,19, we unveil a number of statistical patterns and metrics characterizing the general usage of pitch, timbre, and loudness in contemporary western popular music. Many of these patterns and metrics remain consistently stable for a period of more than 50 years, which points towards a great degree of conventionalism in the creation and production of this type of music. Yet, we find three important trends in the evolution of musical discourse: the restriction of pitch sequences (with metrics showing less variety in pitch progressions), the homogenization of the timbral palette (with frequent timbres becoming more frequent), and growing average loudness levels (threatening a dynamic richness that has been conserved until today). This suggests that our perception of the new would be essentially rooted on identifying simpler pitch sequences, fashionable timbral mixtures, and louder volumes. Hence, an old tune with slightly simpler chord progressions, new instrument sonorities that were in agreement with current tendencies, and recorded with modern techniques that allowed for increased loudness levels could be easily perceived as novel, fashionable, and groundbreaking.

Results

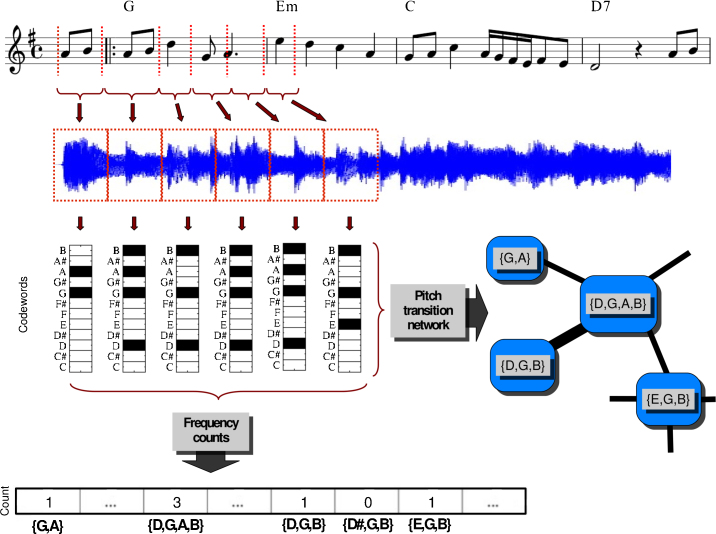
To identify structural patterns of musical discourse we first need to build a ‘vocabulary' of musical elements (Fig. 1). To do so, we encode the dataset descriptions by a discretization of their values, yielding what we call music codewords20 (see Supplementary Information, SI). In the case of pitch, the descriptions of each song are additionally transposed to an equivalent main tonality, such that all of them are automatically considered within the same tonal context or key. Next, to quantify long-term variations of a vocabulary, we need to obtain samples of it at different periods of time. For that we perform a Monte Carlo sampling in a moving window fashion. In particular, for each year, we sample one million beat-consecutive codewords, considering entire tracks and using a window length of 5 years (the window is centered at the corresponding year such that, for instance, for 1994 we sample one million consecutive beats by choosing full tracks whose year annotation is between 1992 and 1996, both included). This procedure, which is repeated 10 times, guarantees a representative sample with a smooth evolution over the years.

Figure 1. Method schematic summary with pitch data.

Figure 1

Open in a new tab

The dataset contains the beat-based music descriptions of the audio rendition of a musical piece or score (G, Em, and D7 on the top of the staff denote chords). For pitch, these descriptions reflect the harmonic content of the piece15, and encapsulate all sounding notes of a given time interval into a compact representation11,12, independently of their articulation (they consist of the 12 pitch class relative energies, where a pitch class is the set of all pitches that are a whole number of octaves apart, e.g. notes C1, C2, and C3 all collapse to pitch class C). All descriptions are encoded into music codewords, using a binary discretization in the case of pitch. Codewords are then used to perform frequency counts, and as nodes of a complex network whose links reflect transitions between subsequent codewords.

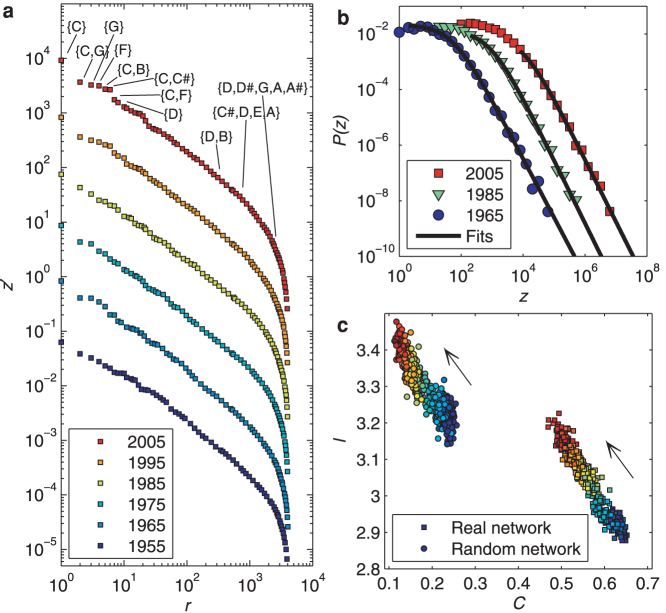
We first count the frequency of usage of pitch codewords (i.e. the number of times each codeword type appears in a sample). We observe that most used pitch codewords generally correspond to well-known harmonic items21, while unused codewords correspond to strange/dissonant pitch combinations (Fig. 2a). Sorting the frequency counts in decreasing order provides a very clear pattern behind the data: a power law17 of the form z ∝ r−α, where z corresponds to the frequency count of a codeword, r denotes its rank (i.e. r = 1 for the most used codeword and so forth), and α is the power law exponent. Specifically, we find that the distribution of codeword frequencies for a given year nicely fits to P(z) ∝ (c + z) −β for z > zmin, where we take z as the random variable22, β = 1 + 1/α as the exponent, and c as a constant (Fig. 2b). A power law indicates that a few codewords are very frequent while the majority are highly infrequent (intuitively, the latter provide the small musical nuances necessary to make a discourse attractive to listeners3,4,5). Nonetheless, it also states that there is no characteristic frequency nor rank separating most used codewords from largely unused ones (except for the largest rank values due to the finiteness of the vocabulary). Another non-trivial consequence of power-law behavior is that when α ≤ 2, extreme events (i.e. very rare codewords) will certainly show up in a continuous discourse providing the listening time is sufficient and the pre-arranged dictionary of musical elements is big enough.

Figure 2. Pitch distributions and networks.

Figure 2

Open in a new tab

(a) Examples of the rank-frequency distribution (relative frequencies z′ such that 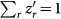Inline graphic). For ease of visualization, curves are chronologically shifted by a factor of 10 in the vertical axis. Some frequent and infrequent codewords are shown. (b) Examples of the density values and their fits, taking z as the random variable. Curves are chronologically shifted by a factor of 10 in the horizontal axis. (c) Average shortest path length l versus clustering coefficient C for pitch networks (right) and their randomized versions (left). Randomized networks were obtained by swapping pairs of links chosen at random, avoiding multiple links and self-connections. Values l and C calculated without considering the 10 highest degree nodes (see SI). Arrows indicate chronology (red and blue colors indicate values for more and less recent years, respectively).

Importantly, we find this power-law behavior to be invariant across years, with practically the same fit parameters. In particular, the exponent β remains close to an average of 2.18 ± 0.06 (corresponding to α around 0.85), which is similar to Zipf's law in linguistic text corpora23 and contrasts with the exponents found in previous small-scale, symbolic-based music studies24,25. The slope of the least squares linear regression of β as a function of the year is negligible within statistical significance (p > 0.05, t-test). This makes a high stability of the distribution of pitch codeword frequencies across more than 50 years of music evident. However, it could well be that, even though the distribution is the same for all years, codeword rankings were changing (e.g. a certain codeword was used frequently in 1963 but became mostly unused by 2005). To assess this possibility we compute the Spearman's rank correlation coefficients26 for all possible year pairs and find that they are all extremely high, with an average of 0.97 ± 0.02 and a minimum above 0.91. These high correlations indicate that codeword rankings practically do not vary with years.

Codeword frequency distributions provide a generic picture of vocabulary usage. However, they do not account for discourse syntax, as well as a simple selection of words does not necessarily constitute an intelligible sentence. One way to account for syntax is to look at local interactions or transitions between codewords, which define explicit relations that capture most of the underlying regularities of the discourse and that can be directly mapped into a network or graph18,19. Hence, analogously to language-based analyses27,28,29, we consider the transition networks formed by codeword successions, where each node represents a codeword and each link represents a transition (see SI). The topology of these networks and common metrics extracted from them can provide us with valuable clues about the evolution of musical discourse.

All the transition networks we obtain are sparse, meaning that the number of links connecting codewords is of the same order of magnitude as the number of codewords. Thus, in general, only a limited number of transitions between codewords is possible. Such constraints would allow for music recognition and enjoyment, since these capacities are grounded in our ability for guessing/learning transitions3,4,8 and a non-sparse network would increase the number of possibilities in a way that guessing/learning would become unfeasible. Thinking in terms of originality and creativity, a sparse network means that there are still many ‘composition paths' to be discovered. However, some of these paths could run into the aforementioned guessing/learning tradeoff9. Overall, network sparseness provides a quantitative account of music's delicate balance between predictability and surprise.

In sparse networks, the most fundamental characteristic of a codeword is its degree k, which measures the number of links to other codewords. With pitch networks, this quantity is distributed according to a power law P(k) ∝ k−γ for k > kmin, with the same fit parameters for all considered years. The exponent γ, which has an average of 2.20±0.06, is similar to many other real complex networks18, and the median of the degree k is always 4. Nevertheless, we observe important trends in the other considered network metrics, namely the average shortest path length l, the clustering coefficient C, and the assortativity with respect to random Γ. Specifically, l slightly increases from 2.9 to 3.2, values comparable to the ones obtained when randomizing the network links. The values of C show a considerable decrease from 0.65 to 0.45, and are much higher than those obtained for the randomized network. Thus, the small-worldness30 of the networks decreases with years (Fig. 2c). This trend implies that the reachability of a pitch codeword becomes more difficult. The number of hops or steps to jump from one codeword to the other (as reflected by l) tends to increase and, at the same time, the local connectivity of the network (as reflected by C) tends to decrease. Additionally, Γ is always below 1, which indicates that the networks are always less assortative than random (i.e. well-connected nodes are less likely to be connected among them), a tendency that grows with time if we consider the biggest hubs of the network (SI). The latter suggests that there are less direct transitions between ‘referential' or common codewords. Overall, a joint reduction of the small-worldness and the network assortativity shows a progressive restriction of pitch transitions, with less transition options and more defined paths between codewords.

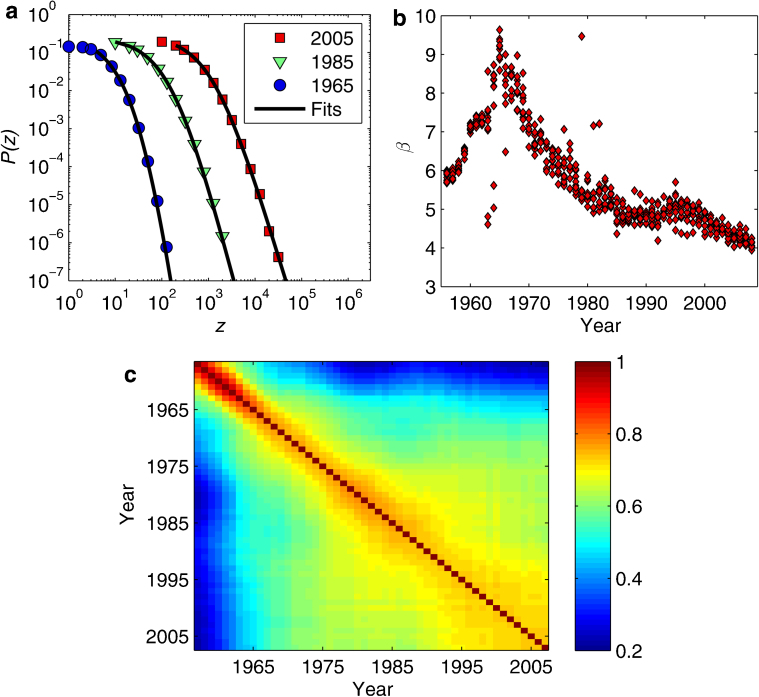
As opposed to pitch, timbre provides a different picture. Even though the distribution of timbre codeword frequencies is also well-fitted by a power law (Fig. 3a), the parameters of this distribution vary across years. In particular, since 1965, β constantly decreases to values approaching 4 (Fig. 3b). Although such large values of β would imply that other fits could also be acceptable, the power law provides a simple parameterization to compare the changes over the years (and is not rejected in a likelihood ratio test in front of other alternatives). Smaller values of β indicate less timbral variety: frequent codewords become more frequent, and infrequent ones become even less frequent. This evidences a growing homogenization of the global timbral palette. It also points towards a progressive tendency to follow more fashionable, mainstream sonorities. Interestingly, rank correlation coefficients are generally below 0.7, with an average of 0.57 ± 0.15 (Fig. 3c). These rather low rank correlations would act as an attenuator of the sensation that contemporary popular music is becoming more homogeneous, timbrically speaking. The fact that frequent timbres of a certain time period become infrequent after some years could mask global homogeneity trends to listeners.

Figure 3. Timbre distributions.

Figure 3

Open in a new tab

(a) Examples of the density values and fits taking z as the random variable. (b) Fitted exponents β. (c) Spearman's rank correlation coefficients for all possible year pairs.

Compared to timbre codeword frequencies, metrics obtained from timbre transition networks show no substantial variation. Again, similar median degrees (all equal to 8) and degree distributions were observed for all considered years. However, we were not able to achieve a proper fit for the latter (SI). Values of Γ are larger than 1 and increasing since 1965. Thus, in contrast to pitch, timbre networks are more assortative than random. The values of l fluctuate around 4.8 and C is always below 0.01. Noticeably, both are close to the values obtained with randomly wired networks. This close to random topology quantitatively demonstrates that, as opposed to language, timbral contrasts (or transitions) are rarely the basis for a musical discourse1. This does not regard timbre as a meaningless facet. Global timbre properties, like the aforementioned power law and rankings, are clearly important for music categorization tasks2,11 (one example is genre classification31). Notice however that the evolving characteristics of musical discourse have important implications for artificial or human systems dealing with such tasks. For instance, the homogenization of the timbral palette and general timbral restrictions clearly challenge tasks exploiting this facet. A further example is found with the aforementioned restriction of pitch codeword connectivity, which could hinder song recognition systems (artificial song recognition systems are rooted on pitch codeword-like sequences, cf.32).

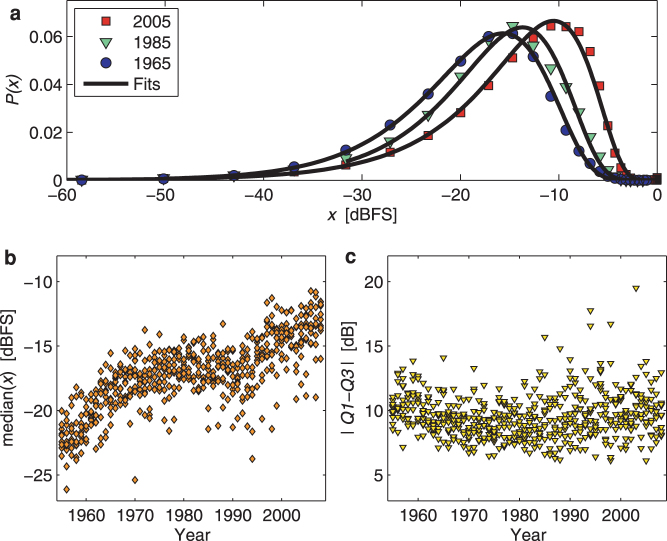
Loudness distributions are generally well-fitted by a reversed log-normal function (Fig. 4a). Plotting them provides a visual account of the so-called loudness race (or loudness war), a terminology that is used to describe the apparent competition to release recordings with increasing loudness33,34, perhaps with the aim of catching potential customers' attention in a music broadcast (from our point of view, loudness changes are not only the result of technological developments but, in part, also the result of conscious decisions made by musicians and producers in the musical creation process, cf.33). The empiric median of the loudness values x grows from −22 dBFS to −13 dBFS (Fig. 4b), with a least squares linear regression yielding a slope of 0.13 dB/year (p < 0.01, t-test). In contrast, the absolute difference between the first and third quartiles of x remains constant around 9.5 dB (Fig. 4c), with a regression slope that is not statistically significant (p > 0.05, t-test). This shows that, although music recordings become louder, their absolute dynamic variability has been conserved, understanding dynamic variability as the range between higher and lower loudness passages of a recording34. However, and perhaps most importantly, one should notice that digital media cannot output signals over 0 dBFS35, which severely restricts the possibilities for maintaining the dynamic variability if the median continues to grow.

Figure 4. Loudness distributions.

Figure 4

Open in a new tab

(a) Examples of the density values and fits of the loudness variable x. (b) Empiric distribution medians. (c) Dynamic variability, expressed as absolute loudness differences between the first and third quartiles of x, |Q1 − Q3|.

Finally we look at loudness transition networks, which show comparable degree distributions, a median degree between 13 and 14, values of l between 8 and 10, and a Γ fluctuating around 1.08. Noticeably, l is appreciably beyond the values obtained by randomly wired networks. The values of C have an average of 0.59 ± 0.02, also much above the values obtained by the random networks. These two observations suggest that the network has a one-dimensional character, inferring that no extreme loudness transitions occur (one rarely finds loudness transitions to drive a musical discourse). The very stable metrics obtained for loudness networks imply that, despite the race towards louder music, the topology of loudness transitions is maintained.

Discussion

Beyond the specific outcomes discussed above, we now focus on the evolution of musical discourse. Much of the gathered evidence points towards an important degree of conventionalism, in the sense of blockage or no-evolution, in the creation and production of contemporary western popular music. Thus, from a global perspective, popular music would have no clear trends and show no considerable changes in more than fifty years. Pitch codeword frequencies are found to be always under the same underlying pattern: a power law with the same exponent and fitting parameters. Moreover, frequency-based rankings of pitch codewords are practically identical, and several of the network metrics for pitch, timbre, and loudness remain immutable. Frequency distributions for timbre and loudness also fall under a universal pattern: a power law and a reversed log-normal distribution, respectively. However, these distributions' parameters do substantially change with years. In addition, some metrics for pitch networks clearly show a progression. Thus, beyond the global perspective, we observe a number of trends in the evolution of contemporary popular music. These point towards less variety in pitch transitions, towards a consistent homogenization of the timbral palette, and towards louder and, in the end, potentially poorer volume dynamics.

Each of us has a perception of what is new and what is not in popular music. According to our findings, this perception should be largely rooted on the simplicity of pitch sequences, the usage of relatively novel timbral mixtures that are in agreement with the current tendencies, and the exploitation of modern recording techniques that allow for louder volumes. This brings us to conjecture that an old popular music piece would be perceived as novel by essentially following these guidelines. In fact, it is informally known that a ‘safe' way for contemporizing popular music tracks is to record a new version of an existing piece with current means, but without altering the main ‘semantics' of the discourse.

Some of the conclusions reported here have historically remained as conjectures, based on restricted resources, or rather framed under subjective, qualitative, and non-systematic premises. With the present work, we gain empirical evidence through a formal, quantitative, and systematic analysis of a large-scale music collection. We encourage the development of further historical databases to be able to quantify the major transitions in the history of music, and to start looking at more subtle evolving characteristics of particular genres or artists, without forgetting the whole wealth of cultures and music styles present in the world.

Methods

Detailed method descriptions are provided in the SI.

Author Contributions

J.S., A.C., and M.B. performed research. All authors designed research, discussed results, and wrote the paper.

Supplementary Material

Supplementary Information

Supplementary Information

srep00521-s1.pdf (1.1MB, pdf)

Acknowledgments

This work was partially supported by Catalan Government grants 2009-SGR-164 (A.C.), 2009-SGR-1434 (J.S. and J.Ll.A.), 2009-SGR-838 (M.B.) and ICREA Academia Prize 2010 (M.B.), European Comission grant FP7-ICT-2011.1.5-287711 (M.H.), Spanish Government grants FIS2009-09508 (A.C.), FIS2010-21781-C02-02 (M.B.) and TIN2009-13692-C03-01 (J.Ll.A.), and Spanish National Research Council grant JAEDOC069/2010 (J.S.). The authors would like to thank the million song dataset team for making this massive source of data publicly available.

References

  1. Patel A. D. Music, language, and the brain (Oxford University Press, Oxford, UK, 2007). [Google Scholar]
  2. Ball P. The music instinct: how music works and why we can't do without it (Bodley Head, London, UK, 2010). [Google Scholar]
  3. Huron D. Sweet anticipation: music and the psychology of expectation (MIT Press, Cambridge, USA, 2006). [Google Scholar]
  4. Honing H. Musical cognition: a science of listening (Transaction Publishers, Piscataway, USA, 2011). [Google Scholar]
  5. Levitin D. J., Chordia P. & Menon V. Musical rhythm spectra from Bach to Joplin obey a 1/f power law. Proc. of the National Academy of Sciences of the USA 109, 3716–3720 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Lerdahl F. & Jackendoff R. A generative theory of tonal music (MIT Press, Cambridge, USA, 1983). [Google Scholar]
  7. Temperley D. Music and probability (MIT Press, Cambridge, USA, 2007). [Google Scholar]
  8. Juslin P. & Sloboda J. A. Music and emotion: theory and research (Oxford University Press, Oxford, UK, 2001). [Google Scholar]
  9. Reynolds R. The evolution of sensibility. Nature 434, 316–319 (2005). [DOI] [PubMed] [Google Scholar]
  10. Zanette D. H. Playing by numbers. Nature 453, 988–989 (2008). [DOI] [PubMed] [Google Scholar]
  11. Casey M. A. et al. Content-based music information retrieval: current directions and future challenges. Proc. of the IEEE 96, 668–696 (2008). [Google Scholar]
  12. Müller M., Ellis D. P. W., Klapuri A. & Richard G. Signal processing for music analysis. IEEE Journal of Selected Topics in Signal Processing 5, 1088–1110 (2011). [Google Scholar]
  13. Michel J.-B. et al. Quantitative analysis of culture using millions of digitized books. Science 331, 176–182 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Bertin-Mahieux T., Ellis D. P. W., Whitman B. & Lamere P. The million song dataset. In: Proc. of the Int. Soc. for Music Information Retrieval Conf. (ISMIR), 591–596 (2011). [Google Scholar]
  15. Jehan T. Creating music by listening. Ph.D. thesis, Massachussets Institute of Technology, Cambridge, USA (2005). [Google Scholar]
  16. Bak P. How nature works: the science of self-organized criticality (Copernicus, New York, USA, 1996). [Google Scholar]
  17. Newman M. E. J. Power laws, Pareto distributions and Zipf's law. Contemporary Physics 46, 323–351 (2005). [Google Scholar]
  18. Newman M. E. J. Networks: an introduction (Oxford University Press, Oxford, UK, 2010). [Google Scholar]
  19. Barrat A., Barthélemy M. & Vespignani A. Dynamical processes on complex networks (Cambridge University Press, Cambridge, UK, 2008). [Google Scholar]
  20. Haro M., Serrà J., Herrera P. & Corral A. Zipf's law in short-time timbral codings of speech, music, and environmental sound signals. PLoS ONE 7, e33993 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. De Clercq T. & Temperley D. A corpus analysis of rock harmony. Popular Music 30, 47–70 (2011). [Google Scholar]
  22. Adamic L. A. & Huberman B. A. Zipf's law and the internet. Glottometrics 3, 143–150 (2002). [Google Scholar]
  23. Zipf G. K. Human behavior and the principle of least effort (Addison-Wesley, Boston, USA, 1949). [Google Scholar]
  24. Zanette D. Zipf's law and the creation of musical context. Musicae Scientiae 10, 3–18 (2006). [Google Scholar]
  25. Beltrán del Río M., Cocho G. & Naumis G. G. Universality in the tail of musical note rank distribution. Physica A 387, 5552–5560 (2008). [Google Scholar]
  26. Hollander M. & Wolfe D. A. Nonparametric statistical methods (Wiley, New York, USA, 1999), 2nd edn. [Google Scholar]
  27. Sigman M. & Cecchi G. A. Global organization of the Wordnet lexicon. Proc. of the National Academy of Sciences of the USA 99, 1742–1747 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Ferrer i Cancho R., Solé R. V. & Köhler R. Patterns in syntactic dependency networks. Physical Review E 69, 051915 (2004). [DOI] [PubMed] [Google Scholar]
  29. Amancio D. R., Altmann E. G., Oliveira O. N. & Costa L. d. F. Comparing intermittency and network measurements of words and their dependence on authorship. New Journal of Physics 13, 123024 (2011). [Google Scholar]
  30. Watts D. J. & Strogatz S. H. Collective dynamics of ‘small-world' networks. Nature 393, 440–442 (1998). [DOI] [PubMed] [Google Scholar]
  31. Scaringella N., Zoia G. & Mlynek D. Automatic genre classification of music content: a survey. Signal Processing Magazine 23, 133–141 (2006). [Google Scholar]
  32. Serrà J., Gómez E. & Herrera P. Audio cover song identification and similarity: background, approaches, evaluation, and beyond. In Raś Z. W., & Wieczorkowska A. A., (eds.) Advances in Music Information Retrieval, vol. 274 of Studies in Computational Intelligence, chap. 14, 307–332 (Springer, Berlin, Germany, 2010).
  33. Milner G. Perfecting sound forever: an aural history of recorded music (Faber and Faber, London, UK, 2009). [Google Scholar]
  34. Deruty E. ‘Dynamic range' and the loudness war. Sound on Sound – September 2011 22–24 (2011). [Google Scholar]
  35. Oppenheim A. V., Schafer R. W. & Buck J. R. Discrete-time signal processing (Prentice-Hall, Upper Saddle River, USA, 1999), 2nd edn. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Information

srep00521-s1.pdf (1.1MB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES