Open-loop, closed-loop and compensatory control: performance improvement under pressure in a rhythmic task

Abstract

According to explicit monitoring theories, the phenomenon of choking under pressure is due to actors focusing their attention on the execution of the skill. This step-by-step perceptually guided control may then interfere with automatic execution. In order to examine the changes in control at the sensorimotor level, we examined the rhythmic task of ball bouncing which affords detailed quantification of indicators of control based on previous research. The hypothesis was that under psychological pressure perceptually guided control should lead to decreased performance due to over-emphasis on closed-loop control and decreased compensatory control. In two experiments of different difficulty psychological stress was induced via setting up a fake competition. Results showed that, contrary to the hypothesis, performance accuracy and consistency improved together with an increase in compensatory control. Indicators for open- and closed-loop processes did not change. Only under more challenging conditions in Experiment 2, enhanced performance under pressure was accompanied by more active, closed-loop and less passive control. The results are discussed in light of task demands and the continuous rhythmic nature of the task: in more challenging tasks, control appears to be more prone to disturbance due to psychological stress. The different control demands in continuous rhythmic tasks may be less prone to interference due to psychological stress than in discrete tasks.

Introduction

If it were not for the phenomenon of “choking under pressure” watching sports events would be half as fascinating. In all types of sports, from golf to basketball to gymnastics, we can witness that in competitive situations athletes sometimes fail. This phenomenon has been dubbed “choking under pressure” (as defined by Baumeister and Showers 1986). Investigations into this phenomenon have primarily focused on attentional mechanisms to account for such performance changes. It is generally recognized that at an expert stage motor skills are executed “automatically” and control appears to be relegated to lower levels of the central nervous system (e.g. Schneider and Fisk 1983; Milton et al. 2004). It has been hypothesized that when athletes are under pressure to perform exceptionally well, they turn their focus of attention towards the process of execution and monitor the execution of their movements more explicitly (Baumeister 1984). This may result in a more perceptually-guided, closed-loop control of the movement leading to a constrained execution and the occasional breakdown of performance (e.g. Beilock and Carr 2001; Beilock et al. 2002).

Several studies have lent support to this hypothesis, although explicit monitoring in psychological stress situations and changes in control have been inferred rather indirectly. For example Beilock and Carr (2001) showed that participants did not choke when—during a fake competition—they had to solve a secondary cognitive task in addition to the primary motor task. Hence, the authors argued that choking was prevented because the secondary task inhibited self-focus by directing attention to the distractor task. Research by Lewis and Linder (1997) showed that participants did not choke under pressure when they were already used to self-monitoring. In a study by Masters (1992) participants only choked when they had learned the task explicitly, i.e. they had acquired declarative knowledge about the task. Masters argued that self-monitoring under pressure leads to a “reinvestment” of that knowledge; implicit learning therefore prevents choking (see also Hardy et al. 1996; Gucciardi and Dimmock 2008). Beilock and Carr (2001) also showed that at the beginning of a learning process, explicit monitoring due to psychological pressure improved performance. Later, however, when the skill was more proceduralized, explicit monitoring could lead to a breakdown of performance.

More direct evidence for explicit monitoring of execution under pressure was provided by Gray (2004). In a baseball batting task participants performed a secondary discrimination task that required either focusing on movement execution or on a sound unrelated to the movement. Under pressure, significantly fewer errors occurred when the secondary task implied focus on the movement, seen as evidence for movement-focused attention under pressure. Vickers and Williams (2007) found performance improvement under pressure in a shooting task to be correlated with a more steady gaze fixation on a target. This was seen as support for externally directed visual attention and, inversely, an indication of less efficient perceptual strategies in cases of choking. While these observations imply that choking under pressure coincides with altered perceptual processes, it has not been shown how perceptual information is integrated in motor control processes under pressure.

Whereas these studies only analyzed task performance, Higuchi (2000) also examined kinematic variables in a ball throwing task in order to test for constrained movement under pressure. He found that impaired performance under stress was associated with increased variability of joint coordination but reduced variability of the release point. In another study Higuchi et al. (2002) used an interceptive task and again found reduced variability of kinematics under stress. Similarly, Collins et al. (2001) reported less variable movement patterns in a continuous rhythmic stepping task, and Pijpers et al. (2005) in climbing behavior; in both studies psychological pressure was manipulated by participants performing at elevated heights. The results of reduced movement variability in the pressure situation are interpreted as evidence for a more tightly controlled and constrained execution.

Yet, reduced kinematic variability is not per se a characteristic of less skilled movements. A classic study on pistol shooting showed that skilled marksmen exhibit remarkable invariance in the tip of the pistol while at the same time exhibiting considerable variability in the joint angles of the arm (Arutyunyan et al. 1968). Evidently, the fluctuations in the joint angles must have compensated or covaried with each other. With many more recent studies that followed this seminal paper covariation between component variables has become the signature of skilled movement control (Scholz and Schoner 1999; Cusumano and Cesari 2006; Cohen and Sternad 2009). With additional psychological pressure that generally constrains movement execution, it can be expected that such seemingly subtle features of skilled coordination are affected.

The present study aims to probe further into the changes in sensorimotor coordination and the control processes when psychological stress is applied. To this end the task of bouncing a ball was chosen as a testbed as previous theoretical and experimental work has provided a foundation to tease apart automatic open-loop processes from more perceptually-guided closed-loop processes (Schaal et al. 1996; Wei et al. 2007, 2008). In addition, covariation and compensatory control can be assessed as the task can be parsed into two levels execution and results, in analogy to the distinction into the levels of joint angles and endpoint (de Rugy et al. 2003).

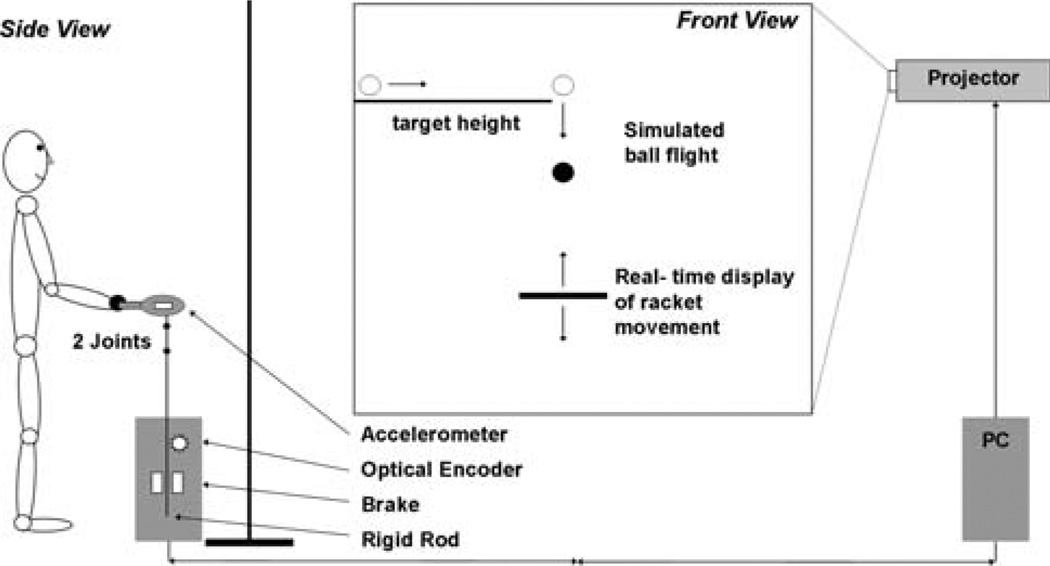
In the experimental task the actor holds a racket in his/her hand and rhythmically hits a ball into the air aiming to consistently hit a target height (Fig. 1). Mathematical analyses of a model of the task have revealed that successful task performance is possible with open-loop control, once racket-ball contact are tuned to be in the right “ballpark”. Specifically, stability analyses of the model consisting of a planar surface moving vertically in sinusoidal fashion and bouncing a ball showed that the system has dynamical stability (Schaal et al. 1996; Sternad et al. 2001). For the model system such dynamical or “passive” stability is indicated when the surface or the racket impacts the ball during the decelerating portion of the racket’s upward motion. Assuming ballistic fight of the ball, this means that balls from a larger height contact the racket later in time; at this point, the racket trajectory has decelerated to a smaller velocity; smaller racket velocity at contact means smaller all height in the next fight cycle (Fig. 2). Hence, a higher ball amplitude is followed by a lower amplitude, implicitly correcting itself. Dynamically stable performance implies that small errors converge back to stable performance without requiring active corrections (for details see Dijkstra et al. 2004). Performance with dynamical stability can also be regarded as open-loop control, as the racket trajectories are generated in an open-loop fashion. In experiments that closely copied the physical model, subjects indeed showed negative accelerations of the racket at contact which provided evidence that humans indeed exploited dynamical stability that, arguably, simplified computational demands of the task (de Rugy et al. 2003).

Fig. 1.

Virtual set-up of the ball bouncing task. Participants were positioned in front of a screen and moved a racket. The ball and racket were displayed onto the screen. The objective was to hit the ball rhythmically and accurately to the target line

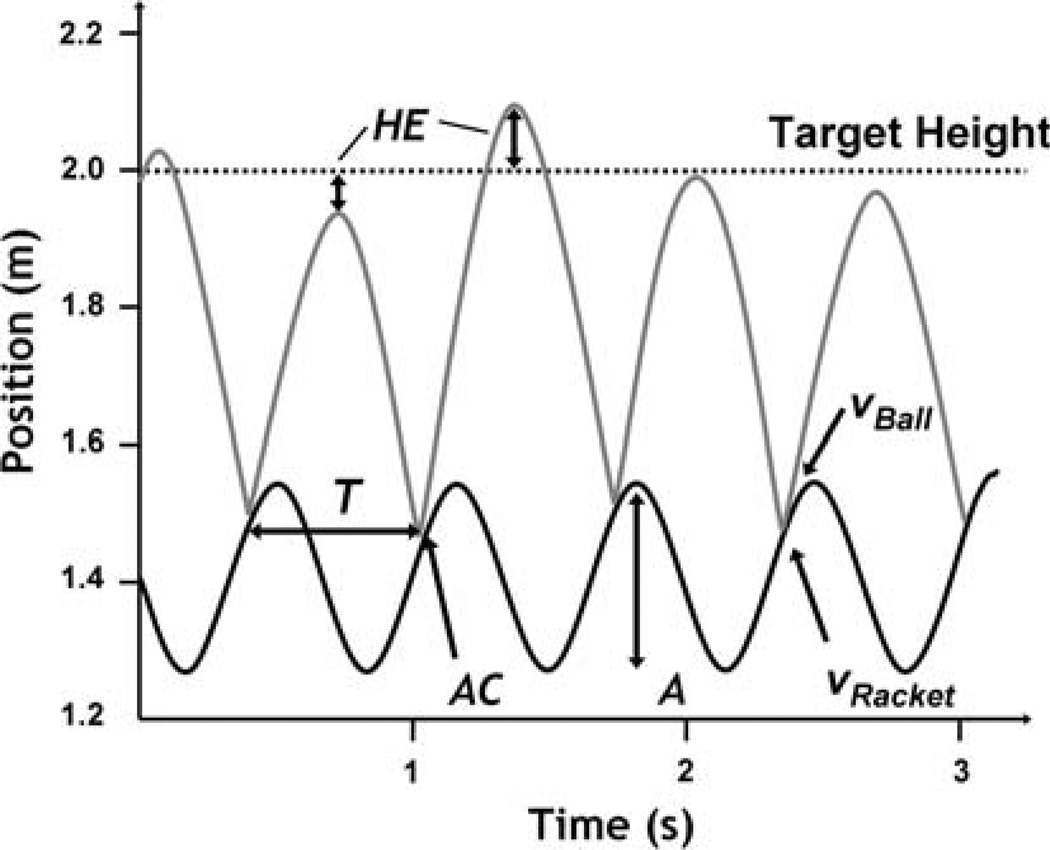
Fig. 2.

Time series of racket trajectory and ball position. Dependent measures are shown: signed height error (HE), racket period (T), racket amplitude (A), and racket acceleration at impact (AC)

More recent work extended these results and showed that, in addition, human actors also apply error corrective control, i.e. closed-loop control. Actors have sensory information and they perceive errors in the trajectory of the ball, both visually and via proprioception. A first study applied perturbations and showed that return to steady state is faster than relying on self-correction only (Wei et al. 2007, 2008). But also at steady state, theoretical analyses provided a way to tease apart indicators of closed-loop control from dynamically stable performance (Wei et al. 2007; Ronsse et al. 2008a, b; Wei et al. 2008). Interestingly, the relative contribution of active and passive contributions changed with experience: more experienced actors relied more on dynamical stability but, at the same time, also showed more active error corrections. In addition, skilled actors have been shown to exploit compensatory processes to achieve stable performance, as evidenced by covariation of execution variables (see de Rugy et al. 2003). Due to constraints in the virtual set-up, task performance, i.e. accuracy in hitting a target height, is completely determined by three variables at impact: racket velocity at impact, ball velocity before impact, and impact height. As the functional relation between execution variables and the result is known, the amount of covariation can be calculated (Müller and Sternad 2003).

The aim of this study was to analyze performance in ball bouncing during a pressure situation in order to identify how open- and closed-loop control strategies and variability change with psychological stress. Based on explicit monitoring, we hypothesized that under pressure performers should (1) show decrements in task performance, (2) rely less on dynamical stability and open-loop control, (3) increase the closed-loop error correction processes, and (4) show less exploitation of compensatory processes. More explicitly, we expected that under pressure, performers (1) become less accurate and more variable, (2) show less negative racket accelerations at impact, (3) show increased correlations between result and execution variables as signature of perceptual feedback-based corrections, and (4) show less covariation of execution variables.

These hypotheses were tested in two experiments. In Experiment 1, we used the standard configuration of the virtual set-up where subjects bounce a ball to a target height. This should allow subjects to achieve relatively stable performance within one session of 30 trials (Dijkstra et al. 2004). However, there has been some evidence that performance in such simple tasks improves under (social evaluative) pressure (Travis 1925; Strauss 2002). Possibly, relatively easy tasks may not require further corrections or any other changes in control, such as compensation, and the effect of explicit monitoring under pressure may not be visible. In ball bouncing, previous studies have shown that especially under more difficult conditions in which bounces were extrinsically perturbed, active control was evidenced to a larger extent (Dijkstra et al. 2004; Wei et al. 2007, 2008). Consequently, Experiment 2 increased the difficulty of the task by introducing perturbations at selected impacts that resulted in unpredictable ball amplitudes. The stress manipulations were the same in both experiments.

Methods

Participants

48 undergraduate students (19 male, 29 female, age 18–23 years) were recruited as participants for Experiment 1. None of the participants had any practice with this task before. Data of nine participants (1 male, 8 female) had to be discarded because they did not appear for the second session or due to technical problems. 24 undergraduate students (10 male, 15 female, age 20–28 years) were recruited for Experiment 2 who had not participated before and could also be regarded as novices. Data of one participant had to be discarded because of technical problems in recording. In both experiments participants received extra credit for an undergraduate class as compensation and were given $10 as reward in the competition (see below). The participants were informed about the experimental procedure and prior to participation signed the consent form in compliance with the Regulatory Committee of the Pennsylvania State University.

Apparatus and material

A virtual reality set-up was used in which the participant manipulated a real table-tennis racket to bounce a virtual ball rhythmically to a target height. As in previous studies ball and racket displacements were restricted to the vertical dimension (de Rugy et al. 2003). Participants were positioned in front of a large backprojection screen (1.80 m wide and 1.33 m high) onto which the visual display was projected. The display consisted of a red horizontal line (the target line) from the left edge to the middle of the screen and a magenta horizontal bar (length: 0.2 m, width: 0.02 m) representing the paddle in the middle of the screen (Fig. 1). The target line was displayed at a height of 2.0 m (length: 0.9 m, width: 0.02 m), the paddle’s minimum position was 1.2 m above the floor. The ball was displayed as a yellow filled circle, 0.06 m in diameter. The participant stood upright at a distance of 1 m from the screen and held the racket horizontally at a comfortable height. A rigid rod with two hinge joints was attached below the racket surface and ran through a noose that was part of a heavy weight floor piece. The material and coating of the rod and the noose presented minimal friction. The joints allowed the racket to be moved and tilted freely in three dimensions although only up-and-down movements of the rod were recorded and displayed. Due to the display the actual racket movements deviated only negligibly from vertical. By its vertical motion the rod rotated a wheel whose revolutions were measured by an optical encoder. The signal from the optical encoder was transformed by a digital board (Data Translation, Inc) and sent online to the PC that controlled the virtual display.

The projection onto the screen was in real time with an average time delay between real and virtual racket movement of 22 ms (±0.5; see Wei et al. 2007). The gain between displacement of the real and the virtual racket was 1. Acceleration of the racket was measured with an accelerometer attached to the base of the paddle. The sampling frequency was set to its maximum which varied across the cycle due to different computational demands and averaged to 400 Hz. In order to simulate the impact of the racket and the virtual ball, a mechanical brake was attached to the rod. The brake was activated by a solenoid that, in turn, was triggered by the software controlling the interactive display. The trigger was started 15 ms before the estimated actual (i.e. visual) impact time. Impact time was estimated by using the distance between racket and ball divided by the relative velocity between them. The brake was applied at each impact for a duration of 30 ms. The electronic delay had a duration of only one sampling interval; the mechanical delay between the control signal and the onset of the brake was approximately 10 ms. The force developed by this brake was adjusted to that produced by a tennis ball falling on the racket; it was approximately constant for all contacts.

Custom-written software computed the ball trajectories online based on the measured racket movements and the contact parameters of ball and racket. The simulated ball trajectories were projected onto the screen so that the subject only interacted virtually with the ball (Open GL Graphics). The visual display was calculated every 3 ms and was projected to the screen with an update rate of 60 Hz. The ball’s trajectory was calculated using the equations of ballistic fight and inelastic instantaneous impact. The energy loss at impact was captured by the coefficient of restitution α.

Experimental conditions and procedure

After the participants were positioned in front of the screen they were given details about the task. The instruction was to rhythmically hit the ball such that the apex of the ball trajectory would be as exactly at the target line as possible. They were advised that when the trial started, it was helpful to actively approach the first falling ball before it hit the racket. The experiment consisted of two sessions scheduled on two consecutive days. On Day 1, participants completed 32 trials with short rests after trials 8, 16 and 24. Each trial lasted 40 s that allowed for 50–60 bounces, depending on the impact position chosen by the participant. Immediately after each trial, information about their average score was presented on the screen. This score gave the average absolute error (in cm) between the maximum ball amplitude and the target height across all bounces of the trial. Participants were informed that they should minimize this deviation across trials. A fading procedure was applied to this performance feedback that reduced the frequency of feedback from every single trial to every 8th trial across practice. The displayed score always only related to the last trial. Between two successive trials there was a 5-s break. On Day 2, participants performed three warm-up trials followed by a Baseline Test of 10 trials and a Performance Test of 10 trials. Feedback was only given after each warm-up trial. Participants were instructed to demonstrate how much they had learned on the previous day.

Before the Performance Test, participants were assigned to either the No-Stress or the High-Stress group. Participants from the High-Stress group were given additional instructions that consisted of four steps to increase psychological pressure. This manipulation has become standard in research investigating choking under pressure (Beilock and Carr 2001; Gray 2004). Participants received a sheet explaining that (1) they were to enter a competition for which they were teamed with another participant of this study. If both team-mates could raise their performance by 25% in the final Performance Test compared to their individual average performance in the Baseline Test, each would be rewarded $10. (2) If one of them could not raise his or her performance, the other would not receive the reward either. (3) Furthermore they were told that a list of the teams with results and potential rewards would be openly posted after the experiment. (4) Prior to starting the first trial of the Performance Test participants were told that their team-mate had already successfully raised his/her performance by 25%. After the experiment, participants were given a debriefing statement, explaining that every participant would receive $10, independent of theirs or others’ performance. Participants in the No-Stress group were simply instructed to again demonstrate their level of expertise.

In order to raise the difficulty of the task, Experiment 2 introduced perturbations during the last 8 trials on Day 1 and continued throughout all trials on Day 2. At every 8th impact within each trial the coefficient of restitution α was randomly changed from its normal value (α = 0.50) resulting in an unexpected velocity of the ball that resulted in higher or lower ball amplitudes. To obtain sufficiently large perturbations, the perturbed coefficient of restitution (α-P) was changed by at least 0.10 from its normal value 0.50. To prevent too large perturbations, the maximum change was 0.20. To achieve an equal proportion of atypically high and low ball amplitudes, α-P was randomly determined for each perturbed impact to be within the ranges 0.3 ≤ α-P_low ≤ 0.4 or 0.6 ≤ α-P_high ≤ 0.7. Previous studies had shown that participants needed an average of five cycles to return to steady state after perturbations (de Rugy et al. 2003). With the aim to ensure that all participants resumed a stable rhythm after a perturbation an interval of seven bounces between perturbations was chosen. Given the random magnitudes of the perturbations participants could not anticipate the perturbation.

To evaluate the level of anxiety, participants from both groups filled out the state-version of the State-Trait-Anxiety Inventory before the Baseline Test and a second time before the Performance Test (STAI, Spielberger et al. 1983). Following prescriptions from the manual, sum scores across the 20 items were calculated.¹ Thus, scores on the STAI range between 20 (low anxiety) and 80 (high anxiety). Previous studies used the STAI as well as the Competitive State Anxiety Inventory-2 (CSAI-2, Martens et al. 1990). This study used the STAI as several questions in CSAI-2 directly refer to competition, which would be confusing to participants in the No-Stress group (e.g. “I’m concerned about this competition”). Upon completion of the last trial, participants were given a debriefing statement.

Data reduction and dependent measures

The raw data of racket displacement and acceleration were filtered with a Savitzky-Golay filter (Orfanidis 1986). This procedure included interpolation of the data to a constant sampling frequency of 500 Hz. Subjects’ kinematic data was evaluated to test the four hypotheses. Hypothesis 1 stated that at the level of task result, the absolute ball height error, AE, should increase. AE was defined as the mean absolute difference between the maximum ball height and the target height. For each trial, the average of all bounces was calculated. Additionally, to assess variability, the standard deviations of the signed height error, the variable error VE, was calculated. Concomitantly, at the level of task execution, the period of the racket movement T was defined between the impacts of successive bounces; the amplitude of the racket movement A was defined as the distance from the minimum to the maximum of the racket trajectory during one cycle (peak-to-peak). The standard deviations of racket period, SD-T, and racket amplitude, SD-A, were calculated to evaluate consistency in execution. Outliers of more than three standard deviations from individual means were deleted before calculating averages.

To evaluate control strategies as posed by hypotheses 2 and 3 indicators for open- and closed-loop strategies were assessed. For the presence of open-loop strategy or dynamical stability, the acceleration of the racket at impact, AC, was evaluated. AC was determined from the raw accelerometer signal one sample before the impact (for details see Wei et al. 2007). To assess active error compensation via closed-loop strategies, linear regression analyses were conducted of racket velocity at bounce k + 1 on the height error at bounce k (see Wei et al. 2008 for rationale). Unlike for the performance assessment that used the absolute error AE, this analysis needed the signed height error HE. Before the regression analyses, the data of each individual were first pooled across all 10 trials of the Baseline Test and separately for the 10 trials of the Performance Test (between 500 and 600 data points each); outliers greater than three standard deviations from the mean were deleted. The slope of the regression indicated the scaling of racket velocity of the preceding height error, i.e., whether for example an overshoot of the target height was followed by a reduced racket velocity at the next contact. Therefore, the regression slope expressed the gain of the error control.

Hypothesis 4 stated that compensatory control should decrease. Straightforward mechanical analysis shows that the task is redundant: ball amplitude and its height error at each bounce are fully determined by the velocity of the racket at impact, the incoming velocity of the ball, and the position of the impact (see de Rugy et al. 2003). However, many different combinations of the three variables can lead to the same ball amplitude, the task is redundant. Hence, at each bounce the three variables can covary such that a deviation in one variable can be compensated for by a change in another variable. To assess how much the resulting ball amplitude is brought about by a covariation of the three variables, the empirically measured variability in the result is compared with a covariation-free variability V₀ (see Müller and Sternad 2003). This covariation-free variability V₀ is obtained by permutation of the three execution variables. Performing this randomization, an alternative height error can be calculated for each of the bounces of a trial. If covariation contributed to achieving desired ball amplitude, the height error for the permutated variables will be higher on average. Repeating this permutation method 1,000 times to obtain 1,000 estimates for covariation-free variability V₀, the average V₀ can be calculated. Finally, covariation was quantified by COV = (V_act/V₀) − 1 (eq. 18 in Müller and Sternad 2003). This coefficient was calculated for both absolute and variable error, COV-AE and COV-VE.

Statistical analyses

To test the four hypotheses, the dependent measures were subjected to a 2 (group) × 2 (test) mixed-effects analysis of variance (ANOVA) with repeated measurements on the second factor. For effect size of the ANOVAs Cohen’s f was calculated, with f = 0.25 representing a medium effect size. For testing the interaction between group and test the level of significance was set to α = 0.05.

For testing the null hypothesis that groups were equal at the end of Day 1 and for testing equal performance at Baseline the level of significance was adjusted in order to reduce type-II error and raise the power to 1 − β = 0.80. In Experiment 1, α was set to α = 0.45 (N = 39, f = 0.25) for group differences on Day 1, for Baseline differences α was set to α = 0.55 (N = 29, f = 0.25). In Experiment 2, for testing equal performance at the end of Day 1 the level of significance was set to α = 0.61 (N = 23, f = 0.25), for testing equal performance at Baseline α was set to α = 0.64 (N = 20, f = 0.25). The α-corrections were performed with G*Power software (Faul et al. 2007).

Following a rationale introduced by Vickers and Williams (2007) we also explored the contribution of changes in the execution and control variables to changes in the dependent performance measures, AE and VE. To this end, multiple regression analyses were performed. First, difference scores were calculated for all variables. Difference scores of SD-T, SD-A, COV AE, COV-VE, AC, regression slope as well as of the STAI-anxiety scores were entered into stepwise multiple regression, independently for AE and VE. Because of the explorative nature, we used both forward and backward stepwise regression. Similar to Vickers and Williams (2007), we only analysed the High-Stress group.

Experiment 1: results

Performance on day 1

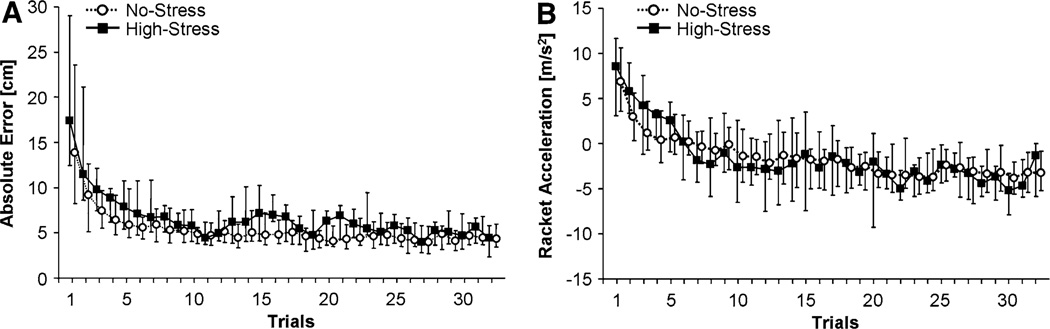
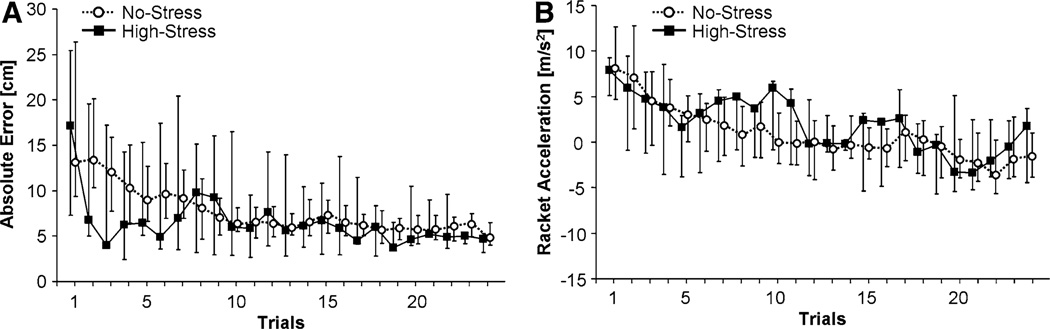
The purpose of the session on Day 1 was that participants who were all novices to the task could practice to achieve a relatively steady performance level. Figure 3a shows the result variable AE across all 32 trials for the two groups. Each data point represents the median of all participants per group at each trial and the error bars represent the interquartile range. As can be seen, participants improved their task performance and asymptotically approached a performance level from the middle of the session onwards. The interquartile ranges are asymmetric as the distributions were skewed to values closer to zero. To test whether the groups reached the same level of skill, an exponential function, y(t) = a + b × e^−ct, was fitted to each individual subject’s data across the 32 trials (mean R² = 0.64 ± 0.28). The fitted value at the last trial was determined for each participant and these values were compared between groups. There was no significant difference between the High-Stress group (5.21 ± 1.67 cm) and the No-Stress group (5.38 ± 2.08 cm), F(1, 37) = 0.07, p > 0.45.

Fig. 3.

Time series across the 32 trials of practice on Day 1 for all participants. The medians and the 25 and 75 percentiles of the No-Stress and the High-Stress groups are displayed (assignment occurred on Day 2). a Absolute error from target height, AE, b Racket acceleration at impact, AC

For a more theoretically grounded evaluation of their performance strategy, the execution variable racket acceleration at impact, AC, is plotted in Fig. 3b. The trial medians per group show an exponential time course starting with positive values and approaching negative AC values with practice. Error bars representing interquartile range indicate a large interindividual variance. As for AE, exponential functions were fitted to each participant’s data (mean R² = 0.54 ± 0.28). Comparison of the mean fitted values of the exponential function at the last trial showed no significant difference between the High-Stress group (−3.30 ± 3.43 m/s²) and the No-Stress group (−3.60 ± 2.94 m/s²), F(1, 37) = 0.09, p > 0.45.

Manipulation check

Before testing performance under stress on Day 2, the effectiveness of the pressure manipulation was evaluated. Using the STAI questionnaire the level of anxiety was compared between groups for the Baseline and Performance Tests. Initially, the expected interaction between Group and Test, which should show a significant increase for the High-Stress group but not for the No-Stress group, was not significant, F(1, 37) = 3.50, p > 0.05. To achieve the necessary group differences, we scrutinized participants for the effectiveness of the manipulation. In the High-Stress group, six participants reported decreases in state anxiety, contrary to expectation. As the goal of this study was to evaluate the effect of stress on performance, these subjects were eliminated from all further analyses. With the same rationale, we excluded four participants from the No-Stress group from further analyses, because they reported increases in state anxiety of more than 1 point. After exclusion of these participants, the state anxiety score showed the desired increase in anxiety from Baseline to Performance Test in the High-Stress group (32.21 ± 6.83–38.86 ± 8.67) and no change in the No-Stress group (28.27 ± 4.68–25.80 ± 4.57), evidenced by a significant interaction between group and test, F(1, 27) = 42.37, p < 0.05, f = 1.25. However, the difference at Baseline was significant, F(1, 27) = 3.34, p < 0.55, f = 0.35.

Performance on day 2

Task result

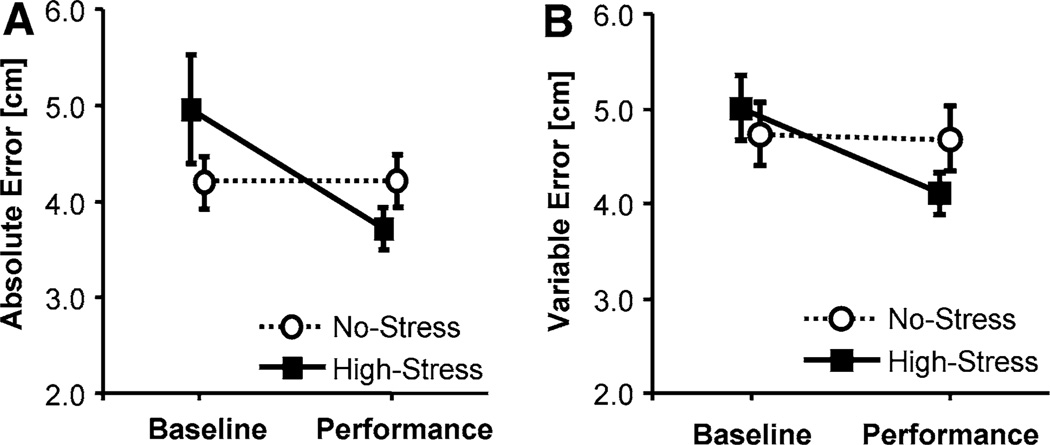
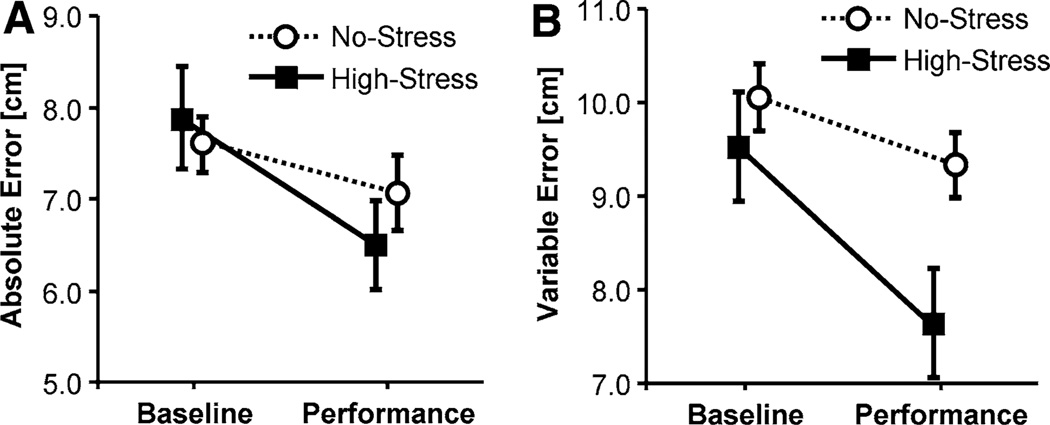
A first goal was to test the changes in performance due to stress from the Baseline to the Performance Test. Submitting averages of AE for the 10 trials in the Baseline and Performance Tests to a two-way ANOVA rendered the interaction between group and test as significant, F(1, 27) = 6.15, p < 0.05, f = 0.48 (Fig. 4a). Counter to expectations participants in the High-Stress group decreased their error from the Baseline Test to the Performance Test, whereas participants in the No-Stress group did not show further improvements. However, there was a significant difference between the two groups in the Baseline Test, F(1, 27) = 1.56, p < 0.55, f = 0.24.

Fig. 4.

Means of absolute error, AE (a), and variable error, VE (b), during the 10 trials of the Baseline Test and the Performance Test; the error bars indicate standard error

Participants also became more consistent under pressure: the variable error VE in the High-Stress group decreased in the Performance Test, while the No-Stress group did not show any changes in their consistency across tests, F(1, 27) = 9.54, p < 0.05, f = 0.59 (see Fig. 4b). Unlike for AE, there was no significant group difference at Baseline.

Task execution

The two variability measures for racket period and amplitude, SD-T and SD-A, did not indicate any significant changes nor group differences in consistency for the High-Stress group compared to the No-Stress group (Table 1).

Table 1.

Means (M) and standard errors (SE) of racket period (SD-T) and racket amplitude (SD-A) in Experiment 1

	No-Stress Group, N = 15		High-Stress Group, N = 14
	M	SE	M	SE
SD-T (ms)
Baseline Test	32.06	1.64	31.26	1.64
Performance Test	30.37	1.72	28.24	1.66
SD-A (cm)
Baseline Test	1.82	0.09	1.69	0.09
Performance Test	1.86	0.09	1.64	0.11

Indicators of control

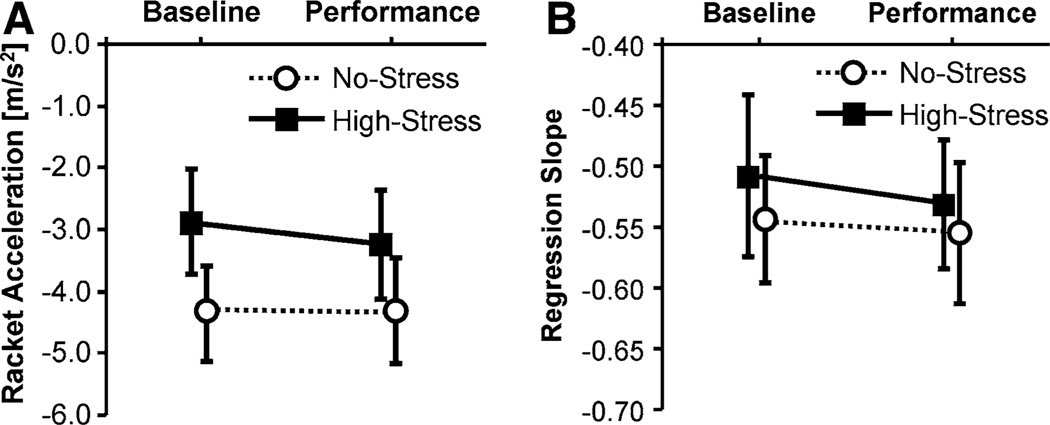
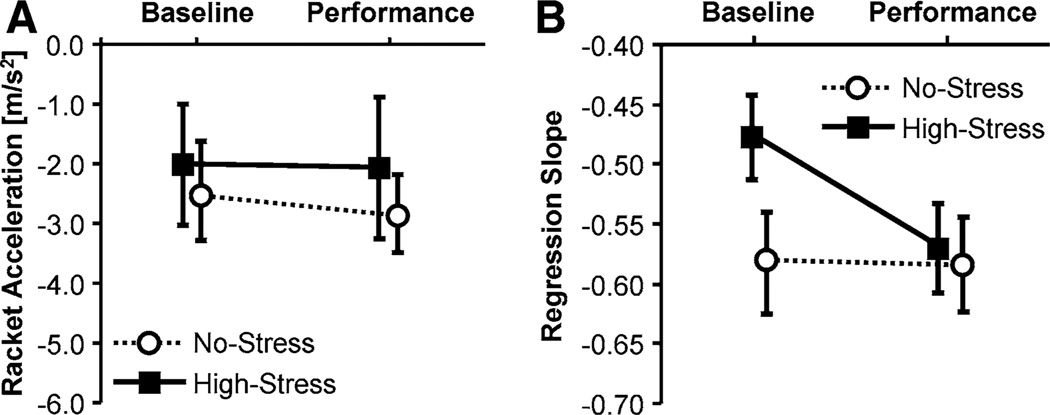
Average AC values in the 10 trials of the Baseline and the Performance Tests are shown together with the standard errors in Fig. 5a. There were visible differences in the mean AC values between the two groups in both tests. However, a 2 × 2 ANOVA did not yield any significant main effect. Further, no significant interaction indicated differential changes in AC between groups. Figure 5b shows the average slope of the regressions of racket velocity on height error for the two groups. The average slope coefficients of the regressions pooled for both groups was −0.53 ± 0.2. Again, no statistically significant results were obtained.

Fig. 5.

Means of racket acceleration at impact, AC (a) and of regression slopes of racket period on HE (b), during the 10 trials of the Baseline Test and the Performance Test; the error bars indicate standard error

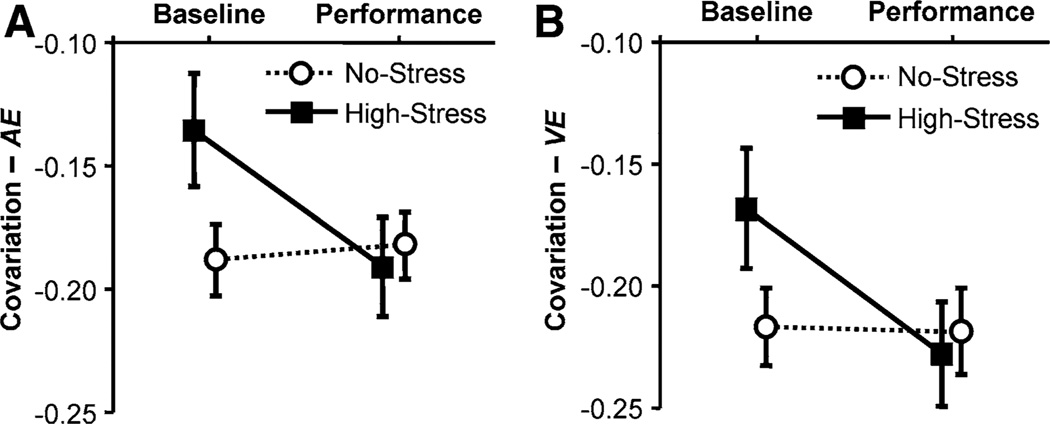
However, there was a significant interaction for Covariation of execution variables in COV-AE, F(1, 27) = 4.63, p < 0.05, f = 0.41, and COV-VE, F(1, 27) = 4.71, p < 0.05, f = 0.42. As Fig. 6a and b suggest, there was a significant group difference at Baseline, F(1, 27) = 3.84, p < 0.55, in COV-AE and COV-VE, F(1, 27) = 2.83, p < 0.55.

Fig. 6.

Covariation of impact parameters evaluated during the 10 trials of the Baseline Test and the Performance Test. a Covariation with respect to absolute error, COV-AE. b Covariation with respect to variable error, COV-VE. Means and standard error

Contribution to performance differences

Differences in the absolute error AE were significantly predicted by difference scores of only Covariation COV-AE using forward stepwise regression, F(1,12) = 29.79, p < 0.05, adj. R² = 0.69. Using backward stepwise regression, three variables were identified as significant predictors: difference scores of COV-AE and COV-VE and the standard deviations of racket period, SD-T, F(3,10) = 27.12, p < 0.05, adj. R² = 0.86. With respect to difference scores of the variable error VE, the forward stepwise regression identified the two difference scores of COV-VE and of SD-T as significant predictors, F(2,11) = 67.09, p < 0.05, adj. R² = 0.91. The backward stepwise regression again identified the difference scores of COV-VE, and of SD-T but also the regression slope, F(3,10) = 57.06, p < 0.05, adj. R² = 0.93.

Experiment 2: results

Performance on day 1

As in Experiment 1 participants arrived at a relatively steady performance level. Figure 7a shows the time series of the result variable AE across trials for both groups. As can be seen, subjects improved their task performance and arrived at an asymptotic performance level. An exponential function, y(t) = a + b × e^−ct, was fitted to each subject’s data across the first 24 (non-perturbed) trials (mean R² = 0.66 ± 0.28). There was no significant difference between mean fitted values of the last trial for the High-Stress group (6.04 ± 1.94 cm) and the No-Stress group (6.08 ± 2.98 cm), F(1, 21) < 0.01, p > 0.61. The execution variable racket acceleration at impact AC is plotted in Fig. 7b and similarly shows an exponential time course starting with positive values and approaching negative values with practice (mean R² = 0.54 ± 0.29). Also, there was no significant difference between mean fitted values of the last trial for the High-Stress group (−3.04 ± 3.38 m/s²) and the No-Stress group (−3.46 ± 3.03 m/s²), F(1, 21) = 0.10, p > 0.61.

Fig. 7.

Time series across the 24 trials of practice on Day 1 for all participants. The medians and the 25 and 75 percentiles of the No-Stress and the High-Stress groups are displayed (assignment occurred on Day 2). a Absolute error from target height, AE. b Racket acceleration at impact, AC

Manipulation check

In order to assess the effectiveness of the pressure manipulation the level of state anxiety between Baseline and Performance Tests was compared. Similar to Experiment 1, three participants in the No-Stress group were excluded from further analyses because they reported increases in state anxiety of more than two points. No participant had to be excluded from the High Stress group. After exclusion of the participants, the state anxiety score showed the necessary increase in anxiety in the High-Stress group (32.82 ± 9.18–41.27 ± 11.59) and a small decrease in the No-Stress group (29.33 ± 6.22–27.78 ± 6.22), evidenced by a significant interaction between Group and Test, F(1, 18) = 22.27, p < 0.05, f = 1.11. There was a significant group difference at Baseline, F(1, 18) = 0.94, p < 0.64.

Performance on day 2

Task result

In the Baseline Test the average AE did not significantly differ between the two groups, F(1, 18) = 0.18, p > 0.64. But participants in the High-Stress group were more successful in improving performance than participants in the No-Stress group and reduced their average absolute error AE, as indicated by a significant interaction, F(1, 18) = 4.69, p < 0.05, f = 0.51 (Fig. 8a). Participants in the High-Stress group were also more consistent (VE) in the Performance Test compared to Baseline whereas the No-Stress group did not change, F(1, 18) = 5.63, p < 0.05, f = 0.56 (Fig. 8b).

Fig. 8.

Means of absolute error, AE (a), and variable error, VE (b), during the 10 trials of the Baseline Test and the Performance Test; the error bars indicate standard error

Task execution

Additionally, variability in execution, SD-T and SD-A, significantly decreased in both groups from Baseline to Performance Test, F(1, 18) = 24.72, p < 0.05, f = 1.17 but the interaction between groups and test was not significant (Table 2).

Table 2.

Means (M) and standard errors (SE) of variability of racket period (SD-T) and racket amplitude (SD-A) in Experiment 2

	No-Stress Group, N = 9		High-Stress Group, N = 11
	M	SE	M	SE
SD-T (ms)
Baseline Test	59.07	1.54	56.12	2.42
Performance Test	54.56	2.27	51.29	2.15
SD-A (cm)
Baseline Test	2.46	0.20	1.88	0.11
Performance Test	2.22	0.18	1.75	0.09

Indicators of control

Average AC shown in Fig. 9a did not reveal differences in changes between tests for the two groups, F(1, 18) = 0.22, p > 0.05. Figure 9b shows the average slopes of regression of racket velocity on height error indicating error corrections. The average values are comparable to Experiment 1 and previous results. There was a significant interaction indicating an increase in the regression slopes in the High-Stress group from Baseline to Performance Test, F(1, 18) = 5.09, p < 0.05, f = 0.53. Group differences at the Baseline Test were significant, F(1, 18) = 3.98, p < 0.64, f = 0.47.

Fig. 9.

Means of racket acceleration at impact, AC (a) and of regression slopes of racket period on HE (b), during the 10 trials of the Baseline Test and the Performance Test; the error bars indicate standard error

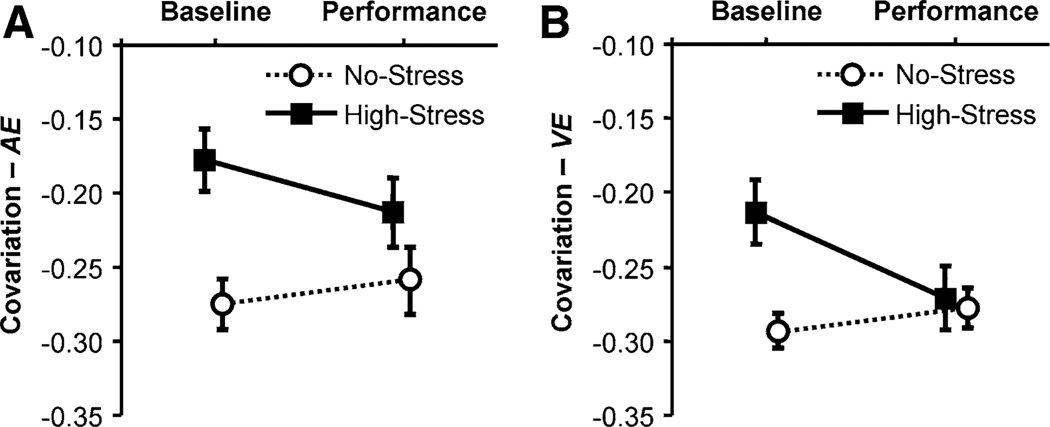
However, there was a significant interaction for covariation of execution variables in COV-AE, F(1, 18) = 7.73, p < 0.05, f = 0.65, and COV-VE, F(1, 18) = 13.14, p < 0.05, f = 0.85. As Fig. 10 suggests, there was also a significant group difference at Baseline, F(1, 18) = 12.52, p < 0.64, in COV-AE and COV-VE, F(1, 18) = 10.82, p < 0.64.

Fig. 10.

Means of covariation of impact parameters with respect to absolute error, COV-AE (a), and with respect to variable error, COV-VE (b), during the 10 trials of the Baseline Test and the Performance Test; the error bars indicate standard error

Contribution to performance differences

No variables were found to significantly predict differences in the absolute error AE using forward stepwise regression. Using backward stepwise regression, two variables were identified: difference scores of covariation, COV-AE, and of the standard deviation of racket amplitude, SD-A, F(2,8) = 5.10, p < 0.05, adj. R² = 0.45. With respect to difference scores of variable error VE, in forward stepwise no variable was identified as a significant predictor. In backward stepwise regression, difference scores of COV-VE, of the regression slope, and of the standard deviation of racket period SD-T were identified, F(3,7) = 3.65, p < 0.05, adj. R² = 0.44.

Discussion

In two experiments, all participants practiced for one session of 32 trials and showed the expected performance improvements towards a steady level. The absolute error asymptoted to a value of about 5 cm at the end of Day 1 which was similar to levels in a related study with novice participants (Wei et al. 2008). In parallel, the racket accelerations showed an exponential time course where AC values changed from initially positive values to negative values during practice, indicating that participants learnt to exploit passive stability. Importantly, both experimental groups had reached a relatively steady level of performance before undergoing differing stress manipulations on Day 2.

Based on theoretical understanding and previous empirical results in the ball bouncing task, we hypothesized that explicit monitoring under pressure should lead to decreased accuracy and increased variability in the task variable, less open-loop control (i.e., less negative racket acceleration at contact), more feedback-based control (i.e., negative regression slopes between height error and racket velocity) and less compensation (i.e. covariation of impact variables). Most notably and contrary to the hypotheses, the participants in the stressed groups did not choke but rather improved their task performance under pressure: participants became more accurate and more consistent in bouncing the ball accurately to a target height.

Evaluation of racket accelerations at impact that are indicative of performance with dynamical stability control did not reveal any change as a result of the pressure manipulation. Note, though, that this variable did show visible changes during the first practice sessions, giving evidence that it is a sensitive measure of performance quality. Although large inter-individual variance was seen across learning, both groups reached a stable region in both experiments. Even though the No-Stress groups showed slightly more negative values than the High-Stress groups, theoretically this difference does not indicate different control strategies. In fact, previous studies identified highest stability for AC values in the range between −3 and −5 m/s² (Schaal et al. 1996). Only changes from negative to positive values can be interpreted as changes in control.

The expectation that pressure leads to an increase in active, closed-loop control could only partly be confirmed. When perturbations were introduced in Experiment 2, this more demanding task rendered some effects in the degree of perceptually based corrections: participants in the High-Stress group showed more active error corrections of racket movements. The increase in active error correction can also be linked to performance enhancement because difference scores in regression slopes contributed to predicting changes in the variable error in both experiments. However, due to group differences at Baseline, it must be noted that the High-Stress group only increased to the level of the No-Stress group. Still, in both experiments the slope coefficients of the regressions were similar to the results observed in novices in a previous experiment (Wei et al. 2008). Importantly, the slopes were more negative than what would be expected from the stochastic version of the model, thus suggesting the existence of active error correction.

Whereas the variability of the racket amplitudes and periods did not change, covariation of impact variables increased in the High-Stress groups. This compensation between execution variables appears to underlie the performance improvement under stress: regression analyses of performance variables on execution variables and indicators of control showed that covariation contributed significantly in all cases. This highlights that understanding the relationship between execution variables is insightful over and above single variables (Higuchi 2000; Higuchi et al. 2002). Taken all results together, our study did not elicit the expected changes in performance.

These mostly unexpected results need to be scrutinized for possible methodological limitations. A first concern relates to the obvious fact that experiments on choking under pressure need “pressure”. The experiments used a standard paradigm to induce psychological pressure similar to an athletic competition. However, the test of the manipulation via self-report in questionnaires revealed that this manipulation was not successful with all participants. To enhance group differences according to the experimental goal we therefore discarded participants that had not responded to the pressure manipulation; participants in the control group were also eliminated if they showed anxiety responses. Thus, although the manipulation may not have been as successful as anticipated, the slightly modified group composition should have reflected effects of psychological pressure. It might also be argued that anxiety scores were relatively low. However, they were similar to those reported in related studies that report decrements in performance, as for example the study by Masters (1992). In conclusion, the conditions were sufficient to test our hypotheses regarding how psychological stress affects performance and sensorimotor processes in the ball bouncing task.

A second methodological concern are the group differences in some of the measures. There were notable differences at Baseline primarily for measures of execution but also for indicators of control. Improvements in these measures thus may just reflect these initial differences rather than reflect adaptations to stress. However, no group differences were observed during learning; furthermore, at the result level experimental control lead to similar levels of performance between groups in the Baseline test.

A third concern relates to the expertise of the participants: some studies suggested that, while increased explicit monitoring impairs performance in experts, it may actually be helpful for novices learning a new task (Beilock and Carr 2001; Perkins-Ceccato et al. 2003). If participants in this study were still novices in the ball bouncing task, then this may explain the enhancing effects of psychological pressure. On the other hand, participants’ learning curve speaks against this explanation: The exponential change in the task variable absolute height error, AE with a leveling off to a mean absolute error of less than 5 cm at the end of Day 1 indicated that performance had approached a steady state. Standard deviations of racket amplitude and period were well below the range of non-experienced performers and participants used AC values that have been identified to produce stable bouncing behavior (Wei et al. 2008).

A fourth concern refers to the nature of the task. It has been a matter of debate what aspects of a task may be subject to choking under pressure (overviews for example in Bond and Titus 1983; Strauss 2002). Candidate features have been complexity of the task, type of performance measures, i.e. quantitative versus qualitative ones. In addition, motor abilities of the performer, such as coordination or physical fitness, may also determine the influence of stress. Although the descriptor complexity is hard or impossible to define, the task of ball bouncing may rank as a rather simple skill: the experimental set-up constrained the task to only one dimension (vertical up-and-down movement of racket and ball trajectories) where the ball cannot be lost and performance improvements happen relatively fast. Some evidence exists that in these types of tasks performance are actually enhanced in pressure situations, consistent with the results of the two experiments. On the other hand, the ball bouncing task performance affords accuracy and for these types of tasks pressure can be detrimental (Bond and Titus 1983; Strauss 2002).

A feature that has not been discussed in this context is whether continuous rhythmic tasks may be less prone to choking. The tasks in previous studies on choking under pressure were almost exclusively discrete tasks such as a golf putt or basketball throws (Masters 1992; Hardy et al. 1996; Beilock and Carr 2001). In these skills a considerable amount of time is spent with preparation for and planning of the movement and the success of the task is determined at one single instant (Wrisberg and Pein 1992). Continuous tasks, on the other hand, with their longer duration may leave room for action-control strategies to overcome pressure and explicit monitoring (Pijpers et al. 2005; Jordet et al. 2009). Further, the conditions always change depending on the previous bounce and errors propagate from one bounce to the next. For each new ball contact actors need to adjust to the ball trajectory resulting from the previous bounce. As such, error correction and continuous monitoring is an inherent part of this skill. Hence, it is conceivable that additional focus on execution due to pressure may therefore not affect the control strategy in the same manner as in a discrete task.

More evidence in support for this argument that a continuous rhythmic skill requires a very different control strategy come from brain imaging and modeling results. Schaal et al. (2004) showed that discrete movements, even when confined to single-joint wrist movements, are associated with significantly more cortical and subcortical activation in both cerebral hemispheres. Specifically, there is a significant activation of the parietal and prefrontal areas in discrete performance. In contrast, rhythmic movements were associated mostly with primary motor areas. Hence, continuous skills may thus not be as prone to interferences from higher cognitive processes. This potential difference in control strategies is supported by theoretical studies that aimed to model discrete and rhythmic movements. With the goal to obtain accurate discrete movements precise setting of parameters is required, where small deviations may significantly affect the result (de Rugy and Sternad 2003; Hogan and Sternad 2007; Ronsse et al. 2009). As such it is viable that rhythmic tasks may be less subject to psychological interference.

In summary, to fully understand the phenomenon of choking under pressure it is important to understand and investigate the sensorimotor mechanisms involved. Previous studies have inferred explicit monitoring from task performance and have shown effects of pressure on the execution, i.e. kinematics of a movement. This study aimed to probe deeper and analyzed the kinematics with more fine-grained analyses, where specific measures were associated with control strategies based on previous modeling work. While we found evidence for more closed-loop error correction and increased compensatory control that permit inference of increased explicit monitoring, we also conclude that the effect of pressure on performance, or lack thereof, is mitigated by the rhythmic nature of the task.