A Computational Model for Rhythmic and Discrete Movements in Uni- and Bimanual Coordination

Abstract

Current research on discrete and rhythmic movements differs in both experimental procedures and theory, despite the ubiquitous overlap between discrete and rhythmic components in everyday behaviors. Models of rhythmic movements usually use oscillatory systems mimicking central pattern generators (CPGs). In contrast, models of discrete movements often employ optimization principles, thereby reflecting the higher-level cortical resources involved in the generation of such movements. This letter proposes a unified model for the generation of both rhythmic and discrete movements. We show that a physiologically motivated model of a CPG can not only generate simple rhythmic movements with only a small set of parameters, but can also produce discrete movements if the CPG is fed with an exponentially decaying phasic input. We further show that a particular coupling between two of these units can reproduce main findings on in-phase and antiphase stability. Finally, we propose an integrated model of combined rhythmic and discrete movements for the two hands. These movement classes are sequentially addressed in this letter with increasing model complexity. The model variations are discussed in relation to the degree of recruitment of the higher-level cortical resources, necessary for such movements.

1 Introduction

In current research on motor control, a large portion of studies focuses on a relatively small set of actions, most notably discrete prehension movements and rhythmic locomotion. With a view to everyday behavior, these two classes of movement represent only a small section of the rich movement repertoire of humans and animals. Furthermore, there appears to be a conceptual gap between research focusing on discrete movements—movements bounded by two rest intervals such as reaching, pointing, or aiming—and research focusing on rhythmic movements—movements executed in a sustained manner with a repetitive pattern, such as walking or drumming (Schaal, Sternad, Osu, & Kawato, 2004; Hogan & Sternad, 2007). This gap is reflected in both the respective experimental methodologies and the theoretical approaches. This state appears unsatisfactory, as not only do many behaviors constitute combinations of rhythmic patterns with discrete movements, as, for example, seen in playing musical instruments, but also both types of behavior are ultimately controlled by the same central nervous system.

Phylogenetically, rhythmic movements are old behaviors and are found in most species, ranging from worms and insects to primates. These are mostly locomotory behaviors but also chewing, rocking, and grooming. Discrete movements are pervasive in phylogenetically younger species, particularly in primates with developed upper extremities, and are controlled by more elaborate cortical areas (see, e.g., Kalaska, Scott, Cisek, & Sergio, 1997; Desmurget et al., 2001; Shadmehr & Wise, 2005). In recent years, evidence has been accumulated that the control of rhythmic and discrete movements is processed differently by the central nervous system (Hogan & Sternad, 2007; Huys, Studenka, Rheaume, Zelaznik, & Jirsa, 2008; Sternad, 2008). Behavioral studies (see, e.g., van Mourik & Beek, 2004; Buchanan, Park, & Shea, 2006; Smits-Engelsman, Swinnen, & Duysens, 2006) demonstrated that rhythmic movements between two targets are in general more accurate than corresponding isolated discrete movements. These results make the hypothesis that rhythmic arm movements are concatenations of discrete submovements unlikely. In support of this inference from behavioral data, Schaal et al. (2004) presented imaging results showing that the major areas activated in extremely simple discrete movements are the parietal and prefrontal cortex typically associated with higher cognitive functions. In contrast, rhythmic movements showed activation concentrated in the primary motor areas and considerably less bilateral cerebellar activity.

In animals, the neural control of locomotion and other rhythmic activities is known to be processed by dedicated low-level neural circuitries, the Central Pattern Generators (CPGs; see, e.g., Marder, 2000; Marder & Bucher, 2001). In vertebrates, the first evidence for CPGs was revealed by Brown (1914), who showed that cats with a transected spinal cord showed rhythmic alternating contractions in ankle flexors and extensors (see also Duysens & van de Crommert, 1998). These early documentations that the locomotory CPGs are located—at least partly—at the spinal level were supplemented by further support from nonprimates and primates, including humans (Cohen, Rossignol, & Grillner, 1988; Collins & Richmond, 1994; Dimitrijevic, Gerasimenko, & Pinter, 1998; Duysens & van de Crommert, 1998; Swinnen, 2002; Kawashima, Nozaki, Abe, Akai, & Nakazawa, 2005). More recently, the concept of CPG has been extended to rhythmic actions in the upper extremities (Dietz, 2002; Zehr et al., 2004; Zehr & Duysens, 2004; White et al., 2008), suggesting the presence of similar lower-level circuitries for voluntary rhythmic arm movements. These last findings are in good agreement with the imaging results reported by Schaal et al. (2004), as far fewer high-level cortical areas were involved in rhythmic compared to discrete movements.

Based on these neurophysiological findings, especially those on phylogenetically older species where CPG circuitries are easily identifiable and separable, numerous studies have successfully modeled CPGs. For example, Wilson (1999) reported a model of the lamprey’s CPG, which drives the muscles generating swimming activities, and Vavoulis et al. (2007) developed a model of the snail feeding network. Ijspeert, Crespi, Ryczko, and Cabelguen (2007) used a network of extremely simple oscillators for a salamander robot that can robustly walk and swim. For more complex circuitries, researchers have opted for more phenomenological models, in which an abstract oscillatory structure captures the global behavior (Buchli, Righetti, & Ijspeert, 2006). A common characteristic of various CPG models is to separate the circuitry into two symmetrical and mutually inhibitory substructures, that is, half-centers (Matsuoka, 1985; Nagashino & Kelso, 1991, 1992; Grossberg, Pribe, & Cohen, 1997). These two half-centers can be viewed as drivers of a pair of antagonistic muscles. While the presence of such half-centers has been established for “simple” species, there is only indirect evidence that such circuitries also exist in primates, including humans.

The modeling of the cortical processing involved in the planning, control, and sensory integration of discrete reaching movements has recently been reviewed in the context of optimization principles (see Jordan & Wolpert, 1999; Wolpert & Ghahramani, 2000; Todorov & Jordan, 2002; Todorov, 2004). The key principle in this approach is that the central nervous system optimally extracts the information from priors and sensory inflow and generates an end-effector trajectory that minimizes a given cost function. For instance, minimizing movement jerk (third derivative of position) is one such optimality criterion that has successfully accounted for the bell-shaped velocity profiles in simple reaching movements (Flash & Hogan, 1985). While optimization approaches are successful for discrete movements, it has not been discussed how the generative processing of discrete movements can be related to rhythmic movements, which arguably exploit low-level structures.

In the past decade, researchers have experimentally demonstrated that forearm movements combining rhythmic and discrete components highlight some coupling between those two units of action: the discrete movement is triggered during a limited phase window of the rhythmic cycle, which is in turn reset by the discrete movement (Sternad, Dean, & Schaal, 2000; de Rugy & Sternad 2003). Moreover, recent investigations revealed that the interaction between rhythmic and discrete components is necessary to finely control an external object (a bouncing ball), either to correct for unexpected perturbations (Wei, Dijkstra, & Sternad, 2007) or to adapt the control strategy to various movement frequencies or visual feedback conditions (Ronsse, Lefèvre, & Sepulchre, 2008; Ronsse, Thonnard, Lefèvre, & Sepulchre, 2008). Taken together, these findings suggest that even if they are largely nonoverlapping primitives, discrete and rhythmic movements are combined in a nonarbitrary manner by the central nervous system. The aim of this letter is to present a modeling framework that explicitly cuts across the divide between discrete and rhythmic movements. This model is based on a parsimonious half-center structure, whose mutual inhibition ensures steady-state oscillations as long as it is provided with a tonic input. Subsequently, we will show that this inhibitory structure can also be recruited for the generation of discrete movements when the alternating activation of the antagonistic muscles is decreased. Finally, our model embeds a coupling mechanism that can account for the most fundamental coordination properties appearing in bimanual movements.

In conclusion, we aim at providing a comprehensive model to capture the low-level circuitry of the motor apparatus. This model sheds some light on the physiology of the actual system, arguing that the half-center structure is efficiently recruited in the generation of both rhythmic and discrete movements. A simple coupling between two such structures can account for some coordination findings in bimanual movements. The basic model is detailed in the next section; sections 3 to 6 address movements with increasing complexity that this model can simulate.

2 Modeling Approach

The modeling of an autonomous oscillator is usually captured by a set of nonlinear differential equations ẋ = f(α_f, x), where x denotes the state vector of the oscillating system and α_f the parameter vector. The function f is such that the limit cycle defined by x^★(t + T) = x^★(t), ∀t ≥ 0 (T is the cycle period) is a stable attractor in the state space of x. In the case of a CPG, the model also includes an input vector u, representing, for example, the global contribution of synaptic inputs to the CPG neurons: ẋ = f(α_f, x, u). For simplicity, we assume that the system is linear in the input and that the input and autonomous contributions to the dynamical equations can be separated, ẋ = f(α_f, x) + α_uu, with α_u weighting the input contribution. Finally, it is also meaningful to integrate a coupling term to capture how two or more of these structures “talk” to each other in order to synchronize their frequency or lock their phase. For the ith oscillator, the model is as follows:

$${\stackrel{.}{x}}_i=f({\alpha }_f,x_i)+\sum _{j\ne i}g({\alpha }_g,x_i,x_j)+{\alpha }_u{u}_i,$$

assuming that the coupling g, parameterized through the vector α_g, can be isolated from the autonomous dynamics. Accordingly, the vector x_j denotes the state of any other oscillator coupled with the one of interest (the ith). With a particular design of f and g, Haken, Kelso and Bunz (1985) proposed a model based on the van der Pol and Raleigh oscillators that capture the bifurcation route in phase stability occurring in human hand movements under the influence of a scalar change in cycling frequency: both in-phase and antiphase movements are stable at low frequency, while only in-phase movements remain stable at high frequency. Similarly, Grossberg et al. (1997) designed a neural network of two excitatory and two inhibitory neurons obeying the Hodgkin-Huxley membrane equation, which displayed the same bifurcation route via particular coupling function g and parameters α_g.

2.1 Background: The Matsuoka Oscillator

We will use a simple CPG model that captures the basic properties for the generation of a one-degree-of-freedom rhythmic movement, the half-center Matsuoka oscillator (Matsuoka 1985, 1987). This CPG model consists of two antagonistic (groups of) neurons and produces rhythmic patterns with a tonic (constant) external input. The magnitude of this input determines the frequency and amplitude of the output, such that the stable limit cycle of this oscillator is not unique, but is shaped by the input. The Matsuoka oscillator has already been used to model the rhythmic component in complex arm movements (Sternad et al., 2000; de Rugy et al., 2003; de Rugy & Sternad, 2003), investigate the mechanisms of resonance tuning in rhythmic movements (Williamson, 1998; Verdaasdonk, Koopman, & van der Helm, 2006; Williams & DeWeerth, 2007; White et al., 2008), and produce coordinated patterns in the musculoskeletal system of the lower extremities in human locomotion (Taga, 1995a, 1995b).

In the Matsuoka oscillator, the autonomous dynamics f are based on a piece-wise linear set of differential equations modeling the dynamics of the neural discharge rates: the oscillator consists of a pair of mutually inhibitory (groups of) neurons whose (average) rates of discharge are denoted by ψ_i and ψ_j, respectively. The firing rates obey the following equations:

$$\begin{array}{l}{t}_1{\stackrel{.}{\psi }}_i=-{\psi }_i-\beta {\varphi }_i-\eta {[{\psi }_j]}^{+}+u_i,\\ t_1{\stackrel{.}{\psi }}_j=-{\psi }_j-\beta {\varphi }_j-\eta {[{\psi }_i]}^{+}+u_j,\end{array}$$ (2.1)

where t₁ is the time constant for the rate of discharge, β the constant of self-inhibition, and η the constant of mutual inhibition. The symbol [•]⁺ = max(0, •) denotes that only positive discharge rates are considered for mutual inhibition. The self-inhibition is governed by two other state variables, ϕ_i and ϕ_j, which obey the following equations:

$$\begin{array}{l}{t}_2{\stackrel{.}{\varphi }}_i=-{\varphi }_i+{[{\psi }_i]}^{+},\\ t_2{\stackrel{.}{\varphi }}_j=-{\varphi }_j+{[{\psi }_j]}^{+}.\end{array}$$ (2.2)

These equations capture the well-known phenomenon of adaptation or fatigue (see, e.g., Wilson, 1999), whose time constant is t₂. Adaptation refers to the fact that the rate of discharge of a neuron whose external input u(t) is constant will first rapidly increase to a maximum value (at a fast timescale governed by t₁) and then gradually decrease to a lower value (at a slower timescale governed by t₂). Adaptation plays an essential role in the generation of the oscillations by the Matsuoka oscillator (see Matsuoka, 1985, and references therein).

The structure of the Matsuoka oscillator is very similar to other half-center CPGs (e.g., Nagashino & Kelso, 1991, 1992; Grossberg et al., 1997). Robust oscillations emerge as a consequence of the balance between mutual inhibition (either direct, as in the Matsuoka oscillator, or through an intermediate neuron, as in Nagashino and Kelso’s or Grossberg et al.’s models) and self-inhibition (via adaptation, as in the Matsuoka oscillator, or through the same intermediate neuron in Nagashino and Kelso’s or Grossberg et al.’s models). While the models by Nagashino and Kelso (1991, 1992) and Grossberg et al. (1997) considered each half-center as the pacemaker of one limb, we assume here that each of both half-centers of the oscillator controls the activity of one muscle of the joint, whose outputs are opposing (antagonistic) torques linearly dependent on the truncated rates of discharge (see Sternad et al., 2000; de Rugy et al., 2003; de Rugy & Sternad, 2003). Assuming that ψ_i and ψ_j are proportional to the torque generated in the positive and negative directions, respectively, the total produced torque is then

$${\psi }_T=h_{\psi }({[{\psi }_i]}^{+}-{[{\psi }_j]}^{+}),$$ (2.3)

where h_ψ is the torque gain. The torque is converted into effector velocity through a simple inertial mechanical system,

$$I\ddot{\theta }+\gamma \stackrel{.}{\theta }-{\psi }_T=0,$$ (2.4)

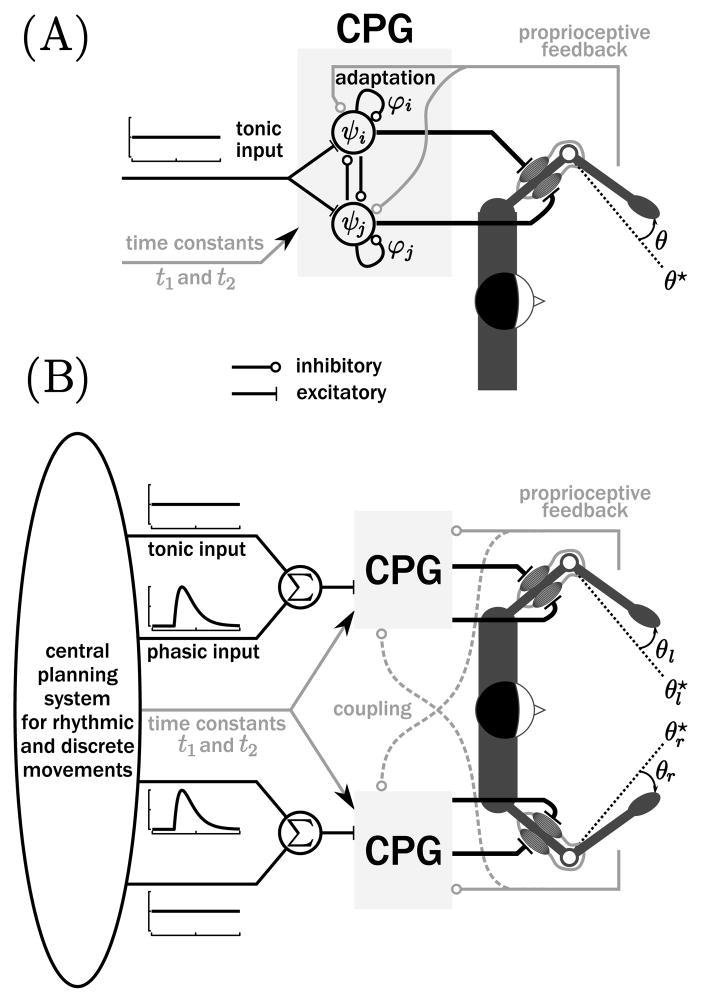
where I and γ are the moment of inertia and the damping. This effector’s angular position, velocity, and acceleration are given by θ, θ̇, and θ̈, respectively. For simplicity, we neglected the passive stiffness of the effector, assuming that the equilibrium of the mechanical equation 2.4 (i.e., $\overline{{\psi }_T}=\overline{\stackrel{.}{\theta }}=\overline{\ddot{\theta }}=0$) is not confined to a single position θ̄, but can be attained throughout a larger range (see, e.g., Esposti, Cavallari, & Baldissera, 2007). A picture of this CPG driving the two antagonistic muscles of the elbow is represented in Figure 1A.

Figure 1.

(A) Matsuoka oscillator as a model for the CPG driving the two antagonistic (cartoon) muscles of the elbow generating single degree-of-freedom movements. Proprioceptive feedback (in gray) provides inhibitory input to the CPG. More details can be found in the text. (B) Complete model for the generation of bimanual rhythmic and discrete movements.

More recently, the Matsuoka oscillator was extended with a term representing the feedback information from the afferent pathways originating from the muscle spindles (Dimitrijevic et al., 1998; van de Crommert, Mulder, & Duysens, 1998; Kuo, 2002; Buschges, 2005; Frigon & Rossignol, 2006; Simoni & DeWeerth, 2007). One way to include this sensory feedback into the firing rate equations (2.1) is in terms of a negative inhibitory influence (Williamson, 1998):

$$\begin{array}{l}{t}_1{\stackrel{.}{\psi }}_i=-{\psi }_i-\beta {\varphi }_i-\eta {[{\psi }_j]}^{+}-\sigma {[\theta -{\theta }^{★}]}^{+}+u_i,\\ t_1{\stackrel{.}{\psi }}_j=-{\psi }_j-\beta {\varphi }_j-\eta {[{\psi }_i]}^{+}-\sigma {[-(\theta -{\theta }^{★})]}^{+}+u_j,\end{array}$$ (2.5)

where σ quantifies the strength of this sensory coupling and θ^★ is the reference position of the output. This proprioceptive feedback is represented by the light gray path in Figure 1A. Initially, such sensory input of the Matsuoka oscillator was studied to reproduce the energy exchanges between the oscillator and the mechanical system that leads to frequency locking and resonance tuning (Williamson, 1998; Verdaasdonk et al., 2006; Williams & DeWeerth, 2007). Note that Taga (1995a, 1995b) used similar feedback terms to stabilize the musculoskeletal system in his locomotion model, including the so-called global angle between centers of pressure and gravity. Since the mechanical limb system (equation 2.4) is not an oscillator (it does not include gravity or passive stiffness), there is no resonance tuning, and the output frequency is determined only by the frequency of the CPG. Besides this property, the extended system (equation 2.5) has additional advantages for the present simulations: sensory feedback is undoubtedly present at the spinal level, and sensory feedback stabilizes the average position around θ^★ via an active stiffness mechanism. Without this term, system 2.1 oscillates around an arbitrary position and is dynamically unstable.

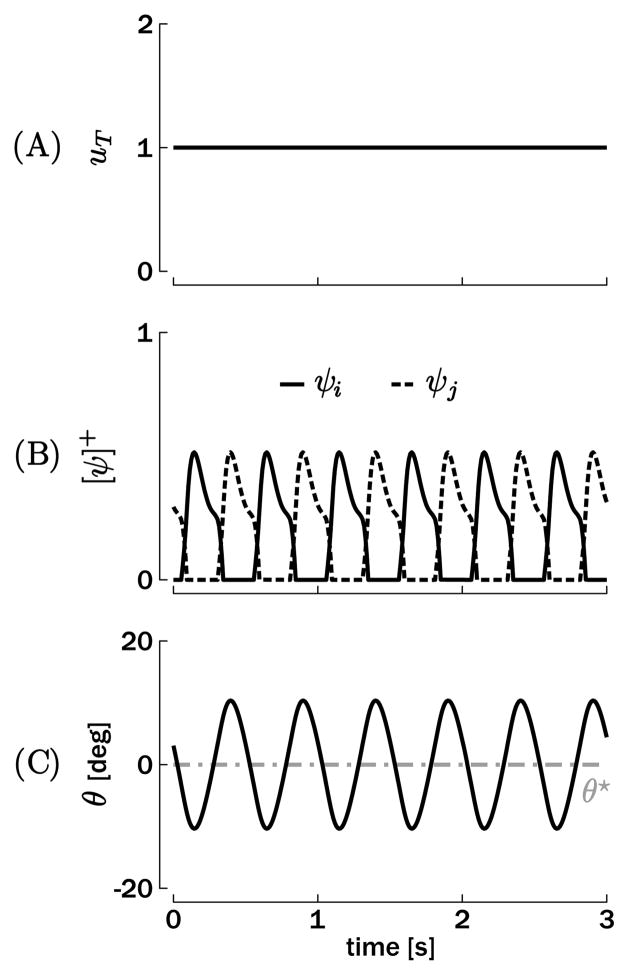
The Matsuoka oscillator produces an oscillatory output for a constant tonic input u_i(t) = u_j(t) = u_T. A typical input-state-output plot is shown in Figure 2 for t₁ = 0.05 s, t₂ = 0.125 s, u_T = 1, β = 2.5, η = 2.5, σ = 1.5, h_ψ = 5 (arb. units), γ = 0.5Nm.s/rad, I = 0.08Nm.s²/rad, and θ^★ = 0 deg. The parameters γ and I correspond to previously measured values for rhythmic elbow movements (Bennett, Hollerbach, Xu, & Hunter, 1992). The time constants t₁ and t₂ are tuned such that the oscillation period lies around 0.5 s, with a plausible time course of the adaptation. Moreover, it can be shown that both the period and amplitude of the steady-state oscillation are dependent on the time constants t₁ and t₂ and the tonic input u_T (see the appendix).

Figure 2.

Simulation of a single degree-of-freedom rhythmic movement. (A) Tonic input u_T. (B) Muscles input (rates of discharge of the corresponding neurons ψi and ψj), which produce the torque ψ_T. (C) Position output θ oscillating around the reference position θ^★ = 0.

2.2 Bimanual Coupling

This section proposes a design for the coupling function g, capturing how several oscillators can “talk” to each other to synchronize their frequency or lock their phase. We will focus on a network of two oscillators, each representing the CPG structure of a single limb. Based on the single-limb equations, 2.2 to 2.5, we assume that the right limb is described by the following state variables ψ_r,i, ψ_{r, j}, ϕ_r,i, ϕ_{r, j}, θ_r, θ̇_r and the inputs u_r,i and u_{r, j}. Similarly, the left limb is described by the following state variables ψ_l,i, ψ_{l, j}, ϕ_l,i, ϕ_{l, j}, θ_l, θ̇_l and the inputs u_l,i and u_{l, j}. For simplicity, we assume that the time constants t₁ and t₂ are equal for the two limbs.

With a view to oscillator 2.5, three types of dynamical coupling g can be considered:

1. Following the principle of muscle homology (i.e., postulating that homologous muscles are (partly) controlled by a common neural network in the brain), the coupling should be at the level of the inputs: u_r,i = u_l,i and u_{r, j} = u_{l, j}. However this coupling does not constrain the phase between the oscillators: relative phase does not converge to one or several attractors, and the oscillators behave as two independent units.

2. Matsuoka (1985, 1987) suggested a coupling at the level of the internal state variables (e.g., discharge rates) when considering networks of more than two oscillators. However, this type of network converges robustly to one particular phase relationship, and the coexistence of two mutually exclusive attractors, such as in-phase and antiphase, is very hard to obtain within a simple network structure.

3. The coupling can be at the level of the output variables θ_r and θ_l, suggesting a connection between the two effectors via the afferent pathways. In the case of rhythmic movements, in-phase and antiphase stability can be obtained via the homologous coupling (θ_r with ψ_r,i and ψ_{r, j}, and vice versa) and the nonhomologous coupling (θ_r with ψ_l,i and ψ_{l, j}, and vice versa), respectively (see section 5).

Due to the shortcomings of types 1 and 2, we focus on the third type of coupling. The coupled Matsuoka oscillator is thus described by the following equations (only for the right effector for brevity):

$$\begin{array}{l}{t}_1{\stackrel{.}{\psi }}_{r,i}=-{\psi }_{r,i}-\beta {\varphi }_{r,i}-\eta {[{\psi }_{r,j}]}^{+}-\sigma {[{\theta }_r-{\theta }_r^{★}]}^{+}-\mu {[{\theta }_l-{\theta }_l^{★}]}^{+}-\nu {[-{\theta }_l+{\theta }_l^{★}]}^{+}+u_{r,i},\\ t_2{\stackrel{.}{\varphi }}_{r,i}=-{\varphi }_{r,i}+{[{\psi }_{r,i}]}^{+},\\ t_1{\stackrel{.}{\psi }}_{r,j}=-{\psi }_{r,j}-\beta {\varphi }_{r,j}-\eta {[{\psi }_{r,i}]}^{+}-\sigma {[-{\theta }_r+{\theta }_r^{★}]}^{+}-\mu {[-{\theta }_l+{\theta }_l^{★}]}^{+}-\nu {[{\theta }_l-{\theta }_l^{★}]}^{+}+u_{r,j},\\ t_2{\stackrel{.}{\varphi }}_{r,j}=-{\varphi }_{r,j}+{[{\psi }_{r,j}]}^{+}.\end{array}$$ (2.6)

An equivalent system is used for the left oscillator. The mechanical systems are equivalent to equation 2.4. The couplings introduced in equation 2.6 correspond to sensory couplings, since the μ and ν terms depend on the position of the other limb. In equation 2.6, μ parameterizes the homologous coupling (since μ and σ play similar roles for θ_r and θ_l in the equation), and ν parameterizes the nonhomologous coupling (since ν and σ play opposite roles for θ_r and θ_l in the equation). Similar to the feedback term σ introduced in equation 2.5, both μ and ν are inhibitory in equation 2.6. An overview picture of the coupled oscillators driving the two elbows is shown in Figure 1B, with the bimanual coupling represented by the dashed gray paths. In the following sections, two types of inputs to these oscillators, tonic and phasic, will be used to simulate rhythmic and discrete movements, respectively.

3 Unimanual Discrete Movements

As reviewed in section 2.1, the single-effector oscillator (see equation 2.5; not including coupling terms) produces steady-state oscillations around its reference position θ^★. This mechanism has been exploited to generate rhythmic movements (see Figure 2). Discrete movements—movements that are clearly delimited by pause intervals such as reaching or pointing (Hogan & Sternad, 2007)—are another class of movements.

In this section, we will use the Matsuoka oscillator as a generator for discrete movements. Since the Matsuoka oscillator is a simple model of CPG, which is supposed to lie at a very low level in the motor pathway (at least partly spinal), we hypothesize that such a structure cannot be bypassed in the generation of discrete movements. We will show that the mutually inhibitory structure of the Matsuoka oscillator can be similarly constructive in the generation of the alternating antagonistic muscular bursts as typical for discrete movements (Wachholder & Altenburger, 1926; Sternad & Corcos, 2001). Our objective is thus to demonstrate how the discrete movements generator could use an oscillatory CPG at the end of its pathway.

3.1 Methods

One way to generate discrete movements with oscillators is by characterizing their equilibrium points, that is, the fixed points of the state space for constant inputs (see, e.g., Schöner, 1990; Jirsa & Kelso, 2005). The equilibrium point or λ-model for human movement control was initially proposed by Asatryan and Feldman (1965) and Feldman (1966a, 1966b). More recently, other equilibrium point models have been developed to study discrete and rhythmic movements (see, e.g., Jirsa & Kelso, 2005; Kistemaker, van Soest, & Bobbert, 2007). In the case here, the equilibrium point is set through the reference position θ^★. The sensory inputs correcting for the difference between θ and θ^★ in equation 2.5 are inhibitory, such that they make ψ_i and ψ_j negative in the absence of any external input (u_i = u_j = 0). Given equation 2.3, negative rates of discharge cannot produce any torque, such that the output θ will stay constant and will not converge to θ^★. Stated differently, our model requires the design of inputs u_i and u_j that compensate for the inhibitory influence of the sensory feedback and drive the output toward the equilibrium θ^★.

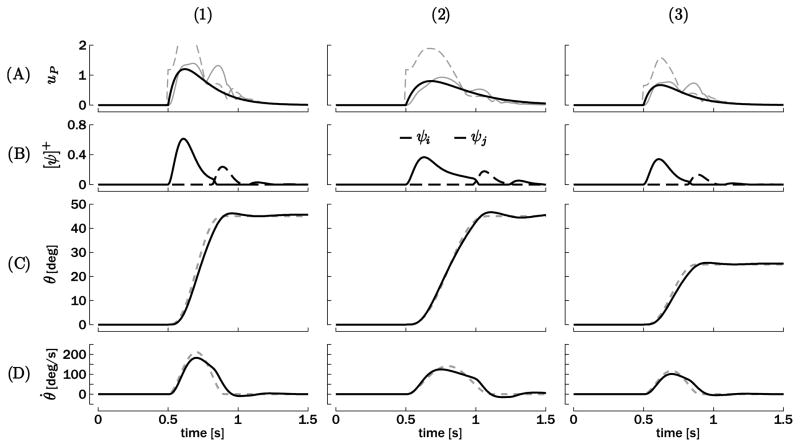
A first way to compute the inputs u_i and u_j with the goal of producing a bell-shaped velocity output is to invert the oscillator (equations 2.4 and 2.5). Using H to denote the transfer function of the Matsuoka oscillator, that is, the frequency mapping between the inputs (u_i and u_j) and the output (θ) the dynamical inverter G of this transfer function will ensure G × H ≃ 1 for a large frequency range. Figure 3A depicts examples of three typical bell-shaped velocity profiles computed from inputs that were obtained through dynamical inversion. The solid gray curves represent u_i, and the dashed gray curves represent u_j.

Figure 3.

Typical examples of discrete movements triggered at t = 0.5 s: (1) amplitude θ^★ = 45 deg and duration τ = 0.4 s, (2) amplitude θ^★ = 45 deg and duration τ = 0.6 s, and (3) amplitude θ^★ = 25 deg and duration τ = 0.4 s. (A) Phasic inputs computed by equation 3.1 (solid black) in comparison to the input resulting from a dynamical inversion of the perfect bell-shaped velocity output (solid and dashed gray for the agonistic and antagonistic sides, respectively). (B) Corresponding neuronal discharge rates ψ_i and ψ_j (only positive parts). (C) Resulting trajectories (solid black) compared to the ideal bell-shaped velocity profile (dotted gray). (D) Corresponding velocity profiles. Ideal bell-shaped velocity profiles are again shown in dashed gray lines.

We do not want to suggest that dynamical inversion of the Matsuoka oscillator is explicitly computed by the central nervous system in order to generate movements such as point-to-point reaching (see Wolpert, Miall, & Kawato, 1998; Kawato, 1999; Todorov & Jordan, 2002, for contributions discussing the presence of inverse internal models in the brain). However, we will use these “ideal” (meaning that these inputs generate a perfectly bell-shaped velocity output) inputs for u_i and u_j to find a simple phasic input u_P for both muscles that generates an output with approximate bell-shaped velocity with very few parameters. This fit was obtained by a product of two exponentials: one of the form (e^{t τ₁} − 1), which models the rising time constant τ₁, and one of the form e^−t/τ₂, whose time constant τ₂ depends on the desired movement duration. In sum, this input corresponds to a filtered decaying pulse as used by de Rugy and Sternad (2003) to generate ballistic discrete movements from a similar model. The parameters have been obtained from fitting many inputs u_i computed by dynamical inversion (see Figure 3A). We propose the following phasic input for both muscles: u_i = u_j =

$$u_P(t)={\left[0.07\frac{\mid {\theta }^{★}\mid }{\tau }\left(e^{\frac{1.4(t-t_0)}{\tau }}-1\right)e^{\frac{-4.1(t-t_0)}{\tau },}\right]}^{+},$$ (3.1)

where θ^★ is the desired movement amplitude (and consistently the equilibrium point of the inhibitory proprioceptive feedback), τ is the desired movement duration, and t₀ is the movement onset.

3.2 Results

Figure 3 displays three typical reaching movements obtained from different parameter tunings and compares them with the corresponding “ideal” movement (i.e., a perfect bell-shaped velocity trajectory of same amplitude and duration and their corresponding inverted inputs). This “ideal” trajectory should correspond to one that minimizes jerk (third derivative of position; see, e.g., Flash & Hogan, 1985; Hogan & Sternad, 2007). Note that the reference position θ^★ switches abruptly (step function) from 0 deg to its final value at the movement onset: t₀ = 0.5 s. The input u_p is equal for both muscles (see equation 3.1). However, dynamical inversion predicts large differences between the “ideal” u_i and u_j for—at least—the first movement phase. During this phase, the fit (see equation 3.1) is much closer to u_i than u_j (see Figure 3A), thus closer to the input corresponding to the active muscle (i.e., ψ_i; see Figure 3B). Nonetheless, this discrepancy between u_p and the “ideal” u_j will not affect the corresponding output very much. Indeed, the corresponding ψ_j is negative in both cases during this first movement phase, and the model relies on the fact that negative ψ’s are truncated to zero in both the torque generation and mutual inhibition. In sum, a common input for both units is simpler than dynamical inversion and does not significantly influence the position output if the fit is made with the input corresponding to the active muscle.

The EMG bursts in point-to-point movements are typically triphasic, arising from the successive activation of the agonist (acceleration of the effector), the antagonist (braking), and the agonist (stabilization). Figure 3B shows a similar sequence of activations. This is due to mutual inhibition that attracts them into the oscillatory mode (as in sustained rhythmic movements) and the exponential decay of the input that limits the number of bursts to three. Our method thus generates terminated discrete movement while exploiting the oscillatory structure (crossed-inhibition) of the Matsuoka oscillator. It is interesting to point out that Wachholder and Altenburger (1926) already speculated that the triphasic sequence of bursts was a consequence of the fundamentally rhythmic alternation of the antagonistic muscles (see Sternad & Corcos, 2001, for the English translation).

Figure 3 illustrates that a large range of reaching movements can be generated from a simple input, equation 3.1, and that the control of amplitude and duration can be determined independently by θ^★ and τ, respectively. In sum, equation 3.1 can be viewed as a simplified implementation of a discrete movement inverter. Rather than relying on a complex computational structure, it relies on two parameters, θ^★ and τ, and therefore requires fewer computational resources. The controller generates the phasic input on the basis of the desired duration and amplitude, while the bell-shaped velocity profile emerges as a consequence of the intrinsic sequential activation of the antagonistic muscles.

4 Rhythmic and Discrete Combination in Unimanual Movement

In this section, we describe simulation results that were obtained when combining rhythmic and discrete movements within a single limb. An example for such type of movement occurs in locomotion, where stepping over an obstacle corresponds to a change in the step length, that is, a change in the average position of the effectors. Based on section 3, the reference position (the average position θ^★) of the ongoing oscillation is abruptly changed at some arbitrary phase in order to elicit a discrete component to the ongoing rhythmic movement. However, there is no need for compensating the inhibitory effect of the sensory feedback with a phasic input, since the tonic input generating the rhythmic component already plays this compensatory role. Since only the reference position changes in the simulations and the tonic input remains constant, the proposed model can be viewed as a purely “equilibrium point model,” keeping in mind that θ = θ^★ is not a stable equilibrium point, but stabilizes the average position of the oscillation. Simulation results will be compared to experimental results from human performance as previously reported by Sternad and colleagues (Sternad et al., 2002; Sternad, de Rugy, Pataky, & Dean, 2002; de Rugy & Sternad, 2003).

4.1 Methods

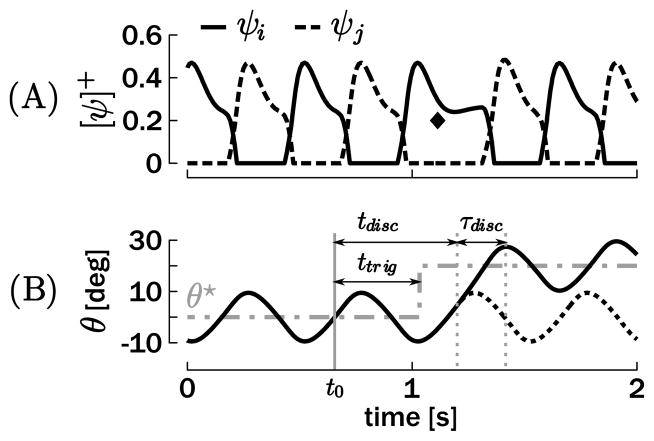
We simulated the following experimental results on a combined rhythmic and discrete movement using the unimanual model, equation 2.5. A baseline rhythmic movement around θ^★ = 0 deg was generated with an amplitude of A = 20 deg—oscillations between −10 deg and 10 deg—and five different periods: T = 0.4 s, 0.5 s, 0.6 s, 0.8 s, or 1 s. At a certain phase of the rhythmic cycle, θ^★ was switched abruptly (step function) to 20 deg, forcing the oscillator to oscillate around this novel reference position of oscillations between 10 deg and 30 deg (see Figure 4).

Figure 4.

Example of a unimanual combination of rhythmic and discrete movement. (A) Positive truncated neuronal discharge rates. (B) Resulting effector position θ with respect to the reference position θ^★. With respect to t₀ (the beginning of the cycle), t_trig denotes the time of the stimulus indicating a switch in θ^★; t_disc denotes the onset time of the discrete movement at which the trajectory actually differs from the original rhythmic movement (dotted line); and τ_disc denotes the duration of the discrete movement (between the onset, defined previously, and the first peak in the following oscillation). On A, the diamond highlights the ψ_i burst, which generates the discrete submovement.

For each of the five tested periods T, 100 movements were generated, for which the phase of the abrupt switch in θ^★ was randomly selected from the range of 0 to 2π rad with a uniform distribution. We tested the validity of our model with respect to three main results from the literature (Sternad et al., 2000, 2002; de Rugy & Sternad, 2003):

1. Regardless of the phase of the shift signal, the onset of the overt discrete movement occurs within a finite phase window of the rhythmic cycle.

2. The phase of the rhythmic movement is reset by the discrete movement.

3. The duration and the peak velocity of the discrete movement scale with the rhythmic movement period.

In order to quantitatively evaluate and compare the simulation and human results, it is necessary to define some variables. First, t₀ defines the beginning of the cycle and is used as reference time: it is the last time the position passes through θ = θ^★ with positive velocity before the perturbation (see Figure 4). t_trig and t_disc define the times when the discrete movement was triggered and when the trajectory differed from a continuous rhythmic movement with respect to t₀. The difference threshold was set to 0.03 deg between the normal and the changed trajectories. Consequently, the phases of stimulation and discrete onset are defined as

$$\begin{array}{l}{\phi }_{\mathit{trig}}=mod\left(2\pi \frac{t_{\mathit{trig}}}{T},2\pi \right),\\ {\phi }_{\mathit{disc}}=mod\left(2\pi \frac{t_{\mathit{disc}}}{T},2\pi \right).\end{array}$$ (4.1)

The duration of the discrete movement is denoted by τ_disc and is defined as the time between the movement onset (defined previously) and the first peak in the following oscillation: the end of the discrete movement.

For the 500 simulated movements (5 periods T × 100 phase onsets), we calculated φ_disc, τ_disc, and the velocity peak during the discrete movement: the time window defined by τ_disc.

4.2 Results

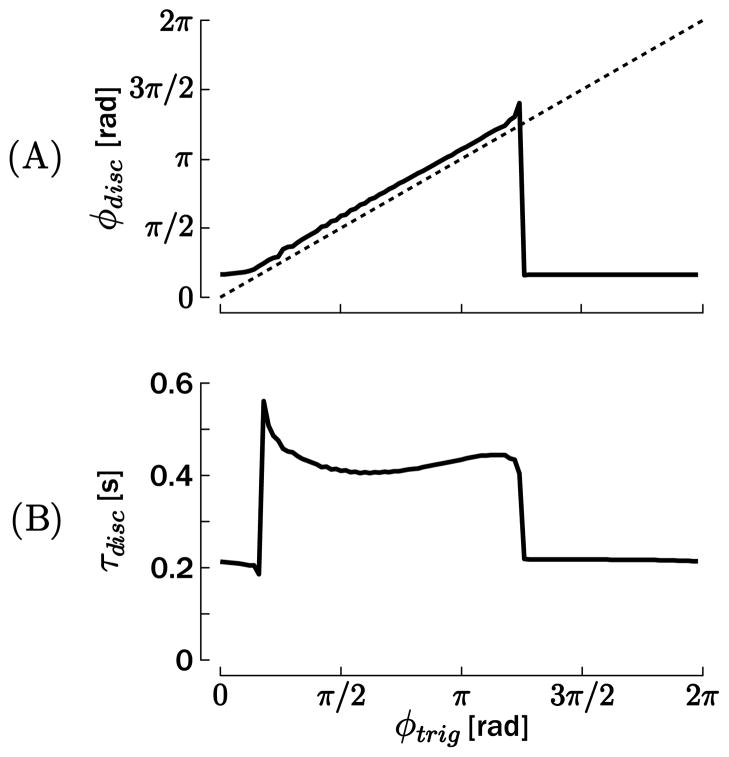
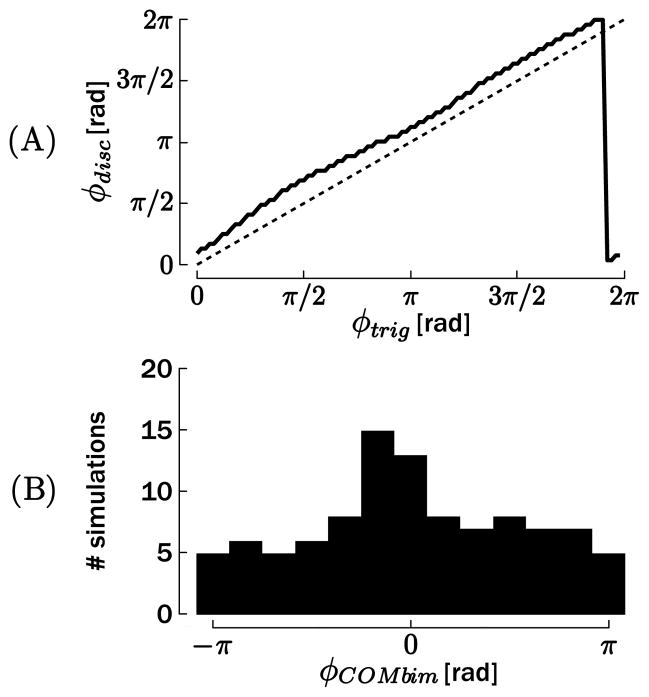
The phase of the switch in θ^★(φ_trig) and the phase of the actual onset of the discrete movement φ_disc are compared in Figure 5A for T = 0.5 s. The relationship between the two phases would be a straight line parallel to the dotted identity line if the discrete movement started at a constant phase (corresponding to a constant delay for a given frequency) after the trigger t_trig, that is, if the phase of the discrete movement onset did not depend on the rhythmic cycle. This was the case for trigger phases in the approximate interval 0 < φ_trig < 5π/4, where a small but constant offset is observed between φ_trig and φ_disc. However, for the remaining phases, only one onset phase at φ_disc ≃ π/6 was obtained.¹ This result is consistent with the finding that the phase of the discrete movement onset is dependent on the trigger phase. Similar figures were obtained for the other four periods T. This result can be directly compared with actual human data (Sternad et al., 2002; de Rugy & Sternad, 2003), in which the distributions of the onset phase of the discrete movement also appeared to be clustered around particular values.

Figure 5.

(A) Phase of the onset of the discrete movement φ_disc, with respect to φ_trig, the phase of the switch in the reference position θ^★. (B) Duration of the discrete movement τ_disc, with respect to φ_trig. These simulations have been obtained for T = 0.5 s.

To illustrate phase resetting after completion of the discrete movement, we compared the duration of the discrete movement τ_disc with the trigger phase φ_trig (see Figure 5B, for T = 0.5 s). Once again, if no phase reset existed, this relationship would be linearly growing between 0 and T, since the first peak after the discrete movement would not be constrained by its onset. In contrast, Figure 5B illustrates that τ_disc evolved along two “plateaus” of almost constant value. Within each of these plateaus, the first peak in the oscillation following the discrete movement appears after a constant time after the triggering the discrete movement, hence demonstrating that the oscillator phase is reset by the discrete movement.

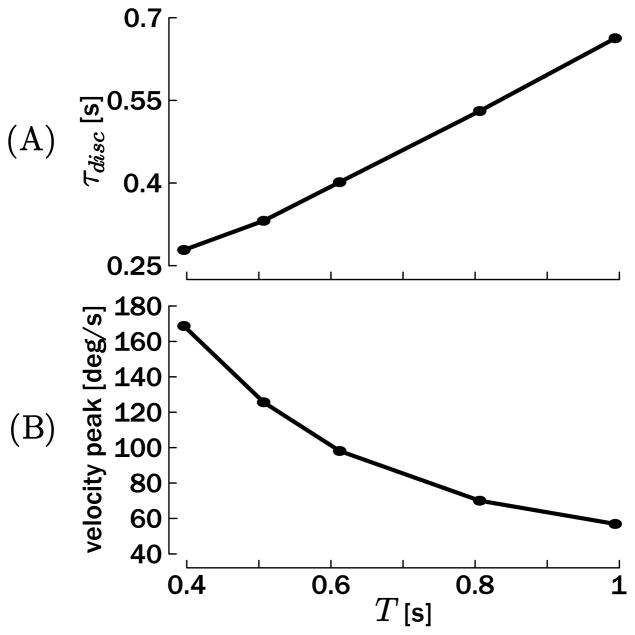
Figure 6A replicates the third result: the average duration of the discrete movement scales almost linearly with the period of the rhythmic movement. Consistently, as shown in Figure 6B, the velocity peak during the discrete movement is higher when the duration is shorter. This can be explained by the fact that the period of the rhythmic movement is determined by the oscillator time constants (t₁, t₂; see the appendix). Consequently, since the discrete movement is initiated by a step change in the reference position θ^★ (switch of equilibrium point), its dynamical profile is also determined by the parameters of the oscillator, in particular, its time constants.

Figure 6.

(A) Average duration of the discrete movement τ_disc with respect to the period T of the baseline rhythmic movement. (B) Velocity peak of the discrete movement with respect to the period T of the baseline rhythmic movement.

These results can be quantitatively compared with the results reported by Sternad et al. (2002), since the tested periods T were the same and the mechanical parameters of the model were tuned for the forearm. While the qualitative match is very good (a decrease of the duration with T, and hence an increase of the velocity peak), Sternad et al. (2002) reported that peak velocity in the discrete movement was about twice as fast in human subjects as reported in the present simulations. Consistently, the duration of the discrete movement was reported to be shorter than in the simulations. A potential reason for this difference is the rather simplistic tonic input u_T used in the present simulation. Actual discrete movements could be accelerated by superimposing a phasic transient (e.g. equation 3.1) on the tonic input at the time of the discrete movement onset or execution.

5 Bimanual Coupling: The Test Case of Rhythmic Movements

Section 2.2 extended the model to couple two Matsuoka oscillators. Here we describe how this coupled structure can produce bimanual rhythmic movements as a natural extension of the unimanual case reviewed in section 2.1. The test case for the model will be two prominent phenomena in rhythmic bimanual coordination: the stability of in-phase and antiphase coordination and the transition from antiphase to in-phase as the movement frequency increases. These two basic coordination phenomena cannot be inferred from single-limb movements since the movements of the coupled limbs are constrained by each other.

As demonstrated in many studies, relative phase between two symmetric rhythmically moving effectors has the tendency to converge toward 0 rad (in-phase) or π rad (antiphase), even though other modes also exist (Swinnen, 2002). From an egocentric frame of reference, in-phase corresponds to simultaneous activation of homologous muscle groups, while antiphase corresponds to alternating activation of these homologous muscle groups between the limbs.

Research on rhythmic bimanual movements has shown that the in-phase mode is usually more stable and less variable (Kelso, Southard, & Goodman, 1979; Haken et al., 1985; Schöner & Kelso, 1988; Turvey, 1990; Beek, Peper, & Daffertshofer, 2002) and requires less effort than the antiphase mode to maintain stability (Swinnen, 2002). Accordingly, increasing the movement frequency ultimately results in a loss of stability of the antiphase mode, such that the in-phase mode becomes the only remaining attractor. In this section, we show how the interlimb coupling proposed in section 2.2 is used to reproduce these two phenomena. Such results have already been obtained by the model of Haken et al. (1985) in which both limb movements are modeled by nonlinear oscillators (see also Schöner & Kelso, 1988; Kelso, 1995). Grossberg et al. (1997) obtained the same result with another model composed of four neurons obeying Hodgkin-Huxley membrane equations. Our objective here is to demonstrate that the same results can be obtained by a model that separates mechanical and neural levels for which each state variable can be mapped onto physiological and mechanical variables. While Grossberg et al.’s model necessitates different parameters for the inhibitory coupling of the two half-centers to elicit either in-phase or antiphase as the unique attractor, we will demonstrate that both attractors coexist with the same parameters’ vector through proper tuning of the sensory coupling terms in equation 2.6.

5.1 Methods

Since this section is on rhythmic movements, the inputs of the two oscillators (see equation 2.6) are tonic: u_r,i = u_{r, j} = u_r,T and u_l,i = u_{l, j} = u_l,T (constant over time). Moreover, we will focus on the case where these two inputs are equal u_r,T = u_l,T = u_T. Since the time constants t₁ and t₂ are also equal for the two limbs, only movements of same period (frequency) and amplitude will be discussed here. For simplicity, we will consider only rhythmic movements around ${\theta }_r^{★}={\theta }_l^{★}=0$. The in-phase mode corresponds to simultaneous activation of the homologous muscles—(ψ_r,i and ψ_l,i) and (ψ_{r, j} and ψ_{l, j})—such that θ_r = θ_l, while the antiphase mode corresponds to simultaneous activation of the nonhomologous muscles—(ψ_r,i and ψ_{l, j}) and (ψ_{r, j} and ψ_l,i)—such that θ_r = −θ_l. We will characterize the basin of attraction of the in-phase and antiphase coordination patterns that defines the portion of the state space in which the considered pattern acts as an attractor. The size of the basins of attraction of the in-phase and antiphase coordination patterns can be tuned via the coupling terms μ and ν of equation 2.6, respectively.

In order to analyze the phase relationship between the two coupled oscillators, we compute their individual phase assuming that the oscillators’ outputs are purely sinusoidal (e.g., θ_r = Asin (ωt + φ_r), θ_l = Asin (ωt + φ_l)). The phase difference is thus obtained by computing

$$\mathrm{\Delta }\phi ={\phi }_l-{\phi }_r=arctan\left(\frac{\lfloor {\theta }_l\rfloor \lfloor {\stackrel{.}{\theta }}_r\rfloor -\lfloor {\theta }_r\rfloor \lfloor {\stackrel{.}{\theta }}_l\rfloor }{\lfloor {\stackrel{.}{\theta }}_r\rfloor \lfloor {\stackrel{.}{\theta }}_l\rfloor +\lfloor {\theta }_r\rfloor \lfloor {\theta }_l\rfloor }\right),$$ (5.1)

where ⌊•⌋ represents the variable • normalized between −1 and 1. While neither the positions nor the velocities are truly sinusoidal, equation 5.1 provides a reasonable estimate of the phase relationship between the two signals. More important, Δφ = 0 rad if θ_r = θ_l (in-phase) and Δφ = π rad if θ_r = −θ_l (antiphase), for all θ_r and θ_l periodic.

5.2 Results

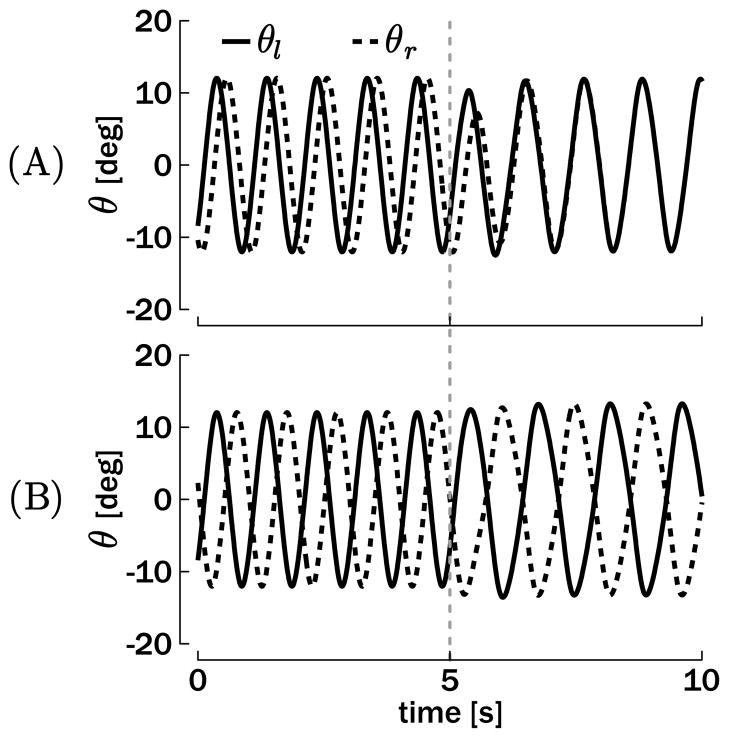
The first result established in this section is the existence of two attractors in the oscillators’ state space, corresponding to the in-phase and the antiphase modes. Figure 7 represents the position outputs (θ_r and θ_l) of two coupled oscillators converging to in-phase and antiphase. At the beginning of the simulations, the interlimb coupling terms are set to zero (μ = ν = 0), such that the two oscillators are independent. Even if the tonic input is the same in the two oscillators in this condition, no particular phase relationship is dynamically stable. At t = 5 s the coupling terms are switched on to μ = 0.75 and ν = 0.49, and the self-coupling term simultaneously decreases from σ = 1.5 to σ = 0.75, such that σ + μ is a constant over time.² All other parameters remain at the values given in section 2. In Figure 7A, the oscillators are initialized with approximately 0.4π rad of phase difference. This phase difference belongs to the basin of attraction of the in-phase mode (0 rad) when the coupling terms are switched on. In contrast, the antiphase mode (π rad) is the asymptotic attractor when the oscillators are initialized with a phase difference from its own basin of attraction, for example, with 0.8π rad (see Figure 7B).

Figure 7.

Simulation of bimanual rhythmic movements converging toward in-phase (A) or antiphase (B) coordination. The plots depict the position output θ_r and θ_l for T = 1 s and A_θ = 12 deg. The interlimb coupling terms μ and ν are turned on at t = 5 s in the simulations.

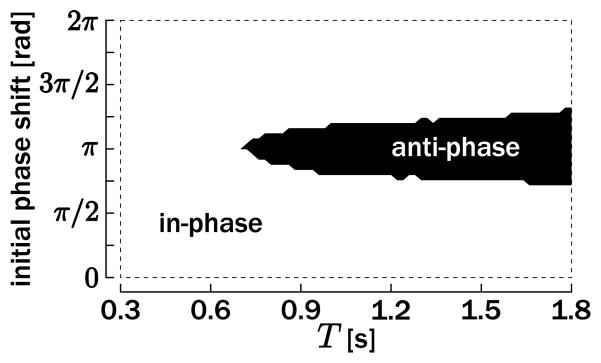
Simulations have been executed for a wide range of initial phase differences and movement periods T, and the results are presented in Figure 8. As revealed by this figure, the in-phase and the antiphase modes are the sole attractors for the coupled oscillators. The basin of attraction of the in-phase mode is large and encompasses initial phase differences of 0 rad and 2π rad. The basin of attraction of the antiphase mode is narrower and is almost symmetrical around the initial difference of π rad. Interestingly, only the in-phase mode remains a stable attractor when the movement period becomes faster than a certain value (around T = 0.7 s), as qualitatively observed in many behavioral experiments (see, e.g., Kelso et al., 1979, for finger-tapping movements).

Figure 8.

Simulation of bimanual rhythmic movements for a broad set of desired movement period T and initial phase difference between the two oscillating units. The conditions for which oscillators converge to the in-phase mode are denoted by the white area (delimited by the dotted rectangle); if they converge to the antiphase mode, this is denoted by the black area.

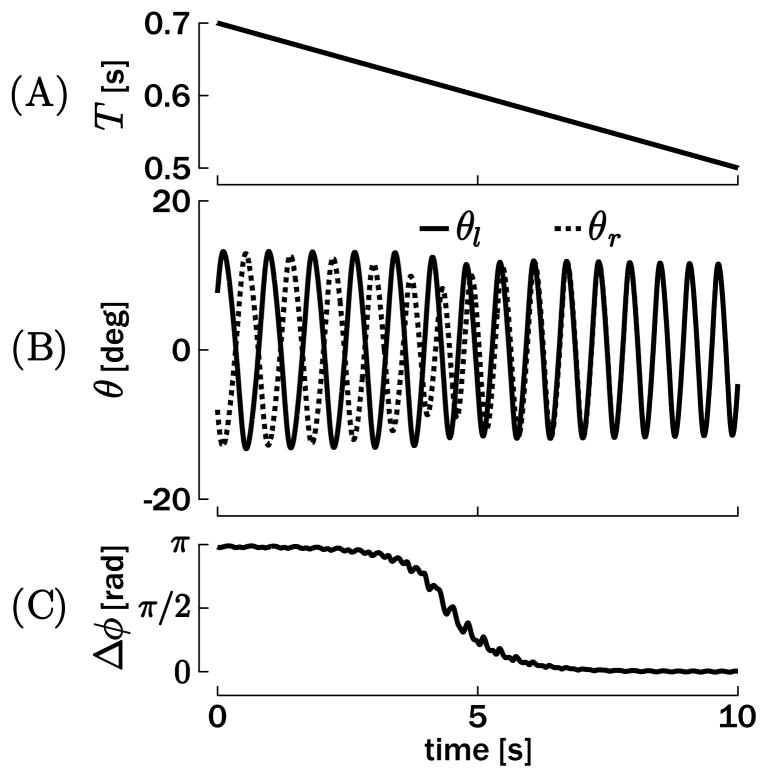
This is further confirmed by Figure 9, which represents a bimanual rhythmic movement that is performed at an increasing tempo (the desired period T decreases linearly over time during the simulation; see Figure 9A). At the beginning, the antiphase mode is stable and attracts the oscillators. However, with T decreasing below a certain threshold (about T = 0.6 s), the antiphase mode becomes unstable (the basin of attraction does not exist for T = 0.6 s in Figure 8) and the outputs are rapidly attracted to the in-phase mode. Note that if the period T is further increased after having been attracted into the in-phase mode, both oscillators remain in-phase, since the in-phase mode is a stable attractor across the entire range of periods.

Figure 9.

Simulation of bimanual rhythmic movements with a decreasing movement period T. (A) Desired period T. (B) Position output of the oscillators. (C) Phase difference between θ_l and θ_r (computed by equation 5.1). A transition from antiphase (π rad) to in-phase (0 rad) occurs when T goes below about 0.6 s.

6 Rhythmic and Discrete Combination in Bimanual Movement

This section combines discrete and rhythmic movements in a bimanual paradigm: one limb executes a rhythmic movement, while the other limb executes a discrete movement. The interactions between these two movements will reveal how the two are coupled to each other. Similar protocols have been experimentally used to establish whether rhythmic and discrete actions result from two different control regimes (Wei, Wertman, & Sternad, 2003) and how their coupling is impaired when the corpus callosum is lesioned (Sternad, Wei, Diedrichsen, & Ivry, 2007).

The coupling between rhythmic and discrete movements will be developed on the basis of the structure presented in section 2.2: one limb is activated by the tonic input to produce a rhythmic movement and the other with the phasic input (see equation 3.1) to produce the discrete movement. The model will exploit the full capabilities of equation 2.6, and the resulting trajectories are the most complex in the framework of this letter. The model outcomes will be compared to two primary experimental results obtained with human elbow movements (Wei et al., 2003; Sternad et al., 2007):

1. In contrast to unimanual rhythmic-discrete movements (see section 4.2), in bimanual performance, discrete movements can be initiated at any arbitrary phase of the simultaneous rhythmic movement.

2. The baseline rhythmic movement is perturbed by the onset of the discrete movement.

6.1 Methods

The model used in this section is the bimanual model presented in section 2.2. First, one limb (e.g., right) receives a phasic input u_P = u_r,i = u_{r, j} (given in equation 3.1) to generate a discrete movement. Second, the other limb (e.g., left) receives a tonic input u_T = u_l,i = u_{l, j} to generate a rhythmic movement around ${\theta }_l^{★}=0$.

For simplicity, the simulations have been computed with only one period T for the baseline rhythmic movement (i.e., with the nominal parameters t₁ and t₂ defined in section 2.1). Similar to the unimanual case in section 4.2, we simulated a rhythmic movement oscillating between −10 deg and 10 deg and a discrete movement starting at ${\theta }_r^{★}=0deg$ and terminating at ${\theta }_r^{★}=20deg$ (amplitude 20 deg).

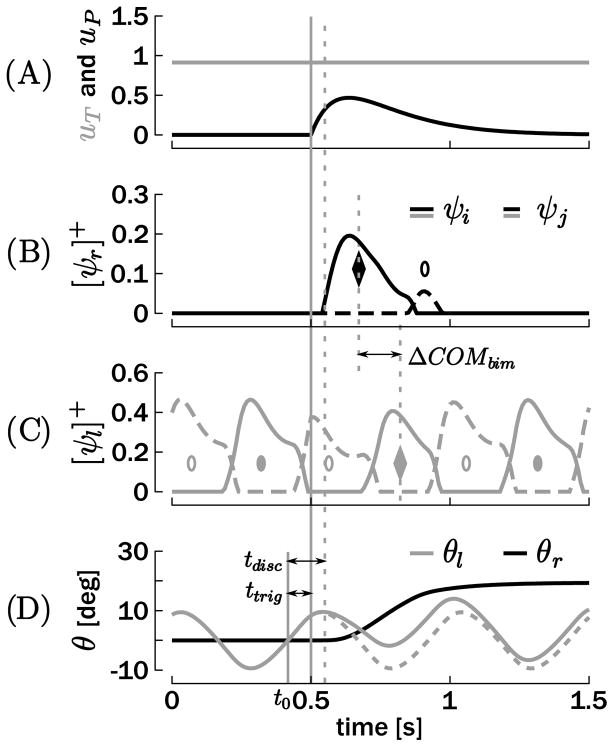
Figure 10 depicts an example of a simulation of such combined bimanual movement. As in Figure 4, t_trig and t_disc define the times of trigger and actual onset of the discrete movement with respect to t₀. The corresponding phases were calculated following equation 4.1. In order to quantify the coupling between both units, the center-of-mass (COM) of each activation burst was computed as the half-area point of each burst. A result reported in Wei et al. (2003) is that the bursts of these two limbs following the discrete movement onset tend to synchronize. This runs counter to the expectation that if the onset of the discrete movement was uniformly distributed, the distance between them should also be uniformly distributed. To quantify this tendency, ΔCOM_bim was defined as the interval delimited by the first COM of the discrete unit and the closest COM of the homologous unit in the rhythmic effector, that is, the two diamonds in Figures 10B and 10C. The corresponding phase was calculated following

Figure 10.

Example of a bimanual rhythmic and discrete movement. Both inputs are represented in A: u_P is the phasic input of the discrete effector and u_T is the tonic input of the rhythmic effector. (B, C) Positive parts of the neuronal discharge rates for both effectors. (D) Resulting effector trajectories with θ_r for the discrete and θ_l for the rhythmic unit. t_trig denotes the time at which the discrete movement is initiated, while t_disc denotes the time at which the position of the discrete effector deviates from 0. The circles and the diamonds represent the COMs of the ψ_i (filled) and ψ_j (empty) bursts. ΔCOM_bim is the time difference between the first COM burst of the discrete effector, and the closest COM of the homologous muscle in the rhythmic effector, that is, the two diamonds.

$${\phi }_{\mathit{COMbim}}=2\pi \frac{\mathrm{\Delta }CO{M}_{\mathit{bim}}}{T}.$$

For simplicity, the desired duration of the discrete movement was fixed (τ = 0.46 s). Simulations were run 100 times with the phase φ_trig uniformly distributed between 0 and 2π. For each of these 100 movements, φ_disc and φ_{C OMbim} were calculated.

6.2 Results

In contrast to results in the unimanual case, Figure 11A reveals that there is almost no influence of the initiation phase φ_trig on the phase relationship between the actual onset of the discrete movement and the rhythmic cycle φ_disc.³ Stated differently, the model is able to generate the discrete movement almost independently from the rhythmic movement. No local attractor appeared on Figure 11A (in contrast to Figure 5A), and the entire phase circle emerged as a solution: only a small and rather constant phase difference is reported between φ_trig and φ_disc. This delay is partly due to the time necessary to compensate for the inhibition due to the activation of the other limb (see equation 2.6). Logically, this inhibitory effect is slightly larger—around φ_trig = π/2 rad and φ_trig = 3π/2 rad.

Figure 11.

(A) Phase of the onset of the discrete movement φ_disc, with respect to the phase of initiation of the discrete movement φ_trig. (B) Phase difference φ_{C OMbim} between the first discharge burst of the discrete effector and the closest burst of the homologous muscle in the rhythmic effector.

This result is in good agreement with the data reported by Wei et al. (2003): no phase dependence was observed in the initiation of the discrete movement, particularly when subjects were instructed to focus their attention on the discrete movement.

However, there is some interaction between both effectors. The example represented in Figure 10 illustrates that the rhythmic movement diverges from the baseline oscillation (dotted lines) at the discrete movement onset. The rhythmic movement rapidly returns to steady-state oscillation with a slightly modified phase. To quantify this interaction, we computed the histogram of φ_{C OMbim} in Figure 11B. If there was no mutual influence between the two effectors, the histogram should be flat since φ_trig is uniformly distributed. However, a peak appeared around 0 rad, which shows a tendency toward synchronization of the bursts, as previously reported for human data (Wei et al., 2003).

7 General Discussion

This letter proposes a computational model of a pattern generator for rhythmic and discrete movements that is based on a half-center structure. Although this model is formulated at a phenomenological level, it nevertheless captures the main properties of the CPGs: (1) generation of robust oscillations with nonrhythmic input, (2) organization around two mutually inhibitory half-centers, and (3) the presence of local feedback loops simulating afferent pathways that act as stiffness terms (Dimitrijevic et al., 1998; van de Crommert et al., 1998; Kuo, 2002; Buschges, 2005; Frigon & Rossignol, 2006; Simoni & DeWeerth, 2007). This model is based on the Matsuoka oscillator, which has been used successfully to simulate a large body of rhythmic movements (Matsuoka, 1985, 1987; Taga, 1995a, 1995b; Williamson, 1998; Sternad et al., 2000; de Rugy et al., 2003; de Rugy & Sternad, 2003; Verdaasdonk et al., 2006; Williams & DeWeerth, 2007; White et al., 2008). The objective of this study was to shed light on the functional relevance of this oscillator structure for a low-level circuitry coupled with the motor apparatus. We propose that this low-level circuitry is recruited in the generation of rhythmic as well as discrete movements, two potentially fundamental units of action (see Hogan & Sternad, 2007). It simulates the alternating activation of antagonistic muscles and the decaying train of antagonistic bursts that are measured in the execution of these two types of movement. Moreover, we tested the model with several paradigms of increasing complexity and reproduced behavioral results reported in the literature. The main features of the model architecture are outlined as follows:

• The model is based on the assumption that CPGs exist and are fundamental components in the circuitry for human upper-limb movements. These CPGs are supposed to be modulated by (local) afferent pathways.

• The model hypothesizes that these CPGs are not bypassed in the execution of discrete movement but instead are recruited to generate the typical train of EMG bursts measured in discrete movements.

• The model establishes that homologous and nonhomologous afferent coupling between two oscillators is sufficient to reproduce the main findings of bimanual coordination.

• The model reproduces specific findings on the coordination between discrete and rhythmic movements, highlighting that these two movement types constitute two units of action that interact with each other via the CPG circuitry.

The existence of CPGs has been identified in animals (both invertebrates and vertebrates) as dedicated low-level (spinal in vertebrates) circuitries for the generation of a broad range of rhythmic activities, including locomotion, respiration, and mastication (Marder, 2000; Marder & Bucher, 2001). Claims that the locomotory CPGs are located—at least partly—at the spinal level were supplemented by further support in nonprimates and primates including humans (Cohen et al., 1988; Collins & Richmond, 1994; Dimitrijevic et al., 1998; Duysens & van de Crommert, 1998; Swinnen, 2002; Kawashima et al., 2005). Supporting the evolutionary view from quadrupedal to bipedal locomotion, later findings accumulated to indirectly support for the presence of CPGs in the generation of voluntary rhythmic movements by the upper limbs (Dietz, 2002; Zehr et al., 2004; Zehr & Duysens, 2004). Interestingly, experimental studies on the mechanisms of resonance tuning further supported the separation between neural (CPG) and mechanical oscillators for the upper limb in the gravitational plane (Verdaasdonk et al., 2006; Williams & DeWeerth, 2007; Raftery, Cusumano, & Sternad, 2008; White et al., 2008).

Finally, it has been established that sensory feedback also regulates the CPG activity and assists in mediating interlimb coordination (Zehr & Duysens, 2004), highlighting the role of the afferent pathways in low-level sensorimotor loops (Dimitrijevic et al., 1998; van de Crommert et al., 1998; Kuo, 2002; Buschges, 2005; Frigon & Rossignol, 2006; Simoni & DeWeerth, 2007). The model presented in this letter clearly relies on the existence of CPGs in the upper-limbs circuitry and proposes a conceptual model of these CPGs, including the afferent pathway (see Figure 1A). For unimanual rhythmic movements, this model achieves fine control of the main movement properties—amplitude, frequency, and average position—via dedicated inputs. The movement amplitude and frequency were controlled by the tonic input u_T and the time constants t₁ and t₂ (see the appendix). The average position around which the oscillation takes place was controlled by the (unstable) equilibrium point θ^★, defining the reference of the afferent pathway.

This reference position also plays a crucial role for the generation of discrete movements, since it determines the stable equilibrium point of the model when the tonic input is zero. However, due to the inhibitory contribution of the sensory feedback, a step change in θ^★ while maintaining the input at zero is not sufficient to move the joints to another equilibrium position. Instead, a particular phasic input is needed that can compensate for the sensory inhibition and produce a bell-shaped velocity profile. This contrasts with the λ-model of Feldman and colleagues (see, e.g., Asatryan & Feldman, 1965; Feldman, 1966a, 1966b, 1986; Latash, 1993; Adamovich, Levin, & Feldman, 1997), in which a movement is brought about by a ramplike or N-shaped change in the r-command that produces a change in the force and length characteristics of the effector (the so-called invariant characteristic). In our model, the input is phasic of a shape given by equation 3.1 to produce a bell-shaped velocity profile. However, other phasic inputs could be considered depending on the task’s objective.

Although the shape of the input is different, the general notion is consistent with the equilibrium point hypothesis. Yet we do not rule out that this phasic input that drives the effector from the old to the new equilibrium point may be adapted to different demands using optimization principles (see, e.g., Todorov & Jordan, 2002). Interestingly, Liu and Todorov (2007) reported how an optimization principle based on a speed-accuracy trade-off accounts for the fact that perturbations introduced late in reaching movements are not fully compensated, seemingly violating the condition of equifinality (see also Hinder & Milner, 2003). In our model, equifinality is not mandatory either, since the task’s objective (e.g., speed-accuracy trade-off) could require a phasic input u_P to bring the output θ to a position other than the equilibrium θ^★.

In the generation of discrete movements, the optimization algorithms mentioned above usually compute the corresponding torque as a succession of positive (accelerating) and negative (breaking) pulses. Such alternating trains of pulses have also been observed in actual data (Wach-holder & Altenburger, 1926; Sternad & Corcos, 2001). We showed that if a lowlevel CPG is recruited for generating a discrete movement, its oscillatory structure facilitates the alternating activations of the two antagonistic muscles. In the example given here, only one common phasic input u_P is computed rather than the desired torque of two different muscles (see also de Rugy & Sternad, 2003). The λ-model also predicts the generation of the three-burst pattern if one-incorporates a velocity-sensitive term into the stretch reflex response (see, e.g., Adamovich et al., 1997). However, the mechanisms involved are very different from our model: in the λ-model, this velocity-sensitive term accounts modulates the stretch reflex to produce the three-bursts pattern, while in our model, it is the low-level oscillatory structure of the CPG that gives rise to this pattern.

The presented mathematical framework also captures some fundamental bimanual coordination properties. The exact source of the bimanual coordination has not yet been clearly identified in the literature as the observed frequency and phase locking could emerge as a consequence of neural cross-hemispheric interactions at the planning or execution stage, interactions in feedback processing, perceptual biases, or any combination of those (see Swinnen & Wenderoth, 2004). The coupling introduced in section 5 suggested a physiologically motivated model of coupled CPGs that can account for the preference for in-phase and antiphase frequency locking in coordinated movements (Turvey, 1990; Kelso, 1995; Swinnen, 2002; Temprado, Swinnen, Carson, Tourment, & Laurent, 2003; Swinnen & Wenderoth, 2004; Levin, Suy, Huybrechts, Vangheluwe, & Swinnen, 2004). The interlimb coupling terms present inhibitory interference between the sensory feedbacks (afferent pathways; see Figure 1B) of the two limbs and isolate the in-phase and the antiphase mode as unique attractors. Importantly, by tuning these coupling terms, we reproduced the loss of stability of the antiphase mode when movement frequency increases.

Other CPG networks have produced bifurcations (see, e.g., Nagashino & Kelso, 1991, 1992; Grossberg et al., 1997), and one model has also been extended to generate discrete movements through tuning of their equilibrium point (Jirsa & Kelso, 2005). While these models rely on equilibrium-point switching by changing parameters, the mechanism we use produces discrete movements by temporarily recruiting the oscillatory structure of the CPG. Stated differently and going back to the formalism introduced in section 2, we generated both discrete and rhythmic movements from the same parameter vector α by changing only the shape of the external input u, while the other approaches manipulate the stability of equilibrium points and limit cycles via the parameters vector. We thereby emphasize the importance of the final stages of the motor pathways in shaping the output and deemphasize the higher-level cortical routes that have been central in other work.

This of course does not deny the fact that cortical mechanisms and interhemispheric coupling are important for bimanual coordination. Specifically, the corpus callosum has been shown to be an important pathway for interhemispheric exchanges. For example, acallosal patients have less difficulty in simultaneously producing movements with divergent directional requirements (Eliassen, Baynes, & Gazzaniga, 1999; Swinnen, 2002). A study by Sternad et al. (2007) examining the mutual influence of rhythmic and discrete movements in bimanual coordination showed that acallosal individuals failed to show phase entrainment at the initiation of a rhythmic movement with one limb while the other was moving rhythmically; in contrast, the perturbation on the baseline rhythmic movement when the other limb produces a discrete movement was similar to control subjects. These results led to the conclusion that the coupling between the two effectors (the dotted gray lines on Figure 1B) arises at several levels in the control loop. Moreover, this interaction was different for rhythmic and discrete movements.

The approach using the half-center oscillator for the generation of both rhythmic and discrete movements provides a mathematical formalism that is consistent with fMRI imaging results (Schaal et al., 2004). Consistent with the higher computational demands of the discrete movement generation, the fMRI results showed that cortical and cerebellar activation of human subjects is more important in the execution of discrete wrist movements (flexion extension) than during a similar rhythmic movement. Indeed in our model, the input profiles for the discrete movement generator are more complex than the constant input required for rhythmic movements. The additional circuitries involved in the discrete movement execution could thus be dedicated to the computation and the timed generation of this complex input. This and other behavioral findings have led to the hypothesis that rhythmic and discrete movements are two fundamental and distinct units of action, controlled by largely nonoverlapping circuitries. This viewpoint is consistent with the simulations presented here on the coordination between rhythmic and discrete submovements within a single or two different effectors. Bimanual simulations revealed that the trigger of the discrete movement in one hand is relatively independent of the phase of the rhythmic movement executed by the other hand, in contrast to the strong phase coupling that has been described when the two hands execute rhythmic movements. However, the unimanual combination of a rhythmic and a discrete component does support the hypothesis that these two units of action share a common circuitry (presumably the low-level CPG), since the trigger of the discrete movement has been shown to be constrained by the phase of the rhythmic cycle in both simulations and experiments.

In conclusion, we have developed a model for the generation of unimanual and bimanual rhythmic and discrete movements. We proposed a parsimonious model that is physiologically motivated by using a half-center CPG. Moreover, we reproduced a number of experimental findings on the coordination of complex movements. More specifically, we aimed at focusing on the biological relevance of our model and proposing a role of the CPG in the generation of (coordinated) discrete movements.

Appendix: Empirical Relationship Between the Rhythmic Output and Oscillator Parameters

The empirical relationships between the parameters of the single-limb oscillator (see equation 2.5) and the features of its output (mainly amplitude and frequency) are briefly summarized.

First, the period T of the oscillation depends on only the time constants t₁ and t₂. Over the range t₁ = [15: 2.5: 250] ms, the following empirical correlation can be established:

$$T=1.47t_1+2.92\sqrt{t_1}-0.2304,$$ (A.1)

with t₂ = 2.5t₁. Over this range, the output consequently oscillates with a period between 149 ms (for t₁ = 15 ms) and 1597 ms (for t₁ = 250 ms). The mean of the absolute error between the estimated period, equation A.1, and the actual period is equal to 6 ms. Without the sensory coupling (i.e., σ = 0 in equation 2.5), the relationship between T and t₁ is close to linear (Williamson, 1998).

Second, Williamson (1998) revealed that the amplitude of the torque ψ_T depends almost linearly on the tonic input u_T. In the model here, the relationship of the tonic input, the time constant t₁, and the position (i.e., output) amplitude A_θ (in degree) is as follows:

$$A_{\theta }=(-323t_1^2+361t_1-6.306)u_T$$ (A.2)

over the range t₁ = [15: 2.5: 250] ms (with t₂ = 2.5t₁) and u_T = [0.1: 0.05: 2]. The mean of the absolute error between the estimated amplitude, equation A.2, and the actual amplitude is equal to 0.452 deg.

Equations A.1 and A.2 permit a direct way to invert the Matsuoka oscillator to produce a rhythmic movement with a desired period T and amplitude A_θ. Assuming that both the time constants t₁ and t₂ and the tonic input u_T are parameters of the oscillator, the inverse of equations A.1 and A.2 is

$$\begin{array}{l}{t}_1=2.13+0.6804T-\sqrt{4.512+2.685T}\\ t_2=2.5t_1\end{array}$$ (A.3)

$$u_T=\frac{A_{\theta }}{-323t_1^2+361t_1-6.306}.$$ (A.4)

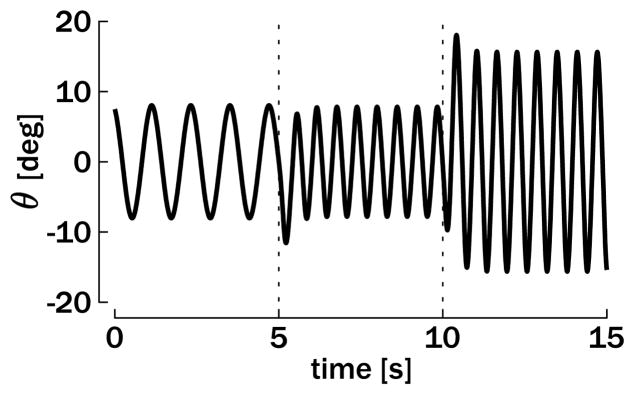
Figure 12 illustrates that both the period and the amplitude of this oscillator can be changed online. At t = 5 s, the period shortened to half its duration (from T = 1.2 s to T = 0.6 s) and at t = 10 s, the amplitude is doubled (from A_θ = 8 deg to A_θ = 16 deg). Steady-state oscillations are rapidly recovered, and the transitions are smooth.

Figure 12.

Simulation of a unimanual rhythmic movement. The plot depicts the position output θ when the reference period is T = 1.2 s for the first 5 seconds of the simulation and T = 0.6 s for the last 10 seconds. The reference amplitude is A_θ = 8 deg for the first 10 seconds and A_θ = 16 deg for the last 5 seconds.

In conclusion, both period and amplitude of the oscillatory output can be controlled through inversion of the oscillator properties. Note that de Rugy and Sternad (2003) established in a similar Matsuoka oscillator that the phase of the cycle at which the change in amplitude onset actually produces a change in the rate of discharge pattern is in good agreement with human data (see also section 4.2).

Note that Matsuoka (1987) showed that different parameters can tune the oscillation frequency in either the time constants or the crossed-inhibition term η.