Planar covariation of limb elevation angles during bipedal walking in the Japanese macaque

Abstract

We investigated the planar covariation of lower limb segment elevation angles during bipedal walking in macaques to elucidate the mechanisms underlying the origin and evolution of the planar law in human walking. Two Japanese macaques and four adult humans walking on a treadmill were recorded, and the time course of the elevation angles at the thigh, shank and foot segments relative to the vertical axis were calculated. Our analyses indicated that the planar law also applies to macaque bipedal walking. However, planarity was much lower in macaques, and orientations of the plane differed between the two species because of differences in the foot elevation angle. The human foot is rigidly structured to form a longitudinal arch, whereas the macaque's foot is more flexible and bends at the midtarsal region in the stance phase. This difference in midfoot flexibility between the two species studied was the main source of the difference in the planar law. Thus, the evolution of a stable midfoot in early hominins may have preceded the acquisition of the strong planar intersegmental coordination and possibly facilitated the subsequent emergence of habitual bipedal walking in the human lineage.

1. Introduction

It is well established that elevation angles of the thigh, shank and foot segments, or the orientation of these segments with respect to the vertical axis, are consistent across subjects in human bipedal walking, and the temporal changes of these segmental angles covary to form a regular loop within a single plane in three-dimensional space [1–11]. Such tight planar coupling of limb segment motions was also reported to be observed in postural control in cats [12] and quadrupedal walking in macaques [13]. The same relationship could also be expected in locomotion of a variety of mammals [14]. However, what is unique about the planar law in human walking is that the constraint of planar covariation of the elevation angles is very strong and the plane could account for greater than 99 per cent of the total variance [1]. Since this planar law was first proposed by Borghese et al. [1], many experimental and theoretical studies have attempted to clarify the origin and functional significance of this kinematic law in human locomotion [2–11].

The existence of a planar law in human walking is suggested to indicate simplified control of human bipedal walking by coordinated kinematic synergies. Indeed, the planar constraint of the inter-segmental coordination reduces the number of effective degrees of freedom requiring control during bipedal walking from three to two. Given that planarity was consistently observed in biomechanically different walking conditions, such as backward walking [3] or walking with body weight support [5], planar covariation has been suggested to emerge from neuronal rather than biomechanical constraints. Ivanenko et al. [7,8] hypothesized that the planar law of inter-segmental coordination may exist because the endpoint of the limb is controlled by the nervous system based on two global variables of the limb: limb axis orientation and limb length. However, biomechanical constraints may also play a part in emergence of the planar law. For example, Hicheur et al. [9] suggested that the planar law arises mainly due to the strong coupling of foot and shank movements resulting from a restricted range of ankle joint movement. Barliya et al. [10] argued that biomechanical constraints due to biarticular muscles and passive coupling of limb segments may also play a role, although the inter-segmental plane may not emerge only from such biomechanical factors.

Bipedal walking of non-human primates has been well studied in the field of physical anthropology [15–28] and, among these, we have examined bipedal walking in bipedally trained Japanese macaques (Macaca fuscata) [29–36]. The acquisition of bipedal walking in an inherently quadrupedal primate could be regarded as a modern analogue for the evolution of bipedal walking, thereby offering an interesting model for understanding the evolution of human bipedalism. Bipedal walking of non-human primates, whose musculoskeletal system is not as adapted to bipedalism as that of humans, may provide insights into the mechanisms underlying the origin and evolution of the planar law in human bipedalism. We therefore investigated planar covariation of the elevation angles during bipedal walking in Japanese macaques for comparative understanding of the mechanisms underlying the emergence of the planar law in human bipedal walking. Specifically, we tested whether the degree of planarity and the orientation of the covariance plane differ between macaque and human bipedal walking and explored possible sources of any such differences.

2. Methods

Analyses of temporal changes in lower limb segment elevation angles during bipedal walking in the Japanese macaque are mainly based on previously published kinematic data [35], but some additional data are also included in the present study. Two highly trained, adult Japanese macaques (KA, 12.3 kg; KU, 9.2 kg) were filmed walking bipedally on a treadmill at 3, 4 and 5 km h^–1 using synchronized high-speed cameras (HotShot 1280; Nac Image Technology, USA) at 125 frames per second for purposes of locomotor kinematics analysis. Five landmarks (head of the fifth metatarsal, lateral malleolus of the fibula, lateral epicondyle of the femur, greater trochanter and acromion) on the right-hand side of the body were manually digitized frame-by-frame (figure 1a). Coordinates of markers were then calculated using three-dimensional motion analysis software (Frame-DIAS II; DKH, Japan). The change in the position of each coordinate over time was filtered at 12 Hz using a zero-phase shift digital low-pass filter. The walking cycles analysed in each subject and speeds are listed in table 1. It must be noted that the bipedal training does affect the way the macaques walk. See Hirasaki et al. [29] for more information.

Figure 1.

Measurement of bipedal walking kinematics. (a) The three-dimensional coordinates of five markers placed on the right-hand side of the body were monitored. (b) Definitions of joint angles. Joint angles are all zero when the torso, thigh, shank and instep of the foot segments are in a straight line. Hip and knee joint angles were defined to increase during flexion, while the ankle joint angle increased during dorsiflexion. (c) Definitions of elevation angles. Elevation angles were defined to increase during counterclockwise rotation of the segments with respect to the vertical axis.

Table 1.

Cycle duration and Froude number of bipedal walking in Japanese macaques and humans.

	ID	speed (km h–1)	N	cycle duration (s)		effective leg length (m)	Fr
				mean	s.d.
macaque	KA	3	9	0.85	0.025	0.352	0.20
		4	16	0.75	0.025	0.351	0.36
		5	16	0.62	0.018	0.353	0.56
	KU	3	12	0.82	0.024	0.332	0.21
		4	13	0.72	0.019	0.323	0.39
		5	11	0.63	0.014	0.323	0.61
human	KH	3	9	1.25	0.019	0.825	0.09
		4	10	1.18	0.022	0.824	0.15
		5	10	1.05	0.024	0.821	0.24
		6	10	1.02	0.022	0.822	0.34
	MO	3	10	1.27	0.024	0.866	0.08
		4	9	1.15	0.024	0.868	0.14
		5	9	1.05	0.014	0.874	0.23
		6	10	0.99	0.013	0.849	0.33
	HA	4	10	1.08	0.013	0.842	0.15
	IS	4	10	1.22	0.009	0.885	0.14

For comparisons, four healthy adult human males (KH, 57 kg; MO, 68 kg; HA, 61 kg; IS, 70 kg) were recorded walking on a treadmill using a three-dimensional optical motion capture system (MAC3D, MotionAnalysis, USA). The infrared reflective markers were attached to the same five landmarks on the right-hand side of the body and the positions were recorded at 100 Hz. Two subjects (KH and MO) walked on the treadmill at 3, 4, 5 and 6 km h^–1, but the other two subjects walked only at 4 km h^–1. Subjects were instructed to walk freely near the middle of the treadmill. Because there are many previous studies that published human data [1–11], we provided only minimal human data in the present study. As we shall show in the result section, our human data agree well with those previously published.

Elevation angles of the thigh, shank and foot segments for both macaques and humans were calculated as the sagittally projected angles of the corresponding limbs with respect to the vertical axis (figure 1c). Calculated angle profiles were interpolated over the cycle duration to fit a 100-point time base for normalization of the time. Joint angles of the lower limbs (anatomical angles of extension and flexion of joints) were also calculated.

To evaluate inter-segmental coordination, time courses of the elevation angles were plotted in a three-dimensional space and trajectories were fitted by a plane using a least-squares method [1]. Principal component analysis (PCA) of the covariance matrix of the elevation angles was performed for this purpose. The covariance matrix of elevation angles M was diagonalized as

2.1

where D is the diagonal matrix of the eigenvalues of M, and P is the eigenvector matrix. We used Matlab (MathWorks, USA) to compute eigenvectors and eigenvalues (matrices P and D, respectively). As reported in prior studies, the covariance matrix based on non-normalized angles was used in PCA. The first two eigenvectors describe the best-fitting plane and the third vector represents the orientation of the plane. The direction cosines of the ith eigenvector with the positive axis of the thigh, shank and foot elevation angles are denoted as u_it, u_is and u_if, respectively. These values are used to quantify the differences in directions of the eigenvectors. The variance accounted for by the ith eigenvector is expressed by its percentage variance; that is, the proportion of the ith eigenvalue compared with the sum of the three eigenvalues. The planarity of the trajectories was quantified by the sum of the percentage variances of the first and second eigenvectors. A third eigenvalue of zero was equivalent to 100 per cent planarity. Further details of the calculation method employed in this study have been described elsewhere [1,4,8].

To evaluate similarities between pairs of elevation angles, we calculated correlation coefficients as described previously [9]. We also approximated elevation angle profiles using the first Fourier decomposition harmonics to quantify phase shifts between pairs of elevation angles [2,10].

For normalization of walking speed between the two species under study, we calculated the Froude number (Fr), defined as

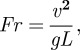2.2

where v is the velocity, g is the gravitational acceleration and L is the effective leg length (mean distance between markers placed at the hip joint and metatarsal head during the entire stance phase), taking into account the digitigrade posture of the macaque foot during bipedalism. Analysis of variance and post-hoc Tukey's honestly significant difference multiple comparisons tests were performed using Statistica v. 06J software (StatSoft, USA) to test for significant differences in the percentage variances, directions of the eigenvectors, correlation coefficients and phase shifts.

3. Results

Mean joint angle profiles during bipedal walking in Japanese macaques and humans were plotted against the gait cycle in figure 2. Hip and knee joint angles were defined to increase during flexion, while the ankle joint increased during dorsiflexion (figure 1b). The number of gait cycles analysed for each subject and velocity, and means and standard deviations of the gait cycle durations are listed in table 1. The 3, 4 and 5 km h^–1 bipedal walking of the macaques corresponded to Fr of about 0.2, 0.4 and 0.6, respectively, whereas the 3, 4, 5 and 6 km h^–1 walking of the humans corresponded to Fr of about 0.1, 0.15, 0.25, 0.33, respectively. The 3 and 4 km h^–1 walking of macaques roughly corresponded to the 4 and 6 km h^–1 walking of the humans in the present study. It has been reported that the change in plane orientation with increasing walking velocity is very small in human walking [2,8]; therefore, the exact match of relative speeds is not critical to the interspecific comparison and to the interpretation of the results.

Figure 2.

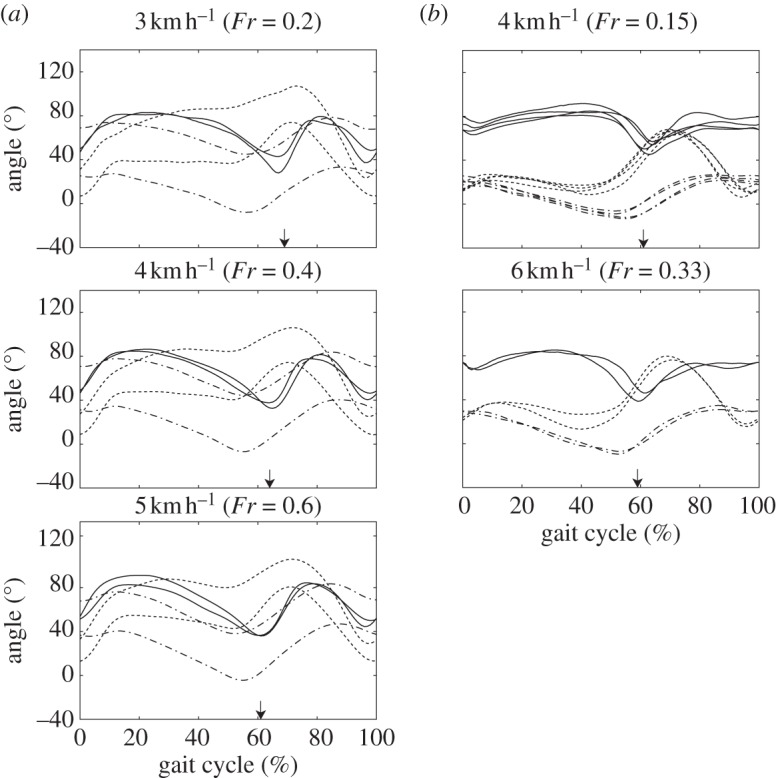
Comparisons of mean joint angle profiles during bipedal walking between (a) Japanese macaques and (b) humans. Curves were averaged across all cycles for each subject and walking speed. 0%, Right foot contact; 100%, next foot contact of the same limb. Solid lines, ankle; dotted lines, knee; dashed-dotted lines, hip. Arrows indicate time of foot off.

As illustrated in figure 2, the kinematics of bipedal walking in the two Japanese macaques were substantially different from each other. While the trunk was more erect, and the hip and knee joints were more extended throughout the gait cycle of KA's bipedal locomotion, KU's gait cycle was marked by substantial inclination of the trunk segment and more flexed hip and knee joints [35]. Nevertheless, the hip and knee joints were relatively more flexed at the time of foot-contact and at mid-stance, respectively, in both macaques than in humans. Furthermore, the foot was more plantarflexed in macaque walking than in human walking at the time of foot-contact and toe-off.

Mean profiles of leg segment elevation angles were plotted against the gait cycle in figure 3. Elevation angles were defined to increase during counterclockwise rotation of the segments (figure 1c). Although thigh elevation angles of macaques and humans resembled each other, elevation angles of the shank and foot segments differed between species. Specifically, the shank elevation angle during the stance phase was relatively smaller in macaque walking than in human walking. Furthermore, although foot elevation angle decreased shortly after foot contact in macaque walking, the angle remained almost constant during the early to mid-stance phase in human walking.

Figure 3.

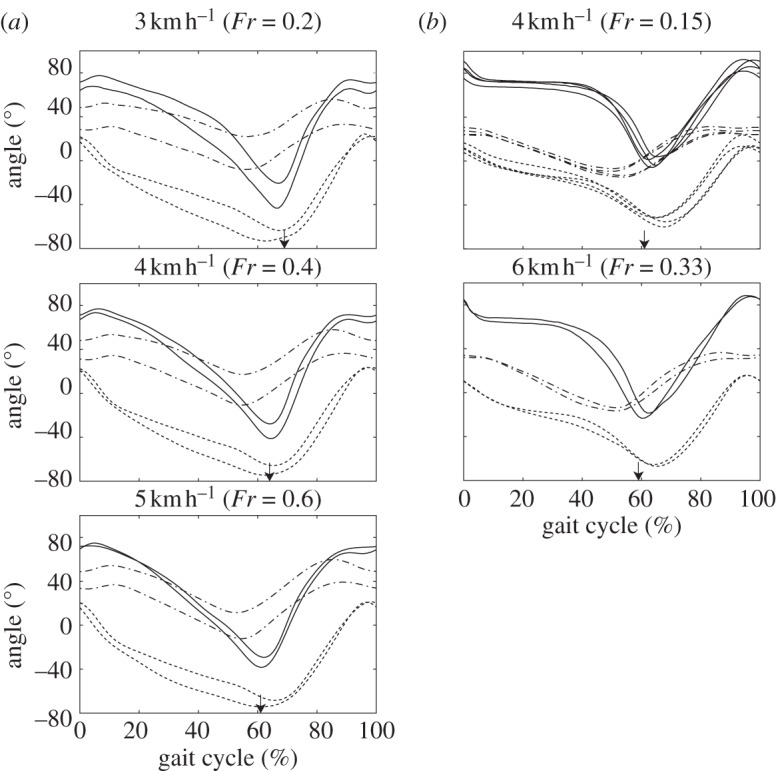
Comparisons of mean elevation angle profiles during bipedal walking in (a) Japanese macaques and (b) humans. Curves were averaged across all cycles per subject and walking speed. 0%, Right foot contact; 100%, next foot contact of the same limb. Solid lines, foot; dotted lines, shank; dashed-dotted lines, thigh. Arrows indicate time of foot off.

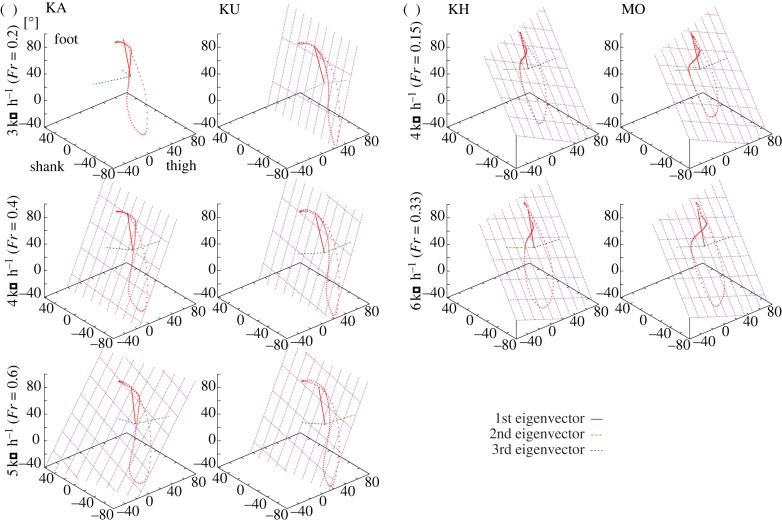
Figure 4 illustrates three-dimensional plots of the mean time courses of the elevation angles of two Japanese macaques (KA and KU) walking at 3, 4 and 5 km h^–1, and two humans (KH and MO) walking at 4 and 6 km h^–1. The trajectories progress in time in the counterclockwise direction, and foot contact and foot-off correspond to the top and bottom of the ‘tear-drop’ loops, respectively. Table 2 lists the eigenvectors of the covariance matrix of the elevation angles plotted in figure 4, as well as the percentage variance accounted for by each eigenvector. If the percentage variance of the third eigenvector (i.e. residual variance not accounted for by planar regression) is less than or equal to 3 per cent, the best-fitting planes of the corresponding loop trajectories were drawn (figure 4).

Figure 4.

Planar covariation of elevation angles for (a) two macaques and (b) two human subjects. Three-dimensional plots of the mean time courses of the elevation angles, the best-fitted planes of the corresponding loop trajectories and the eigenvectors are presented. Trajectories progress counterclockwise. Foot contact corresponds to the top of the loop. The mean value of each angular coordinate has not been subtracted in this study in order to indicate the differences in mean elevation angles. Calculation of Fr indicated that the 3 and 4 km h^–1 walking of the macaques roughly corresponded to the 4 and 6 km h^–1 walking of the humans. (Online version in colour.)

Table 2.

Eigenvectors of covariance matrix of elevation angles and corresponding percentage variance.

	ID	speed (km h–1)	1st eigenvector			2nd eigenvector			3rd eigenvector			% variance (s.d.)
			ut	us	uf	ut	us	uf	ut	us	uf	i = 1	i = 2	i = 3
macaque	KA	3	0.280	0.615	0.737	−0.597	−0.433	0.586	−0.681	0.603	−0.247	92.2 (1.0)	4.5 (0.8)	3.3 (0.5)
	KU	3	0.197	0.629	0.752	0.146	−0.773	0.608	−0.964	0.010	0.245	93.1 (1.0)	5.5 (0.8)	1.4 (0.2)
	KA	4	0.318	0.591	0.741	0.245	−0.792	0.527	−0.898	−0.013	0.398	93.1 (0.6)	4.7 (0.5)	2.2 (0.3)
	KU	4	0.229	0.618	0.751	0.222	−0.774	0.568	−0.932	−0.035	0.316	93.0 (0.9)	5.4 (0.9)	1.5 (0.4)
	KA	5	0.347	0.577	0.739	0.402	−0.784	0.422	−0.823	−0.150	0.506	93.0 (0.8)	5.5 (0.7)	1.5 (0.7)
	KU	5	0.285	0.597	0.750	0.278	−0.786	0.518	−0.899	−0.061	0.390	92.3 (0.9)	5.9 (0.5)	1.8 (0.7)
human	KH	3	0.179	0.630	0.755	−0.941	−0.110	0.315	0.282	−0.768	0.574	89.6 (0.9)	9.1 (0.8)	1.3 (0.1)
	MO	3	0.184	0.627	0.756	−0.932	−0.131	0.336	0.310	−0.767	0.561	83.8 (0.8)	15.4 (0.8)	0.7 (0.1)
	KH	4	0.245	0.617	0.747	−0.932	−0.062	0.356	0.267	−0.784	0.560	88.3 (0.8)	10.3 (1.0)	1.4 (0.2)
	MO	4	0.226	0.626	0.747	−0.941	−0.057	0.332	0.251	−0.777	0.576	85.6 (0.6)	13.6 (0.7)	0.8 (0.1)
	HA	4	0.192	0.596	0.779	−0.923	−0.159	0.349	0.332	−0.787	0.520	85.5 (0.5)	13.8 (0.5)	0.7 (0.1)
	IS	4	0.192	0.642	0.742	−0.931	−0.120	0.344	0.310	−0.757	0.575	86.5 (0.3)	12.5 (0.3)	1.0 (0.1)
	KH	5	0.284	0.608	0.740	−0.918	−0.041	0.388	0.266	−0.790	0.548	89.5 (0.8)	9.2 (1.0)	1.3 (0.3)
	MO	5	0.222	0.595	0.772	−0.958	−0.014	0.286	0.181	−0.803	0.567	87.1 (0.3)	11.9 (0.4)	0.9 (0.1)
	KH	6	0.287	0.574	0.766	−0.939	0.013	0.341	0.186	−0.818	0.543	89.0 (0.7)	9.1 (0.8)	1.8 (0.3)
	MO	6	0.262	0.591	0.763	−0.947	0.004	0.322	0.187	−0.807	0.560	87.4 (0.4)	11.8 (0.4)	0.8 (0.1)

Percentage variances of the third eigenvector were less than or equal to 3 per cent for all subjects and all speeds, except for 3 km h^–1 walking of the macaque KA (table 2), indicating that loop trajectories of the elevation angles were essentially planar for both humans and macaques. However, percentage variance of the third eigenvector was found to be significantly higher in macaques (1.4–3.3%) than in humans (0.7–1.8%; p < 0.05 for all combinations except for macaque 5 km h^–1 versus human 6 km h^–1). This finding indicates that planar covariation was comparatively weaker in macaques. In addition, direction cosines of the third eigenvectors (u_3t and u_3s) were significantly different between macaques and humans (p < 0.001 for all combinations), demonstrating that orientations of the best-fitting plane of angular covariation differed substantially between species. Furthermore, although the change in plane orientation with increasing speed was very small in human walking [2,8], it was significantly altered with increasing speed in macaque walking. The directions of the first eigenvector underwent very little change with increasing speed, indicating that the covariance plane rotated monotonically about the first eigenvector (the long axis of the gait loop) with increasing speed. However, it rotated in a clockwise direction in macaque walking, even though it slightly rotated in a counterclockwise direction in human walking [2].

The eigenvectors for human walking were similar between human subjects (table 2), and are in a range consistent with values reported in the literature [1]. Comparisons of eigenvectors for macaque and human walking indicate that the first eigenvector was very similar between the two species (table 2). However, direction cosines of the second eigenvector (u_2t and u_2s) were significantly different (p < 0.001 for all combinations), indicating that the difference in direction of the second eigenvector distinguished the orientation of the plane between macaque and human bipedal walking. Furthermore, the mean percentage variance accounted for by the first and second eigenvectors was approximately 93 per cent and 5 per cent, respectively, in macaques, and 86–88% and 10–12%, respectively, in humans (p < 0.001 for all combinations). This finding indicates that the percentage variance accounted for by the first eigenvector is significantly larger for macaque walking than for human walking.

Correlations and phase shifts between pairs of elevation angles are presented in table 3. As shown in table 3, the correlation between foot and shank elevation angle was found to be significantly higher in human walking (approx. 0.95; p < 0.001 for all combinations) than in macaque walking (approx. 0.9). However, correlations between the other two pairs of elevation angles (shank and thigh, and foot and thigh) were significantly higher in macaque walking (> 0.75; p < 0.001 for all combinations) and the coefficients were much smaller in human walking. Furthermore, the phase shift between shank and thigh elevation angles was found to be significantly smaller in macaques (table 3), indicating that elevation angles actually fluctuated more in-phase in macaque walking.

Table 3.

Correlations and phase shifts between pairs of elevation angles. r, Correlation coefficient; Δφ, phase shift. Subscripts FS, ST and FT denote elevation angles between foot and shank, shank and thigh, and foot and thigh, respectively.

	ID	speed (km h–1)	rFS		rST		rFT		ΔφFS		ΔφST
			mean	s.d.	mean	s.d.	mean	s.d.	mean	s.d.	mean	s.d.
macaque	KA	3	0.908	0.011	0.780	0.029	0.758	0.042	16.1	3.5	18.0	3.2
	KU	3	0.884	0.021	0.766	0.024	0.834	0.029	17.5	3.8	6.8	2.4
	KA	4	0.894	0.011	0.815	0.033	0.877	0.017	13.5	3.6	9.4	4.9
	KU	4	0.887	0.019	0.766	0.035	0.853	0.038	15.5	3.6	6.5	3.0
	KA	5	0.891	0.011	0.789	0.032	0.915	0.033	5.9	6.5	10.9	3.7
	KU	5	0.877	0.020	0.770	0.021	0.872	0.035	14.8	5.4	8.0	2.8
human	KH	3	0.955	0.005	0.536	0.044	0.400	0.041	11.9	1.5	46.5	4.2
	MO	3	0.945	0.004	0.485	0.032	0.244	0.043	19.0	1.1	49.9	3.1
	KH	4	0.949	0.005	0.612	0.026	0.479	0.033	11.9	1.1	42.5	2.1
	MO	4	0.959	0.004	0.534	0.017	0.360	0.022	15.2	1.2	45.6	2.4
	HA	4	0.945	0.005	0.536	0.023	0.299	0.023	18.4	1.3	46.3	1.9
	IS	4	0.949	0.003	0.520	0.009	0.320	0.013	14.5	0.9	48.6	0.9
	KH	5	0.951	0.006	0.688	0.028	0.568	0.058	11.9	2.6	34.7	2.8
	MO	5	0.966	0.004	0.526	0.015	0.413	0.026	11.7	1.4	45.4	1.4
	KH	6	0.946	0.009	0.655	0.038	0.582	0.046	11.3	1.3	36.2	3.8
	MO	6	0.968	0.004	0.589	0.011	0.474	0.010	11.7	1.4	41.3	1.5

4. Discussion

Although the planar law of inter-segmental coordination also applies to bipedal walking in Japanese macaques, this study demonstrated that the planarity of the three-dimensional trajectory of the elevation angle is significantly lower in macaques than in humans. Furthermore, the leg movements are relatively more confined to one component axis along the first eigenvector in macaques. In both species, the first eigenvector was projected in nearly the same direction. However, the direction of the second eigenvector (and therefore the orientation of the plane) was found to differ between species.

Courtine et al. [13] studied the planar covariation of hindlimb elevation angles in quadrupedal walking in rhesus macaques (Macaca mulatta). In comparison with macaque quadrupedal walking, the shape of the trajectory and the orientation of the plane during bipedal walking are more similar to each other than to those of humans. However, the variance accounted for by the first and second eigenvectors are higher and lower, respectively, in macaque bipedal walking, indicating that leg movements are relatively more confined to one component axis only when they walk bipedally.

Ivanenko et al. [7,8] demonstrated that the first and second eigenvectors are correlated with limb axis orientation and length, respectively, and suggested that limb movements are basically controlled according to these two variables; hence, the angular covariance of the three limb segments is confined to a single plane in three-dimensional space. Lower planarity in macaque walking therefore suggests that facilitation of control by using fewer degrees of freedom is less effective. The smaller percentage variance accounted for by the second eigenvector in macaque walking indicates that excursion of the limb length component is smaller, possibly because of comparatively weaker control of the limb axis. On the other hand, limb length in human walking varied greatly, resulting in a larger percentage variance accounted for by the second eigenvector.

This difference may be attributed to different phase relationships among the elevation angles of the limb segments during the stance phase of bipedal walking. In human walking, the foot elevation angle remained nearly constant during the early to mid-stance phase, while the change in the elevation angle occurred mainly in the thigh segment. The three-dimensional trajectory of the elevation angle therefore moved parallel to the thigh axis to form the plane. On the other hand, foot elevation angle in macaques continued to decrease after the initial contact of the foot until foot push-off during bipedal walking (figure 5). Fluctuations in the elevation angle of the three segments in macaques thus more closely resembled each other (table 3), resulting in the larger and smaller percentage variance accounted for by the first and second eigenvectors, respectively. Consequently, the species difference in foot motion with respect to the ground was considered to make a difference in the planar law of inter-segmental coordination during bipedal walking.

Figure 5.

Foot motion during the stance phase of bipedal walking in a Japanese macaque (KA) from foot contact to foot take-off. The foot was initially placed in a plantigrade position. Intermediate dorsiflexion at the midfoot, midtarsal break, is observed shortly afterwards. (Online version in colour.)

This study also demonstrated that the spatial orientation of the plane altered substantially with increasing speed in macaque bipedal walking, although the change is minimal in human walking. This is due to an increased range of movement of the thigh elevation angle in macaques. It has been suggested that the change in orientation of the plane correlates with net mechanical power expended during human walking, compensating for the increase in energy required for faster walking [2]. However, the plane drastically rotates in the opposite direction with increasing speed in macaque walking, suggesting that the same might not be applied to macaque bipedal walking. The mechanism underlying this drastic change in the plane orientation is currently obscure, but the trajectory is more collapsed and confined to one dimension in macaque walking. In such cases, a small change in trajectory affects the orientation of the plane to a large degree. The large change in orientation could thus also be attributable to the weaker planarity of interlimb coordination in macaques.

The noted differences between these two species may result from a difference in the anatomy and mechanics of the foot of humans and macaques. In human walking, the heel contacts the ground first, the foot is then placed flat, and the heel and midfoot are simultaneously lifted in the middle to late stance phase. Further, humans are completely plantigrade and their foot structure is comparatively stiff [37,38], acting as a rigid lever for effective push-off as an adaptation for bipedal walking. Conversely, although the foot was initially placed in a plantigrade position, macaques are digitigrade. As illustrated in figure 5, the heel is lifted independently from the other part of the foot during macaque bipedal walking, because the midfoot region is more mobile and dorsiflexion occurs at both cuboid-metatarsal and calcaneocuboid joints [39]. This characteristic dorsiflexion at the midfoot during stance phase, termed midtarsal break, has been observed across primate species [24,40–45], but not in humans. This suggests that the absence of midtarsal break is a derived feature acquired through the course of the evolution of human bipedalism [39]. Owing to this difference in foot structure, the heel is gradually raised from the early stance phase in macaque walking, resulting in the continuous decrease in foot elevation angle. The human foot segment, which is specialized for terrestrial bipedalism, therefore contributes in a major way to the emergence of the strong planar constraint of the inter-segmental coordination in human walking.

Debate is ongoing as to whether the planar law of inter-segmental coordination is mainly due to biomechanical factors or to the existence of an underlying neural control strategy [7–10]. The present findings suggest that the anatomy and mechanics of the human foot contributed much to the emergence of strong planarity in human walking. However, this does not necessarily mean that the emergence of the planar law is a simple consequence of the strong correlation between the foot and shank elevation angles, with nothing to do with control of walking. Even though planar constraint may have originated from biomechanical factors, such coordinated kinematic synergies could certainly be exploited by the nervous system. The musculoskeletal system of the lower limb in humans is possibly better designed for simplified control of bipedal locomotion based on the two global parameters of orientation and length of the limb axis.

Morphological analyses of hominin foot bones suggest that the plantigrade foot with a stiff midfoot region had evolved by the time of Australopithecus afarensis [39,46–48]. If this is accurate, the planar law of inter-segmental coordination in human bipedal walking was acquired around 3 million years ago, possibly in an effort to facilitate bipedal walking by reducing the number of degrees of freedom needing to be controlled. In addition, the plantigrade structure of the human foot has also been suggested to reduce the energy cost of human walking. Using oxygen consumption as a measure of the energy cost of walking, Cunningham et al. [49] found that human walking is much more efficient if the heel contacts the ground first (plantigrade posture), rather than if the heel slightly raised (digitigrade posture). The difference in efficiency arises because less energy is dissipated during collisions between the heel and the ground, and because muscle activity generated by the ankle plantiflexors is smaller. As a result of acquiring a stable midfoot, early hominins may have achieved simplification of locomotor control owing to the planar law of inter-segmental coordination, along with improvements in the energy cost of transport with bipedal walking. These progressive changes may have facilitated the subsequent evolution of habitual bipedal walking in the human lineage.